1 Introduction

The study of time-delay systems [4, 8, 30, 31] has attracted considerable attention due to the fact that time delays often occur in practical systems and may cause poor system performance or even instability [24]. Many representative results on the stability analysis and control synthesis of time-delay systems were investigated in [5, 15, 20].

Sliding mode control (SMC), recognized as an effective robust control algorithm, can handle model parameter uncertainties and external disturbances. Over the past decades, some influential results for nonlinear or linear uncertain time-delay systems by utilizing SMC method have been published [2, 9, 10, 12, 13, 15, 21, 27]. In [2], the mean-square and mean-module filtering problems for a nonlinear polynomial stochastic system subject to Gaussian white noises were addressed. The problem of SMC approach for uncertain stochastic systems with time delay was studied in [20].

Moreover, Markov jump systems (MJSs) with time delays have widely used in power systems, aerospace systems, networked control systems, and so on. The mode switching [16] is determined by a Markov process where the transition probabilities are memoryless. In another research frontier, the transition rates of semi-Markov jump systems (S-MJSs) are related to jump time, and the transition rates are memory, that is, the transition probabilities rely on the full history knowledge of previous switching sequences at each time. Many representative results on the synthesis work of S-MJSs have been investigated [7, 32, 33, 42, 45]. For instance, the authors in [45] investigated the problem of robust adaptive SMC for S-MJSs with actuator faults. Contrary to S-MJSs, the jump time of MJSs complies with exponential distribution, i. e., the transition rate is not connected with jump time. Many problems of stability analysis and stabilization for MJSs have been researched [3, 11, 14, 19, 23, 25, 28, 29, 34, 38, 44] and references therein. To mention a few, in [9], a novel augmented sliding mode observer was proposed to tackle the stabilization problem for a type of Markovian stochastic jump systems. The problem of SMC for a type of nonlinear uncertain stochastic systems with Markovian switching in [19] was discussed. However, the transition probabilities of MJSs mentioned in previous work are assumed to be totally known. In fact, the exact information of the transition probabilities is hard to obtain. Consequently, many studies on MJSs with unknown transition probabilities were reported in [6, 39,40,41, 43]. For instance, the authors investigated the problems of a class of continuous-time and discrete-time Markov jump linear systems (MJLSs) with partly unknown transition probabilities in [40]. The robust control problem of stochastic stability for MJLSs with respect to norm-bounded transition probabilities was considered in [6].

As we know, the system states are not available [1, 26, 35] and the inevitable parameter uncertainties often arise in practical systems. Therefore, the \(H_{\infty }\) control and state estimation problems of state-delayed MJSs with partly unknown transition probabilities, unknown matched nonlinearities and model parameter uncertainties have not been fully addressed due to the following difficulties: (i) the system states are generally not available; (ii) the upper bounds of nonlinearities caused the instability of the closed-loop system are difficult to obtain such that they are hard to be tackled; (iii) the detail knowledge of transition probabilities is tough to obtain.

In this paper, the state estimation and \(H_{\infty }\) control problems are studied for state-delayed MJSs with partly unknown transition probabilities, matched nonlinearity, matched disturbance and model parameter uncertainties. The main contributions of the work are as follows: firstly, this paper considers the SMC problem of state-delayed MJSs subject to parameter uncertainties, unknown nonlinearities and unknown transition probabilities, which are more general in the realistic industrial systems. Secondly, compared with existing control approaches for MJSs [29, 38], a novel adaptive sliding mode controller is constructed to guarantee that all variables of state-delayed MJSs can be driven onto the designed sliding mode surface in the presence of admissible uncertainties, nonlinearities and external disturbance. Thirdly, the theoretical results of this paper can be extended to some existing studies on MJSs without time delay. Finally, simulation results are exploited to display the effectiveness of the proposed method.

The six sections of this paper are organized as follows. The system description and some preliminaries are given in Sect. 2. Sections 3 and 4 design the integral sliding mode surface and adaptive sliding mode controller, respectively. A numerical example is used to testify the validity of the proposed control method in Sect. 5, and we conclude this paper in Sect. 6.

Notations: The superscript “T” represents the matrix transposition, and \(\mathbb {R}^{n}\) shows the n -dimensional Euclidean space. (\(\Omega ,\mathcal {F},\mathcal {P}\)) denotes the probability space, where \(\left\{ \mathcal {F}_{t}\right\} _{t\ge 0}\) satisfies the usual condition. \(\mathbf {P}\left\{ {\cdot }\right\} \) represents the probability. \(L_{\mathcal {F}_{0}}^{P}\left( \left[ -\tau \text {,}0\right] \text {;}\mathbb {R}^{n}\right) \) is the family of all \( \mathcal {F}_{0}\)-measurable \(\mathbb {C}\left( \left[ -\tau ,0\right] ; \mathbb {R}^{n}\right) \)-valued random variables \(\vartheta \) \(=\left\{ \vartheta \left( \theta \right) :-\tau \le \theta \le 0\right\} \) so that sup\(\mathbf {E}\left\| \vartheta \left( \theta \right) \right\| _{2}^{2}<\infty ,\) where \(\mathbf {E}\{\cdot \}\) denotes the mathematical expectation on the given probability measure \(\mathcal {P}\). I and 0 indicate the identity matrix and zero matrix, respectively. The notation \( X_{i}>0\) implies that \(X_{i}\) is real symmetric and positive definite. \( \left\| \cdot \right\| _{1}\) and \(\left\| \cdot \right\| \) refer to the 1-norm and usual Euclidean vector norm, respectively. \(\lambda _{\max }(P)\) indicates the maximum eigenvalue of a real symmetric matrix P. The notation \(\hbox {diag}\{\cdot \}\) represents a diagonal matrix. \( L_{2}[0,\infty )\) stands for the space of square integral vector function. The symbol “\(*\)” denotes a symmetric term.

2 System description and preliminaries

Assume that \(\{r_{t}\), \(t\ge 0\}\) is a finite-state Markov jumping process taking discrete values in state space \(S=\left\{ 1,2,\ldots ,s\right\} .\) Then the transition probabilities \(\Pi =\left( \pi _{ij}\right) _{s\times s}\) \(\left( i,j=1,2,\ldots ,s\right) \) can be denoted as follows:

$$\begin{aligned} \Pr \left( r_{t+\upsilon }=j\mid r_{t}=i\right) =\left\{ \begin{array}{l} \pi _{ij}\upsilon +o\left( \upsilon \right) ,\quad i\ne j, \\ 1+\pi _{ii}\upsilon +o\left( \upsilon \right) ,\quad i=j, \end{array} \right. \end{aligned}$$

where \(\pi _{ij}\) satisfies \(\pi _{ij}>0\) when \(i\ne j\); \(\upsilon >0\) and \( \lim _{\upsilon \rightarrow 0}o(\upsilon )/\upsilon =0,\) \(\pi _{ii}=-\sum _{j=1,\text { }j\ne i}^{s}\pi _{ij}\) for each mode i.

The following state-delayed MJSs are defined on a complete probability space (\(\Omega ,\mathcal {F},\mathcal {P}\)):

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( t\right) =\left( A\left( r_{t}\right) +\triangle A\left( r_{t},t\right) \right) x\left( t\right) \\ \quad \quad \qquad +\left( A_{d}\left( r_{t}\right) +\triangle A_{d}\left( r_{t},t\right) \right) x\left( t-\tau \right) \\ \quad \quad \qquad +B\left( u\left( t\right) +f\left( x,t\right) +d\left( t\right) \right) , \\ x\left( t,r_{0}\right) =\phi \left( t,r_{0}\right) ,\text { }t\in \left[ -\tau ,0\right] ,r_{0}\in S \\ y\left( t\right) =C\left( r_{t}\right) x\left( t\right) \end{array} \right. \end{aligned}$$
(1)

where \(x\left( t\right) \in \mathbb {R}^{n},\) \(u\left( t\right) \in \mathbb {R} ^{m},\) \(f\left( x,t\right) \in \mathbb {R}^{m},\) \(d\left( t\right) \in \mathbb {R}^{m}\) and \(y\left( t\right) \in \mathbb {R}^{p}\) are, respectively, the state vector, control input, nonlinear function, disturbance and system output. For each \(r_t\in S\), \(A\left( r_{t}\right) \in \mathbb {R}^{n\times n},\) \(A_{d}\left( r_{t}\right) \in \mathbb {R}^{n\times n},\) \(B\in \mathbb {R}^{n\times m}\) and \( C\left( r_{t}\right) \in \mathbb {R}^{p\times n}\) are constant system matrices with appropriate dimensions. \(\triangle A\left( r_{t},t\right) \in \mathbb {R}^{n\times n}\) and \(\triangle A_{d}\left( r_{t},t\right) \in \mathbb {R}^{n\times n}\) are system parameter uncertainties. \(\phi \left( t,r_{0}\right) \in L_{\mathcal {F}_{0}}^{P}\left( \left[ -\tau ,0\right] ; \mathbb {R}^{n}\right) \) denotes a initial vector-valued continuous function. \(\tau \) is a known time delay.

The specific information of transition probabilities is hard to be achieved such that some elements in matrix \(\Pi \) are unknown. For instance, for system (1) with four operation modes, the transition probability matrix \(\Pi \) may be written as

$$\begin{aligned} \Pi =\left[ \begin{array}{cccc} ? &{} \pi _{12} &{} ? &{} ? \\ ? &{} \pi _{22} &{} \pi _{23} &{} ? \\ \pi _{31} &{} ? &{} ? &{} ? \\ \pi _{41} &{} ? &{} ? &{} \pi _{44} \end{array} \right] , \end{aligned}$$

where “?” denotes the inaccessible elements. For notational convenience, \(\forall i\in S,\) define \(S=S_{\kappa }^{i}\cup S_{u\kappa }^{i}\) with

$$\begin{aligned} S_{\kappa }^{i}\overset{\vartriangle }{=}\left\{ j:\pi _{ij}\,\,\text {is known} \right\} ,S_{u\kappa }^{i}\overset{\vartriangle }{=}\left\{ j:\pi _{ij}\text { is unknown}\right\} . \end{aligned}$$

Denote \(\pi _{\kappa }^{i}\overset{\vartriangle }{=}\sum _{j\in S_{\kappa }^{i}}\pi _{ij}\) throughout the article. For simplicity, state-delayed MJSs (1) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( t\right) =\left( A_{i}+\triangle A(i,t)\right) x\left( t\right) \\ \quad \quad \qquad +\left( A_{di}+\triangle A_{d}\left( i,t\right) \right) x\left( t-\tau \right) \\ \quad \quad \qquad +B\left( u\left( t\right) +f\left( x,t\right) +d\left( t\right) \right) , \\ x\left( t,r_{0}\right) =\phi \left( t,r_{0}\right) ,\text { }t\in \left[ -\tau ,0\right] ,r_{0}\in S \\ y\left( t\right) =C_{i}x\left( t\right) , \end{array} \right. \end{aligned}$$
(2)

where \(A\left( r_{t}\right) =A_{i},\) \(A_{d}\left( r_{t}\right) =A_{di}\) and \( C\left( r_{t}\right) =C_{i}\). \(\triangle A\left( r_{t},t\right) =\triangle A(i,t)\) and \(\triangle A_{d}\left( r_{t},t\right) =\triangle A_{d}\left( i,t\right) \) denote the system parameter uncertainties, which satisfy the following forms:

$$\begin{aligned} \left[ \triangle A\left( i,t\right) \text { }\triangle A_{d}\left( i,t\right) \right] =E_{i}F\left( i,t\right) \left[ H_{i}\text { }H_{di}\right] , \end{aligned}$$
(3)

where \(E_{i}\), \(H_{i}\) and \(H_{di}\) are constant matrices with compatible dimensions for each \(i\in S\), and unknown time-varying matrix function \(F\left( i,t\right) \) satisfies

$$\begin{aligned} F^{T}\left( i,t\right) F\left( i,t\right) )\le I\text {, }i\in S. \end{aligned}$$
(4)

The matched disturbance \(d\left( t\right) \) is bounded as \(\Vert d\left( t\right) \Vert \le d,\) where d is a known scalar. The nonlinear function \( f\left( x,t\right) \) satisfies

$$\begin{aligned} \Vert f\left( x,t\right) \Vert \le \alpha +\beta \Vert y\left( t\right) \Vert , \end{aligned}$$
(5)

where \(\alpha >0\) and \(\beta >0\) are unknown constants. Besides, assume rank\( \left( B\right) =m\) for each \(i\in S.\)

The following definitions are necessary for this paper.

Definition 1

[17] Introduce the stochastic positive functional candidate of system (2) as \(V\left( x\left( t\right) ,i\right) \), which has twice differentiable on \(x\left( t\right) \). Its infinitesimal operator \(\mathcal {L}V\left( x\left( t\right) ,i\right) \) is defined as

$$\begin{aligned}&\mathcal {L}V\left( x\left( t\right) ,i\right) = \\&\lim _{\bigtriangleup t\rightarrow 0^{+}}\frac{1}{\bigtriangleup t}\left[ \mathbf {E}\{V\left( x\left( t+\bigtriangleup t\right) ,r_{t+\bigtriangleup t}\right) \ |\ x\left( t\right) ,r_{t}=i\}\right. \\&\quad \left. -V\left( x\left( t\right) ,i\right) \right\} . \end{aligned}$$

Definition 2

[22] For system (2) with \( u\left( t\right) =0\), the equilibrium point is stochastically stable, if for any \(x\left( t\right) \) defined on \(\left[ -\tau ,0\right] ,\) and \(r_{0}\in S\)

$$\begin{aligned} \int _{0}^{\infty }\mathbf {E}\{\left\| x\left( \theta ,x\left( t\right) ,r_{0}\right) \right\| ^{2}\}d\theta <+\infty . \end{aligned}$$

3 Observer-based sliding mode control

In fact, the exact information of nonlinearity is generally not available. Therefore, the unknown constant parameters \(\alpha \) and \(\beta \) are estimated by \(\hat{\alpha }\left( t\right) \) and \(\hat{\beta }\left( t\right) \) via adaptive control strategy, respectively. Define the estimation errors of each parameter as \(\tilde{\alpha }\left( t\right) =\hat{ \alpha }\left( t\right) -\alpha \) and \(\tilde{\beta }\left( t\right) =\hat{ \beta }\left( t\right) -\beta \).

3.1 Observer design

For state-delayed MJSs (1), a sliding mode observer is synthesized as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{\hat{x}}\left( t\right) = A_{i}\hat{x}\left( t\right) +A_{di}\hat{x} \left( t-\tau \right) +B\left( u\left( t\right) +u_{e}\left( t\right) \right) &{} &{} \\ \quad \quad \qquad +L_{i}\left( y\left( t\right) -C_{i}\hat{x}\left( t\right) \right) , &{} &{} \\ \hat{y}\left( t\right) = C_{i}\hat{x}\left( t\right) , &{} &{} \end{array} \right. \end{aligned}$$
(6)

where \(\hat{x}\left( t\right) \in \mathbb {R}^{n}\) is the estimator state and \(L_{i}\in \mathbb {R}^{n\times p}\) is the observer gain matrix to be designed later for each \(i\in S\). \(u_{e}\left( t\right) \) is designed to weaken the effect of unknown nonlinearity \(f\left( x,t\right) \). Assume \(s_{e}\left( t\right) =B^{T}X_{i}e\left( t\right) \) in state estimation error space for the following derivations, and \(X_{i}>0\) satisfies equation \(B^{T}X_{i}=N_{i}C_{i}\), in which \(N_{i}\) will be designed later.

Let the estimation error be \(e\left( t\right) \overset{\vartriangle }{=}\) \( x\left( t\right) -\hat{x}\left( t\right) .\) Recalling (6) and (2), the estimate error dynamics can be obtained as follows:

$$\begin{aligned} \dot{e}\left( t\right)= & {} \left( A_{i}+\triangle A\left( i,t\right) -L_{i}C_{i}\right) e\left( t\right) \nonumber \\&\quad +\,\left( A_{di}+\triangle A_{d}\left( i,t\right) \right) e\left( t-\tau \right) \nonumber \\&\quad +\,\triangle A\left( i,t\right) \hat{x}\left( t\right) +\triangle A_{d}\left( i,t\right) \hat{x}\left( t-\tau \right) \nonumber \\&\quad +\,B\left( f\left( x,t\right) +d\left( t\right) -u_{e}\left( t\right) \right) , \nonumber \\ y_{e}\left( t\right)= & {} C_{i}e\left( t\right) , \end{aligned}$$
(7)

where \(y_{e}(t)\) denotes the error system output. Now introduce the following \(H_{\infty }\) performance index:

$$\begin{aligned} J=\mathbf {E}\left\{ \int _{0}^{\infty }\left( y_{e}^{T}\left( \theta \right) y_{e}\left( \theta \right) -\gamma ^{2}d^{T}\left( \theta \right) d\left( \theta \right) \right) d\theta \right\} . \end{aligned}$$

The performance \(J<0\) can be converted into the following form:

$$\begin{aligned} \mathbf {E}\left( \sup _{0\ne d\left( t\right) \in L_{2}}\frac{ \left\| y_{e}\left( t\right) \right\| }{\left\| d\left( t\right) \right\| }\right) <\gamma . \end{aligned}$$

Define the following integral sliding mode surface:

$$\begin{aligned} \zeta \left( t\right) =F\hat{x}\left( t\right) -\int _{0}^{t}F\left( A_{i}+BK_{i}\right) \hat{x}\left( h\right) dh, \end{aligned}$$
(8)

where \(F\in \mathbb {R}^{m\times n}\) is a constant matrix and \(K_{i}\in \mathbb {R}^{m\times n}\) is selected such that \(A_{i}+BK_{i}\) is Hurwitz and \( FB>0 \) (see [18]).

Remark 1

It should be pointed out that the terms \(F\hat{x}\left( t\right) \) and \( \int _{0}^{t}F\left( A_{i}+BK_{i}\right) \hat{x}(\varphi )d\varphi \) are continuous in sliding mode surface (8). Thus, the designed integral sliding manifold (8) is always continuous despite the presence of switching term \(\left( A_{i}+BK_{i}\right) \).

It follows from (8) that

$$\begin{aligned} \dot{\zeta }\left( t\right)&=F\dot{\hat{x}}\left( t\right) -F\left( A_{i}+BK_{i}\right) \hat{x}\left( t\right) \nonumber \\&=FB\left( u\left( t\right) +u_{e}\left( t\right) \right) +FA_{di}\hat{x} \left( t-\tau \right) \nonumber \\&\quad +FL_{i}C_{i}e\left( t\right) -FBK_{i}\hat{x}\left( t\right) . \end{aligned}$$

Let \(\dot{\zeta }\left( t\right) =0,\) the equivalent control law can be derived as

$$\begin{aligned} u_{eq}\left( t\right)= & {} K_{i}\hat{x}\left( t\right) -\left( FB\right) ^{-1}FA_{di}\hat{x}\left( t-\tau \right) \nonumber \\&\quad -\left( FB\right) ^{-1}FL_{i}C_{i}e\left( t\right) -u_{e}\left( t\right) . \end{aligned}$$
(9)

Substituting (9) into (6) yields

$$\begin{aligned} \dot{\hat{x}}\left( t\right) = \left( A_{i}+ BK_{i}\right) \hat{x}\left( t\right) +\bar{F}A_{di}\hat{x}\left( t-\tau \right) + \bar{F} L_{i}C_{i}e\left( t\right) . \end{aligned}$$
(10)

where \(\bar{F}=I-B\left( FB\right) ^{-1}F.\) The robust control term \( u_{e}\left( t\right) \) is designed as

$$\begin{aligned} u_{e}\left( t\right)= & {} \left( \left| \hat{\alpha }\left( t\right) \right| +\left| \hat{\beta }\left( t\right) \right| \left\| y\left( t\right) \right\| +\rho _{1}\right) \hbox {sgn}(s_{e}\left( t\right) ), \nonumber \\ \dot{\hat{\alpha }}\left( t\right)= & {} c_{\alpha }\left\| s_{e}\left( t\right) \right\| ,\quad \dot{\hat{{\beta }}}\left( t\right) =c_{\beta }\left\| s_{e}\left( t\right) \right\| \left\| y\left( t\right) \right\| , \end{aligned}$$
(11)

where \(c_{\alpha }\) and \(c_{\beta }\) are chosen positive constants.

3.2 Stability analysis

The sufficient conditions of stochastic stability for augmented system consisted of (7) and (10) are derived in the following theorem.

Theorem 1

Given a scalar \(\gamma >0,\) the sliding mode surface is given by (8). If there exist positive definite symmetric matrices \( X_{i}\in \mathbb {R}^{n\times n}\), matrices \(Y_{i}\in \mathbb {R}^{n\times p},\) \(N_{i}\in \mathbb {R}^{m\times p},\) \(L_{i}\in \mathbb {R}^{n\times p},\) positive scalars \(\varepsilon _{i1},\) \(\varepsilon _{i2},\) \(\varepsilon _{i3}\) and \(\varepsilon _{i4}\) , \(\forall i\in S\) such that

$$\begin{aligned}&\left[ \begin{array}{cc} \Psi _{1i} &{} \Psi _{2i} \\ *&{} \Psi _{3i} \end{array} \right] <0,\quad \forall i\in S_{\kappa }^{i}, \end{aligned}$$
(12)
$$\begin{aligned}&\left[ \begin{array}{cc} \Delta _{1i} &{} \Delta _{2i} \\ *&{} \Delta _{3i} \end{array} \right] <0,\quad \forall i\in S_{u\kappa }^{i}, \end{aligned}$$
(13)
$$\begin{aligned}&X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+X_{j}\ge 0, \nonumber \\&\quad \forall j\in S_{u\kappa }^{i},\quad j=i, \end{aligned}$$
(14)
$$\begin{aligned}&A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+X_{j}\ge 0, \nonumber \\&\quad \forall j\in S_{u\kappa }^{i},\quad j=i, \end{aligned}$$
(15)
$$\begin{aligned}&X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+X_{j}\le 0, \nonumber \\&\quad \forall j\in S_{u\kappa }^{i},\quad j\ne i, \end{aligned}$$
(16)
$$\begin{aligned}&A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+X_{j}\le 0, \nonumber \\&\quad \forall j\in S_{u\kappa }^{i},\quad j\ne i, \end{aligned}$$
(17)
$$\begin{aligned}&B^{T}X_{i}=N_{i}C_{i}, \end{aligned}$$
(18)

where

$$\begin{aligned} \Psi _{1i}= & {} \left[ \begin{array}{ccccc} \Psi _{11i} &{} X_{i}\bar{F}A_{di} &{} 0 &{} 0 &{} 0 \\ *&{} \Psi _{22i} &{} 0 &{} 0 &{} 0 \\ *&{} *&{} \Psi _{33i} &{} X_{i}A_{di} &{} X_{i}B \\ *&{} *&{} *&{} \Psi _{44i} &{} 0 \\ *&{} *&{} *&{} *&{} -\gamma ^{2}I \end{array} \right] ,\\ \Psi _{2i}= & {} \left[ \begin{array}{cccccc} X_{i}\bar{F} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} X_{i}E_{i} &{} X_{i}E_{i} &{} X_{i}E_{i} &{} X_{i}E_{i} &{} C_{i}^{T}Y_{i}^{T} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] , \\ \Psi _{11i}= & {} \left( 1+\pi _{\kappa }^{i}\right) \left[ X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] \\&+\,Q_{1}+\varepsilon _{i1}H_{i}^{T}H_{i}+\sum _{j\in S_{\kappa }^{i}, j\ne i}\pi _{ij}X_{j}+\pi _{ii}X_{i}, \\ \Psi _{33i}= & {} \left( 1+\pi _{\kappa }^{i}\right) \left( A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}\right) \\&+\,\varepsilon _{i4}H_{i}^{T}H_{i}+C_{i}^{T}C_{i}+\sum _{j\in S_{\kappa }^{i}, \text { }j\ne i}\pi _{ij}X_{j}+\pi _{ii}X_{i}, \\ \Delta _{1i}= & {} \left[ \begin{array}{ccccc} \Delta _{11i} &{} X_{i}\bar{F}A_{di} &{} 0 &{} 0 &{} 0 \\ *&{} \Delta _{22i} &{} 0 &{} 0 &{} 0 \\ *&{} *&{} \Delta _{33i} &{} X_{i}A_{di} &{} X_{i}B \\ *&{} *&{} *&{} \Delta _{44i} &{} 0 \\ *&{} *&{} *&{} *&{} -\gamma ^{2}I \end{array} \right] , \\ \Delta _{2i}= & {} \left[ \begin{array}{cccccc} X_{i}\bar{F} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} X_{i}E_{i} &{} X_{i}E_{i} &{} X_{i}E_{i} &{} X_{i}E_{i} &{} C_{i}^{T}Y_{i}^{T}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] , \\ \Delta _{11i}= & {} \left( 1+\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}\right) \left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] +\varepsilon _{i1}H_{i}^{T}H_{i} \\&+\,\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}X_{j},\\ \Delta _{33i}= & {} \left( 1+\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}\right) \left( A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}\right. \\&\left. -\,C_{i}^{T}Y_{i}^{T}\right) +\varepsilon _{i4}H_{i}^{T}H_{i}+\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}X_{j} \\&+\,Q_{2}+C_{i}^{T}C_{i}, \\ \Psi _{22i}= & {} \Delta _{22i}=-\,Q_{1}+\varepsilon _{i2}H_{di}^{T}H_{di}, \\ \Psi _{44i}= & {} \Delta _{44i}=-\,Q_{2}+\varepsilon _{i3}H_{di}^{T}H_{di}, \\ \Psi _{3i}= & {} \Delta _{3i}=-\,diag \{X_{i},\varepsilon _{1i}I,\varepsilon _{2i}I,\varepsilon _{3i}I,\varepsilon _{4i}I,X_{i}\}, \end{aligned}$$

then the resulting closed-loop system composed of (7) and ( 10) is stochastically stable. In addition, the state observer gain is calculated by

$$\begin{aligned} L_{i}=X_{i}^{-1}Y_{i},\quad i\in S. \end{aligned}$$

Proof

Take the Lyapunov functional as follows:

$$\begin{aligned} V_{1}\left( \hat{x},e,i\right)= & {} \hat{x}^{T}\left( t\right) X_{i}\hat{x} \left( t\right) +e^{T}\left( t\right) X_{i}e\left( t\right) \nonumber \\&+\,\int _{t-\tau }^{t}\hat{x}^{T}\left( t\right) Q_{1}\hat{x}\left( t\right) dt+\,c_{\alpha }^{-1}\tilde{\alpha }^{2}\left( t\right) \nonumber \\&+\,\int _{t-\tau }^{t}e^{T}\left( t\right) Q_{2}e\left( t\right) dt+c_{\beta }^{-1}\tilde{\beta }^{2}\left( t\right) .\nonumber \\ \end{aligned}$$
(19)

Letting \(d\left( t\right) =0\), by Definition 1, we have

$$\begin{aligned} \mathcal {L}V_{1}\left( \hat{x},e,i\right)= & {} 2\hat{x}^{T}\left( t\right) X_{i}\left[ (A_{i}+BK_{i})\hat{x}\left( t\right) \right. \nonumber \\&\left. +\,\bar{F}L_{i}C_{i}e\left( t\right) +\bar{F}A_{di}\hat{x}\left( t-\tau \right) \right] \nonumber \\&+\,\hat{x}^{T}\left( t\right) Q_{1}\hat{x}\left( t\right) \nonumber \\&+\,2e^{T}\left( t\right) X_{i}(A_{i}+\triangle A\left( i,t\right) \nonumber \\&-\,L_{i}C_{i})e\left( t\right) \nonumber \\&+\,2e^{T}\left( t\right) X_{i}\triangle A\left( i,t\right) \hat{x}\left( t\right) \nonumber \\&+\,2c_{\alpha }^{-1}\tilde{\alpha }\left( t\right) \dot{\tilde{\alpha }} \left( t\right) \nonumber \\&+\,2e^{T}\left( t\right) X_{i}\left( A_{di}+\triangle A_{d}\left( i,t\right) \right) e\left( t-\tau \right) \nonumber \\&+\,2e^{T}\left( t\right) X_{i}\triangle A_{d}\left( i,t\right) \hat{x}\left( t-\tau \right) \nonumber \\&+\,2e^{T}\left( t\right) X_{i}B\left( f\left( x,t\right) -u_{e}\left( t\right) \right) \nonumber \\&-\,\hat{x}^{T}\left( t-\tau \right) Q_{1}\hat{x}\left( t-\tau \right) \nonumber \\&+\,e^{T}\left( t\right) Q_{2}e\left( t\right) \nonumber \\&+\,e^{T}\left( t-\tau \right) Q_{2}e\left( t-\tau \right) \nonumber \\&+\,\hat{x}^{T}\left( t\right) \sum _{j=1}^{s}\pi _{ij}X_{j}\hat{x}\left( t\right) \nonumber \\&+\,e^{T}\left( t\right) \sum _{j=1}^{s}\pi _{ij}X_{j}e\left( t\right) \nonumber \\&+\,2c_{\beta }^{-1}\tilde{\beta }\left( t\right) \dot{\tilde{\beta }}\left( t\right) . \end{aligned}$$
(20)

The following term in (20) can be converted into

$$\begin{aligned} 2\hat{x}^{T}\left( t\right) X_{i}\bar{F}L_{i}C_{i}e\left( t\right)\le & {} \hat{x}^{T}\left( t\right) X_{i}\bar{F}X_{i}^{-1}\bar{F}^{T}X_{i}\hat{x} \left( t\right) \nonumber \\&+\,e^{T}\left( t\right) C_{i}^{T}L_{i}^{T}X_{i}L_{i}C_{i}e\left( t\right) .\nonumber \\ \end{aligned}$$
(21)

From (3) and (4), the following terms can be also, respectively, simplified as

$$\begin{aligned}&2e^{T}\left( t\right) X_{i}\triangle A\left( i,t\right) \hat{x}\left( t\right) \nonumber \\&\quad \le \varepsilon _{i1}^{-1}e^{T}\left( t\right) X_{i}E_{i}E_{i}^{T}X_{i}e\left( t\right) \nonumber \\&\qquad +\,\varepsilon _{i1}\hat{x}^{T}\left( t\right) H_{i}^{T}H_{i}\hat{x}\left( t\right) , \end{aligned}$$
(22)
$$\begin{aligned}&2e^{T}\left( t\right) X_{i}\triangle A_{d}\left( i,t\right) \hat{x}\left( t-\tau \right) \nonumber \\&\quad \le \varepsilon _{i2}^{-1}e^{T}\left( t\right) X_{i}E_{i}E_{i}^{T}X_{i}e\left( t\right) \nonumber \\&\qquad +\,\varepsilon _{i2}\hat{x}^{T}\left( t-\tau \right) H_{di}^{T}H_{di}\hat{x} \left( t-\tau \right) , \end{aligned}$$
(23)
$$\begin{aligned}&2e^{T}\left( t\right) X_{i}\triangle A_{d}(i,t)e\left( t-\tau \right) \nonumber \\&\quad \le \varepsilon _{i3}^{-1}e^{T}\left( t\right) X_{i}E_{i}E_{i}^{T}X_{i}e\left( t\right) \nonumber \\&\qquad +\,\varepsilon _{i3}e^{T}\left( t-\tau \right) H_{di}^{T}H_{di}e\left( t-\tau \right) , \end{aligned}$$
(24)
$$\begin{aligned}&2e^{T}\left( t\right) X_{i}\triangle A\left( i,t\right) e\left( t\right) \nonumber \\&\quad \le \varepsilon _{i4}^{-1}e^{T}\left( t\right) X_{i}E_{i}E_{i}^{T}X_{i}e\left( t\right) \nonumber \\&\qquad +\,\varepsilon _{i4}e^{T}\left( t\right) H_{i}^{T}H_{i}e\left( t\right) . \end{aligned}$$
(25)

Similarly, by the condition \(s_{e}\left( t\right) =B^{T}X_{i}e\left( t\right) ,\) one can obtain

$$\begin{aligned}&2c_{\alpha }^{-1}\tilde{\alpha }\left( t\right) \dot{\tilde{\alpha }}\left( t\right) +2c_{\beta }^{-1}\tilde{\beta }\left( t\right) \dot{\tilde{\beta }} \left( t\right) \nonumber \\&\quad +\,2e^{T}\left( t\right) X_{i}B\left[ f\left( x,t\right) \right. \nonumber \\&\quad \left. -\left( \left| \hat{\alpha }\left( t\right) \right| +\left| \hat{\beta }\left( t\right) \right| \left\| y\left( t\right) \right\| +\rho _{1}\right) \hbox {sgn}\left( s_{e}\left( t\right) \right) \right] \nonumber \\&\le -2\rho _{1}\left\| s_{e}\left( t\right) \right\| <0. \end{aligned}$$
(26)

Substituting (21)–(26) into (20) yields

$$\begin{aligned} \mathcal {L}V_{1}\left( \hat{x},e,i\right) \le \eta ^{T}\left( t\right) \Phi \left( i\right) \eta \left( t\right) , \end{aligned}$$

where

$$\begin{aligned} \Phi \left( i\right)= & {} \left[ \begin{array}{cccc} \Sigma _{11i} &{} X_{i}\bar{F}A_{di} &{} 0 &{} 0 \\ *&{} \Sigma _{22i} &{} 0 &{} 0 \\ *&{} *&{} \Sigma _{33i} &{} X_{i}A_{di} \\ *&{} *&{} *&{} \Sigma _{44i} \end{array} \right] , \nonumber \\ \eta \left( t\right)= & {} \left[ \begin{array}{cccc} \hat{x}^{T}\left( t\right)&\hat{x}^{T}\left( t-\tau \right)&e^{T}\left( t\right)&e^{T}\left( t-\tau \right) \end{array} \right] ^{T}, \nonumber \\ \Sigma _{11i}= & {} X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+Q_{1} \nonumber \\&\quad +\,\varepsilon _{i1}H_{i}^{T}H_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j}\nonumber \\&\quad +\,X_{i}\bar{F} X_{i}^{-1}\bar{F}^{T}X_{i}, \end{aligned}$$
(27)
$$\begin{aligned} \Sigma _{22i}= & {} -Q_{1}+\varepsilon _{i2}H_{di}^{T}H_{di},\nonumber \\ \Sigma _{44i}= & {} -Q_{2}+\varepsilon _{i3}H_{di}^{T}H_{di}, \nonumber \\ \Sigma _{33i}= & {} A_{i}^{T}X_{i}+X_{i}A_{i}+\varepsilon _{i1}^{-1}X_{i}E_{i}E_{i}^{T}X_{i} \nonumber \\&\quad +\,\varepsilon _{i2}^{-1}X_{i}E_{i}E_{i}^{T}X_{i}+\varepsilon _{i3}^{-1}X_{i}E_{i}E_{i}^{T}X_{i} \nonumber \\&\quad +\,\varepsilon _{i4}^{-1}X_{i}E_{i}E_{i}^{T}X_{i}+Q_{2}+C_{i}^{T}Y_{i}^{T}X_{i}^{-1}Y_{i}C_{i} \nonumber \\&\quad -\,Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+\sum _{j=1}^{s}\pi _{ij}X_{j}. \end{aligned}$$
(28)

For \(i\in S_{\kappa }^{i}\), the term \(X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j}\) in (27) can be rewritten as follows:

$$\begin{aligned} \Theta \left( i\right)= & {} X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+\sum _{j=1}^{s}\pi _{ij}X_{j} \\= & {} \left( 1+\sum _{j\in S_{\kappa }^{i}}\pi _{ij}\right) \left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\quad \left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] +\sum _{j\in S_{\kappa }^{i}}\pi _{ij}X_{j} \\&\quad +\,\sum _{j\in S_{u\kappa }^{i}}\pi _{ij}\left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\quad \left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] +\sum _{j\in S_{u\kappa }^{i}}\pi _{ij}X_{j} \\= & {} \left( 1+\pi _{\kappa }^{i}\right) \left[ X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] \\&\quad +\,\sum _{j\in S_{\kappa }^{i}}\pi _{ij}X_{j}+\sum _{j\in S_{u\kappa }^{i}}\pi _{ij}\left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\quad \left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+X_{j}\right] . \end{aligned}$$

Then, \(\forall j\in S_{u\kappa }^{i}\) and if \(i\in S_{\kappa }^{i},\) obviously, \(\Theta \left( i\right) <0\) can be achieved by (12) and (16). Besides, \(\forall j\in S_{u\kappa }^{i}\) and if \( i\notin S_{\kappa }^{i}\), we have

$$\begin{aligned} \Theta \left( i\right)= & {} \left( 1+\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}\right) \left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\quad \left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}\right] +\sum _{j\in S_{\kappa }^{i},\text { }j\ne i}\pi _{ij}X_{j} \\&\quad +\,\pi _{ii}\left[ X_{i}\left( A_{i}+BK_{i}\right) +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+X_{i}\right] \\&\quad +\,\sum _{j\in S_{u\kappa }^{i},\text { }j\ne i}\pi _{ij}\left[ X_{i}\left( A_{i}+BK_{i}\right) \right. \\&\quad \left. +\left( A_{i}+BK_{i}\right) ^{T}X_{i}+X_{j}\right] . \end{aligned}$$

Then, we can obtain \(\Theta \left( i\right) <0\) by (13), (14) and (16).

Similarly, for \(i\in S_{\kappa }^{i}\), the term \(A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+\sum _{j=1}^{s}\pi _{ij}X_{j}\) in (28) can be simplified as:

$$\begin{aligned} \Omega \left( i\right)= & {} \left( 1+\pi _{\kappa }^{i}\right) \left( A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}\right) \\&\quad +\sum _{j\in S_{\kappa }^{i}}\pi _{ij}X_{j}+\sum _{j\in S_{u\kappa }^{i}}\pi _{ij}\left( A_{i}^{T}X_{i}+X_{i}A_{i}\right. \\&\quad \left. - Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+X_{j}\right) . \end{aligned}$$

Then, \(\forall j\in S_{u\kappa }^{i}\) and if \(i\in S_{\kappa }^{i},\) it is straightforward that \(\Omega \left( i\right) <0\) can be obtained by (12) and (17). Besides, \(\forall j\in S_{u\kappa }^{i}\) and if \(i\notin S_{\kappa }^{i}\), we have

$$\begin{aligned} \Omega \left( i\right)= & {} \left( 1+\sum _{j\in S_{\kappa }^{i},j\ne i}\pi _{ij}\right) \left( A_{i}^{T}X_{i}+X_{i}A_{i}\right. \\&\quad \left. - Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}\right) +\sum _{j\in S_{\kappa }^{i}, j\ne i}\pi _{ij}X_{j} \\&\quad +\pi _{ii}\left( A_{i}^{T}X_{i}+X_{i}A_{i}-Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+X_{i}\right) \\&\quad +\sum _{j\in S_{u\kappa }^{i},j\ne i}\pi _{ij}\left( A_{i}^{T}X_{i}+X_{i}A_{i}\right. \\&\quad \left. - Y_{i}C_{i}-C_{i}^{T}Y_{i}^{T}+X_{j}\right) . \end{aligned}$$

Then, we can obtain \(\Omega \left( i\right) <0\) by (13), (15) and (17).

It can be shown that \(\Phi _{i}<0\) are obtained by linear matrix inequalities (LMIs) (12)–( 18). Then we have \(\mathcal {L}V_{1}\left( \hat{x},e,i\right) <0\) for \( \forall \eta \left( t\right) \ne 0\). The resulting closed-loop system with \( d\left( t\right) =0\) is stochastically stable.

Next, under sliding mode observer (6) and sliding mode surface (8), we will approve that state-delayed MJSs (2) are stochastically stable with a disturbance attenuation level \(\gamma ,\) i.e., \(d\left( t\right) \ne 0.\) Hence, the infinitesimal generator of stochastic Lyapunov functional \(V_{1}\left( \hat{x },e,i\right) \) as (19) is deduced as follows:

$$\begin{aligned} \mathcal {L}V_{1}\left( \hat{x},e,i\right) =\eta ^{T}\left( t\right) \Phi _{i}\eta \left( t\right) +2e^{T}\left( t\right) X_{i}Bd\left( t\right) . \end{aligned}$$

According to \(\mathbf {E}{V}_{1}\left( \hat{x},e,i\right) =\mathbf {E} \int _{0}^{\infty }\mathcal {L}V_{1}\left( \hat{x},e,i\right) dt>0\), for \( d\left( t\right) \in L_{2}[0,\infty )\), the system performance J can be converted into

$$\begin{aligned} J\le & {} \mathbf {E}\left\{ \int _{0}^{\infty }\left( y_{e}^{T}\left( t\right) y_{e}\left( t\right) -\gamma ^{2}d^{T}\left( t\right) d\left( t\right) \right. \right. \nonumber \\&\quad \left. \left. +\,\mathcal {L}V_{1}\left( \hat{x},e,i\right) \right) \right\} dt \nonumber \\= & {} \mathbf {E}\int _{0}^{\infty }\xi ^{T}\left( t\right) \Xi _{i}\xi \left( t\right) dt, \end{aligned}$$

where \(\displaystyle \xi \left( t\right) {=}\left[ \hat{x}^{T}\left( t\right) \hat{x}^{T}\left( t{-}\tau \right) e^{T}\left( t\right) e^{T}\left( t{-}\tau \right) d^{T}\left( t\right) \right] ^{T}\).

By employing LMIs (12)–(18), we have \(\Xi _{i}<0,\) which implies that \(J<0\). Thus, it yields

$$\begin{aligned} \mathbf {E}\left( \sup _{0\ne d(t)\in L_{2}}\frac{\left\| y_{e}\left( t\right) \right\| }{\left\| d\left( t\right) \right\| } \right) <\gamma . \end{aligned}$$

Note that equality constraint (18) can be rewritten as

$$\begin{aligned} \hbox {tr}\left[ \left( B^{T}X_{i}-N_{i}C_{i}\right) ^{T}\left( B^{T}X_{i}-N_{i}C_{i}\right) \right] =0. \end{aligned}$$

Introduce the following condition:

$$\begin{aligned} \left( B^{T}X_{i}-N_{i}C_{i}\right) ^{T}\left( B^{T}X_{i}-N_{i}C_{i}\right) <\sigma _{i}I, \end{aligned}$$

where scalar \(\sigma _{i}>0\), which will be designed later. Then, by Schur complement, one can obtain

$$\begin{aligned} \left[ \begin{array}{cc} -\sigma _{i}I &{} \left( B^{T}X_{i}-N_{i}C_{i}\right) ^{T} \\ *&{} -I \end{array} \right] <0. \end{aligned}$$
(29)

Hence, the above feasible problem with equality constraint will be converted into the following minimization problem:

$$\begin{aligned} \min \sigma _{i},\text {subject to}\,\, (12){-}(17) \,\,\hbox {and} \,\,(29). \end{aligned}$$
(30)

Thus, the overall closed-loop system composed of (7) and ( 10) is stochastically stable by Definition 2. The proof is completed. \(\square \)

Remark 2

It is worthwhile to point out that (12), (14) and ( 15) in Theorem 1 will not be checked simultaneously due to \(S _{\kappa }^{i}\cap S _{u\kappa }^{i}=\emptyset .\)

Remark 3

Note that (30) is a minimization problem involving linear objective and LMIs constraints, it admits a global infimum and if this infimum equals zero, the observed-based adaptive SMC problem is solvable.

Remark 4

It is seen that conditions (12)–(18) will unavoidably contain LMIs. For each \(i\in S\), these unknown variables \(X_{i}\), \(Y_{i}\) and \(L_{i}\) in Theorem 1 are connected with system mode i. Therefore, the system mode of state-delayed MJSs in (2) decides the computational complexity of the proposed methodology.

4 Adaptive sliding mode controller design

In this section, we will design an adaptive SMC law to guarantee the finite-time reachability of the sliding mode surface.

Theorem 2

Suppose that Theorem 1 has feasible solution, the adaptive SMC law is synthesized as

$$\begin{aligned} u\left( t\right) =u_{ib}+u_{ic},\quad i\,=\,1,2,\ldots ,s, \end{aligned}$$
(31)

where \(u_{ib}\) and \(u_{ic}\) are linear control input part and discontinuous control input part, respectively. They are, respectively, designed as

$$\begin{aligned} u_{ib}= & {} -l_{i}\zeta \left( t\right) +K_{i}\hat{x}\left( t\right) -FA_{di}\hat{ x}\left( t-\tau \right) ,\\ u_{ic}= & {} -\,\left( \delta _{i}\left( t\right) +\left| \hat{\alpha }\left( t\right) \right| +\left| \hat{\beta }\left( t\right) \right| \left\| y\left( t\right) \right\| \right. \\&\quad \left. +\,\kappa +\rho _{1}\right) sgn (\zeta \left( t\right) ), \end{aligned}$$

where \(\kappa \) and \(\rho _{1}\) are small positive constants, \(\delta _{i}\left( t\right) \) is given by

$$\begin{aligned} \delta _{i}\left( t\right)= & {} \max _{i\in S}\left\{ \left\| \left( FB\right) ^{-1}FL_{i}\right\| \left\| y\left( t\right) \right\| \right. \nonumber \\&\quad \left. +\left\| \left( FB\right) ^{-1}FL_{i}C_{i}\right\| \left\| \hat{x}\left( t\right) \right\| \right\} , \end{aligned}$$
(32)

the above two adaptive gains are designed as

$$\begin{aligned} \dot{\hat{\alpha }}\left( t\right) =c_{\alpha }\left\| s_{e}\left( t\right) \right\| ,\quad \dot{\hat{{\beta }}}\left( t\right) =c_{\beta }\left\| s_{e}\left( t\right) \right\| \left\| y\left( t\right) \right\| . \end{aligned}$$
(33)

Then the state trajectories will be attracted to sliding mode surface (8) in finite time.

Proof

The Lyapunov function candidate of system (6) is taken as

$$\begin{aligned} V_{2}\left( t\right) =\frac{1}{2}\zeta ^{T}\left( t\right) \left( FB\right) ^{-1}\zeta \left( t\right) . \end{aligned}$$

The infinitesimal generator of \(V_{2}\left( t\right) \) along the trajectories of sliding mode dynamics (10) is derived as follows:

$$\begin{aligned} \mathcal {L}V_{2}\left( t\right)= & {} -l_{i}\zeta ^{T}\left( t\right) \zeta \left( t\right) -\delta _{i}\left( t\right) \zeta ^{T}\left( t\right) \hbox {sgn}\left( \zeta \left( t\right) \right) \nonumber \\&\quad -\left( \left| \hat{\alpha }\left( t\right) \right| +\left| \hat{\beta }\left( t\right) \right| \left\| y\left( t\right) \right\| +\rho _{1}\right) \nonumber \\&\qquad s^{T}\left( t\right) \hbox {sgn}\left( \zeta \left( t\right) \right) \nonumber \\&\quad +\,\zeta ^{T}\left( t\right) \left( FB\right) ^{-1}FL_{i}\left( y\left( t\right) -C_{i}\hat{x}\left( t\right) \right) \nonumber \\&\quad +\,\zeta ^{T}\left( t\right) u_{e}\left( t\right) -\kappa \zeta ^{T}\left( t\right) \hbox {sgn}(\zeta \left( t\right) ). \end{aligned}$$
(34)

By employing \(\zeta ^{T}\left( t\right) \hbox {sgn}(s_{e}\left( t\right) )\le \left\| \zeta \left( t\right) \right\| _{1}\), the following term in (34) can be converted into

$$\begin{aligned}&-\left( \left| \hat{\alpha }\left( t\right) \right| +\left| \hat{\beta }\left( t\right) \right| \left\| y\left( t\right) \right\| +\rho _{1}\right) \zeta ^{T}\left( t\right) \hbox {sgn}\left( \zeta \left( t\right) \right) \nonumber \\&+\zeta ^{T}\left( t\right) u_{e}\left( t\right) \le 0. \end{aligned}$$
(35)

According to conditions (32) and (35), one can get

$$\begin{aligned} \mathcal {L}V_{2}\left( t\right)\le & {} -l_{i}\left\| \zeta \left( t\right) \right\| ^{2}-\kappa \left\| \zeta \left( t\right) \right\| \nonumber \\\le & {} -\kappa \left\| \zeta \left( t\right) \right\| \le -\tilde{ \kappa }V_{2}^{\frac{1}{2}}\left( t\right) , \end{aligned}$$

where \(\tilde{\kappa }=\kappa \sqrt{2/\lambda _{\max }[(FB)^{-1}]}>0.\) Hence, there exists an instant \(\tilde{t}=2\sqrt{V_{2}(0)}/\tilde{\kappa }\) to ensure \(V_{2}\left( t\right) =0\), i.e., \(\zeta \left( t\right) =0\) when \( t\ge \tilde{t}\). Meanwhile, the system state trajectories can reach the predefined sliding mode surface in finite time. The proof is finished. \(\square \)

The design procedure of the work is generalized as follows.

Detailed design procedure:

  1. (I)

    According to equation (8), we choose the proper matrices F and \(K_{i}\).

  2. (II)

    Addressing the optimization problem in (30), we can obtain the optimal solutions \(X_{i}\), \(Y_{i}\) and \(N_{i}\). Then, the observer gains can be computed as \(L_{i}=X^{-1}_{i} Y_{i}\).

  3. (III)

    Design the robust controller \(u_{e}(t)\) and the adaptive SMC law according to (11) and (31), respectively, where the adaptive laws of \(\alpha (t)\) and \(\beta (t)\) are designed in (33).

Remark 5

It should be pointed out that according to the physical characterization of the nonlinearity, it is difficult to capture the exact information of every component \(f_i\left( x,t\right) \) of the vector-valued function nonlinearity \(f\left( x,t\right) \). Therefore, we can integrate the adaptive control strategy into SMC problem for state-delayed MJSs. Then, an adaptive SMC law is synthesized to guarantee that all variables of state-delayed MJSs are drawn to the designed sliding manifold in the existence of admissible uncertainties, nonlinearities and disturbance.

5 Numerical example

The matrices in (1) with four operation modes are given as follows:

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{rrr} -1.86 &{} 1.5 &{} 0.2 \\ 0 &{} -3.279 &{} -2.3 \\ 0 &{} 2.928 &{} -2.082 \end{array} \right] , \\ A_{2}= & {} \left[ \begin{array}{rrr} -1.86 &{} 1.5 &{} 0.2 \\ 0 &{} -4.279 &{} -2.3 \\ 0 &{} 2.928 &{} -2.082 \end{array} \right] , \\ A_{3}= & {} \left[ \begin{array}{rrr} -1.86 &{} 1.5 &{} 0.2 \\ 0 &{} -5.279 &{} -2.3 \\ 0 &{} 2.928 &{} -2.082 \end{array} \right] , \\ A_{4}= & {} \left[ \begin{array}{rrr} -1.86 &{} 1.5 &{} 0.2 \\ 0 &{} -6.279 &{} -2.3 \\ 0 &{} 2.928 &{} -2.082 \end{array} \right] ,\quad B=\left[ \begin{array}{r} -2 \\ -2 \\ -1 \end{array} \right] , \\ A_{d1}= & {} \left[ \begin{array}{rrr} 0.5 &{} 0.5 &{} 0.1 \\ 0.1 &{} 0.1 &{} 0 \\ 0 &{} 0.1 &{} 0.2 \end{array} \right] ,\quad A_{d2}=\left[ \begin{array}{rrr} 0.2 &{} 0.1 &{} 0.1 \\ 0.1 &{} 0.1 &{} 0 \\ 0 &{} 0.1 &{} 0.2 \end{array} \right] , \\ A_{d3}= & {} \left[ \begin{array}{rrr} 0.2 &{} 0.1 &{} 0 \\ 0.1 &{} 0.1 &{} 0 \\ 0.2 &{} 0.1 &{} 0.8 \end{array} \right] ,\quad A_{d4}=\left[ \begin{array}{rrr} 0.2 &{} 0.2 &{} 0.1 \\ 0.1 &{} 0.1 &{} 0 \\ 0 &{} 0.1 &{} 0 \end{array} \right] , \\ C_{1}= & {} \left[ \begin{array}{ccc} 0.5 &{} -0.2 &{} 0.1 \\ -0.2 &{} 0.1 &{} -0.5 \\ 0.2 &{} 0.2 &{} 0 \end{array} \right] , \\ C_{2}= & {} \left[ \begin{array}{ccc} 0.5 &{} -0.2 &{} 0.1 \\ -0.2 &{} 0.1 &{} -0.15 \\ 0.2 &{} 0.2 &{} 0 \end{array} \right] , \\ C_{3}= & {} \left[ \begin{array}{ccc} 0.5 &{} -0.2 &{} 0.1 \\ -0.2 &{} 0.1 &{} -0.15 \\ 0.2 &{} 0.2 &{} 0 \end{array} \right] , \\ C_{4}= & {} \left[ \begin{array}{ccc} 0.5 &{} -0.2 &{} 0.1 \\ -0.2 &{} 0.1 &{} -0.25 \\ 0.2 &{} 0.2 &{} 0 \end{array} \right] , \\ E_{1}= & {} \left[ \begin{array}{ccc} 0.2 &{} 0.2 &{} 0.2 \\ 0 &{} 0.2 &{} 0.1 \\ 0 &{} 0 &{} 0.3 \end{array} \right] ,\quad E_{2}=\left[ \begin{array}{ccc} 0.2 &{} 0.2 &{} 0.2 \\ 0 &{} 0.2 &{} 0.1 \\ 0 &{} 0 &{} 0.3 \end{array} \right] , \\ E_{3}= & {} \left[ \begin{array}{ccc} 0.2 &{} 0.2 &{} 0.2 \\ 0 &{} 0.2 &{} 0.1 \\ 0 &{} 0 &{} 0.3 \end{array} \right] ,\quad E_{4}=\left[ \begin{array}{ccc} 0.2 &{} 0.2 &{} 0.2 \\ 0 &{} 0.2 &{} 0.1 \\ 0 &{} 0 &{} 0.5 \end{array} \right] ,\\ H_{1}= & {} \left[ \begin{array}{ccc} 0.2 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0.2 &{} 0.2 &{} 1 \end{array} \right] ,\quad H_{2}=\left[ \begin{array}{ccc} 0.2 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0.2 &{} 0.2 &{} 1 \end{array} \right] , \\ H_{3}= & {} \left[ \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0.2 &{} 0.2 &{} 1 \end{array} \right] ,\quad H_{4}=\left[ \begin{array}{ccc} 0.1 &{} 0.1 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0.2 &{} 0.2 &{} 1 \end{array} \right] , \\ H_{d1}= & {} \left[ \begin{array}{ccc} 0.2 &{} 0 &{} 0.1 \\ 0 &{} 0.1 &{} 0 \\ 0.2 &{} 0.2 &{} 0.1 \end{array} \right] ,\quad H_{d2}=\left[ \begin{array}{ccc} 0.2 &{} 0 &{} 0.1 \\ 0 &{} 0.1 &{} 0 \\ 0.2 &{} 0.2 &{} 0.1 \end{array} \right] , \end{aligned}$$
$$\begin{aligned} H_{d3}= & {} \left[ \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0.2 &{} 0 &{} 0 \end{array} \right] ,\quad H_{d4}=\left[ \begin{array}{ccc} 0.1 &{} 0.1 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} 0.1 \end{array} \right] . \end{aligned}$$

The transition matrix \(\Pi \) is given as

$$\begin{aligned} \Pi =\left[ \begin{array}{cccc} -2.4 &{} 2.2 &{} ? &{} ? \\ ? &{} -1.9 &{} 1.7 &{} ? \\ 1.2 &{} ? &{} -1.8 &{} ? \\ 2.6 &{} ? &{} ? &{} -2.8 \end{array} \right] , \end{aligned}$$

where “?” is unavailable element. The matrices \(K_{1}\), \(K_{2}\), \(K_{3}\) and \(K_{4}\) are computed as

$$\begin{aligned} K_{1}= & {} \left[ \begin{array}{ccc} 1.1560&0.1524&-0.0334 \end{array} \right] , \\ K_{2}= & {} \left[ \begin{array}{ccc} 1.3392&-0.4797&-0.2292 \end{array} \right] , \\ K_{3}= & {} \left[ \begin{array}{ccc} 2.1802&-0.7285&-0.1829 \end{array} \right] ,\\ K_{4}= & {} \left[ \begin{array}{ccc} 1.8693&-1.2579&-0.0559 \end{array} \right] . \end{aligned}$$

The nonlinearity \(f\left( x,t\right) \), external disturbance \(d\left( t\right) \) and time-varying matrix function \(F\left( i,t\right) \) for four subsystems are given as \( f\left( x,t\right) =0.28+0.2\sin (200t)x_{1}\left( t\right) ,\) \( d\left( t\right) =\exp \left( -t\right) \sqrt{ x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}, \) \(F\left( 1,t\right) =F\left( 2,t\right) =F\left( 3,t\right) =F\left( 4,t\right) =0.02\sin \left( 200t\right) ,\) respectively.

For delay \(\tau \in [-2.5,0)\), the initial conditions are, respectively, set as \(x\left( 0\right) =\left[ \begin{array}{ccc} 0.5&-0.5&0.2 \end{array} \right] ^{T}\) and \(\hat{x}\left( 0\right) =\left[ \begin{array}{ccc} 0.2&-0.1&0.1 \end{array} \right] ^{T}\). We set \(F=\big [ -0.3\quad -0.2 -0.1\big ] .\) The adaptive parameters are, respectively, selected as \(\hat{\alpha }\left( 0\right) =0\), \(\hat{\beta } \left( 0\right) =0\), \(c_{\alpha }=0.4\) and \(c_{\beta }=2.5\) in (33). The observer-based adaptive SMC law is designed in (31) with \(l_{1}=l_{3}=0.85,\) \(l_{2}=l_{4}=0.80,\) \(\kappa =0.1\) and \( \rho _{1}=1.\) By handling the optimal problem in (30), we have

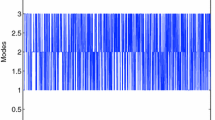
$$\begin{aligned} L_{1}= & {} \left[ \begin{array}{rrr} 0.9544 &{} 0.0485 &{} 1.3991 \\ -1.8289 &{} -0.6447 &{} 3.4118 \\ -2.1039 &{} -2.6729 &{} 1.3803 \end{array} \right] , \\ L_{2}= & {} \left[ \begin{array}{ccc} 1.1280 &{} 0.1743 &{} 1.0889 \\ -3.1106 &{} -2.5079 &{} 5.0254 \\ -6.1187 &{} -12.7171 &{} 1.0538 \end{array} \right] , \\ L_{3}= & {} \left[ \begin{array}{ccc} 2.7137 &{} 2.9771 &{} -0.7232 \\ -1.7651 &{} -1.2084 &{} 3.0056 \\ -2.1684 &{} -5.5754 &{} -1.1733 \end{array} \right] , \\ L_{4}= & {} \left[ \begin{array}{ccc} 2.1372 &{} 1.0096 &{} 1.6076 \\ -2.6619 &{} -0.5535 &{} 7.0478 \\ -1.7736 &{} -3.6856 &{} 2.4934 \end{array} \right] . \end{aligned}$$

The simulation results are illustrated in Figs. 1–7. Figure 1 shows the switching signal \(r\left( t\right) \), and Fig. 2 plots the error trajectories. Figures 3 and 4 depict original system state responses and state estimation responses, respectively. In Fig. 5, the curve denotes the integral sliding mode surface function \(\zeta \left( t\right) \). Figures 6 and 7 demonstrate the responses of estimation values \(\hat{\alpha }\left( t\right) \) and \(\hat{\beta }\left( t\right) \), respectively.

Fig. 1
figure 1

Trajectory of \(r\left( t\right) \)

Full size image
Fig. 2
figure 2

State estimation error trajectories \(e\left( t\right) \)

Full size image
Fig. 3
figure 3

State trajectories \(x\left( t\right) \)

Full size image
Fig. 4
figure 4

State estimation trajectories \(\hat{x}\left( t\right) \)

Full size image
Fig. 5
figure 5

Sliding mode surface \(\zeta \left( t\right) \)

Full size image
Fig. 6
figure 6

Estimation of \({\alpha }\left( t\right) \)

Full size image
Fig. 7
figure 7

Estimation of \({\beta }\left( t\right) \)

Full size image

6 Conclusion

The SMC problem has been studied for state-delayed MJSs with disturbances, matched nonlinearities, parameter uncertainties, partly unknown transition probabilities and unmeasured states. Construct an appropriate sliding mode surface to ensure the sliding motion to be stochastically stable. The designed observer-based adaptive sliding mode controller can regulate the effect of unknown nonlinearity and guarantee the finite-time reachability. The effectiveness of the proposed control scheme has been illustrated via a numerical example. Future research will focus on the control problem for nonlinear state-delayed MJSs by using fuzzy control approach [36, 46].