Robust Finite-Time Output Feedback $H_\infty$ Control for Stochastic Jump Systems with Incomplete Transition Rates

Abstract

This article aims to investigate the problem of robust finite-time output feedback $H_\infty$ control for stochastic jump systems with incomplete transition rates. Firstly, for the nominal stochastic jump systems, the sufficient conditions for the finite-time boundedness and finite-time output feedback stabilization are developed, respectively. Then, a robust finite-time $H_\infty$ output feedback controller is designed by means of linear matrix inequalities. A key point of this work is to relax the special requirement of completely known transition rates to more general form that mixes two cases of completely known and completely unknown transition rates. Finally, a numerical example is given to demonstrate the applicability of the main results.

1 Introduction

Owing to the existence of abrupt changes in practical applications, many systems can be effectively modeled as stochastic jump systems, such as manufacturing systems [18], economic systems [4], communication systems [2], and so on. Similar to a switched system [19], a stochastic jump system consists of a family of continuous or discrete time subsystems and a set of Markovian chain that orchestrates the switching between them. Recently, stochastic jump systems have attracted considerable attention and a large number of results have been published. For example, please see [11–13, 15, 23] and references therein. In particular, the problem of $H_\infty$ filtering for Markovian jump singular system was considered and a weighted gain was reached under a quantisation condition in [15]. After that, more results of filtering for discrete time stochastic Markov jump systems were reported in [6, 7, 27]. Using the linear matrix inequality approach, a number of interesting results on Markovian jump neural networks systems with time delay have appeared in [25, 26].

It is well acknowledged that stochastic stability, defined in an infinite-time interval, is one of the crucial issues in the study of stochastic jump systems [20, 30, 31]. To some extent, the stochastic stability plays a critical role in reality. However, in some cases, the stability property in infinite time is not acceptable. For instance, the control process of a robot arm is not allowed to be beyond some given threshold in a finite-time interval [23]. To deal with this situation, the notion of finite-time stability was presented by Peter Dorato [8]. Later on, the finite-time stability was also extended to stochastic jump systems, and many relevant results have been derived [22]. Moreover, the transition rates determine the performance of systems [9, 14, 28, 29]. Usually, the assumption that the transition rates are completely known or bounded may lead to some conservativeness. Actually, the information of transition rates might not be exactly known in many practical control problems, because it is difficult and expensive to gain precisely the information of transition rates or even the bounds. Thus, in recent years, much attention has been focused on the study of stochastic jump systems with incomplete transition rates [30, 31]. The problem of robust finite-time $H_\infty$ control for stochastic jump systems was discussed in [16]. It is required that the bounds of transition rates are known. [30] discussed the stochastic stabilization problem of stochastic jump systems with partly unknown transition probabilities by the fixed weighting matrices method. To a certain degree, the results relax the traditional assumptions that all the transition rates or the bounds must be completely known.

In addition, when the state is measurable, the state feedback $H_{\infty }$ control problem has been widely explored, and a large amount of useful and interesting achievements have been reported in the literature [32, 33]. It should be pointed out that the requirement of the availability of the state at each time in state feedback control is shown to be more conservative because state is immeasurable in real world [5, 10, 24]. Therefore, it is extremely imperative and significant to construct a $H_{\infty }$ output feedback controller. Meanwhile, it is difficult to obtain the conditions in the form of linear matrix inequalities ensuring the finite-time $H_\infty$ output feedback stabilization.

To the best of our knowledge, the synthesis issue of robust finite-time output feedback $H_{\infty }$ control for stochastic jump systems with incomplete transition rates has not been fully investigated so far. This is mainly due to the difficulty in extending the existing results to stochastic jump systems with incomplete transition rates. This motivates the present study.

In this paper, we study the problem of robust finite-time output feedback $H_\infty$ control for stochastic jump systems with incomplete transition rates. The main contribution lies in three aspects. First, some sufficient conditions are provided to guarantee the finite-time boundedness and finite-time output feedback stabilization. Second, a robust finite-time $H_\infty$ output feedback controller is designed. Third, we do not introduce any confinement to the unknown transition rates, which is less conservative. Finally, a practical example of a single-link robot arm system is given to demonstrate the applicability of the main results.

Notations For real symmetric matric $A$, the notation $A\ge 0$ ($A>0$) means that the matrix $A$ is positive semi-definite (positive definite). $A^T$ and $A^{-1}$ denote, respectively, the transpose of a matrix $A$ and the inverse of a matrix $A$. $\lambda _{\max }(B)$ ($\lambda _{\min }(B)$) is the maximum (minimum) eigenvalue of a matrix $B$. diag$\{A, B\}$ represents the block diagonal matrix of $A$ and $B$. $I$ is the unit matrix with appropriate dimension, and in a matrix, the term of symmetry is stated by the asterisk $*$. $\mathbb {R}^n$ stands for the $n$-dimensional Euclidean space, $\mathbb {R}^{n\times m}$ is the set of all $n\times m$ real matrices, and $\mathcal {M}=\{1, 2, \ldots , N\}$ means a set of positive numbers. $\Vert *\Vert$ denotes the Euclidean norm of vectors. $\ L_2^n[0, +\infty )$ is the space of $n$-dimensional square integrable function vector over $[0, +\infty )$. ${ \Omega }$ is the sample space, $\mathcal {F}$ is the algebra of events, and $\mathcal {P}$ is the probability measure defined on $\mathcal {F}$. $\mathbb {E}\{\cdot \}$ denotes the mathematics expectation of the stochastic process or vector.

2 Problem Formulation and Preliminaries

Consider the following stochastic jump system in the probability space (${ \Omega }$, $\mathcal {F}$, $\mathcal {P}$):

$$\begin{aligned} \left\{ \begin{array}{lllll} dx(t)&{}=&{} [(A(r_t)+\triangle A(r_t))x(t)+(B(r_t)+\triangle B(r_t))u(t)+E_x(r_t)v(t)]dt\\ &{}&{}+\,\, G(r_t)x(t)dW(t), \\ y(t)&{}=&{} C_y(r_t)x(t), \\ z(t)&{}=&{} C_z(r_t)x(t)+D_z(r_t)u(t)+E_z(r_t)v(t), \\ x(t_0)&{}=&{} x_{0},\,r_{t_0}= r_{0},\,t = 0, \end{array} \right. \end{aligned}$$

(1)

where $x(t)\in {\mathbb {R}^{n}}$ is the state vector, $u(t)\in {\mathbb {R}^{m}}$ is the control input, $v(t)\in {L_2^n[0, +\infty )}$ is an arbitrary external disturbance, $y(t)\in {\mathbb {R}^{p}}$ is the measure output, $z(t)\in {\mathbb {R}^{q}}$ is the control output, $W(t)\in \mathbb {R}$ is a standard Wiener process, which is independent of the Markovian process, $x_{0}, r_{0}$, and $t_{0}$, respectively, represent the initial state, initial mode, and initial time. {$r_{t}, t\ge 0$} is a Markovian process which takes values in a finite space $\mathcal {M}=\{1, 2, \ldots , N\}$ with the transition rate matrix $\Pi =\{\pi _{ij}\}$ ($i, j\in \mathcal {M}$ ) given by

$$\begin{aligned} \,P \{r_{t+\Delta t}=j|r_t=i\}= \left\{ \begin{array}{ll} \pi _{ij}\Delta t+o(\Delta t), &{} i\ne j,\\ 1+\pi _{ii}\Delta t+o(\Delta t), &{} i= j, \end{array} \right. \end{aligned}$$

where $\Delta t>0$, and $\displaystyle {}\lim _{\Delta t\rightarrow \,0}\frac{o(\Delta t)}{\Delta t}=0$. $\pi _{ij}\ge 0$ ($i,j\in \mathcal {M}, i\ne j$ ) is the transition rates from mode $i$ at time $t$ to mode $j$ at time $t+\Delta t$, and $\displaystyle {}{\sum _{j=1,i\ne j}^{N}}{\pi _{ij}}=-\pi _{ii}$. $A(r_t)$, $B(r_t)$, $E_x(r_t)$, $C_y(r_t)$, $C_z(r_t)$, $D_z(r_t)$, $E_z(r_t)$ and $G(r_t)$ are known constant matrices with appropriate dimensions. $\Delta A(r_t)$ and $\Delta B(r_t)$ represent the uncertainties in the matrices $A(r_t)$ and $B(r_t)$, which satisfy

$$\begin{aligned} \triangle A(r_t)=M_1(r_t)F(t,r_t)N_1(r_t), \,\,\,\,\,\,\,\,\,\,\triangle B(r_t)=M_2(r_t)F(t,r_t)N_2(r_t), \end{aligned}$$

(2)

where $M_1(r_t)$, $N_1(r_t)$, $M_2(r_t)$, and $N_2(r_t)$ are known matrices with appropriate dimensions, and $F(t,r_t)$ is the time-varying unknown matrix function with Lebesgue norm measurable elements satisfying

$$\begin{aligned} {F(t,r_t)^T}{F(t,r_t)}\le I. \end{aligned}$$

(3)

The controller to be designed is described by the following structure

$$\begin{aligned} u(t)=K(r_t)y(t)=K(r_t)C_y(r_t)x(t), \end{aligned}$$

(4)

where $K(r_t)$ is the output feedback gain to be designed. Then the closed-loop system is as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} dx(t)&{}=&{} [(A(r_t)+\triangle A(r_t)+(B(r_t)+\triangle B(r_t))K(r_t)C_y(r_t))x(t)\\ &{}&{}+\,E_x(r_t)v(t)]dt+G(r_t)x(t)dW(t), \\ y(t)&{}=&{} C_y(r_t)x(t), \\ z(t)&{}=&{} (C_z(r_t)+D_z(r_t)K(r_t)C_y(r_t))x(t)+E_z(r_t)v(t), \\ x(t_0)&{}=&{} x_{0},\,r_{t_0}= r_{0},\,t = 0. \end{array} \right. \end{aligned}$$

(5)

For notational simplicity, when $r(t)=i, i\in \mathcal {M}$, $A(r_t)$, $B(r_t)$, $K(r_t)$, $E_x(r_t)$, $C_y(r_t)$, $C_z(r_t)$, $D_z(r_t)$, $E_z(r_t)$, $\Delta A(r_t)$, $\Delta B(r_t)$, $M_1(r_t)$, $N_1(r_t)$, $M_2(r_t)$, $N_2(r_t)$, and $G(r_t)$ are respectively denoted as $A_i$, $B_i$, $K_i$, $E_{xi}$, $C_{yi}$, $C_{zi}$, $D_{zi}$, $E_{zi}$, $\Delta A_i$, $\Delta B_i$, $M_{1i}$, $N_{1i}$, $M_{2i}$, $N_{2i}$, and $G_i$.

On the other hand, the transition rates of the Markovian process are assumed to be partly available, i.e., some elements in matrix $\Pi =\{\pi _{ij}\}$ are unknown. For instance, for the stochastic jump system (1) with four subsystems, the transition rate matrix $\Pi$ may be as:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} ? &{} \pi _{12} &{} ? &{} \pi _{14} \\ \pi _{21}&{} ? &{} ? &{} \pi _{24} \\ \pi _{31} &{} ? &{} \pi _{33} &{} ? \\ ? &{} ? &{} ? &{} \pi _{44} \end{array}\right] , \end{aligned}$$

(6)

where ‘?’ represents the inaccessible transition rate. For $\forall i\in \mathcal {M}$, seeking describable convenience, we denote $\mathcal {M}=L_k^i+L_{uk}^i$, and

$$\begin{aligned} L_k^i&\triangleq \{j: \pi _{ij} \,\,\hbox {is \,\,known, \,\,for} \,\,j\in \mathcal {M}\}, \\ \nonumber L_{uk}^i&\triangleq \{j: \pi _{ij} \,\,\hbox {is \,\,unknown, \,\,for} \,\,j\in \mathcal {M}\}. \end{aligned}$$

(7)

Moreover, if $L_k^i \ne \mathbf 0$, $L_k^i$ is further described as

$$\begin{aligned} L_k^i=\{k_1^i, k_2^i, \ldots k_m^i \}, \,\,\,\,1\le m \le \mathcal {M}, \end{aligned}$$

(8)

where $k_m^i \in \mathcal {M}$ represents the $m \hbox {th}$ known transition rate of the set $L_k^i$ in the $i \hbox {th}$ row of the transition rate matrix $\Pi$.

Remark 1

The transition rates are required that all information are completely known ($L_{uk}^i = \mathbf 0 , L_k^i = \mathcal {M}$) or completely unknown ($L_k^i= \mathbf 0 , L_{uk}^i = \mathcal {M}$) in some existing works. Here, we consider a general form.

We now introduce some assumptions, definitions, and lemmas, which are useful in our later development.

Assumption 1

The external disturbance $v(t)$ is time-varying and satisfies the condition

$$\begin{aligned} \int _{t_0}^{T}{v^{T}(s)}{v(s)}ds \le d, \,\,\,d\ge 0. \end{aligned}$$

(9)

Definition 1

(FTS [8]) For a given constant $T>0$, the stochastic jump system (1) ($u(t)=0, v(t)=0$) is said to be finite-time stable with respect to ($c_1, c_2, T, H_i$), if

$$\begin{aligned} {\mathbb {E}\{x_0^TH_ix_0\}\le c_1}\Longrightarrow {\mathbb {E}\{{x(t)}^TH_ix(t)\} < c_2}, \,\,\forall t\in [0, T], \end{aligned}$$

(10)

where $0<c_1<c_2, H_i>0$.

Definition 2

(FTB [1]) For a given constant $T>0$, the stochastic jump system (1) ($u(t)=0$) is said to be finite-time bounded with respect to ($c_1, c_2, T, H_i,$ $d$) for any disturbance satisfying (9), if condition (10) holds with $0<c_1<c_2, H_i>0$.

Definition 3

(The Finite-Time $H_\infty$ Control) For the stochastic jump system (1), the finite-time $H_\infty$ control problem is solvable with disturbance attenuation level $\gamma >0$, if there exists a output feedback controller in the form of (4), such that the following two conditions are satisfied:

• 1. The stochastic jump system (1) is finite-time bounded with respect to ($c_1, c_2, T,$ $H_i, d$);

• 2. Under zero initial condition ($x(t_0)=0, t_0=0$), for any external disturbance $v(t)\ne 0$ satisfying condition (9), the control output $z(t)$ of the stochastic jump system (1) satisfies

  $$\begin{aligned} \mathbb {E}\bigg \{\int _{0}^{T}z^T(t)z(t)dt \bigg \} \le \gamma ^2\int _{0}^{T}v^T(t)v(t)dt. \end{aligned}$$

  (11)

Definition 4

[17] In the Euclidean space$\{\mathbb {R}^n \times \mathcal {M} \times \mathbb {R^+} \}$, introduce the stochastic Lyapunov function for the stochastic jump system (1) as $V(x(t),i)$, and the weak infinitesimal operator satisfies

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= \lim _{\Delta _t \rightarrow 0} \frac{1}{\Delta _t} [\mathbb {E}\{V(x(t+\Delta _t), r(t+\Delta _t))\}-V(x(t),i)] \nonumber \\&= \frac{\partial }{\partial t}V(x(t),i)+\frac{\partial }{\partial x}V(x(t),i) \dot{x}(t)+{\sum _{j=1}^N}{\pi _{ij}}V(x(t),j) \\&+\,\frac{1}{2}tr[x^T(t)G_i^TV_{xx}(x(t),i)G_ix(t)].\nonumber \end{aligned}$$

(12)

Remark 2

Unlike the classical Lyapunov stability is a system property on an infinite-time interval, the finite-time stability defines in the finite-time interval, that is, a system is said to be finite-time stable, if once we fix a finite-time interval, the state of system does not exceed the prescribed bound during this time interval.

Lemma 1

[21] Let $T, M, F$, and $N$ be real matrices of appropriate dimension with $F^TF\le I$, then for any positive scalar $\varepsilon >0$, there holds

$$\begin{aligned} T+MFN+{N^T}{F^T}{M^T}\le T+\varepsilon M{M^T}+\varepsilon ^{-1}{N^T}N. \end{aligned}$$

(13)

Lemma 2

Given $T>0$. The stochastic jump system (1) ($u(t)=0, v(t)=0$) under incomplete transition rates is finite-time stable with respect to $(c_1, c_2, T, H_i )$, if there exist a positive constant $\alpha >0$, symmetric positive definite matrices $P_i \in \mathbb {R}^{n\times n}, S \in \mathbb {R}^{p\times p}$ and symmetric matrices $Q_i\in \mathbb {R}^{n\times n}$, such that for every $i \in \mathcal {M}$

$$\begin{aligned}&A_i^TP_i+P_iA_i+\sum _{j\in {L_k^i}}{\pi _{ij}}(P_j-Q_i)+G_i^TP_iG_i-\alpha {P_i}<0, \end{aligned}$$

(14)

$$\begin{aligned}&P_j-Q_i\le 0, \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j\ne i,\end{aligned}$$

(15)

$$\begin{aligned}&P_j-Q_i\ge 0, \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j=i, \end{aligned}$$

(16)

$$\begin{aligned}&c_1e^{\alpha T}\frac{\lambda _{\max }(\tilde{P}_i)}{\lambda _{\min }(\tilde{P}_i)}<c_2, \end{aligned}$$

(17)

where $\tilde{P}_i = {H_i^{-1/2}}P_i{H_i^{-1/2}}$.

Proof

See the Appendix. $\square$

Lemma 3

Given $T>0$. The stochastic jump system (1) $(u=0)$ under incomplete transition rates is finite-time bounded with respect to $(c_1, c_2, T, H_i, d )$, if there exist two positive constants $\alpha >0, \gamma >0$, symmetric positive definite matrices $P_i \in \mathbb {R}^{n\times n}, S \in \mathbb {R}^{p\times p}$ and symmetric matrices $Q_i\in \mathbb {R}^{n\times n}$, such that for every $i \in \mathcal {M}$

$$\begin{aligned}&\left[ \begin{array}{cccccc} {{A_{i}}^T}P_i+P_i{A_{i}}+\sum _{j\in {L_k^i}}{\pi _{ij}}(P_j-Q_i)+G_i^TP_iG_i-\alpha {P_i} &{} \,\,P_i E_{xi} \\ *&{} \,\,-\gamma ^2I\\ \end{array} \right] <0,\qquad \end{aligned}$$

(18)

$$\begin{aligned}&P_j-Q_i\le 0, \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j\ne i,\end{aligned}$$

(19)

$$\begin{aligned}&P_j-Q_i\ge 0, \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j=i, \end{aligned}$$

(20)

$$\begin{aligned}&{c_1}{\lambda _{\max }(\tilde{P}_i)+\frac{\gamma ^2d}{\alpha }(1-e^{-\alpha T})}<e^{-\alpha T}c_2\lambda _{\min }(\tilde{P}_i), \qquad \end{aligned}$$

(21)

where $\tilde{P}_i = {H_i^{-1/2}}P_i{H_i^{-1/2}}$.

Proof

See the Appendix. $\square$

3 Main Results

In this section, we firstly give the finite-time $H_{\infty }$ performance analysis for the nominal system of the stochastic jump system (1) and then investigate the issues of robust finite-time $H_{\infty }$ control.

3.1 Finite-Time Output Feedback $H_{\infty }$ Control

In this subsection, we construct a output feedback controller for the nominal system of the stochastic jump system (1) with $F(t, r_t)=0$ for all $t \ge 0$, and then give the finite-time $H_{\infty }$ performance analysis. The nominal system of the stochastic jump system (1) is described as follows

$$\begin{aligned} \left\{ \begin{array}{lllll} dx(t)&{}=&{} [(A_ix(t)+B_iu(t)+E_{xi}v(t)]dt+G_ix(t)dW(t), \\ y(t)&{}=&{} C_{yi}x(t), \\ z(t)&{}=&{} C_{zi}x(t)+D_{zi}u(t)+E_{zi}v(t), \\ x(t_0)&{}=&{} x_{0},\ r_{t_0}= r_{0},\,t = 0. \end{array} \right. \end{aligned}$$

(22)

Under the output feedback controller (4), the closed-loop system is

$$\begin{aligned} \left\{ \begin{array}{lll} dx(t)&{}=&{} [(A_i+B_iK_iC_{yi})x(t)+E_{xi}v(t)]dt+G_ix(t)dW(t), \\ y(t)&{}=&{} C_{yi}x(t), \\ z(t)&{}=&{} (C_{zi}+D_{zi}K_iC_{yi})x(t)+E_{zi}v(t), \\ x(t_0)&{}=&{} x_{0},\,r_{t_0}= r_{0},\,t = 0. \end{array} \right. \end{aligned}$$

(23)

Theorem 1

Consider $T>0$ and $v(t)$ satisfying (9). The stochastic jump system (22) under incomplete transition rates is finite-time stabilizable via a output feedback controller (4) with respect to ($c_1, c_2, T, H_i, d$) and the inequality (11) is satisfied, if there exist two positive constant $\alpha >0, \gamma >0$, symmetric positive definite matrices $P_i \in \mathbb {R}^{n\times n}$ and symmetric matrices $Q_i\in \mathbb {R}^{n\times n}$, such that for all $i \in \mathcal {M}$

$$\begin{aligned}&\left[ \begin{array}{cccccc} \Xi _i&{} \,\,P_i E_{xi} &{} \,\,(C_{zi}+D_{zi}K_iC_{yi})^T \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T\\ *&{} \,\,*&{} \,\,-I \\ \end{array} \right] <0, \end{aligned}$$

(24)

$$\begin{aligned}&P_j-Q_i\le 0, \quad \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j\ne i,\end{aligned}$$

(25)

$$\begin{aligned}&P_j-Q_i\ge 0, \quad \quad \quad \quad \quad \,\,\,j\in L_{uk}^i, \quad \,\,j=i, \end{aligned}$$

(26)

$$\begin{aligned}&{c_1}{\lambda _{\max }(\tilde{P}_i)+\frac{\gamma ^2d}{\alpha }(1-e^{-\alpha T})}<e^{-\alpha T}c_2\lambda _{\min }(\tilde{P}_i), \end{aligned}$$

(27)

where

$$\begin{aligned} \Xi _i&= {(A_i+B_iK_iC_{yi})^T}P_i+P_i(A_i+B_iK_iC_{yi})+\sum _{j\in L_k^i}\pi _{ij}(P_j-Q_i)\nonumber \\&+\,\, G_i^TP_iG_i-\alpha P_i, \\ \tilde{P}_i&= {H_i^{-1/2}}P_i{H_i^{-1/2}}. \end{aligned}$$

Proof

By Schur complement lemma, condition (24) can be written as

$$\begin{aligned}&\left[ \begin{array}{cccccc} \Xi _i&{} \,\,P_i E_{xi} &{} \,\,(C_{zi}+D_{zi}K_iC_{yi})^T \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T\\ *&{} \,\,*&{} \,\,-I \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{cccccc} \Xi _i&{} \,\,P_i E_{xi} \\ *&{} \,\,-\gamma ^2I \\ \end{array} \right] + \left[ \begin{array}{cccccc} (C_{zi}+D_{zi}K_iC_{yi})^T \\ E_{zi}^T\\ \end{array} \right] \left[ \begin{array}{cccccc} C_{zi}+D_{zi}K_iC_{yi} &{} \,\,E_{zi} \\ \end{array} \right] <0.\qquad \end{aligned}$$

(28)

Moreover, we obtain

$$\begin{aligned} \left[ \begin{array}{cccccc} (C_{zi}+D_{zi}K_iC_{yi})^T \\ E_{zi}^T\\ \end{array} \right] \left[ \begin{array}{cccccc} C_{zi}+D_{zi}K_iC_{yi} &{} \,\,E_{zi} \\ \end{array} \right] >0. \end{aligned}$$

(29)

Obviously, (24) implies (18). Then based on Lemma 3, the finite-time boundedness of the stochastic jump system (23) can be guaranteed by the above condition.

Then, for the stochastic jump system (23), choose a Lyapunov function candidate as

$$\begin{aligned} V(x(t), i)=x(t)^T{P_i}x(t). \end{aligned}$$

(30)

We have

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= \lim _{\Delta _t \rightarrow 0} \frac{1}{\Delta _t} [\mathbb {E}\{V(x(t+\Delta _t)r(t+\Delta _t))\}-V(x(t),i)] \nonumber \\&= \frac{\partial }{\partial t}V(x(t),i)+\frac{\partial }{\partial x}V(x(t),i) \dot{x}(t)+{\sum _{j=1}^N}{\pi _{ij}}V(x(t),j)\nonumber \\&+\,\frac{1}{2}tr[x^T(t)G_i^TV_{xx}(x(t),i)G_ix(t)].\nonumber \\&= x^T(t)\bigg [{A_i^T}P_i+P_iA_i+{\sum _{j=1}^N}{\pi _{ij}}P_j\bigg ]x(t)+x^T(t)P_i G_i w(t) \nonumber \\&+\,w^T(t)G_i^TP_ix(t)+x^T(t)G_i^TP_i(x(t),i)G_ix(t). \end{aligned}$$

(31)

Due to $\sum _{j=1}^N{\pi _{ij}Q_i}=0$ for arbitrary symmetric matrices $Q_i$, we can write the inequality (31) as

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= x^T(t)\bigg [{A_i^T}P_i+P_iA_i+{\sum _{j=1}^N}{\pi _{ij}}(P_j-Q_i)+G_i^TP_iG_i\bigg ]x(t)\nonumber \\&+\,x^T(t)P_i E_{xi} v(t)+v^T(t)E_{xi}^TP_ix(t) \nonumber \\&= x^T(t)\bigg [{A_i^T}P_i+P_iA_i+{\sum _{j\in L_k^i}}{\pi _{ij}}(P_j-Q_i) \\&+{\sum _{j\in L_{uk}^i}}{\pi _{ij}}(P_j-Q_i)+G_i^TP_iG_i\bigg ]x(t)+x^T(t)P_i E_{xi} v(t)\nonumber \\&+\,v^T(t)E_{xi}^TP_ix(t). \nonumber \end{aligned}$$

(32)

Notice that $\pi _{ij}\ge 0$ for all $i\ne j$, and $\pi _{ii}=-{\sum _{j=1,i\ne j}^{N}}{\pi _{ij}}<0$ for all $i\in \mathcal {M}$, in view of the inequality (24–26), we have

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&\le \alpha V(x(t),i)+ \gamma ^2v^T(t)v(t)-z^T(t)z(t). \end{aligned}$$

(33)

Further, multiplying (33) by $e^{-\alpha t}$ yields

$$\begin{aligned} \mathcal {L}[{e^{-\alpha t} V(x(t),i)}]&\le e^{-\alpha t} [\gamma ^2 v^T(t)v(t)-z^T(t)z(t)]. \end{aligned}$$

(34)

Under the zero initial condition, integrating the above inequality between $0$ and $t$, we have

$$\begin{aligned} {e^{-\alpha t} V(x(t),i)}&\le \int _{0}^{t} e^{-\alpha s} [\gamma ^2v^T(s)v(s)-z^T(s)z(s)]ds. \end{aligned}$$

(35)

Thus, the following condition holds

$$\begin{aligned} \mathbb {E}{\int _{0}^{t} e^{-\alpha s} z^T(s)z(s) ds }&\le \int _{0}^{t} e^{-\alpha s} \gamma ^2 v^T(s)v(s)ds. \end{aligned}$$

(36)

Note that $t\in [0, T]$, it follows

$$\begin{aligned} \mathbb {E}{\int _{0}^{T}z^T(s)z(s) ds }&\le \gamma ^2e^{\alpha T} \int _{0}^{T}v^T(s)v(s)ds. \end{aligned}$$

(37)

Therefore, (11) holds with $\bar{\gamma }=\sqrt{e^{\alpha T}}\gamma$.

This completes the proof. $\square$

Remark 3

It is clearly seen that (24) is a nonlinear matrix inequality due to the existence of the nonlinear terms $K_i^TB_i^TC_{yi}^TP_i$ and $P_iC_{yi}B_iK_i$. In order to solve the desired controller $K_i$, we give the following result.

Theorem 2

Consider $T>0$ and arbitrary $v(t)$ satisfying (9). The stochastic jump system (22) under incomplete transition rates is finite-time stabilizable via a output feedback controller with respect to $(c_1, c_2, T, H_i, d )$ and the inequality (11) is satisfied, if there exist three positive scalars $\alpha , \gamma , \lambda$, symmetric positive definite matrices $X_i \in \mathbb {R}^{n\times n}$ and $Y_i\in \mathbb {R}^{m\times m}$, symmetric matrices $R_i\in \mathbb {R}^{n\times n}$ and matrices $L_i\in \mathbb {R}^{n\times m}$, such that for all $i \in \mathcal {M}$

$$\begin{aligned}&\left[ \begin{array}{cccccc} \Pi _{1i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T &{} \,\,S_{1i}(x) \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,-X_i &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-M_{1i}(x) \\ \end{array} \right] < 0, \,i\in L_k^i, \end{aligned}$$

(38)

$$\begin{aligned}&\left[ \begin{array}{cccccc} \Pi _{2i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T &{} \,\,S_{2i}(x) \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,-X_i &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-M_{2i}(x) \\ \end{array} \right] <0, \,i\in L_{uk}^i, \end{aligned}$$

(39)

$$\begin{aligned}&\left[ \begin{array}{cccccc} -R_i &{} \,\,X_i \\ *&{} \,\,-X_j\\ \end{array} \right] \le 0, \quad \quad \,\,\,\,j\in L_{uk}^i, \,\,j\ne i, \end{aligned}$$

(40)

$$\begin{aligned}&X_j-R_j \ge 0, \,\quad \quad \quad \quad \,\,\,\,j\in L_{uk}^i, \,\,j=i, \end{aligned}$$

(41)

$$\begin{aligned}&Y_iC_{yi}=C_{yi}X_i, \end{aligned}$$

(42)

$$\begin{aligned}&\left[ \begin{array}{cccccc} -e^{-\alpha T} c_2+ \frac{\gamma ^2d}{\alpha } (1-e^{-\alpha T}) &{} \,\,\,\sqrt{c_1} \\ \sqrt{c_1} &{} \,\,\,-\lambda \end{array} \right] <0, \end{aligned}$$

(43)

$$\begin{aligned}&\lambda H_i^{-1}<X_i<H_i^{-1}, \end{aligned}$$

(44)

where

$$\begin{aligned} \Pi _{1i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i+\pi _{ii}X_i-\alpha X_i, \\ \Pi _{2i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i-\alpha X_i, \\ S_{1i}(x)&= \bigg [\sqrt{\pi _{ik_1^i}}X_i,\cdots , \sqrt{\pi _{ik_{r-1}^i}}X_i, \sqrt{\pi _{ik_{r+1}^i}}X_i,\cdots , \sqrt{\pi _{ik_m^i}}X_i\bigg ], \\ M_{1i}(x)&= \hbox {diag} \{X_{k_1^i} ,\cdots , X_{k_{r-1}^i}, X_{k_{r+1}^i}, \cdots , X_{k_m^i}\}, \\ S_{2i}(x)&= \bigg [\sqrt{\pi _{ik_1^i}}X_i,\cdots ,\sqrt{\pi _{ik_m^i}}X_i\bigg ], \\ M_{2i}(x)&= \hbox {diag} \{X_{k_1^i} ,\cdots , X_{k_m^i}\}, \end{aligned}$$

with $k_1^i, k_2^i, \ldots k_m^i$ given in (8) and $k_r^i=i$. Moreover, the finite-time $H_{\infty }$ output feedback controller gains are given by $K_i=L_iY_i^{-1}$.

Proof

If the conditions (24–27) are satisfied, it is easy to achieve that the system (22) is finite-time $H_{\infty }$ output feedback stabilizable.

Firstly, pre-and post- multiplying the inequality (24) by diag$\{P_i^{-1} \ \,I \,\,I \}$ and performing a congruence transformation to (24) by $X_i=P_i^{-1}, K_i=L_iY_i^{-1}, Y_iC_{yi}=C_{yi}X_i, R_i=P_i^{-1}Q_iP_i^{-1}$, we get

$$\begin{aligned} \left[ \begin{array}{cccccccccc} \Xi _{1i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T \\ *&{} \,\,*&{} \,\,-I \\ \end{array} \right] < 0, \end{aligned}$$

(45)

where

$$\begin{aligned} \Xi _{1i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}+\sum _{j\in L_k^i}\pi _{ij}X_iX_j^{-1}X_i \nonumber \\&-\sum _{j\in L_k^i}\pi _{ij}R_i+X_iG_i^TX_i^{-1}G_iX_i-\alpha X_i. \end{aligned}$$

Since $\pi _{ii}<0, \forall i\in \mathcal {M}$, inequality (45) is dealt with in the following two cases.

Case I: $i\in L_k^i$. The inequality (45) becomes

$$\begin{aligned}&\left[ \begin{array}{cccccccccc} \Xi _{2i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,0 -X_i \\ \end{array} \right] \nonumber \\&\quad + \left[ \begin{array}{cccccccccc} \sum _{j\in L_k^i,j \ne i}\pi _{ij}X_iX_j^{-1}X_i &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] <0, \end{aligned}$$

(46)

where $\Xi _{2i} = X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i-\alpha X_i+\pi _{ii}X_i.$

Applying Schur complement lemma to (46) immediately gives (38).

Case II: $i\in L_{uk}^i$. The inequality (45) turns into

$$\begin{aligned}&\left[ \begin{array}{cccccccccc} \Xi _{3i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,0 -X_i \\ \end{array} \right] \nonumber \\&\quad +\left[ \begin{array}{cccccccccc} \sum _{j\in L_k^i,j \ne i}\pi _{ij}X_iX_j^{-1}X_i &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] <0, \end{aligned}$$

(47)

where $\Xi _{3i}= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i-\alpha X_i.$

Using the similar proof, we can see that (39) is true.

Then, pre- and post-multiplying the inequalities (25) and (26) by $P_i^{-1}$ respectively and letting $X_i=P_i^{-1}, R_i=P_i^{-1}Q_ iP_i^{-1}$, we have

$$\begin{aligned}&X_iX_j^{-1}X_i-R_i\le 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j\in L_{uk}^i, \,\,\,\,j\ne i,\end{aligned}$$

(48)

$$\begin{aligned}&X_j-R_j\ge 0 \,\,\quad \quad \quad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j\in L_{uk}^i, \,\,\,\,j=i. \end{aligned}$$

(49)

It is clear that inequality (48) is equivalent to LMI (40). Denoting $\tilde{X}_i=\tilde{P}_i^{-1}=H_i^{1/2} X_i H_i^{1/2}$ and taking $\lambda _{\max }(\tilde{X}_i)=\frac{1}{\lambda _{\min }(\tilde{P}_i)}$ into consideration, we conclude that condition (27) holds. Further, the following condition

$$\begin{aligned} \lambda <{\lambda _{\min }(\tilde{X}_i)}, \,\,\,\,{\lambda _{\max }(\tilde{X}_i)}<1, \end{aligned}$$

(50)

guarantees that

$$\begin{aligned} \frac{c_1}{\lambda }+ \frac{\gamma ^2d}{\alpha }(1-e^{-\alpha t})<e^{-\alpha t}c_2. \end{aligned}$$

(51)

It is easy to see that condition (50) implies LMI (44) and (51) is equivalent to (43). Therefore, if LMIs (38–44) hold, the closed-loop system (23) is $H_{\infty }$ finite-time bounded. The stochastic jump system (22) can be stabilized via the output feedback controller (4) with $K_i=L_iY_i^{-1}$.

This completes the proof. $\square$

3.2 Robust Finite-Time $H_{\infty }$ Control

In this subsection, a robust finite-time $H_{\infty }$ output feedback controller is designed to guarantee the finite-time output feedback stabilization of the stochastic jump system (1) with disturbance attenuation level $\gamma >0$.

Theorem 3

Given $T>0$ and $v(t)$ satisfying (9). The problem of robust finite-time $H_{\infty }$ control for the the stochastic jump system (1) with incomplete transition rates is solvable with disturbance attenuation level $\gamma >0$, if there exist positive scalars $\alpha , \gamma , \lambda , \varepsilon _{1i}, \varepsilon _{2i}$, symmetric positive definite matrices $X_i \in \mathbb {R}^{n\times n}$ and $Y_i\in \mathbb {R}^{m\times m}$, symmetric matrices $R_i\in \mathbb {R}^{n\times n}$ and matrices $L_i\in \mathbb {R}^{n\times m}$, such that for all $i \in \mathcal {M}$, (40–44) and the following inequalities hold

$$\begin{aligned} \left[ \begin{array}{ccccccccc} \displaystyle {}\Psi _{1i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T &{} \,\,X_iN_{1i}^T &{} \,\,C_{yi}^TL_i^TN_{2i}^T &{} \,\,S_{1i}(x) \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,-X_i &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-\varepsilon _{1i}I &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-\varepsilon _{2i}I &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-M_{1i}(x) \\ \end{array} \right] < 0, \nonumber \\ i\in L_k^i, \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(52)

$$\begin{aligned} \left[ \begin{array}{ccccccccc} \displaystyle {}\Psi _{2i} &{} \,\,E_{xi} &{} \,\,X_iC_{zi}^T+C_{yi}^TL_i^TD_{zi}^T &{} \,\,X_iG_i^T &{} \,\,X_iN_{1i}^T &{} \,\,C_{yi}^TL_i^TN_{2i}^T &{} \,\,S_{2i}(x) \\ *&{} \,\,-\gamma ^2I &{} \,\,E_{zi}^T &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,-I &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,-X_i &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-\varepsilon _{1i}I &{} \,\,0 &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-\varepsilon _{2i}I &{} \,\,0 \\ *&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,*&{} \,\,-M_{2i}(x) \\ \end{array} \right] <0, \nonumber \\ i\in L_{uk}^i, \quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(53)

where

$$\begin{aligned} \Psi _{1i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i+\pi _{ii}X_i \nonumber \\&+\,\varepsilon _{1i}M_{1i}M_{1i}^T+ \varepsilon _{2i}M_{2i}M_{2i}^T -\alpha X_i, \\ \Psi _{2i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i+\varepsilon _{1i}M_{1i}M_{1i}^T\nonumber \\&+ \,\varepsilon _{2i}M_{2i}M_{2i}^T-\alpha X_i, \\ S_{1i}(x)&= \bigg [\sqrt{\pi _{ik_1^i}}X_i,\cdots , \sqrt{\pi _{ik_{r-1}^i}}X_i, \sqrt{\pi _{ik_{r+1}^i}}X_i,\cdots , \sqrt{\pi _{ik_m^i}}X_i\bigg ], \\ M_{1i}(x)&= \hbox {diag} \{X_{k_1^i} ,\cdots , X_{k_{r-1}^i}, X_{k_{r+1}^i}, \cdots , X_{k_m^i}\}, \\ S_{2i}(x)&= \bigg [\sqrt{\pi _{ik_1^i}}X_i,\cdots ,\sqrt{\pi _{ik_m^i}}X_i\bigg ], \\ M_{2i}(x)&= \hbox {diag} \{X_{k_1^i} ,\cdots , X_{k_m^i}\}, \end{aligned}$$

with $k_1^i, k_2^i, \ldots k_m^i$ described as in (8) and $k_r^i=i$. The controller gains are given by $K_i=L_iY_i^{-1}$.

Proof

In (38) and (39), by replacing $A_i$ and $B_i$ with $(A_i+\triangle A_i)$ and $(B_i+\triangle B_i)$, respectively, the following conditions are obtained

$$\begin{aligned} \tilde{\Pi }_{1i}&= \Pi _{1i}+X_i \Delta A_i^T+\Delta A_iX_i+C_{yi}^TL_i^T\Delta B_i^T+\Delta B_iL_iC_{yi}, \\ \tilde{\Pi }_{2i}&= \Pi _{2i}+X_i \Delta A_i^T+\Delta A_iX_i+C_{yi}^TL_i^T\Delta B_i^T+\Delta B_iL_iC_{yi}, \end{aligned}$$

where

$$\begin{aligned} \Pi _{1i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i+\pi _{ii}X_i-\alpha X_i, \\ \Pi _{2i}&= X_iA_i^T+A_iX_i+C_{yi}^TL_i^TB_i^T+B_iL_iC_{yi}-\sum _{j\in L_k^i}\pi _{ij}R_i-\alpha X_i. \\ \end{aligned}$$

We now deal with the uncertainties described as $\Delta A_i, \Delta B_i$. By Lemma 1, there exist scalars $\varepsilon _{1i}, \varepsilon _{2i}$ such that

$$\begin{aligned} X_i\Delta A_i^T+\Delta A_i X_i&= X_i N_{1i}^TF_{i}^T(t)M_{1i}^T+ M_{1i}F_{i}(t)N_{1i}X_i \nonumber \\&\le \varepsilon _{1i}M_{1i}M_{1i}^T+\varepsilon _{1i}^{-1}X_iN_{1i}^TN_{1i}X_i, \end{aligned}$$

(54)

$$\begin{aligned} C_{yi}^TL_i^T\Delta B_i^T+\Delta B_iL_iC_{yi}&= C_{yi}^TL_i^TN_{2i}^TF_{i}^T(t)M_{2i}^T+M_{2i}F_{i}(t)N_{2i}L_iC_{yi} \nonumber \\&\le \varepsilon _{2i}M_{2i}M_{2i}^T+\varepsilon _{2i}^{-1}C_{yi}^TL_i^TN_{2i}^TN_{2i}L_iC_{yi}. \end{aligned}$$

(55)

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} X_i\Delta A_i^T+\Delta A_i X_i &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Phi _{1i} &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} X_i N_{1i}^T \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] F_i^T(t) \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} M_{1i}^T &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] + \left[ \begin{array}{cccccccccccccc} M_{1i} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] F_i(t) \left[ \begin{array}{cccccccccccccc} N_{1i}X_i &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \nonumber \\&\quad \le \varepsilon _{1i}\left[ \begin{array}{cccccccccccccc} M_{1i} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] \left[ \begin{array}{cccccccccccccc} M_{1i}^T &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] + \varepsilon _{3i}^{-1}\left[ \begin{array}{cccccccccccccc} X_iN_{1i}^T \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] \left[ \begin{array}{cccccccccccccc} N_{1i}X_i &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varepsilon _{1i}M_{1i}M_{1i}^T &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] + \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,X_iN_{1i}^T \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ *&{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,-\varepsilon _{1i}I \\ \end{array} \right] . \end{aligned}$$

(56)

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{yi}^TL_i^T\Delta B_i^T+\Delta B_iL_iC_{yi} &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,\\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Phi _{2i} &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\ 0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \ \ 0 &{} \ \ 0 &{} \ \ 0 &{} \ \ 0 &{} \ \ 0 \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{cccccccccccccc} C_{yi}^TL_i^TN_{2i}^T \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] F_{i}^T(t) \left[ \begin{array}{cccccccccccccc} M_{2i}^T &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] + \left[ \begin{array}{cccccccccccccc} M_{2i} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] F_{i}(t) \left[ \begin{array}{cccccccccccccc} N_{2i}L_iC_{yi} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \nonumber \\&\quad \le \varepsilon _{2i}\left[ \begin{array}{cccccccccccccc} M_{2i} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] \left[ \begin{array}{cccccccccccccc} M_{2i}^T &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right] + \varepsilon _{2i}^{-1}\left[ \begin{array}{cccccccccccccc} C_{yi}^TL_i^TN_{2i}^T \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \right] \left[ \begin{array}{cccccccccccccc} N_{2i}L_iC_{yi} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] .\nonumber \\&\quad = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varepsilon _{2i}M_{2i}M_{2i}^T &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] {+} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,C_{yi}^TL_i^TN_{2i}^T \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ 0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,-\varepsilon _{2i}I \\ *&{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 &{} \,\,0 \\ \end{array} \right] ,\nonumber \\ \end{aligned}$$

(57)

where

$$\begin{aligned} \Phi _{1i}&= X_i N_{1i}^TF_{i}^T(t)M_{1i}^T+ M_{1i}F_{i}(t)N_{1i}X_i, \\ \Phi _{2i}&= C_{yi}^TL_i^TN_{2i}^TF_{i}^T(t)M_{2i}^T+M_{2i}F_{i}(t)N_{2i}L_iC_{yi} . \\ \end{aligned}$$

Applying Schur complement Lemma to (54) and (55) leads to (52). Then, similar to the derivation of (52), we can easily prove that (53) holds.

Therefore, if LMIs (40–44) and (52–53) hold, the closed-loop system (5) is robust $H_{\infty }$ finite-time bounded, and the stochastic jump system (1) can be stabilized via the output feedback controller (4) with $K_i=L_iY_i^{-1}$.

This completes the proof. $\square$

Remark 4

Notice that the condition (42) is not in the strictly linear matrix inequality form. In order to deal with this problem, we can replace (42) by the inequality:

$$\begin{aligned}&\left[ \begin{array}{cccccc} -\beta I &{} \,\,\,Y_iC_{yi}-C_{yi}X_i \\ *&{} \,\,\,-I \end{array} \right] <0. \end{aligned}$$

(58)

When $\beta$ is a sufficiently small positive scalar, (58) is closed to (42). The linear matrix inequality (58) may be conservative, but we have to notice that the condition (58) can be solved using the LMI toolbox, see [3].

Remark 5

Theorem 3 presents the sufficient condition of designing the robust finite-time $H_{\infty }$ output feedback controller for stochastic jump systems with incomplete transition rates. Note that the coupled LMIs (52–53) and (40–44) include $X_i$, $Y_i$, $R_i$, $L_i$, $H_i$, $\alpha$, $\beta$, $\gamma ^2$, $\lambda$, $\varepsilon _{1i}$, $\varepsilon _{2i}$, $c_1$, $c_2$, $T$, and $d$. Therefore, for given scalars $\alpha$, $\lambda$, $c_1$, $c_2$, $T$, and $d$, we can take $\gamma ^2$ as the optimized variable to obtain an optimized robust finite-time $H_{\infty }$ output feedback controller. The attenuation lever $\gamma ^2$ can be reduced to the minimum value that satisfies LMIs (52–53) and (40–44). The optimization problem can be described as follows:

$$\begin{aligned}&\displaystyle \min _{X_i, Y_i, R_i, L_i, H_i, \varepsilon _{1i}, \varepsilon _{2i}}\,\,\rho \\&\hbox {s.t. \,\,LMIs} \left\{ \begin{array}{cccc} (52)-(53) \\ (40)-(44) \end{array}\right. \,\,\hbox {with} \,\rho =\gamma ^2. \end{aligned}$$

Remark 6

By using the MATLAB LMIs Toolbox, it is straightforward to check the feasibility of Theorem 3.

Remark 7

Time delay frequently occurs in various engineering systems, which is usually a source of instability and often causes undesirable performance and even makes the system out of control [25–27]. For stochastic jump systems with time delay, we may look for an appropriate Lyapunov–Krasovskii functions. Then, the sufficient condition, which can be easily tackled in the form of LMIs, can be obtained.

4 Simulation Results

In this section, we provide two examples to show the effectiveness of the main results in this paper.

Example 1

The four-mode uncertain stochastic jump system with paraments are given by

Mode 1

$$\begin{aligned} A_{1}&= \left[ \begin{array}{cc} -2 \,&{}\quad -0.5 \\ 0 &{}\quad -1 \end{array} \right] , \, B_{1}=\left[ \begin{array}{cc} 0.6 \,&{}\quad 0\\ -0.1 \,&{}\quad 0.8 \end{array} \right] ,\ \ M_{11}=\left[ \begin{array}{cc} 0.1 \\ 0.2 \end{array} \right] ,\quad \ N_{11}=\left[ \begin{array}{cc} 0.1 \,&0.01 \end{array}\right] ,\\ M_{21}&= \left[ \begin{array}{cc} 0.1 \\ 0 \end{array}\right] , \quad \quad \ \ N_{21}=\left[ \begin{array}{cc} 0.2 \,&0.01 \end{array} \right] ,\ \ E_{x1}\!=\!\left[ \begin{array}{cc} 1 \,&{} -0.1 \\ 0.1 \,&{} 1 \end{array} \right] , \ \ C_{z1}\!=\!\left[ \begin{array}{cc} 1\,&{} 0\\ 0 \,&{} 1 \end{array} \right] ,\\ D_{z1}\!&= \!\left[ \begin{array}{cc} 1 \,&{} 0\\ 0 \,&{} 1 \end{array} \right] , \quad \quad E_{z1}\!=\!\left[ \begin{array}{cc} 1\,&{} 0\\ 0 \,&{} 1 \end{array} \right] , \quad \quad \ \ G_{1}\!=\!\left[ \begin{array}{cc} 0.1\,&{} 0\\ 0 \,&{} 0.1 \end{array} \right] , \quad \ C_{y1}\!=\!\left[ \begin{array}{cc} 0.4 \,&{} 0 \\ 0 \,&{}0.1 \end{array} \right] , \end{aligned}$$

Mode 2

$$\begin{aligned} A_{2}\!&= \!\left[ \begin{array}{cc} -3 \,&{}\quad -0.5\\ 1 \,&{}\quad -2.5 \end{array} \right] , \quad B_{2}=\left[ \begin{array}{cc} 1\,&{}\quad 0.1\\ 0 \,&{}\quad 0.8 \end{array} \right] , \qquad M_{12}\!=\!\left[ \begin{array}{cc} 0.1 \\ 0.13 \end{array} \right] , \ N_{12}\!=\!\left[ \begin{array}{cc} 0.1 \,&\quad 0.3 \end{array} \right] ,\\ M_{22}\!&= \!\left[ \begin{array}{cc} 0.1 \\ 0 \end{array} \right] , \quad \ \,\,N_{22}\!=\!\left[ \begin{array}{c@{\quad }c} 0.01 \,&0.1 \end{array} \right] , \,\,E_{x2}\!=\!\left[ \begin{array}{c@{\quad }c} 1 \,&{} 0\\ 0.1 \,&{} 1 \end{array} \right] , \quad \, C_{z2}\!=\!\left[ \begin{array}{c@{\quad }c} 1\,&{} 0\\ 0 \,&{} 1 \end{array} \right] , \\ D_{z2}\!&= \!\left[ \begin{array}{c@{\quad }c} 1 \,&{} 0\\ 0 \,&{} 1 \end{array} \right] , \quad E_{z2}\!=\!\left[ \begin{array}{c@{\quad }c} 1\,&{} 0\\ 0 \,&{} 1 \end{array} \right] , \quad \quad G_{2}\!=\!\left[ \begin{array}{c@{\quad }c} 0.2 \,&{} 0\\ 0 \,&{} 0.2 \end{array} \right] ,\quad \,C_{y2}\!=\!\left[ \begin{array}{c@{\quad }c} -0.1 \,&{} 0 \\ 0 \,&{}0.2 \end{array} \right] , \end{aligned}$$

Mode 3

$$\begin{aligned} A_{3}\!&= \!\left[ \begin{array}{cc} 2 \,&{}\quad -1.8\\ 0 \,&{}\quad 1.5 \end{array} \right] , \quad B_{3}\!=\!\left[ \begin{array}{cc} 1 \,&{}\quad 0\\ 0.1 \,&{}\quad 1.3 \end{array} \right] , \,M_{13}\!=\!\left[ \begin{array}{cc} 0.1 \\ 0.19 \end{array} \right] , \quad \,N_{13}=\left[ \begin{array}{cc} 0.2 \,&\quad 0.15 \end{array} \right] ,\\ M_{23}\!&= \!\left[ \begin{array}{cc} 0.1 \\ 0.05 \end{array} \right] , \quad \quad \,\,\,N_{23}=\left[ \begin{array}{cc} 0.1 \,&\quad 0.11 \end{array} \right] , \ E_{x3}=\left[ \begin{array}{cc} 1 \,&{}\quad 0\\ 0 \,&{}\quad 1 \end{array} \right] , \quad \,\, C_{z3}\!=\!\left[ \begin{array}{cc} 1 \,&{}\quad 0\\ 0 \,&{}\quad 1 \end{array} \right] , \\ D_{z3}\!&= \!\left[ \begin{array}{cc} 1 \,&{}\quad 0\\ 0 \,&{}\quad 1 \end{array} \right] , \quad \,\,\, E_{z3}\!=\!\left[ \begin{array}{cc} 1 \,&{}\quad 0\\ 0 \,&{}\quad 1 \end{array} \right] , \quad \quad \,G_{3}\!=\!\left[ \begin{array}{cc} 0.1 \,&{}\quad 0\\ 0 \,&{}\quad 0.1 \end{array} \right] , \,C_{y3}\!=\!\left[ \begin{array}{cc} 0.2 \,&{}\quad 0 \\ 0 \,&{}\quad 0.3 \end{array} \right] , \end{aligned}$$

Mode 4

$$\begin{aligned} A_{4}\!&= \!\left[ \begin{array}{cc} -2 &{}\quad -0.4\\ 2 &{}\quad -1.5 \end{array} \right] , \quad B_{4}\!=\!\left[ \begin{array}{cc} 1&{}\quad 0\\ 0 &{}\quad 1 \end{array} \right] , \qquad M_{14}=\left[ \begin{array}{cc} 0.1 \\ 0.09 \end{array} \right] , \,\,N_{14}\!=\!\left[ \begin{array}{cc} 0.1&\quad 0.05 \end{array} \right] ,\\ M_{24}\!&= \!\left[ \begin{array}{cc} 0.2 \\ 0 \end{array} \right] , \quad \quad \qquad \,N_{24}=\left[ \begin{array}{cc} 0&\quad 0.1 \end{array} \right] , \quad \,\,E_{x4}\!=\!\left[ \begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad 1 \end{array} \right] , \quad \, C_{z4}\!=\!\left[ \begin{array}{cc} 1&{} 0\\ 0 &{} 1 \end{array} \right] , \\ D_{z4}\!&= \!\left[ \begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad 1 \end{array} \right] , \quad \quad \! \quad \,\, E_{z4}\!=\!\left[ \begin{array}{cc} 1&{}\quad 0\\ 0 &{}\quad 1 \end{array} \right] , \quad \quad G_{4}\!=\!\left[ \begin{array}{cc} 0.2&{}\quad 0\\ 0 &{}\quad 0.2 \end{array} \right] ,\,C_{y4}\!=\!\left[ \begin{array}{cc} 0.1 &{}\quad 0 \\ 0 &{}\quad 0.2 \end{array} \right] , \end{aligned}$$

Choose the positive scalars $c_1=2, c_2=8.8, T=8, d=1, \alpha =0.01$ and the matrices $H_i=4I, i=1, 2, 3, 4$. The transition rate matrices are given respectively in four cases:

Case I		Completely	known
	1	2	3	4
1	-0.7	0.4	0.1	0.2
2	0.1	-1	0.3	0.6
3	0.5	0.4	-1.3	0.4
4	0.9	0.1	0.5	-1.5
Case II		Partially	known
	1	2	3	4
1	?	0.4	?	0.2
2	?	-1	0.3	?
3	0.5	?	-1.3	?
4	?	0.1	?	?
Case III		Partially	known
	1	2	3	4
1	-0.7	?	0.1	?
2	0.1	?	?	0.6
3	?	0.4	?	0.4
4	0.7	?	0.5	-1.5
Case VI		Completely	unknown
	1	2	3	4
1	?	?	?	?
2	?	?	?	?
3	?	?	?	?
4	?	?	?	?

Based on the LMIs (40–44), (52), and (53) in Theorem 3, the robust finite-time $H_{\infty }$ output feedback controller gains are obtained below:

Case I	Completely known
Controller gains	$K_{1}=[-12.7862 \ \ \ 0.4678 ; \ \,\,1.2536 \,-63.9580]$
	$K_{2}= [\,48.9090 \,\,\,\,0.6281 ; \,\,\,\,1.5609 \,-27.4897]$
	$K_{3}= [-19.4609 \,-1.2617 ; -0.0442 \,-26.6781]$
	$K_{4}= [-40.6328 \,-0.8940 ; -0.1791 \,-20.4902]$
Case II	Partially known
Controller gains	$K_{1}=[-10.2508 \,\,\,\,0.3927 ; \,\,\,1.4609 \,-63.9080]$
	$K_{2}= [\,56.2721 \,\,\,\,0.4527 ; \,\,\,\,0.4161 \,-34.2997]$
	$K_{3}= [-25.5304 \,-0.0179 ; -0.0162 \,-15.6604]$
	$K_{4}= [-46.2473 \,-0.8945 ; -0.8522 \,-29.4492]$
Case III	Partially know
Controller gains	$K_{1}=[-9.4198 \,\,\,\,2.7156 ; \,\,\,0.0562 \,-51.3098]$
	$K_{2}= [\,68.0098 \,\,\,\,0.0805 ; \,\,\,\,0.9362 \,-25.5802]$
	$K_{3}= [-13.5304 \,-0.0179 ; -2.4642 \,-17.1818]$
	$K_{4}= [-33.6230 \,-0.7473 ; -1.6999 \,-20.0095]$
Case VI	Completely unknown
Controller gains	$K_{1}=[-18.0008 \,\,\,\,0.8931 ; \,\,\,1.5302 \,-56.2220]$
	$K_{2}= [\,50.4821 \,\,\,\,0.0290 ; \,\,\,\,0.2198 \,-30.6413]$
	$K_{3}= [-25.4777 \,-0.3519 ; -0.0602 \,-14.9994]$
	$K_{4}= [-50.2001 \,-0.6600 ; -0.4516 \,-28.4370]$

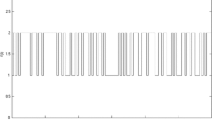
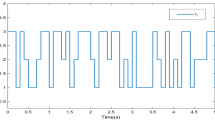
Figures 1–2 show the effectiveness of the design method. Figure 1 describes the state trajectories of the closed-loop system. It can be seen that the stochastic jump system (5) with incomplete transition rates is robust finite-time stable. Figure 2 presents the corresponding control signal, which further shows the effectiveness of the designed controller (4).

Fig. 1

State response of the closed-loop system

Fig. 2

Control signal of the closed-loop system

Example 2

We consider a single-link robot arm in [16, 23]. To demonstrate the effectiveness of the results, we assume that a white noise interferes with a single-link robot arm system. The dynamic equation is given by

$$\begin{aligned} d^2{\theta }(t)&= \bigg [-\frac{MgL}{J}sin(\theta (t))-\frac{D(t)}{J}\dot{\theta }(t)+\frac{1}{J}u(t)+\frac{L}{J}v(t)\bigg ]dt\nonumber \\&+\,G dW(t). \end{aligned}$$

(59)

where $\theta (t)$ is the angle position of the arm, $u(t)$ is the control input, $v(t)$ is the external disturbance, and $W(t)$ is a white noise. $M$ is the mass of the payload, $J$ is the moment of inertia, $g$ is the acceleration of gravity, $L$ is the length of the arm, and $D(t)$ is the viscous friction. The values of parameters $g$, $D(t)$ and $L$ are given by $g=9.81$, $D(t)=2$ and $L=0.5$, respectively. The parameters $M$ and $J$ have four different modes. The transition rate matrices are given, respectively, in four cases:

Case I		Completely	known
	1	2	3	4
1	-0.7	0.2	0.2	0.3
2	0.2	-1	0.5	0.3
3	0.8	0.4	-1.3	0.1
4	0.7	0.2	0.6	-1.5
Case II		Partially	known
	1	2	3	4
1	?	0.2	?	0.3
2	?	-1	0.5	?
3	0.8	?	-1.3	?
4	?	0.2	?	?
Case III		Partially	known
	1	2	3	4
1	-0.7	?	0.2	?
2	0.2	?	?	0.3
3	?	0.4	?	0.1
4	0.7	?	0.6	-1.5
Case VI		Completely	unknown
	1	2	3	4
1	?	?	?	?
2	?	?	?	?
3	?	?	?	?
4	?	?	?	?

The linearized system with four modes systems (59) is represented by

$$\begin{aligned} \left\{ \begin{array}{lllll} dx(t)&{}=&{} \bigg [\left[ \begin{array}{cc} 0 &{} 1\\ -gl &{} -\frac{2}{J(r)} \end{array} \right] x(t)+\left[ \begin{array}{cc} 0 \\ \frac{1}{J(r)} \end{array} \right] u(t)+\left[ \begin{array}{cc} 0 \\ \frac{1}{J(r)} \end{array} \right] v(t)\bigg ]dt\\ &{}&{}+\left[ \begin{array}{cc} 0.1 &{} 0\\ 0 &{} 0.1 \end{array} \right] x(t)dW(t), \\ y(t)&{}=&{} \left[ \begin{array}{cc} 0.1 &{} 0.2 \end{array} \right] x(t), \\ z(t)&{}=&{} \left[ \begin{array}{cc} 1 &{} 1 \end{array} \right] x(t), \end{array} \right. \end{aligned}$$

(60)

where $x(t)=[x_1(t)^T \ x_2(t)^T]^T$, $r=\{1, 2, 3, 4\}$, $J(r)$ depends on the jump mode $r$, $J(1)=1$, $J(2)=5$, $J(3)=10$, $J(4)=15$. We consider the uncertain parameters as follows:

$$\begin{aligned} M_{11}=\left[ \begin{array}{cc} 0.1 \\ 0.2 \end{array} \right] ,\quad \ N_{11}=\left[ \begin{array}{cc} 0.1&0.01 \end{array} \right] ,\ \ M_{12}=\left[ \begin{array}{cc} 0.1 \\ 0.13 \end{array} \right] , \ N_{12}=\left[ \begin{array}{cc} 0.1&0.3 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} M_{13}=\left[ \begin{array}{cc} 0.1 \\ 0.19 \end{array} \right] , \quad \ N_{13}=\left[ \begin{array}{cc} 0.2&0.15 \end{array} \right] , \ \ M_{14}=\left[ \begin{array}{cc} 0.1 \\ 0.09 \end{array} \right] , \ \ N_{14}=\left[ \begin{array}{cc} 0.1&0.05 \end{array} \right] , \end{aligned}$$

and choose the positive scalars $c_1=2, c_2=8.8, T=10, d=1, \alpha =0.01$ and the matrices $H_i=4I, i=1, 2, 3, 4$.

Our purpose is to design a robust finite-time output feedback $H_\infty$ controller in the form of (4) such that the closed-loop system is finite-time stable with an optimal $H_\infty$ performance index. Based on the LMIs (40–44), (52), and (53) in Theorem 3, the robust finite-time $H_{\infty }$ output feedback controller gains are obtained:

Case I	Completely known
Controller gains	$K_{1}=-21.9938$ $K_{2}=-78.6534$ $K_{3}= -115.6020$ $K_{4}=-168.7598$
Case II	Partially known
Controller gains	$K_1=-19.9571$ $K_{2}= -103.4801$ $K_{3}= -155.5879$ $K_{4}=-260.8996$
Case III	Partially know
Controller gains	$K_{1}=-13.5207$ $K_{2}=-45.8019$ $K_{3}=-92.0787$ $K_{4}=-144.2625$
Case VI	Completely unknown
Controller gains	$K_{1}=-29.9364$ $K_{2}=-88.7656$ $K_{3}=-184.3426$ $K_{4}=-119.6302$

We take the initial condition $x_0=[-0.1, 0.1]$. Figure 3 describes the state trajectories of the closed-loop system. It can be seen that the stochastic jump system (5) with incomplete transition rates is robust finite-time stable, which implies that the stochastic jump system (1) is robust finite-time $H_{\infty }$ output feedback stabilizable via the designed output feedback controller (4). The corresponding control signal is presented in Fig. 4, which further shows the effectiveness of the designed controller (4).

Fig. 3

State response of the closed-loop system

Fig. 4

Control signal of the closed-loop system

5 Conclusions

This study has concerned with the problem of robust finite-time output feedback $H_\infty$ control for stochastic jump systems with incomplete transition rates. The sufficient conditions have been developed to ensure the finite-time boundedness and finite-time output feedback stabilization for the given system. We have also designed a robust finite-time $H_\infty$ output feedback controller, which guarantees the $H_\infty$ finite-time boundedness of the closed-loop system. Finally, a numerical example has been provided to demonstrate the applicability of the main results.

Appendix

1.1 Proof of Lemma 2

Proof

For the stochastic jump system (1) ($u(t)=0, v(t)=0$, and $F(t, r_t)=0$), choose a Lyapunov function candidate as (30). Then, by Definition 4, we obtain

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= x^T(t)\bigg [A_i^TP_i+P_iA_i+\sum _{j=1}^N{\pi _{ij}}P_j\bigg ]x(t) \nonumber \\&+\,x^T(t)G_i^TP_iG_ix(t). \end{aligned}$$

(61)

If the transition rates are not accessible completely, the following equation hold for arbitrary symmetric matrices $Q_i$ due to $\sum _{j=1}^N{\pi _{ij}}Q_i=0$

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= x^T(t)\bigg [A_i^TP_i+P_iA_i+{\sum _{j=1}^N}{\pi _{ij}}P_j-\sum _{j=1}^N{\pi _{ij}}Q_i\bigg ]x(t)\nonumber \\&+\,x^T(t)G_i^TP_iG_ix(t) \nonumber \\&= x^T(t)\bigg [A_i^TP_i+P_iA_i+\sum _{j\in L_k^i}{\pi _{ij}}(P_j-Q_i)+\sum _{j\in L_{uk}^i}{\pi _{ij}}(P_j-Q_i)\nonumber \\&+\,G_i^TP_iG_i\bigg ]x(t). \end{aligned}$$

(62)

If $i\in L_k^i$(the elements of the diagonal are known), by inequalities (14) and (15), the following inequality holds

$$\begin{aligned} \displaystyle {} \mathcal {L}{V(x(t),i)}\le \alpha V(x(t),i). \end{aligned}$$

(63)

If $i\in L_{uk}^i$(the elements of the diagonal are unknown), according to inequalities (14–16), the inequality (63) holds. Multiplying (63) by $e^{-\alpha t}$ yields

$$\begin{aligned} \mathcal {L}({e^{-\alpha t}}{V(x(t),i)})\le 0. \end{aligned}$$

(64)

According to Dynkin’s formula for (64), we get

$$\begin{aligned} \displaystyle {}{e^{-\alpha t}}{V(x(t),i)}-{V(x_0,t_0)}\le 0, \end{aligned}$$

(65)

which shows

$$\begin{aligned} V(x(t),i)\le e^{\alpha t}V(x_0,t_0). \end{aligned}$$

(66)

This together with $\tilde{P}_i={H_i^{-1/2}}P_i{H_i^{-1/2}}$ gives rise to

$$\begin{aligned} \begin{array}{ll} V(x(t),i)\le e^{\alpha t} {c_1} \lambda _{\max }(\tilde{P}_i). \end{array} \end{aligned}$$

(67)

Consider

$$\begin{aligned} V(x(t),i)=x^T(t){P_i}x(t) \ge \lambda _{\min }(\tilde{P}_i) x^T(t){H_i}x(t). \end{aligned}$$

(68)

For $\forall t\in [0, T]$, we obtain

$$\begin{aligned} \mathbb {E}\{x^T(t){H_i}x(t)\}\le {c_1}e^{\alpha t}\frac{{\lambda _{\max }(\tilde{P}_i) }}{\lambda _{\min }(\tilde{P}_i)}<c_2. \end{aligned}$$

(69)

This completes the proof. $\square$

1.2 Proof of Lemma 3

Proof

For the stochastic jump system (1) ($u = 0$ and $F(t, r_t)=0$), choose a Lyapunov function candidate as (30). Based on Definition 4, we have

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= x^T(t)\big [A_i^TP_i+P_iA_i+\sum _{j=1}^N{\pi _{ij}}P_j+G_i^TP_iG_i\big ]x(t)\nonumber \\&+\,v^T(t)E_{xi}^TP_ix(t)+x^T(t)P_i E_{xi}v(t). \end{aligned}$$

(70)

Since $\sum _{j=1}^N{\pi _{ij}}Q_i=0$ is always true for arbitrary symmetric matrices $Q_i$, (70) can be rewritten as

$$\begin{aligned} \mathcal {L}{V(x(t),i)}&= x^T(t)\left[ A_i^TP_i+P_iA_i+{\sum _{j=1}^N}{\pi _{ij}}P_j-\sum _{j=1}^N{\pi _{ij}}Q_i+G_i^TP_iG_i\right] x(t)\nonumber \\&+\,v^T(t)E_{xi}^TP_ix(t) \nonumber \\&+\,x^T(t)P_i E_{xi}v(t)\nonumber \\&= x^T(t)\Big [A_i^TP_i+P_iA_i+\sum _{j\in L_k^i}{\pi _{ij}}(P_j-Q_i)+\sum _{j\in L_{uk}^i}{\pi _{ij}}(P_j-Q_i)\nonumber \\&+\,G_i^TP_iG_i\Big ]x(t) \nonumber \\&+\,v^T(t)E_{xi}^TP_ix(t)+x^T(t)P_i E_{xi}v(t). \end{aligned}$$

(71)

Notice that $\pi _{ij}\ge 0$ for all $i\ne j$, and $\pi _{ii}=-\displaystyle {}{\sum _{j=1,i\ne j}^{N}}{\pi _{ij}}<0$ for all $i\in \mathcal {M}$, if $i\in L_k^i$ (the elements of the diagonal are known), by inequalities (18) and (19), the following inequality holds

$$\begin{aligned} \displaystyle {} \mathcal {L}{V(x(t),i)}\le \alpha V(x(t),i)+ \gamma ^2 v^T(t)v(t). \end{aligned}$$

(72)

If $i\in L_{uk}^i$(the elements of the diagonal are unknown), according to inequalities (18–20), the inequality (72) holds. Multiplying (72) by $e^{-\alpha t}$ yields

$$\begin{aligned} \mathcal {L}({e^{-\alpha t}}{V(x(t),i)})\le \gamma ^2 e^{-\alpha t}v^T(t)v(t). \end{aligned}$$

(73)

Using Dynkin’s formula to (73), we obtain

$$\begin{aligned} \displaystyle {}{e^{-\alpha t}}{V(x(t),i)}-{V(x_0,t_0)}\le \gamma ^2 \int _{0}^{t}e^{-\alpha s}v^T(t)v(t) ds, \end{aligned}$$

(74)

which in turn shows

$$\begin{aligned} V\big (x(t),i\big )&\le e^{\alpha t}V(x_0,t_0)+\gamma ^2 e^{\alpha t} \int _{0}^{t}e^{-\alpha s}v^T(s)v(s) ds \nonumber \\&\le e^{\alpha t}\left[ V(x_0,t_0)+\gamma ^2 d \frac{1-e^{-\alpha t}}{\alpha }\right] . \end{aligned}$$

(75)

This together with $\tilde{P}_i={H_i^{-1/2}}P_i{H_i^{-1/2}}$ gives rise to

$$\begin{aligned} \begin{array}{ll} V(x(t),i)\le e^{\alpha t} \big [{c_1} \lambda _{\max }(\tilde{P}_i)+\gamma ^2d \frac{(1-e^{-\alpha t})}{\alpha }\big ]. \end{array} \end{aligned}$$

(76)

Taking into account the fact that

$$\begin{aligned} V(x(t),i)=x^T(t){P_i}x(t) \ge \lambda _{\min }(\tilde{P}_i) x^T(t){H_i}x(t), \end{aligned}$$

(77)

$\forall t\in [0, T]$, we have

$$\begin{aligned} \mathbb {E}\{x^T(t){H_i}x(t)\}\le \frac{e^{\alpha t}\big [{c_1}{\lambda _{\max }(\tilde{P}_i)+\gamma ^2d \frac{(1-e^{-\alpha t})}{\alpha }}\big ]}{\lambda _{\min }(\tilde{P}_i)}<c_2. \end{aligned}$$

(78)

This completes the proof. $\square$