1 Introduction

The motions of large-scale atmospheres and oceans are described by a series of primitive equations including the continuity equation and the momentum equations. Investigators are trying to simplify them according to scale analysis or in specific situations, for example, the quasi-geostrophic approximation is mostly used. Among the theories, Rossby waves are more important. Kinds of nonlinear equations with multiple physical factors, such as shear basic flow and topography, were derived to simulate the evolution of Rossby solitary waves in the past. Long obtained a Korteweg–deVries (KdV) equation for Rossby wave amplitude under beta-plane approximation [1]. Redekopp and Wadati obtained KdV equation and modified KdV (mKdV) equation [2, 3]. Redekopp and Weidman also studied the formation of Rossby solitons with a shear basic flow and obtained necessary conditions for the existence of Rossby solitons [4]. Boyd and Li [5,6,7] derived KdV, mKdV equations in describing the equatorial Rossby solitary wave from primitive equations. Ono put forward to an integral–differential equation [8]. Luo used a nonlinear Schrödinger equation (NLS) to describe the evolution of Rossby solitary wave packets [9], which pointed out that the NLS equation was also appropriate for the Rossby solitons as other equations. Recently, kinds of nonlinear equations, such as integro-differential equation, mBO–mKdV–Burgers equation, ILW-Burgers equation and nonlinear Schrödinger equation, were derived by multiscale method by Yang et al. [9,10,11,12,13] to describe the evolution of Rossby solitary waves or wave packets. At the same time, it is also worth noting that Le and Nguyen have made great progress in investigating the nonlinear waves by the variational–asymptotic method in recent years [14,15,16], which is an effective method for the multiscale and perturbation analysis.

Looking at the above research, on the one hand, most research did the assumption of constant Rossby parameter; Liu and Tan discussed the variation of it along with latitude in a generalized beta approximation [17]. Luo further used the generalized form to study the dipole blocking phenomenon in atmospheres [18]. Song et al. [19, 20] extended the beta effect to a general case indicating its importance in inducing the evolution of Rossby solitary waves. On the other hand, \((1+1)\)-dimensional nonlinear partial differential equations were mainly used in describing the evolution of nonlinear Rossby waves. However, real atmospheric and oceanic motions are not just in one spatial direction. Providing higher-dimensional theories for the nonlinear Rossby waves is necessary. To our knowledge, Gottwald firstly derived the \((2+1)\)-dimensional Zakharov–Kuznetsov (ZK) equation for nonlinear Rossby waves from the quasi-geostrophic barotropic vorticity equation [21]. Recently, Yang et al. [22] obtained ZK–Burgers equation in simulating the \((2+1)\)-dimensional Rossby solitary waves. But they did not consider the variation of Rossby parameter neither. Moreover, topography makes important effects on the study of solitons [10, 23,24,25]. However, no attentions are paid to such effect on the higher-dimensional Rossby waves.

Analytical solutions for nonlinear partial differential equations are also important, and many methods have been proposed [26,27,28,29,30,31,32,33,34,35,36,37,38]. However, each method was only appropriate for special kinds of equations. For example, Yang et al. [22] used sine–cosine and rational methods to give analytical solutions for the ZK equation they obtained, but did not get analytical solution for the ZK–Burgers equation because of the limitation of their method. It is also necessary for us to choose appropriate method to obtain the analytical solutions for the equation we encounter in the present paper.

Considering all of the above discussions, the main purpose of this paper is to consider a \((2+1)\)-dimensional nonlinear Rossby waves with effects of generalized beta, topography and dissipation. The paper is organized as follows: In Sect. 2, we derive a generalized forced Zakharov–Kuznetsov (fZK) equation which includes basic topographical effect part, slowly varying effect part and dissipative effect to describe the evolution of Rossby solitary wave. In Sect. 3, analytical solutions of ZK equation are obtained by elliptic function expansion method; meanwhile, fZK equation is solved by efficient reduced differential transform method, respectively. In Sect. 4, discussions are done on the effects of slowly varying topography and dissipation by the graphical presentations of the analytical solutions. Brief conclusions are given at last.

2 Derivation of fZK equation

2.1 Governing equations and boundary conditions

Beginning with a dimensionless barotropic potential vorticity equation with topography and turbulent dissipation, it is written as [20]

$$\begin{aligned}&\left( \frac{\partial }{\partial t}+\frac{\partial \varPsi }{\partial x}\frac{\partial }{\partial y}-\frac{\partial \varPsi }{\partial y}\frac{\partial }{\partial x}\right) \left( \nabla ^{2}\varPsi +f+h(x,y)\right. \nonumber \\&\quad \left. +h_1 (t)\right) =-\mu \nabla ^{2}\varPsi +Q, \end{aligned}$$
(1)

where \(\varPsi \) is the total stream function, \(f=f_0 +\beta (y)y\) is the vertical component of Coriolis parameter with \(f_0 =2\varOmega \sin \varphi _0 \), \(\varOmega \) is the angular velocity of the earth rotation and \(\varphi _0\) is the local latitude. \(\beta (y)\) is the generalized Rossby parameter [19, 20], h(x, y) is the basic topography part, and \(h_1 (t)\) represents the slowly variation of topography with time. \(\mu \) is the turbulent dissipation parameter. Q denotes the external heating source, and \(\nabla ^{2}\) is the two-dimensional Laplace operator.

Boundary conditions are necessary to solve the problem completely; they are written as

$$\begin{aligned} \left. {\frac{\partial \varPsi }{\partial x}} \right| _{y=0} =\left. {\frac{\partial \varPsi }{\partial x}} \right| _{y=1} =0 \end{aligned}$$
(2)

2.2 Multiscale method and perturbation expansion method

The form of total stream function is assumed to be

$$\begin{aligned} \varPsi =-\int \limits _0^y {\left[ \bar{{u}}(s)-c_0 \right] \hbox {d}s} +\varepsilon ^{2}{\varPsi }'(x,y,t) \end{aligned}$$
(3)

where \(\bar{{\varPsi }}=-\int \nolimits _0^y {[\bar{{u}}(s)-c_0 ]\hbox {d}s}\) is the basic stream function and \({\varPsi }'\) is the perturbed one. \(\varepsilon \) is a small parameter which characterizes the weak nonlinearity. The external heating source balances the diffusion of the basic flow \(\bar{{u}}\) according to the assumption by Caillol et al. [39]. Further assumptions are made in order to satisfy the balance between topography and nonlinearity

$$\begin{aligned} h(x,y)= & {} \varepsilon ^{2}{h}'(y), \nonumber \\ h_1 (t)= & {} \varepsilon ^{2}{h}'_1 (t),\mu =\varepsilon ^{3}\mu _0. \end{aligned}$$
(4)

It is reasonable to neglect the zonal variation of topography for the study of large-scale atmospheric motions. Substituting Eqs. (3) and (4) into Eqs. (1) and (2) yields

$$\begin{aligned}&\left[ \frac{\partial }{\partial t}+(\bar{{u}}-c_0)\frac{\partial }{\partial x}\right] \nabla ^{2}{\varPsi }'+p(y)\frac{\partial {\varPsi }'}{\partial x} \nonumber \\&\qquad +\,\varepsilon ^{2}J\left[ {\varPsi }',\nabla {\varPsi }'+{h}'\right] +\frac{\hbox {d}{h}'_1 (t)}{\hbox {d}t} \nonumber \\&\quad =-\varepsilon ^{3}\mu _0 \nabla ^{2}{\varPsi }', \end{aligned}$$
(5)
$$\begin{aligned}&\left. {\frac{\partial {\varPsi }'}{\partial x}} \right| _{y=0} =\left. {\frac{\partial {\varPsi }'}{\partial x}} \right| _{y=1} =0, \end{aligned}$$
(6)

where \(p(y)=[\beta (y)y-{\bar{{u}}}'{]}'\) represents the shear basic flow effect and generalized \(\beta (y)\) effect, \(J[a,b]=\frac{\partial a}{\partial x}\frac{\partial b}{\partial y}-\frac{\partial a}{\partial y}\frac{\partial b}{\partial x}\) is the Jacobi operator.

Introducing multiple scales

$$\begin{aligned} X=\varepsilon x,\quad Y=\varepsilon y,\quad T=\varepsilon ^{3}t, \end{aligned}$$
(7)

and perturbation expansions

$$\begin{aligned} {\varPsi }'=\varPsi _0 +\varepsilon \varPsi _1 +\varepsilon ^{2}\varPsi _2 +\cdots . \end{aligned}$$
(8)

Substituting Eqs. (7) and (8) into Eqs. (5) and (6) yields

$$\begin{aligned}&O(\varepsilon )\left\{ \begin{array}{l} \left( \bar{u} - {c_0}\right) \frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _0}}}{{\partial {y^2}}}\right) + p(y)\frac{{\partial {\varPsi _0}}}{{\partial X}} = 0\\ \frac{{\partial {\varPsi _0}}}{{\partial X}} = 0,\quad \qquad y = 0,1 \end{array} \right. . \end{aligned}$$
(9)
$$\begin{aligned}&O({\varepsilon ^2})\left\{ \begin{array}{l} (\bar{u} - {c_0})\frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _1}}}{{\partial {y^2}}}\right) + p(y)\frac{{\partial {\varPsi _1}}}{{\partial X}}\\ = - 2(\bar{u} - {c_0})\frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _0}}}{{\partial y\partial Y}}\right) \\ \frac{{\partial {\varPsi _1}}}{{\partial X}} = 0,\quad \qquad y = 0,1 \end{array} \right. . \end{aligned}$$
(10)
$$\begin{aligned}&O({\varepsilon ^3})\quad \left\{ \begin{array}{l} (\bar{u} - {c_0})\frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _2}}}{{\partial {y^2}}}\right) + p(y)\frac{{\partial {\varPsi _2}}}{{\partial X}}\\ = - \frac{\partial }{{\partial T}}\left( \frac{{{\partial ^2}{\varPsi _0}}}{{\partial {y^2}}}\right) - (\bar{u} - {c_0})\frac{\partial }{{\partial X}}{\nabla ^2}{\varPsi _0}\\ - 2(\bar{u} - {c_0})\frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _1}}}{{\partial y\partial Y}}\right) \quad - \frac{{\partial {\varPsi _0}}}{{\partial X}}\frac{\partial }{{\partial y}}\left( \frac{{{\partial ^2}{\varPsi _0}}}{{\partial {y^2}}}\right) \\ - \frac{{d{{h'}_1}(t)}}{{\hbox {d}T}} + \frac{{\partial {\varPsi _0}}}{{\partial y}}\frac{\partial }{{\partial X}}\left( \frac{{{\partial ^2}{\varPsi _0}}}{{\partial {y^2}}}\right) \\ - \frac{{\partial {\varPsi _0}}}{{\partial X}}\frac{{\hbox {d}h'}}{{\hbox {d}y}} - {\mu _0}\frac{{{\partial ^2}{\varPsi _0}}}{{\partial {y^2}}}\\ \frac{{\partial {\varPsi _2}}}{{\partial X}} = 0,\quad \qquad y = 0,1 \end{array} \right. . \end{aligned}$$
(11)

2.3 Derivation of fZK equation

Assuming a separable formal solution of Eq. (9) is

$$\begin{aligned} \varPsi _0 =A(X,Y,T)\varphi _0 (y). \end{aligned}$$
(12)

Substituting (12) into Eq. (9) yields

$$\begin{aligned} \left\{ {\begin{array}{l} (\bar{{u}}-c_0){\varphi }''_0 (y)+p(y)\varphi _0 (y)=0 \\ \varphi _0 (0)=\varphi _0 (1)=0 \\ \end{array}} \right. . \end{aligned}$$
(13)

When \(\bar{{u}}-c_0 \ne 0\), it becomes

$$\begin{aligned} \left\{ {\begin{array}{l} {\varphi }''_0 (y)+\frac{p(y)}{(\bar{{u}}-c_0)}\varphi _0 (y)=0 \\ \varphi _0 (0)=\varphi _0 (1)=0 \\ \end{array}} \right. . \end{aligned}$$
(14)

Equation (14) is the well-known Rayleigh–Kuo equation, which determines the meridional structure of the waves. We need to solve higher-order equations to determine the evolution of amplitude A(X, Y, T) with time and space.

Assuming a separable solution of Eq. (10) is

$$\begin{aligned} \varPsi _1 =B(X,Y,T)\varphi _1 (y). \end{aligned}$$
(15)

Substituting (15) into Eq. (10) yields

$$\begin{aligned}&\frac{\partial B}{\partial X}{\varphi }''_1 (y)+\frac{p(y)}{\bar{{u}}-c_0 }\varphi _1 (y)\frac{\partial B}{\partial X} \nonumber \\&\quad =-2\frac{\partial ^{2}A}{\partial X\partial Y}{\varphi }'_0 (y). \end{aligned}$$
(16)

Without loss of generality, we set

$$\begin{aligned} \frac{\partial B}{\partial X}=\frac{\partial ^{2}A}{\partial X\partial Y}. \end{aligned}$$
(17)

Equation (16) becomes into the following

$$\begin{aligned} \left\{ {\begin{array}{l} {\varphi }''_1 (y)+\frac{p(y)}{(\bar{{u}}-c_0)}\varphi _1 (y)=-2{\varphi }'_0 (y) \\ \varphi _1 (0)=\varphi _1 (1)=0. \\ \end{array}} \right. \end{aligned}$$
(18)

Equation (18) does not determine the structure of A(X, Y, T) neither. Substituting (12) and (15) into Eq. (11) and using (14) and (18) yield

$$\begin{aligned} \left( \bar{{u}}-c_0\right) \frac{\partial }{\partial X}\left( \frac{\partial ^{2}\varPsi _2 }{\partial y^{2}}\right) +p(y)\frac{\partial \varPsi _2 }{\partial X}=F. \end{aligned}$$
(19)

where

$$\begin{aligned} F= & {} -\frac{\partial A}{\partial T}\left( \frac{\partial ^{2}\varphi _0 }{\partial y^{2}}\right) -(\bar{{u}}-c_0)\varphi _0 (y)\frac{\partial ^{3}A}{\partial X^{3}}\nonumber \\&-(\bar{{u}}-c_0)\left[ \varphi _0 (y)+2{\varphi }'_1 (y)\right] \frac{\partial ^{3}A}{\partial X\partial Y^{2}} \nonumber \\&-A\frac{\partial A}{\partial X}\left[ \varphi _0 (y){\varphi }'''_0 (y)-{\varphi }'_0 (y){\varphi }''_0 (y)\right] \nonumber \\&-\frac{\partial A}{\partial X}\frac{\hbox {d}{h}'}{\hbox {d}y}\varphi _0 (y)-\mu _0 A{\varphi }''_0 (y)-\frac{\hbox {d}{h}'_1 }{\hbox {d}T}. \end{aligned}$$
(20)

The homogeneous part of Eq. (19) is the same as Eq. (9), and non-singular condition must be satisfied in order to obtain a regular solution of Eq. (19) as follows

$$\begin{aligned} \int \limits _0^1 {\frac{\varphi _0 (y)}{\bar{{u}}-c_0 }F\hbox {d}y} =0. \end{aligned}$$
(21)

Substituting (20) into Eq. (21) yields

$$\begin{aligned}&\frac{\partial A}{\partial T}+a_1 A\frac{\partial A}{\partial X}+a_2 \frac{\partial A}{\partial X}+a_3 \frac{\partial ^{3}A}{\partial X^{3}} \nonumber \\&\quad +a_4 \frac{\partial ^{3}A}{\partial X\partial Y^{2}}+\mu _0 A=a_6 \frac{\hbox {d}{h}'_1 }{\hbox {d}T} , \end{aligned}$$
(22)

where the coefficients are

$$\begin{aligned} a_1= & {} {I_1 }/I,\quad a_2 ={I_2 }/I,\quad a_3 ={I_3 }/I,\quad a_4 ={I_4 }/I,\\ a_6= & {} {I_6 }/I \quad \hbox {and}\\ I= & {} \int \limits _0^1 {\frac{p(y)}{(\bar{{u}}-c_0)^{2}}\varphi _0^2 (y)\hbox {d}y} ,\\ I_1= & {} \int \limits _0^1 {\left( \frac{p(y)}{\bar{{u}}-c_0 }\right) {'}\frac{\varphi _0^3 (y)}{\bar{{u}}-c_0 }\hbox {d}y} ,\\ I_2= & {} -\int \limits _0^1 {\frac{\varphi _0^2 (y)}{\bar{{u}}-c_0 }\frac{\hbox {d}{h}'}{\hbox {d}y}\hbox {d}y} ,\\ I_3= & {} -\int \limits _0^1 {\varphi _0^2 \hbox {d}y} ,\\ I_4= & {} -\int \limits _0^1 {\left[ 2\varphi _0 (y){\varphi }'_1 (y)+\varphi _0^2 (y)\right] \hbox {d}y} ,\\ I_6= & {} \int \limits _0^1 {\frac{\varphi _0 (y)}{(\bar{{u}}-c_0)}\hbox {d}y} ,\quad \hbox {respectively}. \end{aligned}$$

Equation (22) is a \((2+1)\)-dimensional generalized fZK equation. Term with coefficient \(a_1\) indicates that both the generalized \(\beta (y)\) and the shear basic flow are essential in inducing the nonlinear Rossby waves. It is noted that the variation of \(\beta (y)\) can still induce nonlinear Rossby solitary waves even if without shear basic flow. Term with coefficient \(a_2\) represents the basic topography effect, and it is a phase shift factor, which is consistent with some previous investigations. \(\mu _0\) represents dissipation. The right-hand side term represents slowly varying topography effect, and it is a external forced factor, which is an important factor with respect to the evolution of Rossby solitary waves in a long time aspect. In addition, Eq. (22) reduces to the case by Yang et al. [22] when generalized beta effect and topography are absent. When \(\mu _0 =0\), it reduces to the traditional ZK equation by Gottwald [21]. So, in conclusion, Eq. (22) we obtained at present is a generalization of some previous studies, which can simulate more physical mechanism for the evolution of nonlinear Rossby solitary waves.

3 Analytical solutions

3.1 Solution of generalized ZK equation by elliptic function expansion method

In what follows, the dissipation and slowly varying topography are both absent. The elliptic function expansion method is used to solve the generalized ZK equation with only basic topography. Equation (22) becomes into the following form:

$$\begin{aligned} \frac{\partial A}{\partial T}+a_1 A\frac{\partial A}{\partial X}+a_2 \frac{\partial A}{\partial X}+a_3 \frac{\partial ^{3}A}{\partial X^{3}}+a_4 \frac{\partial ^{3}A}{\partial X\partial Y^{2}}=0. \end{aligned}$$
(23)

Doing transformation \(\xi =kX+lY-\omega T\) yields

$$\begin{aligned} \left( a_2 -\frac{\omega }{k}\right) \frac{\hbox {d}A}{\hbox {d}\xi }+a_1 A\frac{\hbox {d}A}{\hbox {d}\xi }+\left( a_3 k^{2}+a_4 l^{2}\right) \frac{\hbox {d}^{3}A}{\hbox {d}\xi ^{3}}=0. \end{aligned}$$
(24)

Assuming the formal solution of Eq. (24) to be

$$\begin{aligned} A(\xi )=\sum _{k=0}^n b_{k} {sn^{k}\xi } , \end{aligned}$$
(25)

according to the balance between nonlinearity and dispersion, it is

$$\begin{aligned} 2n+1=n+3, \end{aligned}$$
(26)

therefore

$$\begin{aligned} A(\xi )=b_0 +b_1 sn\xi +b_2 sn^{2}\xi . \end{aligned}$$
(27)

Substituting (27) into Eq. (24) yields the solution according to the principles of elliptic function expansion method

$$\begin{aligned} A= & {} \frac{8\left( 1+m^{2}\right) \left( a_3 k^{2}+a_4 l^{2}\right) +\omega /k-a_2 }{a_1 } \nonumber \\&-\frac{12m^{2}\left( a_3 k^{2}+a_4 l^{2}\right) }{a_1 }sn^{2}\left( kX+lY-\omega T\right) .\nonumber \\ \end{aligned}$$
(28)

When \(m\rightarrow 1\), the solitary wave solution is

$$\begin{aligned}&A(X,Y,T)=\frac{\omega /k-a_2 -4(a_3 k^{2}+a_4 l^{2})}{a_1 } \nonumber \\&\quad +\frac{12(a_3 k^{2}+a_4 l^{2})}{a_1 }\sec h^{2}(kX+lY-\omega T). \end{aligned}$$
(29)

Especially when \(\omega /k-a_2 -4(a_3 k^{2}+a_4 l^{2})=0\) satisfies, which is just the linear dispersion relation for Eq. (23), the solitary wave becomes into

$$\begin{aligned}&A(X,Y,T) = \frac{{12\left( {a_3}{k^2} + {a_4}{l^2}\right) }}{{{a_1}}}\hbox {sech}^2\left[ kX + lY\right. \nonumber \\&\left. \quad - \left( 4{a_3}{k^3} + 4{a_4}k{l^2} + {a_2}\right) T\right] . \end{aligned}$$
(30)

From (30), phase shifting effect of basic topography and inducing effect of generalized \(\beta (y)\) on the nonlinear Rossby solitary waves are evident.

3.2 Solution of generalized fZK equation by reduced differential transform method

It is noted that the elliptic function expansion method can solve the specific nonlinear equations with only odd derivatives or even derivatives, and it is not so suitable for the obtained generalized fZK equation in the present paper. We will use the efficient reduced differential transform method in the following procedures to solve Eq. (22) [36]

$$\begin{aligned}&\frac{\partial A}{\partial T}+a_1 A\frac{\partial A}{\partial X}+a_2 \frac{\partial A}{\partial X}+a_3 \frac{\partial ^{3}A}{\partial X^{3}} \nonumber \\&\quad +a_4 \frac{\partial ^{3}A}{\partial X\partial Y^{2}}+\mu _0 A=a_6 \frac{\hbox {d}{h}'_1 }{\hbox {d}T}. \end{aligned}$$
(31)

Assume

$$\begin{aligned} A=\sum _{k=0}^\infty {A_k (X,Y)T^{k}} , \end{aligned}$$
(32)
Fig. 1
figure 1

Evolution of amplitude A at different time for \(\mu _0 =5,\gamma =0.5,X=Y\). The horizontal coordinate represents the spatial variable with \(X=Y\), and the vertical coordinate represents the amplitude. a \(T=0\); b \(T=0.5\); c \(T=1\)

Full size image

and

$$\begin{aligned} {h}'_1 (T)=\sin \gamma T=\sum _{k=0}^\infty {{h}'_{1,k} T^{k}}. \end{aligned}$$
(33)

The following iterations are obtained according to the method,

$$\begin{aligned}&A_{k+1} =-\frac{1}{k+1}\left[ a_2 \frac{\partial A_k }{\partial X}+a_3 \frac{\partial ^{3}A_k }{\partial X^{3}} \right. \nonumber \\&\quad +a_4 \frac{\partial ^{3}A_k }{\partial X\partial Y^{2}}+a_1 \sum _{r=0}^k {A_r \frac{\partial A_{k-r} }{\partial X}} \nonumber \\&\quad +\left. \mu _0 A_k \right] +a_6 {h}'_{1,k+1}. \end{aligned}$$
(34)

The initial condition is assumed to be \(A_0 (X,Y)=\sec h^{2}(X+Y)\); consecutive terms can be obtained as follows according to (34) by using Mathematica software

$$\begin{aligned} A_1= & {} \gamma a_6 -\mu _0 \hbox {Sech}[X+Y]^{2}\nonumber \\&+\,2a_1 \hbox {Sech}[X+Y]^{4}\hbox {Tanh}[X+Y]\nonumber \\&+\,2a_2 \hbox {Sech}[X+Y]^{2}\hbox {Tanh}[X+Y] \nonumber \\&-\,a_3 \left( 16\hbox {Sech}[X+Y]^{4}\hbox {Tanh}[X+Y]\right. \nonumber \\&-\left. \,8\hbox {Sech}[X+Y]^{2}\hbox {Tanh}[X+Y]^{3}\right) \nonumber \\&-\,a_4 \left( 12\hbox {Sech}[X+Y]^{4}\hbox {Tanh}[X+Y] \right. \nonumber \\&\left. -\,2\hbox {Tanh}[X+Y](-2\hbox {Sech}[X+Y]^{4}\right. \nonumber \\&\left. +\,4\hbox {Sech}[X+Y]^{2}\hbox {Tanh}[X+Y]^{2})\right) . \end{aligned}$$
(35)
$$\begin{aligned} A_2= & {} (-4+3\hbox {cosh}[2(x+y)])\hbox {sech}[x+y]^{8}a_1^2 \nonumber \\&+\,(-2+\hbox {cosh}[2(x+y)])\hbox {sech}[x+y]^{4}a_2^2 \nonumber \\&-\,272\hbox {sech}[x+y]^{8}a_3 a_4 -136\hbox {sech}[x+y]^{8}a_4^2 \nonumber \\&-\,\frac{1}{2}\gamma a_6 \mu _0 +\frac{1}{2}\hbox {sech}[x+y]^{2}\mu _0^2 \nonumber \\&-\,136\hbox {sech}[x+y]^{8}a_3^2 \nonumber \\&-\,2\hbox {sech}[x+y]^{6}a_2 ((-33+26\hbox {cosh}[2(x+y)]\nonumber \\&-\,\hbox {cosh}[4(x+y)])a_3 +(-33+26\hbox {cosh}[2(x+y)] \nonumber \\&-\,\hbox {cosh}[4(x+y)])a_4 +\hbox {cosh}[x+y]^{3}\hbox {sinh}[x+y]\mu _0 )\nonumber \\&+\,16\hbox {sech}[x+y]^{4}a_3 \mu _0 \hbox {tanh}[x+y] \nonumber \\&+\,16\hbox {sech}[x+y]^{4}a_4 \mu _0 \hbox {tanh}[x+y]\nonumber \\&+\,1440\hbox {sech}[x+y]^{6}a_3^2 \hbox {tanh}[x+y]^{2} \nonumber \\&+\,2880\hbox {sech}[x+y]^{6}a_3 a_4 \hbox {tanh}[x+y]^{2}\nonumber \\&+\,1440\hbox {sech}[x+y]^{6}a_4^2 \hbox {tanh}[x+y]^{2}\nonumber \\&-\,8\hbox {sech}[x+y]^{2}a_3 \mu _0 \hbox {tanh}[x+y]^{3} \nonumber \\&-\,8\hbox {sech}[x+y]^{2}a_4 \mu _0 \hbox {tanh}[x+y]^{3}\nonumber \\&-\,912\hbox {sech}[x+y]^{4}a_3^2 \hbox {tanh}[x+y]^{4}\nonumber \\&-\,1824\hbox {sech}[x+y]^{4}a_3 a_4 \hbox {tanh}[x+y]^{4}\nonumber \\&-\,912\hbox {sech}[x+y]^{4}a_4^2 \hbox {tanh}[x+y]^{4}\nonumber \\&+\,32\hbox {sech}[x+y]^{2}a_3^2 \hbox {tanh}[x+y]^{6}\nonumber \\&+\,64\hbox {sech}[x+y]^{2}a_3 a_4 \hbox {tanh}[x+y]^{6} \nonumber \\&+\,32\hbox {sech}[x+y]^{2}a_4^2 \hbox {tanh}[x+y]^{6}\nonumber \\&+\,a_1 (2(-3+2\hbox {cosh}[2(x+y)])\hbox {sech}[x+y]^{6}a_2 \nonumber \\&+\,2(74-68\hbox {cosh}[2(x+y)] \nonumber \\&+\,5\hbox {cosh}[4(x+y)])\hbox {sech}[x+y]^{8}a_3 \nonumber \\&+\,22\hbox {sech}[x+y]^{8}a_4 +\gamma \hbox {sech}[x+y]^{2}a_6 \hbox {tanh}[x+y] \nonumber \\&-\,3\hbox {sech}[x+y]^{4}\mu _0 \hbox {tanh}[x+y]\nonumber \\&-\,192\hbox {sech}[x+y]^{6}a_4 \hbox {tanh}[x+y]^{2}+22\hbox {sech}[x+y]^{8}a_4 \nonumber \\&+\,\gamma \hbox {sech}[x+y]^{2}a_6 \hbox {tanh}[x+y]\nonumber \\&-\,3\hbox {sech}[x+y]^{4}\mu _0 \hbox {tanh}[x+y]\nonumber \\&+\,80\hbox {sech}[x+y]^{4}a_4 \hbox {tanh}[x+y]^{4}). \end{aligned}$$
(36)

By taking first three terms, solution of Eq. (31) can be written as

$$\begin{aligned} A=A_0 (X,Y)+A_1 (X,Y)T+A_2 (X,Y)T^{2}. \end{aligned}$$
(37)

This is an analytical solution for the generalized fZK equation, the dissipation and slowly varying topography from (35), (36) and (37) are obviously found. Of course, (37) is complex; it is necessary for us to consider such a problem through graphical representations in order to understand the importance from dissipation and slowly varying topography.

Fig. 2
figure 2

Evolution of amplitude A at different time for \(\mu _0 =0.5,\gamma =0.5,X=Y\). The horizontal coordinate represents the spatial variable with \(X=Y\), and the vertical coordinate represents the amplitude. a \(T=0\); b \(T=0.5\); c \(T=10\)

Full size image
Fig. 3
figure 3

the evolution of amplitude A at different time for \(\mu _0 =0.5,\gamma =5,X=Y\). The horizontal coordinate represents the spatial variable with \(X=Y\) and the vertical coordinate represents the amplitude. a \(T=0.5\); b \(T=10\)

Full size image

4 Discussion

In what follows, we will simply set the coefficients be \(a_1 =1,a_2 =1,a_3 =1,a_4 =1,a_6 =1\) in order to study the dissipation and topography on the \((2+1)\)-dimensional nonlinear solitary Rossby waves by graphical representation for the above analytical solutions. we will use special two-dimensional cases to present the results.

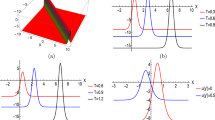
In Figs. 1 and 2, we have plotted the evolution of solitary Rossby wave amplitude for different dissipation parameters. It can be seen the slip effect from dissipation; large dissipation induces much more evident slip effect.

In Figs. 2 and 3, we have characterized the effect from slowly varying topography, and it can be seen that the forcing effect from variation of topography can enhance the evolution of amplitude.

5 Conclusions

We have successfully derived a generalized fZK equation in describing the \((2+1)\)-dimensional nonlinear Rossby solitary waves with generalized beta, topography and dissipation. We specially considered the effect from slowly varying topography. We found that the basic topographical effect is an essential factor in influencing the frequency of the Rossby waves. The effect from slowly varying topography with time is an external forcing factor on impacting the evolution of solitary Rossby waves, and it can enhance the variations of amplitude. And the generalized beta contributes to the induction of nonlinear Rossby solitary waves. Moreover, we obtained analytical periodic and solitary waves for the ZK equation based on the elliptic function expansion method, but the method fails to the fZK equation. The reduced differential transform method is applicable to the fZK equation fortunately. The results demonstrated that both topography and dissipation are important factors for the evolution of higher-dimensional nonlinear Rossby solitary waves.