Keywords

1 Introduction

Geophysical Fluid Mechanics (GFM) is mainly on the study of fluid flows while the rotation effect of planets could not be neglected, such as the atmosphere or ocean in the earth. Among many kinds of wave motions in GFM, the Rossby wave describes the long-term propagations, such as weather or climate phenomena in atmospheres, wave guide in oceans [1]. The durations of such phenomena are usually about 10 days or longer. One distinctive fact is that they can maintain stable, persistent, and large solitary kind waves, such as the Jupiter’s Great Red Spot, the North Atlantic Oscillation (NAO), and the atmospheric blocking [2]. The evolution of Rossby solitary wave is affected by multiple physical factors, such as the bottom topography, the basic flow, the stratification of atmosphere or ocean, and the external heat or dissipation. Such fascinating features enable scholars to explain the physical mechanisms of some extreme weather activities. Historically, several types of nonlinear partial differential equations were derived to disclose the physical mechanisms of Rossby solitary waves. In 1895, Korteweg and de Vries [3] initiated the well-known Korteweg-de Vries (KdV) model equation

$$\begin{aligned} A_t+\alpha A_x+\beta A_{xxx}+\gamma AA_x=0 \end{aligned}$$
(1)

to describe the evolution of nonlinear shallow water waves, where t, x represents the temporal and spatial variable, respectively, and the subscripts denote the partial derivatives to the corresponding variables. It was first derived by Long [4] in 1964 to simulate the evolution of nonlinear Rossby solitary wave amplitude under the \(\beta \)-plane approximation. In 1966, Benny further investigated the Rossby solitary waves according to the KdV model equation [5]. The corresponding results present the relationship between the wave velocity and the wave amplitude, which generalized the results of Long [4]. Later, the modified Korteweg-de Vries (mKdV) [6,7,8]

$$\begin{aligned} A_t+\alpha A_x+\beta A_{xxx}+\gamma A^2A_x=0 \end{aligned}$$
(2)

was obtained to present a stronger nonlinearity of mKdV than that of KdV. Besides, Body [9, 10] obtained the KdV and mKdV model equations by directly using methods of reductive perturbations based on the primitive model equations. Later, other kinds of evolution equations were given to describe the nonlinear Rossby solitary waves, such as KdV-Burgers equation [11], and so on . Interestingly, Ono [12, 13] used an integra-differential model equation, named as Benjamin-Davis-Ono (BDO) equation to simulate the propagation of nonlinear Rossby waves, which declares the existence of algebraic solitary waves in GFM. The BDO equation is

$$\begin{aligned} A_t+\alpha A_x+\beta AA_x+\gamma \frac{\partial ^2\,H(A)}{\partial x^2}=0, \end{aligned}$$
(3)

where \(H(A(x,t))=\frac{1}{\pi }\mathrm {P}\int _{-\infty }^{+\infty }\frac{A(x^\prime , t)}{x-x^\prime }\mathrm {d}x^\prime \) is the Hilbert transformation of A(x, t), and \(\mathrm {P}\) represents the Cauchy Principal Integral. The Boussinesq model equation

$$\begin{aligned} A_{tt}+\alpha A_{xx}+\beta A_{xxxx}+\gamma AA_x=0 \end{aligned}$$
(4)

was obtained to simulate the evolution of nonlinear Rossby solitary waves. It should be denoted that the Boussinesq model equation represents that the wave propagates in two directions while other models yield only one-direction evolutions. With the development in this field, more and more complex and fascinating evolution equations were derived by scholars to reveal the dynamics of nonlinear Rossby waves. For example, Yang and the cooperators have done much progress on the study of Rossby solitary waves in deep rotational fluids [14,15,16,17,18,19]. Most investigations declare that the meridional shear basic flow and the bottom topography have great influence on the excitation, the evolution, and disappearance of Rossby solitary waves. In recent past years, Hoddys et al. [20,21,22,23] considered the effect of zonally varying basic flow on the dynamics of nonlinear Rossby solitary waves. The KdV equation and Boussinesq equation with variable coefficients were derived to simulate the Rossby solitary wave amplitude. The results yield that the zonally varying background flow has obvious influence on both the wave phase speed and the amplitude. Special attention should be paid on the development of Rossby wave packet theory. Luo et al. [24,25,26,27] begun to use the efficient nonlinear Schr\(\ddot{\texttt {o}}\)dinger model equation (NLS)

$$\begin{aligned} iA_{t}+\alpha A_{xx}+|A|^2A_x=0, \end{aligned}$$
(5)

since the 1980s, where i is the square root of \(-1\). They used the NLS model equation to characterize the evolution of kinds of extreme weather event, such as the NAO, all their abovementioned results depict that it is appropriate for the adoption of NLS model equation in simulating the propagation of nonlinear Rossby solitary waves. Much more related work has been done in the recent years [28,29,30,31,32,33,34,35,36].

On the other hand, for most previous studies, such as [20], the “Traditional Approximation” (TA), which neglects the horizontal component of the Coriolis parameter \(f_H=2\varOmega \cos \varphi \), was accepted by most investigators like Eckart [37], and so on, where \(\varOmega \) is the angular velocity of the earth rotation, and \(\varphi \) is the latitude. By now, large amounts of work have been finished on such approximation. Existed theoretical and numerical results have shown that the TA is quite successful in the investigation and understanding for large-scale atmospheric or oceanic motions. However, it is necessary to consider the qualitative dynamics of nonlinear waves with complete Coriolis parameters of both vertical and horizontal components, \(f=2\varOmega \sin \varphi \) and \(f_H=2\varOmega \cos \varphi \), respectively. It is called the “Non-Traditional Approximation” (NTA) [38,39,40,41]. Especially for the case of the equatorial atmospheres or oceans, the horizontal component of the Coriolis parameter is more important compared to the vertical one in this area. Thus, it is essential to study the tropical motions under NTA, such as the instability, the dispersion, and the Madden-Julian Oscillation (MJO). For the study of complete Coriolis parameters, Beckman denoted that the horizontal Coriolis parameter has advantages than both the vertical one and the nonlinearity [42]. Gerkema and Shiria [43, 44], White and Bromley [45] announced that the horizontal Coriolis parameter should not be omitted as it is one of the main factors inducing the equatorial near-inertial waves. Hayashi [46] further denoted that the horizontal Coriolis parameter affects the vertical vorticity, the pressure, the potential temperature, and the density of the equatorial atmosphere under the NTA. Yasuda and Sato [47] presented the influence of complete Coriolis force on the linear near-inertial waves. Kasahara and Gary [48,49,50] gave the numerical solution of the linearized model under the complete Coriolis force. Davies et al. [51] obtained the numerical solution for a general compressible fluids, which has great application for the weather prediction and climate changes. Reznik discussed linearized wave dynamics and the geostrophic problems under the non-traditional approximation [52,53,54,55]. Itano [56], Tort et al. [57] investigated the inertial instability of the zonally symmetric flow under the f-plane approximation of NTA. It discloses that the NTA would enhance the inertial instability. Mass and Harlander studied the equatorial wave attractor and inertial oscillation under the complete Coriolis force [58] and some other results [59,60,61]. Last but not most, the variational approach was also popular for the scholars to study the nonlinear Rossby waves in the past decades [62, 63]. It is worthy of mentioning the fact that Dellar and Salmon [64] obtained a similar conserved potential vorticity equation under NTA just as the classical potential vorticity conserved equation under TA.

However, there is only one spatial variable in abovementioned equations. Actually, the real evolution of nonlinear Rossby solitary waves depends on not only one spatial direction. Therefore, it is quite necessary to generalize the evolution of Rossby waves with respect to higher dimensional cases. In the context of some physical fields, such as plasma physics, ion-acoustic waves, and shallow water waves, some researchers generalized the KdV equation and the mKdV equation in higher dimensional cases. It is well known that the Kadomtsev-Petviashvili (KP) and Zakharov-Kuznetsov (ZK) equations are in two spatial and one temporal coordinates. Kadomtsev and Petviashvili [65] first proposed the KP equation in their study of the evolution of long ion-acoustic waves of small amplitude propagation in plasma. Hereafter, Infeld et al. [66] and Groves et al. [67] investigated the extended KP equation with respect to 2-D shallow water waves and ion-acoustic waves in plasma, respectively. The Zakharov-Kuznetsov equation [68, 69], which is a higher dimensional generalization of the KdV equation, was derived in the area of plasma. Different from the KP equation, Ablowitz et al. [70] proved that the ZK equation is not integrable by the inverse scattering method. In the research of the Rossby waves in GFM, Gottwalld [71] first derived the ZK equation for the evolution of nonlinear Rossby waves from the quasi-geostrophic potential vorticity equation. In recent years, Zhang et al. [72,73,74,75] presented the physical mechanisms of nonlinear Rossby waves by using the ZK model equation, and manifested the existed results a lot. Fu et al. [76] and Guo et al. [77] further derived some kind of fractional ZK model equations to simulate the evolution of nonlinear Rossby solitary waves in stratified fluids. The above studies showed that ZK equation and generalized ZK equation are appropriate model equations in the simulation of the evolution of nonlinear Rossby waves.

Additionally, it is important to construct analytical solutions for the nonlinear partial differential equation (NPDE). In the construction of the solutions to the NPDE, many direct methods have been developed, such as the inverse scattering method [70], the sine-cosine algorithm [78], the Hirota bilinear method [79,80,81], the efficient first integral method by Feng [82], the modified trigonometric function series method [83], The tanh method [84], the homotopy analysis method [85], the homogeneous balance method [86], the multiple exp-function [87], the modified \((G^\prime /G)\)-expansion method [88], and so on [89,90,91,92]. In the present paper, choosing the appropriate method is also necessary for us to obtain the analytical solutions to the new mZK equation. Furthermore, numerical solutions are essential for the investigations of kinds of fluid phenomena. For example, Zeidan et al. [93,94,95], Goncalves et al. [96] studied porous media mixtures containing nanofluids using a hyperbolic conservative two-phase flow model. Goncalves et al. [97, 98] also numerically studied the interaction between a plane incident shock wave and a cylindrical bubble.

To the best of our knowledge, there are not many reports about the generalized formal equation of the ZK in the study of nonlinear Rossby waves yet. It is essential for us to investigate such problems. Now, we will consider a new modified ZK (nmZK) equation for nonlinear Rossby waves. In Sect. 2, we are interested in the derivation of the nmZK equation for nonlinear Rossby waves from the barotropic quasi-geostrophic equation. In Sect. 3, the solitary wave solutions of the nmZK equation are obtained by using weak nonlinear perturbation and efficient reduced differential transform methods. Through numerical calculation, the influence of all kinds of physical parameters on the Rossby wave amplitude is given. In Sect. 4, the conservation laws under the influence of dissipation and slowly varying topography are obtained. Also, the dynamical analysis without considering the slowly varying topography and dissipation is given. Finally, some conclusions and further discussions are presented in Sect. 5.

2 Nonlinear Equatorial Wave Model

2.1 Basic Mathematical Model

In this work, we will go on investigating the nonlinear equatorial waves based on the conserved potential vorticity equation under the NTA [64]

$$\begin{aligned} \bigg (\frac{\partial }{\partial t}+\frac{\partial \varPsi }{\partial x}\frac{\partial }{\partial y}-\frac{\partial \varPsi }{\partial y}\frac{\partial }{\partial x}\bigg )\bigg (\nabla ^{2}\varPsi +f-f_H\frac{\partial B}{\partial y}\bigg )=-\mu \nabla ^{2}\varPsi +Q, \end{aligned}$$
(6)

with boundary conditions

$$\begin{aligned} \frac{\partial \varPsi }{\partial x}\bigg |_{y=0}=\frac{\partial \varPsi }{\partial x}\bigg |_{y=1}=0, \end{aligned}$$
(7)

where \(\varPsi \) is the total stream function, B(x, y) is the topography, \(\mu \) is the turbulent dissipation parameter, Q is the potential vorticity forcing, and \(\nabla \) is the two-dimensional Laplace operator.

In our contribution, we mainly consider the motions of tropical atmospheres. It is obvious that the vertical Coriolis parameter f is weak compared to the horizontal one \(f_H\). Thus, throughout the whole work, the variation of vertical Coriolis parameter f is neglected. Next, introducing L, U to be the characteristics of spatial length and velocity, respectively, and H is the topography characteristic. We have the following non-dimensional equation:

$$\begin{aligned} \bigg (\frac{\partial }{\partial t}+\frac{\partial \varPsi }{\partial x}\frac{\partial }{\partial y}-\frac{\partial \varPsi }{\partial y}\frac{\partial }{\partial x}\bigg )\bigg (\nabla ^{2}\varPsi -\delta \frac{\partial B}{\partial y}\bigg )=-\mu \nabla ^{2}\varPsi +Q \end{aligned}$$
(8)

and the boundary conditions

$$\begin{aligned} \frac{\partial \varPsi }{\partial x}\bigg |_{y=0}=\frac{\partial \varPsi }{\partial x}\bigg |_{y=1}=0, \end{aligned}$$
(9)

where parameter \(\delta =\frac{H}{L}\) denotes the aspect ratio, and the corresponding term with \(\delta \) represents a combined effect of both topography and Coriolis parameter \(f_H\) on the waves.

In order to solve the nonlinear problems (8) and (9) , we assume that

$$\begin{aligned} \varPsi =\bar{\varPsi }(y)+\varPsi '(x,y,t), \end{aligned}$$
(10)

where \(\bar{\varPsi }(y)=-\int _0^y[\bar{u}(s)-c_0]\mathrm {d}s\) is the basic stream function and \(\varPsi ^\prime \) is the perturbed one, \(\bar{u}(y)\)is the shear background current, and \(c_0\) is the wave speed. To obtain the equation governing the amplitude modulation of the Rossby waves, we need to introduce the following slow time and space variables [74]

$$\begin{aligned} X=\varepsilon ^{\frac{1}{4}}x,~~~~~Y=\varepsilon ^{\frac{1}{4}}y,~~~~~T=\varepsilon ^{\frac{3}{4}}t, \end{aligned}$$
(11)

where \(0\le \varepsilon \ll 1\) is small for weak nonlinearity. We expand the perturbation stream function \(\varPsi ^\prime \) with the following form:

$$\begin{aligned} \varPsi '=\varepsilon ^{\frac{1}{4}}\varPsi _1+\varepsilon ^{\frac{1}{2}}\varPsi _2+\varepsilon ^{\frac{3}{4}}\varPsi _3+\cdots . \end{aligned}$$
(12)

It is appropriate to believe that the topography is varying strongly along with the south-north directions but weakly in the east-west directions. Thus, we assume

$$\begin{aligned} B(X,y,Y)=B_0(y)+\varepsilon ^{\frac{1}{4}}B_1(X,Y). \end{aligned}$$
(13)

The topography is in multiple scales, and it is different from most previous studies [18, 99], which considered only basic or slowly varying topography separately. The potential vorticity forcing is believed to balance the dissipation caused by the background shear current [100].

Substituting Eqs.(8)–(11) into Eq.(7) leads to all order perturbation equations about \(\varepsilon \):

$$\begin{aligned} O(\varepsilon ^{\frac{1}{2}}): {\left\{ \begin{array}{ll} (\bar{u}-c_0)\frac{\partial }{\partial X}\big (\frac{\partial ^{2}\varPsi _1}{\partial y^{2}}\big )+p(y)\frac{\partial \varPsi _1}{\partial X}=0\\ \frac{\partial \varPsi _1}{\partial X}=0,~~~~y=0,1, \end{array}\right. } \end{aligned}$$
(14)
$$\begin{aligned} O(\varepsilon ^{\frac{3}{4}}): {\left\{ \begin{array}{ll} (\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _2}{\partial y^{2}})+p(y)\frac{\partial \varPsi _2}{\partial X}=-2(\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y\partial Y}) \\ -\frac{\partial \varPsi _1}{\partial X}\frac{\partial }{\partial y}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})+\frac{\partial \varPsi _1}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})\\ \frac{\partial \varPsi _2}{\partial X}=0,~~~~y=0,1, \end{array}\right. } \end{aligned}$$
(15)
$$\begin{aligned} O(\varepsilon ): {\left\{ \begin{array}{ll} (\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _3}{\partial y^{2}})+p(y)\frac{\partial \varPsi _3}{\partial X}=-\frac{\partial }{\partial T}\frac{\partial ^{2}\varPsi _1}{\partial y^{2}}-(\bar{u}-c_0)\frac{\partial }{\partial X}\nabla ^{2}\varPsi _1 \\ -2(\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _2}{\partial y\partial Y})-3\frac{\partial \varPsi _1}{\partial X}\frac{\partial ^{3}\varPsi _1}{\partial y^{2}\partial Y}-\frac{\partial \varPsi _1}{\partial X}\frac{\partial ^{3}\varPsi _2}{\partial y^{3}} -\frac{\partial \varPsi _2}{\partial X}\frac{\partial ^{3}\varPsi _1}{\partial y^{3}} \\ +2\frac{\partial \varPsi _1}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y\partial Y})+\frac{\partial \varPsi _1}{\partial Y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})+\frac{\partial \varPsi _1}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _2}{\partial y^{2}})+ \\ \frac{\partial \varPsi _2}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})+\delta \frac{\partial \varPsi _1}{\partial y}\frac{\partial ^{2}B_1}{\partial X\partial Y}-\mu _0\frac{\partial ^{2}\varPsi _1}{\partial y^{2}} \\ \frac{\partial \varPsi _3}{\partial X}=0,~~~~y=0,1, \end{array}\right. } \end{aligned}$$
(16)

where \(p(y)=-[\delta B^{\prime \prime }_{0}(y)+\bar{u}^{\prime \prime }(y)]\) and \(\mu =\varepsilon ^{\frac{3}{4}}\mu _0\) are satisfied.

2.2 Model Derivation by Multiple-Scale Method

Assume that a formal solution of Eq. (14) is

$$\begin{aligned} \varPsi _1=A(X,Y,T)\varphi _1(y). \end{aligned}$$
(17)

When \(\bar{u}(y)-c_0\ne 0\) , that is, without critical layer effect [100], it follows from Eqs. (14) and (17) that

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_1(y)+q(y)\varphi _1(y)=0,\\ \varphi _1(0)=\varphi _1(1)=0. \end{array}\right. } \end{aligned}$$
(18)

Equation (18) is the well-known Rayleigh-Kuo equation. \(q(y)=\frac{p(y)}{\bar{u}(y)-c_0}\) is the potential function of the meridional structure equation and it states that the nonlinear topography and shear basic flow are necessary for the motions of the Rossby waves, which is consistent with the real case. Here, it is a new finding that both the Coriolis parameter \(f_H\) and nonlinear topography are important in inducing the evolution of nonlinear Rossby waves. However, Eq. (18) only determines the meridional structure of the waves. Thus, we need to solve higher order equations so as to know more about the spatial-temporal evolution of wave amplitude A(X, Y, T). Assume a formal solution of (15) to be

$$\begin{aligned} \varPsi _2=\varPsi _{21}+\varPsi _{22}, \end{aligned}$$
(19)

where

$$\begin{aligned} \varPsi _{21}=B_1(X,Y,T)\varphi _{21}(y),\varPsi _{22}=B_2(X,Y,T)\varphi _{22}(y). \end{aligned}$$
(20)

According to the method of separable variables, \(B_1,B_2,\varphi _{21},\varphi _{22}\) satisfy the following equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} (\bar{u}-c_0)\frac{\partial B_1}{\partial X}\varphi ''_{21}+p(y)\frac{\partial B_1}{\partial X}\varphi _{21}=-2(\bar{u}-c_0)\frac{\partial ^{2}A}{\partial X\partial Y}\varphi '_1, \\ (\bar{u}-c_0)\frac{\partial B_2}{\partial X}\varphi ''_{22}+p(y)\frac{\partial B_2}{\partial X}\varphi _{22}=A\frac{\partial A}{\partial X}(\frac{p(y)}{(\bar{u}-c_0)})'\varphi ^{2}_1. \end{array}\right. } \end{aligned}$$
(21)

Without loss of generality, we set

$$\begin{aligned} B_1=\frac{\partial A}{\partial Y},~~~B_2=\frac{A^{2}}{2}. \end{aligned}$$
(22)

Then the following equations are satisfied:

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{21}+q(y)\varphi _{21}=-2\varphi '_{1},\\ \varphi _{21}(0)=\varphi _{21}(1)=0. \end{array}\right. } \end{aligned}$$
(23)
$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{22}+q(y)\varphi _{22}=\frac{q'(y)}{\bar{u}-c_0}\varphi ^{2}_{1},\\ \varphi _{22}(0)=\varphi _{22}(1)=0. \end{array}\right. } \end{aligned}$$
(24)

Equations (23) and (24) cannot determine the structure of the amplitude A(X, Y, T). Substituting Eqs. (17) and (20) into Eq. (16) yields the following equation:

$$\begin{aligned} (\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _3}{\partial y^{2}})+p(y)\frac{\partial \varPsi _3}{\partial X}=F, \end{aligned}$$
(25)

where

$$\begin{aligned} F=&-\frac{\partial }{\partial T}\frac{\partial ^{2}\varPsi _1}{\partial y^{2}}-(\bar{u}-c_0)\frac{\partial }{\partial X}\nabla ^{2}\varPsi _1-2(\bar{u}-c_0)\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _2}{\partial y\partial Y})-3\frac{\partial \varPsi _1}{\partial X}\frac{\partial ^{3}\varPsi _1}{\partial y^{2}\partial Y}\\&-\frac{\partial \varPsi _1}{\partial X}\frac{\partial ^{3}\varPsi _2}{\partial y^{3}}-\frac{\partial \varPsi _2}{\partial X}\frac{\partial ^{3}\varPsi _1}{\partial y^{3}}+2\frac{\partial \varPsi _1}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y\partial Y}) +\frac{\partial \varPsi _1}{\partial Y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})\\&+\frac{\partial \varPsi _1}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _2}{\partial y^{2}})+\frac{\partial \varPsi _2}{\partial y}\frac{\partial }{\partial X}(\frac{\partial ^{2}\varPsi _1}{\partial y^{2}})+\delta \frac{\partial \varPsi _1}{\partial y}\frac{\partial ^{2}B_1}{\partial X\partial Y}-\mu _0\frac{\partial ^{2}\varPsi _1}{\partial y^{2}}. \end{aligned}$$

The homogeneous part of Eq. (25) is the same as that of Eq. (14), and non-singular condition is needed in order to obtain a regular solution of Eq. (25) as

$$\begin{aligned} \int \limits _{0}^\text {1}\frac{\varphi _0(y)}{\bar{u}-c_0}F\mathrm {d}y=0. \end{aligned}$$
(26)

Substituting Eqs. (17), (20), and (22) into Eq. (26) yields

$$\begin{aligned} \frac{\partial A}{\partial T}+a_1A^{2}\frac{\partial A}{\partial X}+a_2\frac{\partial ^{3} A}{\partial X^{3}}+a_3\frac{\partial ^{3} A}{\partial X\partial Y^{2}}&+a_4\frac{\partial A}{\partial X}\frac{\partial A}{\partial Y} +a_4A\frac{\partial ^{2}A}{\partial X\partial Y} \nonumber \\&+\bigg (\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0\bigg )A=0. \end{aligned}$$
(27)

The coefficients are \(a_1=\frac{I_1}{I}, a_2=\frac{I_2}{I}, a_3=\frac{I_3}{I}, a_4=\frac{I_4}{I}, a_5=\frac{I_5}{I}\) with representations of

$$\begin{aligned}&I=\int \limits _{0}^\text {1}\frac{q(y)}{(\bar{u}-c_0)}\varphi ^{2}_1(y)\mathrm {d}y, \nonumber \\&I_1=\int \limits _{0}^\text {1}\frac{1}{\bar{u}-c_0}[\frac{3}{2}q'(y)\varphi ^{2}_1(y)\varphi _{22}(y)-\frac{1}{2}\bigg (\frac{q(y)}{\bar{u}-c_0}\bigg )'\varphi ^{4}_1(y)]\mathrm {d}y,\nonumber \\&I_2=-\int \limits _{0}^\text {1}\varphi ^{2}_1(y)\mathrm {d}y,\nonumber \\&I_3=-\int \limits _{0}^\text {1}[2\varphi _1(y)\varphi '_{21}(y)+\varphi ^{2}_1(y)]\mathrm {d}y,\nonumber \\&I_4=\int \limits _{0}^\text {1}\frac{1}{\bar{u}-c_0}[-2(\bar{u}-c_0)\varphi _1\varphi '_{22}+q'(y)\varphi ^{2}_1(y)\varphi _{21}(y)]\mathrm {d}y,\nonumber \\&I_5=\int \limits _{0}^\text {1}\frac{\varphi _1(y)\varphi '_1(y)}{\bar{u}-c_0}\mathrm {d}y. \end{aligned}$$
(28)

Until now, we have obtained Eq. (27) for wave amplitude A(X, Y, T), which is a new mZK equation for the evolution of forced and low-frequency nonlinear Rossby waves. Firstly, the term with coefficient indicates that a necessary condition for the excitation of nonlinear Rossby waves is \(q^\prime (y)\ne 0\). \(q^\prime (y)\) denotes that the combined effects of Coriolis parameter \(h_H\) and topography are of great importance in inducing the nonlinear equatorial Rossby solitary waves, especially in the situation without shear background current. Most previous studies showed that the equatorial beta plane approximation is necessary, but, in our study, it is unnecessary that we treat with the issue of shear background current. Secondly, Eq. (27) represents a stronger nonlinear effect of the ZK model equation in [16,17,18]. It states that the real nonlinear equatorial Rossby waves propagate in two spatial and one temporal coordinates with multiple nonlinearities. Thirdly, the term with coefficient \(a_2\) is the same as that of the classical mKdV or the ZK model. Lastly, the term with the \(\delta a_5\frac{\partial ^2 B_1}{\partial X\partial Y}\) represents linear growth or decay of the evolution of wave amplitude, where \(\mu _0\) is the dissipation from friction. \(\delta a_5\frac{\partial ^2 B_1}{\partial X\partial Y}\) represents a linear growth or decay from the slowly varying topography, which means that the slowly varying topography is an unstable factor for the equatorial Rossby waves. Obviously, \(a_5\) will disappear in the case of constant background flow \(\bar{u}(y)=u_0\). The above analysis reveals the complexity of tropical motions. When the slow variation in meridional direction is absent, Eq. (27) reduces to the mKdV equation.

3 Solutions and Simulations

For a clear understanding of the mechanism about the excitation of nonlinear Rossby solitary waves created by the multiple topography \(B(X,y,Y)=B_0(u)+\varepsilon ^{\frac{1}{4}}B_1(X,Y)\), we let

$$\begin{aligned} \bar{u}(y)=u_0-\varepsilon y,~~~B_0(y)=\frac{1}{2}b_0y^{2}+b_1y+b_2,~~~B_1(X,Y)=\exp (-\gamma X^{2}+\sigma Y), \end{aligned}$$
(29)

where \(u_0,b_0,b_1,b_2\) are all real constants. Here, \(u_0\) represents basic background flow. \(b_0,b_1,b_2\) are coefficients of the parabola. \(\varepsilon \) is a small parameter indicating the weak shear. \(\gamma \) and \(\sigma \) are also real constants representing the rates of change of the topography in zonal and meridional directions, respectively. Then, using the given parameters, we solve Eqs. (18), (23) and (24) through weak nonlinear method to determine the coefficients of Eq. (27). Then, we solve Eq. (27) by reduced differential transform method. Finally, the influence of all parameters on the amplitude of the Rossby waves is obtained through numerical calculation.

3.1 Solutions of the New Modified mZK Equation

Weak nonlinear method is developed to solve Eqs. (18), (23), and (24)

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi _1(y)=\varphi _{11}(y)+\varepsilon \varphi _{12}(y)+\cdots ,\\ c_0=c_{00}+\varepsilon c_{01}+\cdots ,\\ \varphi _{21}(y)=\varphi _{211}(y)+\varepsilon \varphi _{212}(y)+\cdots ,\\ \varphi _{22}(y)=\varepsilon \varphi _{221}(y)+\varepsilon ^{2}\varphi _{222}(y)+\cdots . \end{array}\right. } \end{aligned}$$
(30)

Substituting Eq. (30) into Eqs. (18), (23), and (24) leads to all order perturbation equations about \(\varepsilon \):

\(\varepsilon ^{(0)}\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{11}(y)-\frac{b_0\delta }{u_0-c_{00}}\varphi _{11}(y)=0,\\ \varphi _{11}(0)=\varphi _{11}(1)=0. \end{array}\right. } \end{aligned}$$
(31)
$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{211}(y)-\frac{b_0\delta }{u_0-c_{00}}\varphi _{211}(y)=-2m\pi cos~m\pi y,\\ \varphi _{211}(0)=\varphi _{211}(1)=0. \end{array}\right. } \end{aligned}$$
(32)

By solving the eigenvalue problem of Eqs. (31) and (32) with homogeneous boundary value condition, the solutions can be obtained as

$$\begin{aligned} \varphi _{11}(y)=sin~m\pi y, \end{aligned}$$
(33)
$$\begin{aligned} \varphi _{211}(y)=-ysin~m\pi y, \end{aligned}$$
(34)

with \(c_{00}=u_0+\frac{b\delta }{m^{2}\pi ^{2}}.\)

\(\varepsilon ^{(1)}\):

$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{12}(y)-\frac{b_0\delta }{u_0-c_{00}}\varphi _{12}(y)=-m^{2}\pi ^{2} \frac{y+c_{01}}{u_0-c_{00}}sin~m\pi y,\\ \varphi _{12}(0)=\varphi _{12}(1)=0. \end{array}\right. } \end{aligned}$$
(35)
$$\begin{aligned} {\left\{ \begin{array}{ll} \varphi ''_{212}(y)-\frac{b_0\delta }{u_0-c_{00}}\varphi _{212}(y)=\frac{1}{2(u_0-c_{00})}[(1-m^{2}\pi ^{2}y^{2})sin~m\pi y-m\pi (y-1)cos~m\pi y],\\ \varphi _{12}(0)=\varphi _{12}(1)=0. \end{array}\right. } \end{aligned}$$
(36)

In the same way, from Eqs. (35) and (36), we obtain

$$\begin{aligned} \varphi _{12}(y)=\frac{1}{4(u_0-c_{00})}[-ysin~m\pi y+m\pi (y^{2}-y)cos~m\pi y], with~c_{01}=-\frac{1}{2}, \end{aligned}$$
(37)
$$\begin{aligned} \varphi _{212}(y)=\frac{1}{u_0-c_{00}}\bigg [\frac{1}{4}((y-y^{2})sin~m\pi y)+\frac{1}{2}\bigg (\frac{m\pi }{6}y^{3}-\frac{1}{m\pi }y-\frac{m^{2}\pi ^{2}-6}{6m\pi }\bigg )cos~m\pi y\bigg ], \end{aligned}$$
(38)
$$\begin{aligned} \varphi _{221}(y)=\frac{1}{6(u_0-c_{00})}cos~2m\pi y+\frac{1}{2(u_0-c_{00})}-\frac{2cos~m\pi y}{3(u_0-c_{00})}. \end{aligned}$$
(39)

Thus, Eqs. (18), (23), and (24) have asymptotic solutions as follows:

$$\begin{aligned} \varphi _1(y)=\varphi _{11}(y)+\varepsilon \varphi _{12}(y), \end{aligned}$$
(40)
$$\begin{aligned} \varphi _{21}(y)=\varphi _{211}(y)+\varepsilon \varphi _{212}(y), \end{aligned}$$
(41)

and

$$\begin{aligned} \varphi _{22}(y)=\varepsilon \varphi _{221}(y). \end{aligned}$$
(42)

Substituting Eqs. (29), (40)–(42) into Eq. (28), we obtain the coefficients of Eq. (27).

In the next step, the reduced differential transform method [101] is developed to solve Eq. (22). Assume

$$\begin{aligned} A(X,Y,T)=\sum _{k=0}^{\infty }A_k(X,Y)T^{k}. \end{aligned}$$
(43)

Substituting Eq. (43) into Eq. (27), we obtain the following iterations:

$$\begin{aligned} A&=-\frac{1}{k+1}\bigg [a_1\sum _{s=0}^{k}\bigg (\sum _{r=0}^{s}A_rA_{s-r}\frac{\partial A_{k-s}}{\partial X}\bigg )+a_2\frac{\partial ^{3}A_k}{\partial X^{3}}+a_3\frac{\partial ^{3}A_k}{\partial X\partial Y^{2}}\nonumber \\&+a_4\sum _{r=0}^{k}\frac{\partial A_r}{\partial X}\frac{\partial A_{k-r}}{\partial Y} +a_4\sum _{r=0}^{k}A_r\frac{\partial ^{2} A_{k-r}}{\partial X\partial Y}+\bigg (\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0\bigg )A_k\bigg ]. \end{aligned}$$
(44)

Assume that

$$\begin{aligned} A_0(X,Y)=\mathrm {sech}(X+Y). \end{aligned}$$

From Eq. (44), we can get \(A_0,A_1,A_2,\ldots ,\) through MATLAB. For simplicity, we omit the details. Taking first three terms, we can get the solution to Eq. (27)

$$\begin{aligned} A(X,Y,T)=A_0(X,Y)+A_1(X,Y)T+A_2(X,Y)T^{2}. \end{aligned}$$
(45)

3.2 Results and Discussions

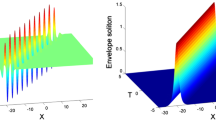
In this paper, we take the small parameter \(\varepsilon \) to be \(\varepsilon =0.0001\) and \(m=2\). In Figs. 1, 2, and 3, we use different expressions to describe the evolution of wave amplitude. These figures show that the evolution process of the amplitude of solitary wave has similar laws of changing in X- and Y-directions under the given parameters because the value of nonlinear item \(a_4\) (in computation, its value is the largest) has the decisive functions in the equations with required amplitude. The term with \(a_4\) of (27) is symmetrical about variables X and Y. Meanwhile, the simulation of Figs. 1, 2, and 3 demonstrates the necessity of considering higher dimensional nonlinear Rossby waves.

Fig. 1
figure 1

\(\delta =0.3,b_0=-0.7,u_0=0.9,\mu _0=0.02,\gamma =1,\sigma =-1\): a The 3D evolutionary plot of amplitude at \(Y=0\). b the amplitude profile at different time at \(Y=0\)

Full size image
Fig. 2
figure 2

\(\delta =0.3,b_0=-0.7,u_0=0.9,\mu _0=0.02,\gamma =1,\sigma =-1\): a The 3D evolutionary plot of amplitude at \(X=0\). b the amplitude profile at \(X=0\)

Full size image
Fig. 3
figure 3

The 3D-plot of amplitude A in spatial direction of X and Y in fixed moment T with \(\delta =0.3,b_0=-0.7,u_0=0.9,\mu _0=0.02,\gamma =1,\sigma =-1\): a \(T=0\); b \(T=0\); c \(T=0\); d \(T=0\)

Full size image
Fig. 4
figure 4

The changes of amplitude A under different aspect ratio\(\delta \) with \(b_0=-0.7,u_0=0.9,\mu _0=0.02,\gamma =1,\sigma =-1\) at time \(T=10\). a at \(Y=0\). b at \(X=0\)

Full size image
Fig. 5
figure 5

The changes of amplitude A under different values of \(b_0\) with \(\delta =0.3,u_0=0.9,\mu _0=0.02,\gamma =1,\sigma =-1\) at time \(T=10\). a at the spatial point \(Y=0\). b at the spatial point \(X=0\)

Full size image
Fig. 6
figure 6

The changes of amplitude A under different topographic parameter \(\gamma \) with \(\delta =0.3,b_0=-0.7,u_0=0.9,\mu _0=0.02\) at \(T=10\); a at \(\sigma =-1, Y=0\); b at \(\sigma =-1, X=0\); c at \(\sigma =1, Y=0\); d at \(\sigma =1, X=0\)

Full size image

Figure 4 shows that with the decrease of aspect ratio, the amplitude becomes larger and larger, which means that shallow water is one important factor in exciting Rossby waves. In Fig. 5, we characterize the effect of basic topography, and it can be seen that the forcing effect of variation of topography can enhance the evolution of amplitude. Also, Fig. 5 reveals that basic topography and its variation have obvious influence on amplitude.

Figure 6 shows that slowly varying topography almost has no influence on amplitude in X-direction. However, when \(\sigma =-1\), slowly varying topography has small influence on the amplitude in the negative half axis of Y and almost no influence on the amplitude in the positive half axis of Y. In the negative half axis of Y, with the increase of \(\gamma \), the amplitude becomes smaller and smaller. When \(\sigma =1\), the influence of slowly varying topography on the amplitude in the direction of Y is opposite. In summary, slowly varying topography has influence on amplitude, but it is much weaker than that of basic topography.

In Fig. 7, we can also see the influence of slowly varying topography parameter \(\sigma \) on amplitude. Similarly, in X-direction, slowly varying topography almost has no influence. But, when \(\sigma =-1\) is negative, slowly varying topography only has small influence in the negative half axis of Y and no influence in the positive half axis of Y. Also, with the increase of \(\sigma \), the amplitude becomes bigger and bigger. When \(\sigma =-1\) is positive, slowly varying topography only has small influence in the positive half axis of Y and no influence in the negative half axis of Y. Also, with the increase of \(\sigma \), the amplitude becomes smaller and smaller. Figure 8 demonstrates the influence of dissipation coefficient on Rossby wave amplitude. We can see that Rossby wave amplitude is influenced in both X- and Y-directions. And the influence in X- and Y-directions is similar. With the increase of dissipation coefficient, amplitude becomes smaller and smaller.

Fig. 7
figure 7

The changes of amplitude A under different topographic parameter \(\sigma \) with \(\delta =0.3,b_0=-0.7,u_0=0.9,\mu _0=0.02,\gamma =1\) at \(T=10\); a at the spatial point \(Y=0,\sigma \) is negative; b at the spatial point \(X=0,\sigma \) is negative; c at the spatial point \(Y=0,\sigma \) is positive; d at the spatial point \(Y=0,\sigma \) is positive

Full size image
Fig. 8
figure 8

The changes of amplitude A under different dissipation parameters \(\mu _0\) with \(\delta =0.3,u_0=0.9,\gamma =1,\sigma =-1\) at time \(T=10\). a at the spatial point \(Y=0\). b at the spatial point \(X=0\)

Full size image

4 Conservation Laws and Dynamical Analysis

The conservation properties and the dynamics of the obtained new mZK equation are analyzed in this section. The conservation laws are essential in characterizing the qualitative properties of mechanical systems, especially for the integrable systems. Infinite number of conservation laws can be obtained from the classical mKdV equation. The present study focuses on the mass and momentum of the motions. The following equations can be easily obtained from Eq.(27):

$$\begin{aligned} \frac{\partial A}{\partial T}+\frac{\partial }{\partial X}\bigg (\frac{1}{3}a_1A^{3}+a_2\frac{\partial ^{2} A}{\partial X^{2}}+a_3\frac{\partial ^{2} A}{\partial Y^{2}}+a_4A\frac{\partial A}{\partial Y}\bigg )+\bigg [\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0\bigg ]A=0, \end{aligned}$$
(46)
$$\begin{aligned} \frac{\partial A^{2}}{\partial T}&+\frac{\partial }{\partial X}\bigg [\frac{a_1}{2}A^{4}+2a_2 A\frac{\partial ^{2} A}{\partial X^{2}}-a_2\bigg (\frac{\partial A}{\partial X}\bigg )^{2}-a_3\bigg (\frac{\partial A}{\partial Y}\bigg )^{2}+2a_4A^{2}\frac{\partial A}{\partial Y}\bigg ]\nonumber \\&+\frac{\partial }{\partial Y}\bigg (2a_3A\frac{\partial ^{2}A}{\partial X\partial Y}\bigg )-a_4\frac{\partial (A^{2})}{\partial X}\frac{\partial A}{\partial Y}+2\bigg [\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0\bigg ]A^{2}=0. \end{aligned}$$
(47)

The mass

$$\begin{aligned} C_1=\iint \limits _{X,Y}A\mathrm {d}X\mathrm {d}Y \end{aligned}$$
(48)

and the momentum

$$\begin{aligned} C_2=\iint \limits _{X,Y}A^{2}\mathrm {d}X\mathrm {d}Y \end{aligned}$$
(49)

satisfy the following equations:

$$\begin{aligned} \frac{\mathrm {d}C_1}{\mathrm {d}T}=-\iint \limits _{X,Y}[\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0]A\mathrm {d}X\mathrm {d}Y, \end{aligned}$$
(50)
$$\begin{aligned} \frac{\mathrm {d}C_2}{\mathrm {d}T}=-\iint \limits _{X,Y}2[\delta a_5\frac{\partial ^{2}B_1}{\partial X\partial Y}+\mu _0]A^{2}\mathrm {d}X\mathrm {d}Y, \end{aligned}$$
(51)

where A and its any order partial derivation are assumed to be zero at infinity.

It is evident that the mass and the momentum are affected by the slowly varying topography and the dissipation, which is consistent with the former qualitative analysis. Equations (50) and (51) enjoy conservation laws when the slowly varying topography and the dissipation are absent. Generally speaking, the mass and momentum of the system are not conserved any more, which is consistent with the real motions of atmospheres and oceans.

On the other hand, benefited from some ideas of [102], we investigate the dynamical analysis of the Eq. (27). Next we neglect the influence of the slowly varying topography and dissipation, that is, \(B_1=0,\mu _0=0\).

Let \(A(X,Y,T)=\phi (\xi ), \xi =mX+nY-lT\) , then

$$\begin{aligned} (a_2m^{3}+a_3mn^{2})\phi '''+a_4mn(\phi '^{2}+\phi \phi '')-I\phi '+a_1m\phi ^{2}\phi '=0. \end{aligned}$$
(52)

Using \((\phi \phi ^\prime )^2=(\phi ^\prime )^2+\phi \phi ^{\prime \prime }\) and integrating Eq. (47) yields

$$\begin{aligned} (a_2m^{3}+a_3mn^{2})\phi ''+a_4mn\phi \phi '-I\phi +\frac{1}{3}a_1m\phi ^{3}=0. \end{aligned}$$
(53)

To facilitate further discussion, assume

$$\begin{aligned} \frac{-I}{a_2m^{3}+a_3mn^{2}}=\alpha ,~~~\frac{a_1m}{3(a_2m^{3}+a_3mn^{2})}=\beta ,~~~\frac{a_4mn}{a_2m^{3}+a_3mn^{2}}=\gamma . \end{aligned}$$

Then Eq. (53) reduces to

$$\begin{aligned} \phi ''+\gamma \phi \phi '+\alpha \phi +\beta \phi ^{3}=0. \end{aligned}$$
(54)

Putting \(\phi ^\prime =y\), then the following planar system is given:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm {d}\phi }{\mathrm {d}\xi }=y,\\ \frac{\mathrm {d}y}{\mathrm {d}\xi }=-\gamma \phi y-\alpha \phi -\beta \phi ^{3}, \end{array}\right. } \end{aligned}$$
(55)

with the Hamiltonian

$$\begin{aligned} H(\phi ,y)=y^{2}+\gamma \phi ^{2}y+\alpha \phi ^{2}+\frac{\beta }{2}\phi ^{4}. \end{aligned}$$
(56)

In order to investigate the phase portrait of the system (55), let

$$\begin{aligned} f(\phi )=-\alpha \phi -\beta \phi ^{3}. \end{aligned}$$

It has three zero points \(\phi _-,\phi _0\), and \(\phi _+\) with

$$\begin{aligned} \phi _-=-\sqrt{-\frac{\alpha }{\beta }},~~~\phi _0=0,~~~\phi _+=\sqrt{\frac{\alpha }{\beta }},~~~\alpha \beta <0. \end{aligned}$$

Letting \((\phi _i,0)\) be one of the singular points of system (55), then the characteristic values of the linearized system of (55) at the singular points \((\phi _i,0)\) are

$$\begin{aligned} \lambda _\pm =\pm \sqrt{f'(\phi _i)}. \end{aligned}$$
(57)

From the qualitative theory of dynamical systems, we deduce that

  1. 1.

    if \(f'(\phi _i)>0\), then \((\phi _i,0)\) is a saddle point;

  2. 2.

    if \(f'(\phi _i)<0\), then \((\phi _i,0)\) is a center point;

  3. 3.

    if \(f'(\phi _i)=0\), then \((\phi _i,0)\) is a degenerate saddle point.

Therefore, we obtain the phase portraits of system (55), see Fig. 9. Let

$$\begin{aligned} H(\phi ,y)=h, \end{aligned}$$
(58)

where h is a Hamiltonian function. Next, we consider the relations between the orbits of (55) and the Hamiltonian. Set

$$\begin{aligned} h^*=|H(\phi _+,0)|=|H(\phi _-,0)|=\frac{\alpha ^{2}}{2|\beta |}. \end{aligned}$$
(59)

Thus, the following conclusions hold:

  • If \(\beta <0\) and \(\alpha >0\), then

    1. A

      When \(h<0\) or \(h>h^*\), system (55) does not have any closed orbit;

    2. B

      When \(0<h<h^*\), system (55) has three periodic orbits \(L_2,L_5\) and \(L_6\);

    3. C

      When \(h=0\), system (55) has two periodic orbits \(L_1\) and \(L_7\);

    4. D

      When \(h=h^*\), system (55) has two heteroclinic orbits \(L_3\) and \(L_4\).

  • If \(\beta >0\) and \(\alpha <0\), then

    1. A

      When \(h<-h^*\), system (55) does not have any closed orbit;

    2. B

      When \(-h^*<h<0\), system (55) has two periodic orbits \(L_8\) and \(L_9\);

    3. C

      When \(h=0\), system (55) has two heteroclinic orbits \(L_{10}\) and \(L_{11}\);

    4. D

      When \(h>0\), system (55) has a periodic orbits \(L_{12}\).

Fig. 9
figure 9

The phase portraits of system (50): a \(\beta <0\) and \(\alpha >0\); b \(\beta >0\) and \(\alpha <0\)

Full size image

5 Conclusions

In this paper, we derived a nmZK model equation with the effects of the horizontal component of Coriolis parameter, the topography, and the dissipation. The influence mechanisms of all kinds of parameters on the Rossby waves are discussed through theoretical analysis and numerical calculations. Moreover, we find that both the horizontal Coriolis parameter and nonlinear topography are important in inducing the evolution of the nonlinear Rossby waves. In addition, the conservation laws and the dynamical analysis without considering dissipation and slowly varying topography are studied.

There are some problems to be addressed in our future research as follows. On one hand, due to the complex dispersive structure of the nmZK equation, we shall study the traveling wave solutions. On the other hand, we shall study the lump solutions.