1 Introduction

In recent years, solitary waves theory has attracted much more attention on mechanics, applied mathematics, physics, atmospheric and oceanic science and other interdisciplinary fields. Many natural phenomena have relationship with Rossby waves, and many nonlinear partial differential equations (NLPDEs) are used to analyze the quasi-geostrophic potential vorticity equation. Rossby waves play a significant role in the oceans and the atmospheres, because it is one of the main wave patterns caused by the effect of Earth’s rotation. To consider the dissipative effect, the generalized Boussinesq equation in the rotating fluid was obtained [1, 2]. The Zakharov-Kuznetsov (ZK) equation, which is also the higher dimensional generalization of the KdV equation, was presented by Gottwald et al. [3] to further study the nonlinear waves in the area of plasma. And Ono [4] discussed algebraic Rossby solitary waves and derived the Benjamin-Ono (BO) equation in stratified fluids. Kadomtsev and Petviashvili [5] first put forward the KP equation in plasma and studied the evolution of long ion-acoustic waves. And Groves et al. [6] derived the KP equation with respect to 2-D shallow water waves. Hereafter, Cong Wang et al. [7] studied the coupled KP equations in the two-layer quasi-geotropic potential vortex equation of unequal depth with bottom topography. Kinds of equations, like the mZK equation, ZK-BO equation, ZK-Burgers equation [8,9,10,11,12,13] and so on, were obtained to study the Rossby waves. Recently, lots of scholars derived NLPDEs from the quasi-geostrophic vorticity equation and investigated the Rossby waves by employing multi-scale analysis and perturbation method. And multiple-scale methods [14,15,16,17,18] are widely used to analyze water wave in wave tank, coastal and oceanic applications.

As mentioned above, the stretch coordinates in employing multi-scale analysis are difference when the order of small parameters are not considered. Large of scholars study the X and Y without the effect of timescale when the basic stream function is considered as \(-\int _{0}^{y}(u(s)-c) {\textbf {d}}s\) [19, 20], or just the X with the effect of timescale when the basic stream function is considered as \(-\int _{0}^{y}u(s)ds\), like Gardner-Morikawa transform [21]. The (1+1)D and (2+1)D version of the multiple scales method has been researched for many years, which the group velocity in fluid usually is considered as an arbitrary constant. Song and Yang [22] point out that \(\int _{0}^{y}(u(s)-c_{0}){\textbf {d}}s\) is a traveling wave transformation made in longitude, and it consists with the character of Gardner-Morikawa transform. Liu et al. [2] introduces the slow stretch coordinates \(X=\epsilon ^{\frac{1}{2}}x, Y=\epsilon (y-c_{1}t), T=\epsilon t\). The authors [23] consider the group velocity of Rossby waves in the stretch coordinates of latitude and longitude \(X=\epsilon (x-c_0t), Y=\epsilon ^2(y-c_1t), T=\epsilon ^3 t\). The essential difference between them is whether the group velocity in latitude or longitude is considered.

However, it is pointed out that the group velocity changes over time in many researches of NLPEDs with variable coefficients, and several effective methods have been established, including \(G'/G-\)expansion method, auxiliary equation method, the symmetric transformation, extended mapping method, and so on [24,25,26,27,28,29,30,31,32]. Bilinear residual network method [33] and Bilinear neural network method [34,35,36] can obtain \(100\%\) accurate analytical solution for partial differential equation, which is far more accurate than traditional neural network numerical method.

In this article, the auxiliary equation is applied to Hirota bilinear method. Its key is that the test function is generalized to the sum of multiple auxiliary equations, which gives the modified method the advantage of enriching the forms of solution and setting up of the test function. And NLPEDs with variable coefficients can be successfully derived from the quasi-geostrophic vorticity equation, when the group velocity is considered as a function of time. The variable coefficients cause the propagation of Rossby wave and the increase of Rossby wave amplitude. All blocking structures move in longitude, when the group velocity of spatial scale y is considered. Hence, this article derives variable coefficients KP equation in Sect. 2, which tries to analyze the influence in Rossby waves and its flow field. There are a large number of scholars to analyze KP equation [7, 37,38,39], but few to discuss variable coefficient. Therefore, we utilize auxiliary equation method and modified Hirota bilinear method to obtain the soliton wave solution and rogue wave solution in Sect. 3, respectively. The variable coefficients are limited to constants, and some explanations are given in Sect. 3.2. The evolution of Rossby waves is studied and the blocking structures of total flow fields are discussed in Sect. 4. Finally, some conclusions are given in Sect. 5.

2 Derivation of Kadomtsev-Petviashvili equation

Starting from the quasi-geostrophic vorticity equation, it can be written as [40]

$$\begin{aligned}{} & {} \left( \frac{\partial }{\partial t}+\frac{\partial \varPsi }{\partial x}\frac{\partial }{\partial y}- \frac{\partial \varPsi }{\partial y}\frac{\partial }{\partial x}\right) (\nabla ^{2}\varPsi +\beta (y)y)=0,\nonumber \\{} & {} \frac{\partial \varPsi }{\partial x}\bigg |_{y=0,1}=0, \end{aligned}$$
(1)

where \(\beta (y)\) is a nonlinear function of the latitude variable y, and \(\nabla ^{2}\) is the 2D Laplace operator.

The total stream function is assumed to be

$$\begin{aligned} \varPsi (x,y,t)=-\int _{0}^{y}u(s)ds+\epsilon ^2\psi (x,y,t), \end{aligned}$$
(2)

where \(-\int _{0}^{y}u(s)ds\) is the basic stream function, \(\psi \) is the disturbance stream function and \(\epsilon \) is a small parameter characterizing the nonlinear property. When \(\epsilon \ll 1\), it is a weakly nonlinear problem. Substituting Eq.(2) into Eq.(1) yields

$$\begin{aligned}{} & {} \left[ \frac{\partial }{\partial t}+u(y)\frac{\partial }{\partial x}\right] \nabla ^{2}\psi +p(y)\frac{\partial \psi }{\partial x}+\epsilon ^2J(\psi ,\nabla ^{2}\psi )=0,\nonumber \\{} & {} \frac{\partial \psi }{\partial x}\bigg |_{y=0,1}\nonumber \\{} & {} =0, \end{aligned}$$
(3)

where \(p(y)=\frac{\partial (\beta (y)y-u(y)')}{\partial y}\), \(J(a,b)=\frac{\partial a}{\partial x}\frac{\partial b}{\partial y}-\frac{\partial a}{\partial y}\frac{\partial b}{\partial x}\).

The perturbation expansion method is applied to find the asymptotic solution of the weakly nonlinear problem. To this purpose, introducing the slow stretch coordinates

$$\begin{aligned} X{} & {} =\epsilon (x-\int c_{0}(t){\textbf {d}}t), Y=\epsilon ^2(y-\int c_{1}(t){\textbf {d}}t), \nonumber \\ T{} & {} =\epsilon ^3t. \end{aligned}$$
(4)

where \(\int c_{0}(t){\textbf {d}}t\) and \(\int c_{1}(t){\textbf {d}}t\) represent the zonal and meridional group velocity of Rossby waves. Then the disturbance stream function is introduced as the following perturbation expansions

$$\begin{aligned} \psi =\psi _{0}+\epsilon \psi _{1}+\epsilon ^2\psi _{2}+O(\epsilon ^{3}). \end{aligned}$$
(5)

Substituting Eq.(4) and (5) into Eq.(3) yields the equations about small parameter \(\epsilon \)

$$\begin{aligned}{} & {} O\left( \epsilon \right) :\left\{ \begin{array}{l} [p(y)+(u(y)-c_0(T))\frac{\partial ^2}{\partial y^2}]\frac{\partial }{\partial X}\psi _{0}=0, \\ \frac{\partial \psi _0}{\partial X}=0, y=0,1 \end{array}\right. \end{aligned}$$
(6)
$$\begin{aligned}{} & {} O\left( \epsilon ^{1}\right) :\left\{ \begin{array}{l} [p(y)+(u(y)-c_0(T))\frac{\partial ^2}{\partial y^2}]\frac{\partial }{\partial X}\psi _{1}=c_{1}(T)\frac{\partial ^{2} }{\partial y^{2}}\frac{\partial }{\partial Y}\psi _0, \\ \frac{\partial \psi _1}{\partial X}=0, y=0,1 \end{array}\right. \end{aligned}$$
(7)
$$\begin{aligned}{} & {} O\left( \epsilon ^{2}\right) :\left\{ \begin{array}{l} [p(y)+(u(y)-c_0(T))\frac{\partial ^2}{\partial y^2}]\frac{\partial }{\partial X}\psi _{2}=-\frac{\partial }{\partial T}\frac{\partial ^2 }{\partial y^{2}}\psi _{0}+\frac{\partial \psi _0}{\partial y}\frac{\partial ^3 }{\partial X\partial y^2} \psi _{0}\\ -\frac{\partial \psi _0}{\partial X}\frac{\partial ^3 }{\partial y^3} \psi _{0}+(-u(y)+c_{0}(T))\frac{\partial ^{3}}{\partial ^{3} X}\psi _{0}+c_{1}(T)\frac{\partial ^2 }{\partial y^{2}}\frac{\partial }{\partial Y}\psi _1 \\ +2(-u(y)+c_{0}(T))\frac{\partial ^{3}}{\partial y\partial X\partial Y }\psi _0\equiv F,\\ \frac{\partial \psi _2}{\partial X}=0, y=0,1 \end{array}\right. \end{aligned}$$
(8)

We suppose that \(\psi _{0}\) have the following separable variables form in Eq.(6)

$$\begin{aligned} \psi _{0}=A(X,Y,T)\varphi _0(y), \end{aligned}$$
(9)

and substituting it into Eq.(6) yields

$$\begin{aligned} \left\{ \begin{array}{l} \varphi _0''(y)+\frac{p(y)}{u(y)-c_{0}(T)}\varphi _0(y)=0, \\ \varphi _0(0)=\varphi _0(1)=0, \end{array}\right. \end{aligned}$$
(10)

In the next order, we set out

$$\begin{aligned} \psi _{1}=B(X,Y,T)\varphi _1(y), \end{aligned}$$
(11)

and substituting it into Eq.(7) yields

$$\begin{aligned} \left\{ \begin{array}{l} [\varphi _1''(y)+\frac{p(y)}{u(y)-c_{0}(T)}\varphi _1(y)]B_{X}=\frac{c_{1}(T)}{u(y)-c_{0}(T)}\varphi _0''(y)A_{Y}, \\ \varphi _1(0)=\varphi _1(1)=0, \end{array}\right. \nonumber \\ \end{aligned}$$
(12)

In hence, B(X, Y, T) can be taken into the forms as follows

$$\begin{aligned} B(X,Y,T)=\partial _{X}^{-1}A(X,Y,T)_{Y}. \end{aligned}$$
(13)

So that Eq.(12) can be written as

$$\begin{aligned} \varphi _1''(y)= & {} -c_{1}(T)\frac{p(y)}{(u(y)-c_{0}(T))^{2}}\varphi _0(y)\nonumber \\{} & {} -\frac{p(y)}{u(y)-c_{0}(T)}\varphi _1(y). \end{aligned}$$
(14)

Lastly, substituting Eq.(9), Eq.(11), Eq.(13) into Eq.(8) and using \(\int _{0}^{1}[\frac{\varphi _0(y)}{u(y)-c_{0}(T)}F]{\textbf {d}}y=0\) yields

$$\begin{aligned}{} & {} A_T+a_1(T)AA_X+a_2(T)A_{XXX}\nonumber \\{} & {} \qquad +a_3(T)\partial _X^{-1}A_{YY}=0 \end{aligned}$$
(15)

where

$$\begin{aligned}{} & {} a_1(T)=\frac{1}{I}\int _0^1\left[ \left( \frac{p(y)}{u(y)-c_{0}(T)}\right) _y\varphi _0(y)^2\right] {\textbf {d}}y,\nonumber \\{} & {} \quad a_2(T)=-\frac{1}{I}\int _0^1\varphi _0(y)^2{\textbf {d}}y,\nonumber \\{} & {} a_3(T)=-\frac{1}{I}\int _0^1 [c_1(T)^2 \frac{p(y)}{(u(y)-c_{0}(T))^3}\varphi _0(y)^2\nonumber \\{} & {} \quad \quad + c_1(T)\frac{p(y)}{(u(y)-c_{0}(T))^2}\varphi _0(y)\varphi _1(y)]{\textbf {d}}y,\nonumber \\{} & {} a_4(T)=-2\frac{1}{I}\int _0^1\varphi _0'(y)\varphi _0(y){\textbf {d}}y=0,\nonumber \\{} & {} \quad I=\int _0^1\left[ \frac{p(y)}{(u(y)-c_{0}(T))^2}\varphi _0(y)^2\right] {\textbf {d}}y\ne 0 \end{aligned}$$
(16)

Obviously, Eq.(15) is variable coefficient KP equation. And we will analyze its solutions hereinafter.

3 Analysis for variable coefficient KP equation

3.1 Soliton wave solutions

Here, the auxiliary equation method is used to study the KP equation. First, a transformation is assumed to be \(A=A(\xi ), \xi =kX+lY+\omega (T)\). Substituting it into Eq.(15) yields

$$\begin{aligned} (k\omega '(T){+}a_3(T)l^2)A'+a_1(T)k^2AA'{+}a_2(T)k^4A'''{=}0. \end{aligned}$$
(17)

Expand A as the following series for the function

$$\begin{aligned} A(\xi )=b_0(T)+b_1(T)f(\xi )+b_2(T)f^2(\xi ), \end{aligned}$$
(18)

where \(f(\xi )\) is Riccati equation \(f'(\xi )=c_0+c_1f(\xi )+c_2f^2(\xi )\), and its solutions are provided in much researches. Substituting above into Eq.(17), and then equating all the coefficients of the \(f^{i}(\xi )\) term to zero. Lastly, soliton wave solution is obtained as follows

$$\begin{aligned} A_1{} & {} =b_0(T)-\frac{12k^2c_1c_2a_2(T)}{a_1(T)}f(\xi )\nonumber \\{} & {} \quad -\frac{12k^2c_2^2a_2(T)}{a_1(T)}f^2(\xi ), \end{aligned}$$
(19)

where \(\xi =kX+lY-\int (k^3c_1^2a_2(T)+8k^3c_0c_2a_2(T)+\frac{l^2}{k}a_3(T)+ka_1(T)b_0(T)){\textbf {d}}T\).

Case 1When \(\varDelta =c_1^2-4c_0c_2>0\), \(f(\xi )=-\frac{(}{c_1}{2c_2}-\frac{\sqrt{\varDelta }}{2c_2}\tanh \,(\frac{\sqrt{\varDelta }}{2}\xi )\).

Case 2When \(\varDelta =0\), \(f(\xi )=-\frac{c_1}{2c_2}-\frac{1}{c_2\xi }\).

Case 3When \(\varDelta <0\), \(f(\xi )=-\frac{c_1}{2c_2}+\frac{\sqrt{-\varDelta }}{2c_2}\tan (\frac{\sqrt{-\varDelta }}{2}\xi )\).

According to the real situation of the ocean and atmosphere and the previous experience, it is necessary to consider the total stream function as a periodic function in the background flow. Thus, we assume that the basic stream function is \(u(s)=s\cos (s)\) to research the evolution of Rossby waves. To analyze the effect of variable coefficient caused by the zonal and meridional group velocity, we take the velocity as \(c_0(t)=c_1(t)=t^2+1\), and other parameters take \(\beta (y)=y, \varphi _0(y)=\varphi _1(y)=y, c_1=1, c_2=2, c_3=-3, k=l=1, b_0(T)=1\). Via mean value theorems for definite integrals, there is \(y'\in [0,1]\) such that \(I=\frac{1}{(u(y')-c_{0}(T))^2}\int _0^1[p(y)\varphi _0(y)^2]{\textbf {d}}y\). \(a_1(T), a_2(T)\) and \(a_3(T)\) also are considered as such. As a result, \(u(y')\) is considered as a constant, and \(u(y')\in [0,u_{MAX}], u_{MAX}\approx 0.56110\).

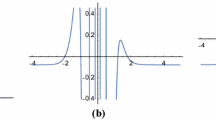
Since the soliton wave solution of KP equation had been studied by many scholars, this paper only shows the solution of Case 1. From Fig. 1a, the solution is bell-shaped solution. Interestingly, as time progresses, not only Rossby wave propagates to the right, but also its amplitude \(A_1\) increases from Fig. 1b, c. This is because that the velocity is not a constant but is growing. Figure 1d shows \(u(y')\) also affects the displacement and the amplitude \(A_1\) of Rossby wave, but does not affect the whole change trend.

Fig. 1
figure 1

Soliton wave solution: (a) with \(T=0\) and \(u(y')=0\); (b) with \(u(y')=0\), and \(Y=0\); (c) with \(u(y')=0.5\), and \(Y=0\); (d) with \(Y=0\), and \(T=0.3\)

Full size image

3.2 Rogue wave solutions

For facilitating calculation, via inserting \(A(X,Y,T)=w_X(X,Y,T)\) into Eq. (15) and integrating it with respect to X yields, Eq. (15) can be transformed into an equivalent form

$$\begin{aligned} w_{XT}{+}a_1(T)w_{X}w_{XX}+a_2(T)w_{XXXX}{+}a_3(T)w_{YY}{=}0. \end{aligned}$$
(20)

Then substituting the rational transformation [32]

$$\begin{aligned} w(X,Y,T)=\frac{F(X,Y,T)}{G(X,Y,T)} \end{aligned}$$
(21)

into Eq.(20), and then the relationship between F and G is obtained \(F(X,Y,T)=\frac{12a_2(T)}{a_1(T)}G_{X}(X,Y,T)\). Next we choose text function as follows

$$\begin{aligned}{} & {} G=b_{1}f_{1}^{2}(\xi _{1})+b_{2}f_{2}^{2}(\xi _{2})+b_{3}f_{3}(\xi _{3})+b_{4},\nonumber \\{} & {} f_{1}'(\xi _{1})=1, f_{2}'(\xi _{2})=1,\nonumber \\{} & {} \quad f_{3}'^2(\xi _{3})=c_0+c_1f_{3}(\xi _{3})+c_2f_{3}^2(\xi _{3}). \end{aligned}$$
(22)

where \(\xi _{i}=b_{i1}X+b_{i2}Y+b_{i3}(T)\), \(b_{i}\) and \(b_{ij}(i,j=1,2,3,4)\) are the complex constants. From it, we can determine the functional representation of \(f_i\), and results are calculated

$$\begin{aligned}{} & {} b_{1}=b_{2}=1,\nonumber \\{} & {} b_{13}(T)=\frac{-2b_{12}b_{21}b_{22}+b_{11}(b_{22}^{2}-b_{12}^{2})}{b_{11}^{2}+b_{21}^{2}}\int a_3(T){{\varvec{d}}}T,\nonumber \\{} & {} b_{23}(T)=\frac{-2b_{11}b_{12}b_{22}+b_{21}(b_{12}^{2}-b_{22}^{2})}{b_{11}^{2}+b_{21}^{2}}\int a_3(T){{\varvec{d}}}T,\nonumber \\{} & {} b_{33}(T)=-b_{31}\frac{8b_{11}b_{12}b_{21}b_{22}-b_{21}^{2}(b_{12}^{2}-3b_{22}^{2})+b_{11}^{2}(3b_{12}^{2}-b_{22}^{2})}{3(b_{11}^{2}+b_{21}^{2})^2}\int a_3(T){\textbf {d }}T,\nonumber \\{} & {} b_{32}=b_{31}\frac{b_{11}b_{12}+b_{21}b_{22}}{b_{11}^{2}+b_{21}^{2}},\nonumber \\{} & {} a_2(T)=\frac{(b_{12}b_{21}-b_{11}b_{22})^2}{3c_{2}(b_{11}^{2}+b_{21}^{2})^{2}b_{31}^{2}}a_{3}(T),\nonumber \\{} & {} b_{4}=\frac{16b_{11}^{4}+16b_{21}^{4}+8c_{1}b_{21}^{2}b_{3}b_{31}^{2}+(c_{1}^{2}-4c_{0}c_{2})b_{3}^{2}b_{31}^{4}+8b_{11}^{2}(4b_{21}^{2}+c_{1}b_{3}b_{31})}{16c_{2}(b_{11}^{2} +b_{21}^{2})b_{31}^2},\nonumber \\{} & {} \frac{12a_2(T)}{a_1(T)}=b_{5}. \end{aligned}$$
(23)
Fig. 2
figure 2

Lump solution: (a) and (b) at \(T=0\); (c) with \(Y=0\)

Full size image
Fig. 3
figure 3

Lump with one soliton solution: (a) and (b) at \(T=2\); (c) with \(Y=-2\)

Full size image

Then, we can obtain the interaction solution of the KP equations as

$$\begin{aligned} A_2= & {} b_5\left[ \frac{2b_{1}b_{11}^{2}+2b_{2}b_{21}^2+b_{3}b_{31}^{2}f_{3}''(\xi _{3})}{b_{1}\xi _{1}^2+b_{2}\xi _{2}^2+b_{3}f_{3}(\xi _{3})+b_{4}}\nonumber \right. \\{} & {} \left. -\left( \frac{2b_{1}b_{11}\xi _{1}+2b_{2}b_{21}\xi _{2}+b_{3}b_{31}f_{3}'(\xi _{3})}{b_{1}\xi _{1}^2+b_{2}\xi _{2}^2+b_{3}f_{3}(\xi _{3})+b_{4}}\right) ^2\right] \nonumber \\ \end{aligned}$$
(24)

Because \(f_{3}\) is one of elliptic equation [41], and its functional form is affected by \(c_0, c_1, c_2\), the solution are classified as follows.

Case 1

When \(b_{3}=0\), the solution of KP is lump solution and \(b_{4}=-\frac{3(b_{11}^{2}+b_{21}^{2})^{3}a_2(T)}{(b_{12}b_{21}-b_{11}b_{22})^{2}a_3(T)}\). We take \(b_{11}=b_{12}=1,b_{21}=-1,b_{22}=2,b_{5}=1,a_3(T)=1\), the solution is shown in Fig. 2.

Case 2

When \(b_{3}\ne 0,\varDelta '=c_2^2-4c_0c_1=0\), the solution is lump and one soliton solution. If parameter \(b_{11}=b_{12}=1,b_{21}=-1,b_{22}=2,b_{3}=-1,b_{31}=1,b_{5}=1,c_{2}=1,c_{1}=2,c_{0}=1,a_3(T)=1\) is selected, the solution is shown in Fig. 3.

Case 3

When \(b_{3}\ne 0,c_2>0,\varDelta '>0\), the solution is lump and one hyperbolic cosine function solution. If parameter \(b_{11}=b_{12}=1,b_{21}=-1,b_{22}=2,b_{3}=1,b_{31}=-1,b_{5}=c_{2}=c_{1}=c_{0}=1,a_3(T)=1\) is selected, the solution is shown in Fig. 4.

Fig. 4
figure 4

Lump with one hyperbolic cosine function solution: (a) and (b) at \(T=0\); (c) with \(Y=0\)

Full size image

Case 4

When \(b_{3}\ne 0,c_2<0,\varDelta '>0\), the solution is lump and one sine function solution. If parameter \(b_{11}=1,b_{12}=-1,b_{21}=1,b_{22}=1,b_{3}=-1,b_{31}=1,b_{5}=1,c_{2}=-2,c_{1}=0,c_{0}=1,a_3(T)=1\) is selected, the solution is shown in Fig. 5.

Fig. 5
figure 5

Lump with one sine function solution: (a) and (b) at \(T=0\); (c) with \(Y=0\)

Full size image

Interestingly, all the variable coefficients in the calculation result become constant coefficients. Through

$$\begin{aligned} \frac{12a_2(T)}{a_1(T)}=b_{5} \end{aligned}$$

in Eq.(23), \(a_1(T)\) and \(a_2(T)\) are linear dependence. Via Eq.(16), we know

$$\begin{aligned} b_{5}= & {} \frac{12a_2(T)}{a_1(T)} \\= & {} \frac{-12\frac{1}{I}\int _0^1\varphi _0(y)^2{\textbf {d}}y}{\frac{1}{I}\int _0^1[(\frac{p(y)}{u(y)-c_{0}(T)})_y\varphi _0(y)^2]{\textbf {d}}y} \\= & {} \frac{-12\int _0^1\varphi _0(y)^2{\textbf {d}}y}{\int _0^1[(\frac{p(y)}{u(y)-c_{0}(T)})_y\varphi _0(y)^2]{\textbf {d}}y}, \end{aligned}$$

where \(b_{5}\) and \(\int _0^1\varphi _0(y)^2{\textbf {d}}y\) are constants. It is necessary that \(c_0(T)\) is a constant. According to

$$\begin{aligned} a_2(T)=\frac{(b_{12}b_{21}-b_{11}b_{22})^2}{3c_{2}(b_{11}^{2}+b_{21}^{2})^{2}b_{31}^{2}}a_{3}(T) \end{aligned}$$

in Eq.(23), \(c_1(T)\) is also a constant. The presence of both \(c_0(T)\) and \(c_1(T)\) serves as the primary catalyst for the emergence of variable coefficient. Therefore, the variable coefficients are reduced to constant coefficients.

Fig. 6
figure 6

Evolution of Rossby wave flow field for \(A_1\), and the parameter takes \(\epsilon =0.2\)

Full size image
Fig. 7
figure 7

Evolution of Rossby wave flow field for \(A_2\) of Case 1, and the parameter takes \(\epsilon =0.1\)

Full size image
Fig. 8
figure 8

Evolution of Rossby wave flow field, and the parameter takes \(\epsilon =0.1\)

Full size image
Fig. 9
figure 9

Evolution of Rossby wave flow field for \(A_2\) of Case 4, and the parameter takes \(\epsilon =0.1\)

Full size image

Here, Figs. 2–5 are explained and analyzed. Figure 2, which has been studied by many scholars, is the common lump solution, so this paper dose not describe it. From Fig. 3a, b, the lump wave and the soliton wave are independent of each other and move in the same direction in time from \(\infty \) to \(-\infty \); they collide at \(T=0\) because of velocity of lump wave than soliton wave; after the collision, the two waves merge into one wave. With the passage of time, the waves move from east to west from Fig. 3c. In Fig. 4, it can be clearly seen that two parallel waves appears phenomenon about swallowed and spited lump wave at \(T\rightarrow \pm 0.6\). Lump wave is separated from one wave, then moves and merges in another wave. Interestingly, Fig. 4 has some similarities with Fig. 3. On the one hand, the expression for Case 2 has one more exponential function than Case 3 because of the parameter values of \(f_3\). On the other hand, Fig. 4b has one more wave than Fig. 3b. Apart from the differences above, the dynamic properties and forms of solution do not change. Lastly, the image of solution for Case 4 is shown in Fig. 5. And from Fig. 5c, the wave changes periodically overtime.

4 Evolution of Rossby waves flow field

In the previous article, the soliton wave solutions and rogue wave solutions are obtained and then the total stream function can be written as

$$\begin{aligned} \varPsi (x,y,t)= & {} -\int _{0}^{y}s\cos (s)ds\nonumber \\{} & {} +\epsilon ^2\varphi _0(y)A(\epsilon (x-\int c_{0}(t){\textbf {d}}t), \epsilon ^2\nonumber \\{} & {} \left( y-\int c_{1}(t){\textbf {d}}t\right) , \epsilon ^3t), \end{aligned}$$
(25)

It is well known that climate changes periodically on a large or small areas. According to the real situations of the ocean and atmosphere and the previous experience, it is necessary to consider the total stream function in the background flow as a periodic function. Thus, the basic stream function is \(u(s)=s\cos (s)\) to study the evolution of Rossby waves flow field. In addition, this section uses the preceding parameter values.

In Fig. 6, the dipole blocking structure appears in Rossby wave flow field. The distribution of blocking structure is not symmetry at any time, the blocking structure in the north tilts to the west, and it in the south tilts to the east, because \(c_0(t)\) and \(c_1(t)\) are the quadratic functions about time, not constants. And the northern air pressure is higher than southern air pressure in the whole flow field. With the passage of time, the entire blocking structure propagates eastward. It can also be found that the change \(u(y')\) affects the altitude of dipole blocking structure, but does not affect the evolution of Rossby waves flow field.

In Fig. 7, Rossby wave flow field constituted by lump wave is shown. The distribution of the blocking structure is symmetry and the northern pressure is also higher than the southern. The entire blocking structure propagates eastward overtime, and rapidly propagates eastward with the increase of \(c_0\). Interestingly, as \(c_1\) changes, it seems that the entire blocking structure has changed. This is because the entire blocking structure shifts in meridian.

In Fig. 8, Rossby wave flow field constituted by the solution for Case 2 and 3 is shown. The blocking structures caused by lump and soliton wave appear together in the Rossby wave flow field. To the left side of (a) and in the middle of (b), we find that the blocking structure is the same as Fig. 8. But elsewhere in (a) and (b), the blocking structures are caused by exp function and sine function, respectively. The southern pressure is also higher than the northern in these blocking structures. The dynamic properties of Fig. 8 are the same as Fig. 7.

In Fig. 9, Rossby wave flow field constituted by the solution for Case 4 is shown. It also has the same dynamic properties as above. When \(c_1\) increases, the blocking structure moves toward the north.

5 Conclusions

Starting with the quasi-geostrophic potential vorticity equation, this article derives variable coefficient KP equation and solves its soliton wave, lump wave, and interaction solution. For evaluating the results, we take the table as follows:

The solution

The parameter

The type of solution

\(A_1\)

\(\varDelta \) in anywhere

The soliton wave

\(A_2\)

\(b_{3}=0\)

Lump wave

\(b_{3}\ne 0,\varDelta '=0\)

The lump and one soliton wave

\(b_{3}\ne 0,c_2>0,\varDelta '>0\)

The lump and one hyperbolic cosine function wave

\(b_{3}\ne 0,c_2<0,\varDelta '>0\)

The lump and one sine function wave

Interestingly, soliton wave could be effected by varied zonal and meridional group velocity, but the lump and interaction are not. In calculation of modified Hirota bilinear method, the variable coefficient meet the need of certain conditions. And according to Eq.(16), the zonal and meridional group velocity are not effected by time. It is pointed that the auxiliary equation method could analyze the variation coefficient, but not solve the rogue wave; Hirota bilinear method is opposite. From 3D, contour and 2D figures, the amplitude of soliton wave is increase overtime when \(c_0(t)=c_1(t)=t^2+1\), and the dynamic characteristic of all solution is shown.

Finally, the blocking structures caused by soliton, lump and interaction wave, are clearly depicted in the Rossby wave flow field. From Figs. 7 and 8, we find that the blocking structures caused by lump wave and others work together, and they keep independent of each other within a certain time frame or a sufficiently small margin of error. In addition, precisely know that the slow stretch coordinates (4) possess the properties of traveling waves transform because of the characteristic of Fig. 9. In essence, all blocking structures in this article move in longitude, but only Fig. 9 is more obvious. Take Fig. 5b for example, the varied range of Y is \((-2,2)\) in the range of \(X\in (-2,2)\), when the time goes in (0, 6). According to the slow stretch coordinates, the spatial scale x and y of Rossby waves flow field are transformed, i.e. y is \((-200,200)\) in the range of \(x\in (-20,20)\) if \(\epsilon =0.1\). From the mathematical point of view, the effect for the spatial scale of Rossby waves flow field is briefly analyzed. There results can be further studied in mechanics, atmospheric and oceanic science and other fields. In addition, there is no general method to solve the Analytical solution of the nonlinear partial differential equation in the field of integrable systems. The symbol calculation method based on neural networks proposed by Zhang et al. [42,43,44,45] open up a general symbolic computing path for the analytic solution of NLPDEs, and lays the foundation for the universal method of symbolic calculation of Analytical expression. The problems studied in this paper can be solved by using this method in the future work.