1 Introduction

In geophysical fluid, nonlinear waves for large scale are important for the dynamics of the ocean and atmosphere [1,2,3,4]. In particular, much attention has been paid to the Rossby solitary wave, the waves amplitude evolution satisfied the KdV equation under plane beta approximation and the effect of horizontal shearing flow  [5, 6]. Subsequently, people make further research on the characteristics of Rossby solitary wave and reach many important conclusions [7,8,9,10,11,12,13,14,15,16]. The nonlinear waves have been discussed by many researches in the atmosphere, especially the solitary waves. For example, the solitary waves have been investigated in the mid-atmosphere where the African easterly waves were propagated [17]. The importance of nonlinear wave was also researched in oceanography, some nonlinear internal waves in the deep basin of the South China Sea have been evaluated the mechanisms for their generation and evolution  [18]. Moreover, some forcing factors such as topography are very important in large-scale motion, so the influences of topography on Rossby solitary wave also attract more attention. The interaction between zonal flow and slowly moving free wave could cause atmosphere blocking under the topographic forcing effect  [19]. What is more, the blocking phenomenon is a kind of covibration characteristic of stabilizing balance state under the effect of external source [20,21,22], the large-scale topographic effect even would affect global atmosphere circulation  [23, 24]. The topography function is in relation to longitude and latitude in many researches [25, 26]. Actually, all things on earth are in movement and variation; therefore, the topography and external source also vary with time in the fluid [27,28,29]. Yang [30, 31] derived some new equations governing the behavior of Rossby solitary waves with the effect of topography, and discussed the changes of nonlinear long wave amplitude and waveform with numerical method. So the topographic variable including the temporal and spatial function which is called unstable topography is so important.

We note that because of the multi-scale feature of atmosphere and ocean, most of the above-mentioned researches were carried out by employing multi-scale analysis and perturbation method. These waves are also called weak nonlinear waves. While, besides of the multi-scale method, the variational-asymptotic method is also an effective method to deal with the problem of amplitude modulation of waves, many work has been done to describe the amplitude modulation of trains of solitons [32,33,34,35]. On the other hand, the study of the exact solutions and feature of solitary wave equations is another important issue, many references were given [36,37,38,39,40].

In the present paper, a new forced KdV equation with the topographic effect is derived, then we discuss the effect excited by the topography. Concretely, starting from the quasi-geostrophic potential vorticity equation, in terms of the unstable topography, using scale analysis method, Rossby solitary wave model is derived in Sect. 2. In terms of different topographic conditions, by comparing the waterfall plots, we give the characteristics of the wave amplitude according to the numerical simulation in Sect. 3. Finally, some conclusions are obtained in Sect. 4.

2 Derivation of governing equation

2.1 Governing equation and boundary conditions

Based on the quasi-geostrophic barotropic model in the paper of Pedlosky [41], it is given the vorticity equation including the unstable topography is

$$\begin{aligned}&\left( {\frac{\partial }{\partial t}+\frac{\partial \Psi }{\partial x}\frac{\partial }{\partial y}-\frac{\partial \Psi }{\partial y}\frac{\partial }{\partial x}} \right) \nonumber \\&\quad \times \,\left[ {f+\nabla ^{2}\Psi +\frac{f_0 }{H}h_b (x,y,t)} \right] =0 \end{aligned}$$
(1)

where \(\Psi \) is the stream function, f is the coriolis parameter, \(\nabla ^{2}=\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\) is Laplace operator, \(h_b (x,y,t)\) is the unstable topography. We make nondimensionalization on Eq. (1)

$$\begin{aligned}&(x,y)=L(x^{*},y^{*}), \quad t=\left( {\frac{L}{U}} \right) t^{*}, \nonumber \\&(u,v)=U(u^{*},v^{*}), \quad \Psi =UL\Psi ^{*}\nonumber \\&f=f_0 +\beta _0 y=f_0 +\frac{U}{L^{2}}\beta ^{*}Ly^{*},\nonumber \\&h_b =\frac{H}{f_0 }\frac{U}{L}h_b^*\end{aligned}$$
(2)

substituting Eq. (2) into Eq. (1) yields

$$\begin{aligned}&\left( {\frac{U}{L}\frac{\partial }{\partial t^{*}}+\frac{UL}{L}\frac{\partial \Psi ^{*}}{\partial x^{*}}\frac{1}{L}\frac{\partial }{\partial y^{*}}-\frac{UL}{L}\frac{\partial \Psi ^{*}}{\partial y{ }^*}\frac{1}{L}\frac{\partial }{\partial x^{*}}} \right) \nonumber \\&\quad \times \,\left[ {f_0 +\frac{U}{L^{2}}\beta ^{*}Ly^{*}+\frac{UL}{L^{2}}\nabla ^{2}\Psi ^{*}+\frac{U}{L}h_b^*)} \right] =0\nonumber \\ \end{aligned}$$
(3)

omitting the asterisk, then the nondimensional equation is

$$\begin{aligned}&\left( \frac{\partial }{\partial t}+\frac{\partial \Psi }{\partial x}\frac{\partial }{\partial y}-\frac{\partial \Psi }{\partial y}\frac{\partial }{\partial x}\right) \nonumber \\&\quad \times \,\left[ \beta y+\nabla ^{2}\Psi +h_b (x,y,t)\right] =0 \end{aligned}$$
(4)

the side boundary condition of nondimensional form is

$$\begin{aligned} \frac{\partial \Psi }{\partial x}=0,y=0,1 \end{aligned}$$
(5)

2.2 Derivation of forced KdV equation with topographic forcing

We assume that the stream function form is

$$\begin{aligned} \Psi (x,y,t)= & {} -\int _0^y [u(y)-c_0 +\varepsilon \alpha ]\mathrm{d}y\nonumber \\&+\,\varepsilon \psi (x,y,t) \end{aligned}$$
(6)

where u(y) is the shearing zonal flow, \(\alpha \) is a measure of the proximity of the system to a resonate, and may be referred to as a detuning parameter, \(c_0 \) is equal to the phase speed of linear long wave in the shearing flow, \(\psi (x,y,t)\) is disturbed stream function, \(\varepsilon \) is a small magnitude parameter. We take the function form of topography as

$$\begin{aligned} h_b (x,y,t)=h_0 (y)+\varepsilon h_1 (x,t) \end{aligned}$$
(7)

here \(h_0 (y)\) is the topographic basic function with zonal changes, \(h_1 (x,t)\) is the disturbed function with meridional direction and time changes, substituting Eqs. (6), (7) into Eq. (4), combined with the boundary condition, we derive the equation regarding the disturbed stream function.

$$\begin{aligned}&\left\{ \frac{\partial }{\partial t}+\varepsilon \frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}-\left[ -(u(y)-c_0 +\varepsilon \alpha )+\varepsilon \frac{\partial \psi }{\partial y}\right] \frac{\partial }{\partial x}\right\} \nonumber \\&\quad \times \, \left[ \varepsilon \nabla ^{2}\psi -{u}'(y)+\beta y+h_0 (y)+\varepsilon h_1 (x,t)\right] =0\nonumber \\ \end{aligned}$$
(8)

We look for the weakly nonlinear problem by the multiple scale method, in order to achieve a balance between nonlinearity and dispersion, so we make Gardner–Morikawa conversion on variables x, t,

$$\begin{aligned} X=\varepsilon ^{\frac{1}{2}}x, \quad T=\varepsilon ^{\frac{3}{2}}t \end{aligned}$$
(9)

here \(\varepsilon (0<\varepsilon \ll 1)\) is a small parameter to measure the degree of nonlinearity, and we set

$$\begin{aligned} h_1 (x,t)=\varepsilon H(X,T) \end{aligned}$$
(10)

In order to obtain the asymptotic solution of weak linear problems, substituting Eqs. (9), (10) into Eq. (8), then we have

$$\begin{aligned}&\frac{\partial \psi }{\partial X}[{h}'_0 (y)+\beta -{u}''(y)]+(u(y)-c_0 )\frac{\partial }{\partial X}\frac{\partial ^{2}\psi }{\partial y^{2}}\nonumber \\&\quad +\,\varepsilon \left[ \alpha \frac{\partial }{\partial X}\frac{\partial ^{2}\psi }{\partial y^{2}}+(u(y)-c_0 )\frac{\partial }{\partial X}\frac{\partial ^{2}\psi }{\partial X^{2}}\right. \nonumber \\&\quad +\,\frac{\partial }{\partial T}\left( \frac{\partial ^{2}\psi }{\partial y^{2}}\right) +J\left( \psi , \frac{\partial ^{2}\psi }{\partial y^{2}}\right) \nonumber \\&\quad \left. +\,(u(y)-c_0 )\frac{\partial H(X,T)}{\partial X}\right] \nonumber \\&\quad +\,O(\varepsilon ^{2})=0 \end{aligned}$$
(11)

where

$$\begin{aligned} J[a,b]=\frac{\partial a}{\partial x}\frac{\partial b}{\partial y}-\frac{\partial a}{\partial y}\frac{\partial b}{\partial x} \end{aligned}$$
(12)

the disturbed stream function has small parameter expansion formula as follows

$$\begin{aligned} \psi= & {} \psi _0 (X,y,T)+\varepsilon \psi _1 (X,y,T)\nonumber \\&+\,\varepsilon ^{2}\psi _2 (X,y,T)+\cdots \end{aligned}$$
(13)

substituting Eq. (13) into Eq. (11),

\(\varepsilon ^{0}\) order

$$\begin{aligned}&[u(y)-c_0 ]\frac{\partial ^{2}}{\partial y^{2}}\left( \frac{\partial \psi _0 }{\partial X}\right) \nonumber \\&\quad +\,\left[ {h}'_0 (y)+\beta -{u}''(y)\right] \frac{\partial \psi _0 }{\partial X}=0 \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial \psi _0 }{\partial X}=0, y=0,1 \end{aligned}$$
(15)

we assume \(\psi _0 =A(X,T)\phi _0 (y)\), according to the boundary condition,

$$\begin{aligned}&\left[ \frac{\hbox {d}^{2}}{\hbox {d}y^{2}}+\frac{{h}'_0 (y)+\beta -{u}''(y)}{u(y)-c_0 }\right] \phi _0 (y)=0 \end{aligned}$$
(16)
$$\begin{aligned}&\phi _0 (0)=\phi _0 (1)=0 \end{aligned}$$
(17)

in order to ascertain amplitude A(X, T), we need to solve high-order problem.

\(\varepsilon ^{1}\) order

$$\begin{aligned}&L_1 [\psi _1 ]=-\left\{ L_0 [\psi _0 ]+J\left[ \psi _0,\frac{\partial ^{2}\psi _0 }{\partial y^{2}}\right] \right. \nonumber \\&\quad \left. \left. +\,[u(y)-c_0 ]\frac{\partial H(X,T)}{\partial X}\right] \right\} \end{aligned}$$
(18)
$$\begin{aligned}&\frac{\partial \psi _1 }{\partial X}=0, \quad y=0,1 \end{aligned}$$
(19)

here

$$\begin{aligned} L_0= & {} [u(y)-c_0 ]\frac{\partial ^{3}}{\partial y^{2}\partial X}\nonumber \\&+\,[{h}'_0 (y)+\beta -{u}''(y)]\frac{\partial }{\partial X} \end{aligned}$$
(20)
$$\begin{aligned} L_1= & {} [u(y)-c_0 ]\frac{\partial ^{3}}{\partial X^{3}}+\frac{\partial ^{3}}{\partial T\partial y^{2}}+\alpha \frac{\partial }{\partial X}\frac{\partial ^{2}}{\partial y^{2}} \end{aligned}$$
(21)

according to Eq. (18), we make integration along y interval [0, 1], and get

$$\begin{aligned}&\int _0^1 {\frac{\phi _0 (y)L_1 [\psi _1 ]}{u(y)-c_0 }} \mathrm{d}y =\int _0^1 {\phi _0 (y)} \frac{\partial ^{3}\psi _1 }{\partial y^{2}\partial X}\mathrm{d}y\nonumber \\&\quad +\,\int _0^1 {\frac{1}{u(y)-c_0 }\phi _0 (y)} [{h}'_0 (y)+\beta -{u}''(y)]\frac{\partial \psi _1 }{\partial X}\mathrm{d}y\nonumber \\ \end{aligned}$$
(22)

assuming

$$\begin{aligned} \psi _1 =B(X,T)\phi _1 (y) \end{aligned}$$
(23)

we get

$$\begin{aligned}&\int _0^1 {\frac{\phi _0 (y)L_1 [\psi _1 ]}{u(y)-c_0 }} \mathrm{d}y=\frac{\partial B(X,T)}{\partial X}\nonumber \\&\quad \times \,\left[ \int _0^1 {\phi _0 (y)} \frac{\partial ^{2}\phi _1 (y)}{\partial y^{2}}\mathrm{d}y\right. \nonumber \\&\quad \left. +\int _0^1 {\frac{\phi _0 (y)\phi _1 (y)}{u(y)-c_0 }} ({h}'_0 (y)+\beta -{u}''(y))\mathrm{d}y\right] \end{aligned}$$
(24)

because of

$$\begin{aligned} \phi _0 \frac{\partial ^{2}\phi _1 }{\partial y^{2}}= & {} \frac{\partial }{\partial y}\left( \phi _0 \frac{\partial \phi _1 }{\partial y}\right) -\frac{\partial }{\partial y}\left( \phi _1 \frac{\partial \phi _0 }{\partial y}\right) \nonumber \\&+\,\phi _1 \frac{\partial ^{2}\phi _0 }{\partial y^{2}} \end{aligned}$$
(25)

making integration on both ends along y interval [0, 1], then

$$\begin{aligned}&\int _0^1 {\phi _0 (y)} \frac{\partial ^{2}\phi _1 (y)}{\partial y^{2}}\mathrm{d}y\\&\quad =\int _0^1 \left[ \frac{\partial }{\partial y}\left( \phi _0 \frac{\partial \phi _1 }{\partial y}\right) -\frac{\partial }{\partial y}\left( \phi _1 \frac{\partial \phi _0 }{\partial y}\right) +\phi _1 \frac{\partial ^{2}\phi _0 }{\partial y^{2}} \right] \mathrm{d}y\nonumber \end{aligned}$$
(26)

based on the boundary condition Eq. (19), there is \(\phi _1 (0)=\phi _1 (1)=0\), then the above equation can be written as

$$\begin{aligned} \int _0^1 {\phi _0 (y)} \frac{\partial ^{2}\phi _1 (y)}{\partial y^{2}}\mathrm{d}y=\int _0^1 {\phi _1 \frac{\partial ^{2}\phi _0 }{\partial y^{2}}} \mathrm{d}y \end{aligned}$$
(27)

substituting Eq. (27) into Eq. (24) leads to

$$\begin{aligned}&\int _0^1 {\frac{\phi _0 (y)L_1 [\psi _1 ]}{u(y)-c_0 }} \mathrm{d}y=\frac{\partial B(X,T)}{\partial X}\nonumber \\&\quad \times \,\left[ \int _0^1 \phi _1 \left( \frac{\partial ^{2}\phi _0 }{\partial y^{2}} +\frac{\phi _0 (y)}{u(y)-c_0 }({h}'_0 (y)+\beta -{u}''(y))\right) \mathrm{d}y\right] \nonumber \\ \end{aligned}$$
(28)

based on Eq. (16), we get

$$\begin{aligned} \int _0^1 {\frac{\phi _0 (y)L_1 [\psi _1 ]}{u(y)-c_0 }} \mathrm{d}y=0 \end{aligned}$$
(29)

so

$$\begin{aligned}&\int _0^1 {\phi _0 (y)} \frac{\partial H(X,T)}{\partial X}\mathrm{d}y\nonumber \\&\quad +\,\alpha \int _0^1 {\frac{\phi _1 (y)}{u(y)-c_0 }} \frac{\partial }{\partial X}\frac{\partial ^{2}\psi _1 }{\partial y^{2}}\mathrm{d}y\nonumber \\&\quad +\,\int _0^1 {\frac{\phi _0 (y)}{u(y)-c_0 }} L_0 [\psi _0 ]\mathrm{d}y\nonumber \\&\quad \left. +\int _0^1 {\frac{\phi _0 (y)}{u(y)-c_0 }} J\left[ \psi _0 ,\frac{\partial ^{2}\psi _0 }{\partial y^{2}}\right] \right\} \mathrm{d}y=0 \end{aligned}$$
(30)

based on Eq. (24),

$$\begin{aligned}&\int _0^1 {\frac{{h}'_0 (y)+\beta -{u}''(y)}{(u(y)-c_0 )^{2}}\phi _0^2 (y)} \mathrm{d}y\frac{\partial A}{\partial T}\nonumber \\&\left. \quad +\int _0^1 {\frac{\phi _0^3 (y)}{u(y)-c_0 }} \frac{\hbox {d}}{\hbox {d}y}\left( \frac{{h}'_0 (y)+\beta -{u}''(y)}{u(y)-c_0 }\right) \right] dyA\frac{\partial A}{\partial X}\nonumber \\&\quad +\,\alpha \frac{\partial A}{\partial X}\int _0^1 {\frac{\phi _1 (y)}{u(y)-c_0 }} \frac{\partial ^{2}\phi _1 (y)}{\partial y^{2}}\mathrm{d}y\nonumber \\&\quad -\,\int _0^1 {\phi _0^2 (y)} \mathrm{d}y\frac{\partial ^{3}A}{\partial X^{3}}=\frac{\partial H(X,T)}{\partial X}\int _0^1 {\phi _0 (y)} \mathrm{d}y \end{aligned}$$
(31)

Finally we get

$$\begin{aligned} \frac{\partial A}{\partial T}+\alpha \frac{\partial A}{\partial X}+\alpha _1 A\frac{\partial A}{\partial X}+\alpha _2 \frac{\partial ^{3}A}{\partial X^{3}}=\alpha _3 \frac{\partial H(X,T)}{\partial X}\nonumber \\ \end{aligned}$$
(32)

where

$$\begin{aligned}&I=\int _0^1 {\frac{{h}'_0 (y)+\beta -{u}''(y)}{(u(y)-c_0 )^{2}}\phi _0^2 (y)} \mathrm{d}y \end{aligned}$$
(33)
$$\begin{aligned}&\alpha _1 =\left. \frac{1}{I}\int _0^1 {\frac{\phi _0^3 (y)}{u(y)-c_0 }} \frac{\hbox {d}}{\hbox {d}y}\left( \frac{{h}'_0 (y)+\beta -{u}''(y)}{u(y)-c_0 }\right) \right] \mathrm{d}y \end{aligned}$$
(34)
$$\begin{aligned}&\alpha _2 =-\frac{1}{I}\int _0^1 {\phi _0^2 } (y)\mathrm{d}y \end{aligned}$$
(35)
$$\begin{aligned}&\alpha _3 =\frac{1}{I}\int _0^1 {\phi _0 } (y)\mathrm{d}y \end{aligned}$$
(36)

Regarding Eq. (32), in terms of X, we make integration from \(-\infty \) to \(+\infty \). Setting \(\left| X \right| \rightarrow \infty \), \(A(X,T)\rightarrow 0\), and we get the mass equation about the solitary wave.

$$\begin{aligned} \frac{\partial }{\partial T}\int _{-\infty }^\infty {A(X,T)\mathrm{d}X=} \int _{-\infty }^\infty {\frac{\partial H(X,T)}{\partial X}\mathrm{d}X} \end{aligned}$$
(37)

Eq. (37) indicates that because of the forced effect, the solitary wave mass is not conserved, with time changes, when the forced member value becomes zero, the mass will be conserved. Then, A(X, T) multiply by Eq. (32), and making integration on X from \(-\infty \) to \(+\infty \), we set \(\left| X \right| \rightarrow \infty \), \(A(X,T)\rightarrow 0\), and get the energy equation about the solitary wave.

$$\begin{aligned}&\frac{\partial }{\partial T}\int _{-\infty }^\infty \frac{1}{2}A^{2}(X,T)\mathrm{d}X\nonumber \\&\quad = \alpha _3 \int _{-\infty }^\infty {A(X,T)\frac{\partial H(X,T)}{\partial X}\mathrm{d}X} \end{aligned}$$
(38)

obviously, the energy of solitary wave will change with the topographic forcing.

In the absence of topographic forcing and parameter \(\alpha \), Eq. (32) degenerates to the standard KdV equation. The solution of KdV equation has been studied all the time, and single solitary and double solitary wave solutions were obtained by the inverse scattering [42], the position solutions were found later which exhibit the positive eigenvalues embedded into the continuous spectrum [43, 44], the periodic wave solutions were obtained with Jacobian elliptic functions and the Exp-function methods [45,46,47]. Meanwhile, the exact n-soliton solution is given by Ablowitz and Clarkson [48]. Le and Nguyen developed the theory of amplitude modulation of waves governed by KdV equation with the variational-asymptotic method [33], and two asymptotic solutions describing the amplitude modulation of trains of solitons and of positon show quite agreement with the exact solutions [34]. In all of the above studies, the clock shape solitary wave solution is \(A(X,T)=M\sec h^{2}\Big (\sqrt{\frac{\alpha _1 M}{12\alpha _2 }}(X-\frac{\alpha _1 M}{3}T)\Big ]\), where M is the maximum amplitude at the initial moment, \(\frac{\alpha _1 M}{3}\) is the moving speed of the solitary waves, and \(\sqrt{\frac{12\alpha _2 }{\alpha _1 M}}\)is the width of the solitary waves, \(\alpha _1 \) and \(\alpha _2 \) are determined by the solution of Eqs. (16), (17). When the right end is inhomogeneous, Eq. (32) has no analytical solution and needs to be solved with the numerical method.

3 Numerical method and conclusion

3.1 Calculation method and process

Considering the weak shear zonal flow: \(u=u_0 +\delta y\), (\({h}'_0 (y)=H_0 +\delta y)\), \(0<\delta \ll 1\), \(H_0 \) is a constant and the topographic slope changes slowly, let \(\delta =0.0024\), \(u_0 =0.5\), \(H_0 =1\), and the shearing characteristic of base flow u(y), in terms of Eq. (16) with eigenvalue problem. We make asymptotic solution, and set

$$\begin{aligned} \phi _0= & {} \phi _0 ^{(0)}+\delta \phi _0 ^{(1)}+\cdots \nonumber \\ c_0= & {} c_{00} +\delta c_{01} +\cdots \end{aligned}$$
(39)

the approximate equations of each order about \(\delta \) can be written as

\(\delta ^{0}\) order:

$$\begin{aligned} \left\{ {\begin{array}{ll} \frac{\hbox {d}^{2}\phi _0 ^{(0)}}{\hbox {d}y^{2}}+\frac{\beta +H_0 }{u_0 -c_{00} }\phi _0 ^{(0)}=0 \\ \phi _0 ^{(0)}(y)=0,y=0,1 \\ \end{array}} \right. \end{aligned}$$
(40)

obviously the solution of Eq. (40) is

$$\begin{aligned} \phi _0 ^{(0)}=\sin m\pi y, \quad c_{00} =u_0 -\frac{\beta +H_0 }{m^{2}\pi ^{2}} \end{aligned}$$

\(\delta ^{1}\) order:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\hbox {d}^{2}\phi _0 ^{(1)}}{\hbox {d}y^{2}}+\frac{\beta +H_0 }{u_0 -c_{00} }\phi _0 ^{(1)}=-\frac{(y-c_{01} )}{u_0 -c_{00} }\frac{\hbox {d}^{2}\phi _0 ^{(0)}}{\hbox {d}y^{2}}-\frac{y\phi _0 ^{(0)}}{u_0 -c_{00} } \\ \phi _0 ^{(1)}(y)=0,y=0,1 \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(41)

we get

$$\begin{aligned} \left\{ {\begin{array}{lll} \frac{\hbox {d}^{2}\phi _0 ^{(1)}}{\hbox {d}y^{2}}+\frac{\beta +H_0 }{u_0 -c_{00} }\phi _0 ^{(1)}&{}=\frac{y-c_{01} }{u_0 -c_{00} }m^{2}\pi ^{2}\sin m\pi y\\ &{}\quad -\frac{y}{u_0 -c_{00} }\sin m\pi y \\ \phi _0 ^{(1)}(y)=0,y=0,1 \\ \end{array}} \right. \end{aligned}$$
(42)

\(c_{01} =\frac{m^{2}\pi ^{2}\hbox {-}1}{2m^{2}\pi ^{2}},\) the solution of Eq. (42) is

$$\begin{aligned} \phi _0 ^{(1)}= & {} \frac{1}{4m\pi }\left( \frac{m^{2}\pi ^{2}-1}{u_0 -c_{00} }\right) \nonumber \\&\times \left[ (y-y^{2})\cos m\pi y+\frac{y}{m\pi }\sin m\pi y\right] \end{aligned}$$
(43)

Finally, \(\phi _0 \) approximate solution is

$$\begin{aligned} \phi _0= & {} \sin m\pi y+\frac{\delta }{4m\pi }\left( \frac{m^{2}\pi ^{2}-1}{u_0 -c_{00} }\right) \nonumber \\&\times \left[ (y-y^{2})\cos m\pi y+\frac{y}{m\pi }\sin m\pi y\right] \end{aligned}$$
(44)

Considering the particularity of Eq. (32), by means of the pseudo-spectral method [49], we find out the numerical solution of Eq. (32). The concrete method is using discrete Fourier transform from the aspect of space, and fourth-order Runge–Kutta method from the aspect of time, then we make numerical solution on such a problem by means of Eq. (32), and discuss the problem in one cycle \([-\pi ,\pi ]\) from the aspect of space. First of all, making average segmentation on the interval into N grid points, \(x_j =-\pi +\frac{2\pi j}{N}\), here \(j=0,\ldots ,N-1\), we take the discrete Fourier transform \(\hat{{u}}(k,t)\), let

$$\begin{aligned}&\hat{{u}}(k,t)=F(u)=\frac{1}{N}\sum _{j=0}^N {u(x_j } ,t)e^{-\hbox {i}kx_j }, \nonumber \\&k=-\frac{N}{2}+1,\ldots ,\frac{N}{2} \end{aligned}$$
(45)

then the discrete Fourier transform can be approximately indicated as

$$\begin{aligned} u(x_j, t)=F^{-1}(\hat{{u}})=\sum _{k=-N/2+1}^{N/2} {\hat{{u}}(k,t)e^{\hbox {i}kx_j }} \end{aligned}$$
(46)

and the differential expression formula on the Fourier transform is

$$\begin{aligned} \frac{\partial ^{n}\hat{{u}}(k,t)}{\partial x^{n}}=(\hbox {i}k)^{n}\hat{{u}}(k,t) \end{aligned}$$
(47)

according to the above formulas, \(A_x =F^{-1}(\hbox {i}kF(A))\), \(A_{xxx} =-F^{-1}(\hbox {i}k^{3}F(A))\), we use the fourth-order Runge–Kutta method from the aspect of time

$$\begin{aligned} A_T= & {} -\alpha _1 AF^{-1}(\hbox {i}kF(A))\nonumber \\&+\,\alpha _2 F^{-1}(\hbox {i}k^{3}F(A))\nonumber \\&+\,\alpha _3 F^{-1}(\hbox {i}kF(H)) \end{aligned}$$
(48)

let

$$\begin{aligned}&f(A_n, T_n )=-\alpha _1 AF^{-1}(\hbox {i}kF(A_n ))\nonumber \\&\quad +\,\alpha _2 F^{-1}(\hbox {i}k^{3}F(A_n )) \end{aligned}$$
(49)
$$\begin{aligned}&a=f(A_n ,T_n )+\alpha _3 F^{-1}(\hbox {i}kF(H(T_n ))) \end{aligned}$$
(50)
$$\begin{aligned}&b=f\left( A_n +\frac{\Delta T}{2}a,T_{n+\frac{1}{2}}\right) \nonumber \\&\quad +\,\alpha _3 F^{-1}\left( \hbox {i}kF\left( H\left( T_{n+\frac{1}{2}}\right) \right) \right) \end{aligned}$$
(51)
$$\begin{aligned}&c=f\left( A_n +\frac{\Delta T}{2}b,T_{n+\frac{1}{2}} \right) \nonumber \\&\quad +\,\alpha _3 F^{-1}\left( \hbox {i}kF\left( H\left( T_{n+\frac{1}{2}} \right) \right) \right) \end{aligned}$$
(52)
$$\begin{aligned}&d=f(A_n +c\Delta T,T_{n+1} )\nonumber \\&\quad +\,\alpha _3 F^{-1}\left( \hbox {i}kF\left( H\left( T_{n+1} \right) \right) \right) \end{aligned}$$
(53)
$$\begin{aligned}&A_{n+1} =A_n +\frac{1}{6}\Delta T(a+2b+2c+d) \end{aligned}$$
(54)

3.2 The effects of unstable topography and steady topography

During numerical calculation process, we get the topography expression formula as

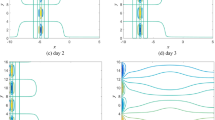
$$\begin{aligned} H(X,T)=-e^{\frac{-(X+50)^{2}}{4}+MT} \end{aligned}$$
(55)

M is given parameter, regarding the correlation coefficient of given base flow u(y) and Eq. (16). When meridional wave number \(m=1\), we can calculate the coefficients \(\alpha _1, \alpha _2, \alpha _3 \) in Eq. (32) and get \(\alpha _1 =-0.003, \alpha _2 =-0.02\), \(\alpha _3 =-0.03\), it is given for a detuning parameter \(\alpha =0.2\), and we provide the initial condition \(A(X,T)=0\), \(T=0\), Figs. 1, 2, 3, 4, 5 and 6 show the numerical results.

When \(M=0\), the solitary wave excited by the topography in the forced area, the amplitude almost remains invariant. Cnoidal wave trains are produced in the downstream position, and no wave movement is produced in the upward position. When \(M<0\), for \(M=-1\times 10^{-2}\), it is shown that the solitary wave amplitude first increases and then decreases with time. The amplitude of cnoidal wave trains produced in the downstream position comparatively strengthen and wavelength shortens. When \(M=1\times 10^{-2}\), the results tend to be different circumstances, the solitary wave amplitude increases rapidly with time T.

When meridional wave number \(m=2\), we can calculate the coefficients \(\alpha _1 =1.3\times 10^{-4}\), \(\alpha _2 =-8\times 10^{-4}\), \(\alpha _3 =1.5\times 10^{-4}\), it is given a detuning parameter \(\alpha =0.01\), here giving the initial condition \(A(X,T)=0 T=0\), Figs. 7, 8 show the numerical results.

Fig. 1
figure 1

The waveform excited by the topography (\(m=1\)), T from 0 to 200, \(M=0\)

Full size image
Fig. 2
figure 2

The waveform excited by the topography (\(m=1\)), \(T=200\), \(M=0\)

Full size image
Fig. 3
figure 3

The waveform excited by the topography (\(m=1\)), T from 0 to 200, \(M=-0.01\)

Full size image
Fig. 4
figure 4

The waveform excited by the topography (\(m=1\)), \(T=200\), \(M=-0.01\)

Full size image
Fig. 5
figure 5

The waveform excited by the topography (\(m=1\)), T from 0 to 200, \(M=0.01\)

Full size image
Fig. 6
figure 6

The waveform excited by the topography (\(m=1\)), \(T=200\), \(M=0.01\)

Full size image
Fig. 7
figure 7

The waveform excited by the topography (\(m=2\)), T from 0 to 5000, \(M=0\)

Full size image
Fig. 8
figure 8

The waveform excited by the topography (\(m=2\)), T from 0 to 5000, \(M=-0.01\)

Full size image

Because of the changes of value \(\alpha \), \(\alpha _1 \), \(\alpha _2 \), the wave trains shown in Figs. 7 and 8 demonstrate the characteristics of long exciting time, slow propagation speed and small amplitude. It is seen that the opposite signs of \(\alpha _3 \) make the topography forms changes, thereby the amplitude form of solitary wave is sunken downward. Comparing \(m=2\) with \(m=1\), the amplitude of solitary wave becomes much smaller. When M changes, comparing Fig. 1 with Fig. 7, it can be observed that the amplitude of wave changes are similar with meridional wave number \(m=1\), but \(M=-1\times 10^{-2}\), the position of the solitary wave moves downstream with time.

4 Conclusion

This paper derives the nonlinear forced KdV equation with unstable topography, and discusses the mass and energy conservation of solitary wave. Without the topographic effect, the mass and energy will be conserved. With the topographic forcing, the mass and energy will not be conserved. The related results are numerically simulated with the pseudo-spectral method.

  1. (1)

    The interaction effect between solitary waves and stable topographic forms, no matter the meridional wave number \(m=1\) or \(m=2\), the amplitude of solitary wave is almost unchanged. Comparing with the train of waves \(m=1\), the amplitude of the solitary waves and downstream train of waves are weaker when \(m=2\) under the effect of the topography.

  2. (2)

    The differences between the stable topography and the solitary wave excited by the unstable topography. When \(M<0\), the wave trains amplitude change obviously, the amplitude of the solitary wave decrease, the downstream cosine wave amplitude increases with the time, wavelength becomes shorter. When \(M>0\), the topographic effect is obvious, the amplitude of the solitary wave is the largest at the end of calculation time.

  3. (3)

    The change of topography variable of \(h_0 (y)\) has relationship with the coefficient of forced KdV equation, and it has an effect on the numerical solution of whole model. Therefore, the topography affects not only the spatial structure of wave, but also the amplitude of wave.

  4. (4)

    The model of Rossby solitary waves is derived by perturbation expansions and stretching transformations of time and space; it is interesting to derive the equations by using the direct variational-asymptotic analysis [32, 33], so the study of amplitude modulation of n-soliton solutions for the Rossby waves will be the topics of our following work.