Introduction

Vibration control has always been a research hotspot in engineering applications, wherein passive vibration control is widely applied due to the advantages of its simple structure, low cost, and lack of demand for external energy. However, appropriately designed linear vibration absorbers can only reduce structural vibration in a relatively narrow frequency range [1, 2]. Therefore, nonlinear elements were introduced into linear vibration absorbers to broaden the vibration reduction frequency band [3]. Vakakis [4] first proposed a nonlinear energy sink (NES), which has the advantages of small added mass and a wide working frequency band. As a passive shock absorber, the NES has quickly attracted much attention in the field of vibration reduction [5,6,7,8,9]. Furthermore, the target energy transfer characteristics of an NES further improve its vibration absorption performance [10,11,12].

The introduction of nonlinearity complicates the dynamic response of the associated system. Thus, many investigations have been devoted to the dynamics of systems consisting of coupled linear and nonlinear oscillators. Zang and Chen [13] investigated the complex dynamic behaviors of a single-degree-of-freedom oscillator coupled with an NES subjected to harmonic excitation. Grinberg et al. [14] studied the periodic, quasiperiodic and chaotic responses of a primary system coupled to a two-degrees-of-freedom (2DOF) NES and found that the additional degree-of-freedom of the NES could considerably improve its vibration reduction performance. Tsakirtzis et al. [15] studied the complex dynamics of linear oscillators coupled to NESs with multiple degrees of freedom. Substantial passive targeted energy transfer from the linear to the nonlinear subsystem can be archived over a wide frequency. Furthermore, combining multiple NESs in parallel can effectively improve the target energy transmission capacity [16, 17]. Sun and Chen [18] analyzed the dynamic behavior of a coupled system composed of a nonlinear primary oscillator and an NES under harmonic excitation. The results showed that properly reducing the nonlinear stiffness of the NES could eliminate the high branch response and improve the damping efficiency of the NES with respect to the primary system.

However, in most engineering applications, the main systems are usually modeled as continuous structures, such as beams and plates, rather than discrete systems. Georgiades and Vakakis [19] first extended the applicability of NESs to continuous systems. They numerically showed that an appropriately designed and placed NES could irreversibly absorb and locally dissipate a large portion of the vibration energy of a beam subjected to impulse excitations. Their results provided an insight into the implementation of the NESs for vibration reduction in practical engineering structures. Samani [20] demonstrated the effectiveness of NESs applied to beams excited by axially moving loads and considered several optimization strategies to enhance the vibration absorption performance. Modeling an aircraft's motion as an axial moving beam, Zhang et al. [21] studied the vibration suppression performance of an NES to the aircraft under heat-induced vibration and found that the appropriate NES parameters could realize the rapid vibration suppression for the main structure. Mamaghani et al. [22] studied the vibration control of a flow transmission pipeline with an NES and analyzed the influences of the NES position, damping, fluid velocity, and other factors on the dynamic response of the structure. Ahmadabadi [23] analyzed the vibration reduction performance of a cantilever beam attached with grounded and ungrounded configurations of NESs, respectively. The necessary conditions for achieving target energy transfer were discussed by evaluating the nonlinear normal modes. Parseh et al. [24] investigated the steady-state dynamics of a beam attached with an NES subjected to harmonic excitation under different boundary conditions. To study the targeted energy transfer from a nonlinear continuous system to an NES, Kani et al. [25] analyzed the targeted energy transfer between multiple modes of a nonlinear beam and an NES as well as the dissipation of the oscillating energy of the beam. Zhang et al. [26] studied the vibration control effects of an NES on a laminated composite beam in hygrothermal and thermal environments environment. Zhang and Chen [27] analyzed the vibration reduction effect of an NES on a geometric nonlinear plate.

There are strict requirements for the mass of an additional shock absorber in aerospace and structural engineering, so research on the optimal designs of shock absorbers has always been a problem worthy of study. In 2002, Smith [28] proposed an inertial element, known as inerter which could provide inertia several times its own mass. Recently, the inerter has been successfully applied for vibration absorption and reduction for many structures, such as aircrafts [29, 30], vehicles [31], and buildings [32]. Zhang et al. [33, 34] integrated an inerter into an NES to enhance the vibration reduction of the NES on elastic structures. They revealed that the inertial NES could suppress elastic beams' multimodal transverse bending vibration.

Some recent studies on the reduction of vibrations of elastic structures have focused on elastic or nonlinear boundaries instead of classical boundaries. Ding et al. [35, 36] investigated the force transmission of a viscoelastic beam with a new vertical elastic support boundary. The study provided a new direction for the study of vibration isolation of elastic structures. Mao [37] first introduced an analytical method for analyzing flexible structures with nonlinear elastic boundary conditions. Ye et al. [38] studied the complex dynamic characteristics of micro bending beams with nonlinear boundary conditions. The results showed that both nonlinear boundary conditions and the initial curvature could significantly affect the vibration of curved flexible structures.

As reviewed above, although many studies have been dedicated to improving the vibration reduction performance of NESs to beams with normal boundary conditions, the applicability of inertial NESs to the vibration mitigation of beams with asymmetric elastic supports is still limited. This particular beam model with asymmetric elastic supports can be degenerated into a cantilever beam or clamped-elastically supported beam.

The present paper establishes a dynamic model for a cantilever beam with a vertical spring on its free end by Hamilton's principle. A light inertial NES is installed at the elastic support end to suppress the multi-modal resonance of the beam. The Dirac function is used to deal with the nonlinearity introduced by the NES on the boundary. The finite element method verifies the frequencies and modes obtained in this paper. Then, the steady-state response of the beam is obtained according to the Runge–Kutta method, and the correctness of the results is verified by the harmonic balance method (HBM). Finally, the suppression effect of the NES on the resonant amplitude of the beam is analyzed, and the parameters of the NES are optimized to improve its performance.

Dynamic model

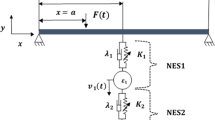
Figure 1 shows the dynamic model of an elastic beam with a nonlinear energy sink attached to its right end. The left end of the beam is clamped, and the right end of the beam is linearly elastically supported. \(L\) denotes the length of the beam. \(t\) and \(x\) represent the time and axial coordinate of the beam, respectively. k means the stiffness of the vertical springs at the right end of the beam. \(w\left( {x,t} \right)\) is the displacement of the transverse vibration of the beam with respect to the \(x\) coordinate. \(v\left( t \right)\) and \(w_{0}\) are the displacements of the NES and the right end of the beam, respectively. The beam is excited by a uniformly distributed harmonic force excitation \(f\left( {x,t} \right) = f_{0} \cos \left( {\Omega t} \right)\), where \(f_{0}\) and \(\Omega\) are the amplitude and frequency of the uniformly distributed harmonic force, respectively. \(b_{m}\) is the inertance of the NES installed on the right end of the beam. \(k_{nes}\) and \(\mu\) are the cubic nonlinear stiffness and the linear damping of the NES, respectively.

Fig. 1
figure 1

Dynamic model of an elastic beam with an inertial NES

Full size image

The beam is considered as the Euler–Bernoulli beam model with a uniform cross-section. The kinetic energy of the beam is given as

$$T = \frac{1}{2}\int_{0}^{L} {\rho A\left( {\frac{\partial w}{{\partial t}}} \right)^{2} } dx$$
(1)

where \(\rho\) and \(A\) are the density and the cross-sectional area of the beam, respectively.

The potential energy of the beam is obtained as

$$U_{v} = \frac{1}{2}\int_{0}^{L} {EI\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} dx}$$
(2)

where \(E\) and \(I\) are Young's modulus and the moment of inertia of the cross section, respectively.

The potential energy of the vertically supported spring can be expressed as

$$U_{s} = \frac{1}{2}kw_{0}^{2}$$
(3)

where \(w_{0}\) is the displacement of the right end of the beam.

Therefore, the potential energy of the beam-spring system is

$$U = \frac{1}{2}\int_{0}^{L} {EI\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)}^{2} dx{ + }\frac{1}{2}kw_{0}^{2}$$
(4)

At the right end of the beam, the force generated by the NESs can be expressed as

$$F_{nes} = k_{nes} (w_{0} - v)^{3} + \mu \left(\frac{{\partial w_{0} }}{\partial t} - \frac{\partial v}{{\partial t}}\right)$$
(5)

In addition, the damping term is introduced by using the Kelvin material constitutive model [39]

$$E = E + c\frac{d}{dt}$$
(6)

where \(c\) is the viscous damping coefficient of the beam.

The virtual work done by the force of the NES and the external force is given as

$$\delta W{ = }\delta W_{nes} + \delta W_{f} = - F_{nes} \delta w_{0} - \int_{0}^{L} {f\delta wdx}$$
(7)

where \(\delta W_{nes}\) and \(\delta W_{f}\) represent the virtual work done by the NES and the uniformly distributed harmonic force, respectively.

Hamilton's principle is applied to obtain the governing equations of the beam with the NES. Hamilton's principle takes the following form

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta W} \right)} dt = 0$$
(8)

The dimensionless variables and parameters are introduced as follows

$$\overline{x} = \frac{x}{L},\overline{w} = \frac{w}{L},\overline{w}_{0} = \frac{{w_{0} }}{L},\overline{v} = \frac{v}{L},\overline{t} = \frac{t}{L}\sqrt {\frac{E}{\rho }} ,$$
$$\omega = \Omega L\sqrt {\frac{\rho }{E}} ,\lambda = \frac{1}{L}\sqrt{\frac{I}{A}} ,\alpha = \frac{c}{L}\sqrt {\frac{1}{E\rho }} ,\overline{k} = \frac{{kL^{3} }}{EI}$$
$$\overline{f}_{0} = \frac{L}{EA}f_{0} ,\zeta = \frac{{b_{m} }}{\rho AL},\overline{k}_{nes} = \frac{{L^{3} }}{EA}k_{nes} ,\overline{\mu } = \frac{\mu }{A}\sqrt {\frac{1}{E\rho }}$$
(9)

Substituting Eqs. (1)–(7) and (9) into Eq. (8), the dimensionless governing equations of the clamped-elastically supported beam can be obtained as

$$\frac{{\partial^{2} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{t}^{2} }} + \lambda^{2} \frac{{\partial^{4} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{4} }} + \alpha \lambda^{2} \frac{{\partial^{5} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{4} \partial \overline{t}}} + \overline{f}_{0} \cos \left( {\omega \overline{t}} \right) = 0$$
(10)

The dimensionless nonlinear boundary conditions of the beam can be written as

$$\left. {\overline{w}\left( {\overline{x},\overline{t}} \right)} \right|_{{\overline{x} = 0}} = 0,\left. {\frac{{\partial \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}}}} \right|_{{\overline{x} = 0}} = 0,\left. {\frac{{\partial^{2} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{2} }}} \right|_{{\overline{x} = 1}} { = 0}$$
$$\left. {\frac{{\partial^{3} \left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{3} }}} \right|_{{\overline{x} = 1}} = \overline{k}\overline{w}_{0} + \overline{k}_{nes} \left( {\overline{w}_{0} - \overline{v}} \right)^{3} + \overline{\mu }\left( {\frac{{\partial \overline{w}_{0} }}{{\partial \overline{t}}} - \frac{{\partial \overline{v}}}{{\partial \overline{t}}}} \right)$$
(11)

The dimensionless governing equation of the NES mounted at the right end of the beam is derived as

$$\zeta \frac{{\partial^{2} \overline{v}}}{{\partial \overline{t}^{2} }} + \overline{k}_{nes} \left( {\overline{v} - \overline{w}_{0} } \right)^{3} + \overline{\mu }\left( {\frac{{\partial \overline{v}}}{{\partial \overline{t}}} - \frac{{\partial \overline{w}_{0} }}{{\partial \overline{t}}}} \right) = 0$$
(12)

In the references [40, 41], Ding et al. treated the nonlinear restoring force and damping force in the boundary conditions as the external excitations subjecting to the beam and verified this special treatment by the finite difference method. According to this treatment for dealing with nonlinear boundary conditions, the Dirac function \(\delta \left( {\overline{x}} \right)\) is applied to transfer the nonlinear term and damping term in Eq. (11) into the external excitations acting to the right end of the beam. Consequently, Eqs. (10) and (11) can be rewritten as

$$\begin{gathered} \int_{0}^{1} {\left( {\frac{{\partial^{2} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{t}^{2} }} + \lambda^{2} \frac{{\partial^{4} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{4} }} + \alpha \lambda^{2} \frac{{\partial^{5} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{4} \partial \overline{t}}} + \overline{f}_{0} \cos \left( {\omega \overline{t}} \right)} \right)} dx \hfill \\ + \left[ {\overline{k}_{nes} \left( {\overline{w}_{0} - \overline{v}} \right)^{3} + \overline{\mu }\left( {\frac{{\partial \overline{w}_{0} }}{{\partial \overline{t}}} - \frac{{\partial \overline{v}}}{{\partial \overline{t}}}} \right)} \right]\delta \left( {\overline{x} - 1} \right) = 0 \hfill \\ \end{gathered}$$
(13)
$$\left. {\overline{w}\left( {\overline{x},\overline{t}} \right)} \right|_{{\overline{x} = 0}} \,=\, 0,\left. {\frac{{\partial \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}}}} \right|_{{\overline{x} = 0}} = 0,\left. {\frac{{\partial^{2} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{2} }}} \right|_{{\overline{x} = 1}} { = 0},\left. {\frac{{\partial^{3} \left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{3} }}} \right|_{{\overline{x} = 1}} \,=\, \overline{k}\overline{w}_{0}$$
(14)

where the Dirac delta function \(\delta \left( {\overline{x} - 1} \right)\) indicates the location of the interaction force.

Free Vibration

In this section, the natural frequencies and modal functions of the linear system are solved. Without nonlinear terms and damping, the corresponding Eq. (13) of the linear transverse vibration of the beam can be rewritten as

$$\frac{{\partial^{2} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{t}^{2} }} + \lambda^{2} \frac{{\partial^{4} \overline{w}\left( {\overline{x},\overline{t}} \right)}}{{\partial \overline{x}^{4} }}\,{ = }\,0$$
(15)

The transverse vibration displacement can be assumed as

$$\overline{w}\left( {\overline{x},\overline{t}} \right) = \varphi \left( {\overline{x}} \right)q\left( {\overline{t}} \right)$$
(16)

where \(\varphi \left( {\overline{x}} \right)\) denotes the mode function of the beam and \(q\left( {\overline{t}} \right)\) represents the corresponding generalized coordinate. Satisfying the boundary conditions that are clamped at one side and elastically supported on the other side, the mode function \(\varphi \left( {\overline{x}} \right)\) can be defined as

$$\varphi \left( {\overline{x}} \right) = C_{1} \cos \beta \overline{x} + C_{2} \sin \beta \overline{x} + C_{3} {\text{ch}} \beta \overline{x} + C_{4} {\text{sh}} \beta \overline{x}$$
(17)

Substituting Eq. (16) into Eq. (14), the following equations are obtained

$$\varphi \left( 0 \right) = 0,\varphi^{\prime}\left( 0 \right) = 0,\varphi^{\prime\prime}\left( 1 \right) = 0,\varphi^{\prime\prime\prime}\left( 1 \right) - \overline{k}\varphi \left( 1 \right) = 0$$
(18)

The undetermined coefficients \(C_{i} \left( {i = 1,\;2,\;3,\;4} \right)\) and the eigenvalue \(\beta\) can be obtained by solving Eqs. (18). Besides, the relationship \(\beta\) and natural frequencies \(\omega\) can be derived as

$$\beta^{4}\, { = }\,\frac{{\omega^{2} }}{{\lambda^{2} }}$$
(19)

Substituting Eq. (17) into Eq. (18) leads to

$$\left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ { - \cos \beta } & { - \sin \beta } & {{\text{ch}} \beta } & {{\text{sh}} \beta } \\ {\beta^{3} \sin \beta - \overline{k}\cos \beta } & { - \beta^{3} \cos \beta - \overline{k}\sin \beta } & {\beta^{3} {\text{sh}} \beta - \overline{k}{\text{ch}} \beta } & {\beta^{3} {\text{ch}} \beta - \overline{k}{\text{sh}} \beta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ \end{array} } \right] = \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right]$$
(20)

For a nontrivial solution \(C_{i} \ne 0\), the determinant of the coefficient matrix of Eq. (20) should be zero. Thus, the values of \(\beta\) and \(\omega\) can be obtained. Table 1 shows the geometric and material parameters of an aluminum alloy beam considered in the present paper [34].

Table 1 Geometric and material parameters of an aluminum alloy beam
Full size table

Based on the parameters in Table 1, the first four values of \(\beta_{i} \left( {i = 1,2,3,4} \right)\) can be calculated as \(\beta_{1} = 3.4009\), \(\beta_{2} = 5.2012\), \(\beta_{3} = 7.9642\), \(\beta_{4} = 11.0342\). The undetermined coefficients \(C_{i} \left( {i = 1,\;2,\;3,\;4} \right)\) can be accordingly solved, and the corresponding modal functions of the first four orders are obtained as follows.

\(\varphi_{1} \left( {\overline{x}} \right) = 1.0482\cos \left( {3.4009\overline{x}} \right) - \sin \left( {3.4009\overline{x}} \right) - 1.0482{\text{ch}} \left( {3.4009\overline{x}} \right) + {\text{sh}} \left( {3.4009\overline{x}} \right)\),

\(\varphi_{2} \left( {\overline{x}} \right)\, =\, 0.9851\cos \left( {5.2012\overline{x}} \right) - \sin \left( {5.2012\overline{x}} \right) - 0.9851{\text{ch}} \left( {5.2012\overline{x}} \right) + {\text{sh}} \left( {5.2012\overline{x}} \right)\),

\(\varphi_{3} \left( {\overline{x}} \right) = 1.0008\cos \left( {7.9642\overline{x}} \right) - \sin \left( {7.9642\overline{x}} \right) - 1.0008{\text{ch}} \left( {7.9642\overline{x}} \right){ + }{\text{sh}} \left( {7.9642\overline{x}} \right)\),

$$\varphi_{4} \left( {\overline{x}} \right) = \cos \left( {11.0342\overline{x}} \right) - \sin \left( {11.0342\overline{x}} \right) - {\text{ch}} \left( {11.0342\overline{x}} \right) + {\text{sh}} \left( {11.0342\overline{x}} \right)$$
(21)

Then, the analytically derived frequencies and modal functions are compared with results obtained using the finite element method. In software ABAQUS, the finite element numerical calculation is conducted to establish the 2D model of the elastic beam with boundary conditions in which one side is clamped and the other side is elastically supported by a vertical spring. Table 2 shows the comparative results of the frequencies of the beam with the same parameters. Figure 2 demonstrates the first four mode shapes obtained by the present modal functions and the finite element method in software ABAQUS, respectively. A good agreement can be observed by comparing frequencies and mode shapes, verifying the accuracy of the proposed method.

Table 2 Comparison of the first four frequencies of the beam
Full size table
Fig. 2
figure 2

Comparison of the first four mode shapes

Full size image

Numerical and Analytical Solutions

Galerkin Method

The Galerkin method is applied to truncate the partial differential governing Eqs. (12) and (13) into nonlinear ordinary differential equations. The solution of the beam's transverse vibration is assumed as

$$\overline{w}\left( {\overline{x},\overline{t}} \right) = \sum\limits_{k = 1}^{K} {q_{k} \left( {\overline{t}} \right)\varphi_{k} \left( {\overline{x}} \right)}$$
(22)

where \(K\) is the Galerkin truncation order. The trial function \(\varphi_{k} \left( {\overline{x}} \right)\) and the weight function \(\psi_{n} \left( {\overline{x}} \right)\) are expressed as the mode functions of the beam as shown in Eq. (17). The ordinary differential equations of the beam and NES are derived as

$$\begin{gathered} M_{n} \ddot{q}_{n} \left( {\overline{t}} \right) + \lambda^{2} K_{n} q_{n} \left( {\overline{t}} \right) + \alpha \lambda^{2} K_{n} \dot{q}_{n} \left( {\overline{t}} \right){ + }\overline{f}_{0} F_{n} \cos \left( {\omega \overline{t}} \right) \hfill \\ + \left\{ {\overline{k}_{nes} \left[ {\sum\limits_{k = 1}^{K} {\varphi_{k} \left( 1 \right)q_{k} \left( {\overline{t}} \right)} - \overline{v}\left( {\overline{t}} \right)} \right]^{3} + \overline{\mu }\left[ {\sum\limits_{k = 1}^{K} {\varphi_{k} \left( 1 \right)\dot{q}_{k} \left( {\overline{t}} \right) - \dot{\overline{v}}\left( {\overline{t}} \right)} } \right]} \right\}\psi_{n} \left( 1 \right) = 0 \hfill \\ \end{gathered}$$
(23)

where

$$M_{n} = \int_{0}^{1} {\psi_{n} \left( {\overline{x}} \right)} \;\varphi_{n} \left( {\overline{x}} \right)d\overline{x},K_{n} = \int_{0}^{1} {\psi_{n} \left( {\overline{x}} \right)} \;\varphi_{n}^{\left( 4 \right)} \left( {\overline{x}} \right)d\overline{x},F_{n} = \int_{0}^{1} {\varphi_{n} } \left( {\overline{x}} \right)d\overline{x}$$
(24)
$$\zeta \ddot{\overline{v}}\left( {\overline{t}} \right) + \overline{k}_{nes} \left[ {\overline{v}\left( {\overline{t}} \right) - \sum\limits_{k = 1}^{K} {\varphi_{k} \left( 1 \right)} \;q_{k} \left( {\overline{t}} \right)} \right]^{3} + \overline{\mu }\left[ {\dot{\overline{v}}\left( {\overline{t}} \right) - \sum\limits_{k = 1}^{K} {\varphi_{k} \left( 1 \right)\dot{q}_{k} \left( t \right)} } \right] = 0$$
(25)

The response of the beam can be numerically calculated by the fourth-order Runge–Kutta method based on Eqs. (23) and (25). The parameters of the inertial NES are given as mass of the inerter \(m_{nes} = 0.0028{\text{kg}}\), Inertance coefficient \(\gamma = 100\), Damping \(\mu = 1{\text{N}} \cdot {\text{s}} \cdot {\text{m}}^{ - 1}\), and Nonlinear stiffness \(k_{nes} = 1 \times 10^{7} {\text{N}} \cdot {\text{m}}^{{ - 3}}\). Based on the reference [42], this paper adopts a ballscrew inerter whose mass is less than 1% of that of the elastic beam. The inertance of the inerter is given as

$$b_{m} = \gamma m_{nes}$$
(26)

where \(m_{nes}\) is the mass of the inerter of the NES, and the inertance coefficient \(\gamma\) is in the range of \(60 - 240\). The initial values are given as

$$q_{1} = 0.025,\dot{q}_{1} = 0,q_{i}\, \left( {i = 2,3,4...,K} \right) = 0,\dot{q}_{i} = 0,\overline{v} = \dot{\overline{v}} = 0$$
(27)

Then, the effects of the Galerkin truncation order \(K\) on the calculation accuracy are analyzed. Figure 3 shows the free vibration responses of the beam with respect to the 2nd, 4th and 6th order Galerkin truncations. It can be observed that the responses of the 4th and 6th order truncation are almost consistent. In contrast, these results are different from the responses of the 2nd order truncation. Consequently, considering the calculation accuracy and convenience, the 4th order Galerkin truncation is employed in the following analysis.

Fig. 3
figure 3

Time history of the free vibration of the beam at right end with different truncation orders

Full size image

Harmonic Balance Method

The accuracy of the numerical results obtained for the governing Eqs. (23) and (25) are verified with the approximate analytical solutions derived by the harmonic balance method. The cubic nonlinearity feature is applied in the NES. Therefore, the odd harmonics are considered for the solutions of the beam and the intertial NES as

$$q_{n} = \sum\limits_{i = 0}^{N} {\left\{ {a_{n,2i + 1} \cos \left[ {\left( {2i + 1} \right)\omega \overline{t}} \right] + b_{n,2i + 1} \sin \left[ {\left( {2i + 1} \right)\omega \overline{t}} \right]} \right\}} ,$$
$$\overline{v}_{n} = \sum\limits_{i = 0}^{N} {\left\{ {a_{2i + 1} \cos \left[ {\left( {2i + 1} \right)\omega \overline{t}} \right] + b_{2i + 1} \sin \left[ {\left( {2i + 1} \right)\omega \overline{t}} \right]} \right\}}$$
(28)

where \(N\) is the nonnegative integer, \(n\) is the Galerkin truncation order, and \(2i + 1\) is the harmonic order.

In the following, an example of the derivation process of the analytical solution is given, where the first order Galerkin truncation and the first order of harmonic order are considered. Let \(i = 0,n = 1\), the governing equations of the beam coupled with the intertial NES are rewritten as

$$\begin{aligned} M_{1} \ddot{q}_{1} + \lambda^{2} K_{1} q_{1} + \alpha \lambda^{2} K_{1} \dot{q}_{1} { + }\overline{f}_{0} F_{1} \cos \left( {\omega \overline{t}} \right) \nonumber \\ \quad + \left[ {\overline{k}_{nes} \left( {\varphi_{11} q_{1} - \overline{v}} \right)^{3} + \overline{\mu }\left( {\varphi_{11} \dot{q}_{1} - \dot{\overline{v}}} \right)} \right]\psi_{11} = 0, \end{aligned}$$
(29)
$$\zeta \ddot{\overline{v}} + \overline{k}_{nes} \left( {\overline{v} - \varphi_{11} q_{1} } \right)^{3} + \overline{\mu }\left( {\dot{\overline{v}} - \varphi_{11} \dot{q}_{1} } \right) = 0$$
(30)

where \(\varphi_{11} = \varphi_{1} \left( 1 \right),\psi_{11} = \psi_{1} \left( 1 \right)\).

The first order harmonic hypothesis solution is

$$q_{1} = a_{1,1} \cos \left( {\omega t} \right) + b_{1,1} \sin \left( {\omega t} \right),$$
$$\overline{v} = a_{1} \cos \left( {\omega t} \right) + b_{1} \sin \left( {\omega t} \right)$$
(31)

Substituting Eq. (31) into Eqs. (29) and (30), making the coefficients before \(\cos \left( {\omega \overline{t}} \right)\) and \(\sin \left( {\omega \overline{t}} \right)\) equal to zero, a set of algebraic equations are obtained

$$- \frac{3}{4}\overline{k}_{nes} A\psi_{11} \left( {A^{2} + B^{2} } \right) - \overline{\mu }\omega B\psi_{11} - a_{11} \omega^{2} M_{1} + a_{11} \lambda^{2} K_{1} + b_{11} \omega \alpha \lambda^{2} K_{1} + \overline{f}_{0} F_{1} = 0,$$
$$- \frac{3}{4}\overline{k}_{nes} B\psi_{11} \left( {A^{2} + B^{2} } \right) + \overline{\mu }\omega A\psi_{11} - b_{11} \omega^{2} M_{1} + b_{11} \lambda^{2} K_{1} - a_{11} \omega \alpha \lambda^{2} K_{1} = 0,$$
$$\frac{3}{4}\overline{k}_{nes} A\left( {A^{2} + B^{2} } \right) - \zeta a_{1} \omega^{2} + \overline{\mu }B\omega = 0,$$
$$\frac{3}{4}\overline{k}_{nes} B\left( {A^{2} + B^{2} } \right) - \zeta b_{1} \omega^{2} - \overline{\mu }A\omega = 0$$
(32)

where

$$a_{11} = a_{1,1} ,A = \left( {a_{1} - a_{11} \varphi_{11} } \right),$$
$$b_{11} = b_{1,1} ,B = \left( {b_{1} - b_{11} \varphi_{11} } \right),$$
(33)

The coefficients in the above algebraic equations can be obtained by the pseudo-arc length continuation method. Figure 4 shows the amplitude-frequency response curve of the numerical solution based on the Runge–Kutta method and the analytical solution obtained by the harmonic balance method. A good agreement can be observed for the two methods, which verifies the accuracy and reliability of the numerical solution.

Fig. 4
figure 4

Comparison of analytical solution and numerical solution

Full size image

Vibration Reduction Effect

This section focuses on the suppression effect of the NES on beam vibration, including the free vibration response, transient response, and steady-state response. Based on the derived governing equation, the numerical results for the response of the beam's right point are obtained by the fourth order Runge–Kutta method.

Free Vibration

Neglecting the force terms related to the NES and setting \(\overline{f}_{0} = 0\) in Eq. (23), the free vibration response of the beam without NES can be numerically determined. Two kinds of spring stiffness (\(k = 46025.2{\text{ N}} \cdot {\text{m}}^{{ - 1}}\) and \(k = 0{\text{ N}} \cdot {\text{m}}^{{ - 1}}\)) are considered to investigate the suppression effect of the NES on the beam's free vibration. According to the parameters given in Table 1, for \(k = 46025.2{\text{ N}} \cdot {\text{m}}^{{ - 1}}\), the free vibration responses of the right point of the beam with and without the NES are plotted in Fig. 5a. It shows that by introducing an NES, the free vibration response of the beam decays to zero more quickly after the initial transient response. For the special case in which \(k = 0{\text{ N}} \cdot {\text{m}}^{{ - 1}}\), the boundary condition of the beam changes from the clamped-elastic support to clamped-free. Figure 5b depicts the vibration suppression effect of the free vibration response at the right point end of the cantilever beam. An effective reduction of the free vibration can also be observed.

Fig. 5
figure 5

Vibration suppression effect of the free vibration response at the beam’s right point: (a) elastically supported beam, (b) cantilever beam

Full size image

Transient Response

The reduction effect of the NES on the transient response of the clamped-elastic support beam under different external excitation frequencies is analyzed in the time domain. In the following analysis, the external excitation amplitude is taken as \(f_{0} = 30{N \mathord{\left/ {\vphantom {N m}} \right. \kern-\nulldelimiterspace} m}\). First, when the excitation frequency \(\Omega { = }105.4Hz\) is near the first natural frequency \(\omega_{1}\), the first four order response of the beam's right point is shown in Fig. 6a. It illustrates that the first order primary oscillation can be observed, while the response of the other three orders is minimal and have little impact on the total response of the beam. Figure 6b demonstrates the first four order responses of the beam with an NES. It can be observed from Fig. 6 that the beam's amplitude will decrease from 11 to 6 mm. Therefore, introducing an NES can efficiently reduce the amplitude of the transient response of the beam.

Fig. 6
figure 6

The first four order transient response of the beam: (a) without an NES, (b) with an NES

Full size image

Figure 7 illustrates the comparison of the beam's right point response when the excitation frequency \(\Omega { = 246}{\text{.6}}Hz\) is near the second natural frequency \(\omega_{2}\). It can be found that the second order response is the main component of the beam's response, and a noticeable vibration reduction effect can also be observed.

Fig. 7
figure 7

The first four order transient response of the beam: (a) without an NES, (b) with an NES

Full size image

Steady State Response

The steady-state response means the stable periodic response after which the transient response completely expires due to the damping effect. To evaluate the vibration suppression effect of the NES on the steady-state response, the reduction percentage of the primary resonance peak \(R\) is introduced as the following form

$$R = \frac{{A_{u} - A_{n} }}{{A_{u} }} \times 100\%$$
(34)

where \(A_{u}\) and \(A_{n}\) represent the primary resonance peak of the vibration at the right point of the beam without and with an NES, respectively.

Figure 8 shows the vibration suppression effect of the steady-state response of the beam under different excitation frequencies. The reduction rates of the first three primary resonance peaks at the right point of the beam are \(42.27\%\),\(35.28\%\) and \(8.27\%\). The vibration suppression effect of the NES on the first two orders of primary resonance is more effective than that of the third order response.

Fig. 8
figure 8

Vibration suppression effect of the steady-state response of the right point of the beam: (a) the first primary resonance, (b) the second primary resonance, (c) the third primary resonance

Full size image

Parameter Analysis

This section is dedicated to the improvement of the NES's reduction performance based on the first primary resonance response obtained in the above analysis. Therefore, a parametric study is conducted by concurrently altering the NES's nonlinear stiffness and damping coefficient for the inertia coefficients \(\gamma { = }50\), \(100\) and \(150\), as presented in Figs. 9, 10 and 11, respectively.

Fig. 9
figure 9

The vibration suppression effect for the first primary resonance when the nonlinear stiffness \(k_{nes}\) and linear damping \(\mu\) change simultaneously for \(\gamma\, { = }\,50\): (a) 3-D surface map for the right end, (b) 2-D contour map for the right end

Full size image
Fig. 10
figure 10

The vibration suppression effect for the first primary resonance when the nonlinear stiffness \(k_{nes}\) and linear damping \(\mu\) change simultaneously for \(\gamma\, { = }\,100\): (a) 3-D surface map for the right end, (b) 2-D contour map for the right end

Full size image

A slight ridge region found in the three-dimensional (3-D) surface graph indicates the optimal area for the suppression effect. The two-dimensional (2-D) graph demonstrates the details of the related ridge region, which indicates the optimal intervals for both nonlinear stiffness and linear damping. It reveals that increasing the inertia coefficient \(\gamma\) can achieve a better reduction effect. Consequently, the optimized parameter intervals of the NES can be concluded from Fig. 11, which are suggested as: \(k_{nes} = 10^{8} \sim 10^{9} {N \mathord{\left/ {\vphantom {N {m^{3} }}} \right. \kern-\nulldelimiterspace} {m^{3} }}\), \(\mu = 120 \sim 160N \cdot {s \mathord{\left/ {\vphantom {s m}} \right. \kern-\nulldelimiterspace} m}\), \(\gamma { = 1}50\).

Fig. 11
figure 11

The vibration suppression effect for the first primary resonance when the nonlinear stiffness \(k_{nes}\) and linear damping \(\mu\) change simultaneously for \(\gamma\, { = 1}\,50\): (a) 3-D surface map for the right end, (b) 2-D contour map for the right end

Full size image

Any set of values in the optimized intervals can achieve the best vibration suppression effect. Figure 12 shows the vibration suppression effect of the optimized NES with \(\gamma { = 1}50\), \(k_{nes} = 10^{8} \sim 10^{9} {N \mathord{\left/ {\vphantom {N {m^{3} }}} \right. \kern-\nulldelimiterspace} {m^{3} }}\) and \(\mu = 120 \sim 160N \cdot {s \mathord{\left/ {\vphantom {s m}} \right. \kern-\nulldelimiterspace} m}\). The result shows that the reduction percentage for the first primary resonance can approach to 99.41%. Although the optimized parameters are obtained according to the first primary resonance response, they can also effectually reduce the amplitude of the second and third-order primary resonance. Based on this set of optimization values, the time history response of free vibration is depicted in Fig. 13. This reveals that the response time of free vibration is remarkably reduced.

Fig. 12
figure 12

The vibration reduction effect of the optimized NES on the steady-state response of the right end of the beam: (a) the first primary resonance, (b) the second primary resonance, and (c) the third primary resonance

Full size image
Fig. 13
figure 13

Comparison of the time history responses of the optimized NES and the unoptimized NES at the right end of the beam

Full size image

Conclusions

In this paper, an inertial NES is installed on the boundary of a beam that is clamped at one end and elastically supported on another end to suppress the multimodal vibration of the beam. Based on Euler–Bernoulli theory and Hamiltonian principle, the dynamic equation of the beam is established. The natural frequency of the beam is analytically solved and verified by the finite element method. The nonlinear terms due to the NES attached to the boundary are transferred into the external excitations. Furthermore, applying the Runge–Kutta method, the beam's transient and steady-state responses are numerically solved and compared with those of the same beam without the NES. The main conclusions of this paper are given as follows.

  1. (1)

    Introducing an NES can efficiently reduce the free vibration, transient response, as well as steady-state response of the clamped-elastically supported beam.

  2. (2)

    The optimized NES can achieve a good vibration suppression effect, where the reduction percentage for the first primary resonance can approach 99%. Besides, the NES can also effectually reduce the amplitudes of the second and third-order primary resonances.

  3. (3)

    With the enhanced inertial NES, it is possible to significantly reduce the additional mass of the attached vibration absorber. Besides, installing the NES on the boundary can promote the practical implementation of NES in engineering applications.

  4. (4)

    Based on the results obtained in the present paper, further investigations can be conducted to implement the inertial NESs on the vibration reduction of different elastically supported structures on engineering, such as the wings of aircrafts, bridges, and vehicles suppressions.