1 Introduction

The axially moving behaviors can occur in many engineering devices. However, when the moving speed is faster, the transverse amplitude of the structure turns to be excessive larger. In order to control the undue vibration, the axially moving behaviors have been widely studied by various researchers. In the early time, the axially moving behaviors had been studied by the model of string [1] and plate [2]. Chen and Yang [3] used the method of multiple scales to investigate the nonlinear free transverse vibration of an axially moving beam. Ding and Chen [4] applied the fast Fourier transform to explore the natural frequencies of nonlinear vibration of axially moving beams. Chen and Tang [5] presented the method of multiple scales for the steady-state response of axially moving viscoelastic beams with pulsating speed. Based on the differential quadrature method, Zhou and Wang [6] investigated the vibrations of axially moving viscoelastic plate with parabolically varying thickness. Ghayesh et al. [7] used the Von Kármán plate theory to study the nonlinear dynamics for forced motions of an axially moving plate. Marynowski and Kapitaniak [8] put forward some suggestions for the directions of further research in the field of dynamics of axially moving continua. Wu and Zhu [9] used different numerical methods to investigate the parametric instability in a taut string with a periodically moving boundary. Özhan and Pakdemirli [10] applied the steady-state solutions based on the model with arbitrary linear and cubic operators to study the axially moving Euler–Bernoulli beam and axially moving viscoelastic beam. Ghayesh et al. [11] investigated an axially moving beam with coupled longitudinal and transverse displacements by considering the case with a three-to-one internal resonance. Pakdemirli et al. [12] used the method of multiple scales and the method of matched asymptotic expansions to investigate the transverse vibrations of an axially moving beam with small flexural stiffness.

In order to suppress the transverse vibration of the axially moving system, axial speed-dependent controllability of the system has attracted much attention. Various active control methodologies, including boundary control method and distributed control method, were proposed for stabilizing the axially moving continua [13–18]. It is noted that most these methodologies require the controllers and actuators to make a closed loop system for sensing the axial speed and exerting control force. However, these methodologies are more complex than passive ones. The passive strategies are inherently stable and simple to design. Targeted energy transfers (TETs) are a one-way irreversible form that energy is directed from a source (donor) to a receiver (recipient). The nonlinear energy sink (NES) has been reported to engage in resonance over a broad frequency range, has a small additional mass, and can perform TETs. Georgiadesa and Vakakis [19] provided numerical evidence of passive and broadband targeted energy transfer from a linear flexible beam under shock excitation to a local essentially nonlinear lightweight attachment. Costa et al. [20] investigated energy transfer between vibrating systems under linear and nonlinear interactions. Kerschen et al. [21] studied the dynamics of passive energy transfer from a damped linear oscillator to an essentially nonlinear end attachment. Mehmood et al. [22] investigated the effects of a nonlinear energy sink (NES) on vortex-induced vibrations of a circular cylinder. Costa and Balthazar [23] studied suppression of vibrations in strongly nonhomogeneous 2DOF systems. Luongo and Zulli [24, 25] applied a mixed multiple scale/harmonic balance method to study the dynamic analysis of externally excited NES-controlled systems and the aeroelastic instability analysis of NES-controlled systems. Panagopoulos et al. [26] used the method of multiple scales to investigate the damped dynamics of an elastic rod with an essentially nonlinear end attachment. Tsakirtzis et al. [27] studied the complex dynamics and targeted energy transfer in linear oscillators coupled to multi-degree-of-freedom essentially nonlinear attachments. Georgiadesa and Vakakis [28] examined TETs from a shock-excited plate on an elastic foundation to nonlinear and linear attachments of alternative configurations.

So far, the structures tend to reduce the total mass. Therefore, it is important to develop new absorbers for reducing the additional vibration energy by adding as less as possible extra mass to the main structure. Vaurigaud et al. [29, 30] put forward to a new method using parallel nonlinear energy sinks for targeted energy transfer.

In this paper, we use the parallel NES based on the idea of nonlinear TET to suppress excessive vibration of an axially moving beam. The Galerkin method is applied to analysis equations of motion, and the effect of vibration suppression is displayed. Although the total mass of the parallel NES system is less than that of the single NES system, the effectiveness of vibration suppression is good or even better.

2 Equation of motion

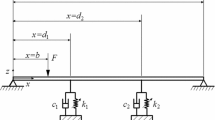
As shown in Fig. 1, the target system consists of a simple supported axially moving beam, with parallel attached essentially nonlinear, damped attachment. The attachment represents the parallel NES, which is hoped to irreversibly absorb the vibration energy.

Fig. 1
figure 1

An axially moving beam with parallel nonlinear energy sinks (NES)

Full size image

The length of the axially moving beam is \(L\); the axial speed is \(V\). The displacements of the beam, the NES1 and the NES2 relative to the horizontal \(X\)-axis are represented as \(U(X,T), \overline{U} _1 (X,T)\) and \(\overline{U}_2 (X,T)\), respectively. The governing equation of motion can be obtained by Newton’s second law as follows

$$\begin{aligned}&\rho A\left( \frac{\partial ^{2}U(X,T)}{\partial T^{2}}+2V\frac{\partial ^{2}U(X,T)}{\partial X\partial T}+V^{2}\frac{\partial ^{2}U(X,T)}{\partial X^{2}}\right) \nonumber \\&\qquad - P\frac{\partial ^{2}U(X,T)}{\partial X^{2}} \nonumber \\&\qquad + EI\frac{\partial ^{4}U(X,T)}{\partial X^{4}}+\eta I\frac{\partial ^{5}U(X,T)}{\partial X^{4}\partial T}\nonumber \\&\quad =[R_1 (t)+\hbox {R}_2 (\hbox {t})]\delta (X-d) \end{aligned}$$
(1)

where \(\rho \) is the linear density, \( A\) is the cross-sectional area, P is the initial tension, \(E\) is the modulus of elasticity, \(I\) is the moment of inertia, \(\eta \) is the viscosity coefficient of the beam material and \(R(t)\) is the interaction force between the beam and the NES.

The equation of motion for the NES is

$$\begin{aligned}&m_\mathrm{NES1} \frac{\partial ^{2}U_1 (X,T)}{\partial T^{2}}+R_1 (t)=0 \end{aligned}$$
(2)
$$\begin{aligned}&m_\mathrm{NES2} \frac{\partial ^{2}U_2 (X,T)}{\partial T^{2}}+R_2 (t)=0 \end{aligned}$$
(3)

where \(m_\mathrm{NES1}\) and \(m_\mathrm{NES2}\) are the mass of the NES1 and NES2, respectively.

The interaction force \(R(t)\) can be written as

$$\begin{aligned} R_1 (t)= & {} K_1 \left[ {\bar{{U}}_1 (T)-Z(T)} \right] ^{3}\nonumber \\&\quad +D_1 \left( {\frac{\partial \bar{{U}}_1 (T)}{\partial T}-\frac{\partial Z(T)}{\partial T}} \right) \end{aligned}$$
(4)
$$\begin{aligned} R_2 (t)= & {} K_2 \left[ {\bar{{U}}_2 (T)-Z(T)} \right] ^{3}\nonumber \\&\quad +D_2 \left( {\frac{\partial \bar{{U}}_2 (T)}{\partial T}-\frac{\partial Z(T)}{\partial T}} \right) \end{aligned}$$
(5)

where \(K_{1}, K_{2}\) is nonlinear (cubic) spring stiffness, \(D_{1}, D_{2}\) is the NES dissipation.

The attachment point displacement and velocity can be expressed as [31]

$$\begin{aligned} Z(T)= & {} U(d,T), \quad \frac{\partial Z(T)}{\partial T}=\frac{\partial U(d,T)}{\partial T}\nonumber \\&\quad +V\frac{\partial U(d,T)}{\partial X} \end{aligned}$$
(6)

where \(d\) is the NES adding position on the beam.

The following is nondimensional quantities

$$\begin{aligned} x= & {} \frac{X}{L},u=\frac{U}{L},t=\frac{T}{L}\sqrt{\frac{P}{\rho A}}, \hbox {v}=V\sqrt{\frac{\rho A}{P}},v_f^2 =\frac{EI}{PL^{2}} \nonumber \\ k= & {} \frac{KL^{4}}{P},\sigma =\frac{DL}{\sqrt{\rho AP}}, \varepsilon =\frac{m_\mathrm{NES} }{\rho AL},\alpha =\frac{I\eta }{L^{3}\sqrt{\rho AP}} \end{aligned}$$
(7)

Substituting Eq. (7) into Eqs. (1) to (6) yields the following dimensionless form

$$\begin{aligned}&\frac{\partial ^{2}u(x,t)}{\partial t^{2}}+2v\frac{\partial ^{2}u(x,t)}{\partial x\partial t}\nonumber \\&\quad + (\hbox {v}^{2}-1)\frac{\partial ^{2}u(x,t)}{\partial x^{2}}+v_f^2 \frac{\partial ^{4}u(x,t)}{\partial x^{4}}+\alpha \frac{\partial ^{5}u(x,t)}{\partial x^{4}\partial t} \nonumber \\&\quad +\,\left[ k_1 \left[ {u(d,t)-\bar{{u}}_1 (t)} \right] ^{3}+\sigma _1 \left( \frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}\right. \right. \nonumber \\&\quad \left. \left. -\frac{\partial \bar{{u}}_1 (t)}{\partial t} \right) \right] \delta (x-d) +\,\left[ k_2 \left[ {u(d,t)-\bar{{u}}_2 (t)} \right] ^{3}\right. \nonumber \\&\quad +\,\sigma _2 \left( \frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}\right. \nonumber \\&\quad \left. \left. -\frac{\partial \bar{{u}}_2 (t)}{\partial t} \right) \right] \delta (x-d)=0\end{aligned}$$
(8)
$$\begin{aligned}&\varepsilon _1 \frac{\partial ^{2}\bar{{u}}_1 (\hbox {x,t})}{\partial t^{2}}+k_1 \left[ {\bar{{u}}_1 (t)-u(d,t)} \right] ^{3} \nonumber \\&\quad +\,\sigma _1 \left( {\frac{\partial \bar{{u}}_1 (t)}{\partial t}-\frac{\partial u(d,t)}{\partial t}-v\frac{\partial u(d,t)}{\partial x}} \right) =0 \end{aligned}$$
(9)
$$\begin{aligned}&\varepsilon _2 \frac{\partial ^{2}\bar{{u}}_2 (\hbox {x,t})}{\partial t^{2}}+k_2 \left[ {\bar{{u}}_2 (t)-u(d,t)} \right] ^{3}\nonumber \\&\quad +\,\sigma _2 \left( {\frac{\partial \bar{{u}}_2 (t)}{\partial t}-\frac{\partial u(d,t)}{\partial t}-v\frac{\partial u(d,t)}{\partial x}} \right) =0 \end{aligned}$$
(10)

3 Galerkin method

Based on the Galerkin method, the governing equations (8), (9) and (10) can be approximated by a more tractable finite dimensional dynamical system. The displacement expansion is assumed as following

$$\begin{aligned} u(x,t)=\sum _{r=1}^N {\phi _r (x)q_r (t)} \end{aligned}$$
(11)

where \(\phi _{r}(x)\) are the eigenfunctions for the free undamped vibration of a beam and are required to satisfy the same boundary conditions, and \(q_{r}(t)\) are the generalized coordinates of the discretized system.

Substituting Eq. (11) into Eqs. (8), (9) and (10)

$$\begin{aligned}&\sum _{r=1}^N \left[ \phi _{r} (x)\ddot{q}_{r} (t)+2v{\phi }'_{r} (x)\dot{q}_{r} (t)+(v^{2}-1){\phi }''_{r} (x)q_{r} (t)\right. \nonumber \\&\quad \left. + v_f^2 \phi _{r}^{(4)} (x)q_{r} (t)+\alpha \phi _{r}^{(4)} (x)\dot{q}_{r} (t) \right] \nonumber \\&\quad + \left[ k_1 \left[ {u(d,t)-\bar{{u}}_1 (t)} \right] ^{3}\right. \nonumber \\&\quad \left. + \sigma _1 \left( \frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_1 (t)}{\partial t} \right) \right] \delta (x-d) \nonumber \\&\quad +\left[ k_2 \left[ {u(d,t)-\bar{{u}}_2 (t)} \right] ^{3}\right. \nonumber \\&\quad \left. +\,\sigma _2 \left( {\frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_2 (t)}{\partial t}} \right) \right] \delta (x-d)\nonumber \\&\quad =0\end{aligned}$$
(12)
$$\begin{aligned}&\quad \varepsilon _1 \ddot{\bar{{u}}}_1 (t)+k_1 \left( {\bar{{u}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)q_{r} (t)} } \right) ^{3}\nonumber \\&\quad +\,\sigma _1 \left( {\dot{\bar{{u}}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0 \end{aligned}$$
(13)
$$\begin{aligned}&\quad \varepsilon _2 \ddot{\bar{{u}}}_2 (t)+k_2 \left( {\bar{{u}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)q_{r} (t)} } \right) ^{3}\nonumber \\&\quad +\, \sigma _2 \left( {\dot{\bar{{u}}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0 \end{aligned}$$
(14)

The beam is supported by pinned ends so we designate \(\phi _{r} (\hbox {x})=\sqrt{2}\sin \lambda _{r} x \quad \lambda _{r} =r\pi \) where the \(\sqrt{2}\) factor is for ensuring orthonormality. Multiplying Eq. (12) by \({\phi }_\mathrm{s}(x)\) and integrating over the domain [0, 1] yield.

$$\begin{aligned}&\delta _\mathrm{sr} \ddot{q}_{r} (t)+(2vb_\mathrm{sr} +\alpha e_\mathrm{sr} )\dot{q}_{r} (t)\nonumber \\&\quad + [(v^{2}-1)c_\mathrm{sr} +v_f^2 e_\mathrm{sr} ]q_{r} (t) \nonumber \\&+ \left[ k_1 \left[ {u(d,t)-\bar{{u}}_1 (t)} \right] ^{3}+\sigma _1 \left( \frac{\partial u(d,t)}{\partial t}\right. \right. \nonumber \\&\quad \left. \left. +v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_1 (t)}{\partial t} \right) \right] \phi _{r} (\hbox {d}) \nonumber \\&+ \left[ k_2 \left[ {u(d,t)-\bar{{u}}_2 (t)} \right] ^{3}+\sigma _2 \left( \frac{\partial u(d,t)}{\partial t}\right. \right. \nonumber \\&\quad \left. \left. +v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_2 (t)}{\partial t} \right) \right] \phi _{r} (\hbox {d})=0\end{aligned}$$
(15)
$$\begin{aligned}&\varepsilon _1 \ddot{\bar{{u}}}_1 (t)+k_1 \left( {\bar{{u}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)q_{r} (t)} } \right) ^{3}\nonumber \\&\quad + \sigma _1 \left( {\dot{\bar{{u}}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0\end{aligned}$$
(16)
$$\begin{aligned}&\varepsilon _2 \ddot{\bar{{u}}}_2 (t)+k_2 \left( {\bar{{u}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)q_r (t)} } \right) ^{3}\nonumber \\&\quad + \sigma _2 \left( {\dot{\bar{{u}}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0 \end{aligned}$$
(17)

where

$$\begin{aligned} \delta _\mathrm{sr}= & {} \int _0^1 {\phi _\mathrm{s}} (x)\phi _{r} (x)\mathrm{d}x, \quad b_\mathrm{sr} =\int _0^1 {\phi _\mathrm{s}} (x){\phi }'_{r} (x)\mathrm{d}x, \quad \nonumber \\ c_\mathrm{sr}= & {} \int _0^1 {\phi _s } (x){\phi }''_{r} (x)\mathrm{d}x, \quad e_\mathrm{sr} =\int _0^1 {\phi _\mathrm{s}} (x)\phi _{r}^{(4)} (x)\mathrm{d}x\nonumber \\ \end{aligned}$$
(18)

\(\delta _\mathrm{sr}\) is the Kronecker’s delta, \(\lambda _{r}\) is the \(r\)th eigenvalues for the free undamped vibration of a beam with the same boundary conditions.

Equations (15), (16), (17) can be written as

$$\begin{aligned}&\mathrm{M}\ddot{q}_{r} (t)+\mathbf{C}\dot{q}_{r} (t)+\mathbf{K}q_{r} (t) \nonumber \\&\quad + \left[ k_1 \left[ {u(d,t)-\bar{{u}}_1 (t)} \right] ^{3}\right. \nonumber \\&\qquad \left. +\,\sigma _1 \left( {\frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_1 (t)}{\partial t}} \right) \right] \phi _{r} (\hbox {d}) \nonumber \\&\quad +\left[ k_2 \left[ {u(d,t)-\bar{{u}}_2 (t)} \right] ^{3}\right. \nonumber \\&\qquad \left. +\, \sigma _2 \left( {\frac{\partial u(d,t)}{\partial t}+v\frac{\partial u(d,t)}{\partial x}-\frac{\partial \bar{{u}}_2 (t)}{\partial t}} \right) \right] \phi _{r} (\hbox {d})\nonumber \\&\qquad =0 \end{aligned}$$
(19a)
$$\begin{aligned}&\varepsilon _1 \ddot{\bar{{u}}}_1 (t)+k_1 \left( {\bar{{u}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)q_r (t)} } \right) ^{3}\nonumber \\&\qquad +\, \sigma _1 \left( {\dot{\bar{{u}}}_1 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0\end{aligned}$$
(19b)
$$\begin{aligned}&\varepsilon _2 \ddot{\bar{{u}}}_2 (t)+k_2 \left( {\bar{{u}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)q_r (t)} } \right) ^{3}\nonumber \\&\qquad +\, \sigma _2 \left( {\dot{\bar{{u}}}_2 (t)-\sum _{r=1}^N {\phi _{r} (d)\dot{q}_{r} (t)-v\sum _{r=1}^N {\phi _{r} ^{\prime }(d)q_{r} (t)} } } \right) \nonumber \\&\quad =0 \end{aligned}$$
(19c)

where

$$\begin{aligned} M= & {} \delta _\mathrm{sr} , \quad C=2vb_\mathrm{sr} +\alpha e_\mathrm{sr} ,\nonumber \\ K= & {} (v^{2}-1)c_\mathrm{sr} +v_f^2 e_\mathrm{sr} =\omega _{r}^2 \end{aligned}$$
(20)

where M, C and K are, respectively, the mass, damping and stiffness matrices, \(\omega \) \(_{r}\) is the \(r\)th natural frequency of the axially moving beam. Equation (19) shows a multi-degree-of-freedom nonlinear system. It can be seen that the parallel NES couple to all modes of the beam thereby being able to extract vibration energy from each mode of the beam.

4 Effectiveness of the parallel NES

In this part, a series of study about the effectiveness of the parallel NES for stabilizing the axially moving beam will be carried out. The effectiveness of the parallel NES attached to an axially moving beam with varying axial speed is examined and compared with that of the single NES, meanwhile.

It is usually to truncate the expansion to a finite number of modes when dealing with the high-dimensional nonlinear dynamical system as Eq. (19). McDonald and Namachchivaya [32] presented that it is indispensable to take at least two modes of the amplitude of the displacement for a good approximation in the Galerkin procedure for gyroscopic systems. Therefore, N \(=\) 1, 2, 3 and 4 is taken, respectively, to examine the numerical convergence via the following quantitative measure

$$\begin{aligned} E_\mathrm{NES} (t)=\frac{\sigma _1 \int _0^t {[\dot{\bar{{u}}}_1 (\tau )-\sum \nolimits _{i=1}^N {\Phi _i (d)\dot{q}_i (t)} ]^{2}d\tau } +\sigma _2 \int _0^t {[\dot{\bar{{u}}}_2 (\tau )-\sum \nolimits _{i=1}^N {\Phi _i (d)\dot{q}_i (t)} ]^{2}d\tau } }{(X^{2}/2)}\times 100 \end{aligned}$$
(21)

The \(E_\mathrm{NES}(t)\) [33] indicates the percentage of the impulsive energy that is absorbed and dissipated by the parallel NES up to time \(t\). It is noted that in the following numerical simulations, \(E_\mathrm{NES}\) are all calculated up to \(t=\) 150. The initial vibration of the axially moving devices is caused by initial speed. So, the following initial distributed velocity is imposed

$$\begin{aligned} \dot{q}_1 (0)= & {} X, \quad q_{r} (0)=\dot{q}_2 (0)=\cdots =\dot{q}_{r}\nonumber \\= & {} \bar{{u}}_1 (0)=\dot{\bar{{u}}}_1 (0)=\bar{{u}}_2 (0)=\dot{\bar{{u}}}_2 (0)=0 \end{aligned}$$
(22)

where \(X\) is a constant.

And the system parameters are \(\sigma _{1} = 0.04, {\sigma }_{2} = 0.06, k_{1}=6000, k_{2}=2000, {\varepsilon }_{1} = 0.03, {\varepsilon }_{2}=0.07, v_{f} = 0.8, v = 1, {\alpha } = 0.001\) and \(X=\) 0.18. Based on the above, Table 1 is obtained so as to show the \(E_\mathrm{NES}\) as a function of \(N \)and \(d\). Obviously, the value of \(E_\mathrm{NES}\) when \(N = 1\) has much difference compared with that when \(N= 2, 3\) and 4. It can be found that \(N = 1\) does not meet the requirements of convergence, but \(N = 2, 3\) and 4 does. So, in this paper, the 2-term Galerkin truncation is applied.

Table 1 Convergence study of the \(E_\mathrm{NES}\) for the Galerkin truncation term
Full size table

The critical axial speed of the beam \(v_{cri}\) and the dimensional flexural stiffness \(v_{f}\) satisfy the following equation

$$\begin{aligned} v_{cri} =\sqrt{1+\pi ^{2}v_f^2 } \end{aligned}$$
(23)

In this paper, the dimensional flexural stiffness is \(v_{f} = 0.8\); therefore, the critical speed is \(v_{cri} = 2.7\). So, the axial speed of the beam is designated to vary from 0 to 2.5 (close to the critical speed).

Figure 2a depicts the transient response of the axially moving beam and the single NES for different values of the axial speed \(v\) varying from 0 to 2.5 and other parameters \({\sigma }=0.1, k=8000, {\varepsilon }=0.1, d=0.6, v_{f}=0.8, {\alpha }=0.001\) and \(X=\) 0.18\(.\) The solid and the dashed lines, respectively, represent the response of the beam and the single NES. Figure 2b depicts the transient response of the axially moving beam and the parallel NES for different values of the axial speed \(v\) varying from 0 to 2.5 and other parameters \(\sigma _{1}=0.04, {\sigma }_{2}=0.06, k_{1}=6000, k_{2}=2000, {\varepsilon }_{1}=0.03,{\varepsilon }_{2}=0.07, d=0.6, v_{f}=0.8, {\alpha }=0.001\) and \(X=0.18\). The solid, the dashed and the dotted line, respectively, represent the response of the beam, the NES1 and the NES2. It can be seen from Fig. 2 that the amplitudes of the two NES devices are all much higher than the beam. Obviously, the energy transfers from the beam to the NES devices. Then, the energy began to be exchanged between the beam and the NES. During this process, the vibration energy is irreversibly transferred and eventually damped by the NES. So, it can be known that the single NES and the parallel NES each can effectively absorb the vibration energy and prevent the beam from excessive vibration for varying axial speed, and the energy absorbing is realized over a wide range of axial speed.

Fig. 2
figure 2figure 2

a Response of the axially moving beam and the single NES for different axial speeds (solid line response of the axially moving beam \((u)\); dashed line response of the NES \((\overline{u} ))\). b Response of the axially moving beam, the NES1 and the NES2 for different axial speed (solid line response of the axially moving beam (\(u)\); dashed line response of the NES1 \((\overline{u_1 } )\); dotted line response of the NES2 \((\overline{u_2 } ))\)

Full size image

As shown in Fig. 3, we compare the response of the beam without NES, with the single NES and with the parallel NES for varying speed \(v\) from 0 to 2.5 so as to further demonstrate the effectiveness of the parallel NES. Parameters of the parallel NES are \(\sigma _{1}=0.04, {\sigma }_{2}=0.06, k_{1}=6000, k_{2}=2000, {\varepsilon }_{1}=0.03,{\varepsilon }_{2}=0.07, d=0.6, v_{f}=0.8, {\alpha }=0.001\) and \(X=0.18,\) and that of the single NES are \(\sigma =0.1, k=8000, {\varepsilon }=0.1, d=0.6, v_{f}=0.8, {\alpha }=0.001\) and \(X=0.18\). Visibly, the total parameters of the parallel NES system are the same as that of the single NES system. The dashed, dotted and solid lines, respectively, represent the response of the beam without NES, with the single NES and with the parallel NES. It can be known from Fig. 3, as time goes on, the response of the beam without NES slowly decays, in contrast, parallel NES and single NES attached to the beam both cause rapidly decay of the transient response of the beam. Comparing the dotted and the dashed lines, the dashed line performs better than another in the aspect of close to 0. In particular, in Fig. 3c, when \(v \)= 1, after 7th seconds, the amplitude of the dashed line is already less than 0.0005; however, the same amplitude of the dotted line is achieved until after 17th seconds. These show that for vibration suppression of the axially moving beam, compared to the single NES system, the parallel NES system has the good or even better effectiveness.

Fig. 3
figure 3

Comparison of the transient response of axially moving beam without NES, with single NES and with parallel NES (dashed line beam without NES; dotted line beam with single NES; solid line beam with parallel NES)

Full size image

Based on Fig. 3, in order to reduce the mass of the parallel NES, Fig. 4 is demonstrated. Parameters of the parallel NES are \(\sigma _{1}=0.02, {\sigma }_{2}=0.08, k_{1}=6500, k_{2}=1500, {\varepsilon }_{1}=0.01,{\varepsilon }_{2}=0.04, d=0.5, v_{f}=0.8, {\alpha }=0.001\) and \(X=0.18,\) and that of the single NES are \(\sigma =0.1, k=8000, {\varepsilon }=0.1, d=0.5, v_{f}=0.8, {\alpha }=0.001\) and \(X=0.18\). The total parameters except the mass of these two systems are the same. Although the total mass of the parallel NES system is much less than that of the single NES system, the effectiveness of vibration suppression is good or even better. In particular, when the axial speed is \(v\) = 0.5 as shown in Fig. 4b, the superiority of the parallel NES system for vibration suppression is remarkable.

Fig. 4
figure 4

Comparison of the transient response of axially moving beam without NES, with single NES and with parallel NES (dashed line beam without NES; dotted line beam with single NES; solid line beam with parallel NES)

Full size image

In Fig. 5, the response of the beam without NES and with the parallel NES for different adding position \(d\) varying from 0.3 to 0.7 is presented. Parameters of the parallel NES system are \(\sigma _{1}=0.02, {\sigma }_{2}=0.08, k_{1}=6500, k_{2}=1500, {\varepsilon }_{1}=0.01,{\varepsilon }_{2}=0.04, v_{f}=0.8, \hbox {v}=0.5, {\alpha }=0.001\) and \(X=0.18\). The dashed and the solid lines, respectively, represent the response of the beam without the NES and with the parallel NES. It can be known from Fig. 5 that different adding positions lead to different effectiveness of vibration suppression. When the adding position \(d\) is around the 0.5, the approximate optimum vibration suppression effectiveness is achieved.

Fig. 5
figure 5

Response of the axially moving beam without NES and with parallel NES for different adding position (dashed line beam without NES; solid line beam with parallel NES)

Full size image

5 Conclusions

In this study, the vibration suppression of the axially moving beam based on the nonlinear TET theory is investigated. The effectiveness of the single NES and the parallel NES attached to the axially moving beam for stabilizing the axially moving beam with varying axial speed is compared. Although the total mass of the parallel NES is much less than that of the single NES, the effectiveness of vibration suppression is good or even better.