1 Introduction

Nonlinear energy sink (NES) is an essentially nonlinear oscillator which is used as passive control device. Its main feature, due to the lack of linear stiffness, is the capability of getting tuned to the primary structure in a wide range of frequencies, representing a considerable asset to the passive control performance, and overtaking the intrinsic limitations of more common devices such as tuned mass damper [1–3]. An extensive study on the use of NES is given in [4], where analytical, numerical and experimental verification on the characteristics of such a device is provided. There and in many other papers, the analytical studies are carried out by means of the application of the Complexification Averaging Method (CX-A, see [5]). Under this framework, in [6], a main linear oscillator excited by a harmonic force and equipped with NES is studied; in [7], an internally resonant two-d.o.f. system is considered as primary structure, still under the application of harmonic excitation; in [8, 9], the use of NES is extended to aeroelastic problems, in order to suppress or reduce oscillations induced by wind. Discussion on energy pumping between linear and essentially nonlinear oscillators such as NES is given in [10, 11], while extension of the use of NES to control non-ideal main structures are presented in [12, 13]. NES attached to continuum primary linear structures, such as beams or plates, is considered in [14–19]. The possible occurrence of multiple coexisting solutions, sometimes thwarting the beneficial effects of the NES as control device in single-d.o.f. systems, is discussed in [20, 21].

Other analytical studies of oscillators endowed with NES make use of the combination of the Multiple Scale Method and the Harmonic Balance (referred as MSHBM): the case of multi-d.o.f. dynamical systems under harmonic external force is considered in [22]; a two-d.o.f. nonlinear airfoil under wind effects is analyzed in [23]; the chatter in the turning process is studied in [24]; lateral vibrations of a rotor are evaluated in [25]. In [26], a nonlinear elastic string under harmonic force is considered when a NES is attached at a certain position of the span, and the internally nonresonant case is analyzed, being the string supported at one end by a mass-spring system which detunes the first few natural frequencies. There, as well as in [22, 23], the lacking of internal resonance causes the dynamics of the principal structure to be described by just one active mode, while all the other modes turn out to be passive. Moreover, in [26], the perturbation scheme is applied in direct approach, i.e., the Multiple Scale Method is directly imposed on the partial differential equations, as done (for systems without NES) in [27–31].

In this paper, the analysis of [26] is extended to internally resonant taut strings. The same model of [26] is used, except for the right boundary condition, where a fixed support is now considered, which entails the typical internal resonance conditions among the infinite natural frequencies of the string to occur. As it was discussed in [28], when NES is absent, the dominant dynamics of a nonlinear, double supported, taut string under harmonic excitation resonant to a generic mode (say the \(r\)th), is ruled just by the resonant (\(r\)th) mode itself, while the amplitudes of the infinite remaining modes give higher-order contribution. The effect of the NES on this peculiar behavior is discussed here, further extending the MSHBM to systems which include internal resonances, possibly involving more than one active mode of the principal structure. Relevant amplitude modulation equations are obtained and some numerical results are reported, compared to those provided by integration of the system after the application of a multi-mode Galerkin projection.

2 The model

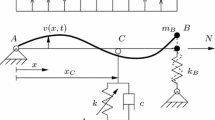
A double supported extensible elastic string is considered here, as shown in Fig. 1. Its initial length is \(\ell \) and prestress tensile force \(N\), and an external force, ruled by the law \(f(x,t)=p(x)\cos (\Omega t)\), is applied along the span. Here \(x\) is the abscissa measured in the prestressed configuration and \(t\) is the time. The linear mass density is \(\rho \) and the axial stiffness is EA. The equations of motion of the string are taken from [27, 28, 32]: they are valid for moderately large displacements, under the hypothesis that the longitudinal versus transverse celerity-rate is large. A NES is applied to the string at point \(C\), corresponding to the abscissa \(x_C\). The mass of the NES is \(m\), its linear damping \(c\) and cubic stiffness \(k\). The in-plane transverse displacement of a generic point of the string is \(v(x,t)\) while the displacement of the mass of the NES is \(y(t)\). The equations read:

$$\begin{aligned}&Nv''(x,t)+\frac{EA}{\ell }v''(x,t)\left[ \int _0^{\ell }\!\!\frac{v'^2(x,t)}{2}\hbox {d}x\right] \!-\!\rho \ddot{v}(x,t)\nonumber \\&\quad \,+\,p(x)\cos (\varOmega t)-\left[ k(v(x,t)-y(t))^3\right. \nonumber \\&\quad \,\left. +\,c(\dot{v}(x,t)-\dot{y}(t))\right] \delta (x-x_C)=0\nonumber \\&\quad \,\quad m\ddot{y}(t)-\left[ k(v(x_C,t)-y(t))^3\right. \nonumber \\&\quad \left. +\,c(\dot{v}(x_C,t)-\dot{y}(t))\right] =0 \end{aligned}$$
(1)

where \(\delta (x)\) is the Dirac delta, the dot indicates time-derivative and the prime space-derivative.

Fig. 1
figure 1

String equipped with a NES

Full size image

The geometric boundary conditions at the supports read

$$\begin{aligned} v(0,t)= & {} 0\nonumber \\ v(\ell ,t)= & {} 0 \end{aligned}$$
(2)

Relevant initial conditions must be added too.

Nondimensional quantities are defined as:

$$\begin{aligned} \tilde{x}= & {} \frac{x}{\ell },\;\tilde{t}=\bar{\omega } t,\; \tilde{y}=\frac{y}{L},\; \tilde{v}=\frac{v}{L},\;\tilde{x}_C=\frac{x_C}{\ell },\nonumber \\ \tilde{\delta }= & {} \ell \delta ,\; \tilde{p}=\frac{p\ell }{N}\sqrt{\frac{\hbox {EA}}{N}},\; \tilde{\varOmega }=\frac{\varOmega }{\bar{\omega }},\nonumber \\ \kappa= & {} \frac{k\ell ^3}{\hbox {EA}},\;\xi =\frac{c}{\sqrt{\rho N}},\;\tilde{m}=\frac{m}{\rho \ell } \end{aligned}$$
(3)

where \(L\) is a characteristic length defined as \(L\mathrel {\mathop :}=\ell \sqrt{\frac{N}{\hbox {EA}}}\), and \(\bar{\omega }=\frac{1}{\ell }\sqrt{\frac{N}{\rho }}\). After the substitutions of the definitions (3) in Eq. (1), the nondimensional version of the equations of motion is obtained. Omitting the tilde, including the contribution of linear structural damping (\(\zeta \dot{v}(x,t)\), where \(\zeta \) is the damping coefficient), and introducing the relative displacement between the main structure at point \(C\) and NES, namely \(z(t)\mathrel {\mathop :}=v(x_C,t)-y(t)\), Eq. (1) become

$$\begin{aligned}&\ddot{v}+\zeta \dot{v}-v''- v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}\hbox {d}x\right] \nonumber \\&\quad +\left[ \kappa z^3+\xi \dot{z}\right] \delta (x-x_C)=p\cos (\varOmega t)\nonumber \\&\qquad m(\ddot{z} -\ddot{v}_C)+\kappa z ^3+\xi \dot{z} =0 \end{aligned}$$
(4)

where \(v_C(t)\mathrel {\mathop :}=v(x_C,t)\), and the boundary conditions

$$\begin{aligned} v(0,t)= & {} 0 \nonumber \\ v(1,t)= & {} 0 \end{aligned}$$
(5)

where the dot and the prime stand here for differentiation with respect to the nondimensional time and abscissa, respectively.

3 The Multiple Scale/Harmonic Balance Method

In order to obtain the perturbation equations, the procedure described in [26] is used here; it is briefly recalled for the sake of completeness. A nondimensional small parameter \(\epsilon \) is introduced to rescale the dependent variables and the parameters: the displacements are \((v,z)\mathrel {\mathop :}=\epsilon ^{1/2}( \tilde{v},\tilde{z})\), consistently with the presence of cubic nonlinearity; the damping factor is \(\zeta =\epsilon \tilde{\zeta }\) and the external force is \(p=\epsilon ^{3/2}\tilde{p}\), consistently with the idea to let both the terms appear at the same level of the nonlinearity. The external excitation is considered 1:1 resonant with one of the linear modes (the \(r\)th, of frequency \(\omega _r=r\pi \)) of the string with NES disengaged. A detuning parameter \(\sigma \) is introduced for the external excitation, as \(\varOmega =\omega _r+\sigma \); it is rescaled as \(\sigma =\epsilon \tilde{\sigma }\). The parameters of the NES are rescaled too, since both its mass and damping are assumed small: \((m,\xi )\mathrel {\mathop :}=\epsilon ( \tilde{m},\tilde{\xi })\). After the application of the rescaling, the omission of tilde and division by \(\epsilon ^{1/2}\), Eq. (4) become:

$$\begin{aligned}&\ddot{v}-v''+\epsilon \biggl [\zeta \dot{v}- v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}\hbox {d}x\right] \nonumber \\&\quad +[\kappa z^3+\xi \dot{z}]\delta (x-x_C)-p\cos (\varOmega t)\biggr ]=0\nonumber \\&\quad \epsilon [m(\ddot{z} -\ddot{v}_C)+\kappa z ^3+\xi \dot{z}]=0 \end{aligned}$$
(6)

Independent time scales \(t_0:=t\), \(t_1:=\epsilon t\), \(t_2=\epsilon ^2t,\ldots \) are introduced and the relevant derivatives are expressed as \(\frac{\partial }{\partial t}=d_0+\epsilon d_1+\epsilon ^2 d_2+\cdots \) and \(\frac{\partial ^2}{\partial t^2}=d_0^2+2\epsilon d_0 d_1+\epsilon ^2(d_1^2+2d_0d_2)+\cdots \), where \(d_j\mathrel {\mathop :}=\partial /\partial t_j\), for \(j=0,1,2,\ldots \). Series expansion of the dependent variables is applied as:

$$\begin{aligned} \begin{Bmatrix} v\\ z \end{Bmatrix}=\begin{Bmatrix} v_0\\ z_0 \end{Bmatrix}+\epsilon \begin{Bmatrix} v_1\\ z_1 \end{Bmatrix}+\epsilon ^2\begin{Bmatrix} v_2\\ z_2 \end{Bmatrix}+\cdots \end{aligned}$$
(7)

After substitution in Eq. (6) and boundary conditions, the collection of terms at the same order in \(\epsilon \) gives the perturbation equations:

$$\begin{aligned}&\hbox {order }\epsilon ^0:\nonumber \\&\quad d_0^2v_0-v''_0=0\end{aligned}$$
(8)
$$\begin{aligned}&\hbox {order }\epsilon ^1:\nonumber \\&d_0^2v_1-v''_1=-2 d_0d_1v_0-\zeta d_0v_0+p\cos (\varOmega t_0)\nonumber \\&\quad -(\xi d_0z_0+\kappa z_0^3)\delta (x-x_C)+ v_0''\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}\hbox {d}x\right] \end{aligned}$$
(9)
$$\begin{aligned}&m(d_0^2z_{0}-d_0^2v_{C_0})+\xi d_0 z_{0} +\kappa z_{0}^3 =0\end{aligned}$$
(10)
$$\begin{aligned}&\hbox {order }\epsilon ^2{:}\nonumber \\&d_0^2v_2-v''_2=- (d_1^2v_0+2 d_0d_2v_0+2d_0d_1v_1)\nonumber \\&\quad -\zeta (d_2v_0+d_1v_1)-\left[ \xi (d_0z_1+d_1z_0)+3\kappa z_0^2z_1\right] \nonumber \\&\quad \delta (x-x_C)+ v_1''\left[ \int _0^{1}\!\!\frac{v_0'^2}{2}\hbox {d}x\right] + v_0''\left[ \int _0^{1}\!\!v'_0v_1'\hbox {d}x\right] \nonumber \\\end{aligned}$$
(11)
$$\begin{aligned}&m(d_0^2 z_{1}-d_0^2v_{C_1})+\xi d_0 z_{1} +3\kappa z_{0}^2z_{1}\nonumber \\&\quad =-2m(d_0d_1z_{0}-d_0d_1v_{C_0})-\xi d_1z_{0} \end{aligned}$$
(12)

At any order, the boundary conditions are trivial:

$$\begin{aligned}&\hbox {order }\epsilon ^k\!:\nonumber \\&v_k(0,t_0,t_1,\ldots )=0,\nonumber \\&v_k(1,t_0,t_1,\ldots )=0 \end{aligned}$$
(13)

for \(k=0,1,2\). So far, except for the boundary condition at the point \(B\), the perturbation equations are identical to those reported in [26] and valid for the internally nonresonant case. It should be noted that no equation relevant to the NES appears at order \(\epsilon ^0\), where just the linearized problem of the string (with NES disengaged) is retained. This occurrence is due to the small value of mass and damping of the NES, as well as to the fact that its stiffness is essentially nonlinear. The solution of Eqs. (8) and (13), which represents the generating solution of the perturbation procedure, should contain all the infinite components relevant to the infinite eigenfunction of the linear system (see [28]). However, driven by inspection of the shape of the equations of motion and by the presence in them of the cubic nonlinearity, and being aimed at obtaining approximated solutions for the system, just the resonant (\(j=r\)) and a superharmonic (\(j=s\mathrel {\mathop :}=3r\)) components are chosen to be retained in the solution:

$$\begin{aligned} v_0(x,t_0,t_1,\ldots )= & {} A_r(t_1,\ldots )\varphi _r(x) e^{i\omega _r t_0}\nonumber \\&+A_s(t_1,\ldots )\varphi _s(x) e^{i\omega _s t_0} +cc \end{aligned}$$
(14)

where: \(A_j(t_1,\ldots )\) are the complex modal amplitudes to be evaluated, depending on the slower timescales; \(i\) is the imaginary unit; \(\omega _j=j\pi \) and \(\varphi _j(x)=\sin (\omega _j x)\) are the \(j\)th eigenvalue and (real) eigenfunction of the problem with NES disengaged; \(cc\) stands for complex conjugate (\(j=r,s\)).

Passing at order \(\epsilon \), the Harmonic Balance method [27] is applied to the NES Eq. (10), assuming as solution for it a one-term Fourier expansion:

$$\begin{aligned} z_0(t_0,t_1,\ldots )= B_{0_r}(t_1,\ldots )e^{i \omega _r t_0} +cc \end{aligned}$$
(15)

where \(B_{0_r}(t_1,\ldots )\) is the complex amplitude depending on slower time scales, to be evaluated. The substitution of Eqs. (14) and (15) in Eq. (10) and the balance of frequency \(\omega _r\) is carried out while, still in the idea of approximation, other frequencies are neglected (see [22] for a discussion on the contribution of higher frequencies). The procedure gives rise to the following algebraic equation:

$$\begin{aligned} -m\omega _r^2(B_0- A_r\varphi _r(x_c))+i\xi \omega _r B_0+3\kappa B_0^2\bar{B}_0=0\nonumber \\ \end{aligned}$$
(16)

where the overbar stands for complex conjugate. To obtain the real form of Eq. (16), the following steps are covered: (a) application of the polar transformation for both \(A_r\) and \(B_0\), which reads \(A_r\mathrel {\mathop :}=\frac{1}{2}a_re^{i\alpha _r}\) and \(B_0\mathrel {\mathop :}=\frac{1}{2}be^{i\beta }\); (b) separation of real and imaginary parts; (c) squaring and adding the two obtained parts. The equation for the invariant manifold which describes a first approximation of a Nonlinear Normal Mode of the system is therefore written:

$$\begin{aligned} m^2\omega _r^4 \varphi _r(x_c)^2 a_r^2=\left( m\omega _r^2 b-\frac{3}{4}\kappa b^3\right) ^2+\xi ^2\omega _r^2 b^2\nonumber \\ \end{aligned}$$
(17)

The dynamics outside the manifold (17) is ruled by the equations of the string at the same order, namely Eqs. (9) and (13) as well as the NES equation at the order \(\epsilon ^2\), which will be tackled ahead. In particular, the solution of Eq. (9) is sought in the form

$$\begin{aligned} v_1(x,t_1,t_2)= & {} \psi _r(x,t_1,t_2)e^{i\omega _r t_0}+\psi _s(x,t_1,t_2)e^{i\omega _s t_0}\nonumber \\&+\,\psi _{2s-r}(x,t_1,t_2)e^{i\omega _{2s-r} t_0}\nonumber \\&+\,\psi _{2s+r}(x,t_1,t_2)e^{i\omega _{2s+r} t_0}\nonumber \\&+\,\psi _{3s}(x,t_1,t_2)e^{i\omega _{3s} t_0}+cc \end{aligned}$$
(18)

where \(\psi _q(x,t_1,t_2)\) are complex functions to be determined (\(q=r,s,2s-r,2s+r,3s\)). This expression for \(v_1\) in Eq. (19) is suggested by the presence of cubic nonlinear terms in Eq. (9) but, in the spirit of the approximation, just components in \(q=r,s\) are actually retained, while the other terms are considered as higher-order harmonics. Then, Eq. (18) is replaced by

$$\begin{aligned} v_1(x,t_1,t_2)= & {} \psi _r(x,t_1,t_2)e^{i\omega _r t_0}\nonumber \\&+\,\psi _s(x,t_1,t_2)e^{i\omega _s t_0}+cc \end{aligned}$$
(19)

and substituted in Eqs. (9) and (13), and terms multiplying \(\exp (i\omega _r t_0)\) and \(\exp (i\omega _s t_0)\) are separated, giving two ordinary differential equations with relevant boundary conditions, respectively. They read:

$$\begin{aligned} \psi _j''+\omega _j^2\psi _j=-f_j(x,t_1,t_2) \end{aligned}$$
(20)

with boundary conditions

$$\begin{aligned} \begin{aligned}&\psi _j(0,t_1,t_2)=0\\&\psi _j(1,t_1,t_2)=0 \end{aligned} \end{aligned}$$
(21)

where

$$\begin{aligned}&f_j(x,t_1,t_2)\mathrel {\mathop :}=-2i\omega _j\varphi _j(x) d_1A_j-i\zeta \omega _j\varphi _j(x) A_j\nonumber \\&\quad -[(i\omega _j\xi B_0+3\kappa B_0^2\bar{B}_0)\varDelta _{j,r}+\kappa B_0^3\varDelta _{j,s}]\delta (x-x_C)\nonumber \\&\quad +\biggl [A_r\varphi ''_r(x)\sum _{h=r,s}A_h\bar{A}_h\int _0^1\!\!\varphi _h'(x)^2\hbox {d}x\nonumber \\&\quad +\biggl (\frac{A_r^2\bar{A}_r}{2}\varphi _r''(x)+\frac{A_s\bar{A}_r^2}{2}\varphi _s''(x)\biggr )\int _0^1\!\!\varphi _r'(x)^2\hbox {d}x\biggr ]\varDelta _{j,r} \nonumber \\&\quad +\biggr [\biggl (\frac{A_r^3}{2}\varphi _r''(x)+A_sA_r\bar{A}_r\varphi _s''(x)\biggr )\int _0^1\!\!\varphi _r'(x)^2\hbox {d}x\nonumber \\&\quad +\biggl (\frac{A_s\bar{A}_s^2}{2}\varphi _s''(x)+A_s^2\bar{A}_s\varphi _s''(x)\biggr )\int _0^1\!\!\varphi _s'(x)^2\hbox {d}x\biggr ]\varDelta _{j,s}\nonumber \\&\quad +\frac{p(x)}{2}e^{i\sigma t_1}\varDelta _{j,r} \end{aligned}$$
(22)

and

$$\begin{aligned} \varDelta _{j,h}={\left\{ \begin{array}{ll} 1&{}j=h\\ 0&{}j\ne h \end{array}\right. } \end{aligned}$$
(23)

for \(j=r,s\).

In order to get a not diverging solution from Eqs. (20) and (21), the solvability condition must be enforced on them, which reads:

$$\begin{aligned} \int _0^1\!\!&f_j(x,t_1,t_2)\varphi _j(x)\hbox {d}x=0 \end{aligned}$$
(24)

Substitution of Eq. (22) in Eq. (24) for \(j=r,s\) provides:

$$\begin{aligned} d_1A_r= & {} -\frac{\zeta }{2}A_r-\biggl [\xi B_{0}-\frac{3i \kappa }{\omega _r} B_0^2\bar{B}_0\biggr ]\varphi _r(x_C)\nonumber \\&+\,i\frac{\omega _r}{4}A_r\left[ \frac{3}{2}\omega _r^2A_r\bar{A}_r\,+\,\omega _s^2A_s\bar{A}_s\right] \!-\!\frac{i p_r}{2\omega _r}e^{i\sigma t_1}\nonumber \\ d_1A_s= & {} -\frac{\zeta }{2}A_s-\frac{i \kappa }{\omega _s} B_0^3\varphi _r(x_C)\nonumber \\&+\,i\frac{\omega _s}{4}A_s\biggl [\omega _r^2A_r\bar{A}_r+\frac{3}{2}\omega _s^2A_s\bar{A}_s\biggr ] \end{aligned}$$
(25)

where \(p_r=\int _0^1\!\!p(x)\varphi _r(x)\hbox {d}x\). It is worth noticing that the external force contribution \(p_r\) appears just in the equation ruling the resonant amplitude \(A_r\) [Eq. (25a)]. Moreover, the single component \(B_0\) of the NES amplitude of relative oscillation appears in both the equations (25a, b). However, it would not appear in equations relevant to amplitudes \(A_j\), for \(j\ne r,s\), if those amplitudes were considered in the generating solution (14). That means that the possible equations ruling all the other amplitudes different than \(A_r\) and \(A_s\) would give trivial solution for them (\(A_j\rightarrow 0\), for \(j\ne r,s\), as it happens for the string with NES disengaged for \(j\ne r\) [28]), confirming the good choice of retaining just the resonant and superharmonic contributions. On the other hand, if a more precise solution for the NES oscillation \(z_0\) were considered in (15), containing, e.g., the component \(r\) as well as the component \(s\), they would couple the amplitude modulation equations relevant to string amplitudes of index \(j=r,s,2s-r,2s+r,3s\), which in this case should be retained in the generating solution (14).

The substitution of Eq. (25) in Eqs. (20) and (21) allows one to obtain a solution for this system, which reads:

$$\begin{aligned} \psi _r(x,t_1)= & {} -\frac{\omega _r^2\omega _s^2}{4}A_s\bar{A}_r^2J_{rs}(x)\nonumber \\&+\left[ i\xi \omega _r B_0+3\kappa B_0^2\bar{B}_0\right] [I_r(x,x_C)\nonumber \\&-2\varphi _r(x)J_r(x)]\!-\!\left[ \frac{P_r(x)}{2}\!-\!p_r J_r(x)\right] e^{i\sigma t_1}\nonumber \\ \psi _s(x,t_1)= & {} \kappa B_0^3(I_s(x,x_C)-2\varphi _s(x)J_s(x))\nonumber \\&-\frac{\omega _r^4}{4}A_r^3J_{rs}(x) \end{aligned}$$
(26)

where

$$\begin{aligned} \begin{aligned}&I_j(x,x_C)=\frac{1}{\omega _j}\sin (\omega _j(x-x_C))H(x-x_C)\\&J_j(x)=\frac{1}{2\omega _j}(\sin (\omega _j x)-\omega _j x\cos (\omega _j x))\\&J_{rs}(x)=\frac{\omega _r\sin (\omega _s x)-\omega _s\sin (\omega _r x)}{\omega _r(\omega _r^2-\omega _s^2)}\\&P_r(x)=\frac{1}{\omega _r}\int _0^x\!\!p(\theta )\sin (\omega _r(x-\theta ))\hbox {d}\theta \end{aligned} \end{aligned}$$
(27)

and \(H(x)\) is the Heaviside step (Dirac delta and Heaviside step are used in the paper in the sense of the distributions). In Eq. (26), the normalization condition consisting in a vanishing amplitude for the complementary solution is assumed.

Equation (12) is considered and a further harmonic balance is applied to it, still assuming a one-term Fourier expansion for \(z_1\):

$$\begin{aligned} z_1(t_0,t_1,\ldots )= B_{1}(t_1,\ldots )e^{i \omega _r t_0} +cc \end{aligned}$$
(28)

Substituting Eqs. (14), (15) and (19) in Eq. (12) and balancing frequency \(\omega _r\), the following equation is obtained:

$$\begin{aligned}&- m\bigl [\omega _r^2B_{1}-2i\omega _r d_1B_{0}+2i\omega _r\varphi _r(x_C)d_1A_r\bigr ]\nonumber \\&\quad +\,\xi d_1B_{0}+i\xi \omega _r B_{1}+3\kappa B_{0}^2\bar{B}_{1}\nonumber \\&\quad -\,m\frac{\omega _r^2\omega _s^2}{4}A_s\bar{A}_r^2J_{rs}(x_C)\nonumber \\&\quad -\,2m\left[ i\xi \omega _r B_0+3\kappa B_0^2\bar{B}_0\right] \varphi _r(x_C)J_r(x_c)\nonumber \\&\quad -\,m\left[ \frac{P_r(x_C)}{2}-p_r J_r(x_C)\right] e^{i\sigma t_1}=0 \end{aligned}$$
(29)

Equations (16) and (29) can be reconstituted, using the definition \(B\mathrel {\mathop :}= B_0+\epsilon B_1\); coming back to the true time, reabsorbing \(\epsilon \) for those and for Eq. (25) one obtains:

$$\begin{aligned} \dot{A}_r= & {} -\frac{\zeta }{2}A_r-\left[ \xi B-\frac{3i \kappa }{\omega _r} B^2\bar{B}\right] \varphi _r(x_C)\nonumber \\&+\,i\frac{\omega _r}{4}A_r\left[ \frac{3}{2}\omega _r^2A_r\bar{A}_r+\omega _s^2A_s\bar{A}_s\right] -\frac{i p_r}{2\omega _r}e^{i\sigma t}\nonumber \\ \dot{A}_s= & {} -\,\frac{\zeta }{2}A_s-\frac{i \kappa }{\omega _s} B^3\varphi _r(x_C)\nonumber \\&+\,i\frac{\omega _s}{4}A_s\left[ \omega _r^2A_r\bar{A}_r+\frac{3}{2}\omega _s^2A_s\bar{A}_s\right] \nonumber \\&-\,2i\omega _r m\varphi _r(x_C)\dot{A}_r+(\xi +2i\omega _r m)\dot{B}\nonumber \\= & {} -\,m\omega _r^2 \varphi _r(x_C)A_r+(m\omega _r^2-i\xi \omega _r)B\nonumber \\&-\,3\kappa B^2\bar{B} +m\frac{\omega _r^2\omega _s^2}{4}A_s\bar{A}_r^2J_{rs}(x_C)\nonumber \\&+\,2m\left[ i\xi \omega _r B_0+3\kappa B_0^2\bar{B}_0\right] \varphi _r(x_C)J_r(x_c)\nonumber \\&+\,m\left[ \frac{P_r(x_C)}{2}-p_r J_r(x_C)\right] e^{i\sigma t_1} \end{aligned}$$
(30)

Equation (30) are the complex amplitude modulation equations (AME) ruling the slow dynamics of the string and NES, also outside the manifold (16). The derivatives of \(B\) and \(A_r\) have been obtained at the second order, due to the fact that they are multiplied by small coefficients \(\xi \) and \(m\). Equation (30) can be written in real form through the polar transformation \(A_j(t)\mathrel {\mathop :}=\frac{1}{2}a_j(t)e^{i\alpha _j(t)}\) (\(j=r,s\)) and \(B(t)\mathrel {\mathop :}=\frac{1}{2}b(t)e^{i\beta (t)}\), separating real and imaginary parts, and defining phase differences as \(\gamma (t)\mathrel {\mathop :}=\sigma t-\alpha _r(t)\), \(\chi (t)\mathrel {\mathop :}=\alpha _s(t)+3\gamma (t)-3\sigma t\) and \(\vartheta (t)\mathrel {\mathop :}=\sigma t-\beta (t)\). They read

$$\begin{aligned}&\dot{a}_r=\mathcal {F}_1(a_r,a_s,b,\gamma ,\chi ,\vartheta )\nonumber \\&\dot{a}_s=\mathcal {F}_2(a_r,a_s,b,\gamma ,\chi ,\vartheta )\nonumber \\&m\omega _r\dot{b}+m\omega _r a_r\dot{\gamma }\sin (\omega _r x_C)\sin (\gamma -\vartheta )\nonumber \\&\quad -\frac{1}{2}\xi b\dot{\vartheta }-m\omega _r\dot{a}_r\sin (\omega _rx_C)\cos (\gamma -\vartheta )\nonumber \\&\quad =\mathcal {F}_3(a_r,a_s,b,\gamma ,\chi ,\vartheta )\nonumber \\&a_r\dot{\gamma }=\mathcal {F}_4(a_r,a_s,b,\gamma ,\chi ,\vartheta )\nonumber \\&a_s \dot{\chi }-3a_s\dot{\gamma }=\mathcal {F}_5(a_r,a_s,b,\gamma ,\chi ,\vartheta )\nonumber \\&m\omega _rb\dot{\vartheta }-m\omega _r a_r\dot{\gamma }\sin (\omega _r x_C)\cos (\gamma -\vartheta )\nonumber \\&\quad +\frac{1}{2}\xi \dot{b}-m\omega _r\dot{a}_r\sin (\omega _rx_C)\sin (\gamma -\vartheta )\nonumber \\&\quad =\mathcal {F}_6(a_r,a_s,b,\gamma ,\chi ,\vartheta ) \end{aligned}$$
(31)

The nonlinear functions \(\mathcal {F}_k\) (\(k=1,\ldots ,6\)) are reported in Appendix 1.

If one defines the columns \(\mathbf {u}\mathrel {\mathop :}=\{a_r,a_s,b,\gamma ,\chi ,\vartheta \}\), \(\mathcal {F}\mathrel {\mathop :}=\{\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3,\mathcal {F}_4,\mathcal {F}_5,\mathcal {F}_6\}\) and the mass matrix \(\mathcal {M}(\mathbf {u})\) (the expression of \(\mathcal {M}(\mathbf {u})\) is reported in Appendix 1), Eq. (31) can be written as

$$\begin{aligned} \mathcal {M}(\mathbf {u})\dot{\mathbf {u}}=\mathcal {F}(\mathbf {u}) \end{aligned}$$
(32)

which in normal form becomes (provided \(\det (\mathcal {M})\ne 0\))

$$\begin{aligned} \dot{\mathbf {u}}=\mathcal {G}(\mathbf {u}) \end{aligned}$$
(33)

where \(\mathcal {G}(\mathbf {u})\mathrel {\mathop :}=\mathcal {M}(\mathbf {u})^{-1}\mathcal {F}(\mathbf {u})\)

Equilibrium points of system (33), describing periodic motions of the variables \(v(x,t)\) and \(z(t)\), are evaluated by solving the same system for \(\dot{a}_r=\dot{a}_s=\dot{b}=\dot{\gamma }=\dot{\vartheta }=\dot{\chi }=0\), and their stability properties are detected looking at the real part of the eigenvalues of the Jacobian matrix; periodic solutions of Eq. (33), giving rise to quasiperiodic motions in \(v(x,t)\) and \(z(t)\), are numerically obtained through direct integration of Eq. (31), while semi-analytical detection of the bands of existence of the SMR (see e.g., [22]) is not carried out here as a consequence of the increased dimension of the system, which makes the procedure not computationally easy. The computations, carried out by means of the softwares Auto [33] and Mathematica [34], are presented in the following Section for a case study.

4 Numerical results

Numerical results are evaluated for a string of damping coefficient \(\zeta =1.119\,\%\) (the value is reconstructed from [35] where modal damping ratios are experimentally measured for a stay). The external force is assumed as uniform (\(p(x)\equiv p\)), and the nondimensional parameters of the NES are \(m=0.05\), \(\kappa =70\), \(\xi =0.01\).

From now on, the external force is assumed to be resonant to the first mode, therefore \(r=1\), \(s=3\), moreover \(\omega _r\mathrel {\mathop :}=\pi \), \(\omega _s\mathrel {\mathop :}=3\pi \) and \(\varphi _r(x)\mathrel {\mathop :}=\sin (\pi x)\), \(\varphi _s(x)=\sin (3\pi x)\).

The position of the NES along the span changes the invariant manifold (17) in the way shown in Fig. 2. In particular, if the NES is located at the mid-span (orange point in Fig. 2a, \(x_C=0.5\)), which is the antinode of both the first and third modes (blue and red lines in Fig. 2a, respectively), for a fixed value of amplitude of oscillation \(b\) of the NES, a smaller amplitude of oscillation \(a\) of the principal structure occurs, than the case where the NES is elsewhere (i.e., the orange curve is always underneath the black and green ones, corresponding to \(x_C=0.3\) and \(x_C=0.2\) in Fig. 2a, respectively). Therefore, the NES is more capable to absorb energy from the main structure, which is the main objective of the control problem, when its position corresponds to the node of the mode shape.

Fig. 2
figure 2

Position of the NES on the span: \(x_C=0.5\), orange point; \(x_C=0.3\), black point; \(x_C=0.2\), green point; first mode (blue line) and third mode (red line) of the string (a); invariant manifolds corresponding to the three positions of the NES (b). (Color figure online)

Full size image

Amplitude of periodic motions of both the string and NES, for force amplitude value \(p=0.0084\), are shown in Fig. 3. In Fig. 3a, the black line corresponds to the response \(a_r\) without NES, which is the unique contribution to the solution of the string; it is superimposed to the response curve obtained when NES is engaged, in terms of \(a_r\) (red line) and \(a_s\) (blue line). The strong reduction of the peak amplitude is evident, which is a beneficial effect of the NES, as well as the participation of the superharmonic component \(a_s\) to the dynamics. In Fig. 3b, the amplitude of oscillation \(b\) of the NES is shown.

Fig. 3
figure 3

Frequency–response curves: a amplitude \(a_r\) with NES disengaged (black line), amplitude \(a_r\) (red line) and \(a_s\) (blue line) with NES engaged; b amplitude of NES \(b\) (red line). Force \(p=0.0084\), position of the NES \(x_C=0.5\). Continuous line stable; dashed line unstable. (Color figure online)

Full size image

A more detailed view of the same frequency–response curves is shown in Fig. 4. There, Hopf bifurcation points (HB) are highlighted; they induce the arising of quasiperiodic oscillations of the string and NES, which are stable close to the left HB point (dark filled regions) and representing weakly modulated responses (WMR). After secondary bifurcations, they become unstable (light filled regions) and the response jumps to Strongly Modulated Responses (which are not shown in the pictures). In Fig. 5, WMR and SMR (black lines) are shown as superimposed to the invariant manifold (red lines), for \(\sigma =0.046\) (WMR, Fig. 5a) and \(\sigma =0.060\) (SMR, Fig. 5b). The time evolution of the same SMR is shown in Fig. 6, where the three components \(a_r\), \(a_s\) and \(b\) experience relaxation oscillations. In Fig. 7, the reconstituted displacement of the midpoint of the string (\(v_m\mathrel {\mathop :}=v(1/2,t)\)) and of the NES (\(z(t)\)) are shown. They are in good agreement with the time evolutions provided by integration of a system of ordinary differential equations obtained by a Galerkin projection of Eqs. (4) and (5), using the first eight odd eigenfunctions as trial functions (Fig. 8).

Fig. 4
figure 4

Frequency–response curves of the amplitudes \(a_r\) (a), \(a_s\) (b) and \(b\) (c), for \(p=0.0084\) and \(x_C=0.5\). Continuous line stable; dashed line unstable. Dark filled regions stable quasiperiodic oscillations. Light filled regions unstable quasiperiodic oscillations

Full size image
Fig. 5
figure 5

Weakly modulated response [\(\sigma =0.048\), black line (a)] and strongly modulated response [\(\sigma =0.060\), black line (b)] with NES at the antinode, for \(p=0.0084\) and \(x_C=0.5\); red line invariant manifold. Continuous line stable; dashed line unstable. (Color figure online)

Full size image
Fig. 6
figure 6

Strongly modulated response (\(\sigma =0.06\), \(p=0.0084\), \(x_C=0.5\)). Time evolution of \(a_r\) (a); time evolution of \(a_s\) (b); time evolution of \(b\) (c)

Full size image
Fig. 7
figure 7

Strongly modulated response (\(\sigma =0.06\), \(p=0.0084\), \(x_C=0.5\)). Time evolution of \(v_m\) (a); time evolution of \(z\) (b)

Full size image
Fig. 8
figure 8

Strongly modulated response from the Galerkin model (\(\sigma =0.06\), \(p=0.0084\), \(x_C=0.5\)). Time evolution of \(v_m\) (a); time evolution of \(z\) (b)

Full size image

5 Conclusions

An internally resonant elastic string is considered here under the action of an external harmonic force. A NES is engaged at a generic point of the string in order to reduce the amplitude of oscillations as a passive control device. The MSHBM, extended in order to deal with internally resonance cases, is applied in direct approach to the system of partial differential equations, to get amplitude modulation equations ruling the slow dynamics of the system.

Differently than the case with NES disengaged, where the dominant dynamics of the string is ruled just by the directly excited resonant mode, the presence of the NES involves (in a first approximation) both the resonant and a superharmonic components in the response, and amplitude modulation equations ruling the slow dynamics of them are coupled to the equation relevant to the NES slow amplitude of oscillation.

Numerical results for a case study are presented, denoting the contribution of both the components in periodic and quasiperiodic solutions, and the beneficial effect of the NES to reduce the amplitude of oscillation of the string. Results are in good agreement with those provided by a discrete, approximated, system of ordinary differential equations obtained by means of a Galerkin projection of the infinite dimensional problem.