Nonlinear modeling for dynamic analysis of a rotating cantilever beam

Abstract

This paper proposes a nonlinear model for more accurate and efficient dynamic analysis of a rotating cantilever beam with elastic deformation. The proposed nonlinear model is described by partial integro-differential equations with non-Cartesian deformation variables, i.e., the stretch, chordwise and flapwise deformations. After the equations of motion are discretized by using the mode superposition method, dynamic responses are computed by applying the Newmark time integration method to the discretized equations. To show the accuracy and efficiency of the proposed model, convergence characteristics and dynamic responses for the present model are compared with those for previous models. This study shows that the proposed model not only yields good accuracy and efficiency in terms of computation, but also overcomes the limitations of a previous conventional nonlinear model expressed by Cartesian variables.

1 Introduction

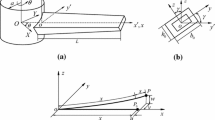
The dynamic analysis of a rotating flexible beam is an interesting topic because rotating beams have a variety of applications such as turbine blades, space appendages, helicopter blades and flying robot wings. As a result, a more reliable dynamic model for a rotating beam requires the stable operation and performance of a rotating machine. Before analyzing previous research, definitions for the various deformations of a rotating beam need to be introduced, because they may be helpful for understanding the research trends for rotating beams. A flexible cantilever beam, as shown in Fig. 1, rotates about the axis perpendicular to the xy plane. In this paper, the deformations in the x, y and z directions are called the axial, chordwise (or lagwise) and flapwise deformations, respectively, and the extensional deformation along the curve of a deformed beam is called the stretch deformation. The elastic deformation of a beam can be described by two sets of deformation variables: Cartesian variables and non-Cartesian variables. The Cartesian deformation variables consist of the axial, chordwise and flapwise deformations. Meanwhile, the non-Cartesian deformation variables use the stretch deformation instead of the axial deformation; therefore, the non-Cartesian variables are composed of the stretch, chordwise and flapwise deformations.

Fig. 1

Configuration of a rotating flexible cantilever beam: a the top view and b the side view

Many linear models for rotating beams have been introduced to avoid computational burden for dynamic analyses. The linear vibrations using Cartesian variables were investigated by various methods such as the finite element method (FEM) [1, 2], the mode superposition method (MSM) [3, 4] and the method of series solution (MSS) [5]. In this study, the MSM represents the Galerkin method with mode functions, assumed mode method, Rayleigh–Ritz method and modal expansion method, collectively. Hoa [1] introduced a linear dynamic model for a rotating beam in which only the flapwise deformation is included with the centrifugal force effect. He obtained discretized equations by using the FEM. Taking into account the Coriolis and centrifugal forces, Simo and Vu-Quoc [2] derived linear equations for the axial and chordwise motions and also discretized the equations by using the FEM. Pesheck et al. [3, 4] derived nonlinear equations considering the axial and flapwise deformations without the chordwise deformation and then obtained partial differential equations linearized about an equilibrium state. The linearized equations were discretized by the MSM. Banerjee and Kennedy [5] derived the equations of axial and chordwise motions considering the centrifugal tension of a beam and then solved the equations by the MSS. Some papers have been published for linear models that are represented with non-Cartesian variables [6–10]. In these papers, the stretch deformation was used instead of the axial deformation. On the basis of solution methods, these papers may be categorized into the MSM [6–8] and the FEM [9, 10].

In most previous studies, the Cartesian variables were used to obtain nonlinear models of rotating beams. To derive nonlinear equations of motion using Cartesian variables, Huang et al. [11] and Kim et al. [12] adopted the nonlinear von Karman strain, but they used linearized stress instead of nonlinear stress. When discretizing the equations, Huang et al. [11] used the MSS while Kim et al. [12] used the MSM. On the other hand, some studies on rotating beams used the FEM to analyze the nonlinear dynamic behaviors of rotating beams [13–15]. Adopting von Karman strain theory, Sharf [13] established a nonlinear FEM to analyze the dynamics of the axial, chordwise and flapwise deformations. Apiwattanalunggarn et al. [14] developed a nonlinear one-dimensional finite element model representing the axial and flapwise motions of a cantilevered rotating beam. Arvin and Bakhtiari-Nejad [15] performed a nonlinear modal analysis of a rotating beam. They derived nonlinear equations for the axial and flapwise motions and discretized the equations using the MSM. Based on the discretized equations, nonlinear normal modes and nonlinear natural frequencies with or without internal resonance were investigated. However, they did not compute the dynamic responses from the discretized equations obtained by the MSM. Using both the FEM and MSM, Wang [16] obtained interesting results for nonlinear dynamic simulations of the axial and chordwise motions. He found that the MSM has poor convergence characteristics compared to the FEM.

In addition to the models mentioned above, various models for the nonlinear vibration analyses of rotating beams have been discussed. Valverde and García-Vallejo [17] used the absolute nodal coordinate formulation to derive nonlinear differential equations, and they showed the similarities between the absolute nodal coordinate formulation and the substructuring technique. Younesian and Esmailzadeh [18] analyzed the nonlinear vibration of a viscoelastic rotating beam. Using the classical steps of the special Cosserat theory of rods, Lacarbonara et al. [19] and Arvin et.al. [20] derived fully nonlinear equations of motion of rotating blades. They investigated the natural frequencies of unshearable blades including coupling between flapping, lagging, axial and torsional motions and discussed the nonlinear modes of vibration which are away from internal resonances. Yao et al. [21] studied the nonlinear dynamic responses of a rotating blade under high-temperature supersonic gas flow when rotating speed varies. Coupling the Galerkin method with the balance harmonic method, Bekhoucha et al. [22] investigated the forced vibration for nonlinear rotating anisotropic beams.

It is well known that most of convergence tests in nonlinear problems generally exhibit the superiority of the MSM to the FEM in terms of convergence. This well-known fact is opposed to a claim of Wang [16]. When computing the dynamic responses of some nonlinear dynamic systems using the MSM, poor converged computation results may be often encountered. Therefore, it is necessary to disclose the reason why the MSM yields poor convergence when applying it to certain nonlinear models. Furthermore, the nonlinear model of a rotating beam, which shows good convergence characteristics even when using the MSM, needs to be developed.

In this paper, a nonlinear model for a rotating cantilever beam is presented, which is described using non-Cartesian variables, i.e., the stretch, chordwise and flapwise deformations. Using the nonlinear von Karman strain and the corresponding nonlinear stress, partial integro-differential equations for the stretch, chordwise and flapwise motions are derived from the Hamilton principle. The equations of motion are discretized by the MSM with the mode functions for the longitudinal and transverse vibrations of a stationary cantilevered beam, and then, the dynamic responses are computed from the discretized equations by applying the Newmark time integration method. Moreover, previous dynamic models for rotating beams are classified into three categories: two of them use nonlinear equations expressed with the Cartesian variable and the other one uses linear equations. When applying the MSM to compute dynamic responses, the poor convergence characteristics of a previous nonlinear model are examined and compared to those of the proposed model. The comparisons of dynamic responses are performed between the proposed and previous models.

2 Equations of motion

As shown in Fig. 1, a flexible cantilever beam fixed to a rigid hub of radius a rotates with an angular speed $\varOmega$. The cantilever beam, which is homogeneous and uniform, has mass density $\rho$, Young’s modulus E, length L and cross-sectional area A. Assuming that the beam length is long enough compared to the dimensions of the cross section, the beam is regarded as an Euler–Bernoulli beam in this study. As discussed in the Sect. 1, the beam deformation may be defined by two sets of deformation variables. The axial, chordwise and flapwise deformations of the Cartesian variables are denoted by u, v and w, respectively. The stretch deformation in non-Cartesian variables is denoted by s. In this study, the non-Cartesian variables of s, v and w are used to derive the nonlinear equations of motion for a rotating beam.

The stretch, axial, chordwise and flapwise deformations, which are functions of the time t and position x, are depicted in Fig. 1, and they are related to the following equation:

$$\begin{aligned} \varepsilon =\frac{\partial s}{\partial x}=\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}, \end{aligned}$$

(1)

where $\varepsilon$ is the normal strain due to the stretch deformation. The relation between the stretch deformation (s) and Cartesian deformations (u, v and w) was derived by Yoo et al. [7], in which more detail derivation procedure can be found. When the strain $\varepsilon$ is expressed in terms of u, v and w, this strain is called the von Karman strain. As shown in (1), the strain expressed by s is linear, while the strain expressed by u, v and w is nonlinear. Integrating (1) with respect to x, the stretch deformation may be written as

$$\begin{aligned} s=u+h_{v} +h_{w}, \end{aligned}$$

(2)

where

$$\begin{aligned} h_{v} =\frac{1}{2}\int _{0}^{x} {\left( {\frac{\partial v}{\partial \xi }} \right) ^{2}\hbox {d}\xi } ,\quad h_{w} =\frac{1}{2}\int _{0}^{x} {\left( {\frac{\partial w}{\partial \xi }} \right) ^{2}\hbox {d}\xi } \end{aligned}$$

(3)

in which $\xi$ is a dummy variable.

The kinetic and potential energies and the work done by non-conservative forces are all required to obtain the equations of motion. When small elastic deformations as well as large overall motions are considered, the kinetic energy can be expressed as

$$\begin{aligned} T= & {} \rho A\int _{0}^{L} \left\{ \left( {\frac{\partial u}{\partial t}-\varOmega v} \right) ^{2}\right. \nonumber \\&\left. +\,\left[ {\frac{\partial v}{\partial t}+\varOmega \left( {a+x+u} \right) } \right] ^{2}+\left( {\frac{\partial w}{\partial t}} \right) ^{2} \right\} \hbox {d}x.\nonumber \\ \end{aligned}$$

(4)

The potential energy (or strain energy) due to the stretch, chordwise and flapwise deformations is given by

$$\begin{aligned} U= & {} \frac{1}{2}\int _{0}^{L} \left[ EA\left( {\frac{\partial s}{\partial x}} \right) ^{2}\right. \nonumber \\&\left. +\,EI_{z} \left( {\frac{\partial ^{2}v}{\partial x^{2}}} \right) ^{2}+EI_{y} \left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right) ^{2} \right] \hbox {d}x, \end{aligned}$$

(5)

where $I_{y}$ and $I_{z}$ are the area moments of inertia about the y and z axes, respectively. The work done by non-conservative pressures may be written as

$$\begin{aligned} W=\int _{0}^{L} {\left( {p_{v} v+p_{w} w} \right) \hbox {d}x}, \end{aligned}$$

(6)

where $p_{v}$ and $p_{w}$ are the distributed forces per unit length in the chordwise and flapwise directions, respectively.

The partial integro-differential equations of motion for a rotating cantilever beam are derived by substituting the above kinetic and potential energies and the work into the Hamilton principle. Using (2), the equations of motion expressed in terms of the stretch, chordwise and flapwise deformations can be written as

$$\begin{aligned}&\rho A\left[ \frac{\partial ^{2}s}{\partial t^{2}}-\frac{\partial ^{2}h_v }{\partial t^{2}}-\frac{\partial ^{2}h_w }{\partial t^{2}}-2\varOmega \frac{\partial v}{\partial t}\right. \nonumber \\&\quad \left. -\,\varOmega ^{2}\left( {s-h_v -h_w } \right) -{\dot{\varOmega }}v \right] \nonumber \\&\quad -\,EA\frac{\partial ^{2}s}{\partial x^{2}}=\rho A\varOmega ^{2}\left( {a+x} \right) , \end{aligned}$$

(7)

$$\begin{aligned}&\rho A\left[ \frac{\partial ^{2}v}{\partial t^{2}}+2\varOmega \left( {\frac{\partial s}{\partial t}-\frac{\partial h_v }{\partial t}-\frac{\partial h_w }{\partial t}} \right) -\varOmega ^{2}v\right. \nonumber \\&\quad \left. +\,{{\dot{\varOmega }}}\left( {s-h_v -h_w } \right) \right] {-}EA\frac{\partial }{\partial x}\left( {\frac{\partial s}{\partial x}\frac{\partial v}{\partial x}} \right) +EI_z \frac{\partial ^{4}v}{\partial x^{4}}\nonumber \\&\qquad =p_{v} -\rho A{\dot{\varOmega }}\left( {a+x} \right) , \end{aligned}$$

(8)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-EA\frac{\partial }{\partial x}\left( {\frac{\partial s}{\partial x}\frac{\partial w}{\partial x}} \right) +EI_y \frac{\partial ^{4}w}{\partial x^{4}}=p_w , \end{aligned}$$

(9)

where a superposed dot represents differentiation with respect to time. The associated boundary conditions are given by

$$\begin{aligned}&s=v=w=\frac{\partial v}{\partial x}=\frac{\partial w}{\partial x}=0 \quad \quad {\hbox {at }} x=0, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial s}{\partial x}=\frac{\partial ^{2}v}{\partial x^{2}}=\frac{\partial ^{2}w}{\partial x^{2}}=\frac{\partial ^{3}v}{\partial x^{3}}=\frac{\partial ^{3}w}{\partial x^{3}}=0 \quad \quad \hbox {at } x=L.\nonumber \\ \end{aligned}$$

(11)

Note that (7)–(9) are nonlinear integro-differential equations because $h_{v}$ and $h_{w}$ are of nonlinear integral form, as shown in (3), and the second terms of (8) and (9) are also nonlinear. However, the boundary conditions given by (10) and (11) are linear with respect to the stretch, chordwise and flapwise deformations.

3 Model classification

The proposed nonlinear model for a rotating beam is compared to other previous models. Four models considered for comparison are called Models 1–4 in this study: Models 1–3 are nonlinear models, while Model 4 is a linear model. Model 1, which is the proposed model in this study, is represented by the equations of motion given by (7)–(9) and the corresponding boundary conditions given by (10) and (11). Therefore, Model 1 is a nonlinear model described by the stretch, chordwise and flapwise deformations.

On the other hand, Model 2 is defined as a nonlinear model described by the axial deformation u (instead of the stretch deformation s), the chordwise deformation v and the flapwise deformation w. The equations of motion and the associated boundary conditions are obtained by introducing (2) into (7)–(11). The obtained equations of motion are given by

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}u}{\partial t^{2}}-2\varOmega \frac{\partial v}{\partial t}-\varOmega ^{2}u-{{\dot{\varOmega }}}v} \right) -EA\frac{\partial }{\partial x}\left[ \frac{\partial u}{\partial x}\right. \nonumber \\&\quad \left. +\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2} +\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2} \right] =\rho A\varOmega ^{2}\left( {a+x} \right) ,\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}+2\varOmega \frac{\partial u}{\partial t}-\varOmega ^{2}v+{{\dot{\varOmega }}}u} \right) -EA\frac{\partial }{\partial x}\left\{ \left[ \frac{\partial u}{\partial x}\right. \right. \nonumber \\&\quad \left. \left. +\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2} \right] \frac{\partial v}{\partial x} \right\} +EI_z \frac{\partial ^{4}v}{\partial x^{4}}\nonumber \\&\qquad =p_v -\rho A{{\dot{\varOmega }}}( {a+x} ), \end{aligned}$$

(13)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-EA\frac{\partial }{\partial x}\left\{ \left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}\right. \right. \nonumber \\&\quad \left. \left. +\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2} \right] \frac{\partial w}{\partial x} \right\} +EI_y \frac{\partial ^{4}w}{\partial x^{4}}=p_w. \end{aligned}$$

(14)

The associated boundary conditions are given by

$$\begin{aligned}&u=v=w=\frac{\partial v}{\partial x}=\frac{\partial w}{\partial x}=0 \quad \quad \hbox {at } x=0, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}=\frac{\partial ^{2}v}{\partial x^{2}}=\frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad =\frac{\partial ^{3}v}{\partial x^{3}}=\frac{\partial ^{3}w}{\partial x^{3}}=0 \quad \quad \hbox {at } x=L. \end{aligned}$$

(16)

Note that Model 2 is defined by the equations of motion given by (12)–(14) and the boundary conditions given by (15) and (16). As shown in (12)–(16), the equations of motion are not only nonlinear, but one of the boundary conditions is also nonlinear. Neglecting the chordwise deformation, Arvin and Bakhtiari-Nejad [15] derived the equations of motion corresponding to Model 2. The models proposed by Sharf [13] and Apiwattanalunggarn et al. [14] can be classified as Model 2.

Another nonlinear model obtained by using the nonlinear strain and linearized stress is called Model 3, which was presented by Huang et al. [11] and Kim et al. [12]. The equations of motion for Model 3, derived by Kim et al. [12], may be expressed as

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}u}{\partial t^{2}}-2\varOmega \frac{\partial v}{\partial t}-\varOmega ^{2}u-{{\dot{\varOmega }}}v} \right) -EA\frac{\partial ^{2}u}{\partial x^{2}}\nonumber \\&\qquad =\rho A\varOmega ^{2}(a+x), \end{aligned}$$

(17)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}+2\varOmega \frac{\partial u}{\partial t}-\varOmega ^{2}v+{{\dot{\varOmega }}}u} \right) \nonumber \\&\quad -EA\frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}} \right) +EI_z \frac{\partial ^{4}v}{\partial x^{4}}\nonumber \\&\qquad =p_v -\rho A{{\dot{\varOmega }}}(a+x), \end{aligned}$$

(18)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-EA\frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}} \right) +EI_y \frac{\partial ^{4}w}{\partial x^{4}}=p_w . \end{aligned}$$

(19)

The boundary conditions for Model 3 are given by (15) and the following equation:

$$\begin{aligned} \frac{\partial u}{\partial x}=\frac{\partial ^{2}v}{\partial x^{2}}=\frac{\partial ^{2}w}{\partial x^{2}}=\frac{\partial ^{3}v}{\partial x^{3}}=\frac{\partial ^{3}w}{\partial x^{3}}=0 \quad \quad \hbox {at } x=L. \end{aligned}$$

(20)

Note that the equations for the chordwise and flapwise motions, (18) and (19), are nonlinear; however, the equation for the axial motion, (17), and the boundary conditions, (15) and (20), are linear. Huang et al. [11] presented the same model as Model 3; however, they neglected the chordwise deformation during derivation of the equations of motion.

Finally, a linear model for a rotating cantilever beam, presented by many researchers [1–10], is Model 4 in this paper. Typical equations for the stretch, chordwise and flapwise motions, which are linear partial differential equations, can be expressed as [9]

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}s}{\partial t^{2}}-2\varOmega \frac{\partial v}{\partial t}-\varOmega ^{2}s-{{\dot{\varOmega }}}v} \right) -EA\frac{\partial ^{2}s}{\partial x^{2}}\nonumber \\&\qquad =\rho A\varOmega ^{2}\left( {a+x} \right) , \end{aligned}$$

(21)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}+2\varOmega \frac{\partial s}{\partial t}-\varOmega ^{2}v+{{\dot{\varOmega }}}s} \right) -\frac{\partial }{\partial x}\left( {F\frac{\partial v}{\partial x}} \right) \nonumber \\&\quad +EI_z \frac{\partial ^{4}v}{\partial x^{4}}=p_v -\rho A{{\dot{\varOmega }}}\left( {a+x} \right) , \end{aligned}$$

(22)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-\frac{\partial }{\partial x}\left( {F\frac{\partial w}{\partial x}} \right) +EI_y \frac{\partial ^{4}w}{\partial x^{4}}=p_w , \end{aligned}$$

(23)

where

$$\begin{aligned} F=\rho A\varOmega ^{2}\left[ {a\left( {L-x} \right) +\frac{1}{2}\left( {L^{2}-x^{2}} \right) } \right] . \end{aligned}$$

(24)

The boundary conditions associated with this model are given by equations as (10) and (11). Gunjal and Dixit [10] used this model for vibration analysis of rotating cantilever beams. Some authors, e.g., Pesheck et al. [3, 4] and Banerjee and Kennedy [5], used the axial deformation u instead of the stretch deformation s to derive the equations of motion, which can be classified as Model 4. However, they derived the same equations for the axial and flapwise motions without considering the chordwise motion.

Table 1 Comparison of the four models for linearity, deformation variables, equations of motion, boundary conditions and related papers

In Table 1, the deformation variables, equations of motion, boundary conditions and related papers are compared between the four models. As depicted in Table 1, Model 1 is described by the stretch, chordwise and flapwise deformation variables; however, Models 2–4 can be described by the axial, chordwise and flapwise deformation variables. It is also observed in this table that the equations of motion for Models 1–3 are nonlinear, while the boundary conditions for Models 1, 3 and 4 are linear.

4 Discretization

Discretized equations are required to obtain numerical solutions from the integro-differential (or differential) equations discussed in the previous sections. As shown in (7)–(9), the stretch deformation is coupled with the chordwise and flapwise deformations. However, if the flapwise force $p_{w}$ does not exists, a rotating beam has only the stretch and chordwise deformations without the flapwise deformation. Moreover, the flapwise deformation is not directly influenced by the rotation of a beam but the stretch and chordwise deformations are. Therefore, for simplicity of comparison between the four models, neglecting the flapwise deformation, only the stretch (or axial) and chordwise deformations are considered in the further discussion.

First, consider the discretization of the equations for Model 1 by using the MSM. Before discretization, the variational equations need to be derived from the equations of motion and corresponding boundary conditions. The weighting functions for the stretch and chordwise deformations are denoted by ${\bar{s}}$ and ${\bar{v}}$, respectively, which are arbitrary functions. These functions have values of zero at the boundaries where the essential boundary conditions are prescribed. Multiplying (7) and (8) by ${\bar{s}}$ and ${\bar{v}}$, respectively, integrating the resultant equations over the beam length, and then applying integration by parts, the following variational equations can be obtained:

$$\begin{aligned}&\rho A\int _0^L \left[ {\bar{s}}\left( {\frac{\partial ^{2}s}{\partial t^{2}}-\frac{\partial ^{2}h_v }{\partial t^{2}}} \right) -2\varOmega {\bar{s}}\frac{\partial v}{\partial t}-\varOmega ^{2}{\bar{s}}\left( {s-h_v } \right) \right. \nonumber \\&\quad \left. -{{\dot{\varOmega }}}{\bar{s}}v \right] \hbox {d}x +EA\int _0^L {\frac{\partial {\bar{s}}}{\partial x}\frac{\partial s}{\partial x}\hbox {d}x}\nonumber \\&\qquad =\rho A\varOmega ^{2}\int _0^L {{\bar{s}}\left( {a+x} \right) } \hbox {d}x, \end{aligned}$$

(25)

$$\begin{aligned}&\rho A\int _0^L \left[ {\bar{v}}\frac{\partial ^{2}v}{\partial t^{2}}+2\varOmega {\bar{v}}\left( {\frac{\partial s}{\partial t}-\frac{\partial h_v }{\partial t}} \right) \right. \nonumber \\&\quad \left. -\varOmega ^{2}{\bar{v}}v +{{\dot{\varOmega }}}{\bar{v}}\left( {s-h_v } \right) \right] \hbox {d}x \nonumber \\&\quad +\int _0^L {\left( {EA\frac{\partial {\bar{v}}}{\partial x}\frac{\partial s}{\partial x}\frac{\partial v}{\partial x}+EI_z \frac{\partial ^{2}{\bar{v}}}{\partial x^{2}}\frac{\partial ^{2}v}{\partial x^{2}}} \right) \hbox {d}x} \nonumber \\&\qquad =\int _0^L {\left[ {p_v -\rho A{{\dot{\varOmega }}}(a+x)} \right] {\bar{v}}} \hbox {d}x. \end{aligned}$$

(26)

Using the MSM, the approximate solutions for the stretch and chordwise deformations, often called the trial functions, may be expressed as a series of the basis functions. The trial functions for s and v can be written as

$$\begin{aligned} s(x,t)=\sum _{j=1}^N {S_j (x)T_j^s (t)},\quad v(x,t)=\sum _{n=1}^N {V_n (x)T_n^v (t)}, \end{aligned}$$

(27)

where N is the total number of basis functions, $S_{j}$ and $V_{n}$ are the basis functions, and $T_{j}^{s}$ and $T_{n}^{v}$ are unknown functions of time to be determined. The basis functions $S_{j}$ and $V_{n}$ are selected as the mode functions for the longitudinal and transverse vibration of a stationary cantilevered beam:

$$\begin{aligned}&S_j (x)=\sqrt{2}\sin \left( {2j-1} \right) \frac{\pi x}{2L}, \end{aligned}$$

(28)

$$\begin{aligned}&V_n \left( x \right) =\cosh \lambda _n x-\cos \lambda _n x\nonumber \\&\quad -\frac{\sinh \lambda _n L-\sin \lambda _n L}{\cosh \lambda _n L+\cosh \lambda _n L}\left( {\sinh \lambda _n x-\sin \lambda _n x} \right) ,\nonumber \\ \end{aligned}$$

(29)

where $\lambda _{n}$ is the nth root of the following frequency equation:

$$\begin{aligned} \cos \lambda _n L\cosh \lambda _n L+1=0. \end{aligned}$$

(30)

It should be noted that the basis functions given by (28) and (29) are the comparison functions because they satisfy the essential boundary conditions given by (10) and the natural boundary conditions given by (11). In other words, the comparison functions can be selected as the basis functions for Model 1 because the boundary conditions for Model 1 are linear, as shown in (10) and (11). The weighting functions for the stretch and chordwise deformations can be also represented by a series of basis functions as follows:

$$\begin{aligned} {\bar{s}}(x,t)=\sum _{i=1}^N {S_i (x){\bar{T}}_i^s (t)},\quad {\bar{v}}(x,t)=\sum _{m=1}^N {V_m (x){\bar{T}}_m^v (t)}, \end{aligned}$$

(31)

where ${\bar{T}}_{i}^{s}$ and ${\bar{T}}_{m}^{v}$ are arbitrary functions of time.

The discretized equations for Model 1 are obtained by substituting (27) and (31) into (25) and (26). The arbitrariness of ${\bar{T}}_{i}^{s}$ and ${\bar{T}}_{m}^{v}$ leads to the following discretized equations:

$$\begin{aligned}&\sum _{j=1}^N {\left( {m_{ij}^s {\ddot{T}}_j^s +k_{ij}^s T_j^s } \right) } +\sum _{n=1}^N {\left( {g_{in}^{sv} {\dot{T}}_n^v +k_{in}^{sv} T_n^v } \right) }\nonumber \\&\quad +N_i^s =f_i^s\quad \hbox {for } i=1,2,\ldots ,N, \end{aligned}$$

(32)

$$\begin{aligned}&\sum _{n=1}^N {\left( {m_{mn}^v {\ddot{T}}_n^v +k_{mn}^v T_n^v } \right) } +\sum _{j=1}^N {\left( {g_{mj}^{vs} {\dot{T}}_j^s +k_{mj}^{vs} T_j^s } \right) } \nonumber \\&\quad +N_m^v =f_m^v \quad \hbox {for } m=1,2,\ldots N, \end{aligned}$$

(33)

where

$$\begin{aligned}&m_{ij}^s =\rho A\int _0^L {S_i (x)S_j (x)\hbox {d}x},\nonumber \\&m_{mn}^v =\rho A\int _0^L {V_m (x)V_n (x)\hbox {d}x},\nonumber \\&g_{in}^{sv} =-2\rho A\varOmega \int _0^L {S_i (x)V_n (x)\hbox {d}x},\nonumber \\&g_{mj}^{vs} =2\rho A\varOmega \int _0^L {V_m (x)S_j (x)\hbox {d}x},\nonumber \\&k_{ij}^s =\int _0^L {\left[ {EA{S}'_i (x){S}'_j (x)-\rho A\varOmega ^{2}S_i (x)S_j (x)} \right] \hbox {d}x},\nonumber \\&k_{mn}^v {=}\int _0^L {\left[ {EI_z {V}^{\prime \prime }_m (x){V}^{\prime \prime }_n (x){-}\rho A\varOmega ^{2}V_m (x)V_n (x)} \right] \hbox {d}x},\nonumber \\&k_{in}^{sv} =-\rho A{{\dot{\varOmega }}}\int _0^L {S_i (x)V_n (x)\hbox {d}x},\nonumber \\&k_{mj}^{vs} =\rho A{{\dot{\varOmega }}}\int _0^L {V_m (x)S_j (x)\hbox {d}x},\nonumber \\&f_i^s =\rho A\varOmega ^{2}\int _0^L {\left( {a+x} \right) S_i (x)\hbox {d}x},\nonumber \\&f_m^v =\int _0^L {\left[ {p_v -\rho A{{\dot{\varOmega }}}\left( {a+x} \right) } \right] V_m (x)\hbox {d}x}, \end{aligned}$$

(34)

and $N_{i}^{s}$ and $N_{m}^{v}$ are nonlinear internal forces given by

$$\begin{aligned} N_i^s= & {} \sum _{n=1}^N \sum _{p=1}^N \beta _{inp}^{sv} \left( {\ddot{T}}_n^v T_p^v +2{\dot{T}}_n^v {\dot{T}}_p^v \right. \nonumber \\&\left. +T_n^v {\ddot{T}}_p^v -\varOmega ^{2}T_n^v T_p^v \right) ,\nonumber \\ N_m^v= & {} \sum _{j=1}^N {\sum _{n=1}^N {\alpha _{mjn}^v T_j^s T_n^v}}+\sum _{n=1}^N \sum _{p=1}^N \beta _{mnp}^v \left[ 2\varOmega ({\dot{T}}_n^v T_p^v \right. \nonumber \\&\left. +T_n^v {\dot{T}}_p^v )+{{\dot{\varOmega }}}T_n^v T_p^v \right] , \end{aligned}$$

(35)

in which

$$\begin{aligned} \alpha _{mjn}^v= & {} EA\int _0^L {{V}'_m (x){S}'_j (x){V}'_n (x)\hbox {d}x},\nonumber \\ \beta _{inp}^s= & {} -\frac{1}{2}\rho A\int _0^L {S_i (x)\int _0^x {{V}'_n (\xi ){V}'_p (\xi )\hbox {d}\xi } \hbox {d}x},\nonumber \\ \beta _{mnp}^v= & {} -\frac{1}{2}\rho A\int _0^L {V_m (x)\int _0^x {{V}'_n (\xi ){V}'_p (\xi )\hbox {d}\xi } \hbox {d}x}.\nonumber \\ \end{aligned}$$

(36)

In (34) and (36), the superposed prime ($\prime$) represents differentiation with respect to the spatial coordinate x (or $\xi$). The discretized equations for the stretch and chordwise motions can be written in matrix-vector form:

$$\begin{aligned} \mathbf{M}{\ddot{\mathbf{T}}}+\mathbf{G}{\dot{\mathbf{T}}}+\mathbf{KT}+\mathbf{N}(\mathbf{T},{\dot{\mathbf{T}}},{\ddot{\mathbf{T}}})=\mathbf{F}, \end{aligned}$$

(37)

where

$$\begin{aligned}&\mathbf{M}=\left[ {{\begin{array}{ll} {\mathbf{m}_s }&{} \mathbf{0} \\ \mathbf{0}&{} {\mathbf{m}_v } \\ \end{array} }} \right] , \mathbf{G}=\left[ {{\begin{array}{ll} \mathbf{0}&{} {\mathbf{g}_{sv} } \\ {\mathbf{g}_{vs} }&{} \mathbf{0} \\ \end{array} }} \right] , \mathbf{K}=\left[ {{\begin{array}{ll} {\mathbf{k}_s }&{} {\mathbf{k}_{sv} } \\ {\mathbf{k}_{vs} }&{} {\mathbf{k}_v } \\ \end{array} }} \right] ,\nonumber \\&{} \mathbf{T}=\left\{ {{\begin{array}{ll} {\mathbf{T}_s } \\ {\mathbf{T}_v } \\ \end{array} }} \right\} , \mathbf{N}=\left\{ {{\begin{array}{ll} {\mathbf{N}_s } \\ {\mathbf{N}_v } \\ \end{array} }} \right\} , \mathbf{F}=\left\{ {{\begin{array}{ll} {\mathbf{f}_s } \\ {\mathbf{f}_v } \\ \end{array} }} \right\} , \end{aligned}$$

(38)

in which $\mathbf{m}_{s}$, $\mathbf{m}_{v}$, $\mathbf{g}_{sv}$, $\mathbf{g}_{vs}$, $\mathbf{k}_{s}$, $\mathbf{k}_{v}$, $\mathbf{k}_{sv}$ and $\mathbf{k}_{vs}$ are $N\times N$ matrices, and $\mathbf{N}_{s}$, $\mathbf{N}_{v}$, $\mathbf{f}_{s}$ and $\mathbf{f}_{v}$ are $N\times 1$ column vectors:

$$\begin{aligned}&{} \mathbf{m}_s =\left[ {m_{ij}^s } \right] , \mathbf{m}_v =\left[ {m_{mn}^v } \right] , \mathbf{g}_{sv} =\left[ {g_{in}^{sv} } \right] ,\nonumber \\&{} \mathbf{g}_{vs} =\left[ {g_{mj}^{vs} } \right] , \mathbf{k}_s =\left[ {k_{ij}^s } \right] , \mathbf{k}_v =\left[ {k_{mn}^v } \right] , \mathbf{k}_{sv} =\left[ {k_{in}^{sv} } \right] , \nonumber \\&{} \mathbf{k}_{vs} =\left[ {k_{mj}^{vs} } \right] , \mathbf{N}_s =\left\{ {N_i^s } \right\} , \mathbf{N}_v =\left\{ {N_m^v } \right\} , \mathbf{T}_s =\left\{ {T_i^s } \right\} , \nonumber \\&{} \mathbf{T}_v =\left\{ {T_m^v } \right\} , \mathbf{f}_s =\left\{ {f_i^s } \right\} , \mathbf{f}_v =\left\{ {f_m^v } \right\} . \end{aligned}$$

(39)

5 Time integration

The trapezoidal rule of the Newmark time integration method is used to obtain dynamic responses for (37). The approximate values of $\mathbf{T}$, ${\dot{\mathbf{T}}}$ and ${\ddot{\mathbf{T}}}$ at time $t=t_{n}$ are denoted by $\mathbf{d}_{n}$, $\mathbf{v}_{n}$ and $\mathbf{a}_{n}$, respectively. The ordinary differential equation, given by (37), at $t=t_{n+1}$ can be written as the following balance equation:

$$\begin{aligned}&\mathbf{Ma}_{n+1} +\mathbf{Gv}_{n+1} +\mathbf{Kd}_{n+1} \nonumber \\&\quad +\mathbf{N}(\mathbf{d}_{n+1} ,\mathbf{v}_{n+1} ,\mathbf{a}_{n+1} )=\mathbf{F}_{n+1}, \end{aligned}$$

(40)

where $\mathbf{F}_{n+1}$ is the value of F at $t=t_{n+1}$. When using the trapezoidal rule, the approximate displacement and velocity vectors, $\mathbf{d}_{n+1}$ and $\mathbf{v}_{n+1}$, respectively, are determined by the following displacement and velocity update equations:

$$\begin{aligned} \mathbf{d}_{n+1}= & {} \mathbf{d}_n +\Delta t\mathbf{v}_n +\frac{1}{4}\Delta t^{2}\left( {\mathbf{a}_n +\mathbf{a}_{n+1} } \right) , \end{aligned}$$

(41)

$$\begin{aligned} \mathbf{v}_{n+1}= & {} \mathbf{v}_n +\frac{1}{2}\Delta t\left( {\mathbf{a}_n +\mathbf{a}_{n+1} } \right) , \end{aligned}$$

(42)

where $\Delta t$ is the time step size defined by $\Delta t=t_{n+1}-t_n$.

To initialize time integration, the initial value of the acceleration vector $\mathbf{a}_{0}$ should be computed with the known initial displacement and velocity vectors, $\mathbf{d}_{0}$ and $\mathbf{v}_{0}$. Substitution of the initial values into (40) leads to

$$\begin{aligned} \mathbf{Ma}_0 +\mathbf{Gv}_0 +\mathbf{Kd}_0 +\mathbf{N}(\mathbf{d}_0 ,\mathbf{v}_0 ,\mathbf{a}_0 )=\mathbf{F}_0 , \end{aligned}$$

(43)

where $\mathbf{a}_{0}$ is an unknown vector. Since (43) is a nonlinear equation for $\mathbf{a}_{0}$, The Newton–Raphson iteration method needs to be applied to determine $\mathbf{a}_{0}$ from (43). The iteration procedure is given by

$$\begin{aligned} \mathbf{a}_0^{(k+1)} =\mathbf{a}_0^{(k)} +\Delta \mathbf{a}_0^{(k)} , \end{aligned}$$

(44)

where k is an iteration number and $\Delta \mathbf{a}_{0}^{(k)}$ is determined from the following equation:

$$\begin{aligned} \mathbf{J}_0^{(k)} \Delta \mathbf{a}_0^{(k)}= & {} -\mathbf{Ma}_0^{(k)} -\mathbf{Gv}_0 -\mathbf{Kd}_0\nonumber \\&-\mathbf{N}\left( {\mathbf{d}_0 ,\mathbf{v}_0 ,\mathbf{a}_0^{(k)} } \right) +\mathbf{F}_0 , \end{aligned}$$

(45)

where $\mathbf{J}_{0}^{(k)}$ is the Jacobian matrix given by

$$\begin{aligned} \mathbf{J}_0^{(k)} =\mathbf{M}+\frac{\partial \mathbf{N}\left( {\mathbf{d}_0 ,\mathbf{v}_0 ,\mathbf{a}_0^{(k)} } \right) }{\partial \mathbf{a}_0^{(k)} }. \end{aligned}$$

(46)

After obtaining the initial values for the displacement, velocity and acceleration vectors, it is required to advance the solutions using the displacement and velocity update equations, given by (41) and (42). The updated acceleration $\mathbf{a}_{n+1}$ should be determined first to compute the updated displacement and velocity vectors $\mathbf{d}_{n+1}$ and $\mathbf{v}_{n+1}$ from (41) and (42) for specified time step size $\Delta t$, and the known vectors $\mathbf{d}_{n}$ and $\mathbf{v}_{n}$. Introduction of (41) and (42) into (40) yields a nonlinear equation for the unknown vector $\mathbf{a}_{n+1}$. The Newton–Raphson method should be applied again to solve the nonlinear equations for $\mathbf{a}_{n+1}$. The iteration procedure to compute $\mathbf{a}_{n+1}$ is given by

$$\begin{aligned} \mathbf{a}_{n+1}^{(k+1)} =\mathbf{a}_{n+1}^{(k)} +\Delta \mathbf{a}_{n+1}^{(k)} , \end{aligned}$$

(47)

where $\Delta \mathbf{a}_{n+1}^{(k)}$ is computed from

$$\begin{aligned} \mathbf{J}_{n+1}^{(k)} \Delta \mathbf{a}_{n+1}^{(k)}= & {} -\mathbf{Ma}_{n+1}^{(k)} -\mathbf{Gv}_{n+1}^{(k)} -\mathbf{Kd}_{n+1}^{(k)}\nonumber \\&-\mathbf{N}\left( {\mathbf{d}_{n+1}^{(k)} ,\mathbf{v}_{n+1}^{(k)} ,\mathbf{a}_{n+1}^{(k)} } \right) +\mathbf{F}_{n+1} , \end{aligned}$$

(48)

where

$$\begin{aligned} \mathbf{J}_{n+1}^{(k)}= & {} \mathbf{M}+\frac{\partial \mathbf{N}\left( {\mathbf{d}_{n+1}^{(k)} ,\mathbf{v}_{n+1}^{(k)} ,\mathbf{a}_{n+1}^{(k)} } \right) }{\partial \mathbf{a}_{n+1}^{(k)} }\nonumber \\&+\frac{1}{2}\Delta t\left[ {\mathbf{G}+\frac{\partial \mathbf{N}\left( {\mathbf{d}_{n+1}^{(k)} ,\mathbf{v}_{n+1}^{(k)} ,\mathbf{a}_{n+1}^{(k)} } \right) }{\partial \mathbf{v}_{n+1}^{(k)} }} \right] \nonumber \\&+\frac{1}{4}\Delta t^{2}\left[ {\mathbf{K}+\frac{\partial \mathbf{N}\left( {\mathbf{d}_{n+1}^{(k)} ,\mathbf{v}_{n+1}^{(k)} ,\mathbf{a}_{n+1}^{(k)} } \right) }{\partial \mathbf{d}_{n+1}^{(k)} }} \right] .\nonumber \\ \end{aligned}$$

(49)

6 Convergence characteristics

The convergence characteristics for only Models 1 and 2 are investigated in this section, because the characteristics for Models 3 and 4 were discussed in previous studies [1, 4, 9, 11, 12]. First of all, a convergence test is performed to find the number of basis functions with which reliable numerical results are obtained from Model 1. For the convergence test, dynamic responses of the stretch and chordwise deformations are computed for a cantilever beam with varying rotating speed that was presented by Wang [16]. To generalize the further discussions, the following dimensionless parameters are introduced in this study:

$$\begin{aligned}&\tau =\frac{t}{T}, \xi =\frac{x}{T}, s^*=\frac{s}{L}, u^*=\frac{u}{L}, v^*=\frac{v}{L},\nonumber \\&\sigma ^*=\frac{\sigma }{E}, \gamma =T\varOmega , \lambda =T^{2}{{\dot{\varOmega }}}, \delta =\frac{a}{L}, \alpha =\sqrt{\frac{AL^{2}}{I_z }},\nonumber \\ \end{aligned}$$

(50)

where

$$\begin{aligned} T=L^{2}\sqrt{\frac{\rho A}{EI_z }}. \end{aligned}$$

(51)

In (50), $\tau$ is the dimensionless time, $\xi$ is the dimensionless position, $s^{*}$ is the dimensionless stretch deformation, $u^{*}$ is the dimensionless axial deformation, $v^{*}$ is the dimensionless chordwise deformation, $\sigma ^{*}$ is the dimensionless stress, $\gamma$ is the dimensionless rotating speed, $\lambda$ is the dimensionless rotating acceleration, $\delta$ the dimensionless hub radius, and $\alpha$ is the slenderness of a beam.

The rotating cantilever beam, which is the same beam studied by Sharf [13] and Wang [16], has a beam length of $L = 10\hbox { m}$, hub radius of $a = 0$, cross-sectional area of $A = 4\times 10^{-4}\hbox { m}^{2}$, density of $\rho = 3000\hbox { kg}/\hbox {m}^{3}$, Young’s modulus of $E = 7\times 10^{8}\hbox { N}/\hbox {m}^{2}$, and area moment of inertia of $I_{z} = 1.333\times 10^{-8}\hbox { m}^{4}$. These values for the physical parameters correspond to the dimensionless parameters of $\delta =0$ and $\alpha =447.22$ . The zero values are imposed on the initial conditions for the stretch and chordwise deformations; furthermore, no external force is exerted on the cantilever beam. The rotating speed profile of Sharf [13] and Wang [16] can be expressed as the following dimensionless angular speed:

$$\begin{aligned} \gamma \left( \tau \right) =\frac{2}{5}\left( {\tau -\frac{15}{2\pi }\sin \frac{2\pi \tau }{15}} \right) . \end{aligned}$$

(52)

The dimensionless speed, given by (52), and the corresponding dimensionless acceleration are plotted in Fig. 2, which shows that the rotating speed increases smoothly and the acceleration has a maximum value at $\tau =7.5$. The dimensionless time step size of $10^{-4}$ is used to compute the dynamic responses for the deformations.

Fig. 2

Dimensionless rotating speed and acceleration profiles

Fig. 3

Dynamic responses of the deformations at the free beam end, computed by applying the mode superposition method to Model 1, for various numbers of the basis functions: a the stretch deformations, b the axial deformations and c the chordwise deformations

Table 2 Convergence characteristics of the RMS values of the deformations for the number of basis functions N, when applying the MSM to Model 1

Fig. 4

Dynamic responses of the deformations at the free beam end, computed by applying the mode superposition method to Model 2, for various numbers of the basis functions: a the stretch deformations and b the chordwise deformations

The convergence test for the dynamic responses is performed by investigating the dynamic responses of the deformations at the free beam end, i.e., at $\xi =1$, as the number of basis functions N increases. When applying the MSM to Model 1, the dimensionless stretch and chordwise deformations for the various number of basis functions are plotted in Fig. 3a and c, respectively. The dimensionless axial deformations, shown in Fig. 3b, are computed by using (2). As presented in Fig. 3, it is difficult to distinguish the differences between the curves for various values of N because these curves are overlapped. This implies that the dynamic response at the free end converges fast as N increases. Table 2 exhibits the convergence characteristics for the root-mean-square (RMS) values of the dynamic responses shown in Fig. 3. The errors in Table 2 are computed based on the RMS values when $N = 20$. Explaining in more detail, the error when $N=i$ is calculated by dividing the difference between the RMS values for $N=i$ and 20 by the RMS value for $N = 20$. Table 2 also confirms that the RMS values of the stretch, axial and chordwise deformations converge fast as the number of the basis functions increases.

The convergence test is also performed when applying the MSM to Model 2. To discretize the equations of Model 2, given by (12) and (13), neglecting the flapwise deformation, the approximate solutions for the axial and chordwise deformations are assumed as

$$\begin{aligned} u(x,t)=\sum _{j=1}^N {U_j (x)T_j^u (t)},\quad v(x,t){=}\sum _{n=1}^N {V_n (x)T_n^v (t)} , \end{aligned}$$

(53)

where $U_{j}$ is the same as $S_{j}$ defined by (28) and $V_{n}$ is given by (29). In other words, the discretized equations for Model 2 are obtained with the same basis functions used for Model 1. Using the similar procedures presented in Sects. 4 and 5, the dynamic responses of the beam deformations at the free end are computed. The computed results for various numbers of the basis functions are illustrated in Fig. 4, where it is seen that the dynamic response converges very slowly as the number of basis function increases. Comparison of Figs. 3 and 4 demonstrates considerable differences between the dynamic responses of Models 1 and 2 when the MSM is used. The RMS values of the deformations of Model 2 for the number of basis functions are listed in Table 3, which demonstrates poor convergence. Comparison of Tables 2 and 3 shows that the RMS values of Model 2 when $N = 20$ are significantly different from the converged values in Table 2. It may be concluded that the RMS values obtained by applying the MSM to Model 2 are not converged ones. In other words, the MSM applied to Model 2 has poor convergence characteristics.

Table 3 Convergence characteristics of the RMS values of the deformations for the number of basis functions N, when applying the MSM to Model 2

In addition, the convergence characteristics are also investigated when the FEM is applied to Model 2. The equations of Model 2, given by (12) and (13), are discretized by using two-node beam elements introduced by Chung and Yoo [9]. The dynamic responses of the deformations at the free end, computed by adopting the FEM with various numbers of elements, are plotted in Fig. 5, where n represents the number of elements used for computations. It is seen in this figure that the dynamic responses for the axial and chordwise deformations converge as the number of elements increases. The RMS values for these dynamic responses are summarized in Table 4, which shows that the RMS values of the axial and chordwise deformations converge with an increasing number of elements. Comparing the RMS values of the axial and chordwise deformations in Tables 2, 3, 4, the converged values obtained from the FEM applied to Model 2 are almost the same as the values from the MSM applied to Model 1 and they are significantly different from the converged values from the MSM applied to Model 2. However, the convergence speed of the MSM for Model 1 is much faster than the speed of the FEM for Model 2. The MSM for Model 1 and the FEM for Model 2 lead to converged responses, but the MSM for Model 2 leads to erroneous responses. The converged responses are illustrated in Fig. 6. This figure shows that the MSM for Model 1 and FEM for Model 2 yield almost the same results but the MSM for Model 2 leads to results with large errors. In other words, the MSM for Model 1 can obtain reliable results, while the MSM for Model 2 cannot. This is because the basis functions for Model 1 are the comparison functions, but the basis functions for Model 2 are not.

Fig. 5

Dynamic responses of the deformations at the free beam end, computed by applying the FEM to Model 2, where n is the number of elements: a the axial deformations and b the chordwise deformations

Table 4 Convergence characteristics of the RMS values for the deformations when applying the FEM to Model 2 as the number of elements n increases

To show that the MSM applied to Model 2 yields unreliable computation results, the stress distributions over the beam length are investigated for three cases: the MSM for Model 1, the MSM for Model 2 and the FEM for Model 2. When the rotating acceleration has a maximum value, that is, when the dimensionless time is 7.5 (Fig. 2), the stress distributions are computed by the following stress:

$$\begin{aligned} \sigma _s^*=\sigma _x^*=\frac{\partial s}{\partial x}=\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}, \end{aligned}$$

(54)

The stress distributions over the beam length for various numbers of the basis functions or elements are plotted in Fig. 7, where Fig. 7a–c shows the stress distributions when applying the MSM to Model 1, when applying the MSM to Model 2 and when applying the FEM to Model 2, respectively. As shown in Fig. 7a and c, the stress distributions converge with an increasing number of basis functions or elements, when the MSM is applied to Model 1 or when the FEM is applied to Model 2. However, when the MSM is used for Model 2, the stress distribution is not converged even for a large number of basis functions.

The reason why the MSM applied to Model 2 does not result in a converged stress distribution is because the basis functions used in (53) are not the comparison functions but instead the admissible functions. As is well known, the comparison functions satisfy both the essential and natural boundary conditions, while the admissible functions satisfy the essential boundary conditions. The derivatives of the basis functions for the chordwise motion, given by (29), with respect to x are not equal to zero at $x=L$ (or $\xi =1)$, so the basis functions used in (53) do not satisfy the natural boundary conditions of (16). These basis functions satisfy only the essential boundary conditions of (15). This means that they are not the comparison functions but the admissible functions. In fact, it is practically impossible to find the comparison functions satisfying both boundary conditions of (15) and (16). In Fig. 7b, the stresses at the free end or $\xi =1$ are not equal to zero; however, in Fig. 7a and c, the stresses at $\xi =1$ are equal to zero. The nonzero stresses at $\xi =1$ in Fig. 7b are caused by selecting the admissible functions, which do not satisfy the natural boundary condition given in (16).

Fig. 6

Comparison of the converged responses obtained by applying the MSM to Model 1, the FEM to Model 2, and the MSM to Model 2: a the axial deformations and b the chordwise deformations

In summary, converged computation results can be obtained when the FEM is applied to Model 2, but converged results cannot be obtained when the MSM is applied to Model 2. However, the FEM applied to Model 2 requires a large amount of elements to obtain converged computation results. The convergence characteristics of the axial and chordwise deformations presented in Tables 1 and 3 are plotted in Fig. 8, where Fig. 8a and b are for the axial and chordwise deformations, respectively. In this figure, the solid lines represent converged RMS values, the circle symbol represents the RMS value when applying the MSM to Model 1, and the square symbol represents the RMS value when applying the FEM to Model 2. As shown in Fig. 8, the MSM applied to Model 1 leads to much faster convergence than the FEM applied to Model 2. This means that the FEM applied to Model 2 is much more inefficient than the MSM applied to Model 1.

7 Dynamic response

In this section, the dynamic responses of Model 1 are compared to the responses of the other models. As shown in the previous section, the MSM for Model 2 cannot have correct responses and the FEM for Model 2 has slow convergence characteristics. For this reason, the comparisons of dynamic responses are made between Models 1, 3 and 4. For computation in this section, the dimensionless slenderness ratio is selected as $\alpha =70$ and the dimensionless hub ratio is selected as $\delta =0.1$ . The initial conditions of zero are imposed, and the rotating speed profiles are shown in Fig. 9. The maximum value of the dimensionless rotating speed is 5, and the dimensionless rising time is 10. The smooth rotating speed profile is defined by

$$\begin{aligned} \gamma \left( \tau \right) =\left\{ {\begin{array}{ll} {\tau /2-(5/{2\pi } )\sin ({\pi \tau }/\hbox {5})}&{} {\hbox {for }0\le \tau \le 10} \\ 5&{} {\hbox {for }10\le \tau \le 30} \\ \end{array} } \right. , \end{aligned}$$

(55)

and the non-smooth profile is defined by

$$\begin{aligned} \gamma \left( \tau \right) =\left\{ {{\begin{array}{ll} {\tau /2}&{} {\hbox {for }0\le \tau \le 10} \\ 5&{} {\hbox {for }10\le \tau \le 30} \\ \end{array} }} \right. . \end{aligned}$$

(56)

The dynamic responses when the smooth speed profile is applied to the rotating beam are presented in Fig. 10, where the solid, dashed and dotted lines represent Models 1, 3 and 4, respectively. Figure 10a shows the dimensionless stretch/axial deformations, Fig. 10b shows the dimensionless chordwise deformations, and Fig. 10c shows the dimensionless normal stresses. It should be noted that in Fig. 10a the responses of Models 1 and 4 are for the stretch deformation, while the response of Model 3 is for the axial deformation. In Fig. 10c, the dimensionless normal stresses of Models 1 and 4 are computed by (54), while the dimensionless normal stress of Model 3 is computed by the following linearized stress given by Kim et al. [12]:

$$\begin{aligned} \sigma _x^*=\frac{\partial u}{\partial x}. \end{aligned}$$

(57)

As shown in Fig. 10, when a rotating beam has a smooth speed profile, the stretch/axial deformation and the normal stress do not exhibit significant differences between Models 1, 3 and 4. However, if the dynamic responses are magnified as shown in Fig. 10c, the nonlinear effect, which is the difference between Models 1 (or 4) and 3, is observed.

Fig. 7

Stress distributions over the beam length when the rotating acceleration is maximum, taken from Fig. 2: a when applying the MSM to Model 1, b when applying the MSM to Model 2 and c when applying the FEM to Model 2

It is interesting to observe the dynamic responses of Models 1, 3 and 4 when the rotating speed has a non-smooth profile. The dynamic responses for the non-smooth profile, illustrated in Fig. 11, show larger oscillations than the responses for the smooth profile illustrated in Fig. 10. These large oscillations for the non-smooth rotating speed profile are caused by abrupt changes in the rotating acceleration at $\tau =0$ and 10. Another meaningful observation in Fig. 11 is that the dynamic responses for Model 3 have considerable differences from those for Models 1 and 4. This implies that the linearized stress used in Model 3 may yield some errors when a rotating beam has a non-smooth speed profile. It should be noted that it is hard to observe the differences of the dynamic responses between the nonlinear model (Model 1) and linear model (Model 4) in Fig. 11. This is because the values the rotating speed and acceleration used for the computations are relatively small: the maximum rotating speed is $\gamma =5$ and the rotating acceleration is $\lambda =0.5$ . When these values are large, the differences between Models 1 and 4 are discussed below.

In the rest of this section, only the two models, i.e., Models 1 and 4, are compared and discussed in more detail. The section for convergence characteristics shows that the MSM and FEM for Model 2 show poor and slow convergence characteristics, respectively, compared to Model 1. It is shown in Figs. 10 and 11 that the dynamic responses for Model 3 have larger errors than the responses for Models 1 and 4. For these reasons, Models 2 and 3 are excluded from the following discussion.

Fig. 8

Convergence characteristics for the dynamic responses of the deformation at the free end: a the axial deformation and b the chordwise deformation; the circle and square symbols represent the RMS values for the MSM applied to Model 1 and the FEM applied to Model 2, respectively

Fig. 9

Smooth and non-smooth profiles of the dimensionless rotating speed

Fig. 10

Dynamic responses for the smooth profile of the rotating speed shown in Fig. 9: a the stretch/axial deformations, b the chordwise deformations and c normal stresses

Fig. 11

Dynamic responses for the non-smooth profile of the rotating speed shown in Fig. 9: a the stretch/axial deformations, b the chordwise deformations and c normal stresses

Fig. 12

Non-smooth rotating speed profiles with three different values of the rotating acceleration while maintaining the same maximum value of the rotating speed

The dynamic responses of Models 1 and 4 are compared for the three different values of rotating acceleration during the rising time intervals when maintaining the same maximum value of the non-smooth rotating speed profiles. Since the responses of Model 3 have relatively large errors, they are omitted in comparison. The dynamic responses are computed for the non-smooth rotating speed profiles, shown in Fig. 12, where the three profiles have different values of the rotating acceleration and the same maximum value of the rotating speed. In this figure, the solid, dashed and dotted lines represent the speed profiles with the accelerations, $\lambda =1$, 2 and 3, respectively, during the rising time interval. The stretch deformations for Models 1 and 4 are shown in Fig. 13a–c, and the chordwise deformations for Models 1 and 4 are shown in Fig. 13d–f. In Fig. 13, the solid and dashed lines stand for the responses of Models 1 and 4, respectively. As shown in Fig. 13, the differences of the responses between Models 1 and 4 increase with the rotating acceleration. Comparing the equations of chordwise motion for Models 1 and 4, i.e., (8) and (22), respectively, the terms related to the rotating acceleration are different from each other: ${{\dot{\varOmega }}}\left( {s-h_{v} -h_{w} } \right)$ in (8) and ${{\dot{\varOmega }}}s$ in (22). This is a significant contribution to the response differences between Models 1 and 4, shown in Fig. 13.

The effects of the rotating acceleration on the dynamic responses are investigated for Models 1 and 4. Figure 13 shows that the average values (or DC values) of the responses in the constant speed region are nearly the same even if the rotating acceleration in the rising time interval is changed. This means that the average value of the response is not influenced by the rotating acceleration. However, the rotating acceleration has an influence on the frequency and amplitude of vibration. To examine this influence, by using the fast Fourier transform, the frequency spectra are obtained from the responses in the intervals of constant rotating speed. The frequency spectra of the vibrations in the constant speed intervals are presented in Fig. 14, where Fig. 14a–c is for the stretch deformations when $\lambda =1$, 2 and 3, respectively, and Fig. 14d–f is for the chordwise deformations. As shown in Fig. 14, the vibration amplitude is dependent on the rotating acceleration. The amplitude of Model 4 seems to be proportional to the acceleration, but the amplitude of Model 1 does not. It is interesting that the vibration frequency of Model 1 decreases as the rotating acceleration increases; however, the frequencies of Model 4 remain constant regardless of the acceleration. For the case of Model 1, the dimensionless peak frequencies corresponding to $\lambda =1$, 2 and 3 are 1.006, 0.976 and 0.970, respectively. However, the peak frequencies of Model 4 do not vary for the change of the rotating acceleration, so they are the same at a value of 1.002 for all the three values of $\lambda$ . This implies that Model 1, which is a nonlinear model, has ‘instantaneous’ natural frequencies affected by the rotating acceleration, while Model 4, which is a linear model, has constant natural frequencies unaffected by the acceleration.

Fig. 13

Dynamic responses of Models 1 and 4 for the three non-smooth profiles of the rotating speed shown in Fig. 12: a the stretch deformations for $\lambda =1$, b the stretch deformations for $\lambda =2$, c the stretch deformations for $\lambda =3$, d the chordwise deformations for $\lambda =1$, e the chordwise deformations for $\lambda =2$, f the chordwise deformations for $\lambda =3$

Fig. 14

Frequency spectra for the vibrations of Fig. 13 during the time intervals of constant rotating speed: a the stretch deformations for $\lambda =1$, b the stretch deformations for $\lambda =2$, c the stretch deformations for $\lambda =3$, d the chordwise deformations for $\lambda =1$, e the chordwise deformations for $\lambda =2$, f the chordwise deformations for $\lambda =3$

Consider the dynamic response differences between Models 1 and 4 for the change in rotating speed. To investigate these differences, the dynamic responses are computed for the three non-smooth rotating speed profiles shown in Fig. 15. The maximum dimensionless rotating speeds of the three profiles are selected as $\gamma _{\mathrm{max}} =10$, 20 and 30. However, the dimensionless rotating acceleration maintains a constant value of $\lambda =2$ to eliminate the effect of the acceleration. The dynamic responses computed by using these speed profiles are presented in Fig. 16, in which Fig. 16a–c is for the stretch deformations, while Fig. 16d–f is for the chordwise deformations. The two models have no difference in the average values of the responses in the constant speed intervals if their maximum speeds are the same. The average value of the dimensionless stretch deformation increases with the maximum rotating speed, whereas the average value of the dimensionless chordwise deformation remains zero regardless of the value of $\gamma _{\mathrm{max}}$ . The increasing average value with the rotating speed is caused by the centrifugal force, which is proportional to the square of the rotating speed.

Fig. 15

Non-smooth rotating speed profiles with three different maximum values of the rotating speed when maintaining the same rotating accelerating

Fig. 16

Dynamic responses of Models 1 and 4 for the three non-smooth profiles of the rotating speed shown in Fig. 15: a the stretch deformations for $\gamma _{\mathrm{max}} =10$, b the stretch deformations for $\gamma _{\mathrm{max}} =20$, c the stretch deformations for $\gamma _{\mathrm{max}} =30$, d the chordwise deformations for $\gamma _{\mathrm{max}} =10$, e the chordwise deformations for $\gamma _{\mathrm{max}} =20$, f the chordwise deformations for $\gamma _{\mathrm{max}} =30$

Fig. 17

Frequency spectra for the vibrations of Fig. 16 during the time intervals of constant rotating speed: a the stretch deformations for $\gamma _{\mathrm{max}} =10$, b the stretch deformations for $\gamma _{\mathrm{max}} =20$, c the stretch deformations for $\gamma _{\mathrm{max}} =30$, d the chordwise deformations for $\gamma _{\mathrm{max}} =10$, e the chordwise deformations for $\gamma _{\mathrm{max}} =20$, f the chordwise deformations for $\gamma _{\mathrm{max}} =30$

Similarly to the frequency spectra shown in Fig. 14, the frequency spectra in Fig. 17 are obtained by the fast Fourier transform of the dynamic responses in the constant speed intervals, shown in Fig. 16. This figure shows that the differences of the vibration frequencies between Models 1 and 4 become large as the maximum rotating speed increases. Since Model 1 considers nonlinear terms, which Model 4 does not have, it may be said that the vibration frequencies computed with Model 1 are more reliable than the frequencies with Model 4. On the other hand, it is observed in Fig. 17 that the vibration frequencies of both the stretch and chordwise deformations increase with the maximum rotating speed. In addition, as the maximum rotating speed increases, the vibration amplitude of the stretch deformation increases (Fig. 17a–c), but the amplitude of the chordwise deformation decreases (Fig. 17d–f). These phenomena occur due to the stiffening effect, which is also caused by the centrifugal force.

8 Conclusions

For the dynamic analysis of a rotating flexible beam, the nonlinear model (Model 1) is proposed and compared to the previous models (Models 2–4). The nonlinear integro-differential equations of motion for the proposed model are derived in terms of the stretch, chordwise and flapwise deformations. During the derivation, the nonlinear von Karman strain and the corresponding nonlinear stress are adopted to consider the geometric nonlinearity due to large deformation. After discretizing the nonlinear equations using the MSM, the discretized equations of the dynamic responses are computed by applying the Newmark time integration method.

The dynamic responses of the proposed model are more accurate than the responses of the three previous models. When the MSM is used for discretization, Model 1 has fast converged solutions, but Model 2 cannot have converged solutions. If the FEM is applied to Model 2, converged solutions can be obtained. However, the convergence speed of the FEM applied to Model 2 is much slower than the speed of the MSM applied to Model 1, because applying the FEM to Model 2 requires many more degrees of freedom than the MSM to Model 1. Meanwhile, Model 3 may yield larger errors in computed responses than Models 1 and 4 because the used stress model of Model 3 is linearized. On the other hand, comparing Models 1 and 4, the responses of Model 1 may be considerably different from the responses of Model 4 for some non-smooth rotating speed profiles. Since Model 1 considers nonlinear terms, which Model 4 does not have, it may be concluded that Model 1 produces more reliable responses than Model 4.

For non-smooth rotating speed profiles, the effects of the rotating acceleration and speed are also investigated. When the rotating acceleration varies with the remaining maximum speed, the rotating acceleration does not influence the average value of the dynamic response, but influences the vibration frequency and amplitude. When the maximum rotating speed changes with the same acceleration in the rising time, the rotating speed increases the vibration frequencies for the stretch and chordwise deformation. Furthermore, the speed increases the vibration amplitude of the stretch deformation but decreases the amplitude for the chordwise deformation.