Dynamic analysis of a rotating double-tapered cantilever Timoshenko beam

Abstract

Based on the nonlinear von Kármán strain and the associated linear stress, the coupling nonlinear dynamic equations of a rotating, double-tapered, cantilever Timoshenko beam are derived using the Hamilton principle. The equation of motion is discretized via the Galerkin method in which the eigenfunctions of a clamped-free Euler–Bernoulli beam are utilized. The natural frequencies and the nonlinear responses of the rotating Timoshenko beam are investigated. Some interesting phenomena of frequency veering and mode shift are observed in the rotating tapered beam due to the coupling effect. The effects of the dimensionless parameters on the natural frequencies of a rotating double-tapered Timoshenko beam are studied through numerical examples.

1 Introduction

Rotating cantilever beams, especially tapered ones, are found in several practical engineering examples such as the rotating machinery, helicopter blades, and wind turbine blades. More reliable dynamic models of these structures are required for reliable and practical design of the structures. Rotating beam differs from a nonrotating beam in having an additional centrifugal force and Coriolis effects on its dynamics. The elastic vibrations are caused by axial and transverse deformations, which have been investigated by many researchers.

In the early 1970s, Weidenhammer [1] derived the nonlinear dynamic model of turbine blades in a centrifugal field based on the Euler–Bernoulli beam theory, in which the axial vibration and bending vibrations are coupled with each other for an arbitrary setting angle. Bazoune and Khulief [2] developed a finite beam element for vibration analysis of a rotating double-tapered Timoshenko beam. This work was further extended to account for different boundary conditions [3]. Lee and Lin [4] derived the governing differential equations for the pure bending vibrations of a rotating nonuniform Timoshenko beam without considering the Coriolis force, the influence of taper ratio, elastic root restraint, setting angle, and rotational speed on the bending natural frequencies of a rotating Timoshenko beam, which have been investigated using a semi-exact numerical method. Banerjee [5] developed the dynamic stiffness matrix of a centrifugally stiffened Timoshenko beam and used the matrix to carry out a free vibration analysis. Using the differential transform method in [6], Ozdemir and Kaya [7] investigated flexural vibration of a rotating double-tapered Euler–Bernoulli beam, the flapwise bending vibration of a rotating tapered cantilevered Bernoulli–Euler beam [8], and the flapwise bending vibration of a rotating double-tapered Timoshenko beam [9]. Sapountzakis and Dourakopoulos [10, 11], taking into account the effects of shear deformation and rotary inertia, investigated the vibration of beams with arbitrary doubly symmetric simply or multiply connected constant cross section, undergoing moderate large displacements and small deformations under general boundary conditions by a boundary element method. Zhu [12] investigated the free vibration of a rotating, double-tapered, cantilever Timoshenko beam that undergoes flapwise transverse vibration using the hybrid deformation variables, and the tuned angular speed is found for a uniform rotating Timoshenko beam. In all these studies, the steady-state normal force (or centrifugal force) was used to examine the centrifugally stiffened effect, and the centrifugal force that is directly proportional to the square of the rotational speed and the identical centrifugal force are given by other authors [13–16], However, the extensional deformation was not considered in the centrifugal stiffening force term, even though it might have been considered in the governing differential equations.

Lin and Hsiao [17] used the fully geometrically nonlinear beam theory and a method based on the power series solution to solve the natural frequency of the rotating Timoshenko beam. Lee and Sheu [18] investigated the free vibration of an inclined rotating uniform beam taken into account the effect of extensional deformation and the Coriolis force. These equations of motion are only for the flapwise vibrations analysis of a rotating beam. Huang et al. [19] investigated the natural frequency of the axial, chordwise, and flapwise vibrations for a rotating Euler–Bernoulli beam. The method based on the power series solution described in [17] is used to solve the natural frequency of a slender rotating beam at a high angular velocity. However, these studies are only for the free vibration analysis of a rotating beam. Kim and Yoo [20] investigated the natural frequency and time responses of a rotating Euler–Bernoulli beam, and the axial force due to the centrifugal effect is obtained according to the perturbation method. The results of numerical examples and time responses show that the described equations of motion are more reliable than the equations of the other modeling methods.

In this work, based on the nonlinear von Kármán strain and the associated linear stress, the nonlinear dynamic equations of a rotating, double-tapered, cantilever Timoshenko beam are derived by using the Hamilton principle. The effect of angular speed, hub radius, slenderness ratio, and the height and width taper ratios on the frequencies of the rotating Timoshenko beam is investigated in this study when the rotation beam is in a steady state, in which the extensional deformation of the beam is considered. In addition, the nonlinear responses of the Timoshenko beam are investigated in this study.

Fig. 1

Rotating double-tapered flexible Timoshenko beam and the deformation: a the configuration of the beam; b the setting angle and the local coordinate system; c the deformation on the neural axis of the beam

2 Dynamic modeling and equations of motion

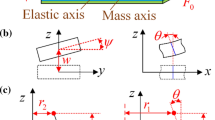
The double-tapered flexible Timoshenko beam is shown in Fig. 1, which is fixed to a rotating rigid hub at point o. The coordinate system OXYZ is the inertial system, fixed on the axis of symmetry of a rigid hub with a radius a, the hub rotates about the vertical axis passing through point O, and the rotating speed of the cantilever beam and hub is $\dot{\theta }$. The coordinate system $o{x}'{y}'{z}'$ is the relative one that is fixed on the beam and rotates with the hub, and the coordinate system oxyz is the local one that is fixed on the beam. The axes x and ${x}'$ are along the undeflected beam, the ${y}'$ axis is in the rotation plane of the beam, and the ${z}'$ axis is parallel to the rotation axis of the beam. The angle between the xy plane and the ${x}'{y}'$ plane (or the xy plane and the ${x}'{y}'$ plane) is the setting angle of the beam $\gamma$. The beam has length L, cross-sectional area A(x), mass density $\rho$, Young’s modulus E, and area moments of inertia about the y and z axes $I_y (x)$ and $I_z (x)$, respectively. The width and height at the root of the beam are defined as $b_0$ and $h_0$, respectively. Assume the planar cross sections that are initially perpendicular to the neutral axis of the beam remain plane, but no longer perpendicular to the neutral axis during the motion. The coupling effect between the bending and torsional motions is neglected, and the torsional behavior of the beam is not discussed in this paper. When point $P_0$ on the beam moves to point P, the deformation of point P in the local coordinate system is described by the axial deformation u and the bending deformations v and w, as shown in Fig. 1c.

The location vector of the point P in the inertial system OXYZ is represented by $\mathbf{R}_\mathrm{p}$ and is given by

$$\begin{aligned} \mathbf{R}_\mathrm{p} =\mathbf{A}_1 \mathbf{A}_2 \mathbf{r}_\mathrm{p} =\mathbf{A}_1 \mathbf{A}_2 (\mathbf{r}_\mathrm{o} +\mathbf{r}_{\mathrm{p}_{0} } +\mathbf{u}_\mathrm{p} ) \end{aligned}$$

(1)

where the matrix $\mathbf{A}_1 =\left[ {{\begin{array}{ccc} {\cos \theta }&{}\quad {-\sin \theta }&{}\quad 0 \\ {\sin \theta }&{}\quad {\cos \theta }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right]$ is the rotational transformation matrix from the relative coordinate system $o{x}'{y}'{z}'$ to the inertial system OXYZ. The matrix $\mathbf{A}_2 =\left[ {{\begin{array}{ccc} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\cos \gamma }&{}\quad {-\sin \gamma } \\ 0&{}\quad {\sin \gamma }&{}\quad {\cos \gamma } \\ \end{array} }} \right]$ is the rotational transformation matrix from the relative coordinate system ${ oxyz}$ to the inertial system $o{x}'{y}'{z}'$. $\mathbf{r}_\mathrm{o} =\left[ {a,0,0} \right] ^{T}$ is the location vector of the origin o of the ${ oxy}$ system in the ${ OXYZ}$ system; the vector $\mathbf{r}_{\mathrm{p}_0}$ is the location vector of the point $P_0$ in the ${ oxyz}$ system, and its coordinate is given by $\left[ { x,y,z} \right] ^{T}$, where the superscript T indicates the transpose of a vector or matrix; and $\mathbf{u}_\mathrm{p}$ is the deformation vector of P in the ${ oxyz}$ system, and its coordinate is represented by

$$\begin{aligned} \mathbf{u}_\mathrm{p} =\left[ {{\begin{array}{ccc} {u-y\varphi _z +z\varphi _y ,}&{}\quad {v,}&{}\quad w \\ \end{array} }} \right] ^{T} \end{aligned}$$

(2)

There is a geometric relation between the arc length stretch s and the Cartesian variables, and the relation is given as [21].

$$\begin{aligned} u=s+u_\mathrm{c} =s-\frac{1}{2}\displaystyle \int _0^x {\left[ {\left( {\frac{\partial v}{\partial \sigma }} \right) ^{2}+\left( {\frac{\partial w}{\partial \sigma }} \right) ^{2}} \right] \hbox {d}\sigma } \end{aligned}$$

(3)

where s is the axial extension quantity; $\varphi _y$ and $\varphi _z$ are the rotational angle of the cross section around the y and z axes, respectively; the parameter $u_\mathrm{c}$ is the second-order coupling term corresponding to the shrinking quantity in the x axial caused by the transverse displacement v and w.

In the zeroth-order approximation coupling model, the small deformation assumption in structural dynamics is adopted, and the second-order term is not taken into account in modeling. However, for a flexible hub–beam system with high-speed rotation, it has significant effect on the system performance and it should be considered in the modeling (see Ref. [22]). This has been demonstrated by numerical simulation and experimental studies, e.g., Ref. [14].

Based on Eq. (1), the inertia velocity of point P on the beam is

$$\begin{aligned} \dot{\mathbf{R}}_\mathbf{p} =\mathbf{A}_1 \mathbf{A}_2 \dot{\mathbf{r}}_\mathbf{p} +\mathbf{A}_{\varvec{\uptheta }} \mathbf{A}_2 \dot{\theta }\left( {\mathbf{r}_\mathbf{o} +\mathbf{r}_{\mathbf{p}_\mathbf{0} } +\mathbf{u}_\mathbf{p} } \right) \end{aligned}$$

(4)

where the superposed dot denotes the time derivative, and

$$\begin{aligned} \mathbf{A}_{\uptheta } =\frac{\partial \mathbf{A}}{\partial \theta }=\left[ {{\begin{array}{ccc} {-\sin \theta }&{}\quad {-\cos \theta }&{}\quad 0 \\ {\cos \theta }&{}\quad {-\sin \theta }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$

Substituting Eqs. (1) and (2) into (4), we obtain

$$\begin{aligned} \dot{\mathbf{R}}=\left[ {{\begin{array}{ccc} {\cos \theta }&{}\quad {-\sin \theta }&{}\quad 0 \\ {\sin \theta }&{} \quad {\cos \theta }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{c} {(\dot{u}-y\dot{\varphi }_z +z\dot{\varphi }_y )-\left[ {(v+y)\cos \gamma -(w+z)\sin \gamma } \right] \dot{\theta }} \\ {(a+x+u-y\varphi _z +z\varphi _y )\dot{\theta }+(\dot{v}\cos \gamma -\dot{w}\sin \gamma )} \\ {\dot{v}\sin \gamma +\dot{w}\cos \gamma } \\ \end{array} }} \right] \end{aligned}$$

(5)

The kinetic energy of the beam can be expressed as

$$\begin{aligned} K=\frac{1}{2}\int _0^L {\rho A\dot{\mathbf{R}}\cdot \dot{\mathbf{R}}\hbox {d}x} \end{aligned}$$

(6)

Substituting Eq. (5) into Eq. (6) and making use of some trigonometric properties, the kinetic energy of the beam can be written as

$$\begin{aligned} K=\frac{1}{2}\int _0^L {\rho A\left\langle {\begin{array}{c} \left[ {(a+x+u-y\varphi _z +z\varphi _y )\dot{\theta }+(\dot{v}\cos \gamma -\dot{w}\sin \gamma )} \right] ^{2} \\ +\left\{ {(\dot{u}-y\dot{\varphi }_z +z\dot{\varphi }_y )-\left[ {(v+y)\cos \gamma -(w+z)\sin \gamma } \right] \dot{\theta }} \right\} ^{2}+(\dot{v}\sin \gamma +\dot{w}\cos \gamma )^{2} \\ \end{array}} \right\rangle \hbox {d}x}\nonumber \\ \end{aligned}$$

(7)

Neglecting the gravitational potential energy and material damping, considering the nonlinearity of the beam, the von Kármán strain theory is adopted in the formulation. Using the von Kármán strain theory, the following strain components can be easily obtained

$$\begin{aligned} \varepsilon _\mathrm{s}= & {} \frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial v}{\partial x}} \right) ^{2}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}-y\frac{\partial \varphi _z }{\partial x}+z\frac{\partial \varphi _y }{\partial x} \end{aligned}$$

(8a)

$$\begin{aligned} \gamma _{xz}= & {} \frac{\partial w}{\partial x}-\varphi _y \end{aligned}$$

(8b)

$$\begin{aligned} \gamma _{xy}= & {} \frac{\partial v}{\partial x}+\varphi _z \end{aligned}$$

(8c)

The corresponding linear stress $\sigma _\mathrm{s}$can be expressed as

$$\begin{aligned} \sigma _\mathrm{s}= & {} E\varepsilon _\mathrm{s} =E\left( {\frac{\partial u}{\partial x}-y\frac{\partial \varphi _z }{\partial x}+z\frac{\partial \varphi _y }{\partial x}} \right) \end{aligned}$$

(9a)

$$\begin{aligned} \tau _{xy}= & {} \kappa G\gamma _{xy} \end{aligned}$$

(9b)

$$\begin{aligned} \tau _{xz}= & {} \kappa G\gamma _{xz} \end{aligned}$$

(9c)

The potential energy of the beam is then given by

$$\begin{aligned} U=\int _0^L {A\left( {\sigma _\mathrm{s} \varepsilon _\mathrm{s} +\tau _{xy} \gamma _{xy} +\tau _{xz} \gamma _{xz} } \right) \mathrm{d}x} \end{aligned}$$

(10)

Substituting Eqs. (8) and (9) into Eq. (10), the total potential energy of the beam can be written as

$$\begin{aligned} U= & {} \frac{1}{2}\int _0^L \left\{ EA\left( {\frac{\partial u}{\partial x}} \right) ^{2}+\frac{1}{2}EA\frac{\partial u}{\partial x}\left[ {\left( {\frac{\partial v}{\partial x}} \right) ^{2}+\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \right] +EI_z \left( {\frac{\partial \varphi _z }{\partial x}} \right) ^{2}\right. \nonumber \\&\left. +\,EI_y \left( {\frac{\partial \varphi _y }{\partial x}} \right) ^{2}+\kappa GA\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) ^{2}+\kappa GA\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) ^{2}\right\} \mathrm{d}x \end{aligned}$$

(11)

The virtual work is given by

$$\begin{aligned} \delta W=0 \end{aligned}$$

(12)

The equation of motion for the rotation Timoshenko beam can be obtained from the following Hamilton’s principle

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left( {\delta K-\delta U+\delta W} \right) \mathrm{d}t} =0 \end{aligned}$$

(13)

Substituting Eqs. (7), (11), and (12) into Eq.(13), we obtain the following differential equations of the deformation u, v, and w, and the rotation angle $\varphi _y,\,\varphi _z$ due to bending:

$$\begin{aligned}&\rho A\left[ {\frac{\partial ^{2}u}{\partial t^{2}}-\dot{\theta }^{2}u-2\dot{\theta }\left( {\frac{\partial v}{\partial t}\cos \gamma -\frac{\partial w}{\partial t}\sin \gamma } \right) -\ddot{\theta }\left( {v\cos \gamma -w\sin \gamma } \right) } \right] -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}} \right) =\rho A\dot{\theta }^{2}(a+x) \end{aligned}$$

(14a)

$$\begin{aligned}&\rho A\left[ {\frac{\partial ^{2}v}{\partial t^{2}}-\dot{\theta }^{2}\left( {v\cos ^{2}\gamma -w\sin \gamma \cos \gamma } \right) +2\dot{\theta }\frac{\partial u}{\partial t}\cos \gamma +\ddot{\theta }u\cos \gamma } \right] \nonumber \\&\quad -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}} \right) -\frac{\partial }{\partial x}\left[ {\kappa GA\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) } \right] =-\rho A\ddot{\theta }(a+x)\cos \gamma \end{aligned}$$

(14b)

$$\begin{aligned}&\rho A\left[ {\frac{\partial ^{2}w}{\partial t^{2}}-\ddot{\theta }u\sin \gamma +\dot{\theta }^{2}\left( {v\cos \gamma \sin \gamma -w\sin ^{2}\gamma } \right) -2\dot{\theta }\frac{\partial u}{\partial t}\sin \gamma } \right] \nonumber \\&\quad -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}} \right) -\frac{\partial }{\partial x}\left[ {\kappa GA\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) } \right] =\rho A\ddot{\theta }(a+x)\sin \gamma \end{aligned}$$

(14c)

$$\begin{aligned}&\rho I_z \left( {\dot{\theta }^{2}\varphi _z -\frac{\partial ^{2}\varphi _z }{\partial t^{2}}} \right) +\frac{\partial }{\partial x}\left( {EI_z \frac{\partial \varphi _z }{\partial x}} \right) +\kappa GA\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) =0 \end{aligned}$$

(14d)

$$\begin{aligned}&\rho I_y \left( {\dot{\theta }^{2}\varphi _y -\frac{\partial ^{2}\varphi _y }{\partial t^{2}}} \right) +\frac{\partial }{\partial x}\left( {EI_y \frac{\partial \varphi _y }{\partial x}} \right) -\kappa GA\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) =0 \end{aligned}$$

(14e)

And furthermore, since the beam is clamped at $x=0$ and free at $x=L$, the boundary conditions of the beam are given by

$$\begin{aligned} {u=v=w=\varphi _y =\varphi _z =0}\quad {\hbox {at}\; x=0;}\quad {\frac{\partial u}{\partial x}=\frac{\partial \varphi _y }{\partial x}=\frac{\partial \varphi _z }{\partial x}=\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) =\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) =0}\quad {\hbox {at}\; x=L}\nonumber \\ \end{aligned}$$

(15)

The dynamic model described by Eq. (14) is a complete representation of the vibration motion for a double-tapered rotating Timoshenko beam. The Coriolis effect of a rotating beam is related to the term $2\dot{\theta }\left( {\frac{\partial v}{\partial t}\cos \gamma -\frac{\partial w}{\partial t}\sin \gamma } \right)$ of Eq. (14a), $2\dot{\theta }\frac{\partial u}{\partial t}\cos \gamma$ of Eq. (14b), and $2\dot{\theta }\frac{\partial u}{\partial t}\sin \gamma$ of Eq. (14c). The term $EA\frac{\partial u}{\partial x}$ in Eqs. (14b) and (14c) represents the axial force of the rotating beam that results in a stiffening effect in the transverse vibrations (v and w). The equations of the axial motion u and transverse motions v and w are coupled with each other for setting angles other than $\gamma =0\,^{\circ }$ and $90\,^{\circ }$.

When $\gamma =0\,^{\circ }$, the equations of motion described by Eq. (14a) can be reduced as

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}u}{\partial t^{2}}-\dot{\theta }^{2}u-2\dot{\theta }\frac{\partial v}{\partial t}-\ddot{\theta }v} \right) -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}} \right) =\rho A\dot{\theta }^{2}(a+x) \end{aligned}$$

(16a)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}-\dot{\theta }^{2}v+2\dot{\theta }\frac{\partial u}{\partial t}+\ddot{\theta }u} \right) -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}} \right) -\frac{\partial }{\partial x}\left[ {\kappa GA\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) } \right] =-\rho A\ddot{\theta }(a+x) \end{aligned}$$

(16b)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}} \right) -\frac{\partial }{\partial x}\left[ {\kappa GA\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) } \right] =0 \end{aligned}$$

(16c)

$$\begin{aligned}&\rho I_z \left( {\dot{\theta }^{2}\varphi _z -\frac{\partial ^{2}\varphi _z }{\partial t^{2}}} \right) +\frac{\partial }{\partial x}\left( {EI_z \frac{\partial \varphi _z }{\partial x}} \right) +\kappa GA\left( {\frac{\partial v}{\partial x}-\varphi _z } \right) =0 \end{aligned}$$

(16d)

$$\begin{aligned}&\rho I_y \left( {\dot{\theta }^{2}\varphi _y -\frac{\partial ^{2}\varphi _y }{\partial t^{2}}} \right) +\frac{\partial }{\partial x}\left( {EI_y \frac{\partial \varphi _y }{\partial x}} \right) -\kappa GA\left( {\frac{\partial w}{\partial x}+\varphi _y } \right) =0 \end{aligned}$$

(16e)

As shown in Eq. (16), the motion u described by Eq. (16a) is called the axial motion, the motion v described by Eqs. (16b) and (16d) is called the chordwise motion (purely in the xy plane), and the motion w described by Eqs.(16c) and (16e) is called the flapwise motion (purely in the xz plane). The chordwise motion and flapwise motion are coupled with the axial motion, and the axial and chordwise motions are coupled with each other. For $\gamma =90\,^{\circ }$, the motion equations have the same expression as those when $\gamma =0\,^{\circ }$, but in this case the motion v is called the flapwise motion and the motion w is called the chordwise motion.

The dynamic model, as represented by Eq. (16), can be reduced if sufficiently large shear stiffness is assumed, meaning $\kappa GA\rightarrow \infty$. In this case, due to Eqs. (16d) and (16e), we have

$$\begin{aligned} \varphi _z =\frac{\partial v}{\partial x}, \quad \varphi _y =-\frac{\partial w}{\partial x} \end{aligned}$$

(17)

This means that the shear deformation is difficult, and only pure flexural deformation takes place. Therefore, the governing Eq. (16) becomes

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}u}{\partial t^{2}}-\dot{\theta }^{2}u-2\dot{\theta }\frac{\partial v}{\partial t}-\ddot{\theta }v} \right) -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}} \right) =\rho A\dot{\theta }^{2}(a+x) \end{aligned}$$

(18a)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}-\dot{\theta }^{2}v+2\dot{\theta }\frac{\partial u}{\partial t}+\ddot{\theta }u} \right) +\frac{\partial }{\partial x}\left[ {\rho I_z \left( {\dot{\theta }^{2}\frac{\partial v}{\partial x}-\frac{\partial ^{3}v}{\partial x\partial t^{2}}} \right) } \right] \nonumber \\&\quad -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}} \right) +\frac{\partial ^{2}}{\partial x^{2}}\left( {EI_z \frac{\partial ^{2}v}{\partial x^{2}}} \right) =-\rho A\ddot{\theta }(a+x) \end{aligned}$$

(18b)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}+\frac{\partial }{\partial x}\left[ {\rho I_y \left( {\dot{\theta }^{2}\frac{\partial w}{\partial x}-\frac{\partial ^{3}w}{\partial x\partial t^{2}}} \right) } \right] -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}} \right) +\frac{\partial ^{2}}{\partial x^{2}}\left( {EI_y \frac{\partial ^{2}w}{\partial x^{2}}} \right) =0 \end{aligned}$$

(18c)

This is governing equation of Rayleigh beams. If we further neglect the influence of rotational inertia, meaning $\rho I_y =\rho I_z =0$, from (18) we then get

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}u}{\partial t^{2}}-\dot{\theta }^{2}u-2\dot{\theta }\frac{\partial v}{\partial t}-\ddot{\theta }v} \right) -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}} \right) =\rho A\dot{\theta }^{2}(a+x) \end{aligned}$$

(19a)

$$\begin{aligned}&\rho A\left( {\frac{\partial ^{2}v}{\partial t^{2}}-\dot{\theta }^{2}v+2\dot{\theta }\frac{\partial u}{\partial t}+\ddot{\theta }u} \right) -\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}} \right) +\frac{\partial ^{2}}{\partial x^{2}}\left( {EI_z \frac{\partial ^{2}v}{\partial x^{2}}} \right) =-\rho A\ddot{\theta }(a+x) \end{aligned}$$

(19b)

$$\begin{aligned}&\rho A\frac{\partial ^{2}w}{\partial t^{2}}-\frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}\frac{\partial w}{\partial x}} \right) +\frac{\partial ^{2}}{\partial x^{2}}\left( {EI_y \frac{\partial ^{2}w}{\partial x^{2}}} \right) =0 \end{aligned}$$

(19c)

This is in accordance with that of Euler–Bernoulli beams given in Refs. [13, 21] once the applied forces are zero $(p_v =p_w =0)$.

In the present study, the following tapering relations for the height and width of the beam are used.

$$\begin{aligned} b(x)= & {} b_0 \left( {1-c_b \frac{x}{L}} \right) \end{aligned}$$

(20a)

$$\begin{aligned} h(x)= & {} h_0 \left( {1-c_h \frac{x}{L}} \right) \end{aligned}$$

(20b)

where $b_0$ and $h_0$ are the width and height at the root of the beam, respectively, and $c_b$, and $c_h$ are the width and height taper ratios, respectively, defined by

$$\begin{aligned} c_b= & {} 1-\frac{b_L }{b_0 } \end{aligned}$$

(21a)

$$\begin{aligned} c_h= & {} 1-\frac{h_L }{h_0 } \end{aligned}$$

(21b)

in which $b_L$ and $h_L$ are the width and height at the free end of the beam, respectively.

With Eq. (20), the variations of the cross-sectional properties can be obtained as

$$\begin{aligned} A(x)= & {} A_0 \left( {1-c_b \frac{x}{L}} \right) \left( {1-c_h \frac{x}{L}} \right) \end{aligned}$$

(22a)

$$\begin{aligned} I_y (x)= & {} I_{y0} \left( {1-c_b \frac{x}{L}} \right) \left( {1-c_h \frac{x}{L}} \right) ^{3} \end{aligned}$$

(22b)

$$\begin{aligned} I_z (x)= & {} I_{z0} \left( {1-c_h \frac{x}{L}} \right) \left( {1-c_b \frac{x}{L}} \right) ^{3} \end{aligned}$$

(22c)

where $A_0$ and $I_0$ are area and the principal moment of inertia at the root cross section of the beam, respectively. Here $b_0 =h_0$ and $c=c_b =c_h$ are used to model a beam with a square cross section and tapers linearly in two planes. Then

$$\begin{aligned} A(x)= & {} A_0 \left( {1-c\frac{x}{L}} \right) ^{2} \end{aligned}$$

(23a)

$$\begin{aligned} I(x)= & {} I_y (x)=I_z (x)=I_0 \left( {1-c\frac{x}{L}} \right) ^{4} \end{aligned}$$

(23b)

With the above tapering relations, we can rewrite the equations of motion in a dimensionless form. For this transformation, several dimensionless variables and parameters are defined as follows:

$$\begin{aligned}&\tau =t\sqrt{\frac{EI_0 }{\rho A_0 L^{4}}},\quad {{\varOmega } =\dot{\theta }\sqrt{\frac{\rho A_0 L^{4}}{EI_0 }},}\quad {\beta =\sqrt{\frac{A_0 L^{2}}{I_0 }},}\quad {\eta =\frac{\kappa G}{E},}\quad {\xi =\frac{x}{L},}\nonumber \\&\quad {\delta =\frac{a}{L},}\quad {\hat{{u}}=\frac{u}{L},}\quad {\hat{{w}}=\frac{w}{L},}\quad {\hat{{\varphi }}_y =\varphi _y }\quad \hat{{v}}=\frac{v}{L},\quad \hat{{\varphi }}_z =\varphi _z \end{aligned}$$

(24)

Substituting the dimensionless variables defined in Eq. (24), and parameters in Eq. (23) into Eqs. (14) and (15), the dimensionless equations of motion can be written as

$$\begin{aligned}&(1-c\xi )^{2}\frac{\partial ^{2}\hat{{u}}}{\partial \tau ^{2}}-2{\varOmega } (1-c\xi )^{2}\left( {\frac{\partial \hat{{v}}}{\partial \tau }\cos \gamma -\frac{\partial \hat{{w}}}{\partial \tau }\sin \gamma } \right) -{\varOmega } ^{2}(1-c\xi )^{2}\hat{{u}}-\dot{{\varOmega } }(1-c\xi )^{2}\left( {\hat{{v}}\cos \gamma -\hat{{w}}\sin \gamma } \right) \nonumber \\&\quad -\,\beta ^{2}\frac{\partial }{\partial \xi }\left( {(1-c\xi )^{2}\frac{\partial \hat{{u}}}{\partial \xi }} \right) ={\varOmega } ^{2}(1-c\xi )^{2}(\delta +\xi ) \end{aligned}$$

(25a)

$$\begin{aligned}&(1-c\xi )^{2}\left[ {\frac{\partial ^{2}\hat{{v}}}{\partial \tau ^{2}}+2{\varOmega } \frac{\partial \hat{{u}}}{\partial \tau }\cos \gamma +\dot{{\varOmega } }\hat{{u}}\cos \gamma -{\varOmega } ^{2}\left( {\hat{{v}}\cos ^{2}\gamma -\hat{{w}}\sin \gamma \cos \gamma } \right) } \right] -\beta ^{2}\frac{\partial }{\partial \xi }\left( {(1-c\xi )^{2}\frac{\partial \hat{{u}}}{\partial \xi }\frac{\partial \hat{{v}}}{\partial \xi }} \right) \nonumber \\&\quad -\,\eta \beta ^{2}\frac{\partial }{\partial \xi }\left[ {(1-c\xi )^{2}\left( {\frac{\partial \hat{{v}}}{\partial \xi }-\hat{{\varphi }}_z } \right) } \right] =-\dot{{\varOmega } }(1-c\xi )^{2}\left( {\delta +\xi } \right) \cos \gamma \end{aligned}$$

(25b)

$$\begin{aligned}&(1-c\xi )^{2}\left[ {\frac{\partial ^{2}\hat{{w}}}{\partial \tau ^{2}}-2{\varOmega } \frac{\partial \hat{{u}}}{\partial \tau }\sin \gamma -\dot{{\varOmega } }\hat{{u}}\sin \gamma +{\varOmega } ^{2}\left( {\hat{{v}}\cos \gamma \sin \gamma -\hat{{w}}\sin ^{2}\gamma } \right) } \right] -\beta ^{2}\frac{\partial }{\partial \xi }\left( {(1-c\xi )^{2}\frac{\partial \hat{{u}}}{\partial \xi }\frac{\partial \hat{{w}}}{\partial \xi }} \right) \nonumber \\&\quad -\,\eta \beta ^{2}\frac{\partial }{\partial \xi }\left[ {(1-c\xi )^{2}\left( {\frac{\partial \hat{{w}}}{\partial \xi }+\hat{{\varphi }}_y } \right) } \right] =\dot{{\varOmega } }(1-c\xi )^{2}\left( {\delta +\xi } \right) \sin \gamma \end{aligned}$$

(25c)

$$\begin{aligned}&(1-c\xi )^{4}\frac{\partial ^{2}\hat{{\varphi }}_z }{\partial \tau ^{2}}+\eta \beta ^{4}(1-c\xi )^{2}\hat{{\varphi }}_z -{\varOmega } ^{2}(1-c\xi )^{4}\hat{{\varphi }}_z -\beta ^{2}\frac{\partial }{\partial \xi }\left( {(1-c\xi )^{4}\frac{\partial \hat{{\varphi }}_z }{\partial \xi }} \right) -\eta \beta ^{4}(1-c\xi )^{2}\frac{\partial \hat{{v}}}{\partial \xi }=0 \end{aligned}$$

(25d)

$$\begin{aligned}&(1-c\xi )^{4}\frac{\partial ^{2}\hat{{\varphi }}_y }{\partial \tau ^{2}}+\eta \beta ^{4}(1-c\xi )^{2}\hat{{\varphi }}_y -{\varOmega } ^{2}(1-c\xi )^{4}\hat{{\varphi }}_y -\beta ^{2}\frac{\partial }{\partial \xi }\left( {(1-c\xi )^{4}\frac{\partial \hat{{\varphi }}_y }{\partial \xi }} \right) +\eta \beta ^{4}(1-c\xi )^{2}\frac{\partial \hat{{w}}}{\partial \xi }=0\nonumber \\ \end{aligned}$$

(25e)

and the boundary conditions

$$\begin{aligned} {\hat{{u}}=\hat{{v}}=\hat{{w}}=\hat{{\varphi }}_y =\hat{{\varphi }}_z =0}&{\hbox {at}\;\xi =0;}\quad {\frac{\partial \hat{{u}}}{\partial \zeta }=\frac{\partial \hat{{\varphi }}_y }{\partial \zeta }=\frac{\partial \hat{{\varphi }}_z }{\partial \zeta }=\left( {\frac{\partial \hat{{v}}}{\partial \zeta }-\hat{{\varphi }}_z } \right) =\left( {\frac{\partial \hat{{w}}}{\partial \zeta }+\hat{{\varphi }}_y } \right) =0}\quad {\hbox {at}\;\zeta =1}\nonumber \\ \end{aligned}$$

(26)

3 Discretization of the equations of motion

In order to analyze the equations numerically, the continuous system is discretized to one with a finite number of degrees of freedom. Galerkin’s discretization method will be applied to the equations of motion. The deformation of beam can be expressed as

$$\begin{aligned} \hat{{u}}(\xi ,\tau )= & {} \sum _{i=1}^N {A_i (\xi )q_i^u (\tau )} \end{aligned}$$

(27a)

$$\begin{aligned} \hat{{v}}(\xi ,\tau )= & {} \sum _{i=1}^N {B_i (\xi )q_i^v (\tau )} \end{aligned}$$

(27b)

$$\begin{aligned} \hat{{w}}(\xi ,\tau )= & {} \sum _{i=1}^N {B_i (\xi )q_i^w (\tau )} \end{aligned}$$

(27c)

$$\begin{aligned} \hat{{\varphi }}_z (\xi ,\tau )= & {} \sum _{i=1}^N {C_i (\xi )q_i^{\varphi z} (\tau )} =\sum _{i=1}^N {\frac{{B}'_i (\xi )}{i\pi }q_i^{\varphi z} (\tau )} \end{aligned}$$

(27d)

$$\begin{aligned} \hat{{\varphi }}_y (\xi ,\tau )= & {} \sum _{i=1}^N {-C_i (\xi )q_i^{\varphi y} (\tau )} =\sum _{i=1}^N {\frac{-{B}'_i (\xi )}{i\pi }q_i^{\varphi y} (\tau )} \end{aligned}$$

(27e)

where N is the total number of comparison functions and $q_i (\tau )$ denotes the $i\hbox {th}$ generalized coordinates of the transverse displacement and rotation, respectively. In the following sections, the modes of a nonrotating Euler–Bernoulli cantilever beam are used as the comparison functions in the simulation. These mode functions are given by

$$\begin{aligned} A_i (\xi )= & {} \sin (2i-1)\frac{\pi \xi }{2} \end{aligned}$$

(28a)

$$\begin{aligned} B_i (\xi )= & {} \cos (\lambda _i \xi )-\cosh (\lambda _i \xi )-\frac{\cosh (\lambda _i )+\cos (\lambda _i )}{\sin (\lambda _i )+\sinh (\lambda _i )}(\sin (\lambda _i \xi )-\sinh (\lambda _i \xi )) \end{aligned}$$

(28b)

where $\lambda _i$ is the $i\hbox {th}$ root of

$$\begin{aligned} \cos \lambda _i \cosh \lambda _i =-1 \end{aligned}$$

Substituted Eq. (27) into Eq. (25), multiplying the resultant equation by corresponding eigenfunction, and integrating with respect $\xi$ over the domain [0, 1], let

$$\begin{aligned} \varvec{A}(\xi )= & {} [A_1 (\xi ),A_2 (\xi ),\ldots ,A_n (\xi )], \nonumber \\ \varvec{B}(\xi )= & {} [B_1 (\xi ),B_2 (\xi ),\ldots ,B_n (\xi )], \nonumber \\ \varvec{C}(\xi )= & {} [C_1 (\xi ),C_2 (\xi ),\ldots ,C_n (\xi )], \nonumber \\ \varvec{q}^{j}(t)= & {} [q_1^j (\tau ),q_2^j (\tau ),\ldots ,q_n^j (\tau )]\qquad (j=u,v,w,\varphi z,\varphi y) \end{aligned}$$

The following discretized equations are derived

$$\begin{aligned}&\left[ {{\begin{array}{ccccc} {{\mathbf {M}}^{{\mathbf {u}}}}&{}\quad &{}\quad &{}\quad &{}\quad \\ &{}\quad {{\mathbf {M}}^{{\mathbf {v}}}}&{}\quad &{}\quad &{}\quad \\ &{}\quad &{}\quad {{\mathbf {M}}^{{\mathbf {w}}}}&{}\quad &{}\quad \\ &{}\quad &{}\quad &{}\quad {{\mathbf {M}}^{\varvec{\varphi }{{\mathbf {z}}}}}&{} \quad \\ &{}\quad &{}\quad &{}\quad &{}\quad {{\mathbf {M}}^{\varvec{\varphi }{\mathbf {y}}}} \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\ddot{{\mathbf {q}}}^{{\mathbf {u}}}} \\ {\ddot{{\mathbf {q}}}^{{\mathbf {v}}}} \\ {\ddot{{\mathbf {q}}}^{{\mathbf {w}}}} \\ {\ddot{{\mathbf {q}}}^{\varvec{\varphi }{{\mathbf {z}}}}} \\ {\ddot{{\mathbf {q}}}^{\varvec{\varphi }{\mathbf {y}}}} \\ \end{array} }} \right\} +\left[ {{\begin{array}{ccccc} 0&{}\quad {{\mathbf {G}}^{{\mathbf {u}}v}}&{}\quad {{\mathbf {G}}^{{\mathbf {uw}}}}&{}\quad &{}\quad \\ {{\mathbf {G}}^{{\mathbf {v}}u}}&{}\quad 0&{} \quad &{} \quad &{}\quad \\ {{\mathbf {G}}^{{\mathbf {wu}}}}&{}\quad &{}\quad 0&{}\quad &{} \quad \\ &{}\quad &{}\quad &{}\quad 0 &{}\quad \\ &{}\quad &{}\quad &{}\quad &{}\quad 0 \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\ddot{{\mathbf {q}}}^{{\mathbf {u}}}} \\ {\ddot{{\mathbf {q}}}^{{\mathbf {v}}}} \\ {\ddot{{\mathbf {q}}}^{{\mathbf {w}}}} \\ {\ddot{{\mathbf {q}}}^{\varvec{\varphi }{\mathbf {z}}}} \\ {\ddot{{\mathbf {q}}}^{\varvec{\varphi }{\mathbf {y}}}} \\ \end{array} }} \right\} \nonumber \\&\quad +\left[ {{\begin{array}{ccccc} {{\mathbf {K}}^{{\mathbf {u}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {uv}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {uw}}}}&{}\quad &{}\quad \\ {{\mathbf {K}}^{{\mathbf {vu}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {v}}}({\mathbf {q}}^{{\mathbf {u}}})}&{}\quad {{\mathbf {K}}^{{\mathbf {vw}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {v}}\varvec{\varphi }{\mathbf {z}}}}&{}\quad \\ {{\mathbf {K}}^{{\mathbf {wu}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {wv}}}}&{}\quad {{\mathbf {K}}^{{\mathbf {w}}}({\mathbf {q}}^{{\mathbf {u}}})}&{}\quad &{} \quad {{\mathbf {K}}^{{\mathbf {w}}{\varvec{\varphi }} {\mathbf {y}}}} \\ &{}\quad {{\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {zv}}}}&{}\quad &{} \quad {{\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {z}}}}&{}\quad \\ &{}\quad &{}\quad {{\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {yw}}}}&{}\quad &{}\quad {{\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {y}}}} \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {{\mathbf {q}}^{{\mathbf {u}}}} \\ {{\mathbf {q}}^{{\mathbf {v}}}} \\ {{\mathbf {q}}^{{\mathbf {w}}}} \\ {{\mathbf {q}}^{{\varvec{\varphi }}{\mathbf {z}}}} \\ {{\mathbf {q}}^{{\varvec{\varphi }} {\mathbf {y}}}} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {{\mathbf {f}}^{{\mathbf {u}}}} \\ {{\mathbf {f}}^{{\mathbf {v}}}} \\ {{\mathbf {f}}^{w}} \\ 0 \\ 0 \\ \end{array} }} \right\} \end{aligned}$$

(29)

where

$$\begin{aligned} {\mathbf {M}}^{{\mathbf {u}}}= & {} \int _0^1 {(1\!-\!c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {A}}\mathrm{d}\xi } ,\quad {{\mathbf {M}}^{{\mathbf {v}}}\!=\!{\mathbf {M}}^{{\mathbf {w}}}\!=\!\int _0^1 {(1\!-\!c\xi )^{2} {\mathbf {B}}^{T}{\mathbf {B}}\mathrm{d}\xi } ,}\quad {{\mathbf {M}}^{{\varvec{\varphi }} {\mathbf {z}}}={\mathbf {M}}^{{\varvec{\varphi }} {\mathbf {y}}}=\int _0^1 {(1-c\xi )^{4}{\mathbf {C}}^{T}{\mathbf {C}}\mathrm{d}\xi } } \\ {\mathbf {G}}^{{\mathbf {uv}}}= & {} -2{\varOmega } \cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {B}}\mathrm{d}\xi } ,\quad {{\mathbf {G}}^{{\mathbf {uw}}}=2{\varOmega } \sin \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {B}}\mathrm{d}\xi } } \\ {\mathbf {G}}^{{\mathbf {vu}}}= & {} 2{\varOmega } \cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {A}}\mathrm{d}\xi } ,\quad {{\mathbf {G}}^{{\mathbf {wu}}}=-2{\varOmega } \sin \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {A}}\mathrm{d}\xi } } \\ {\mathbf {K}}^{{\mathbf {u}}}= & {} \beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {{A}}}^{\prime T}{\mathbf {{A}}}^{\prime }\mathrm{d}\xi } -{\varOmega } ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {A}}\mathrm{d}\xi } ,\quad {{\mathbf {K}}^{{\mathbf {uv}}}=-\dot{{\varOmega } }\cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {B}}\mathrm{d}\xi }} \\ {\mathbf {K}}^{{\mathbf {uw}}}= & {} \dot{{\varOmega } }\sin \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {A}}^{T}{\mathbf {B}}\mathrm{d}\xi } \\ {\mathbf {K}}^{{\mathbf {v}}}({\mathbf {q}}^{{\mathbf {u}}})= & {} -{\varOmega } ^{2}\cos ^{2}\gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {B}}\mathrm{d}\xi } +\beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {{B}}}^{\prime T}{\mathbf {{A}}}^{\prime }{\mathbf {q}} _1 {\mathbf {{B}}}^{\prime }\mathrm{d}\xi } +\eta \beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {{B}}}^{\prime T}{\mathbf {{B}}}^{\prime }\mathrm{d}\xi } \\ {\mathbf {K}}^{{\mathbf {vu}}}= & {} \dot{{\varOmega } }\cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {A}}\mathrm{d}\xi } ,\quad {{\mathbf {K}}^{{\mathbf {vw}}}={\varOmega } ^{2}\sin \gamma \cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {B}}\mathrm{d}\xi } } \\ {\mathbf {K}}^{{\mathbf {w}}}({\mathbf {q}}^{{\mathbf {u}}})= & {} -{\varOmega } ^{2}\sin ^{2}\gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {B}}\mathrm{d}\xi } +\beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {{B}}}^{\prime T}{\mathbf {{A}}}^{\prime }{{\mathbf {q}}}_1 {\mathbf {{B}}}^{\prime }\mathrm{d}\xi } +\eta \beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{\prime T}{\mathbf {{B}}}^{\prime }\mathrm{d}\xi } \\ {\mathbf {K}}^{{\mathbf {wu}}}= & {} -\dot{{\varOmega } }\sin \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {A}}\mathrm{d}\xi } ,\quad {{\mathbf {K}}^{{\mathbf {wv}}}={\varOmega } ^{2}\sin \gamma \cos \gamma \int _0^1 {(1-c\xi )^{2}{\mathbf {B}}^{T}{\mathbf {B}}\mathrm{d}\xi } } \\ {\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {z}}}= & {} {\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {y}}}=\eta \beta ^{4}\int _0^1 {(1-c\xi )^{2}{\mathbf {C}}^{T}{\mathbf {C}}\mathrm{d}x} -{\varOmega } ^{2}\int _0^1 {(1-c\xi )^{4}{\mathbf {C}}^{T}{\mathbf {C}}\mathrm{d}\xi } +\beta ^{2}\int _0^1 {(1-c\xi )^{4}{\mathbf {{C}'}}^{T}{\mathbf {{C}'}}\mathrm{d}\xi } \\ {\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {zv}}}= & {} {\mathbf {K}}^{{\varvec{\varphi }} {\mathbf {yw}}}=-\eta \beta ^{4}\int _0^1 {(1-c\xi )^{2}{\mathbf {C}}^{T}{\mathbf {{B}'}}\mathrm{d}\xi } ,\quad {{\mathbf {K}}^{{\mathbf {v}}{\varvec{\varphi }} {\mathbf {z}}}={\mathbf {K}}^{{\mathbf {w}}{\varvec{\varphi }} {\mathbf {y}}}=-\eta \beta ^{2}\int _0^1 {(1-c\xi )^{2}{\mathbf {{B}'}}^{T}{\mathbf {C}}\mathrm{d}\xi } } \\ {\mathbf {f}}^{{\mathbf {u}}}= & {} {\varOmega } ^{2}\int _0^1 {(1-c\xi )^{2}(\delta +\xi ){\mathbf {A}}^{T}\mathrm{d}\xi } ,\quad {{\mathbf {f}}^{{\mathbf {v}}}=-\dot{{\varOmega } }\cos \gamma \int _0^1 {(1-c\xi )^{2}(\delta +\xi ){\mathbf {B}}^{T}\mathrm{d}\xi } } \\ {\mathbf {f}}^{w}= & {} \dot{{\varOmega } }\sin \gamma \int _0^1 {(1-c\xi )^{2}(\delta +\xi ){\mathbf {B}}^{T}\mathrm{d}\xi }\\ \end{aligned}$$

4 Dynamical characteristics of the steady-state rotating

In the case of steady-state rotating (i.e., $\ddot{\theta }=0$), the term $EA\frac{\partial u}{\partial x}$ in Eqs. (14b) and (14c) represents the axial force of the rotating beam that imposes a stiffening effect on the lateral motions v and w. According to reference [20], the steady-state axial elastic equilibrium equation is obtained

$$\begin{aligned} \frac{\partial }{\partial x}\left( {EA\frac{\partial u}{\partial x}} \right) =-\rho A\dot{\theta }^{2}(a+x+u) \end{aligned}$$

(30)

Because the extensional deformation u is much smaller than $(a+x)$ and is usually ignored on the right-hand side of Eq. (30), the centrifugal stiffening force term can be expressed as follows [6, 16]

$$\begin{aligned} EA\frac{\partial u}{\partial x}=\int _x^L {\rho A\dot{\theta }^{2}\left( {a+x} \right) \mathrm{d}x} =\rho A\dot{\theta }^{2}\left[ {a(L-x)+\frac{1}{2}(L^{2}-x^{2})} \right] \end{aligned}$$

(31)

It is interesting that this axial force is identical to that given by other authors [14, 15] based on a hybrid set of deformation variables.

And when the extensional deformation of the beam is not ignorable, the exact solution of Eq. (30), which satisfies boundary conditions in Eq. (15), may be given by [17–19, 21].

$$\begin{aligned} u(x)=\frac{ak\cos \left[ {k(1-x/L)} \right] +L\sin (kx/L)}{k\cos k}-(a+x) \end{aligned}$$

(32)

where $k=\dot{\theta }L\sqrt{\frac{\rho }{E}}$

Then the centrifugal stiffening force term can be expressed as follows

$$\begin{aligned} EA\frac{\partial u}{\partial x}=EA\left[ {\frac{\cos (kx/L)}{\cos k}-1} \right] +\frac{ka\sin \left[ {k(1-x/L)} \right] }{L\cos k} \end{aligned}$$

(33)

The linearized free vibrations equations around the equilibrium deformation for the transverse motions $\hat{{v}}$ and $\hat{{w}}$ are obtained after introducing $EA\frac{\partial u}{\partial x}$ described by Eqs. (31) or (33) into Eqs. (14b) and (14c).

Table 1 Convergence characteristics of the natural frequencies for the flapwise motion $(\delta =0,\,\gamma =0,\,c=0.4$ and $\beta =12.5$)

Fig. 2

Variation of the dimensionless natural frequencies with the increasing rotating speed when $\delta =0,\,\beta =12.5$, and $c=0$: a the axial and chordwise motions for $\eta =0.33$; b the flapwise motion for $\eta =0.25$

Firstly, the convergence characteristics of the natural frequencies $\omega$ are considered, when the beam is nonrotating and with a zero setting angle $(\dot{\theta }=0,\,\gamma =0)$, the first four natural frequencies for the flapwise motion shown in Table 1. The number of modes “N” represents the number of the assumed modes for each individual deformation variable. It can be seen that the natural frequencies converge rapidly as more modes are added in the computation, and using 12 modes for each individual deformation variable is sufficient to obtain a reasonable accuracy for the first four natural frequencies. In the case of the chordwise motion, the convergence test is identical to those of the bending modes for the flapwise motion presented in Table 1.

4.1 Effect of hub rotational velocity on the natural frequencies

The natural frequencies of the rotating beam obtained from the two different centrifugal stiffening forces described by Eqs. (31) and (33) are considered in this section. For comparison purpose, calculations with $\gamma =0,\,\delta =0,\,\beta =12.5$ and $c=0$ are performed, and the variations of the natural frequencies with respect to the rotational speed are plotted in Fig. 2. In this figure, the solid lines represent the natural frequencies computed with the centrifugal stiffening force described by Eq. (33), while the dotted lines represent the frequencies computed with the centrifugal stiffening force described by Eq. (31). The calculation results are in good agreement with those in Ref. [9, 12, 18]. As expected, the natural frequencies of transverse vibration increase with increasing rotational speed due to the stiffening effect of the centrifugal force. However, the natural frequencies of axial vibration are almost constant, especially for the higher modals.

Fig. 3

Variation of the dimensionless natural frequencies for different setting angle with the increasing rotating speed when $\delta =0$, $\beta =12.5$, $\eta =0.25$, and $c=0$

As shown in Fig. 2b, the natural frequencies of the flapwise motion $(\omega _w)$ monotonically increase with the rotating speed. However, as shown in Fig. 2a, the axial stretching modes $(\omega _u)$ are coupled with the bending modes $(\omega _v)$. This coupling effect between the stretching and bending modes results in the well-known veering phenomena [13, 16, 21, 23], where the two natural frequency loci veer rather than crossing when they are close to each other. For instance, the second mode of axial motion and the fourth mode of the chordwise motion veer at ${\varOmega } =8.9$, and the fifth mode and the sixth mode of the chordwise motion do at ${\varOmega } =14.0$. The natural frequencies computed with different centrifugal stiffening force do not exhibit large differences in the low rotating speed range. However, the natural frequencies of the beam considering the extensional deformation in the centrifugal stiffening force term are greater than those without considering the extensional deformation in the centrifugal stiffening force term in the high rotating speed range, and the differences will be more obvious with the increase in rotational speed.

4.2 Effect of the setting angle $\gamma$ on the natural frequencies

As mentioned in Sect. 2, the axial motion $\hat{{u}}$ and bending motions $\hat{{v}}$ and $\hat{{w}}$ are coupled with each other for setting angles other than $\gamma =0\,^{\circ }$ and $90\,^{\circ }$. For the purpose of convenience, the axial motion $\hat{{u}}$ is assumed to be zero, and the centrifugal stiffening force described by Eq. (31) is used to calculate the natural frequency $\omega _v$ for chordwise motion $\hat{{v}}$, and $\omega _w$ for flapwise motion $\hat{{w}}$. The results of the first two natural frequencies $\omega _v$are shown in Fig. 3. The results indicate that the effect of increasing the setting angle $\gamma$ leads to increasing natural frequency for all modes, where this effect becomes significantly larger as the mode number is decreased. On the contrary, through the similar calculation, we can find that the frequency $\omega _w$for all modes decreases with increasing setting angle $\gamma$. In this study, for the beam with square cross section, $\omega _w$is exactly the same as $\omega _v$ when the setting angle $\gamma =\pi /4$.

Then, when setting angle $\gamma =0\,^{\circ }$, consider the extensional deformation of the beam, the effect of hub radius ratio $\delta$, slenderness ratio $\beta$, and taper ratios c on the natural frequencies, which are discussed in the following section.

4.3 Effect of hub radius ratio $\delta$ on the natural frequencies

Figure 4a shows the variations of the natural frequencies of the axial and chordwise motions of the rotating double-tapered Timoshenko beam with different hub radius ratios, and Fig. 4b shows the first four natural frequencies of the flapwise motion of the beam. $\beta =30,\,c=0.2,\, \eta =0.33$, and three hub radius ratios ($\delta =0$, 0.5, and 1) are considered in the calculation. It can be seen that the natural frequencies of chordwise and flapwise motions increase with the increasing hub radius ratio, but the different of hub radius ratios has no obvious effect on the natural frequencies of the axial motion unless the frequency veering phenomena happens.

Fig. 4

Variation of the dimensionless natural frequencies for the different hub radius ratio when $\eta =0.33,\, \beta =30,\, \gamma =0$, and $c=0.2$: a the axial and chordwise motions; and b the flapwise motion

Fig. 5

Variation of the dimensionless natural frequencies with respect to the slenderness ratio when $\delta =0,\,\gamma =0,\,\eta =0.33$, ${\varOmega } =5$ and $c=0$: a the axial and chordwise motions; and b the flapwise motion

4.4 Effect of slenderness ratio $\beta$ on the natural frequencies

The effect of the slenderness ratio on the natural frequencies is shown in Fig. 5. It is seen that the natural frequencies increase as the slenderness ratio increases. Moreover, for the flapwise motion, it is noticed that the effect of the slenderness ratio is dominant on the higher modes and this effect diminishes rapidly as the slenderness ratio increases. This is something expected because the Timoshenko beam theory is generally used when the higher-mode frequencies are of interest. However, the effect of the slenderness ratio on the natural frequencies for the axial and chordwise motions is complicated due to the frequencies’ veering. In general, the effect of the slenderness ratio is more significant on the higher modes for all axial, chordwise, and chordwise motions.

4.5 Effect of taper ratios c on the natural frequencies

In order to observe the effect of the taper ratios on the natural frequencies, consider the nonrotating beam first. Figure 6 shows the ratios of the natural frequencies over the natural frequencies of a nontapered Timoshenko beam. It is clear that the taper ratios have a significant increasing effect on the first natural frequency for axial and bending (flapwise and chordwise) motion and a little decreasing effect on other frequencies. This conclusion is consistent with those in Ref. [12].

However, consider the effect of rotating speed on the natural frequencies of a rotating double-tapered Timoshenko beam; Fig. 7 shows the effect of the taper ratio on the natural frequencies of a rotating double-tapered Timoshenko beam with a nonzero rotating speed ${\varOmega } =10$. It is seen that the effect of the taper ratio on the natural frequencies is different from that of the nonrotating beam. The taper ratio has a more intense increasing effect on the first natural frequencies of chordwise motion. It is worth noting that a increasing effect on the second natural frequencies of chordwise and flapwise motions is found. At the same time, these effects become more obvious with increasing taper ratio. The taper ratio has a little decreasing effect on the other natural frequencies.

Fig. 6

Effect of the taper ratio on the natural frequencies when $\delta =0,\,\gamma =0,\,{\varOmega } =0,\,\beta =12.5$, and $\eta =0.33$: a the axial motion; b the transverse motions

Fig. 7

Effect of the taper ratio on the natural frequencies when $\delta =0,\,\gamma =0,\,{\varOmega } =10,\,\beta =12.5$, and $\eta =0.33$: a the chordwise motion; b the flapwise motion

5 Time responses at the tip

In this section, time responses for a rotating double-tapered Timoshenko beam are computed when the rotating speed is prescribed. The smooth speed profile is given by

$$\begin{aligned} {\varOmega } =\left\{ {{\begin{array}{ll} {\frac{{\varOmega } _0 }{T}\tau -\frac{{\varOmega } _0 }{2\pi }\sin \left( {\frac{2\pi }{T}\tau } \right) }&{}\quad {\left( {0\le \tau \le T} \right) } \\ {{\varOmega } _0 }&{}\quad {\left( {\tau >T} \right) } \\ \end{array} }} \right. \end{aligned}$$

(34)

where ${\varOmega } _0 =10$ and $T=10$ are the steady-state angular velocity and the time to reach the angular velocity, respectively. This motion smoothly increases the angular velocity until it reaches the steady state and the steady-state angular velocity is sustained. It is so smooth and slow that the lateral oscillation after reaching the steady state remains quite small. The zero initial conditions are imposed on the axial, chordwise, and flapwise deformations. No force is applied in the axial and chordwise directions, but an initial model velocity $\dot{q}_{_1 }^v =0.0001$ is exerted in the flapwise direction. The time responses of the deformation computed at the tip of beam depend on different taper ratios presented in Fig. 8, where the hub radius ratio $\delta =0.01$, slenderness ratio $\beta =30$, and $\eta =0.33$.

Fig. 8

Time responses of the dimensionless deformation at the tip of the beam when $\delta =0.01,\;\gamma =0,\;\omega _0 =10,\;\beta =30\;\hbox {and}\;\eta \hbox {=0.33}$: a the axial deformations; b the chordwise deformations; and c the flapwise deformations (dotted lines represent the responses without considering the extensional deformation in the centrifugal stiffening force)

The dotted lines represent the responses without considering the extensional deformation in the centrifugal stiffening force term, and others are computed considering the extensional deformation in the centrifugal stiffening force term. For the nontapered beam $(c=0)$, comparing the responses of the two studies described by the dotted lines and solid lines, the main differences are found in the time responses of the axial and chordwise deformations, as shown in Fig. 8a, b. The time responses have more high-frequency vibrations in the axial and chordwise motions when considering the extensional deformation in the centrifugal stiffening force. Moreover, the amplitude of the steady-state oscillate is much larger than that computed without considering the extensional deformation in the centrifugal stiffening force. However, the flapwise deformations have little or even no different between the two cases that whether or not considering the extensional deformation in the centrifugal stiffening force. Moreover, comparing the responses of different taper ratios, it is clear that the deformations and the amplitude of steady-state oscillate decrease as the taper ratios increase for all the axial, chordwise, and flapwise motions.

6 Conclusions

The dynamic model derived in this paper provides a complete representation of the vibration motion for a double-tapered rotating Timoshenko beam. Based on whether or not the extensional deformation is considered in the stiffening effect force of the rotating beam, there are two different expressions about the centrifugal stiffening force in previous studies. The effects of different dimensionless parameters on the natural frequencies and time responses are numerically studied. The following results are obtained:

The setting angle has a significant effect on the natural frequencies of transverse vibration for all modes, especially on the lower modes. This paper lays emphasis on the axial and transverse motions when the setting angle is zero, i.e., the axial motion, chordwise motion, and flapwise motion.

The differences in the natural frequencies computed with the two different expressions are small in the low rotating speed range, but the differences become large in the high speed range. Therefore, the centrifugal stiffening force with considering the extensional deformation is more reasonable for a more accurate numerical simulation than that without considering the extensional deformation. The time responses have more high-frequency vibration and larger steady-state oscillation amplitude for the axial and chordwise motions when the extensional deformation is considered in the centrifugal force.

The natural frequencies of the chordwise and flapwise motions increase with the increasing rotational speed and hub radius ratio, and the rate of increase becomes larger with increasing rotation speed and hub radius ratio. The rotation speed and hub radius ratio have no effect on the natural frequencies of the axial motion.

The slenderness ratio has a significant effect on the natural frequencies for all the axial, chordwise, and flapwise motions, especially on the higher modes and when the slenderness ratio is smaller.

The taper ratio for a nonrotating beam has an increasing effect on the first natural frequency of all the axial, chordwise, and flapwise motions, and the other natural frequencies decrease as the taper ratio increases. For the rotating beam, the taper ratio has a slight increasing effect on the second bending natural frequency except on the first. The time responds indicate that higher taper ratio results in the low response amplitude.