1 Introduction

The study of the dynamics of rotating beams in a variety of rotating structures such as the blades of helicopters and turbines is important for design purposes, optimization, and control. The investigation into the dynamic performance and stability of these structures is an essential component of the design process, especially when dealing with the design of control and condition monitoring systems.

The majority of previous studies on rotating blades are based on Euler–Bernoulli beam models for which the geometric nonlinearities are described by the von Karman strain–displacement relationships thereby neglecting shear deformations and often assuming linearized expressions for the elastic curvatures, while a few authors have dealt with more refined nonlinear models of blades.

The research on modeling of rotating blades has been very active in the last three decades and it is difficult to do justice to all work on the topic. A selection of the most significant work is given next while good literature reviews on modeling of composite blades can be found in [1, 2]. Hodges and Dowell [3] derived the equations of motion for a rotating asymmetric, long, straight, slender, homogeneous, isotropic beam with a variable pretwist angle and a small precone angle, undergoing moderate displacements using Hamilton’s principle and the Newtonian method. The ordering scheme was applied according to which the squares of the bending rotations, the torsional deformation, and the chord-to-radius and the thickness-to-radius ratios are taken to be negligible with respect to unity. The strain–displacement relationships were developed from an exact transformation between the deformed and undeformed coordinate systems.

Stafford and Giurgiutiu [4] applied a semi-analytical method to study linear free vibrations of a rotating Timoshenko beam. They used the Frobenius power series method for finding the natural frequencies of a symmetric isotropic blade with a constant rotation speed by ignoring the Coriolis forces. They also investigated the effects of added mass on the flapping and lagging natural frequencies. Torsional modes effects were later accounted for in [5]. The formulation featured the warping effects, based on Saint Venant’s theory of uniform torsion, and the Coriolis effects for pre-twisted uniform and slightly tapered symmetric isotropic blades. The Coriolis effects were ignored in flapping, lagging and torsional motions.

Wright et al. [6] implemented the Frobenius method to study linear free vibration features such as the flapping natural frequencies and mode shapes of a rotating Euler–Bernoulli beam.

Borri and Mantegazza [7] presented the first geometrically exact equations of motion for rotating blades. In the same years, Crespo da Silva and Hodges [8] used Hamilton’s principle to derive the equations of motion of a general rotating beam with a precone angle and a variable pitch angle, by considering the effects of higher-order nonlinearities and aerodynamic forces.

A nonlinear formulation for rotating composite beams was developed by Hodges [9]. He derived the nonlinear intrinsic formulation for the dynamics of rotating pre-curved and twisted anisotropic beams by considering the warping displacements and accounting for the Rodrigues parameters. A mixed approach, based on Newtonian and variational approaches, delivered the equations of motion.

Bauchau and Kang [10] presented a multibody formulation for nonlinear structural dynamic analysis of helicopter blades based on the finite element method and consideration of the Rodrigues parameters. Their model was capable to cover the rigid-body motion as well as elastic motions of rotating multi-component structures. They found excellent correlation between the multibody formulation and analytical solutions for simple rigid-body problems.

Hodges [11] highlighted some special aspects which must be considered in the linear dynamic modeling of rotating Timoshenko beams especially in the derivation of the boundary conditions and the important centrifugal force effects on the linear eigenfunctions. He also stated that the axial instability never occurs for rotating outward beams when they are not subject to external forces.

Lin and Hsiao [12] examined linear vibrations of a rotating Timoshenko beam by means of a method which resorts to the power series solution. They showed that the effects of Coriolis forces on the natural frequencies of the rotating Timoshenko beam are negligible when the beam is linearly elastic and the steady-state axial strain is small.

Hodges [13] formulated exact nonlinear equations of motion for initially curved and twisted anisotropic beams. By implantation of the Kirchhoff analogy, he showed that a time-discretization scheme for the nonlinear dynamics of rigid bodies can be applied in the same manner in space for the nonlinear equilibrium study of beams.

Ozgumus and Kaya [14] studied free vibrations of a rotating, double tapered Timoshenko beam featuring coupling between flapping and torsional vibrations. They used the differential transform method to solve the governing differential equations of motion. They studied the effects of some parameters on the natural frequencies, among which, the angular speed, the hub radius, the breadth-to-taper ratio, the height-to-taper ratio, the flapping-torsional coupling, rotary inertia, and shear deformation.

Avramov et al. [15] derived the equations of motion for a rotating slender cantilever beam with arbitrary cross section using Hamilton’s principle. They considered cross sections having the shear center different from the mass center. They investigated the interaction between flexural and torsional vibrations within the linear and nonlinear models.

Lee et al. [16] investigated the divergence instability and vibrations of a rotating Timoshenko beam with precone and pitch angles. They found that increasing the precone angle results into decreasing the effects of the axial centrifugal force and the pitch angle on the natural frequencies. Moreover, if the precone angle is large enough, the divergence instability occurs.

Recently, Valverde and Garcia-Vallejo [17] studied the stability of a rotating beam including the effects of Coriolis forces by using the absolute nodal coordinate formulation (ANCF) in comparison with a fully geometrically exact nonlinear formulation based on the Cosserat theory of rods. They investigated the effects of the numbers of elements within the ANCF model on the stability analysis.

Arvin and Bakhtiari-Nejad [18] applied the method of multiple scales (MMS) to the discretized equations of motion obtained via Hamilton’s principle to construct the Nonlinear Normal Modes (NNMs) with or without internal resonances. They investigated the stability and bifurcations of the NNMs in the three-to-one and two-to-one internal resonance cases, respectively, between two flapping modes and between one flapping mode and one axial mode.

In this paper, the equations of motion for linearly elastic, isotropic rotating beams with arbitrary cross sections are obtained via a geometrically exact approach which accounts for all geometric terms. The major differences with respect to the equations of motion proposed in the literature are related to the different parametrization of finite rotations and different choices for the generalized nonlinear strain parameters. Moreover, the present geometrically exact modeling has been obtained directly from three-dimensional nonlinear elasticity to justify rationally the adopted generalized nonlinear strains. The material is assumed isotropic and the blades, due to their slenderness, are enforced to be unshearable by the internal unshearability kinematic constraint. The rigidity of the cross sections neglects cross-sectional displacements (which are scaled by Poisson’s ratio for isotropic materials). They are not needed to formulate the beam problem unless one needs to recover the three-dimensional strain field. The governing equations are expanded in Taylor series to obtain the linearized perturbed form about the prestressed configuration under the centrifugal forces. By applying the Galerkin discretization approach to the equations of motion, a system of ordinary differential equations (ODEs) is derived. Linear free vibrations of unshearable blades featuring coupling between flapping, lagging, axial, and torsional modes are investigated as the rotation speed is changed. The results are compared with those of existing papers. Moreover, finite element computations of the frequencies and mode shapes are carried out in COMSOL Multiphysics [19] using the strong form of the present equations of motion and compared with those obtained by the Galerkin procedure. Necessary (but not sufficient) conditions for the existence of 1:1, 2:1 and 3:1 internal resonances are obtained. In the companion paper (part 2), the method of multiple scales is employed to construct the backbone curves of the flapping modes and to investigate how the nonlinearity of the flapping modes changes with the angular speed.

Notation

In this paper, Gibbs notation is adopted for vectors and tensors. Euclidean vectors and vector-valued functions are denoted by lower-case, italic, bold-face symbols. The dot product and cross product of (vectors) u and v are denoted by u⋅v and u×v, respectively. On the other hand, the tensor product between vectors u and v is denoted by uv instead of the more common u⊗v. The value of the second-order tensor A at vector u is expressed as A⋅u. The notation A ⊺ represents the transpose of tensor A. The partial derivative of a function f with respect to the scalar argument s is denoted by either f s or ∂ s f or by f′. The operator ∂ s is assumed to apply only to the term immediately following it. Notation like ∂ s for a total derivative (i.e., a derivative of a composite function) will always be used. The time derivative of a function v is denoted either by ∂ t v or \(\dot{\boldsymbol{v}}\) (according to Newton’s notation for time derivatives). In some places, there may a switch in notation, in the above stated sense, without an explicit warning.

2 Equations of motion

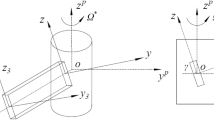
The fully nonlinear equations of motion of rotating blades are obtained through the classical steps of the special Cosserat theory of rods. One of the key steps of the derivation process is associated with the choice of the various reference frames to be used so as to simplify the kinematic and dynamic descriptions [21]. The inertial frame is denoted by {O,i 1,i 2,i 3} where i 1 is the unit vector collinear with the axis of the rotor about which the blade rotates with angular velocity Ω(t) and the origin O lies on this axis (see Fig. 1).

Fig. 1
figure 1

Rotating blade in two configurations: one is the stress-free configuration (dashed lines) while the other is rigidly rotating about i 1 (solid lines). (i 1,i 2,i 3) denotes the inertial frame while (e 1,e 2(t),e 3(t)) is the rotating reference frame

Full size image

A body-fixed rotating frame, denoted by {C,e 1,e 2(t),e 3(t)}, is considered taking {e 1,e 2(t),e 3(t)} collinear, respectively, with {i 1,i 2,i 3}, at time t=0. Unit vector e 3 is collinear with a longitudinal base line of the (stress-free) blade considered rigidly rotating about i 1. Along the base line, the arclength s is chosen to parametrize the positions of the blade cross sections. C is the center of mass of the root cross section through which the blade is connected to the rotor.

A schematic representation of a generic cross section is shown in Fig. 2 where the eccentricity between the shear center, denoted by C E, and the mass center C is described by \((c_{1}^{\mathrm{E}},c_{2}^{\mathrm{E}})\) along the (e 1,e 2) directions, respectively.

Fig. 2
figure 2

The blade cross section and the reference frames

Full size image

The orientation of the (undeformed) cross section is defined by {a 1(s,t),a 2(s,t),a 3(t)} with (a 1, a 2) collinear with the principal inertia axes of the cross section and a 3=a 1×a 2. If e 2 is assumed to be collinear with the chord of the blade cross section in a convenient initial orientation, the principal inertia axes (a 1, a 2) are rotated with respect to (e 1, e 2) by an angle denoted by ϕ o(s). The cross section is further pre-twisted by the angle θ o(s). For convenience, the principal inertia axes are centered in the shear center C E.

The rigidly rotating (stress-free) configuration (see Fig. 3) can be expressed as \(\mathcal{B}_{\mathrm{o}}=\{\breve{\boldsymbol{p}}_{\mathrm{o}}(s,t) =\boldsymbol{r}_{\mathrm{o}}^{\mathrm{E}}(t)+\boldsymbol {r}_{\mathrm{o}}(s,t)+\boldsymbol{x}_{\mathrm{o}}(s,t),\ \boldsymbol{x}_{\mathrm{o}}(s,t)=x_{1}(s)\boldsymbol {a}_{1}(s,t)+ x_{2}(s)\times\boldsymbol{a}_{2}(s,t),\ s \in[s_{1},s_{2}],\ t \in [0,\infty)\}\) where ∂ t a k (s,t)=ω o(s,t)×a k (s,t) and ω o(s,t)=Ω(t)e 1 is the prescribed angular velocity vector. \(\boldsymbol{r}_{\mathrm{o}}^{\mathrm{E}}(t)= \boldsymbol{r}_{\mathrm {o}}^{\mathrm{C}}(t)+\bar{\boldsymbol{x}}^{\mathrm{E}}(t)\) is the position of the elastic center of the root cross section with respect to O at time t and r o(s,t)=s a 3(t)=s e 3(t) is the position vector of the shear center of the cross section at s along the base line. The position of the mass center with respect to O is \(\boldsymbol{r}_{\mathrm{o}}^{\mathrm{C}}(t)=\boldsymbol{d} =d_{2}\boldsymbol{e}_{2}(t)+d_{3}\boldsymbol{e}_{3}(t)\). On the other hand, the position of a material particle of the cross section at s with respect to C E is described by x o(s,t).

Fig. 3
figure 3

The rotating blade in various configurations: initially stress-free configuration (dotted lines), rigidly rotating configuration \(\mathcal{B}_{\mathrm{o}}\) (dashed lines), prestressed \(\mathcal{B}^{\mathrm{o}}\) (dashed-dotted lines) and actual configuration \(\mathcal{B}\) (solid lines)

Full size image

The prestressed effects induced by the centrifugal forces on the rotating blade cause an intermediate (equilibrium) configuration (see Fig. 3) described by \(\mathcal{B}^{\mathrm{o}}=\{\breve {\boldsymbol{p} }^{\mathrm{o}}(s,t) =\boldsymbol{r}_{\mathrm{o}}^{\mathrm {E}}(t)+\boldsymbol{r}^{\mathrm {o}}(s,t)+\boldsymbol{x}^{\mathrm{o}}(s,t),\ \boldsymbol {x}^{\mathrm{o}}(s,t)=x_{1}(s)\boldsymbol{b}_{1}^{\mathrm{o}}(s,t) +x_{2}(s)\boldsymbol{b}_{2}^{\mathrm{o}}(s,t),\ s \in [s_{1},s_{2}],\ t \in[0,\infty)\}\), where r o(s,t) is the position vector of the shear center of the cross section at s in the prestressed configuration with respect to the root cross section. The unit vectors \(\{\boldsymbol{b}_{1}^{\mathrm{o}}(s,t),\boldsymbol{b}_{2}^{\mathrm {o}}(s,t),\boldsymbol{b}_{3}^{\mathrm{o}}(s,t)\}\) describe the orientation of the cross section in \(\mathcal{B}^{\mathrm{o}}\) and are related to a k (s,t) through the orthogonal tensor R o(s,t) according to \(\boldsymbol{b}_{k}^{\mathrm{o}}(s,t)=\boldsymbol{R}^{\mathrm {o}}(s,t)\cdot \boldsymbol{a}_{k}(s,t) \). The curvature vector is obtained by differentiation of \(\boldsymbol{b}_{k}^{\mathrm{o}}(s,t)\) with respect to s as \(\partial_{s} \boldsymbol{b}_{k}^{\mathrm{o}}(s,t)=\boldsymbol{\mu }^{\mathrm {o}}(s,t)\times\boldsymbol{b}_{k}^{\mathrm{o}}(s,t)\). On the other hand, the strains are obtained as the components of the stretch vector:

(1)

where \(\eta_{1}^{\mathrm{o}}\), \(\eta_{2}^{\mathrm{o}}\) are the shear strains in the \(\boldsymbol{b}_{1}^{\mathrm{o}}(s,t)\) and \(\boldsymbol {b}_{2}^{\mathrm{o}}(s,t)\) directions, respectively, and ν o is the blade stretch. The displacement from \(\mathcal{B}_{\mathrm{o}}\) to \(\mathcal {B}^{\mathrm{o}}\) can be introduced according to r o(s,t)=r o(s,t)+u o(s,t) with \(\boldsymbol{u}^{\mathrm{o}}(s,t)=u_{1}^{\mathrm {o}}(s,t)\boldsymbol{e} _{1}+u_{2}^{\mathrm{o}}(s,t)\boldsymbol{e}_{2}(t)+u_{3}^{\mathrm {o}}(s,t)\boldsymbol{e}_{3}(t)\).

Finally, the actual configuration is described by \(\mathcal{B}=\{ \breve{\boldsymbol{p}}(s,t)=\boldsymbol{r}_{\mathrm{o}}^{\mathrm {E}}(t)+\boldsymbol {r}(s,t)+\bar{\boldsymbol{x}}(s,t),\ \bar{\boldsymbol{x}}(s,t) =x_{1}(s)\boldsymbol{b}_{1}(s,t)+x_{2}(s)\boldsymbol{b}_{2}(s,t),\ s \in [s_{1},s_{2}],\ t \in[0,\infty)\}\) where r(s,t) is the actual position vector of the shear center (see Fig. 3) with respect to the root cross section, \(\bar{\boldsymbol{x}}(s,t)=x_{1}\boldsymbol{b}_{1}(s,t)+x_{2}\boldsymbol {b}_{2}(s,t)\) is the position of the material point with respect to C E in the cross section at position s and time t. The unit vectors {b 1(s,t),b 2(s,t),b 3(s,t)}, with b 3(s,t)=b 1(s,t)×b 2(s,t), constitute the cross-section-fixed reference frame introduced to describe the actual orientation of the cross sections. The unit vectors of the current configuration are expressed in terms of the body-fixed unit vectors of the prestressed configuration by means of the incremental orthogonal tensor R(s,t) according to which \(\boldsymbol{b}_{k}(s,t)=\boldsymbol{R}(s,t)\cdot\boldsymbol {b}_{k}^{\mathrm {o}}(s,t)\). Differentiating b k (s,t) with respect to s yields the total curvature vector \(\breve{\boldsymbol{\mu}}\) according to \(\partial_{s} \boldsymbol{b}_{k}(s,t) =\breve{\boldsymbol{\mu}}(s,t)\times\boldsymbol{b}_{k}(s,t)\). The total stretch vector is obtained as \(\breve{\boldsymbol{\nu}}(s,t)=\partial_{s} \boldsymbol {r}(s,t)=\breve{\eta }_{1}(s,t)\boldsymbol{b}_{1}(s,t)+\breve {\eta}_{2}(s,t)\boldsymbol{b}_{2}(s,t)+\breve{\nu}(s,t)\boldsymbol{b}_{3}(s,t)\) where \(\breve{\eta}_{1}\), \(\breve{\eta}_{2}\) are the total shear strains in the b 1(s,t) and b 2(s,t) directions, respectively, while \(\breve{\nu}\) is the total stretch. If u(s,t)=u 1(s,t)e 1+u 2(s,t)e 2(t)+u 3(s,t)e 3(t) denotes the incremental displacement vector from \(\mathcal{B}^{\mathrm{o}}\) to \(\mathcal{B}\), then r(s,t)=r o(s,t)+u(s,t).

Time rates of change of linear and angular momentum

The statements of the balance of linear and angular momentum require the calculation of the velocities which involves the calculation of the time rates of change of the rotating unit vectors. Therefore, differentiation of \(\boldsymbol {b}_{k}^{\mathrm{o}}(s,t)\) and b k (s,t) with respect to time yields \(\partial_{t}\boldsymbol{b}_{k}^{\mathrm{o}}(s,t)= \boldsymbol{\omega }^{\mathrm {o}}(s,t)\times\boldsymbol{b}_{k}^{\mathrm{o}}(s,t)\) and \(\partial _{t}\boldsymbol{b}_{k}(s,t)=\breve {\boldsymbol{\omega} }(s,t)\times\boldsymbol{b}_{k}(s,t)\), respectively.

The velocity and acceleration of material points of the cross section in the prestressed configuration can be expressed as

where \(\breve{\boldsymbol{r}}^{\mathrm{o}}(s,t):=\boldsymbol {r}_{\mathrm{o}}^{\mathrm {E}}(t)+\boldsymbol{r}_{\mathrm{o}}(s,t)+\boldsymbol{u}^{\mathrm {o}}(s,t)\) is the position vector of the shear center of the cross section at s with respect to the origin O in \(\mathcal{B}^{\mathrm{o}}\); \(\breve{\boldsymbol {\omega}}_{\mathrm{R}}(t)\) is the angular velocity vector, and \(\partial_{t}{\boldsymbol{u}}^{\mathrm {oL}}(s,t):=\sum _{k=1}^{3}\partial_{t} u_{k}^{\mathrm{o}}(s,t)\boldsymbol{e}_{k}(t)\) is the local velocity vector (i.e., velocity relative to the rotating frame).

The velocity and acceleration of the material points of the current configuration can be expressed as

where \(\breve{\boldsymbol{r}}=\boldsymbol{r}_{\mathrm{o}}^{\mathrm{E}} +\boldsymbol{r}_{\mathrm{o}}+\breve{\boldsymbol{u}}\) and \(\breve{\boldsymbol{u}}=\boldsymbol{u}^{\mathrm{o}}+\boldsymbol{u}\). The time rate of change of linear and angular momentum in the prestressed and actual configurations are, respectively, defined as

$$ \begin{aligned} &\partial_{t}{\breve{\boldsymbol{l}}}^{\mathrm{o}}:=\int _S\partial_{tt} \breve{\boldsymbol{p}}^{\mathrm{o}}(s,t) \rho \,dA,\\ &\partial_{t} {\breve{\boldsymbol{h}}}^{\mathrm{o}}:=\int _S \breve{\boldsymbol{p}}^{\mathrm{o}}(s,t)\times \partial_{tt} \breve{\boldsymbol{p}}^{\mathrm{o}}(s,t)\rho\,dA, \\ &\partial_{t}{\breve{\boldsymbol{l}}}:=\int_S \partial_{tt} \breve{\boldsymbol{p}} (s,t)\rho \,dA,\\ &\partial_{t} { \breve{\boldsymbol{h}}}:=\int_S\breve{\boldsymbol{p}}(s,t)\times \partial_{tt} \breve{\boldsymbol{p}}(s,t)\rho \,dA. \end{aligned} $$
(2)

The relevant expressions are given in Appendix A.

Equations of motion

The local statement of the balance of linear and angular momentum in the prestressed configuration yields the equations of motion as

(3)
(4)

where n o and m o are the stress resultant and moment resultant over the cross section known as contact force and contact couple, respectively. They are defined as

where t o denotes the first Piola–Kirchhoff stress vector over the cross section normal to a 3(t). Their component representation is \(\boldsymbol{n}^{\mathrm {o}}={Q}_{1}^{\mathrm{o}} \boldsymbol{b}_{1}^{\mathrm{o}}+{Q}_{2}^{\mathrm{o}}\boldsymbol {b}_{2}^{\mathrm{o}}+{N}^{\mathrm {o}}\boldsymbol{b}_{3}^{\mathrm{o}}\) and \({\boldsymbol{m}}^{\mathrm {o}}={M}_{1}^{\mathrm{o}}\boldsymbol{b} _{1}^{\mathrm{o}}+{M}_{2}^{\mathrm{o}}\boldsymbol{b}_{2}^{\mathrm {o}}+{T}^{\mathrm{o}}\boldsymbol{b} _{3}^{\mathrm{o}}\) where \((Q_{1}^{\mathrm{o}},Q_{2}^{\mathrm{o}})\) are the shear forces, N o is the tension, \((M_{1}^{\mathrm{o}},M_{2}^{\mathrm{o}})\) are the bending moments, and T o is the torque. The vectors f o and c o are the external force and couple resultants per unit reference length acting in \(\mathcal{B}^{\mathrm{o}}\).

On the other hand, the balance of linear and angular momentum in the current configuration is stated as

(5)
(6)

where \(\breve{\boldsymbol{n}}=\breve{Q}_{1}\boldsymbol{b}_{1}+\breve {Q}_{2}\boldsymbol{b}_{2}+\breve{N}\boldsymbol{b}_{3}\) and \(\breve{\boldsymbol{m}}=\breve{M}_{1}\boldsymbol{b}_{1}+\breve {M}_{2}\boldsymbol{b}_{2}+\breve{T}\boldsymbol{b}_{3}\) are the generalized stress and moment resultants in the current configuration \(\mathcal{B}\) while \(\breve{\boldsymbol{f}}\) and \(\breve{\boldsymbol{c}}\) are the external force and couple resultants per unit reference length acting in \(\mathcal{B}\). By considering the natural decompositions: \(\breve{\boldsymbol {n}}(s,t)=\boldsymbol{n} ^{\mathrm{o}}(s,t)+\boldsymbol{n}(s,t)\) and \(\breve{\boldsymbol {m}}(s,t)=\boldsymbol{m}^{\mathrm {o}}(s,t)+\boldsymbol{m}(s,t)\), \(\breve{\boldsymbol{f}}(s,t)=\boldsymbol{f}^{\mathrm {o}}(s,t)+\boldsymbol{f}(s,t)\) and \(\breve{\boldsymbol{c} }(s,t)=\boldsymbol{c}^{\mathrm{o}}(s,t)+\boldsymbol{c}(s,t)\), and incorporating equations of motion (3) and (4) holding in the prestressed configuration \(\mathcal{B}^{\mathrm{o}}\), Eqs. (5) and (6) give the incremental form of the equations of motion

(7)
(8)

The vectors n(s,t) and m(s,t) are the incremental contact force and incremental contact couple, respectively, while f(s,t) and c(s,t) are the incremental external force and couple per unit reference length.

3 The prestressed equilibrium and the linearized equations of motion

The linearized form of the equations of motion is obtained by straightforward linearization of the nonlinear equations of motion about the prestressed equilibrium \(\mathcal{B}^{\mathrm{o}}\). For symmetric blades, for which the mass and shear centers coincide, the only strain induced by the rotational motion about i 1 in \(\mathcal {B}^{\mathrm{o}}\) is the generalized stretch which, in linearized form, is \(\nu^{\mathrm{o}}=1+{u_{3}^{\mathrm{o}}}'(s)\) where the prime indicates differentiation with respect to s. In the prestressed (tensile) equilibrium, the shear forces vanish (i.e., \(Q^{\mathrm{o}}_{1}(s)=0=Q^{\mathrm{o}}_{\mathrm {2}}(s)\)), the curvature vector is zero (i.e., μ o=o) and \(\omega ^{\mathrm{o}}_{1}=\omega_{\mathrm{R}}\). The only nontrivial equilibrium equation is

$$ N^{\mathrm{o}\prime}(s)=-\rho A \omega_{\mathrm{R}}^2 \bigl[d_{3}+s+u_{3}^{\mathrm{o}}(s)\bigr] $$
(9)

where ρA is the mass per unit reference length. Equation (9) is formulated in terms of the longitudinal displacement \(u_{3}^{\mathrm{o}}\) only when the constitutive equation is given as \({N^{\mathrm{o}}}(s)=\hat{N}^{\mathrm{o}}(\nu^{\mathrm{o}},s)\). Following [20], we adopt a constitutive function for the equilibrium uniaxial states of stress derived from a stored-energy function proportional to V(ν o):=(ν o)a/a+(ν o)−b/b where a>1 and b>0 are constitutive constants. The ensuing constitutive functions have the form

$$ N^{\mathrm{o}}\bigl(\nu^{\mathrm{o}},s\bigr) =\frac{EA(s)}{ a+b} \biggl[\bigl(\nu^{\mathrm{o}}\bigr)^{a-1} - \frac{1}{(\nu ^{\mathrm {o}})^{b+1}} \biggr] $$
(10)

where EA(s) is the axial stiffness of the blade. The linearly elastic material, represented by the linearized form of Eq. (10), is described by N o(ν o,s)=EA(s)(ν o−1). For the computations, we assume a softening (sublinear) material under tensile states of stress with b=a−1 and \(a=\frac{5}{2}\).

The linearized version of the elastic equilibrium is

$$ \bigl[EA {u_{3}^{\mathrm{o}}}'\bigr]'+\rho A \omega_{\mathrm{R}}^2\bigl(d_{3}+s+u_{\mathrm {3}}^{\mathrm{o}} \bigr)=0 $$
(11)

whose solution for N o is

(12)

where \(\bar{\omega}_{\mathrm{R}}^{a}:={\omega}_{\mathrm {R}}/\omega_{a}\) with \(\omega_{a}:=\sqrt{E A/(\rho A L^{2})}\).

Figure 4 shows the equilibrium stretch of the root cross section vs. the angular speed for the linearly elastic material and the softening material. Below ω R equal to 5⋅103 rpm, the constitutive nonlinearity cannot be appreciated while at higher speeds, some deviations are manifested with consequences on the geometric stiffness and the frequencies.

Fig. 4
figure 4

Variation of the equilibrium stretch ν o at the root cross section with the angular speed ω R. The equilibrium response obtained for a linearly elastic material is contrasted with that exhibited by a nonlinearly elastic (softening) material given by Eq. (10) with b=a−1 and \(a=\frac{5}{2}\). The dashed line indicates the linearly elastic material while the solid line indicates the nonlinear material

Full size image

The linearized equations of motion can be obtained considering the components of the linearized angular speed and curvature vectors (given in Appendix B) which read

(13)
(14)

Thus the linearized equations of motion reduce to

(15)
(16)
(17)
(18)
(19)
(20)

where \((\rho J^{\mathrm{S}}_{11},\rho J^{\mathrm {S}}_{22},\rho J^{\mathrm{S}}_{33})\) are the principal mass moments of inertia of the cross section with respect to the principal inertia axes (b 1,b 2,b 3) with origin in the shear center.

Unshearable rotating blades

The slenderness of typical blades in applications such as helicopter blades or wind turbines allows to consider the blades as being unshearable no matter what the loading conditions are.

This is obtained prescribing two internal kinematic constraints, namely that the shear strains vanish, hence \(\eta^{\mathrm{o}}_{\mathrm {1}}=0=\eta ^{\mathrm{o}}_{2}\). The linearized version of the material constraints leads to the following expressions for the rotations of the cross sections:

(21)

These rotations can be differentiated to yield the linearized bending curvatures.

Solving Eqs. (18) and (19) for the shear forces Q 1 and Q 2 yields

(22)

Substituting Eqs. (22) into Eqs. (15)–(17) and (20) yields the four equations governing the axial, flapping, lagging, and torsional motions

(23)
(24)
(25)
(26)

Linearly elastic isotropic constitutive laws are considered for the eigenvalue problem in the form

$$ \begin{array}{l} \hat{N}^{\mathrm{(1)}}=EA \bigl(\nu^{\mathrm{(1)}}-1\bigr),\qquad \hat {M}_{1} ^{\mathrm{(1)}}=E J^{\mathrm{S}}_{11} \mu_{\mathrm {1}}^{\mathrm{(1)}},\\[6pt] \hat{M}_{2} ^{\mathrm{(1)}}=E J^{\mathrm{S}}_{22} \mu_{\mathrm {2}}^{\mathrm{(1)}},\qquad \hat{T}^{\mathrm{(1)}}=G J^{\mathrm{S}}_{33} \mu_{3}^{\mathrm{(1)}} \end{array} $$
(27)

where G is the shear modulus.

4 Galerkin discretization

The linearized equations of motion can thus be cast in the form

(28)

where the active displacement components and torsional rotations of the unshearable blade are collected in the generalized displacement vector

(29)

I and L are, respectively, the linear, positive-definite, self-adjoint inertia and stiffness operators, while H is the gyroscopic operator.

In the spirit of the method of weighted residuals, the displacements u 1, u 2, u 3 and θ 3 are expressed as linear combination of suitable trial functions, here taken as the eigenfunctions of the free vibration problem of the non-rotating beam having the same boundary conditions; that is,

(30)

where q u(1)(t), q u(2)(t), q u(3)(t) and q θ(3)(t) are, respectively, the flapping, lagging, axial and torsional generalized coordinates, \(\psi^{u(1)}_{j}(s)\), \(\psi^{u(2)}_{j}(s)\), \(\psi ^{u(3)}_{j}(s)\) and \(\psi^{\theta(3)}_{j}(s)\) are, respectively, the flapping, lagging, axial and torsional linear normal modes of the non-rotating blade. The substitution of Eq. (30) into the equations of motion and the minimization of the weighted residuals according to the Galerkin procedure yields the discretized equations of motion as

(31)

where q=[q u(1),q u(2),q u(3),q θ(3)]⊺. The matrices M and K are, respectively, the positive-definite symmetric inertia and stiffness matrices while G is the skew-symmetric gyroscopic matrix (given in Appendix C). The eigenvalue problem is obtained substituting q(t)=e iωt x (i is the imaginary unit) into Eq. (31) to obtain

(32)

It is known (see, e.g., [22]) that the eigenvalues ω of the gyroscopic system (31) (i.e., the solutions of det[−ω 2 M+iω G +K]=0) are real and positive, thus the blade exhibits the full spectrum of real frequencies.

5 Results and discussion

In this section, the linear modal properties of isotropic rotating unshearable blades are investigated. The attention is first directed toward the validation of the adopted discretization scheme. Subsequently, variations of the natural frequencies with the angular speed are studied to highlight scenarios of integer ratios between the frequencies which may give rise to modal interactions resulting into complex three-dimensional motions.

As a first illustrative example, the same geometric and material properties of the rotating beam in [18] are adopted. The properties are summarized in Table 1. The comparisons between the linear natural frequencies calculated by the current approach and those presented in [18] are shown in Table 2, where subscript f and a indicate the flapping and axial modes, respectively. The frequencies of the flapping modes are very close but slightly lower than those found in [18] due to the higher accuracy inherent in the present formulation. On the other hand, the axial natural frequencies are exactly the same as those in [18].

Table 1 Geometric and material properties from Ref. [18]
Full size table
Table 2 The circular frequencies (rad/s) of the flapping and axial modes compared to those of Ref. [18]
Full size table

After a preliminary validation of the results, an aluminum blade is chosen with the following properties: Young’s modulus is 70 GPa, the shear modulus is 26 GPa, the mass density is 2700 kg/m3, the span is 2 m and the cross section is rectangular with the base b=0.005 m, the height h=0.05 m, and the radius of the rotor equal to 0.2 m.

The convergence study of the Galerkin discretization approach at different angular speeds is presented in Tables 3, 4, 5, 6. To evaluate the error by which the frequencies are calculated via the Galerkin discretization, finite element computations are carried out using a finite element general-purpose platform called COMSOL Multiphysics which allows to treat directly the partial-differential equations of motion (strong form) by linearizing them about the prestressed equilibrium. The code discretizes our equations of motion using Lagrangian polynomials.

Table 3 Convergence of the lowest three flapping frequencies calculated by the Galerkin discretization (rad/s)
Full size table
Table 4 Convergence of the lowest three lagging frequencies calculated by the Galerkin discretization (rad/s)
Full size table
Table 5 Convergence of the lowest three torsional frequencies calculated by the Galerkin discretization (rad/s)
Full size table
Table 6 Convergence of the lowest three axial frequencies calculated by the Galerkin discretization (rad/s)
Full size table

In the following tables, the percent error is obtained as 100(ω FE−ω GK)/ω FE for ω R=103 rpm where ω FE is the frequency calculated by COMSOL and ω GK denotes the frequency calculated by the Galerkin procedure. The finite element scheme is based on 100 finite elements with 4th-order Lagrangian interpolant functions. Moreover, N is the number of flapping, lagging, torsional and axial linear normal modes used in the Galerkin discretization approach. In all tables, FE indicates the results obtained via finite elements in COMSOL and GK indicates the results obtained by the Galerkin procedure. A good convergence is attained for all modes for N=8 whereby the error is less than 1 %. However, to achieve a good accuracy in the natural frequencies of rotating blades at high speeds, it is expected that the number N of trial functions (here, the linear normal modes of the non-rotating blade) employed in the discretization increases with the angular speed.

To investigate the dependence of the frequencies of the various modes on the angular speed, variations of the nondimensional natural frequencies of the lowest three flapping, lagging, torsional, and axial modes with the angular speed are shown in Figs. 5, 6, 7, and 8, respectively. Here and henceforth, the dimensional frequencies are rendered nondimensional by scaling them by ω f which is the first flapping natural frequency of the corresponding non-rotating beam. A wide range of angular speeds, namely [0,5⋅103] rpms, is considered so as to span most of the technical operating regimes for rotating beam-like structures.

Fig. 5
figure 5

The (a) first, (b) second, and (c) third flapping natural frequency vs. the angular speed ω R. The solid line and unfilled (filled) circles denote the results obtained by the finite element discretization and those obtained by the Galerkin approach with (without) the effects of the Coriolis forces, respectively

Full size image
Fig. 6
figure 6

The (a) first, (b) second, and (c) third lagging natural frequency vs. the angular speed ω R. The solid line and unfilled (filled) circles denote the results obtained by the finite element discretization and those obtained by the Galerkin approach with (without) the effects of the Coriolis forces, respectively

Full size image
Fig. 7
figure 7

The lowest torsional natural frequency vs. the angular speed ω R. The solid line and unfilled (filled) circles denote the results obtained by the finite element discretization and those obtained by the Galerkin approach with (without) the effects of the Coriolis forces, respectively

Full size image

Moreover, to investigate the relative contribution of the Coriolis forces to the frequencies, the latter are calculated also neglecting the Coriolis forces in the equations of motion. The frequencies of the lowest three flapping modes shown in Fig. 5 do not depend on the Coriolis forces as expected since these forces are orthogonal to the direction of motion. As known, the tension induced by the centrifugal forces has a geometric-type stiffening effect on the flapping modes, thus their frequencies increase with the angular speed. An excellent agreement is found between the results obtained by the Galerkin approach and those obtained by finite elements within COMSOL.

Figure 6 shows variation of the natural frequencies of the lowest three lagging modes in the full range of angular speeds. The Coriolis forces associated with the lagging modes act in the longitudinal direction causing loss of tension which softens the response. This effect is significantly more pronounced in the lowest lagging mode. Of course, by neglecting the Coriolis forces, this effect is lost and the frequencies are off from the actual values exhibiting a discrepancy which grows with the magnitude of the angular speed. This figure shows a good agreement between the results obtained via the Galerkin discretization and those obtained by finite elements for the first mode while for the second and third modes, the Galerkin results are in full agreement with the COMSOL-based results.

Figures 7 and 8 show variations of the frequencies of the lowest torsional and axial modes, respectively. There is a full agreement between the Galerkin-based results and those obtained by finite elements for the first torsional and axial natural frequencies. While the Coriolis forces have no influence on the torsional frequency, they do exert an important effect on the frequency of the lowest axial mode. If the Coriolis forces are neglected, the frequency decreases with the angular speed contrary to the actual increasing trend.

6 Scenarios of internal resonances

A rotating beam-like structure is a powerful example of a nonlinear system which can exhibit a variety of internal resonances [23, 24] depending on a natural tuning parameter, here the angular speed. The internal resonances that may be potentially activated in rotating blades can be predicted by determining the angular speeds at which the frequencies of various modes are in integer ratios. The variety of these possible internal resonances can be appreciated in Fig. 9 which shows variation of the frequencies with the angular speed. In the same plot, twice and three times the natural frequencies of the considered modes are shown so as to locate the speeds at which 1:1, 2:1, and 3:1 ratios arise. All the detected potential internal resonances are listed in Table 7, where subscript “L” and “T” indicate the lagging and torsional modes, respectively, and subscript “f” and “a” denote flapping and axial modes, as before.

Fig. 9
figure 8

The frequencies of elastic isotropic rotating blades vs. the angular speed ω R. The filled circles represent twice the computed frequencies while the unfilled circles denote three times the frequency values. The intersections of the curves with the filled (unfilled) circles with the actual frequency loci denote the angular speeds ω R where 2:1 (3:1) ratios occur

Full size image
Table 7 Possible internal resonances
Full size table

7 Concluding remarks

The geometrically exact equations of motion of elastic isotropic arbitrary pre-twisted blades shown in this work are devoid of restrictions on the geometry of deformation besides the local rigidity of the cross sections. The goal of this work is to study nonlinear vibrations of rotating blades away and near internal resonances by employing a perturbation approach. This justifies the need of the Updated Lagrangian formulation for the geometrically exact equations of motion whose perturbations can be derived consistently and systematically. In particular, in this paper, the linearized form of the equations is obtained for symmetric blades for which the prestressed equilibrium is characterized by a uniaxial tensile state of stress caused by the centrifugal forces. The equations of motion are further simplified by static condensation of the shear forces to reflect the fact that the blades are taken to be unshearable by imposition of two internal kinematic constraints. These material constraints reflect the fact that the blades typically utilized in engineering applications are sufficiently slender and thus they are not prone to shear deformations.

The Galerkin discretization approach was employed to obtain the natural frequencies of the rotating blades as a superposition of the linear mode shapes of the non-rotating blades. In particular, the investigation has addressed the lowest three flapping, lagging, axial, and torsional modes. Besides a validation of the obtained results in comparison with those obtained by finite elements, the results highlight the fact that, as expected, the Coriolis forces have no effects on the flapping and torsional natural frequencies while they play a significant role on the lagging modes, especially the first mode, and on the axial frequencies. The magnitude of the influence of the Coriolis forces increases with the angular speed as shown in Figs. 6 and 8. The rich variety of potential one-to-one, two-to-one and three-to-one internal resonances between flapping, lagging, axial and torsional modes is discussed. The angular speeds at which these resonances may arise are determined numerically. In the companion manuscript (part 2), free nonlinear vibrations of the blades away from internal resonances are studied by the method of multiples scales. The individual nonlinear normal modes are constructed and the backbones of the modes are discussed together with the role of the angular speed on the nonlinearity.

Fig. 8
figure 9

The lowest axial natural frequency vs. the angular speed ω R. The solid line and unfilled (filled) circles denote the results obtained by the finite element discretization and those obtained by the Galerkin approach with (without) the effects of the Coriolis forces, respectively

Full size image