Nonlinear Structural, Inertial and Damping Effects in an Oscillating Cantilever Beam

Abstract

The nonlinear oscillations of a cantilever beam are studied with a theoretical computational model and the results are compared to experimental results obtained in a previous study. In order to explore the various possible nonlinear effects, the cantilevered beam is oscillated by the clamped base in a harmonic motion. Frequency sweeps are conducted in the vicinity of the first and second resonance frequencies of the beam to produce tip displacements of the order of the beam’s length. Three types of nonlinear effects are included in the model and discussed: Inertial, structural, and fluid damping nonlinearities.

Comparison of results from the computational model to previously conducted experiments near the first natural frequency shows reasonable to good agreement, suggesting that this model could be effective in describing large amplitude oscillations. Based on the success of this experimental/computational correlation, a computational study near the second resonant mode suggests that nonlinear inertial effects at a higher resonance frequency have a greater effect on both peak amplitude and the frequency at which it is achieved. For the first resonant mode the effects of nonlinear inertia and nonlinear stiffness are offsetting and hence the peak resonant frequency is little changed from that predicted by linear theory and only a very modest hysteresis is observed. However for the second resonant mode, because the nonlinear inertia effect dominates relative to the nonlinear stiffness effect, there is a greater shift in the peak resonant frequency from its linear value and a more substantial hysteresis is observed.

44.1 Introduction

The dynamic oscillations of cantilevered beams have long been a source of interest in many scientific and engineering applications. The Bernoulli-Euler theory has been generally accepted to describe small amplitude oscillations, but becomes inadequate when the large amplitudes occur.

With recent developments in the aeronautical industry, the large amplitude beam oscillations are utilized in different applications such as flapping UAVs [1, 2] and wind harvesting mechanisms [3,4,5]. The need to predict large amplitude oscillations accurately has encouraged new models to be developed and studied [6,7,8,9,10,11,12,13,14,15,16]. This exploration has led some researchers to the conclusion that the linear viscous damping model, widely used due to its simplicity, is deficient when used in nonlinear model of the beam deflection [16,17,18].

Ozcelic et al. [15] conducted a numerical and experimental study of a flapping slender beam. It was found that while good agreement was reached using viscous damping in a wide range of frequencies up to 1.3 times the first resonance frequency, this was not the case near the primary and secondary harmonic regions. In a following study, Ozcelic and Attar [17] suggested four distinct linear and nonlinear models for the damping force on an oscillation beam. The coefficients for each model were chosen empirically to minimize error near the secondary resonant peak. A damping model based on the third power velocity provided the best prediction of strain response, of the four. Anderson et al. [18] found that that including a quadratic damping model improved the agreement between their theory and experiment. In the studies in [17] and [18] a physical source for the nonlinear damping was not proposed.

In a previous study by the authors [16], a nonlinear model was suggested to describe the response of a cantilever beam to a harmonic base excitation, and compared to experiments. While good agreement between numerical and experimental results was observed, the damping coefficient calculated from experiments varied with excitation amplitude. This led the authors to suggest a nonlinear damping model based on the aerodynamic drag force acting on the beam during oscillation. The initial study showed promising agreement between experiments and the drag induced damping model. It was also found in the study that while nonlinear inertia and stiffness effects arise near the first resonance frequency, these effects are mostly mutually offsetting when combined into the full nonlinear model, leading to a small change in effective resonance frequency and amplitude.

The current study is focused on two aspects of the nonlinear model for cantilever beam oscillations. In the first section the suggested nonlinear fluid damping model is discussed. The effect of the structural (linear) damping and drag coefficient for the nonlinear fluid damping model are studied, and computational results are compared to experiments conducted during the previous study [16] for the first resonant frequency. In the second part of the study the full nonlinear model is used to simulate beam deflection near the second natural frequency of the beam. The partial nonlinearities and their effect on the complete nonlinear model are investigated, and effects that were not as readily visible near the first natural frequency are discussed.

Finally the very interesting work of Luongo et al. [19] and Lenci et al. [20] should be mentioned. In their theoretical/computational work they study the effects of various axial constraints. In the numerical examples it appears they deal with a case of beam fixed at both ends in the transverse direction, but free to move axially [19, 20]. In any event their deformations are much smaller than those considered here.

44.2 Theoretical Background

44.2.1 The Equation of Motion

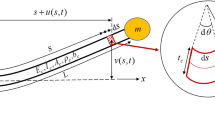
The equation of motion for an inextensible beam can be developed from the potential energy Ub and kinetic energy Tb. For a cantilever beam with a point mass at the free tip undergoing harmonic displacement at the clamped tip, the kinetic and potential energy are defined as follows:

$$ {U}_b=\frac{1}{2}{\int}_0^L EI{\left(\frac{\partial^2w}{\partial {x}^2}\right)}^2\left[1+{\left(\frac{\partial w}{\partial x}\right)}^2\right] dx\vspace*{-4pt} $$

(44.1)

$$ {T}_b=\frac{1}{2}{\int}_0^L{m}_{tot}\left[{\left(\dot{x}+{\dot{w}}_b\right)}^2+{\left(\frac{\partial w}{\partial \zeta}\frac{\partial^2w}{\partial \zeta \partial t} d\zeta \right)}^2\right] dx $$

(44.2)

where the total mass of the system is constructed of both the uniform beam mass as well as the tip mass contribution at x = L.

$$ {m}_{tot}={m}_b+{m}_{tip}\delta \left(x-L\right) $$

(44.3)

Using a Rayleigh-Ritz approach and Lagrange’s equation, and following a process described in Tang and Dowell [6] and extended in Sayag and Dowell [16], a nonlinear equation for the beam’s motion is achieved.

$$ {M}_{bi}{\ddot{q}}_i+{M}_{ti}2{\zeta \omega}_i{\dot{q}}_i+{M}_{bi}{\omega}_i^2{q}_i=-{F}_{w_b}-{F}_{BN}-{F}_{BM}-{F}_{m_{ti p}} $$

(44.4)

The terms on the left hand side of Eq. (44.4) represent the linear, unforced, unloaded part of the equation. A linear term for viscous damping is included in this equation as a simplified model of dissipation. The left hand side of the equation represents external loads as well as internal nonlinear forces acting on the beam: ${F}_{w_b}$ is a load due to the harmonic motion of the clamped base, F _BN and F _BM are the nonlinear structural and inertial forces respectively and ${F}_{m_{tip}}$ is the load generated by a point mass at the free tip of the beam. A detailed description of how these forces are calculated is presented in the appendix.

44.2.2 Damping

For a beam oscillating in any fluid medium, it is reasonable to assume that interaction of the structure with surrounding fluid will cause some energy dissipation. While this may be negligible for small amplitude oscillations, the effect could be more notable when deflections are large enough to be considered nonlinear.

In a previous study by the authors [16] this additional dissipation of energy was described as a drag force acting on the beam due to its rapid motion through the fluid medium. This force is defined by the shape and dimensions of the cross section, as well as the dynamic pressure.

$$ D={C}_D\cdot q\cdot b\cdot \mathit{\operatorname{sign}}\left(\dot{w}\right) $$

(44.5)

The generalized force for the fluid damping can therefore be computed and added to the equation of motion:

$$ {F}_{FD_i}=\frac{1}{2}{C}_D{\rho}_{air}{\dot{q}}_i^2\cdot \mathit{\operatorname{sign}}\left({\dot{q}}_i\right)b{\int}_0^L{\psi}_i^3(x) dx $$

(44.6)

This force is most significant when the oscillation frequency is close to resonance, and under this circumstance the motion of the beam can be closely described by a single mode shape. An instantaneous fluid damping coefficient can be defined by comparing the generalized force caused by drag to the viscous damping term of a single mode from Eq. (44.4), and solving for an equivalent z. The damping coefficient corresponding with the drag force is presented in Eq. (44.7). This time dependent coefficient is computed at each frequency using the dominant mode shape.

$$ {\zeta}_{FD_i}=\frac{C_D}{4}\frac{\rho_{air}{\dot{q}}_i\cdot \mathit{\operatorname{sign}}\left({\dot{q}}_i\right)}{\omega_i\rho h}\frac{\int_0^L{\psi}_i^3(x) dx}{\int_0^L{\psi}_i^2(x) dx} $$

(44.7)

44.3 Experimental System

Numerical simulations conducted for the full nonlinear model were compared with experiments conducted during a previous study. A short description of the experimental system is provided below. More information about the system can be found in Sayag and Dowell [16]. A thin aluminum beam is mounted on a BK 4809 vibration shaker. The beam is clamped to the shaker at the centerline, effectively creating two opposite cantilevered beams. This was done in order to minimize rotational instability of the shaker caused by the large amplitude oscillations of the beam. The shaker is driven by a sine signal generated by a Labview Virtual Instrument (VI), and amplified by a BK 2718 power amplifier. The frequency, w0, and amplitude, W0, of the sine signal are controlled by the VI, allowing a frequency sweep at a desired rate. The beam response was measured using three PCB 352C22 miniature piezoelectric accelerometers. The mass of each accelerometer is 0.5 g. Two accelerometers were placed at the two free beam tips, while a third was attached to the mounting system, near the base of the beam. All accelerometers were connected to a PCB 441A101 signal conditioner. A picture of the shaker, mounting system, two sided beam and three accelerometers is presented in Fig. 44.1.

Fig. 44.1

Experimental system: shaker, two sided beam and three accelerometers

All beams were made of 6061 Aluminum, which was chosen due its high yield stress to Young modulus ratio. The beam dimensions were chosen to allow for large deflections while keeping the maximal stress below the yield point. The beam dimensions are listed in Table 44.1. All numerical simulations were conducted using the same beam dimensions. The length of each cantilever beam, L, is the distance between the edge of the mounting system and the tip of the beam. The material properties of the beam are listed in Table 44.2.

Table 44.1 Beam dimensions

Table 44.2 Beam material properties

44.4 Results and Discussion

Numerical simulations were conducted for a beam with material properties and dimensions described in the experimental system. A nominal value of ζ_st = 0:006 was chosen for structural damping determined from experimental results for a low amplitude oscillation test. Since the cross section of the beam is rectangular, a drag coefficient of a flat plate facing oncoming flow was chosen as a nominal value of C_d = 2.

Numerical simulations were conducted for an increasing or decreasing frequency sweep with increments of 0.1–0.5 Hz, for each run. The amplitude of base displacement was chosen to either be a constant value for an entire numerical simulation, or a combination of specific amplitude per frequency that was observed during experiments. An example of the two possible base displacement input methods is presented in Fig. 44.2. The blue curve displays a base displacement input that does not change in amplitude as input frequency is increased. The yellow curve presents an input amplitude that depends on the instantaneous frequency. This base amplitude was measured during an experimental run. The goal of such simulations was to recreate, as accurately as possible, the oscillations observed during an experiment.

Fig. 44.2

Dimensional base displacement vs. frequency during numerical simulations

Figure 44.3 presents the calculated tip displacement amplitudes for both simulation presented in Fig. 44.2, as well as the measured tip displacement amplitude during the corresponding experiment. Although the resonance frequency measured for both tips of the experimental system is identical, this frequency varies slightly from that calculated numerically. This deviation is likely caused by a small variation in material properties reported by the manufacturer, as explained in previous work [16].

Fig. 44.3

Tip displacement amplitude vs. frequency during numerical simulations and matching experiment

The total instantaneous damping coefficient was also calculated and recorded for each step during the calculation. Figure 44.4 displays the damping coefficient for the two calculated cases described above. The structural damping coefficient in both cases was set to ζ_st = 0:006, therefore the total damping remains above that value for the entire frequency sweep. The increased tip velocity in frequencies close to resonance cause the fluid (nonlinear) component of the damping to become more prominent, and therefore increase the total instantaneous damping significantly. A more in depth discussion of the total damping is included in the next section.

Fig. 44.4

Total instantaneous damping vs. frequency during numerical simulations

44.4.1 Effect of Structural Damping and Drag Coefficient on Computational Results

A sensitivity test for the effect of structural damping and drag coefficient was performed by creating numerical simulations for the beam described above with a wide range of base displacement values. Figure 44.5 presents the maximal tip displacement observed during a numerical run, for a range of different base displacement values and drag coefficients. For this figure the structural (linear) damping was kept as the nominal value of ζ_st = 0:006. A purely linear calculation with structural damping only is also presented, for reference. For small values of base displacement (around 0.1 mm) nonlinear effects are insignificant; The structural damping is most dominant, and drag induced fluid damping is barely noticeable. This causes the tip displacement for all three cases presented here to produce very similar results to the linear case at resonance. As base amplitude increases, the velocity of the beam during deflection becomes greater, causing an increase in the fluid component of damping. The connection between base amplitude and tip amplitude for each value of C_d is well described by a second order concave function, as presented in Fig. 44.5. Base displacement was kept at an amplitude of 1 mm or less to insure that stress in the beam does not exceed yield stress, where material weakening effects (that are not represented in the model) might take place.

Fig. 44.5

Tip displacement amplitude vs. base displacement amplitude at resonance, ζ_st = 0.006, C_d = 1.5–2.5. Markers are computed results. Curves are fitted to data to show trend. Linear model computation with no fluid damping is presented for comparison

Figure 44.6 presents the peak in transfer function between tip and base amplitude for each base amplitude that was simulated. At low base amplitudes these peak values come close to the transfer function achieved by the linear model, presented here as a horizontal line, for comparison. As base displacement increases nonlinear effects become more pronounced, reduce tip amplitude, causing a reduction in peak transfer function values.

Fig. 44.6

Tip displacement to base displacement transfer function vs. base displacement amplitude at resonance, ζ_st = 0.006, C_d = 1.5–2.5. Markers are computed results. Curves are fitted to data to show trend. Linear model computation with no fluid damping is presented for comparison

Figure 44.7 presents the damping coefficient for the previously discussed cases, derived in two ways: ζ_max is the maximal instantaneous total damping coefficient for a single numerical simulation. It represents a combination of structural damping, and the instantaneous fluid damping, caused by drag. This coefficient was detected while the base was oscillated at the frequency which caused maximal tip deflection, and when the beam’s velocity was highest. By contrast, ζ_1/2p is the damping coefficient calculated using the half power method, according to the transfer function between tip and base displacement from the full numerical simulation.

Fig. 44.7

Damping coefficient vs. base displacement amplitude at resonance, ζ_st = 0.006, C_d = 1.5–2.5. ζ_1/2p is calculated using the half power method. ζ_max is maximal instantaneous combined damping (structural and fluid). Linear computation with no fluid damping is presented for comparison

It is seen that for every run presented in this plot, the damping coefficient calculated using the half power method is notably higher than the maximum damping recorded during the run. This can be explained by the variation of total damping presented in Fig. 44.4. The rapid drop in total damping surrounding the resonance frequency causes a change in the shape of the Tip-to-Base transfer function compared to a case with purely linear damping. The maximum damping is well described by a quadratic function that approaches the structural damping as base excitation goes to zero. While the half power method produced an inaccurate coefficient for the linear computation, it is easily seen that this error in ζ_1/2p is greater for the full nonlinear computation, and increases as base displacement (and total damping) increases. This affirms that the half power method is not suitable for accurately predicting damping in nonlinear systems, and particularly systems with nonlinear damping.

A sensitivity test was also performed for the structural damping ζ_st using the same range of base displacements. Figures 44.8, 44.9, and 44.10 present the tip displacement amplitude, peak transfer function value, and calculated damping coefficient vs. base displacement for a constant drag coefficient of C_d = 2:0 and a varying structural damping coefficient of ζ_st = 0.004–0.008. Results computed using the linear model are presented for all ζ_st values, where available.

Fig. 44.8

Tip displacement amplitude vs. base displacement amplitude at resonance, ζ_st = 0.004–0.008, C_d = 2.0

Fig. 44.9

Tip displacement to base displacement transfer function vs. base displacement amplitude at resonance, ζ_st = 0.004–0.008, C_d = 2:0

Fig. 44.10

Damping coefficient vs. base displacement amplitude at resonance, ζ_st = 0.004–0.008, C_d = 2.0

Tip amplitude values versus base displacement for the linear models follow a linear trend, as expected and seen in Fig. 44.7. Computations with lower structural damping produce higher tip displacement. For the nonlinear model computation, all results follow a parabolic curve. Close examination of the curves reveals that as the structural damping increases, the discrepancy between the linear and nonlinear computation decreases. For a base displacement of 0.4 mm and ζ_st = 0:004, a tip displacement of almost 69 mm is observed for the linear computation, compared to only 41 mm for the nonlinear computation. This is a reduction of about 40% in tip amplitude. Increasing the structural damping to ζ_st = 0:008 yields a linear tip displacement of 37 mm, versus 28 mm for the nonlinear case. This is a reduction of only 24%. As base displacement increases, these variations only increase in size, causing the curve with the lowest structural damping, ζ_st = 0:004, to drift further away from its linear counterpart. This is likely due to a fine balance that is achieved between the structural and fluid damping. For a large structural damping, the beam is restricted to smaller displacements and low velocity, preventing fluid damping from reaching high values and greatly affecting the results. As structural damping decreases, beam displacement and velocity increase, allowing for greater fluid damping to take place. Since fluid damping is only present in the nonlinear model, the more dominant it becomes, the greater the difference between the linear and nonlinear models.

Similarly, the transfer functions presented in Fig. 44.9 show the best agreement between linear and nonlinear computations for the highest structural damping and lowest base displacement, and an increasing difference as either base displacement increases, or structural damping decreases.

Figure 44.11 shows two types of damping coefficients, calculated coefficient using half power method, and maximal instantaneous total damping, for various levels of ζ_st. For all levels of structural damping, maximal instantaneous damping approaches the structural base value for small base displacements, as discussed previously. The inherent difference between instantaneous and calculated (half power) damping coefficient is increased as structural damping is decreased. This is due to fluid damping becoming more and more dominant, causing the nonlinearities in the system to grow, and thus decreasing the reliability of the half power method.

Fig. 44.11

Tip displacement amplitude vs. base displacement amplitude at resonance. Markers are experimental results. Shaded area represents simulations using (a) ζ_st = 0.006, C_d = 1.5–2.5 or (b) ζ_st = 0.004–0.008, C_d = 2.0

44.4.2 Comparing Experimental and Computational Results

In order to assess whether variation in structural and fluid damping can explain the results observed in the experimental system, results from the numerical study were compared to results from experimental runs performed using the system described in Sect. 44.4. In each figure a range of simulated results for a single varying parameter (C_d or ζ_st) is presented as a shaded area, while the other parameter is held at a constant value. Experimental results from both tips of the two sided system are presented as discrete points. Some variation between the two tips are observed in most plots. Some possible reasons for these variations are calibration errors of the measurement instruments, or small beam asymmetries. While special considerations were taken to prevent the beam from ever reaching the yield stress during experiments, the repeated oscillatory motion during the full set of experiments may have caused some material fatigue. No indication of deformation or change in system properties were observed in a static test performed post experiment, but these fatigue effects cannot be completely ruled out.

Maximal tip displacement, transfer function at resonance, and measured damping coefficient are all presented versus the corresponding base displacement in Figs. 44.11, 44.12, and 44.13 respectively. The general trend lines produced by the computational model and experimental results in Fig. 44.11 are similar, however a fair amount of scatter is observed in the experimental results. This scatter may reflect in part the difficulty of the measurements in determining the peak response of the tip deflection for systems with relatively low damping, as the one used here. Additionally, uncertainties in material properties, as well as structural damping coefficient and fluid drag coefficient can contribute to the differences between theory and experiment.

Fig. 44.12

Tip displacement to base displacement transfer function vs. base displacement amplitude at resonance. Markers are experimental results. Shaded area represents simulations using (a) ζ_st = 0.006, C_d = 1.5–2.5 or (b) ζ_st = 0.004–0.008, C_d = 2.0

Fig. 44.13

Damping coefficient vs. base displacement amplitude at resonance. Markers are experimental results. Shaded area represents simulations using (a) ζ_st = 0.006, C_d = 1.5–2.5 or (b) ζ_st = 0.004–0.008, C_d = 2.0

The peak transfer function presented on Fig. 44.12 does not show improved agreement between experiment and the numerical model, since the same challenge in locating the exact peak tip amplitude affects results in the same manner described above. It is noted, however, that variation in structural damping (ζ_st) increases the range of results more for low base amplitudes, while changes in fluid damping (C_d) have a larger effect on the range of results for high base amplitudes.

This is consistent with observations made according to Figs. 44.5, 44.6, 44.7, 44.8, 44.9, and 44.10. For the specific range of C_d and ζ_st tested in this work, variation in structural damping produced a much larger range of results than variation in fluid damping. This is likely due to the fact that even at large base displacement, the added damping caused by drag was only comparable to the structural damping in near resonance frequencies, as seen in Fig. 44.4.

The damping coefficient presented in Fig. 44.13 is calculated using the half power method. While this method is normally used for linear systems and is less suitable for nonlinear systems, this is currently the best method to estimate damping effects consistently on a nonlinear system from both experiments and computational simulation data. Maximal instantaneous damping is not presented since such results could not be obtained from experiments. Interestingly, agreement between the two tips, as well agreement in trend between experiments and simulations is far better for the damping coefficient than it was for tip displacement or transfer function. This may be due to damping being a global property of the system, calculated using measurements from a range of frequencies, as opposed to peak tip amplitude and transfer function, which are local spatial and temporal properties.

44.4.3 Nonlinear Effects and Hysteresis Near Second Natural Frequency

Another interesting aspect of the study was to examine how the different components of the nonlinear model affect the beams motion. As it turns out, these differences are greater for the second beam mode than the first beam mode previously studied. Figure 44.14 presents the tip deflection of the beam derived from the computer simulation using four versions of the nonlinear model: Nonlinear Damping only (NLD) – a fluid damping term is added to the linear model; Nonlinear Inertia (NLI) – the nonlinear inertia term, as well as fluid damping, are added to the linear model; Nonlinear Stiffness (NLS) – nonlinear stiffness and fluid damping terms are included in the model; Full nonlinear model (FNL) – all the above mentioned nonlinear terms are included in the model. More information about the various nonlinear terms can be found in Sect. 44.3 and in Sayag and Dowell [16]. Tip response in the vicinity of the first natural frequency, with a base displacement of 1.2 mm is presented in Fig. 44.14a, while the displacement near second resonance frequency with a base amplitude of 1.0 mm is presented in Fig. 44.14b. It is important to note that near the second resonance frequency, the stress at the root of the beam exceeds the yield stress for the type of aluminum used in the experimental study [16]. This could lead to variations in material properties that are not currently represented in the theoretical model. Since this section of the study does not include comparison to experiments, these material effects are neglected, and only the nonlinear effects mentioned above are discussed.

Fig. 44.14

Dimensional tip displacement vs. excitation frequency near first and second resonance frequencies: partial and full nonlinear models. (a) ω₁, A₀ = 1.2 mm; (b) ω₂, A₀ = 1.0 mm

It is seen in Fig. 44.14a that the nonlinear inertia term and nonlinear stiffness term each have a small and opposite effect on the maximum response amplitude and frequency. When the two terms are combined into the full nonlinear model, the effect on both amplitude and frequency is reduced significantly, leading to a tip displacement very similar to the one achieved from linear computation with fluid damping added. Increasing base displacement further might emphasize the slight differences between the models, however this will certainly effect material properties in the experimental model and perhaps lead to failure in the structure.

Near the second resonance frequency, presented in Fig. 44.14b, a slightly lower base amplitude was used. The dimensional tip displacement amplitude is greatly reduced compared to the first resonance frequency, due to both the excitation amplitude and the shape of the dominant mode. Each nonlinear term effects the beams motion in a very similar manner to that observed near the first mode, but the effect is greatly magnified. For example: The NLI model produces a tip amplitude extremum that is about half of the NLD amplitude, at a frequency 98.5 Hz, which is 5.5 Hz below the peak observed using the NLD model. Near the first resonance frequency, the reduction in peak amplitude was about 2.5%, with a frequency variation of about 0.5 Hz. Recall that near the first resonant frequency the total nonlinear effect on the resonant frequency was modest because of the offsetting effects of nonlinear stiffness and inertia. By contrast the total nonlinear effects near the second resonant frequency are more evident because the nonlinear inertia effect is dominant and the nonlinear stiffness effect is less prominent. It is seen in Fig. 44.14b that the FNL computation greatly resembles the results using the NLI model. This indicates that for this range of frequencies, and perhaps higher frequencies as well, the nonlinear inertia has a greater effect on the motion of the beam than nonlinear stiffness.

The tip displacement for the FNL model for both increasing and decreasing frequency sweep is presented in Fig. 44.15. Near the first resonant frequency, presented in Fig. 44.15a, there is no significant difference between the two computations. This is consistent with the previous statements that nonlinear inertia and stiffness effects are mutually canceling in this range of frequencies, therefore no hysteresis is observed. Near the second resonant frequency, presented in Fig. 44.15b, the FNL model, which had proved to be greatly affected by the various nonlinear terms, produced a significant variation in peak amplitude and frequency depending on whether the sweep frequency was increasing or decreasing.

Fig. 44.15

Dimensional tip displacement vs. excitation frequency near first and second resonance frequencies: full nonlinear model, increasing and decreasing frequency sweep. (a) ω₁, A₀ = 1.2 mm; (b) ω₂, A₀ = 1.0 mm

44.5 Summary and Conclusions

It has been widely appreciated that a cantilevered beam has very distinct and different nonlinearities from that of a beam clamped (or at least fixed) at both ends. In the latter case the dominant nonlinearity arises from the tension created by the axial extension induced by the bending of the beam. However for a cantilevered (or free-free) beam the beam is virtually inextensible and indeed a theory based upon the assumption of inextensibility provides a very good model for such a beam. However the deflection that gives rise to the nonlinearity is on the order of the beam length for a cantilevered beam, while by contrast the nonlinearity of a beam clamped at both ends is evident when deflections are only on the order of the beam thickness.

Because the deflections are much larger for a cantilevered beam when nonlinearities come into play the mathematical model is necessarily different and the physical effects are as well. For cantilevered beams stiffness and inertial nonlinearities are both important and indeed their two effects near the first resonance frequency are offsetting to a substantial degree so that the frequency at peak response is relatively little changed from the value predicted by linear theory. However the amplitude of the peak response is modestly changed and perhaps unexpectedly recent work shows that nonlinear damping (which is likely due to fluid drag forces) may be important as well. So the cantilevered beam may exhibit nonlinear damping, inertia and stiffness.

In the present paper several themes are addressed building on the earlier work of Sayag and Dowell [16] and others. All three nonlinear effects are included in the mathematical model and a systematic comparison with the results of earlier experiments [16] is made. Both the mathematical model and the physical experiments show similar trends and quantitative agreement is fair to good. Indeed with the results of this systematic correlation study between theory and experiment in hand, several possible sources of scatter or uncertainty in the experimental data have been identified. These include the modeling of structural and fluid damping with the former being hard to control in an experiment. Ideally the experiments would be repeated in a vacuum chamber which of course makes the experiment more difficult and will require a more elaborate experimental apparatus.

Also in this study the second resonant mode has been studied as well as the first resonant mode. While inertia effects and stiffness effects are substantially offsetting for the first resonant mode, the nonlinear inertia effect is more dominant than the nonlinear stiffness effect for the second resonant mode. It is hypothesized that this will also be true for yet higher resonant modes. This is worthy of further study. Of course it takes higher force levels to bring the higher resonant modes into the nonlinear range.

It likely is significant that the global nonlinear properties of the beam response measured experimentally, i.e. natural frequency and damping as a function of base excitation, show less variation among the experimental measurements and are in better agreement with the theory computational model than the local nonlinear property i.e. tip deflection as a function of base deflection.

There are other possible directions for future work and there is not space here to mention them all. But two are offered as being particularly attractive from both a conceptual and application point of view. One would to be study a free-free beam and the other would be to study a plate rather than a beam. For initial work on these topics see the paper by McHugh and Dowell [7].

Nonlinear Terms of the Computational Model

The internal nonlinear loads and external forces acting on the beam during large amplitude oscillations are presented below. More information about these terms can be found at Tang and Dowell [6] and Sayag and Dowell [16].

$\displaystyle {F}_{w_b}=\left[{m}_b{\int}_0^L{\psi}_i dx+{m}_{tip}{\psi}_0(L)\right]{\ddot{w}}_b\vspace*{2pt}$

$\displaystyle {F}_{BN}=\sum \limits_j\sum \limits_k\sum \limits_lP{4}_{ijkl}\left({q}_j{q}_k{q}_l\right)$

$\displaystyle {F}_{BM}=\sum \limits_j\sum \limits_k\sum \limits_l\left[M{4}_{ijkl}+{m}_{tip}{N}_{ijkl}(L)\right]\left({q}_j{\dot{q}}_k{\dot{q}}_l+{q}_j{q}_k{\ddot{q}}_l\right)$

$\displaystyle {F}_{m_{tip}}={m}_{tip}{\psi}_i(L)\sum \limits_j{\psi}_j(L){\ddot{q}}_j$

Here Mbi is the generalized mass of the beam only, while Mti also includes the tip mass. The following definitions are used:

$\displaystyle {m}_{bi}={\int}_0^L{\psi_i}^2 dx$

$\displaystyle {m}_{ti}={m}_{bi}+{m}_{ti p}{\psi}_i(L)$

$\displaystyle {N}_{ijkl}={\int}_0^x{\psi}_i^{\prime }{\psi}_j^{\prime } d\zeta {\int}_0^x{\psi}_k^{\prime }{\psi}_l^{\prime } d\zeta$

$\displaystyle {M}_{ijkl}={\int}_0^L{m}_b{N}_{ijkl} d x$

$\displaystyle P{4}_{ijkl}=\int EI\left({\psi}_i^{{\prime\prime} }{\psi}_j^{{\prime\prime} }{\psi}_k^{\prime }{\psi}_k^{\prime }+{\psi}_i^{\prime }{\psi}_j^{\prime }{\psi}_k^{\prime}\psi \right) dx$