1 Introduction

Turing instability was proposed by Turing [24] in 1952; it is the phenomenon that initially stable steady state of a dynamical system can become unstable if we additionally consider diffusion in the system. This is surprising and unexpected phenomenon because diffusion usually makes things more smooth and uniform. Loss of stability due to diffusion is called Turing instability. Since the seminal paper of Turing [21], more and more attention is paid on the theoretical models to explain self-organized pattern formation in many different areas of physics, chemistry, biology, geology, and so on, especially biology. Recently, the entrainment and modulation of time-evolutional patterns are investigated numerically in one dimension [26]. Lee and Cho [15] find that the shape and type of Turing patterns depend on dynamical parameters and external periodic forcing. Moreover, Pena and Perez [18] show that slightly squeezed hexagons are locally stable in a full range of distortion angles. The domain coarsening process is strongly affected by the spatial separation among groups created by the Turing pattern formation process [19]. And the robustness problem is also investigated in [11, 17]. The dynamics of spontaneous pattern formation was first introduced to biology by Turing. Several groups have proposed possible candidates generating patterns [4, 10].

In the reaction–diffusion system, diffusion can induce the instability of a uniform equilibrium which is stable with respect to a constant perturbation, as shown by Turing in 1950s. The equilibrium of the nonlinear system is asymptotically stable in the absence of diffusion but unstable in the presence of diffusion [6]. Spatial patterns in reaction–diffusion systems have attracted the interest of experimentalists and theorists during the last decades. Until now, however, there has been no general analysis of the possible role of cross-diffusion in dissipative pattern formation [33]. Shi [20] show that cross-diffusion can destabilize a uniform equilibrium which is stable for the kinetic and self-diffusion reaction systems. On the other hand, cross-diffusion can also stabilize a uniform equilibrium which is stable for the kinetic system but unstable for the self-diffusion reaction system [11, 20]. Cross-diffusion which can lead to Turing pattern formation in biological systems has been reported [3, 9]. The effects of cross-diffusion on pattern formation in reaction–diffusion systems have been discussed in many theoretical papers in which the gradient in the concentration of one species lead to the diffusion in other species [25]. Other two relevant examples are on chemotaxis in E. coli bacteria [8, 25], a phenomenon where cells direct their motion toward or away from higher concentrations of other chemical species.

The above results in the turing instability were focused on the chemistry, ecology, and seldom on gene network. However, synthetic gene network and its dynamics were more and more concerned [27–31, 35–37], and we know that diffusion process is ubiquitous when the gene information was transported from cytoplasm to cell nucleus. In the following, we will investigate the character of diffusion process involving cancer network regulated by microRNA (mir-17–92). MicroRNAs (miRNAs) are an abundant class of small non-coding RNA that functions to regulate the activity and stability of specific mRNA targets through posttranscriptional regulatory mechanism and play a role of repressing translation of mRNA or degrading mRNAs [1, 2, 12, 21]. Recent studies show that miRNAs play a central role in many biological (cellular) processes, including developmental timing, cell proliferation, apoptosis, metabolism, cell differentiation, somitogenesis, and tumor genesis [2]. The induction of specific E2F activities is an essential component in the Myc pathways that control cell proliferation and cell fate decisions [7, 16, 32]. In normal cells, E2F-1 exhibits key negative feedback regulation on c-Myc-induced TERT expression, which is critical to control the transmission of c-Myc-mediated oncogenic signals [14, 22, 34]. The protooncogene Pim-1 is a part of the network that regulates transcription of the human miR-17–92 cluster [5, 23].

In recent years, many scientists deemed that mathematical modeling could be used to investigate the differences at the dynamical level between healthy and pathologic configurations of biological pathways [13]. Using the mathematical model, the researchers can detect the key points regulating main properties of biological system and find the methods to solve the different diseases. In order to understand further the miR-17–92 network involving in Myc and E2F, we also make use the mathematical model to investigate above biological network involving miR-17–92 and look further into the turing instability induced by cross-diffusion, and then understand how the turing pattern inside cells provides the checkpoint that combines mechanical and biochemical information to trigger events during the cell division process.

The paper is organized as follow. In Sect. 2, we give the gene network represented by mathematical model. In Sect. 3, we analyze the stability of pattern formation and selection. In Sect. 4, we show the numerical analysis of the network. Finally, we summarize our results.

2 The model

In this section, we consider a cancer network, where the reaction kinetics describes the interaction between microRNA and protein model. As we all know that molecular diffusion is ubiquitous when molecules interaction or pass though the cytomembrane, we should consider the effect of diffusion on the network. In this paper, we modified the system (1) and (2) given by Aguda et al. [1] and add the diffusion term to the system, obtain the reaction–diffusion system as follows:

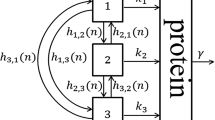
$$\begin{aligned} \frac{\partial {u}}{\partial {t}}-\mathrm{{div}}(\mathcal {D}\nabla u)=G(u), \end{aligned}$$

where \(u\) is a vector \(u_{i}(x, t), i = 1, 2\) of species densities, in which \(u_1\) represents transcription factor \(p\) in Fig. 1c and \(u_2\) represents microRNA in Fig. 1c; \(D\) is a \(2\times 2\) matrix of the diffusion coefficients, where the diagonal element is called the self-diffusion coefficient and the non-diagonals are called cross-diffusion coefficients; and \(G\) is the reaction term indicating the interaction between the involved species. The nonlinear diffusion coefficients matrix of our model as follows:

$$\begin{aligned} \mathcal {D}= \left( \begin{array}{cccc} d_{1} &{} 0\\ d_{2}d_{3}u_{2} &{}\quad d_{2}+d_{2}d_{3}u_{1} \end{array}\right) . \end{aligned}$$

And the interaction contribution is included in the reaction term \(G\). Specifically, the underlying model consists as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial ^{}u_{1}}{\partial t^{}}-d_{1}\triangle u_{1}\!=\!\alpha \!+\!\frac{k_{1}u_{1}^{2}}{a\!+\!u_{1}^{2}+bu_{2}}-\delta u_{1}, \quad (x,t)\in \Omega _{T}\\ \frac{\partial ^{}u_{2}}{\partial t^{}}-d_{2}\triangle (u_{2}+d_{3}u_{1}u_{2})=\beta +k_{2}u_{1}-\gamma u_{2}, \\ \quad (x,t)\in \Omega _{T}\\ \frac{\partial ^{}u_{1}}{\partial \eta ^{}}=\frac{\partial ^{}u_{2}}{\partial \eta ^{}}=0, \quad (x,t)\in \Sigma _{T}\\ u_{1}(x,0)=\psi _{1}(x),u_{2}(x,0)=\psi _{2}(x),\quad x\in \Omega \end{array} \right. \end{aligned}$$
(2.1)

where \(\Omega _{T}=\Omega \times (0,T),\Sigma _{T}=\partial \Sigma \times (0,T)\) for a fixed \(T>0\). In biological terms, the homogeneous Neumann boundary condition indicates that there is no population flux across the boundary. Here, the presence of \(u_{2}\) in the denominator accounting for the miR-dependent down-regulation of protein expression is determined by the term (\(a+bu_{2}\)) in the denominator. The value of the parameter \(b\) is a measure of the efficiency of miRNA inhibition of protein expression, and lumps all factors that could affect the binding of the members of the miR-17–92 cluster to their targets and the inhibition of protein translation. The constant term \(\alpha \) stands for constitutive protein expression due to signal transduction pathways stimulated by growth factors present in the extracellular medium. The parameter \(\alpha \), therefore, corresponds to an experimentally controllable conditions such as the concentration of nutrients in the cell culture medium. \(\delta \) is the rate of the protein degradation. The constant term \(\beta \) represents p-independent constitutive transcription of \(m\). And the last term is a degradation term with rate coefficient \(\gamma \). The presence of the nonlinear diffusion term means basically that the disperse direction of \(u_{2}\) not only contains the self-diffusion (in which way the species move from a region of high density to a region of low density), but also contains cross-diffusion. More specifically, species \(u_{2}\) diffuses with a flux

$$\begin{aligned} \mathbf J&= -\nabla (d_{2}u_{2}+d_{2}d_{3}u_{1}u_{2})\\ {}&= -d_{2}d_{3}u_{2}\nabla u_{1}-(d_{2}+d_{2}d_{3}u_{1})\nabla u_{2}. \end{aligned}$$

Notice that, as \(-d_{2}d_{3}u_{2}<0\), the part \(-d_{2}d_{3}u_{2}\nabla u_{2}\) of the corresponding flux is directed toward the decreasing population density of the species \(u_{1}\).

Fig. 1
figure 1

a A cancer network. This network is part of the mammalian G1-S regulatory network involving miR-17–92, arrowhead represents the activation, hammerhead represents the inhibition, b first stage in the reduction of the model, c the final network model that abstracts the essential structure of the network in a, \(p\) presents the transcription factor (Myc and E2F), \(m\) represents microRNA (miR-17–92) cluster

Full size image

3 Cross-diffusion-driven spatial patterns

In this section, we derive some sufficient conditions for spatial patterns. In particular, we not only show that the patterns formation without cross-diffusion, but also the formation of spatial patterns with cross-diffusion.

3.1 Linear stability analysis

We assume that the system (3.1) is true.

$$\begin{aligned} \left. \begin{array}{l} A-\delta <\gamma \\ 4d_{1}d_{2}k_{2}B>(d_{2}(A-\delta )+d_{1} \gamma )^{2}, \end{array} \right. \end{aligned}$$
(3.1)

where

$$\begin{aligned} A=\frac{2ak_{1}u^{*}_{1}+2bk_{1}u^{*}_{1}u^{*}_{2}}{(a+u^{*2}_{1}+bu^{*}_{2})^{2}}, B=\frac{bk_{1}u^{*2}_{1}}{(2au^{*}_{1}+2bu^{*}_{2})^{2}}. \end{aligned}$$

And we can know from [1] that there is a unique positive equilibrium point to system (2.1), denoted by \(u^{*}=(u^{*}_{1}, u^{*}_{2})\).

In order to study the locally asymptotic stability of the system (2.1), we give the notation as follows.

Notation 3.1

Let \(0=\mu _{1}<\mu _{2}<\cdots \rightarrow \infty \) be the eigenvalues of \(-\triangle \) on \(\Omega \) under no-flux boundary conditions,and \(E(\mu _{i})\) be the space of eigenfunctions corresponding to \(\mu _{i}\). We define the space decomposition as follows:

  1. (i)

    \(\mathbf{X}_{ij}\,{:=}\,\{\mathbf{c}\cdot \phi _{ij}:\mathbf{c}\in R^{2}\}\), where \({\phi _{ij}}\) is an orthonormal basis of \(E(\mu _{i})\) for \(j=1,\ldots , \mathrm{{dim}} E(\mu _{i})\).

  2. (ii)

    \(\mathbf{X}\,{:=}\,\{\mathbf{u} \in [C^1(\overline{\Omega })]^{2}:\frac{\partial u_{1}}{\partial \eta }=\frac{\partial u_{2}}{\partial \eta }=0\) on \(\partial \Omega \}\), and thus \( \mathbf X =\oplus ^{\infty }_{i=1}\mathbf X _{i}\), where \(\mathbf X _{i}=\oplus ^{\mathrm{{dim}}E(\mu _{i})}_{j=1}\mathbf X _{ij}\).

Theorem 3.1

The positive equilibrium point \(u^{*}\) of (2.1) without cross-diffusion is locally asymptotically stable when (3.1) is true.

Proof

First, for the sake of simplicity, we will denote in this paper

$$\begin{aligned} G(u)= \left( {\begin{array}{cc} G_{1}(u) \\ G_{1}(u) \\ \end{array}} \right) = \left( {\begin{array}{cc} \alpha +\frac{k_{1}u_{1}^{2}}{a+u_{1}^{2}+bu_{2}}-\delta u_{1} \\ \beta +k_{2}u_{1}-\gamma u_{2}. \\ \end{array}} \right) \end{aligned}$$

The linearization of (2.1) around the state \(u^{*}\) can be expressed by

$$\begin{aligned} u_{t}=(D\Delta +G_{u}(u^{*}))u, \end{aligned}$$

where \(D=\mathrm{{diag}}(d_{1}, d_{2})\), \(u=(u_{1}, u_{2})\) and

$$\begin{aligned} G_{u}(u^{*})&= \left( {\begin{array}{c@{\quad }c} G_{u_{11}} &{} G_{u_{12}} \\ G_{u_{21}} &{} G_{u_{22}}\\ \end{array}} \right) \\&= \left( {\begin{array}{cc} \frac{2ak_{1}u^{*}_{1}+2bk_{1}u^{*}_{1}u^{*}_{2}}{(a+u^{*2}_{1}+bu^{*2}_{2})^{2}}-\delta &{} \quad \frac{-bk_{1}u^{*2}_{1}}{(a+u^{*2}_{1}+b*u^{*}_{2})^{2}}\\ k_{2} &{} -\gamma \\ \end{array}} \right) . \end{aligned}$$

According to Notation 3.1, the space \(\mathbf X _{i}\) is invariant under the operator \(D\Delta +G_{u}(u^{*})\), and \(\lambda \) is an eigenvalue of this operator on \(\mathbf X _{i}\), if and only if it is an eigenvalue of the matrix \(-\mu _{i}D+G_{u}(u^{*})\). The characteristic polynomial of \(-\mu _{i}D+G_{u}(u^{*})\) is given by

$$\begin{aligned} \psi _{i}(\lambda )=\lambda ^{2}-B_{i} \lambda +C_{i}, \end{aligned}$$

where

$$\begin{aligned} B_{i}&= A-\gamma -k^{2}(d_{1}+d_{2}),\\ C_{i}&= -\gamma A+k_{2}B-\frac{(Ad_{2}-d_{1}\gamma )^{2}}{4d_{1}d_{2}}\\&\quad +\, d_{1}d_{2}(\mu _{i}-\frac{Ad_{2}-d_{1}\gamma }{2d_{1}d_{2}})^{2}. \end{aligned}$$

Recalling condition (3.1), it is easy to verify that \(B_{i}\) and \(-C_{i}\) are negative. Thus, for each \(i\ge 1\), the two roots \(\lambda _{i,1}\) and \(\lambda _{i,2}\) of \(\psi _{i}(\lambda )=0\) have negative real parts, and this completes the proof.

Theorem 3.2

Assume that the system (3.1) holds. If \(\mu _{2}<\widetilde{\mu }\), then there exists a positive constant \(d^{*}_{3}\) such that the equilibrium point \(u^{*}\) of (2.1) is unstable provided that \(d_{2}>d^{*}_{3}\), where \(\mu _{2}\) is given in Notation 3.1 and \(\widetilde{\mu }\) will be given in (3.2).

Proof

For simplicity, we denote \(\Phi (u)=(d_{1}u_{1},d_{2}(u_{2}+d_{3}u_{1}u_{2}))^T\). Linearizing (2.1) around the state \(u^{*}\) yields

$$\begin{aligned} u_{t}=(\Phi _{u}\Delta +G_{u}(u^{*}))u, \end{aligned}$$

where

$$\begin{aligned} \Phi _{u}(u^{*})\!=\! \left( {\begin{array}{c@{\quad }c} \Phi _{u_{11}} &{} \Phi _{u_{12}} \\ \Phi _{u_{21}} &{} \Phi _{u_{22}}\\ \end{array}} \right) \!=\! \left( {\begin{array}{c@{\quad }c} d_{1} &{} 0\\ d_{2}d_{3}u^{*}_{2} \!&{}\! d_{2}+d_{2}d_{3}u^{*}_{1}\\ \end{array}} \right) . \end{aligned}$$

We can obtain that the characteristic polynomial of \(-\mu _{i}\Phi _{u}+G_{u}(u^{*})\) is

$$\begin{aligned} \psi _{i}(\lambda )=\lambda ^{2}-D_{i}\lambda +E_{i}, \end{aligned}$$

where

$$\begin{aligned} D_{i}&= A-\delta -\gamma -(d_{1}+d_{2}+d_{2}d_{3}u^{*}_{1})\mu _{i}\\ E_{i}&= -\gamma (A-\delta )+Bk_{2}-Bd_{2}d_{3}u^{*}_{2}\mu _{i}\\&-\,[(A-\delta )(d_{2}+d_{2}d_{3}u^{*}_{1})-d_{1}\gamma ]\mu _{i}\\&+\,d_{1}(d_{2}+d_{2}d_{3}u^{*}_{1})\mu ^{2}_{i}. \end{aligned}$$

We denote \(\lambda _{1}(\mu _{i})\) and \(\lambda _{2}(\mu _{i})\) be the roots of \(\psi _{i}(\lambda )=0\), and then have

$$\begin{aligned} \lambda _{1}(\mu _{i})+\lambda _{2}(\mu _{i})=D_{i}\quad \hbox {and} \quad \lambda _{1}(\mu _{i})\lambda _{2}(\mu _{i})=E_{i}. \end{aligned}$$

In order to get that \(Re\lambda _{1}(\mu _{i})<0\) and \(Re\lambda _{2}(\mu _{i})>0\), a sufficient condition is \(E_{i}<0\) (based on the fact that \(D_{i}<0\)).

In the following, we look for conditions that make \(E_{i}<0\) hold. First, since \(E_{i}=\mathrm{{det}}(\mu _{i}\Phi _{u}-G_{u}(u^{*}))\), it is easy to deduce that

$$\begin{aligned} F_{i}=Q_{2}\mu ^{2}_{i}+Q_{1}\mu _{i}+\mathrm{{det}}(G_{u}), \end{aligned}$$

where

$$\begin{aligned}&Q_{1}=-Bd_{2}d_{3u^{*}_{2}-(A_\delta )(d_{2}+d_{2}d_{3}u^{*}_{1})}+d_{1}\gamma \\&Q_{2}=d_{1}d_{2}+d_{1}d_{2}d_{3}u^{*}_{1}\\&\mathrm{{det}}(G_{u})=-\gamma (A-\delta )+Bk_{2} \end{aligned}$$

We denote \(Q(\mu )=Q_{2}\mu ^{2}_{i}+Q_{1}\mu _{i}+\mathrm{{det}}(G_{u})\), and \(\widetilde{\mu _{1}}\) and \(\widetilde{\mu _{2}}\) be the roots of \(Q(\mu )=0\) with \(Re(\widetilde{\mu _{1}})<Re(\widetilde{\mu _{2}})\). Condition (3.1) implies that

$$\begin{aligned} \widetilde{\mu _{1}}+\widetilde{\mu _{2}}=-\frac{Q_{1}}{Q_{2}}\quad \hbox {and}\quad \widetilde{\mu _{1}}\widetilde{\mu _{2}}=\frac{\mathrm{{det}}(G_{u})}{Q_{2}}>0. \end{aligned}$$

Furthermore,we have

$$\begin{aligned}&\lim _{d_{3}\rightarrow \infty }\frac{Q_{2}}{d_{3}}=d_{1}d_{2}u^{*}_{1}\\&\lim _{d_{3}\rightarrow \infty }\frac{Q_{1}}{d_{3}}=-Bd_{2}u^{*}_{2}-(A-\delta )d_{2}u^{*}_{1}\\&\lim _{d_{3}\rightarrow \infty }\frac{Q}{d_{3}}=-Bd_{2}u^{*}_{1}\mu _{i}-Ad_{2}u^{*}_{1}\mu _{i}+d_{1}d_{2}u^{*}_{1}\mu ^{2}_{i}. \end{aligned}$$

We see that \(\lim _{d_{3}\rightarrow \infty }\frac{Q}{d_{3}}=0\) has two real roots, one being zero and the other being positive. A continuity argument allows us to show that \(\widetilde{\mu _{1}}\) and \(\widetilde{\mu _{2}}\) are real and positive when \(d_{3}\) is large enough, and in addition

$$\begin{aligned}&\lim _{d_{3}\rightarrow \infty }\widetilde{\mu _{1}}=0,\nonumber \\&\lim _{d_{3}\rightarrow \infty }\widetilde{\mu _{2}}=\frac{u^{*}_{1}+(A-\delta )u^{*}_{1}+Bd_{2}u^{*}_{2}}{d_{1}u^{*}_{1}}=\widetilde{\mu } \end{aligned}$$
(3.2)

Hence, there exists a positive number \(d^{*}_{3}\) such that the inequalities \(\widetilde{\mu }<\mu _{2}\) when \(d_{3}>d^{*}_{3}\), and \(Q(\mu )<0\) when \(\mu \in (0,\widetilde{\mu })\), are valid. Since \(0<\mu _{2}<\widetilde{\mu }\), then \(u_{2}\in (\widetilde{u_{1}}, \widetilde{u_{2}})\). It follows that \(Q(\mu )<0\), which finally implies that \(E_{i}<0\), which completes the proof.

The above theorems reveal that the cross-diffusion effect is able to destabilize the positive equilibrium point, and thereby the solution results in spatial patterns.

3.2 Turing parameter space

In view of Theorem 3.2, the fulfillment of the following conditions is sufficient for the positive equilibrium point \(u^{*}\) being linearly unstable with respect to the particular case of system (2.1):

  1. (i)

    \(A-\delta <\gamma \) and \(4d_{1}d_{2}k_{2}B>(d_{2}(A-\delta )+d_{1} \gamma )^{2}\).

  2. (ii)

    \(\mu _{2}<\frac{u^{*}_{1}+(A-\delta )() u^{*}_{1}+Bd_{2}u^{*}_{2}}{d_{1}u^{*}_{1}}\).

In this paper, the values satisfying the parameter spaces are taken as (3.3)

$$\begin{aligned} \left. \begin{array}{ll} \alpha =\frac{1}{2},\quad \beta =1,\quad a=1,\quad b=1,\quad \gamma =1,\\ k_{1}=1,\quad k_{2}=1,\quad d_{1}=1, \quad d_{2}=1. \end{array} \right. \end{aligned}$$
(3.3)

For this particular choice, the positive stationary uniform solution is given by

$$\begin{aligned} \left. \begin{array}{l} (u^{*}_{1},u^{*}_{2})=(0.6316,1.6316). \end{array} \right. \end{aligned}$$
(3.4)

In Fig. 2, we depict the parameter spaces where instabilities are expected to appear according to conditions (i) and (ii) above. These graphics are obtained by fixing all parameters in (3.3) except for \(a\) and \(b\) (Fig. 2a), \(\gamma \) and \(k_{1}\) (Fig. 2b).

Fig. 2
figure 2

Turing parameter spaces for model (2.1). In the A domain, the solutions remain stable, while in the B, C, D domain, instabilities are expected to appear

Full size image

If no diffusion is considered, then the system (2.1) boils down to the dynamical system

$$\begin{aligned} \frac{\mathrm{{d}}u}{\mathrm{{d}}t}=G(u), \end{aligned}$$

whose phase diagram is presented in Fig. 3a. We show trajectories for different initial values of \(u_{1,0}\) and \(u_{2,0}\) in which the trajectories converge to the equilibrium state (3.4), shown by the intersection of the (nontrivial) nullclines

$$\begin{aligned} \alpha +\frac{k_{1}u_{1}^{2}}{a+u^{2}_{1}+bu_{2}}-\delta u_{1}&= 0\\ \beta +k_{2}u_{1}-\gamma u_{2}&= 0. \end{aligned}$$

We are able to calculate the wavenumber explicitly and determine the pattern selection by linearizing cross-diffusion around the stationary uniform solution and taking \(d_{3}\) as the Turing bifurcation parameter. From the mathematical viewpoint, the Turing bifurcation occurs when \(Im(\lambda _{k})= 0\), \(Re(\lambda _{k})=0\) at \( k\not \equiv 0\), where \(k_{c}\) is the critical wavenumber and \(|k|^{2}\) is equivalent to the eigenvalue \(\mu _{i}\) in Notation 3.1.

Fig. 3
figure 3

a Phase plane for model (2.1). Four trajectories are represented, starting from the initial states \(A,B,C,D\) and reaching the intersection of the nullclines, b plot of the largest of the eigenvalues \(Re(\lambda )\), there is a range of wave numbers which are linearly unstable

Full size image

Now, replacing \(\mu _{i}\) with \(|k|^{2}\), the problem can obtain from the linearization of (2.1) around \(u^{*}\) as follows:

$$\begin{aligned} u_{t}=(G_{u}(U^{*})-|k|^{2}\Phi _{u})u. \end{aligned}$$

And the characteristic equation is as follows:

$$\begin{aligned} \det (G_{u}(U^{*})-|k|^{2}\Phi _{u}-\lambda E)=0. \end{aligned}$$

In order to find out the critical wavenumber, we only need to confirm that

$$\begin{aligned} \mathrm{{min}}_{k^{2}} \det (G_{u}(U^{*})-|k|^{2}\Phi _{u})=0, \end{aligned}$$

which is a quadratic polynomial of \(|k|^{2}\). In this way, the Turing bifurcation threshold is given by \( d^{c}_{3}\) which satisfies the following equation:

$$\begin{aligned} 4\det (G_{u}(u^{*}))\mathrm{{det}}(\Phi _{u})&= (G_{u_{11}}\Phi _{u_{22}} +G_{u_{22}}\Phi _{u_{11}}\\&\quad -G_{u_{12}}\Phi _{u_{21}}-G_{u_{21}}\Phi _{u_{12}})^{2}, \end{aligned}$$

and the critical wavenumber \(k_c\) is given by

$$\begin{aligned} k_{c}\!=\!\sqrt{\frac{G_{u_{11}}\Phi _{u_{22}}\!+\!G_{u_{22}}\!\Phi _{u_{11}}\!-\!G_{u_{12}}\!\Phi _{u_{21}}\!-\!G_{u_{21}}\!\Phi _{u_{12}}}{2\det (\Phi _{u})}}. \end{aligned}$$

4 Numerical analysis

In this section, we will demonstrate Turing pattern according to the previous theoretical results. First, we introduce our numerical scheme using finite difference method. In this paper, we consider zero-flux boundary conditions with region defined as square region \([0, L] \times [0, L] \in \mathfrak {R}^{2}\), then discretize the space and time, in which the square space is divided as \(M\times N\) lattice sites domain with the \(h\) length of lattices, and time step is set as constant \(\tau \). The system (2.1) is performed using the standard five-point approximation for the spatial derivative and an explicit Euler method for the time integration. In this paper, we set \(h=1,\ \tau =0.02\), and select coefficients of self-diffusion \((d_{1},d_{2})=(1,1)\), each frame is \(100\times 100\) space units, we choose parameters \((a,b)=(1,1)\), \((k_{1},k_{2},\alpha ,\beta )=(0.5,1,1,1)\). For our first test, we simulate the section of different patterns depending on the value of the cross-diffusion coefficient \(d_{3}\), and the initial data are taken as a uniformly distributed random perturbation. More precisely, we choose

$$\begin{aligned} u_{1}(x,0)=u^{*}_{1}+\eta _{1},u_{2}(x,0)=u^{*}_{2}+\eta _{2}, \end{aligned}$$

where \(\eta _{1}\in [0,1],\eta _{2}\in [0,1]\).

First, we simulate the section of different patterns based on the the value of cross-diffusion coefficient \(d_{3}\), and depict the real part of the eigenvalues \(Re(\lambda )\) in correspondence with the norm of the wave vector in Fig. 3b. In Fig. 4, we choose the parameter \(d_{3}\) as \(d_{3}=0\), and changed it to \(d_{3}=17, d_{3}=18, d_{3}=19, d_{3}=19.5\) for Figs. 5, 6, 7, and 8, respectively. In addition, we can know that the initial value paly an important role in the selection of patterns and that the modes of the pattern convert from the stripes to the spots as the cross-diffusion coefficient \(d_{3}\) increases. Finally, we also find that the appearance of spots’ pattern will be delayed (\(d_{3}\) will be larger when the spots pattern appear)when the coefficient \(d_{1}\) increases in the simulation, and the delay value is in proportion to \(d_{1}\). From above Figs. 4, 5, 6, 7 and 8, the patterns of protein concentration evolve from stripe to spot pattern, and the spots pattern shows the Stationary localized pulse (dissipative soliton) which corresponds periodical traveling wave. These patterns are starting from a spatially uniform state which turing proved that stable inhomogeneities in “morphogen” concentration could emerge through a diffusion-driven symmetry-breaking instability.

Fig. 4
figure 4

The patterns of species \(u_{1},u_{2}\) at \(d_{3}=0\)

Full size image
Fig. 5
figure 5

The patterns of species \(u_{1},u_{2}\) at \(d_{3}=17\)

Full size image
Fig. 6
figure 6

The patterns of species \(u_{1},u_{2}\) at \(d_{3}=18\)

Full size image
Fig. 7
figure 7

The patterns of species \(u_{1},u_{2}\) at \(d_{3}=19\)

Full size image
Fig. 8
figure 8

The patterns of species \(u_{1},u_{2}\) at \(d_{3}=19.5\)

Full size image

5 Conclusion

In this paper, we have developed a cancer network regulated by microRNA with cross-diffusion and analyze the spatiotemporal dynamics of the cancer network with diffusion under the zero-flux boundary conditions. It is found that the steady state of the system can be globally asymptotically stable under some condition, and Turing patterns can be formed under other conditions. Importantly, we have shown that cross-diffusion can lead to the Turing pattern formation and influence on the distribution of protein and miRNA; obviously, the cross-diffusion is one of drivers which drive the turing pattern in biological system. We also find that the appearance of spots pattern will be delayed (\(d_{3}\) will be larger when the spots pattern appear) when the coefficient \(d_{1}\) increases in the simulation, and the delay value is in proportion to \(d_{1}\). As we know that the formation of Turing patterns in biochemical pathway could then be related to organizing centers in eukaryotic cells playing a role during cell division, and the Turing pattern inside cells could provide a checkpoint that combine mechanical and biochemical information to trigger events during the cell division process, in addition, the cancer is uncheck cell growth, and the unregulated checkpoint can induce to cancer.