Spatial pattern formation in reaction–diffusion models: a computational approach

Abstract

Reaction–diffusion equations have been widely used to describe biological pattern formation. Nonuniform steady states of reaction–diffusion models correspond to stationary spatial patterns supported by these models. Frequently these steady states are not unique and correspond to various spatial patterns observed in biology. Traditionally, time-marching methods or steady state solvers based on Newton’s method were used to compute such solutions. However, the solutions that these methods converge to highly depend on the initial conditions or guesses. In this paper, we present a systematic method to compute multiple nonuniform steady states for reaction–diffusion models and determine their dependence on model parameters. The method is based on homotopy continuation techniques and involves mesh refinement, which significantly reduces computational cost. The method generates one-parameter steady state bifurcation diagrams that may contain multiple unconnected components, as well as two-parameter solution maps that divide the parameter space into different regions according to the number of steady states. We applied the method to two classic reaction–diffusion models and compared our results with available theoretical analysis in the literature. The first is the Schnakenberg model which has been used to describe biological pattern formation due to diffusion-driven instability. The second is the Gray–Scott model which was proposed in the 1980s to describe autocatalytic glycolysis reactions. In each case, the method uncovers many, if not all, nonuniform steady states and their stabilities.

1 Introduction

A fundamental problem in developmental biology is understanding how spatial and temporal patterns form in life, with examples including biofilm formation, cell polarization, fish pigmentation, animal coats, and formation of hair follicles and feather buds (Stoodley et al. 2002; Murray 2002; Liu et al. 2011; Jilkine and Edelstein-Keshet 2011). Mathematical modeling is an important tool in addressing this problem, and both individual-based models and continuum models are used in various contexts (Ben-Jacob et al. 2000; Baker et al. 2009; Wang et al. 2017; Painter et al. 1999; Volkening and Sandstede 2015; Othmer et al. 2009; Xue et al. 2018, 2011, 2015).

Reaction–diffusion equations have been extensively used to describe interactions among molecules and chemical species in biology, and nonuniform steady states of such models are used to describe stationary spatial patterns arising in these systems (Kondo and Miura 2010; Gierer and Meinhardt 1972; Maini et al. 2012; Turing 1952). A reaction–diffusion system takes the form

$$\begin{aligned} {\mathbf {u}}_t = D \varDelta {\mathbf {u}} + {\mathbf {f}}({\mathbf {u}},{\mathbf {p}}), \quad \mathbf {{\mathbf {x}}} \in \varOmega , \; t>0, \end{aligned}$$

(1)

where ${\mathbf {u}}= {\mathbf {u}}({\mathbf {x}}, t)\in \mathbb {R}^n$ represents the concentration of the interacting molecules or chemical species, $D\in \mathbb {R}^{n \times n}$ is the diffusion coefficient matrix, ${\mathbf {p}}\in \mathbb {R}^m$ represents the parameters of the local terms, and the function ${\mathbf {f}}$ denotes reactions and interactions among different species. Homogeneous boundary conditions, such as no-flux or periodic boundary conditions, are frequently imposed at the boundary of the domain. A steady state of the system satisfies the following elliptic system together with the corresponding boundary conditions,

$$\begin{aligned} D \varDelta {\mathbf {u}} + {\mathbf {f}}({\mathbf {u}},{\mathbf {p}}) = 0, \quad \mathbf {{\mathbf {x}}} \in \varOmega . \end{aligned}$$

(2)

With homogeneous boundary conditions, there usually exist one or multiple spatially uniform steady states to (1), satisfying ${\mathbf {f}}({\mathbf {u}},{\mathbf {p}}) = 0$. In the past, much effort has been dedicated to understand whether the system converges to spatially nonuniform steady states by perturbing it from a uniform steady state. One example is due to the interaction of a fast diffusing activator and a slowly diffusing inhibitor known as Turing instability or diffusion-driven instability: when diffusion for both species is absent, the uniform steady state is stable; however, with finite and distinct diffusion rates for the two species, the uniform steady state becomes unstable (Turing 1952; Koch and Meinhardt 1994). A general technique for studying this kind of problems is to perform a linear stability analysis around the uniform steady state and identify conditions under which unstable modes exist. Weakly nonlinear and fully nonlinear methods have been developed to describe the specific structure and stability of nonuniform steady states and transitions at bifurcation points (Cross and Hohenberg 1993; Wollkind et al. 1994; Iron et al. 2004; Wei 2008; Wei and Winter 2008; Kaper et al. 2009).

For reaction–diffusion models with multiple species and/or strongly nonlinear interactions, theoretical analysis of steady states is extremely challenging and computational methods are often used to uncover the structure and stability of the nonuniform steady states. One approach is to numerically integrate the evolutionary system (1) for a long time until the solution does not change much. For explicit numerical methods, many time steps are usually required to overcome the stability constraint of the diffusion and possible stiffness in the reaction terms. For this reason, implicit-explicit and fully implicit time-stepping methods have been developed to numerically solve reaction–diffusion systems (Thomas 2013; Zhao et al. 2011). However, these methods cannot rule out the possibility that the solutions obtained are only metastable. Alternatively, one can discretize (2) and solve the resulting nonlinear system using Newton’s method or multigrid methods (Kelley 1995; Briggs and McCormick 2000; Xu 1994). These methods are faster than the temporal schemes, but their performance highly depends on the initial guess of the solution. In Lo et al. (2012), the idea of combining the robustness of temporal schemes and the fast convergence of steady state solvers was discussed, and a hybrid approach that combines implicit Euler method and Newton’s method was developed to find nonuniform solutions of (2). Since the elliptic system (2) can have multiple solutions, the steady state to which the aforementioned methods converge to is dependent on the initial condition used in the simulation. To completely understand the potential of a specific model in describing stationary patterns in biology, it is desirable to find all nonuniform steady state solutions of the model, i.e., to find all real solutions of the elliptic system (2). Recently, a deflation technique, intended for solving polynomial equations (Wilkinson 1994), has been developed to compute multiple solutions and bifurcations of nonlinear PDEs (Robinson et al. 2017; Farrell et al. 2015). However, this method introduces artificial singularities and may cause numerical instabilities, and even miss roots for a single variable case (Wilkinson 1994).

In this paper, we present a numerical method based on a homotopy continuation technique that can give accurate approximations to many, if not all, solutions to the elliptic system (2) and that does not rely on initial guesses of the solutions. Because ${\mathbf {f}}(\mathbf{u} , \mathbf{p} )$ often describes chemical reactions, we assume that it is either a polynomial or a rational function of ${\mathbf {u}}$, based on mass action kinetics, Michaelis–Menten kinetics or Hill kinetics. We assume no-flux boundary conditions for the variable ${\mathbf {u}}$,

$$\begin{aligned} \displaystyle \frac{\partial {\mathbf {u}}}{\partial \nu } =0, \quad \mathbf {{\mathbf {x}}} \in \partial \varOmega , \end{aligned}$$

(3)

where $\nu$ is the outward normal vector at the boundary. In this paper, we assume that all the solutions of the system (2) are isolated. If there are infinitely many solutions (namely, positive dimensional solutions), we should first consider to regularize the system of nonlinear PDEs. We computationally determine the stability of these solutions and investigate the dependence of the solutions on model parameters. We demonstrate this method using two classic models in mathematical biology. The first is the Schnakenberg model which was proposed in 1970’s to describe biological pattern formation due to diffusion-driven instability (Gierer and Meinhardt 1972). The second is the Gray–Scott model which was proposed in 1980’s to describe autocatalytic glycolysis reactions (Gray and Scott 1983, 1984, 1985).

2 Numerical methods

In this section we describe the numerical methods for computing the solutions to (2) and (3) and determining their stabilities and dependence on parameters.

2.1 Computation of multiple solutions

We will explain the details of spatial discretizations and the homotopy continuation method for solving the discretized polynomial system.

2.1.1 Spatial discretization

The general method starts with the discretization of the system (2) and (3) in space. For a 1D domain [0, L], we divide it into N equidistant subintervals, with grid points $x_j = j h$, $j = 0, \cdots , N$ and $h = L/N$. We approximate the second order spatial derivatives by central difference, and denote the numerical approximation of the solution on the grid points as ${\mathbf {U}}$. Specifically, we have the following discretization

$$\begin{aligned} {\mathbf {F}}_h({\mathbf {U}},{\mathbf {p}}) \equiv D {\mathcal {L}}_h {\mathbf {U}} + {\mathbf {f}} ({\mathbf {U}}, {\mathbf {p}}) = 0, \end{aligned}$$

(4)

where

$$\begin{aligned} \begin{aligned}&{\mathbf {U}} = \begin{pmatrix} {\mathbf {U}}_0 \\ \vdots \\ {\mathbf {U}}_N \end{pmatrix}, \quad {\mathbf {f}} ({\mathbf {U}}, {\mathbf {p}}) = \begin{pmatrix} {\mathbf {f}} ({\mathbf {U}}_0, {\mathbf {p}}) \\ \vdots \\ {\mathbf {f}} ({\mathbf {U}}_N, {\mathbf {p}}) \end{pmatrix}, \\&\Big ({\mathcal {L}}_h {\mathbf {U}}\Big )_j = \frac{ {\mathbf {U}}_{j-1} - 2 {\mathbf {U}}_j + {\mathbf {U}}_{j+1}}{ h^2}, \quad \text{ j } = 1, \ldots N-1, \\&\Big ({\mathcal {L}}_h {\mathbf {U}}\Big )_0 = \frac{ 2{\mathbf {U}}_{1} - 2 {\mathbf {U}}_0 }{ h^2}, \qquad \Big ({\mathcal {L}}_h {\mathbf {U}}\Big )_N = \frac{ 2{\mathbf {U}}_{N-1} - 2 {\mathbf {U}}_N }{ h^2}. \end{aligned} \end{aligned}$$

For a 2D rectangular domain, we use the same discretization in both x and y.

If ${\mathbf {f}}({\mathbf {u}},{\mathbf {p}})$ is given by mass action kinetics, then ${\mathbf {F}}_h$ is a polynomial system which maps ${\mathbf {U}}\in R^K$ to $R^K$ with $K=n(N+1)$. In order to approximate all steady states of the reaction–diffusion system, we aim to find all isolated real solutions of the polynomial system (4). If the reaction terms in ${\mathbf {f}}({\mathbf {u}},{\mathbf {p}})$ contains Michaelis–Menten or Hill function forms, then the system (4) can be transformed into a polynomial system by multiplying the common denominator of these terms.

2.1.2 The homotopy continuation method

In general, it is very hard to solve (4) directly, because the variables ${\mathbf {U}}$ with different index j are coupled together in (4) and because of the potential complex nonlinearities in ${\mathbf {f}} ({\mathbf {U}}, {\mathbf {p}})$. To tackle this problem, we construct a much simpler system ${\mathbf {G}}_h(\mathbf{U} ,\mathbf{p} ) = 0$, called the “start system” (described further below), and apply the homotopy continuation technique described in Bates et al. (2008, 2011). Specifically, we construct a homotopy function

$$\begin{aligned} {\mathbf {H}}({\mathbf {U}},\tau ) := (1-\tau ) {\mathbf {F}}_h({\mathbf {U}},{\mathbf {p}})+\gamma \tau {\mathbf {G}}_h(\mathbf{U} , \mathbf{p} ), \end{aligned}$$

(5)

and aim to solve

$$\begin{aligned} {\mathbf {H}}({\mathbf {U}},\tau ) = 0. \end{aligned}$$

(6)

Here $\tau \in [0, 1]$ is called the homotopy tracking number and $\gamma$ is a randomly chosen complex number. In the function ${\mathbf {H}}$, we suppressed the dependence on ${\mathbf {p}}$ and h for simplicity of notation. When $\tau =1$, we have the start system ${\mathbf {G}}_h(\mathbf{U} , \mathbf{p} )=0$. When $\tau =0$, we recover the target system (4). Let the set $({\mathbf {U}}^1,\ldots ,{\mathbf {U}}^M)$ be the solution set of the start system. The polynomial system (4) is then solved by tracking $\tau$ from 1 to 0 starting from the solutions of the start system along the homotopy curves defined by (6). We note that the homotopy tracking is done in the complex fields, and by the end of tracking we only keep the real solutions to the target system which are relevant to the biological problem.

The start system should be chosen such that: a) it can be solved easily analytically, b) the solution curves of (6) are smooth, and c) every solution of the target system can be reached by a path that originates from a solution of the start system. Mathematical methods have been developed to construct efficient start systems for solving polynomial systems using homotopy. The simplest choice is to use the so-called total degree start system. It arises from the Bézout’s Theorem, which asserts that a system of K polynomial equations in K variables has at most $\varPi _{k=0}^{K-1} d_k$ isolated solution in $\mathbb {C}^K$ when counting multiplicity, where $d_k$ is the degree of the kth polynomial (Sommese and Wampler 2005). A total degree system has exactly $\varPi _{k=0}^{K-1} d_k$ solutions, and one commonly used example is

$$\begin{aligned} \Big ({\mathbf {G}}_h(\mathbf{U} ) \Big )_k = U_k^{d_k}-1, \quad k = 0, 1, 2, \ldots , K-1, \end{aligned}$$

(7)

for which all the solutions are different and can be written explicitly. The disadvantage of using (7) is the large number of solution paths to track $\big (\varPi _{k=0}^{K-1} d_k\big )$ when carrying out homotopy continuation, which is often unnecessary. To reduce the number of solution paths, various methods have been developed by taking the specific polynomial structure into account [see Chapter 8 of Sommese and Wampler (2005)]. In Sects. 3 and 4, we chose start systems based on the structure of the polynomial system discretized from the PDE models. The numerical results obtained using these start systems have been verified and compared with those using the total degree start system (7).

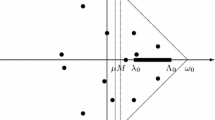
The randomly chosen complex number $\gamma$ is introduced such that none of the solution paths cross each other for $\tau \in (0,1)$ almost surely (Bates et al. 2008; Sommese and Wampler 2005). For all our simulations, we used random number generators to select $\gamma$. In our experience, different $\gamma$ has consistently resulted in the same numerical solutions. The homotopy curves starting at the solution of the start system either end at a solution of the target system or diverge to infinity (Fig. 1a). In our simulations, we chose to terminate the homotopy tracking process once the max-norm of the solution exceeds a large threshold, $10^4$. An alternative method to applying this threshold is to transform the polynomial systems into homogeneous polynomial systems and then apply homotopy continuation on the projective space (Sommese and Wampler 2005).

Fig. 1

Illustration of the homotopy method to solve (4). a Homotopy tracking from the start system to the target system (4). $\mathbb {C}^{K}$ is the K dimensional complex space that the solutions belong to. b The underlying idea of Euler predictor and Newton correction method for each time step $\varDelta \tau$

The numerical method used in path tracking from $\tau = 1$ to $\tau = 0$ involves solving the Davidenko differential equation backward

$$\begin{aligned} \frac{\text{ d }{\mathbf {H}}({\mathbf {U}}(\tau ),\tau )}{\text{ d }\tau }\equiv \nabla _\mathbf{U } {\mathbf {H}} ({\mathbf {U}}(\tau ),\tau ) \frac{\text{ d }{\mathbf {U}}(\tau )}{\text{ d }\tau }+\frac{\partial {\mathbf {H}}({\mathbf {U}}(\tau ),\tau )}{\partial \tau }=0, \end{aligned}$$

(8)

with the initial condition at $\tau = 1$ given by a solution of the start system. Here $\nabla _\mathbf{U } {\mathbf {H}}$ is the Jacobian matrix of $\mathbf{H}$. Since we also have ${\mathbf {H}}({\mathbf {U}},\tau ) = 0$ along the path, we used predictor and corrector methods, such as Euler’s predictor and Newton’s corrector, to solve this initial value problem (Fig. 1b). Denote $\tau ^k = 1- k \varDelta \tau$ and the numerical approximation of $\mathbf{U} (\tau _k)$ as $\mathbf{U} ^k$. Then we have the following algorithm:

Additionally, in our computation we combined the predictor and corrector method with adaptive step size and adaptive precision algorithms to provide reliability and efficiency as in Bates et al. (2008, 2011): if the initial prediction is not adequate or the corrector fails, then the algorithm automatically shortens the step size and solves again.

We note that the homotopy continuation setup (6) guarantees finding all the solutions of the discretized system (4) due to Bézout’s theorem (Bates et al. 2008; Sommese and Wampler 2005). The convergence of the numerical discretization to (2) depends on the specific discretization method, e.g., finite difference, finite element or spectrum methods, and the spatial mesh size.

2.1.3 The bootstrapping method

The mesh size h has to be small such that the discretization error in (4) is small and the solutions of (4) become good approximations of solutions of the elliptic problem (2) and (3). On the other hand, a small h results in a large polynomial system, which in turn leads to extremely high computational cost when carrying out the homotopy method described in Sect. 2.2. This is especially true when the number of PDEs is large and when one needs to solve the PDE in higher dimensional space. To alleviate the computational difficulty, we used the bootstrapping method developed in Hao et al. (2014), which is based on domain decomposition.

Consider two meshes of the domain, a coarse mesh with mesh size H and a fine mesh with mesh size h (Fig. 2). The goal is to solve the system (4) on the fine mesh. Instead of solving it directly, we use the following two-grid method:

The bootstrapping method basically extends the two-grid method by iterating S2 and S3 several times until the mesh is fine enough to ensure the desired accuracy of the discretization. The key idea of the method is to decouple a big polynomial system into many small polynomial subsystems which can be solved in parallel. Although there is no theoretical proof that the bootstrapping method can be used to find all the solutions of the discretized system, it provides a possibility to solve large scale systems arising from discretization of nonlinear PDEs and also shows many advantages in terms of efficiency and robustness compared to the basic homotopy continuation method (Hao et al. 2014).

Fig. 2

Illustration of the two-grid method, or one iteration of the bootstrapping method

2.2 Stability and bifurcation analysis

In this section, we describe the methods that we use to determine the stability of the steady states. Because the steady state solutions are given numerically, their stabilities are also determined numerically.

2.2.1 Linear stability analysis

Let ${\bar{\mathbf{u }}}({\mathbf {x}}, \mathbf{p} )$ be a steady state of (1) and (3), i.e., ${{\bar{\mathbf{u }}}}({\mathbf {x}}, \mathbf{p} )$ satisfies (2) and (3). Let $\mathbf{u} ({\mathbf {x}}, \mathbf{p} ) ={{\bar{\mathbf{u }}}}({\mathbf {x}}, \mathbf{p} ) + {{\hat{\mathbf{u }}}}({\mathbf {x}}, \mathbf{p} )$, where ${{\hat{\mathbf{u }}}}({\mathbf {x}}, \mathbf{p} )$ represents the deviation of the solution $\mathbf{u} ({\mathbf {x}}, \mathbf{p} )$ from the steady state $\bar{\mathbf{u }}({\mathbf {x}})$. Substituting this expression into (1) and (3), and neglecting the nonlinear terms in ${{\hat{\mathbf{u }}}}({\mathbf {x}}, \mathbf{p} )$, we obtain the linearized system

$$\begin{aligned} \frac{\partial {{\hat{\mathbf {u}}}}}{\partial t}= D\varDelta {\hat{\mathbf {u}}}+ \nabla _\mathbf{u }{} \mathbf{f} |_{({\bar{\mathbf {u}}}, \mathbf{p} )}{\hat{\mathbf {u}}}. \end{aligned}$$

(9)

Using separation of variables and assuming ${\hat{\mathbf {u}}}(t,x)=e^{\lambda t}{\mathbf {J}}({\mathbf {x}})$, we have the following eigenvalue problem

$$\begin{aligned} {\mathcal {A}} {\mathbf {J}}= D\varDelta {\mathbf {J}}+ \nabla _\mathbf{u }{} \mathbf{f} |_{({\bar{\mathbf {u}}}, \mathbf{p} )} {\mathbf {J}}=\lambda {\mathbf {J}}. \end{aligned}$$

(10)

with no-flux boundary conditions. The steady state ${\bar{\mathbf {u}}}$ is asymptotically stable if all the eigenvalues of (10) have negative real part.

To numerically approximate the spectrum of (10), we consider the discretized problem corresponding to (1) and (3). For the 1D case described in Sect. 2.1.1, we have

$$\begin{aligned} \displaystyle \frac{\partial {\mathbf {U}}}{\partial t} = {\mathbf {F}}_h({\mathbf {U}},{\mathbf {p}}), \end{aligned}$$

(11)

After linearization around the steady state ${\bar{\mathbf {U}}}$, it becomes

$$\begin{aligned} \displaystyle \frac{\partial {\hat{\mathbf {U}}}}{\partial t} = \mathbf{L} _h({\bar{\mathbf {U}}}) {\hat{\mathbf {U}}}, \qquad \mathbf{L} _h({\bar{\mathbf {U}}}) = \nabla _{{\mathbf {U}}} {\mathbf {f}}_h|_{({\bar{\mathbf {U}}},{\mathbf {p}})}. \end{aligned}$$

(12)

Determining the asymptotic stability of ${\bar{\mathbf {U}}}$ requires calculating the eigenvalues of the matrix $\mathbf{L} _h({\bar{\mathbf {U}}})$: if for a given steady-state solution ${\bar{\mathbf {U}}}$, all the eigenvalues of $\mathbf{L} _h({\bar{\mathbf {U}}})$ have negative real parts, then this steady state is asymptotically stable.

In our investigations, we assume that the stability of ${\bar{\mathbf {U}}}$ can be used to represent the stability of ${\bar{\mathbf {u}}}$. This approximation is based on the convergence of eigenvalues of $\mathbf{L} _h({\bar{\mathbf {U}}})$ to eigenvalues of ${\mathcal {A}}$ (Freiling and Yurko 2001; Kong and Zettl 1996).

2.2.2 One-parameter bifurcation diagram

To understand how the steady state solutions depend on parameters of the model, we compute one-parameter bifurcation diagrams by solving the discretized system (4) with a varying parameter p, i.e., we solve ${\mathbf {F}}_h({\mathbf {U}},p)={\mathbf {0}}$. The method is similar to standard numerical continuation methods. Specifically, we used homotopy tracking with Euler’s predictor and Newton’s corrector, as detailed in Sect. 2.1.2, where ${\mathbf {F}}_h({\mathbf {U}},p)$ is the homotopy function and p is the tracking parameter. Moreover, we used a trial-and-error approach for step-size control with respect to the parameter p: shorten the step-size upon failure, and lengthen it upon repeated successes (Sommese and Wampler 2005). In this paper, we consider the steady state bifurcations only and will explore other types of bifurcations, e.g., Hopf bifurcation, in the future.

2.2.3 Two-parameter solution map

Mathematical models of the form (1) frequently have multiple steady states for the same parameter combination. To understand how the number of steady state solutions depend on a pair of parameters, $p_1$ and $p_2$, we compute two-parameter solution maps, in which the 2D parameter space is divided into different regions, and the number of steady states remains the same within each region but changes across a boundary curve between two neighboring regions.

At each point of a boundary curve, one or multiple steady state solutions change stability, i.e., there exists a steady state solution $\mathbf{u}$ such that the linearized system around $\mathbf{u}$ has zero eigenvalues. Thus the following system holds for parameter combinations on the boundary curves,

$$\begin{aligned}&D \varDelta {\mathbf {u}} + {\mathbf {f}}({\mathbf {u}},p_1,p_2)=0, \quad x \in \varOmega \nonumber \\&D \varDelta \mathbf{j} +\nabla _\mathbf{u } {\mathbf {f}} ({\mathbf {u}},p_1,p_2) \mathbf{j} =0, \quad x \in \varOmega \nonumber \\&\displaystyle \frac{\partial {\mathbf {u}}}{\partial \nu } = \displaystyle \frac{\partial {\mathbf {j}}}{\partial \nu } = 0, \quad \mathbf {{\mathbf {x}}} \in \partial \varOmega , \nonumber \\&\int _{\varOmega } \mathbf{j} (\mathbf{x} ) d{\mathbf {x}} =1. \end{aligned}$$

(13)

where $\mathbf{u} = \mathbf{u} ({\mathbf {x}})$ is a solution to the nonlinear problem and ${\mathbf {j}} = {\mathbf {j}}(\mathbf{x} )$ is a nontrivial solution of the linearized system, i.e., an eigenfuction to the zero eigenvalue. To solve the above system in 1D, we use the same discretization as in Eq. (4). Once the boundary curves are computed, the 2D parameter space is divided into several sub-domains. We then sample points from each sub-domain and compute the number of steady state solutions for that region.

3 Application to the Schnakenberg model

The Schnakenberg system is a Turing model where u is an activator and v is a substrate.

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{\partial u}{\partial t} = \varDelta u + \eta (a - u + u^2 v), \\&\displaystyle \frac{\partial v}{\partial t} = d \varDelta v + \eta (b - u^2 v ). \end{aligned} \end{aligned}$$

(14)

Here both species are produced uniformly in the domain, u decays linearly, and v is converted to u in a nonlinear and autocatalytic manner. The diffusion rate d differentiates the relative dispersal speed of the two species, and the parameter $\eta$ specifies the relative balance between the diffusion and the chemical reaction.

We computed steady-state solutions of the Schnakenberg model in a 1D domain $x\in [0, 1]$ with no-flux boundary conditions. We first considered the situation with fixed parameters $a = 1/3$, $b = 2/3$, $\eta = 50$ and $d=50$. We found three steady state solutions including one unstable constant steady state $\Big (a+b, \frac{b}{(a+b)^2}\Big ) = \big (1, 2/3\big )$ and two stable nonuniform steady states using the bootstrapping method (Fig. 3a, b).

Fig. 3

Steady states of the Schnakenberg model with $\eta = 50$. a, b Three steady state solutions with $d = 50$. The arrows point to two components of the same nonuniform solution. c Bifurcation diagram of the model. The y-axis is u(0) of the steady state solutions. Solid line: stable. Dashed line: unstable. Other parameters used: $a = 1/3$ and $b = 2/3$

The two stable solutions are symmetric with respect to the center of the domain. To understand how the diffusion rate d affects the spatial patterns of u and v, we tracked these solutions by decreasing d from 50 to 30. The bifurcation diagram Fig. 3c shows that one supercritical pitchfork bifurcation occurs near $d^* = 44$, and the constant solution is stable when d is smaller than $d^*$. We note that the parameter $d^*$ we found here is consistent with the critical diffusion rate that one would obtain following linear stability analysis of the uniform steady state.

In these calculations, we used the bootstrapping method that starts with an initial coarse mesh with 9 grid points, i.e., $N=8$, $h = 1/8$. The target system is

$$\begin{aligned} \begin{aligned}&\frac{U_{j-1} - 2 U_j + U_{j+1}}{h^2} + \eta (a - U_j + U_j^2 V_j) = 0, \quad j = 1,\ldots N-1, \\&d\frac{V_{j-1} - 2 V_j + V_{j+1}}{h^2} + \eta (b - U_j^2 V_j ) = 0, \quad j = 1,\ldots N-1, \\&\frac{2U_{1} - 2 U_0 }{h^2} + \eta (a - U_0 + U_0^2 V_0) = 0, \\&d \frac{2V_{1} - 2 V_0 }{h^2} + \eta (b - U_0^2 V_0) = 0, \\&\frac{2U_{N-1} - 2 U_N }{h^2} + \eta (a - U_N + U_N^2 V_N) = 0, \\&d \frac{2V_{N-1} - 2 V_N }{h^2} + \eta (b - U_N^2 V_N) = 0. \end{aligned} \end{aligned}$$

(15)

The start system is

$$\begin{aligned} \begin{aligned}&\kappa + \eta (a - U_j + U_j^2 V_j) = 0,\quad j = 0,\ldots N, \\&\kappa + \eta (b - U_j^2 V_j ) = 0 \quad j = 0,\ldots N. \end{aligned} \end{aligned}$$

(16)

We note that this start system is decoupled for different j. The parameter $\kappa$ is chosen such that the start system has three distinct complex solutions for each j, that is, $3^9=19,683$ solutions on the initial coarse mesh. For model parameters we considered in this paper, we used $\kappa =0$. After tracking all the solution paths along the homotopy curves, we obtained both real and complex solutions to the target system. We kept the real solutions (total of 7) and discarded the complex solutions (total of 19121). Then we refined the mesh by dividing h by 2 each step until $N=256$. For each bootstrapping step we used similar target and start systems but with the desired boundary conditions as described in Algorithm 2. Eventually we had three real solutions as shown in Fig. 3.

We chose the start system (16) for the following reasons. There is only one nonlinear term, $u^2 v$, in the Schnakenberg model (14) and this is also reflected in the discretized system (15). If we add the first component of (15) to the second component, we obtain linear relations between the U’s and the V’s. The same is true for the last four components of (15) which results from discretization of the model at the two boundary points. After this simplification, the total degree of the target system becomes $3^9\approx 2\times 10^5$ for the initial coarse mesh, which is much lower than the total degree without simplification, that is, $9^9\approx 4\times 10^8$ for the initial coarse mesh. The start system (16) kept the nonlinear structure of (15) and essentially is a total degree system if we use the same simplification. It allows us to track significantly fewer homotopy curves than the total degree system (7), which reads, for this example,

$$\begin{aligned} U_j^3 - 1 = 0, \quad V_j^3 - 1 = 0, \quad j = 0,\ldots N \end{aligned}$$

(17)

We simulated the path tracking process with a mesh of 5 grid points using both (16) and (17) and obtained the same solutions for the target system. This benchmark comparison confirmed the validity of (16) numerically.

Through this example, we compared the computational efficiency of the basic homotopy continuation method (no bootstrapping) and the bootstrapping method as described in Sect. 2. The model parameters used in the comparison are the same as in Fig. 3. We considered mesh sizes $h = 0.5, 0.25, 0.125, \text{ and }\; 0.0625$. For $h=0.5$ the two methods are identical. For smaller h, the homotopy method solves the discretized polynomial system on that mesh, while the bootstrapping method starts with the coarse mesh with grid size 0.5 and refines the mesh by adding a middle point for each subinterval until the grid size becomes h. Both methods lead to the same number of solutions. However, as shown in Table 1, the bootstrapping method was significantly faster than the homotopy method. The comparison was implemented in C++ and the computing time was recorded on a Xeon 5410 processor with 64-bit Linux.

Table 1 Computing time comparison between the homotopy continuation method and the bootstrapping method for the Schnakenberg model

To understand how an increased rate of chemical reactions affect the spatial patterns, we performed the same computations for a much larger $\eta$ given by $\eta = 200$. When d = 100, we found a total of 7 steady state solutions including one constant solution and 6 nonuniform solutions. As d decreases from 100 to 30, the number of solutions decreases from 7 to 5 to 3 and finally to 1. The component u is plotted in Fig. 4a–c for $d = 50, 70$ and 100 respectively. Solid lines indicate stable solutions and dashed lines indicate unstable solutions. The bifurcation diagram with respect to d is given in Fig. 4d: solid lines indicate stable solutions and dotted lines indicate unstable solutions. There are three bifurcation points at $d=44, 64, 73$ approximately. The intersection of the two solid lines near $d = 87$ is not a bifurcation point. The stable solution branches labeled by numbers in Fig. 4d correspond to the solutions labeled in Fig. 4a–c. The solution branch labeled with number 1 in Fig. 4d corresponds to the uniform steady state.

Fig. 4

Steady states of the Schnakenberg model with $\eta = 200$. a–c Steady state solutions with $d = 50$, 70, 100. Here y-axis labels u(x). d bifurcation diagram of the model with parameter d. Here y-axis labels u(0). Solid lines: stable. Dashed or dotted lines: unstable. Other parameters used are the same as in Fig. 3

In order to explore how the number of steady state solutions changes with respect to d and $\eta$, we computed the $d-\eta$ curves across which steady state bifurcations occur, using the algorithm described in Sect. 2.2.3. Figure 5 plots these boundary curves and the number in each subregion indicates the number of steady state solutions for each parameter combination in that region. The two dashed lines indicate the situations with $\eta =50$ and $\eta =200$, corresponding to the two cases considered in Figs. 3 and 4. We note that the results of these calculations is consistent with Figs. 3 and 4.

Fig. 5

Two-parameter solution map for the Schnakenberg model. The numbers on the figure label the total number of steady states in each subdomain. The two horizontal dashed lines corresponds to the parameter regimes we used in Figs. 3 and 4. Other parameters used are the same as in Fig. 3

In Kaper et al. (2009), bifurcation analysis near a uniform steady state was developed for Turing systems. In particular, the Schnakenberg model was analyzed with similar parameter ranges as we considered here. Figure 4 in Kaper et al. (2009) suggests that when $a=1/3$, $b=2/3$, $\eta = 50$ (the notation $\gamma$ is used in Kaper et al. (2009) instead of $\eta$), as d increases, the uniform steady state loses stability and perturbation with wavenumber one half from the uniform steady state drives the instability; when $\eta =200$, as d increases, perturbation with wavenumber one changes stability before perturbation with wavenumber one half. The numerical results shown in Figs. 3, 4 and 5 are not only consistent with all the analysis in Kaper et al. (2009) but also give more quantitative information about the nonuniform steady states and their dependence on the parameters d and $\eta$.

4 Application to the Gray–Scott model

The Gray–Scott model was first proposed by Gray and Scott to describe autocatalytic reactions in 1980’s Gray and Scott (1983), Gray and Scott (1984), Gray and Scott (1985). It takes the following form:

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\partial A}{\partial t} = D_A \varDelta A + S A^2 - (\mu +\rho )A,\\ \displaystyle \frac{\partial S}{\partial t} = D_S \varDelta S - S A^2 + \rho (1-S). \end{aligned} \end{aligned}$$

(18)

Here A is the concentration of an activator and S is the concentration of a substrate. The model corresponds to the following reactions

$$\begin{aligned} S + 2A \overset{1}{\rightarrow }3A, \quad A \overset{\mu }{\rightarrow }P, \quad A,S \overset{\rho }{\rightarrow }\phi , \quad \phi \overset{\rho }{\rightarrow }S, \end{aligned}$$

(19)

where P is a terminal product, the third reaction represents a linear decay of A and S, and the last reaction represents a constant feeding of S to the system with rate $\rho$.

Although simple, the system (18) can predict very complicated spatial-temporal patterns including spots, stripes, and dividing spots (Pearson 1993; Lee et al. 1993). We investigated stationary spatial patterns supported by (18) under no-flux boundary conditions (3), with ${\mathbf {u}} = (A, S)$. The default parameter values used in our computations are $D_A=2.5\times 10^{-4}$, $D_S=5\times 10^{-4}$, $\rho =0.04$ and $\mu =0.065$ unless otherwise noted. Under this parameter regime, there is one real uniform steady state $(A, S) = (0, 1)$, which is linearly stable.

4.1 Pattern formation in 1D

We first considered stationary spatial patterns of the Gray–Scott model on a 1D domain [0, 1]. We applied the bootstrapping method with a starting mesh size $h=1/8$ ($N=8$) and ending mesh size $h=1/1024$ ($N=1024$). With a similar consideration as the Schnakenberg model, we used the following start system

$$\begin{aligned} \begin{aligned}&\kappa + S_j A_j^2 - (\mu +\rho )A_j = 0,\quad j = 0,\ldots N, \\&\kappa - S_j A_j^2 + \rho (1-S_j) = 0 \quad j = 0,\ldots N. \end{aligned} \end{aligned}$$

(20)

We found 23 real solutions, including the linearly stable uniform solution (0, 1), 6 linearly stable nonuniform solutions (Fig. 6), and 16 linearly unstable nonuniform solutions (Fig. 7). In these plots, we grouped the solutions based on their peak numbers and symmetries. Of the 6 stable nonuniform solutions, the first two are symmetric with respect to the center of the domain $x = 0.5$ and can be characterized as half-peak solutions. The 3rd solution and the 4th solution are one-peak solutions and identical under the translation $x \rightarrow (x + 0.5)$. The last two solutions are symmetric to the center of the domain as well and both have one and a half peaks.

Fig. 6

Stable nonuniform steady states of the Gray–Scott model in 1D. Blue: A(x). Red: S(x). Parameters used: $D_A=2.5\times 10^{-4}$, $D_S=5\times 10^{-4}$, $\rho =0.04$ and $\mu =0.065$

Fig. 7

Unstable nonuniform steady states of the Gray–Scott model in 1D. Blue: A(x). Red: S(x). Parameters used are the same as in Fig. 6

In Fig. 7 the unstable nonuniform solutions are ordered with increasing peak numbers. We note that the solution pair 13 and 14 are similar but not identical to the solution pair 15 and 16. We refined the mesh to $N = 4096$ and they still appear to be different numerical solutions to the nonlinear system (4). We note that the numerical residual in our calculations is on the order of $10^{-12}$.

We treated $\rho$ as a bifurcation parameter and tracked the solutions for $\rho$ between 0.025 to 0.05. Figure 8a plots the bifurcation diagram with the y-axis given by $\big (1-\max _{0\le x\le 1}{S(x)}\big )$ on the log scale. The uniform steady state has $S = 1$, i.e., zero on the vertical axis, and thus it is not shown in the diagram. The nonuniform steady states form 4 disconnected parts, corresponding to peak number half, one, one and a half, and two from bottom to top shown in Fig. 8a. Because the vertical axis measures the maximum of S(x), each branch corresponds to a solution pair (with certain symmetry) that corresponds to those shown in Figs. 6 and 7.

Fig. 8

Parameter dependence of the Gray–Scott model in 1D. a Bifurcation diagram with respect to $\rho$. The y-axis is $\big (1-\max _{0\le x\le 1}{S(x)}\big )$ calculated for every solution on the logarithmic scale. Solid lines: stable solutions. Dashed lines: unstable solutions. The uniform steady state is a stable isolated solution branch and not shown in this diagram. Si: the ith stable nonuniform solution with the same index as in Fig. 6. Ui: the ith unstable nonuniform solution with the same index as in Fig. 7. b Two-parameter solution map with respect to $\mu$ and $\rho$. The numbers on the figure label the total number of steady states in each subdomain. The vertical dashed line corresponds to the parameter regime used in Figs. 6, 7 and panel A. The four curves appear close near $\mu = 0.065$ but there is no intersection point. Other parameters used are the same as in Fig. 6

To investigate how the number of steady state solutions change with respect to both $\mu$ and $\rho$, we computed the $\mu$ v.s. $\rho$ curves across which steady state bifurcations occur, using the algorithm described in Sect. 2.2.3. Figure 8b shows these curves, and the number in each subregion indicates the number of steady state solutions, including both stable and unstable, for each parameter set in that region. The vertical dashed line indicates the situation with the baseline parameter $\mu =0.065$: as $\rho$ increases from 0 to 0.01, the number of solutions increases from 1 (a single stable uniform steady state) to 5, 11, 19 and finally to 23, consistent with the bifurcation diagram in Fig. 8a. The boundary between 5 solutions and 11 solutions is very close to the boundary between 1 and 5, but these two curves do not intersect.

Finally, we investigated how the steady state solutions depend on the domain size. After increasing the domain size to 2, we found a single stable uniform steady state, 12 stable nonuniform steady states, and 32 unstable nonuniform steady states using the baseline parameters as shown in Figs. 6 and 7. The nonuniform steady states also appear in pairs, and compared with the case with domain size 1, the number of nonuniform solutions and the range of their peak numbers are exactly doubled. Figure 9 plots the stable nonuniform steady states by selecting one representative from each solution pair. The peak number of these solutions increases from half to three.

4.2 Pattern formation in 2D

We then considered stationary spatial patterns that can be described by the Gray–Scott model on a 2D domain. In our simulations, we started with an initial mesh with 3 grid points in both x and y directions, and applied the bootstrapping method by dividing each grid to two halves each time, until there are 33 grid points in each dimension. For the domain $[0, 1]\times [0,1]$, we found 16 stable nonuniform steady states and 198 unstable nonuniform steady states numerically. Similar to the 1D case, these solutions can be grouped using transformations and symmetry conditions. First, we used no-flux boundary conditions for the entire boundary and therefore we expect that if u(x, y) is a solution, then $u(1-x,y)$, $u(x, 1-y)$, $u(1-x,1-y)$ are also solutions. Second, because the domain is symmetric in x and y, we expect that if u(x, y) is a solution, then rotating it by $\pi /2$, $\pi$ and $3\pi /2$ with respect to the center of the domain adds more solutions to the system. Furthermore, for solutions that have certain kinds of symmetry, they can be identified with other solutions. For example, if solution u(x, y) is symmetric to $x = 0.5$, then $u\big ( (x+0.5) \mod 1\big )$ is a solution. Using such transformations and symmetry conditions, the stable nonuniform steady states can be classified to 4 groups, and one representative solution, A(x, y), from each group is plotted in the first 4 panels of Fig. 10. The first three solutions are stripe patterns, which are homogeneous in the y-direction and correspond to the 3 solution pairs in 1D shown in Fig. 6. The last solution is a spot pattern. The unstable nonuniform steady states can be classified as stripe patterns, spot patterns, and stripe-spot patterns. Selected unstable patterns are plotted in Fig. 10.

Fig. 9

Stable nonuniform steady states of the Gray–Scott model in 1D on a larger domain [0, 2]. Blue: A(x). Red: S(x). Parameters used are the same as in Figs. 6 and 7

Fig. 10

Stable and selected unstable nonuniform steady states of the Gray–Scott model in 2D. The contour plots are for the component A(x, y). The horizontal and vertical axes represent x and y respectively. The domain is $[0, 1]\times [0,1]$. Parameters used are the same as in Fig. 6

We then considered the rectangular domain $[0, 2]\times [0,1]$ and found 98 stable nonuniform steady states. The stable patterns include horizontal stripes, vertical stripes, isolated spots, connected dots, as well as stripe-spot patterns. Selected patterns are plotted in Fig. 11. These patterns share many features with the patterns demonstrated in Pearson (1993).

Fig. 11

Selected stable nonuniform steady states of the Gray–Scott model in 2D. The contour plots are for the component A(x, y). The horizontal and vertical axes represent x and y respectively. The domain is $[0, 2]\times [0,1]$. Parameters used are the same as in Fig. 6

5 Discussion

Reaction–diffusion models have been widely used to describe pattern formation in biological contexts. Both steady state patterns and time-dependent, transient patterns have been shown important in modeling phenomena arising in, e.g., cell and developmental biology as well as ecology. The focus of this paper is on the computation of steady state patterns supported by reaction–diffusion models. Frequently the reaction terms take the form of polynomials or rational functions, based on mass action kinetics or other chemical reaction kinetics. In this paper, we described homotopy and bootstrapping methods which can potentially find all steady state solutions with those kinetic terms. We note that the basic homotopy method (no bootstrapping) is guaranteed to find all solutions of the discretized polynomial system if one uses the total degree system or other carefully chosen start system. We also note that in our experience when using bootstrapping, the initial grid number has to be large enough to reconcile the key space scales of the problem. Combined with numerical continuation with regards to a single parameter of the model, these methods were used to generate plots of steady state bifurcation diagrams with respect to that parameter. Finally, we developed a computational method to draw two-parameter solution maps, in which the parameter plane is divided into sub-regions, and the number of steady state solutions remain constant within each sub-region.

We applied these computational methods to find nonuniform steady state solutions for two classic models in mathematical biology. The first is the Schnakenberg model that has been used to describe biological pattern formation due to diffusion-driven instability. Our numerical results are consistent with existing analytical results obtained using dynamic transition theory (Kaper et al. 2009). The second example we considered is the Gray–Scott model, proposed in the 1980s to describe autocatalytic glycolysis reactions. Our 2D simulations for the Gray–Scott model yielded a plethora of spot, stripe, and spot-stripe patterns as well as their stabilities, which also appear to be consistent with previous studies.

These methods can be readily applied to compute multiple steady states for other nonlinear PDE models, as long as after spatial discretization, the resulting nonlinear system can be rewritten as (or approximated by) a system of polynomial equations. One example is PDE models for chemotaxis which is the directed movement of cells in response to external chemical signals. PDE models for chemotaxis usually consist a reaction-drift-diffusion equation for the cell population, called the Patlak–Keller–Segel equation, and reaction–diffusion equations for the external chemical signals. Derivations of such models for bacterial chemotaxis suggests the additional drift term (also called cross-diffusion term or taxis term) to be a rational function of the unknowns (Hillen and Painter 2009; Xue 2015). Chemotaxis models are shown to have steady-state patterns representing cell aggregates and cell stripes, as well as time-dependent patterns such as traveling waves, time-periodic patterns, and even chaotic patterns (Othmer and Stevens 1997; Painter et al. 1999; Xue and Othmer 2009; Painter and Hillen 2011).

The software XPPAUT has been extensively used to perform numerical continuation and bifurcation analysis for ODE systems (Ermentrout 2002). For PDE systems, one can discretize space and reduce the problem to a system of ODEs and use XPPAUT, or use other software packages such as pde2path which is built upon AUTO (Uecker et al. 2014). To use these packages, we start from one point on a solution component, which is a steady state solution for the initially chosen parameters, track the solution by varying one of the model parameters, and this will lead to a bifurcation diagram with a single connected component. For large ODE systems, the number of bifurcation points and connected branches can become large, thus it usually depends on trial-and-error and the researcher’s experience with the software to make sure that all the branches are found. Moreover, if the bifurcation diagram contains multiple components that are not connected, it is essential to find at least one point from each component in order to recover the full bifurcation diagram, which is frequently nontrivial. The computational methods described in this paper address these problems and provide a systematic approach to potentially find all steady state solutions given a specific parameter set. When computing the bifurcation diagrams, we performed solution tracking starting from every solution for the initially chosen parameter set. For this reason, the bifurcation diagrams we obtained were more complete and even able to recover disconnected components. We focused on the computation of steady state solutions for nonlinear PDEs and steady-state bifurcations. In the future, we would like to extend the current methods to compute all periodic solutions in time for reaction–diffusion equations and other evolutionary PDEs and compare with analytical results in, e.g., Sun et al. (2005). We also plan to develop a user-friendly open-source software for the implementation of these methods.

In order to guarantee that one finds all the solutions of the discretized polynomial systems, we carried out the computation on the complex field and using start systems equivalent to total degree systems. As the number of grid points increases, the number of solution paths for homotopy tracking grows exponentially. Moreover, our methods yield a much larger number of complex solutions, which are biologically irrelevant, compared to the number of real solutions. For these reasons, the homotopy method introduced here is computationally expensive and how to reduce the computational cost is a central question. The bootstrapping method is built upon the idea of domain decomposition and can significantly reduce the computational cost in 1D (see Table 1). However, for computations in 2D or 3D, the bootstrapping method still turns out to be slow: for the Gray–Scott model 2D simulations presented in Fig. 10, it took several hours on a single-core CPU. Because the solution tracking process starting from different solutions of the start system is independent of each other, parallel computing can be used to further reduce the computational time. Because the number of solution paths highly depends on the choice of the start system, general guidelines is much needed for constructing minimal start systems for polynomial systems discretized from nonlinear PDEs. For 2D and 3D problems, the target polynomial system is very complicated due to the discretization of the Laplacian operator. One possible direction is to design multi-step homotopy methods that first solve intermediate systems before solving the target system, e.g., by adding the discretization of the spatial derivatives dimension-by-dimension in each homotopy step.