1 Introduction

Nonlinear-system control, particularly in regard to stabilization, tracking, observer design, chaos control and synchronization, has been extensively studied over the past decade, as motivated by numerous potential applications in the field of nonlinear science [1–4]. In practice, actuator nonlinearities (e.g., saturation) are often neglected in controller design for nonlinear systems, which can cause detrimental effects such as overshoot, lag, and even instability [5]. Controlling nonlinear systems under actuator saturation is a challenging issue demanding serious attention. Actuator saturation in linear systems has been dealt with in two well-known ways. The first method is to design a state feedback controller that incorporates knowledge of actuator saturation to deal with the linear [6–8] and the nonlinear systems [9]. The second method is to design an anti-windup compensator (AWC) in addition to the conventional stabilizing or tracking controller [10–15]. The main objective of an AWC is to improve the overall closed-loop performance in the presence of saturating actuators, specifically by utilizing the difference between the controller output and the saturated control signal. Some preliminary results on AWC design for feedback-linearizable and Euler–Lagrange nonlinear systems have already been reported [16–18]. However, AWC design for nonlinear systems is a nontrivial problem that remains still unsolved [5] due to the inherent complexity of nonlinear systems.

One of the simple AWC design techniques for linear systems is the internal model control (IMC)-based scheme. Although this scheme can offer poor performance, an AWC always exists for asymptotically stable plants, and it is highly applicable to other actuator nonlinearities [10, 19, 20]. The goal of this AWC scheme is to make the conventional nominal controllers, which are designed for unconstrained systems, unaware of saturation effects, such that the nominal controller must see the system composed of AWC and saturated plant as indistinguishable from the open-loop plant without saturation. To this end, the IMC-based AWC for linear systems uses an exact copy of the plant. Further, a more general decoupled-architecture-based AWC scheme, due to its performance, robustness, and wide applicability to uncertain, time-delay, unstable, and cascade plants, also has been found to be interesting for linear systems (see, for example, [5, 14, 15], and [21]).

Recently, a preliminary analytical study was conducted to evaluate applicability of IMC- and decoupled-architecture-based AWC schemes to dynamic-inversion-based feedback-linearizable Lipschitz nonlinear systems [22]. However, the nonlinear IMC-based AWC scheme is not able to construct the mapping between controller output and controller input same as the nominal plant model. Based on an a priori assumption of the existence of decoupled architecture, the possibility of a so-called decoupling AWC scheme that uses nonlinear matrix inequalities for globally Lipschitz nonlinear systems is discussed in the same work, although a decoupling architecture is not assured. Nevertheless, in order to explore less conservative AWC architectures, to address AWC design for a variety of nonlinear systems, to develop synthesis conditions for unstable and oscillatory systems, and to investigate noncomplex design methodologies with less parameter tuning effort, further studies are required.

Based on the works [17] and [23], an IMC-based AWC scheme for nonlinear systems is proposed in this paper, which achieves a mapping between the output and the input of a nominal controller same as the nominal plant. It is further shown that a nonlinear IMC-based AWC always exists for asymptotically stable nonlinear systems, regardless of the nonlinearity type. For better performance, a novel full-order decoupling AWC architecture for nonlinear systems is proposed. This study shows that a proper selection of the nonlinear component in the dynamics of a full-order AWC plays a key role in establishing an equivalent decoupled architecture. By means of the proposed decoupled architecture, the Lipschitz condition, a quadratic Lyapunov function, the sector condition, and L 2 gain reduction, a linear matrix inequality (LMI)-based global full-order AWC scheme for asymptotically stable systems with global Lipschitz nonlinearities is developed. To the best of the authors’ knowledge, a global nonlinear full-order LMI-based AWC scheme for asymptotically stable Lipschitz nonlinear systems, by which the optimal AWC parameters can be obtained by solving standard LMI routines, is proposed for the first time. Due to the potential for wide applicability in the field of nonlinear science, a decoupled-architecture-based local AWC scheme for unstable and chaotic systems, which can simultaneously guarantee the region of stability and the closed-loop performance, is derived. The authors believe that this type of local treatment, utilizing LMIs, is applied for the first time to decoupled-architecture-based AWC schemes. The proposed AWC schemes are validated through numerical simulations for controlling a chaotic Chua’s circuit.

The remainder of this paper is organized as follows. Section 2 describes the system, and Sect. 3 discusses the nonlinear IMC-based AWC scheme. Section 4 illustrates the proposed full-order AWC architecture and its equivalent decoupled architecture. Section 5 treats the decoupled-architecture-based AWC design. Section 6 provides the numerical simulation results for the proposed methodology. Finally, Sect. 7 presents the conclusions of this study.

Notation

Standard notation is used throughout the paper. The L 2 gain from d to z is defined as \(\sup_{\Vert d \Vert _{2} \ne 0} ( \Vert z \Vert _{2} / \Vert d \Vert _{2} )\), where \(\Vert \cdot \Vert _{2} = \sqrt{\int_{0}^{\infty} \Vert \cdot \Vert ^{2}\,dt}\) denotes the L 2 norm and ∥⋅∥ represents the Euclidean norm of vector d or z. A symmetric positive (or semi-positive) definite matrix X is represented by X>0 (or X≥0). For the ith-diagonal entry x i for i=1,2,…,m, \(\operatorname {diag}(x_{1},x_{2},\ldots ,x_{m})\) represents a diagonal matrix. For a matrix A, A (i) denotes the ith row of the matrix. For u∈R m, the saturation function is defined as \(\operatorname {sat}(u) = \operatorname {sign}(u_{(i)})\min ( \bar{u}_{(i)},\vert u_{(i)} \vert )\), where \(\bar{u}_{(i)} > 0\) is the ith bound on the saturation.

2 System description

Consider a class of nonlinear systems given by

(1)

where x p ∈R n, \(u_{\operatorname {sat}} = \operatorname {sat}(u) \in R^{m}\), u∈R m, and y∈R p represent the state, the saturated control input, the control input, and the output vectors, respectively. The nonlinear function f(x p )∈R n stands for a time-varying vector. The matrices A∈R n×n, B∈R n×m, C∈R p×n, and D∈R p×m are constant. The nominal open-loop system is defined as

(2)

where x n ∈R n, u n ∈R m, and y n ∈R p are the nominal plant state, the nominal plant input, and the nominal plant output of the system, respectively, in the absence of saturation (i.e., by taking \(u_{n} = u = u_{\operatorname {sat}}\)). Suppose that an output feedback nominal tracking controller, designed for the nominal open-loop system, has the form

$$ \left . \begin{array}{l} \dot{x}_{c} = f_{c}(x_{c},y_{n},r,t) \\ u_{n} = g_{c}(x_{c},y_{n},r,t) \end{array} \right \} K(r,y_{n}), $$
(3)

where r∈R p and x c ∈R q are the desired output reference signal and the controller state vector, respectively. The time-varying nonlinearities f c (⋅) and g c (⋅), representing the controller dynamics, are of appropriate dimensions. The closed-loop system formed by (2) and (3) is called a nominal closed-loop system.

Assumption 1

The nominal closed-loop system is well-posed and asymptotically stable if r=0, and has the desired tracking performance if r≠0.

For a diagonal positive definite matrix W∈R m×m, the classical global sector condition is given by

$$ D_{z}(u)^{T}W \bigl[ u - D_{z}(u) \bigr] \ge 0, $$
(4)

where \(D_{z}(u) = u - \operatorname {sat}(u)\) represents the dead-zone nonlinearity.

3 IMC-based AWC design

The proposed IMC-based AWC parameterization is given by

(5)

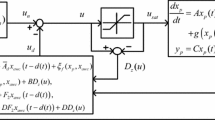
where x aw∈R n and y d ∈R p represent the vectors for the AWC state and output, respectively. The function f IMC(x p ,x aw)∈R n is the nonlinear component of the IMC-based AWC to be determined. The overall closed-loop system with the IMC-based AWC (by assigning u=u n ) is schematized in Fig. 1. The AWC block has two inputs, x p and \(\tilde{u}\), and provides one output, y d , to recover the nominal plant output y n as y n =y+y d . The main objective of the IMC-based AWC is to achieve the same mapping from u n to y n as in the nominal state space model (2), in order that the controller (3) becomes unaware of the saturation effects [10, 19]. To find the nonlinearity f IMC(x p ,x aw), the open-loop system (1) under saturation is rewritten for \(\tilde{u} = u_{n} - u_{\operatorname {sat}}\) as

(6)

Using (5), (6), y n =y+y d , and x n =x p +x aw, we obtain the state space model for the nonlinear mapping from u n to y n as

(7)

The mapping (7) for the IMC-based AWC case will be exactly the same as for the nominal open-loop system (2) if

(8)

Hence, to obtain an appropriate nonlinear IMC-based AWC, the function f IMC(x p ,x aw) must be selected as in (8). For asymptotically stable systems under Assumption 1, the open-loop system (1), the mapping from u n to y n given by (2), and the nominal closed-loop system formed by (2)–(3) are stable. It implies that the output of the IMC-based AWC, given by y d , will remain bounded. Consequently, a stable IMC-based AWC, given by (5) and (8), ensuring the mapping from u n to y n same as the nominal plant, always exists for asymptotically stable nonlinear systems, no matter what type of nonlinear function f(⋅) is used in the plant dynamics.

Fig. 1
figure 1

Proposed IMC-based AWC for asymptotically stable nonlinear systems

Full size image

Remark 1

The present work shows that an IMC-based nonlinear AWC for nonlinear systems always exists regardless of the type of nonlinearity f(x p ). Hence, the selection of f IMC(x p ,x aw), as in [17] and [23], can be used to design a dynamic AWC for a broader class of nonlinear systems.

4 Proposed decoupled AWC architecture

It is well known from the literature (see, for example, [14] and [20]) that the IMC-based AWC schemes are not preferable due to slow response from the AWC. Therefore, a more general nonlinear AWC architecture and its equivalent decoupled architecture for nonlinear systems are developed in this section. The proposed parameterization for decoupled-architecture-based nonlinear AWC is given by

(9)

where x aw∈R n, u d ∈R m, and y d ∈R p are the state, the input, and the output of the AWC, respectively, and F∈R m×n is a constant matrix to be determined. The initial condition of AWC can be taken as x aw(0)=0. Note that the IMC-based AWC parameterization (5) is a special case of the proposed decoupled-architecture-based AWC parameterization (9) for F=0. A schema of the overall closed-loop system formed by plant (1), controller (3), and AWC (9) is shown in Fig. 2. The proposed AWC, as in the IMC-based AWC scheme, has two inputs \(\tilde{u}\) and x p . For compensation of the saturation nonlinearity, the nonlinear AWC provides two signals, u d and y d , in order to modify the controller output u n as u=u n −u d and the constrained plant output y d as y n =y+y d , respectively.

Fig. 2
figure 2

Proposed decoupled-architecture-based AWC for nonlinear systems

Full size image

Figure 3 shows a decoupled architecture equivalent to that in Fig. 2. The overall closed-loop system consists of two components, which are shown separated by a dashed line. The lower component is the nominal nonlinear closed-loop system, and the upper part is the uncertain decoupled nonlinear component. A two-step procedure that is provided shows that the nonlinear mappings Γ n :u n →y n and Γ d :u n →y d are equivalent for the two architectures. First, consider the mapping Γ n :u n →y n in Fig. 2. Applying \(\tilde{u} = u - u_{\operatorname {sat}}\) and u=u n −u d to the nonlinear system (1) yields

(10)

Using u d =Fx aw, the state and output equations for x aw and y d , respectively, can be rewritten as

(11)

Applying the transformations y n =y+y d and x n =x p +x aw and using (9) and (11) yields the mapping Γ n :u n →y n for Fig. 2 as given by (2), which is identical to the state space description for the mapping Γ n :u n →y n shown in Fig. 3. Next, consider the mapping Γ d :u n →y d , described by (9) and u=u n −u d , for the architecture shown in Fig. 2. Using u=u n −u d and \(\tilde{u} = D_{z}(u)\) yields \(\tilde{u} = D_{z}(u_{n} - u_{d})\). Further, using \(\tilde{u} = D_{z}(u_{n} - u_{d})\) and x p =x n −x aw in (9) affords

(12)

which is the same as the state space representation for the mapping Γ d :u n →y d in Fig. 3. Hence, it follows that the architectures shown by Figs. 2 and 3 are equivalent. However, the decoupled architecture shown in Fig. 3 can be used for the selection of the AWC design requirements. By minimizing the L 2 gain of the nonlinear mapping Γ d :u n →y d , we can achieve the performance of the overall closed-loop system with AWC closer to the nominal performance.

Fig. 3
figure 3

Equivalent decoupled architecture of Fig. 2, which can be used for selection of the unknown component of the AWC

Full size image

Remark 2

The term Fx aw in the state equation of AWC (9) can be utilized for multiple performance objectives to ensure the robustness, disturbance rejection, enlargement of the region of stability, and fast convergence rate in contrast to [17] and the IMC-based AWC scheme in the previous section. Furthermore, the proposed AWC architecture is less conservative than [22], for the selection of AWC design objectives, due to existence of a decoupled architecture because of the proposed selection of the function f(x p +x aw)−f(x p ) as a nonlinear AWC component. Owing to these features, a full-order decoupled AWC architecture for more complex nonlinear systems is provided in Appendix A, which can be helpful in future.

5 AWC design

In this section, the LMI-based AWC design for nonlinear systems by means of the proposed decoupled architecture is described. We take the following assumption.

Assumption 2

The nonlinearity f(x) for all \(x,\bar{x} \in R^{n}\) satisfies the following Lipschitz condition:

$$ \bigl \Vert f(x) - f(\bar{x}) \bigr \Vert \le \bigl \Vert L(x - \bar{x}) \bigr \Vert , $$
(13)

where L is a matrix of suitable dimensions.

Note that the AWC architectures proposed in the previous sections are general and applicable to a nonlinear system (1), even if Assumption 2 is not satisfied. A nonlinear matrix inequality-based treatment for locally Lipschitz and non-Lipschitz systems will be addressed later. Now, we provide an LMI-based condition for designing AWC by minimizing the L 2 gain of the mapping Γ d :u n →y d .

Theorem 1

Consider that the overall closed-loop system in Fig. 2 (with architecture equivalent to that in Fig. 3), comprised of plant (1), controller (3), and AWC (9), satisfies Assumptions 1–2. The optimization

$$\min \gamma $$

such that

$$ \gamma > 0,\qquad Q > 0,\quad U > 0, $$
(14)

and

(15)

where γ is a scalar, U∈R m×m and Q∈R n×n are diagonal and symmetric matrices, respectively, and M∈R m×n is a constant matrix, ensures the following:

  1. (i)

    the asymptotic stability of the decoupled nonlinear component Γ d :u n →y d if u n =0

  2. (ii)

    the L 2 gain of the nonlinear mapping Γ d :u n →y d less than γ (that is, ∥y d ∥2/∥u n ∥2<γ) if u n ≠0

Moreover, the optimal value of parameter F can be obtained from F=MQ −1.

Proof

As stated earlier, the goal of AWC design is to minimize the L 2 gain γ for the nonlinear mapping Γ d :u n →y d in Fig. 3. Accordingly, consider a quadratic Lyapunov function given by

$$ V(x_{\mathrm{aw}},t) = x_{\mathrm{aw}}^{T}\gamma Px_{\mathrm{aw}}, $$
(16)

with P=P T>0 and γ>0. Defining

$$ J_{1} = \bigl( \dot{V} + y_{d}^{T}y_{d} - \gamma ^{2}u_{n}^{T}u_{n} \bigr) / \gamma < 0 $$
(17)

and integrating from 0 to T→∞ yields

(18)

which implies the following:

  1. (a)

    if u n =0, (17) implies that \(\dot{V} < 0\) and the decoupled nonlinear component becomes asymptotically stable;

  2. (b)

    given x aw(0)=0, V(x aw,0)=0, and V(x aw,T)>0, (18) ensures that \(\Vert y_{d} \Vert _{2}^{2} < \gamma ^{2}\Vert u_{n} \Vert _{2}^{2}\), that is, the L 2 gain of mapping Γ d :u n →y d is less than γ.

For simplicity, we define

$$ \bar{A} = A + BF,\qquad \bar{C} = C + DF. $$
(19)

Taking the time-derivative of (16) along the state equation in (9), using the resultant and (19), and substituting \(y_{d} = (C + DF)x_{\mathrm{aw}} + D\tilde{u}\) into (17), we obtain

(20)

Using inequality (13) and (20), we obtain J 1≤Z T Π 1 Z<0, where

$$ Z = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} x_{\mathrm{aw}}^{T} & \tilde{u}^{T} & ( f(x_{n}) - f(x_{n} - x_{\mathrm{aw}}) )^{T} & u_{n}^{T} \end{array} \right ]^{T}, $$
(21)
$$ \varPi _{1} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \bar{A}^{T}P + P\bar{A} + L{}^{T}L + (1/\gamma )\bar{C}{}^{T}\bar{C} & PB + (1/\gamma )\bar{C}{}^{T}D & P & 0 \\ * & (1/\gamma )D^{T}D & 0 & 0 \\ * & * & - I & 0 \\ * & * & * & - \gamma I \end{array} \right ] < 0. $$
(22)

Sector condition (4) yields \(\tilde{u}^{T}W [ u_{n} - Fx_{\mathrm{aw}} - \tilde{u} ] \ge 0\) for a diagonal matrix W>0, which can be rewritten as Z T Π 2 Z≥0, where

$$ \varPi _{2} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 0 & - F^{T}W & 0 & 0 \\ * & - 2W & 0 & W \\ * & * & 0 & 0 \\ * & * & * & 0 \end{array} \right ] \ge 0. $$
(23)

Combining (22) and (23) through the S-procedure, Π=Π 1+εΠ 2<0, for a scalar ε>0, taking v=εW and, further, applying the Schur complement and (19), we obtain

$$ \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} (A^{T} + F^{T}B^{T})P + P(A + BF) & PB - F^{T}v & P & 0 & L^{T} & (C + DF)^{T} \\ * & - 2v & 0 & v & 0 & D^{T} \\ * & * & - I & 0 & 0 & 0 \\ * & * & * & - \gamma I & 0 & 0 \\ * & * & * & * & - I & 0 \\ * & * & * & * & * & - \gamma I \end{array} \right ] < 0. $$
(24)

Applying the congruence transform by pre- and post-multiplying the inequality (24) with \(\operatorname {diag}(P^{ - 1},v^{ - 1},I, I,I,I)\), and taking P −1=Q>0, v −1=U>0, and M=FQ, the LMIs (14)–(15) are obtained, which completes the proof of Theorem 1. □

The LMI-based condition developed in Theorem 1, by utilizing the global sector condition, can be used for global AWC design of asymptotically stable systems. If a nonlinear system (e.g., an unstable or a chaotic system) does not verify the asymptotic stability assumption, obtaining global results is difficult owing to infeasibility of the synthesis condition. Therefore, the local sector condition [24] (see also [25]) can be used to design a local decoupled-architecture-based full-order AWC. The main advantage of this type of local sector condition is its utility to enlarge the region of stability for systems under input saturation. Consider a region

$$ S(\bar{u}) = \bigl\{ w \in R^{m}; - \bar{u} \le u - w \le \bar{u} \bigr\}, $$
(25)

where \(\bar{u} \in R^{m}\) is a constant vector representing a bound on saturation. If (25) is satisfied, the local sector condition

$$ \tilde{u}^{T}W [ w - \tilde{u} ] \ge 0 $$
(26)

is ensured by application of Lemma 1 (in [24]) to the dead-zone nonlinearity of the architecture in Fig. 3. By selecting w=u n +Gx aw, (25)–(26) can be rewritten as

$$ S(\bar{u}) = \bigl\{ w \in R^{m}; - \bar{u} \le ( - F - G)x_{\mathrm{aw}} \le \bar{u} \bigr\}, $$
(27)
$$ \tilde{u}^{T}W [ u_{n} + Gx_{\mathrm{aw}} - \tilde{u} ] \ge 0. $$
(28)

Now, we propose an LMI-based sufficient condition for designing a local decoupled-architecture-based AWC for a nonlinear system (1).

Theorem 2

Consider the overall closed-loop system of Fig. 2 (with architecture equivalent to that in Fig. 3), comprised of plant (1), controller (3), and AWC (9), which satisfies Assumptions 1–2. Suppose that the LMIs

$$ \sigma > 0,\qquad \delta > 0,\qquad Q > 0,\qquad U > 0, $$
(29)
$$ \left [ \begin{array}{c@{\quad}c@{\quad}c} Q & - M_{(i)}^{T} - H_{(i)}^{T} \\ * & \delta \bar{u}_{(i)}^{2} \end{array} \right ] \ge 0,\quad i = 1,\ldots,m, $$
(30)

and

(31)

are satisfied, where σ is a scalar, δ −1 is the acceptable bound on the L 2 norm of u n , U∈R m×m and Q∈R n×n are diagonal and symmetric matrices, respectively, and M∈R m×n and H∈R m×n are constant matrices. Then the following are ensured:

  1. (i)

    the decoupled nonlinear component is asymptotically stable with region of convergence \(x_{\mathrm{aw}}^{T}\delta Q^{ - 1}x_{\mathrm{aw}} \le 1\) if u n =0;

  2. (ii)

    the AWC state remains bounded by \(x_{\mathrm{aw}}^{T}\delta Q^{ - 1}x_{\mathrm{aw}} \le 1\), ∀t>0, and the L 2 gain for the mapping Γ d :u n →y d is less than \(\gamma = \sqrt{\sigma}\), that is, ∥y d ∥2/∥u n ∥2<γ.

Moreover, the parameter F can be determined by F=MQ −1.

Proof

To minimize the L 2 gain γ, for the nonlinear mapping Γ d :u n →y d representing the decoupled nonlinear component shown in Fig. 3, consider a quadratic Lyapunov function

$$ V(x_{\mathrm{aw}},t) = x_{\mathrm{aw}}^{T}Px_{\mathrm{aw}} $$
(32)

and P=P T>0 with the inequality

$$ J_{2} = \dot{V} + \sigma ^{ - 1}y_{d}^{T}y_{d} - u_{n}^{T}u_{n} < 0, $$
(33)

where scalars ε>0 and σ=γ 2>0. By integrating the inequality (33) from t=0 to t=T>0, it can be seen that

  1. (a)

    \(V(x_{\mathrm{aw}},T) < \int_{0}^{T} u_{n}^{T}u_{n} \le \Vert u_{n} \Vert _{2}^{2} < \delta ^{ - 1}\ \forall T > 0\), as V(x aw,0)=0 for x aw(0)=0. This shows that the AWC state x aw remains bounded by \(x_{\mathrm{aw}}^{T}\delta Px_{\mathrm{aw}} <\nobreak 1\) for all times t≥0. The LMI (30) implies that the region \(x_{\mathrm{aw}}^{T}\delta Px_{\mathrm{aw}} < 1\) is included in S(u 0). Hence, (27)–(28) are validated.

  2. (b)

    \(\Vert y_{d} \Vert _{2}^{2} < \gamma ^{2}\Vert u_{n} \Vert _{2}^{2}\) is ensured, which can be validated by taking T→∞ as in the proof of Theorem 1. Hence, the L 2 gain of the mapping Γ d :u n →y d is guaranteed to be less than γ.

Additionally, if u n =0 and \(x_{\mathrm{aw}}^{T}(t_{1})\delta Px_{\mathrm{aw}}(t_{1}) < 1\) for all t≥t 1, the decoupled nonlinear component is asymptotically stable as clear from (33). The LMI (31) can be obtained using the local sector condition (28), and inequalities (32)–(33) are derived in a manner similar to the proof of Theorem 1. Note that P −1=Q>0, M=FQ, H=GQ, and U=(εW)−1 are used in the derivation of LMIs (29)–(31). □

The local LMI-based AWC scheme proposed in Theorem 2 can be used to acquire a reasonable regional performance by minimizing σ for a given value of the tolerate-able bound δ −1. Moreover, for a given value of σ, the proposed methodology can be used to provide the largest possible bound on the L 2 norm of u n .

Remark 3

The proposed AWC design techniques by Theorems 1 and 2 can be applied to design a global or local AWC for nonlinear systems, which, unlike those of [17, 18], and [22], are not necessarily feedback-linearizable. The techniques [18] and [22] require bounded-input bounded-state stability or exponentially stability for open-loop plants. By contrast, the local AWC treatment provided in Theorem 2 can be used for unstable nonlinear systems to acquire a large region of stability. In addition, more systematic approaches, than the traditional AWC schemes, are developed in Theorems 1 and 2 for selection of unknown AWC parameters.

Remark 4

A more general parameterization than (9) can also be selected for decoupled-architecture-based AWC design. Motivated by [22], nonlinear matrix inequality-based preliminary approaches for AWC design of locally Lipschitz and non-Lipschitz nonlinear systems based on a more general parameterization are described in Appendix B. The optimization techniques in the work [22] (and references therein) can be used to solve the nonlinear matrix inequalities. The interesting feature of the proposed AWC scheme is its applicability to locally Lipschitz and non-Lipschitz nonlinear systems by means of a less conservative decoupled AWC architecture. However, further work is still needed to investigate the AWC design for locally Lipschitz and non-Lipschitz nonlinear systems.

6 Simulation results

Control of chaotic systems subjected to input saturation nonlinearity [26, 27] is a nontrivial problem owing to complex behavior of chaotic systems. To show the applicability of the proposed AWC scheme to nonlinear science, the following chaotic Chua’s circuit (see [28]) is considered:

$$ A = \left [ \begin{array}{c@{\quad}c@{\quad}c} - 2.548 & 9.1 & 0 \\ 1 & - 1 & 1 \\ 0 & - 14.2 & 0 \end{array} \right ],\qquad B = \left [ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right ], $$
(34)
$$ C = \left [ \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \end{array} \right ],\qquad D = 0, $$
(35)

and

(36)

We can select \(L = \operatorname {diag}(10,0,0)\). Inspired by [29], the state x p(1) can be controlled by employing a feedback-linearizable PI controller given by

(37)

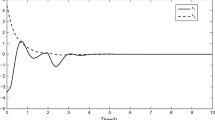
The AWC design scheme in [22] is limited to asymptotically stable systems; therefore, it cannot be applied to the present case. To obtain the implementable AWC parameter F, the values of σ=0.1 and δ=0.001 were fixed. The saturation limit was taken as \(\bar{u} = 2\). By solving the LMIs of Theorem 2, F=[−123.037 −6.88 −0.0136] was obtained. Note that the LMIs of Theorem 2 can also be solved for optimal solution of the L 2 gain from u n to y d . The best value of the L 2 gain was obtained to be γ=3.52×10−6 for δ=0.001. Figure 4 shows the nominal closed-loop response, the closed-loop response with saturation (without an AWC), the closed-loop response with the proposed AWC, and the closed-loop response with the AWC [18] for a square wave reference signal with different controller parameter K P and K I selections. The closed-loop response with the proposed AWC tracks the reference signal, for each selection of K P and K I , with a higher overshoot than the nominal system due to the input constraint, whereas the closed-loop response with saturation exhibits an unstable behavior. The closed-loop response with the AWC [18] does not track the reference signal for K P =K I =30. When K P =K I =40, the performance of the AWC is improved, though instability occurs after time t=40 s. Upon further increasing the controller parameters to K P =K I =50, the response of the AWC [18] was reasonable, but remained inferior to the proposed methodology. The response of the AWC [18] is highly dependent on the overall closed-loop system; this approach therefore can suffer performance limitations due to the slow AWC response caused by slow closed-loop system dynamics. However, selection of a fast nominal controller, producing a fast closed-loop system, can remedy these problems.

Fig. 4
figure 4

Closed-loop response of chaotic Chua’s circuit with the proposed AWC scheme under different controller parameters: (a) K P =K I =30, (b) K P =K I =40, (c) K P =K I =50

Full size image

7 Conclusions

This paper explored the possibilities of a nonlinear full-order AWC design for nonlinear systems under actuator saturation. A nonlinear IMC-based AWC architecture was developed to deal with asymptotically stable nonlinear systems. A more general architecture based on the transformation of an overall closed-loop system into a decoupled architecture was developed, which can be used for stable, unstable, and chaotic systems. Global and local LMI-based sufficient conditions were developed in order to design a decoupled-architecture-based AWC for systems with globally Lipschitz nonlinearities. The proposed local AWC design ensures, simultaneously, a large region of stability and a reasonable closed-loop performance. The proposed AWC schemes were successfully tested using a numerical example, and its results were found to be supportive for resolution of automation-industry and nonlinear science problems.