Multistage anti-windup design for linear systems with saturation nonlinearity: enlargement of the domain of attraction

Abstract

This paper considers the multistage anti-windup (AW) design for linear systems with saturation nonlinearity, with the objective of enlarging the domain of attraction of the resulting closed-loop system. We present results for both static and dynamic AW compensation gains, in terms of linear matrix inequalities. Iterative algorithms are established to obtain the AW compensation gains that maximize the estimate of the domain of attraction. In addition, a particle swarm optimization-based systematic method is proposed to determine the design point of the multistage AW scheme and to set the initial conditions of the established iterative algorithms. Using the proposed method, benefits of the multistage AW on the domain of attraction are illustrated through a benchmark example.

1 Introduction

It has been well recognized that saturation nonlinearity affects virtually all practical control systems. Due to saturation, the actual plant input will be different from the controller output, which causes performance degradation and may even induce instability. Designing a high-performance controller for dynamic systems subject to saturation nonlinearity has received an increasing attention in academia and industry over the past several decades [1–6]. Various design methods for dealing with saturation nonlinearity have been developed, which can be generally classified into two broad classes: the one-step approach and the two-step approach. The one-step approach is an approach that takes the saturation nonlinearity explicitly into account when designing controllers. Although this methodology is satisfactory in principle, it has often been criticized for its conservatism [3]. In the two-step approach, a nominal controller which not accounts for the saturation nonlinearity is first designed to achieve some nominal performance requirements. Then, a compensation term is added to the nominal controller to minimize the adverse effects of saturation. Such an approach is called anti-windup (AW) and the compensation term is referred to as AW compensator. In this paper, we concentrate on the design of the AW compensator.

In traditional AW design, a single AW compensator (or set of gains) is designed and set to be activated as soon as saturation occurs. Almost all AW designs were based on this paradigm (e.g., [7–10]). However, in recent years, several AW schemes that use different activation mechanisms have been proposed in the literature. In [11, 12], a modified AW scheme called as delayed AW was proposed. The delayed AW is not to activate the AW compensator immediately when saturation is encountered, but instead to allow saturated actuators act unassisted up to a pre-designed point. Wu and Lin [13, 14] proposed a modified AW scheme opposite to the delayed AW, which is referred to as anticipatory AW. Considering the system dynamical nature, the basic idea of the anticipatory AW is to activate the AW compensator in anticipation of actuator saturation. Further modification of the AW scheme can be found in [15, 16], in which the proposed AW scheme consists of two AW compensators: one activated at the occurrence of actuator saturation (immediate AW compensator) and the other activated in delayed of actuator saturation (delayed AW compensator).

The modified AW schemes mentioned above add not too much complexity, but indeed have the potential of further improving the closed-loop performance in tracking reference signals. Except the transient performance, enlarging the domain of attraction of the system with saturation nonlinearity is also an important index to measure the improvement in AW design [17–21]. In [22], a linear matrix inequality (LMI)-based analysis approach has been developed to enlarge the domain of attraction of the closed-loop system under a pre-designed nominal controller. Based on the work of [22], several improved analysis approaches have been proposed to reduce the conservativeness of the resulting domains [23, 24]. Typically, it has been shown that the anticipatory AW could obtain a larger domain of attraction than the delayed AW and the traditional AW, both in static case [13] and in dynamic case [25]. We note that the effects of using multiple sets of AW gains on domain of attraction still remain an open problem.

In this paper, we further investigate the possible benefits of the multistage AW scheme proposed in [15, 16], in terms of domain of attraction. Our work is based on extending the AW synthesis approach established in [22, 26] to include a static immediate AW compensator and a static/dynamic delayed AW compensator. The actual saturation element is modeled as a time-varying gain, and the artificial saturation element in the multistage AW scheme is modeled by polytopic representation method. Then, iterative LMI-based algorithms are established to design the AW compensators that lead to the largest estimate of the domain of attraction of the resulting closed-loop system. Both static and dynamic AW compensation gains are considered. Finally, a population-based optimization technique, particle swarm optimization (PSO), is utilized to determine the design point of the multistage AW scheme and to search for the best initialization of the established iterative algorithms. Unlike the traditional methods, in which these free design parameters can only be selected by trial and error according to the computational results, the PSO-based approach provides a systematic way to determine these parameters.

Fig. 1

Multistage AW scheme: $P, C,$ AW and AW$_\mathrm{d}$ are the plant, the linear controller, the immediate AW compensator, and the delayed AW compensator, respectively

The remainder of this paper is organized as follows. In Sect. 2, we give a general description of the multistage AW scheme. In Sect. 3, we establish the LMI-based iterative algorithms to design the AW compensation gains that maximize the estimate of the domain of attraction. Section 4 presents the PSO-based parameter selection method. Section 5 presents the simulation results of a well-known numerical example. A brief conclusion in Sect. 6 ends the paper.

The notation in this paper is standard. ${\mathbb {R}}$ is the set of real numbers. $A^\mathrm{T}$ is the transpose of real matrix $A$. The matrix inequality $A>B (A\ge {B})$ means that $A$ and $B$ are square Hermitian matrices and $A-B$ is positive (semi-)definite. $I$ and $0$ denote the identity matrix and zero matrix with appropriate dimensions, respectively. A block diagonal matrix with sub-matrices $X_{1}, X_{2}, \ldots , X_{p}$ in its diagonal will be denoted by $\hbox {diag}\{ X_{1}, X_{2}, \ldots , X_{p} \}$. For a non-Hermitian real matrix, $\text {He}(A)=A+A^\mathrm{T}$.

2 Problem statement

Consider the following linear plant with saturation nonlinearity

$$\begin{aligned} P:\left\{ \!\!\!\!\! \begin{array}{ll} &{}\dot{x}_{p} = A_{p}x_{p}+B_{p}\hbox {sat}_{h}(u) \\ &{}y= C_{p}x_{p}\\ \end{array} \right. \end{aligned}$$

(1)

where $x_{p}\in {\mathbb {R}}^{n_{p}}$ is the plant state, $u\in {\mathbb {R}}^{n_{u}}$ is the control input, $y\in {\mathbb {R}}^{n_{y}}$ is the measured output, and $A_{p}, B_{p}$, and $C_{p}$ are real constant matrices of appropriate dimensions. The function $\hbox {sat}_{h}(u):{\mathbb {R}}^{n_{u}}\rightarrow {\mathbb {R}}^{n_{u}}$ is the standard decentralized saturation function defined as

$$\begin{aligned}&\hbox {sat}_{h}(u) = \left[ \hbox {sat}_{h^{1}}(u_{1}), \ldots , \hbox {sat}_{h^{n_{u}}}(u_{n_{u}})\right] ^\mathrm{T}, \nonumber \\&\hbox {sat}_{h^{i}}(u_{i}) =\hbox {sign}(u_{i})\hbox {min}\left\{ h^{i},|u_{i}|\right\} \end{aligned}$$

(2)

with $h = \hbox {diag} \{h^{1}, \ldots , h^{n_{u}} \}, h^{i}$ is the saturation limit for $i$th input.

Assume that a linear controller of the form

$$\begin{aligned} C:\left\{ \!\!\! \begin{array}{ll} &{}\dot{x}_{c} = A_{c}x_{c}+B_{c}y \\ &{}u = C_{c}x_{c}+D_{c}y\\ \end{array} \right. \end{aligned}$$

(3)

has been designed. Here, $x_{c}\in {\mathbb {R}}^{n_{c}}$ is the controller state, and $A_{c}, B_{c}, C_{c}$, and $D_{c}$ are real constant matrices of appropriate dimensions. The linear controller guarantees the stability of the closed-loop system and meets some performance requirements in the absence of actuator saturation.

In the traditional AW design, a correction term proportional to the difference between the controller output and the actual plant input $q=u-\hbox {sat}_{h}(u)$ is added to the linear controller, that is,

$$\begin{aligned} \left\{ \!\!\! \begin{array}{ll} &{}\dot{x}_{c} = A_{c}x_{c}+B_{c}y-Eq \\ &{}u = C_{c}x_{c}+D_{c}y\\ \end{array}\right. \end{aligned}$$

(4)

where $E$ is the static AW compensation gain. It is straightforward to see that the compensator is activated as soon as saturation occurs (i.e., $q\ne 0$).

In [16], the multistage AW scheme that consists of an immediate AW compensator and a delayed AW compensator was proposed (see Fig. 1). An artificial saturation element with a higher saturation bound $h/g_\mathrm{d}$ was added; here, $0<g_\mathrm{d}<1$ is a design variable specified by designer. When the two AW compensators both have static gains, the resulting compensated controller can be written as

$$\begin{aligned} \left\{ \!\!\!\!\! \begin{array}{ll} &{}\dot{x}_{c} = A_{c}x_{c}+B_{c}y-Eq-E_\mathrm{d}q_\mathrm{d} \\ &{}u = C_{c}x_{c}+D_{c}y\\ \end{array}\right. \end{aligned}$$

(5)

where $q=u_\mathrm{d}-\hat{u}, q_\mathrm{d}=u-u_\mathrm{d}$, and $E$ and $E_\mathrm{d}$ are the immediate AW compensation gain and the delayed AW compensation gain, respectively.

Letting the delayed AW compensator has dynamic gains, that is,

$$\begin{aligned} \left\{ \!\!\!\!\! \begin{array}{ll} &{}\dot{x}_\mathrm{aw}= A_\mathrm{aw}x_\mathrm{aw}+B_\mathrm{aw}q_\mathrm{d} \\ &{}\eta = C_\mathrm{aw}x_\mathrm{aw}+D_\mathrm{aw}q_\mathrm{d}\\ \end{array}\right. \end{aligned}$$

(6)

where $x_\mathrm{aw}\in {\mathbb {R}}^{n_\mathrm{aw}}$ is the delayed AW compensator state, $A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$ are real constant matrices of appropriate dimensions, $\eta$ is the output of the compensator, then the compensated controller can be correspondingly written as

$$\begin{aligned} \left\{ \!\!\!\!\! \begin{array}{ll} &{}\dot{x}_{c} = A_{c}x_{c}+B_{c}y-Eq+\eta \\ &{}u = C_{c}x_{c}+D_{c}y\\ \end{array}\right. \end{aligned}$$

(7)

In this paper, we will evaluate how the multistage AW scheme affects the size of the achievable domain of attraction of the closed-loop system. Both the controller (5) and (7) will be considered. For simplicity, we first concentrate on single actuator plants, and the results can be readily extended to multiactuator plants, to be presented latter.

3 Multistage AW compensation gain design

3.1 Static AW gains

To rewrite the closed-loop system depicted in Fig. 1, we first replace the actual saturation element with the following time-varying gain $k(t)$,

$$\begin{aligned} k(t)=\frac{\hat{u}(t)}{u_\mathrm{d}(t)} \end{aligned}$$

(8)

When $|u|<h$, no saturation occurs, $k(t)=1$. When $h \le |u| < h/g_\mathrm{d}$, only the actual saturation is in effect, $g_\mathrm{d}<k(t)\le 1$. When $|u|\ge h/g_\mathrm{d}$, both saturation elements are activated, $k(t)=g_\mathrm{d}$. Thus, we have $k(t)\in [g_\mathrm{d}, 1]$. Considering $\hbox {sat}_{h/g_\mathrm{d}}(u) = \frac{h}{g_\mathrm{d}}\hbox {sat}_{1}(\frac{g_\mathrm{d}}{h}u)$, the closed-loop system can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\dot{x} = (A-BF)x+B_{1}\hbox {sat}_{1}(F_{1}x) \\ &{}u = Fx\\ \end{array}\right. \end{aligned}$$

(9)

where

$$\begin{aligned} x= & {} \left[ \begin{array}{l} x_{p} \\ x_{c} \\ \end{array}\right] ,\\ A= & {} \left[ \begin{array}{ll} A_{p} &{}\quad 0 \\ B_{c}C_{p} &{}\quad A_{c}\\ \end{array}\right] ,\quad B= \left[ \begin{array}{l} 0 \\ E_\mathrm{d}\\ \end{array}\right] ,\\ B_{1}= & {} \left[ \begin{array}{l} B_{p}k\frac{h}{g_\mathrm{d}} \\ \left( E_\mathrm{d}-E+EK\right) \frac{h}{g_\mathrm{d}}\\ \end{array}\right] ,\\ F= & {} \left[ \begin{array}{ll} D_{c}C_{p}&C_{c} \end{array}\right] ,\quad F_{1}=\frac{g_\mathrm{d}}{h}F. \end{aligned}$$

Remark 1

Modeling the saturation element as a time-varying gain has been attempted before [11, 13]. In this paper, the synthesis results will be formulated and solved as some LMI-based optimization problems. Due to linearity, we only need to check the resulting LMIs on the extreme values of $k(t){:} 1$ and $g_\mathrm{d}$.

Define the symmetric polyhedron ${\fancyscript{L}}(F_{1})=\{x\in {\mathbb {R}}^{n_{p}+n_{c}}| |f_{1i}x|\le 1, i=1, 2, \ldots , n_{u} \}$, where $f_{1i}$ is the $i$th row of the matrix $F_{1}$. Note that ${\fancyscript{L}}(F_{1})$ stands for the unsaturated zone of the closed-loop system (9).

Similar to [22, 26], we use a contractively invariant ellipsoid to estimate the domain of attraction of the closed-loop system. Define $V(x)=x^\mathrm{T}Px, P\in {\mathbb {R}}^{(n_{p}+n_{c})\times (n_{p}+n_{c})}$ is a positive definite matrix. The ellipsoid $\varOmega (P)=\{x\in {\mathbb {R}}^{n_{p}+n_{c}}| x^\mathrm{T}Px \le 1 \}$ is said to be contractively invariant if $\forall x \in \varOmega (P)\backslash 0$,

$$\begin{aligned} \dot{V}(x)=2x^\mathrm{T}P((A-BF)x+B_{1}\hbox {sat}_{1}(F_{1}x))<0 \end{aligned}$$

(10)

Clearly, if $\varOmega (P)$ is contractively invariant, then it is inside the domain of attraction of the closed-loop system.

For any two matrices $F_{1}, H\in {\mathbb {R}}^{n_{u}\times (n_{p}+n_{c})}$ and a vector $v\in {\fancyscript{V}}, {\fancyscript{V}}=\{v\in {\mathbb {R}}^{n_{u}}|~v_{i}= 1\ \hbox {or} \ 0\}$, denote

$$\begin{aligned} M(v, F_{1}, H)= & {} \hbox {diag}\{v_{1}, v_{2}, \ldots , v_{n_{u}}\}F_{1} \nonumber \\&\quad +\,(I-\hbox {diag}\{v_{1}, v_{2}, \ldots , v_{n_{u}}\})H \end{aligned}$$

(11)

Let $h_{i}$ be the $i$th row of the matrix $H$. We arrive at the following lemma.

Lemma 1

Given an ellipsoid $\varOmega (P)$, if there exists an $H\in {\mathbb {R}}^{n_{u}\times (n_{p}+n_{c})}$ such that

$$\begin{aligned} \begin{array}{l} \left( A-BF+B_{1}M(v, F_{1}, H)\right) ^\mathrm{T}P\\ \qquad +P\left( A-BF +B_{1}M(v, F_{1}, H)\right) \\ \qquad \quad <0,\ \forall v\in {\fancyscript{V}},\ k\in \left\{ 1, g_\mathrm{d}\right\} \end{array} \end{aligned}$$

(12)

and $\varOmega (P) \subset {\fancyscript{L}}(H)$, i.e., $|h_{i}x|\le 1, i=1, 2,\ldots , n_{u}$, for all $x\in \varOmega (P)$, then $\varOmega (P)$ is a contractively invariant set of the closed-loop system (9).

Let $\chi _{R}=\hbox {co}\{x_{1}, x_{2}, \ldots , x_l \}$ be a reference shape set. Here, $x_{1}, x_{2}, \ldots , x_l$ are some priori given points in ${\mathbb {R}}^{n_{p}+n_{c}}, \hbox {co}\{\cdot \}$ denotes the convex hull of a set. With Lemma 1, we can choose the largest ellipsoid through the following optimization problem:

$$\begin{aligned} \begin{array}{lll} &{}&{}\underset{P>0, H}{\hbox {max}} \quad \alpha , \\ \hbox {s.t.}&{}(\hbox {a}) &{}\alpha \chi _{R}\subset \varOmega (P), \\ &{} (\hbox {b}) &{} (A-BF+B_{1}M(v, F_{1}, H))^\mathrm{T}P+P(A-BF \\ &{}&{} \quad +\,B_{1}M(v, F_{1}, H))<0, \forall v\in {\fancyscript{V}}, k\in \{1, g_\mathrm{d}\}, \\ &{} (\hbox {c}) &{} |h_{i}x|\le 1, i=1, 2, \ldots , n_{u}, \forall x \in \varOmega (P). \end{array}\nonumber \\ \end{aligned}$$

(13)

Define $Q=P^{-1},\gamma =\alpha ^{-2}$, and $G=HQ$. Let the $i$th row of $G$ be $g_{i}$. Then, $M(v, F_{1}, H)Q=M(v, F_{1}Q, G)$. The optimization problem (13) can be rewritten as

$$\begin{aligned} \begin{array}{lll} &{}&{}\underset{Q>0, G}{\hbox {min}}\quad \gamma , \\ \hbox {s.t.}&{} (\hbox {a}) &{} \left[ \begin{array}{ll} \gamma &{}\quad x_{i}^\mathrm{T} \\ x_{i} &{}\quad Q \\ \end{array}\right] \ge 0, \ i=1, 2, \ldots , l, \\ &{} (\hbox {b}) &{} Q(A-BF)^\mathrm{T} +(A-BF)Q+ M^\mathrm{T}(v, F_{1}Q,G)B_{1}^\mathrm{T} \\ &{}&{} \quad +\,B_{1}M(v,F_{1}Q,G) < 0,\, \forall v\in {\mathcal {V}},\ k\in \{1, g_\mathrm{d}\}, \\ &{} (\hbox {c}) &{} \left[ \begin{array}{ll} 1 &{}\quad g_{i} \\ g_{i}^\mathrm{T} &{}\quad Q \\ \end{array}\right] \ge 0,\ i=1, 2, \ldots , n_{u}. \end{array} \end{aligned}$$

(14)

Note that the AW compensation gains $E$ and $E_\mathrm{d}$ are embedded in $B$ and $B_{1}$; thus, the optimization (14) cannot be transformed into LMIs in terms of variables $E, E_\mathrm{d}, Q$, and $G$. Denote

$$\begin{aligned} P=\left[ \begin{array}{ll} P_{1} &{}\quad P_{12} \\ P_{12}^\mathrm{T} &{}\quad P_{2} \\ \end{array} \right] ,&\quad M(v, F_{1}, H)=[M_{1} \ M_{2}] \end{aligned}$$

(15)

where $P_{1}\in {\mathbb {R}}^{n_{p} \times n_{p}}, P_{12}\in {\mathbb {R}}^{n_{p} \times n_{c}}, P_{2}\in {\mathbb {R}}^{n_{c} \times n_{c}}, M_{1}\in {\mathbb {R}}^{n_{u} \times n_{p}}$, and $M_{2}\in {\mathbb {R}}^{n_{u} \times n_{c}}$. Then, the condition (b) in (13) can be changed to

$$\begin{aligned} \varSigma =\hbox {He}\left[ \begin{array}{ll} \varSigma _{11} &{}\quad \varSigma _{12} \\ \varSigma _{21} &{}\quad \varSigma _{22} \\ \end{array} \right] <0, \ \forall v\in {\fancyscript{V}}, k\in \left\{ 1, g_\mathrm{d} \right\} \end{aligned}$$

(16)

where

$$\begin{aligned} \varSigma _{11}= & {} P_{1}A_{p}+P_{12}B_{c}C_{p}-P_{12}E_\mathrm{d}D_{c}C_{p}+P_{1}B_{p}k \frac{h}{g_\mathrm{d}}M_{1} \\&\quad +\,P_{12}(E_\mathrm{d}-E+Ek)\frac{h}{g_\mathrm{d}}M_{1}, \\ \varSigma _{12}= & {} P_{12}A_{c}-P_{12}E_\mathrm{d}C_{c}+P_{1}B_{p}k\frac{h}{g_\mathrm{d}}M_{2} \\&\quad +\,P_{12}(E_\mathrm{d}-E+Ek)\frac{h}{g_\mathrm{d}}M_{2}, \\ \varSigma _{21}= & {} P_{12}^\mathrm{T}A_{p}+P_{2}B_{c}C_{p}-P_{2}E_\mathrm{d}D_{c}C_{p}+P_{12}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{1}\\&\quad +\,P_{2}(E_\mathrm{d}-E+Ek)\frac{h}{g_\mathrm{d}}M_{1},\\ \varSigma _{22}= & {} P_{2}A_{c}-P_{2}E_\mathrm{d}C_{c}+P_{12}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{2} \\&\quad +\,P_{2}(E_\mathrm{d}-E+Ek)\frac{h}{g_\mathrm{d}}M_{2}. \end{aligned}$$

The inequality above is LMI in $P_{1}, E$, and $E_\mathrm{d}$. This indicates that with fixed $P_{12}, P_{2}$, and $H$, one can determine the AW compensation gains $E$ and $E_\mathrm{d}$ to make the region $\{x_{p}\in {\mathbb {R}}^{n_{p}}| ~x_{p}^\mathrm{T}P_{1}x_{p}\le 1\}$ as large as possible. Based on the above analysis and the iterative algorithm in [22], we establish the following iterative algorithm.

Algorithm 1

(Iterative algorithm for determining AW compensation gains $E$ and $E_\mathrm{d}$)

Step 1:

For a given reference set $\chi _{R}$ and $E=0, E_\mathrm{d}=0$, solve the optimization problem (14). Denote the solution as $\gamma _{0}, Q_{0}$, and $G_{0}$. Set $\chi _{R}=\gamma _{0}^{-1/2}\chi _{R}$.

Step 2:

Set $i=1$ and $\gamma _\mathrm{opt}=1$. Set $E$ and $E_\mathrm{d}$ with initial values $E^{0}$ and $E_\mathrm{d}^{0}$, respectively.

Step 3:

Solve the optimization problem (14) for $\gamma , Q$, and $G$. Denote the solution as $\gamma _{i}, Q$, and $G$.

Step 4:

Let $\gamma _\mathrm{opt}=\gamma _{i}\gamma _\mathrm{opt}, \chi _{R}=\gamma _{i}^{-1/2}\chi _{R}, P=Q^{-1}$, and $H=GQ^{-1}$.

Step 5:

IF $|\gamma _{i}-1|<\delta$, a predetermined tolerance, GOTO Step 7, ELSE GOTO Step 6.

Step 6:

Solve the following LMI optimization problem

$$\begin{aligned}&\begin{array}{lll} &{}&{}\underset{P_{1}>0, E, E_\mathrm{d}}{\hbox {min}}\quad \gamma , \\ \hbox {s.t.}&{} \hbox {(a}) &{} \left[ \begin{array}{ll} \gamma &{}\quad x_{i}^\mathrm{T} \\ x_{i} &{}\quad P^{-1} \\ \end{array}\right] \ge 0, \quad i=1, 2, \ldots , l, \\ &{} \hbox {(b}) &{} \varSigma <0, \ \forall v\in {\fancyscript{V}}, \ k\in \{1, g_\mathrm{d}\}, \\ &{} \hbox {(c}) &{} \left[ \begin{array}{ll} 1 &{}\quad h_{i} \\ h_{i}^\mathrm{T} &{}\quad P \\ \end{array}\right] \ge 0,\quad i=1, 2, \ldots , n_{u}. \end{array} \end{aligned}$$

(17)

Set the solution as $E$ and $E_\mathrm{d}$, and $i=i+1$, then GOTO Step 3.

Step 7:

IF $\gamma _\mathrm{opt}\le 1$, then $\alpha =\gamma _\mathrm{opt}^{-1/2}$ and $E$ and $E_\mathrm{d}$ are feasible solutions and STOP, ELSE set $E$ and $E_\mathrm{d}$ with another initial values and GOTO Step 2.

3.2 Combination of dynamic and static AW

With a static immediate AW compensator and a dynamic delayed AW compensator, the closed-loop system depicted in Fig. 1 can be written as

$$\begin{aligned} \left\{ \!\!\!\!\! \begin{array}{ll} &{}\dot{x} = (A-BF)x+B_{1}\hbox {sat}_{1}(F_{1}x) \\ &{}u = Fx\\ \end{array}\right. \end{aligned}$$

(18)

where

$$\begin{aligned} x= & {} \left[ \begin{array}{l} x_{p} \\ x_{c} \\ x_\mathrm{aw} \end{array}\right] ,\\ A= & {} \left[ \begin{array}{lll} A_{p} &{}\quad 0 &{}\quad 0 \\ B_{c}C_{p} &{}\quad A_{c} &{}\quad C_\mathrm{aw} \\ 0 &{}\quad 0 &{}\quad A_\mathrm{aw} \end{array} \right] , \quad B=\left[ \begin{array}{l} 0 \\ -D_\mathrm{aw} \\ -B_\mathrm{aw} \end{array}\right] ,\\ B_{1}= & {} \left[ \begin{array}{l} B_{p}k\frac{h}{g_\mathrm{d}} \\ \left( -E+Ek-D_\mathrm{aw}\right) \frac{h}{g_\mathrm{d}} \\ -B_\mathrm{aw}\frac{h}{g_\mathrm{d}} \end{array}\right] ,\\ F= & {} \left[ \begin{array}{lll} D_{c}C_{p}&C_{c}&0 \end{array}\right] ,\quad F_{1}=\frac{g_\mathrm{d}}{h}F. \end{aligned}$$

Define the ellipsoid $\varOmega (P)=\{x\in {\mathbb {R}}^{n_{p}+n_{c}+n_\mathrm{aw}}| ~x^\mathrm{T}Px\le 1\}$ and let $\chi _{R}=\hbox {co}\{x_{1}, x_{2}, \ldots , x_l\}$ be a reference shape set. Here, $x_{1}, x_{2}, \ldots , x_l$ are some priori given points in ${\mathbb {R}}^{n_{p}+n_{c}+n_\mathrm{aw}}$. Based on Lemma 1, we arrive at the following optimization problem to enlarge the estimate of the domain of attraction of the closed-loop system (18),

$$\begin{aligned} \begin{array}{lll} &{}&{} \underset{P>0, H}{\hbox {max}}\quad \alpha , \\ \hbox {s.t.}&{} (\hbox {a}) &{} \alpha \chi _{R}\subset \varOmega (P), \\ &{} (\hbox {b}) &{} (A-BF+B_{1}M(v, F_{1}, H))^\mathrm{T}P+P(A-BF \\ &{}&{} \quad +B_{1}M(v, F_{1}, H))<0, \forall v\in {\fancyscript{V}}, k\in \{1, g_\mathrm{d}\}, \\ &{} (\hbox {c}) &{} |h_{i}x|\le 1, i=1, 2, \ldots , n_{u}, \forall x \in \varOmega (P). \end{array}\nonumber \\ \end{aligned}$$

(19)

where $h_{i}$ is the $i$th row of the matrix $H, H\in {\mathbb {R}}^{n_{u} \times (n_{p}+n_{c}+n_\mathrm{aw})}$.

Define $Q=P^{-1}, \gamma =\alpha ^{-2}$, and $G=HQ$. Let the $i$th row of $G$ be $g_{i}$. The optimization problem (19) can be rewritten as

$$\begin{aligned} \begin{array}{lll} &{}&{} \underset{Q>0, G}{\hbox {min}}\quad \gamma , \\ \hbox {s.t.}&{} (\hbox {a}) &{} \left[ \begin{array}{ll} \gamma &{}\quad x_{i}^\mathrm{T} \\ x_{i} &{}\quad Q \\ \end{array}\right] \ge 0, \quad i=1, 2, \ldots , l, \\ &{} (\hbox {b}) &{} Q(A-BF)^\mathrm{T}+ (A-BF)Q+M^\mathrm{T}(v, F_{1}Q,G)B_{1}^\mathrm{T} \\ &{}&{}\quad +B_{1}M(v,F_{1}Q,G) < 0,\, \forall v\in {\mathcal {V}},\ k\in \{1, g_\mathrm{d}\}, \\ &{} (\hbox {c}) &{} \left[ \begin{array}{ll} 1 &{}\quad g_{i} \\ g_{i}^\mathrm{T} &{}\quad Q \\ \end{array}\right] \ge 0,\quad i=1, 2, \ldots , n_{u}. \end{array} \end{aligned}$$

(20)

Note that the optimization problem above is linear in terms of variables $Q$ and $G$. Next, define

$$\begin{aligned} P&=\left[ \begin{array}{lll} P_{1} &{}\quad P_{12} &{}\quad P_{13} \\ P_{12}^\mathrm{T} &{}\quad P_{2} &{}\quad P_{23} \\ P_{13}^\mathrm{T} &{}\quad P_{23}^\mathrm{T} &{}\quad P_{3} \end{array} \right] ,\nonumber \\&\qquad M(v, F_{1}, H)=\left[ M_{1} \ M_{2} \ M_{3} \right] \end{aligned}$$

(21)

where $P_{1}\in {\mathbb {R}}^{n_{p} \times n_{p}}, P_{12}\in {\mathbb {R}}^{n_{p} \times n_{c}}, P_{13}\in {\mathbb {R}}^{n_{p} \times n_\mathrm{aw}}, P_{2}\in {\mathbb {R}}^{n_{c} \times n_{c}}, P_{23}\in {\mathbb {R}}^{n_{c} \times n_\mathrm{aw}}, P_{3}\in {\mathbb {R}}^{n_\mathrm{aw}\times n_\mathrm{aw}}, M_{1}\in {\mathbb {R}}^{n_{u}\times n_{p}}, M_{2}\in {\mathbb {R}}^{n_{u}\times n_{c}}$, and $M_{3}\in {\mathbb {R}}^{n_{u}\times n_\mathrm{aw}}$. Then, condition (b) in (19) is equivalent to

$$\begin{aligned} \varTheta= & {} \hbox {He} \left[ \begin{array}{lll} \varTheta _{11} &{}\quad \varTheta _{12} &{}\quad \varTheta _{13} \\ \varTheta _{21} &{}\quad \varTheta _{22} &{}\quad \varTheta _{23} \\ \varTheta _{31} &{}\quad \varTheta _{32} &{}\quad \varTheta _{33} \end{array}\right] <0,\nonumber \\&\quad \forall v\in {\fancyscript{V}},\quad k\in \left\{ 1, g_\mathrm{d}\right\} \end{aligned}$$

(22)

where

$$\begin{aligned} \varTheta _{11}= & {} P_{1}A_{p}+P_{12}B_{c}C_{p}-P_{12}D_\mathrm{aw}D_{c}C_{p} \\&\quad -\,P_{13}B_\mathrm{aw}D_{c}C_{p}P_{1}B_{p}k\frac{h}{g_\mathrm{d}}M_{1}\\&\quad +\,P_{12}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{1}-P_{13}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{1}, \\ \varTheta _{12}= & {} P_{12}A_{c}-P_{12}D_\mathrm{aw}C_{c}-P_{13}B_\mathrm{aw}C_{c}P_{1}B_{p}k\frac{h}{g_\mathrm{d}}M_{2} \\&\quad +\,P_{12}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{2}-P_{13}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{2},\\ \varTheta _{13}= & {} P_{12}C_\mathrm{aw}+P_{13}A_\mathrm{aw}P_{1}B_{p}k\frac{h}{g_\mathrm{d}}M_{3} \\&P_{12}(-E+Ek-D_\mathrm{aw})-P_{13}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{3}, \\ \varTheta _{21}= & {} P_{12}^\mathrm{T}A_{p}+P_{22}B_{c}C_{p}-P_{22}D_\mathrm{aw}D_{c}C_{p} \\&\quad -\,P_{23}B_\mathrm{aw}D_{c}C_{p}P_{12}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{1} \\&\quad +\,P_{22}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{1}-P_{23}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{1},\\ \end{aligned}$$

$$\begin{aligned} \varTheta _{22}= & {} P_{22}A_{c}-P_{22}D_\mathrm{aw}C_{c}-P_{23}B_\mathrm{aw}C_{c}+P_{12}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{2} \\&\quad +\,P_{22}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{2}-P_{23}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{2}, \\ \varTheta _{23}= & {} P_{22}C_\mathrm{aw}+P_{23}A_\mathrm{aw}P_{12}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{3} \\&\quad +\,P_{22}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{3}-P_{23}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{3}, \\ \varTheta _{31}= & {} P_{13}^\mathrm{T}+P_{23}^\mathrm{T}B_{c}C_{p}-P_{23}^\mathrm{T}D_\mathrm{aw}D_{c}C_{p} \\&\quad -\,P_{33}B_\mathrm{aw}D_{c}C_{p}P_{13}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{1} \\&\quad +\,P_{23}^\mathrm{T}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{1}-P_{33}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{1},\\ \varTheta _{32}= & {} P_{23}^\mathrm{T}A_{c}-P_{23}^\mathrm{T}D_\mathrm{aw}C_{c}-P_{33}B_\mathrm{aw}C_{c}P_{13}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{2} \\&\quad +\,P_{23}^\mathrm{T}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{2}P_{33}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{2},\\ \varTheta _{33}= & {} P_{23}^\mathrm{T}C_\mathrm{aw}+P_{33}A_\mathrm{aw}P_{13}^\mathrm{T}B_{p}k\frac{h}{g_\mathrm{d}}M_{3} \\&\quad +\,P_{23}^\mathrm{T}(-E+Ek-D_\mathrm{aw})\frac{h}{g_\mathrm{d}}M_{3}-P_{33}B_\mathrm{aw}\frac{h}{g_\mathrm{d}}M_{3}. \end{aligned}$$

The inequality above is linear in terms of variables $P_{1}, E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$. Thus, we arrive at the following iterative algorithm to design the static immediate AW compensation gain and the dynamic delayed AW compensation gains to make the estimate of the domain of attraction of the closed-loop system (18) as large as possible.

Algorithm 2

(Iterative algorithm for determining AW compensation gains $E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$)

Step 1:

For a given reference set $\chi _{R}$ and $E=0, A_\mathrm{aw}=0, B_\mathrm{aw}=0, C_\mathrm{aw}=0$, and $D_\mathrm{aw}=0$, solve the optimization problem (20). Denote the solution as $\gamma _{0}, Q_{0}$, and $G_{0}$. Set $\chi _{R}=\gamma _{0}^{-1/2}\chi _{R}$.

Step 2:

Set $i=1$ and $\gamma _\mathrm{opt}=1$. Set $E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$ with initial values $E^{0}, A_\mathrm{aw}^{0}, B_\mathrm{aw}^{0}, C_\mathrm{aw}^{0}$, and $D_\mathrm{aw}^{0}$, respectively.

Step 3:

Solve the optimization problem (20) for $\gamma , Q$, and $G$. Denote the solution as $\gamma _{i}, Q$, and $G$.

Step 4:

Let $\gamma _\mathrm{opt}=\gamma _{i}\gamma _\mathrm{opt}, \chi _{R}=\gamma _{i}^{-1/2}\chi _{R}, P=Q^{-1}$, and $H=GQ^{-1}$.

Step 5:

IF $|\gamma _{i}-1|<\delta$, a predetermined tolerance, GOTO Step 7, ELSE GOTO Step 6.

Step 6:

Solve the following LMI optimization problem

$$\begin{aligned} \begin{array}{lll} &{}&{} \underset{P_{1}>0, E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}, D_\mathrm{aw}}{\hbox {min}}\quad \gamma , \\ \hbox {s.t.} &{}\hbox {(a}) &{} \left[ \begin{array}{ll} \gamma &{}\quad x_{i}^\mathrm{T} \\ x_{i} &{}\quad P^{-1} \\ \end{array}\right] \ge 0, \quad i=1, 2, \ldots , l, \\ &{} \hbox {(b}) &{} \varTheta <0, \ \forall v\in {\fancyscript{V}}, \ k\in \{1, g_\mathrm{d}\}, \\ &{} \hbox {(c}) &{} \left[ \begin{array}{ll} 1 &{}\quad h_{i} \\ h_{i}^\mathrm{T} &{}\quad P \\ \end{array}\right] \ge 0,\quad i=1, 2, \ldots , n_{u}. \end{array} \end{aligned}$$

(23)

Set the solution as $E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$, and $i=i+1$, then GOTO Step 3.

Step 7:

IF $\gamma _\mathrm{opt}\le 1$, then $\alpha =\gamma _\mathrm{opt}^{-1/2}$ and $E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$ are feasible solutions and STOP, ELSE set $E, A_\mathrm{aw}, B_\mathrm{aw}, C_\mathrm{aw}$, and $D_\mathrm{aw}$ with another initial values and GOTO Step 2.

Remark 2

For multiple input systems (i.e., $n_{u}>1$), the time-varying gain $k(t)$ and the design variable $g_\mathrm{d}$ defined before, respectively, become the following $n_{u}\times n_{u}$ diagonal matrices:

$$\begin{aligned} \begin{array}{lll} K(t) &{} = &{} \hbox {diag}\left\{ k_{1}(t), k_{2}(t), \ldots , k_{n_{u}}(t)\right\} , \\ G_\mathrm{d} &{} = &{} \hbox {diag}\left\{ g_{\mathrm{d}_{1}}, g_{\mathrm{d}_{2}}, \ldots , g_{\mathrm{d}_{n_{u}}}\right\} \end{array} \end{aligned}$$

where $k_{i}(t)\in [g_{\mathrm{d}_{i}}, 1]$. Here, $0<g_{\mathrm{d}_{i}}<1, i=1, 2, \ldots , n_{u}$, is the design point chosen for the $i$th actuator. Define

$$\begin{aligned} {\fancyscript{K}}= & {} \left\{ K(t)= \hbox {diag}\left\{ k_{1}(t), k_{2}(t), \ldots , k_{n_{u}}(t)\right\} \right. \nonumber \\&\left. | ~k_{i}(t)=g_{\mathrm{d}_{i}}\ \hbox {or} \ 1 \right\} \end{aligned}$$

(24)

Due to linearity, any $K(t)$ can be represented as a linear combination of extreme values evaluated at the corners of the parameter hypercube ${\fancyscript{K}}$,

$$\begin{aligned} K(t)=\sum _{i=1}^{2^{n_{u}}}\alpha _{i}(t)\overline{K}^{i} \end{aligned}$$

(25)

where $\overline{K}^{i}\in {\fancyscript{K}}, i=1, 2, \ldots , 2^{n_{u}}$, and $\alpha _{i}(t)\ge 0$ with $\sum _{i=1}^{2^{n_{u}}}\alpha _{i}(t) =1$. Then, in the optimization problems established in this paper, we only need to check the LMIs at the vertices obtained from $K(t)$ (i.e., $\overline{K}^{i}\in {\fancyscript{K}}, i=1, 2, \ldots , 2^{n_{u}}$ ).

Remark 3

Different from [15, 16], in which the authors validated the superiority of the multistage AW scheme by comparing the tracking performance, the results in this section allow one to further investigate the possible benefits of the multistage AW scheme in enlarging the domain of attraction of the resulting closed-loop system. On the other hand, since the multistage AW scheme consists of a traditional AW loop and a delayed AW loop, the obtained results can be also readily extended to the traditional AW scheme and the delayed AW scheme. Let $E_\mathrm{d}=0$, then Algorithm 1 will be reduced to the algorithm obtained in [22] which is for the traditional AW scheme. Let $E=0$, then Algorithm 1 will be reduced to the algorithm obtained in [13] which is for the static delayed AW scheme, and Algorithm 2 will be reduced to the algorithm obtained in [25] which is for the dynamic delayed AW scheme.

4 PSO-based parameter selection

It should be pointed out that the multistage AW scheme can provide better results than the traditional AW scheme, but strongly depends on the choice of the design point $G_\mathrm{d}$. However, no systematic method that determines $G_\mathrm{d}$ is available in the literature until now. On the other hand, it is well recognized that for the nonlinear optimization problems solved by Algorithms 1 and 2, the optimization results depend on the given initial conditions. In the original paper [22], the initialization was left to be given by trial and error based on the obtained optimization results. Such a problem also exists in [23]. In a recent research [24], Li and Lin use an optimal solution from the work of [19] as the initialization, but such a selection does not guarantee the globality of the solution either.

On the other hand, PSO is a population-based global optimization technique developed by Kennedy and Eberhart [27]. In PSO, the system is initialized with a population of random solutions and searches for optima by updating generations. In recent several years, PSO has become quite popular in control engineering [28–32]. As far as our knowledge goes, no work of applying PSO to anti-windup problems has been reported in the literature before. In this paper, we use the PSO algorithm to decide the design point $G_\mathrm{d}$ and to give the initialization values of the established iterative algorithms. With the application of PSO algorithm, one can obtain an optimal selection of the design point $G_\mathrm{d}$ and the initialization values of the iterative algorithms, in a relatively more systematic way. In addition, the algorithm is easy to be implemented, and its benefits will grow when the dimension of the problem increases. For example, for a system with $n_{c}=10$ and $n_{u}=10$, there will be 210 elements in $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$ (510 elements in $G_\mathrm{d}, E^{0}, A_\mathrm{aw}^{0}, B_\mathrm{aw}^{0}, C_\mathrm{aw}^{0}$, and $D_\mathrm{aw}^{0}$), and thus, it is almost impossible to determine these parameters by trial and error. However, the PSO algorithm is a computational intelligence-based technique that is not largely affected by the size of the optimization problem [33].

In PSO, each particle is treated as a potential solution of the optimization problem and initialized with a random position and velocity. Then, all the particles “fly” in the search space to track the feasible solutions. During the fly progress, a particle will track two best positions: One is the best position so far found by the particle itself, and the other is the best position so far found by the swarm. The search path is different for each particle, thus, guarantees that a wide area of the search space is explored, and increases the chance of finding the optimal solution. The $i$th particle in the swarm updates its velocity and position according to the following iterative equations:

$$\begin{aligned} v_{ij}^{k+1}= & {} \omega v_{ij}^{k}+c_{1}r_{1}\left( p_{ij}^{k}-x_{ij}^{k}\right) \nonumber \\&\quad +\,c_{2}r_{2}\left( p_{gj}^{k}-x_{ij}^{k}\right) \end{aligned}$$

(26)

$$\begin{aligned} x_{ij}^{k+1}= & {} x_{ij}^{k}+v_{ij}^{k+1} \end{aligned}$$

(27)

where $i=1, 2, \ldots , N, N$ is the population size, $j=1, 2, \ldots , D, D$ is the dimension of the search space, $k=1, 2, \ldots , k_{\mathrm{max}}, k_{\mathrm{max}}$ is the maximum iteration, $v_{ij}^{k}$ and $x_{ij}^{k}$ are the velocity and position of $j$th dimension of particle $i$ at iteration $k$, respectively, $p_{ij}^{k}$ is the best position of $j$th dimension found by article $i$ until iteration $k, p_{gj}^{k}$ is the best position of $j$th dimension found by the swarm until iteration $k, r_{1}$ and $r_{2}$ are independent random numbers between 0 and 1, $c_{1}$ and $c_{2}$ are learning factors, and $\omega$ is the inertia weight specifying how much the current velocity will affect the new velocity vector. The inertia weight $\omega$ at iteration $k$ can be given as [34]

$$\begin{aligned} \omega ^{k}=\omega _{\mathrm{start}}-\frac{\omega _{\mathrm{start}}-\omega _{\mathrm{end}}}{k_{\mathrm{max}}}\times k \end{aligned}$$

(28)

where $\omega _{\mathrm{start}}$ and $\omega _{\mathrm{end}}$ are the initial value and terminal value of $\omega$, respectively.

Here, we take the case where the two AW compensators both have static gains as example to demonstrate the implementation of PSO. As we hope to obtain a largest domain of attraction, the objective function in PSO algorithm can be straightforward defined as

$$\begin{aligned} J=\frac{1}{\alpha _\mathrm{opt}} \end{aligned}$$

(29)

The decision variables are the design point $G_\mathrm{d}=\hbox {diag}\{g_{\mathrm{d}_{1}}, \ldots , g_{\mathrm{d}_{n_{u}}}\}$ and the given initial values $E^{0}=[e_{ij}^{0}]_{n_{c}\times n_{u}}$ and $E_\mathrm{d}^{0}=[e_{\mathrm{d}, ij}^{0}]_{n_{c}\times n_{u}}$, and in PSO algorithm, they will be expressed as

$$\begin{aligned} X=\left[ g_{\mathrm{d}_{1}}, \ldots , g_{\mathrm{d}_{n_{u}}}, e_{11}^{0}, \ldots , e_{n_{c}n_{u}}^{0}, e_{\mathrm{d},11}^{0}, \ldots , e_{\mathrm{d},n_{c}n_{u}}^{0}\right] \nonumber \\ \end{aligned}$$

(30)

To prevent the values of the obtained AW compensation gains $E$ and $E_\mathrm{d}$ from being too large, we can constrain $E=[e_{ij}]_{n_{c}\times n_{u}}$ and $E_\mathrm{d}=[e_{\mathrm{d},ij}]_{n_{c}\times n_{u}}$ element-by-element by setting

$$\begin{aligned} \varphi _{ij}\le e_{ij}\le \psi _{ij},\quad \varphi _{\mathrm{d},ij}\le e_{\mathrm{d},ij}\le \psi _{\mathrm{d},ij} \end{aligned}$$

(31)

Accordingly, in the PSO algorithm, the search range for the design point $G_\mathrm{d}$ is set to be $g_{\mathrm{d}_{i}}\in (0 \ 1), i=1, 2, \ldots , n_{u}$, and for the AW compensation gains $E$ and $E_\mathrm{d}$,it is set to be $e_{ij}\in [\varphi _{ij} \ \psi _{ij}]$ and $e_{\mathrm{d},ij}\in [\varphi _{\mathrm{d},ij} \ \psi _{\mathrm{d},ij}], i=1, 2, \ldots , n_{c}, \ j=1, 2, \ldots , n_{u}$, respectively.

Thus, the PSO-based iterative algorithm to decide $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$ can be stated as follows:

Algorithm 3

(Iterative algorithm for determining $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$)

Step 1:

Set the swarm population size $N$, the maximal search speed $V_{\mathrm{max}}$, the maximum search iteration number $k_{\mathrm{max}}$, the initial and terminal values of inertia weight $\omega _{\mathrm{satrt}}$ and $\omega _{\mathrm{end}}$, and the search range of the decision variables. Initialize the position and velocity of each particle.

Step 2:

Set $p_{ij}^{1}=x_{ij}^{1}$ and $p_{gj}^{1}=p_{mj}^{1}$, where $p_{mj}^{1}$ satisfies $J(p_{mj}^{1})=\hbox {min}\{J(p_{1j}^{1}), \ldots , J(p_{Nj}^{1})\}$.

Step 3:

Set $k=k+1$. Update the velocity and the position of each particle, and the inertia weight $\omega$ according to (26), (27), and (28), respectively. If $v_{ij}^{k}>V_{\mathrm{max}}$, then $v_{ij}^{k}=V_{\mathrm{max}}$. If $v_{ij}^{k}<-V_{\mathrm{max}}$, then $v_{ij}^{k}=-V_{\mathrm{max}}$. Constrain the position of each particle in the given search range.

Step 4:

For each particle, calculate the objective function (29) using Algorithm 1.

Step 5:

Update the particle itself best position and the swarm best position, respectively, according to

$$\begin{aligned} p_{ij}^{k+1}= & {} \left\{ \begin{array}{ll} p_{ij}^{k}, &{} \quad \hbox {if} \ J\left( p_{ij}^{k}\right) \le J\left( x_{ij}^{k+1}\right) \\ x_{ij}^{k+1}, &{} \quad \hbox {else} \end{array}\right. \end{aligned}$$

(32)

$$\begin{aligned} p_{gj}^{k+1}= & {} \left\{ \begin{array}{ll} p_{gj}^{k},&{} \quad \hbox {if} \ J\left( p_{gj}^{k}\right) \le \hbox {min}\\ &{}\quad \left\{ J\left( p_{1j}^{k+1}\right) , \ldots , J\left( p_{Nj}^{k+1}\right) \right\} , \\ p_{mj}^{k+1},&{} \quad \hbox {else} \end{array}\right. \nonumber \\ \end{aligned}$$

(33)

where $p_{mj}^{k+1}$ satisfies $J(p_{mj}^{k+1})=\hbox {min}\{ J(p_{1j}^{k+1}), \ldots , J(p_{Nj}^{k+1})\}$.

Step 6:

If the number of iteration $k$ reaches the maximum value $k_{\mathrm{max}}$, then GOTO next step, else GOTO Step 3.

Step 7:

The latest swarm best position $p_{gj}^{k_{\mathrm{max}}}$ is an optimal solution to $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$, and $J(p_{gj}^{k_{\mathrm{max}}})$ is the optimal objective function value.

Remark 4

When applying PSO, several settings must be taken into account to facilitate the convergence and avoid fall into local optimal. The search range of the decision variables is decided by the optimization problem itself. For example, in this paper, the design point $g_{\mathrm{d}_{i}}, i=1, 2, \ldots , n_{u}$, is constrained by $0<g_{\mathrm{d}_{i}}<1$, and the AW compensation gains can be limited by $\pm$100. $V_{\mathrm{max}}$ is the parameter that limits the velocity of the particles. If the value of $V_{\mathrm{max}}$ is too high, the particles may fly past good solutions. If the value of $V_{\mathrm{max}}$ is too small, the particles’ movements are limited and may not explore sufficiently beyond local solutions. In general, $V_{\mathrm{max}}$ is set at 10–20 % of the search range of the variable on each dimension [35]. The learning factors are often set to be $c_{1}=c_{2}=2$. Population sizes of 20–50 are most common. The inertia weight controls the exploration property of the algorithm: a larger $\omega$ leads to a more global behavior, and a smaller $\omega$ results in facilitating a more local behavior. In general, $\omega _{\mathrm{start}}$ and $\omega _{\mathrm{end}}$ are set to be 0.9 and 0.4, respectively.

5 Numerical example

We consider here a benchmark example also studied in [22]. The plant and linear controller matrices are given by

$$\begin{aligned} A_{p}= & {} \left[ \begin{array}{ll} -0.1 &{}\quad 0 \\ 0 &{}\quad -0.1 \end{array}\right] ,\quad B_{p}=\left[ \begin{array}{ll} 1.5 &{}\quad 4 \\ 1.2 &{}\quad 3 \end{array} \right] ,\\&\quad C_{p}=\left[ \begin{array}{ll} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{array} \right] ,\\ A_{c}= & {} \left[ \begin{array}{ll} 0 &{}\quad 0 \\ 0 &{}\quad 0 \end{array} \right] ,\quad B_{c}=\left[ \begin{array}{ll} -1 &{}\quad 0 \\ 0 &{}\quad -1 \end{array} \right] ,\\&\quad C_{c}=\left[ \begin{array}{ll} 0.3333 &{}\quad 0 \\ 0 &{}\quad -0.1 \end{array} \right] ,\\ D_{c}= & {} \left[ \begin{array}{ll} -3.333 &{}\quad 0 \\ 0 &{}\quad 1 \end{array} \right] . \end{aligned}$$

We first consider the case that all the AW compensation gains are static. Let $\chi _{R}=[0.6 \ 0.4 \ 0 \ 0]^\mathrm{T}$ and $\delta =10^{-4}$, and constrain each element of the compensation gains by $\pm$100. Figure 2 demonstrates the obtained ellipsoids by different settings of the design point $G_\mathrm{d}$ and the initialization $E^{0}$ and $E_\mathrm{d}^{0}$. We see that the obtained ellipsoids strongly depend on the given values of $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$. As there are 10 elements in these three parameters, it is not easy to find the best group of $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$ that leads to the largest domain of attraction by a trail and error method.

Fig. 2

Ellipsoids with different settings of $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$. Solid line is with $G_\mathrm{d}=\hbox {diag}\{0.80 \ 0.80 \}$, dotted line is with $G_\mathrm{d}=\hbox {diag}\{0.90 \ 0.90 \}$, dash-dotted line is with $G_\mathrm{d}=\hbox {diag}\{0.95 \ 0.95 \}$, and dashed line is with $G_\mathrm{d}=\hbox {diag}\{0.98 \ 0.98 \}$. a $E^0=\left[ \begin{array}{cc} 50 &{} 50\\ 50 &{} 50 \end{array}\right] ,\,E_\mathrm{d}^0=\left[ \begin{array}{cc} 10 &{} 10\\ 10 &{} 10 \end{array}\right]$, b $E^0=\left[ \begin{array}{cc} 10 &{} 10\\ 10 &{} 10 \end{array}\right] ,\,E_\mathrm{d}^0=\left[ \begin{array}{cc} 50 &{} 50\\ 50 &{} 50 \end{array}\right]$, c $E^0=\left[ \begin{array}{cc} 20 &{} 20\\ 20 &{} 20 \end{array}\right] ,\,E_\mathrm{d}^0=\left[ \begin{array}{cc} 80 &{} 80\\ 80 &{} 80 \end{array}\right]$, d $E^0=\left[ \begin{array}{cc} 80 &{} 80\\ 80 &{} 80 \end{array}\right] ,\,E_\mathrm{d}^0=\left[ \begin{array}{cc} 20 &{} 20\\ 20 &{} 20 \end{array}\right]$

Table 1 Settings of PSO algorithm

Then, we use Algorithm 3 to decide $G_\mathrm{d}, E^{0}$, and $E_\mathrm{d}^{0}$. The settings of PSO algorithm are listed in Table 1. The search range of $g_{\mathrm{d}_{i}}, i=1, 2$, is $(0, 1)$. The search range of $e_{ij}^{0}$ and $e_{\mathrm{d},ij}^{0}, i=1, 2, j=1, 2$, is $[-100 \ 100]. V_{\mathrm{max}}$ is set to be 15 % of the search range. We run Algorithm 3 for 10 times, and the evolution histories of the objective function are depicted in Fig. 3. Based on the optimization results, we select

$$\begin{aligned} G_\mathrm{d}&=\hbox {diag}\{0.9752, \ 0.9747\}, \\ E^{0}&=\left[ \begin{array}{ll} 70.9697 &{}\quad 36.4084 \\ 55.8063 &{}\quad 65.0102 \end{array}\right] ,\\&\quad E_\mathrm{d}^{0}=\left[ \begin{array}{ll} 18.2149 &{}\quad 45.6080\\ 18.2149 &{}\quad 84.7193 \end{array}\right] , \end{aligned}$$

which, leads to $\alpha =81.9708$, and

$$\begin{aligned} E&=\left[ \begin{array}{rr} 70.3940 &{} \quad 83.1007 \\ 1.2076 &{}\quad -84.3258 \end{array}\right] ,\\&\quad E_\mathrm{d} =\left[ \begin{array}{ll} 83.6765 &{}\quad -83.7532 \\ 96.1066 &{}\quad -99.8825 \end{array}\right] , \\ P_{1}&=10^{-3}\times \left[ \begin{array}{ll} 2.8254 &{}\quad 2.4486 \\ 2.4486 &{}\quad 2.6776 \end{array}\right] . \end{aligned}$$

Fig. 3

Convergence of the objective function for 10 optimizations

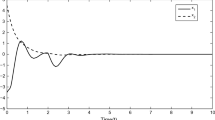
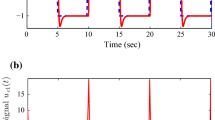
Plotted in Fig. 4 are the obtained ellipsoids, and a state trajectory that starts from a point on its bound. Also plotted in the figure in a dotted line is the ellipsoid obtained in [22]. It can be observed that the multistage AW scheme achieves a significantly larger domain of attraction than the traditional AW scheme. System response corresponding to the trajectory is depicted in Figs. 5 and 6. As these figures suggest, both the immediate AW compensator and the delayed AW compensator are in effect.

Fig. 4

Ellipsoids and a trajectory that starts from a point on the boundary of the larger ellipsoid

Fig. 5

Time history of the plant state

Fig. 6

Plant input: solid line is the time history of $u$, dashed line is the time history of $u_\mathrm{d}$, and dotted line is the time history of $\hat{u}$. a $u_1$, b $u_2$

We next consider the situation when the delayed AW compensator has dynamic gains. Also let $\chi _{R}=[0.6 \ 0.4 \ 0 \ 0]^\mathrm{T}, \delta =10^{-4}$, and constrain each element of the compensation gains by $\pm$100. Using Algorithm 3, we choose

$$\begin{aligned} G_\mathrm{d}&=\hbox {diag}\{0.9979, \ 0.9968\}, \\ E^{0}&=\left[ \begin{array}{rr} -39.9210 &{}\quad 61.8891 \\ 40.9158 &{}\quad 51.4248 \end{array}\right] , \\ A_\mathrm{aw}^{0}&=\left[ \begin{array}{rr} -81.3937 &{}\quad 97.8870 \\ -83.1400 &{}\quad 77.6196 \end{array}\right] ,\\ B_\mathrm{aw}^{0}&=\left[ \begin{array}{ll} -63.8194 &{}\quad 13.8084 \\ 83.0660 &{}\quad 80.0112 \end{array}\right] , \\ C_\mathrm{aw}^{0}&=\left[ \begin{array}{rr} 83.1783 &{}\quad -77.0453 \\ -34.1644 &{}\quad 72.50488 \end{array}\right] ,\\ D_\mathrm{aw}^{0}&=\left[ \begin{array}{ll} 99.9305 &{}\quad -98.4908 \\ 69.2371 &{}\quad -2.4055 \end{array}\right] , \end{aligned}$$

which, leads to $\alpha =109.4719$, and

$$\begin{aligned} E&=\left[ \begin{array}{rr} 38.1685 &{}\quad 23.8691 \\ 34.7836 &{}\quad -45.4089 \end{array}\right] , \\ A_\mathrm{aw}&=\left[ \begin{array}{rr} -49.6898 &{}\quad -66.3143 \\ 18.2308 &{}\quad -53.6246 \end{array}\right] ,\\ B_\mathrm{aw}&=\left[ \begin{array}{ll} 8.0438 &{}\quad -24.0927 \\ 98.9166 &{}\quad -61.6883 \end{array}\right] , \\ C_\mathrm{aw}&=\left[ \begin{array}{ll} -9.4493 &{}\quad 51.9200 \\ -99.3915 &{}\quad -49.4815 \end{array}\right] ,\\ D_\mathrm{aw}&=\left[ \begin{array}{ll} -86.1278 &{}\quad 86.9735 \\ -98.9582 &{}\quad 95.6214 \end{array}\right] , \\ P_{1}&=10^{-3}\times \left[ \begin{array}{ll} 1.6143 &{}\quad -1.4575 \\ -1.4575 &{}\quad 1.6822 \end{array}\right] . \end{aligned}$$

The obtained ellipsoid is plotted in Fig. 7. We note that letting the delayed AW compensator to be dynamic leads to a larger domain of attraction than that obtained by two static AW compensators. The dashed curves in Fig. 7 are the state trajectories with the state initial conditions on the boundary of the ellipsoid and the controller initial state $[x_{c}^\mathrm{T}(0) \ x_\mathrm{aw}^\mathrm{T}(0)]^\mathrm{T}=[0 \ 0]^\mathrm{T}$. Clearly, all trajectories converge to the origin.

Fig. 7

Ellipsoid and state trajectories

6 Conclusion

This paper considered the multistage AW design for linear systems with saturation nonlinearity, with the objective of enlarging the domain of attraction of the resulting closed-loop system. Iterative algorithms were established to obtain the AW compensation gains, and a PSO-based symmetric method was proposed to decide the parameters that cannot be easily determined before. Simulation results confirmed that the multistage AW scheme has the potential of leading to larger domain of attraction than the traditional AW scheme, and PSO algorithm can be a useful compensatory tuner in multistage AW design.