An Input–Output Approach to Anti-windup Design for Sampled-Data Systems with Time-Varying Delay

Abstract

A methodology for designing anti-windup compensators is investigated, for sampled-data systems with delays and actuator saturation. More precisely, criteria for the existence of an anti-windup compensator that ensure simultaneously stability and an $H_{\infty }$ norm bound in closed-loop are developed, thanks to the use of a three-term approximation of the delays, of the scaled small gain theorem, and of a Wirtinger-based inequality. The criteria are in the form of a set of linear matrix inequalities: an optimization algorithm is proposed to maximize the estimated domain of attraction that can be easily implemented. Some simulation examples are also provided to demonstrate the superiority of the proposed approach.

1 Introduction

In practical systems, the control signals are implemented by actuators that are subject to saturation. This issue is receiving significant attention during the last decades (see [38] and references therein ), as closed-loop performance deteriorates, and stability can be lost when the actuators saturate. The most frequent strategy to attenuate this problem is to include an anti-windup compensator in the control system [14], that do not act until the saturation is reached. Many results are available for the anti-windup design: for instance, in [24], the authors used the input delay approach for synthesizing an Anti-windup compensator to AQM in TCP/IP networks. For time delay systems under input saturation constraint via sampled-data, we can cite [25].

With the development of intelligent instruments and the availability of inexpensive digital sensors, digital controllers are generally used for many real-life systems. Thus, continuous-time systems are frequently controlled by discrete-time controllers implemented in digital devices, so the overall system becomes a sampled-data control system. Therefore, considerable attention is also been paid to these sampled-data control systems. For instance, in [27], sampled-data stabilization criteria have been established by using Wirtinger’s integral inequality. A sampled-data strategy was used to study the problem of robust stabilization of uncertain neutral state delayed-systems under input saturation in [17]. In [32], the problem of stabilization of switched systems with actuator faults via the robust reliable sampled-data control was studied.

Time-varying delays arise naturally in most real-world systems. They have been considered in the literature for instance, for AQM/TCP systems, in [5], for wind turbines, in [16, 29], and more general systems as descriptor systems [37] or neutral systems [18, 19]. Moreover, time-delays are often a source of oscillation, poor performance and instability of a control system. Considering these facts, a great deal of attention has been devoted to stability analysis and controller synthesis for time-delay systems [1,2,3,4, 35, 36]. Some useful approaches have already been established for time-delay systems, including the free weighting matrices technique [21], the Wirtinger inequality approach [11, 26, 28] and the input–output (IO) approach [20]. When using the IO approach, the original system is divided into two interconnected subsystems. Then, by using the scaled small gain (SSG) theorem, we can demonstrate that the stability condition can considerably be improved. In the literature, several results can be found concerning the IO approach. In [22] the delayed state $x(t-\tau (t)$ is approximated by its average value $\frac{1}{2}(x(t-\tau _{1})+x(t-\tau _{1}))$ (two-terms approximation) and stability criteria have been proposed. Extension of the two-terms approximation method to study the T-S Fuzzy systems with time-varying delay is considered in [39]. In [12], a new model transformation was proposed for continuous-time systems by using three-terms approximation. This approximation has also been successfully used to investigate the robust stabilization of delta operator systems with time-varying delays in [13], to design an $H_{\infty }$ filter for discrete time-varying delay systems in [40], and to synthesize an anti-windup compensator for delta operator systems with actuator saturation in [31]. The aforementioned consideration shows that the IO approach has been considered by several authors and has an important role in studies embroiled with delay systems. To the authors’ best knowledge, this idea has not yet been done in sampled-data systems under input saturation, and this is the motivation behind the presented work.

In summary, the problem of $H_{\infty }$ sampled-data anti-windup compensator design for time varying delay systems with input saturation will be investigated in this paper via the IO approach. The main novelty and contributions of this paper can be summarized as follows:

• 1. A methodology to design anti-windup compensator is proposed to mitigate the effect of saturation in sample-data systems with delays. The designed compensator ensures asymptotic stability of the closed-loop system and enlarges the domain of attraction.

• 2. The methodology is based on transforming the original sampled-data system with time varying delay and input saturation into two interconnected subsystems. Then, by using and input/output approach and the scaled small gain theorem and using Wirtinger’s integral inequality, LMI-based conditions are derived that can be numerically solved with little conservativeness, as illustrated in the numerical examples provided.

${\mathbf {Notations}}$: ${\mathbf {G}}_{\mathbf{1}}\circ \mathbf{G}_{\mathbf{2}}$ represents the series connection of mapping ${\mathbf {G}}_{\mathbf{1}}$ and ${\mathbf {G}}_{\mathbf{2}}$. $P>0 (\ge 0)$ means that matrix P is positive (semi) definite. $P^{T}$ and $P^{-1}$ denote the transpose and inverse of matrix P, respectively. $*$ stands for the symmetric term of the diagonal elements of square symmetric matrix. $\Vert .\Vert _{\infty }$ represents the $l_{2}$-induced norm of a transfer function matrix or a general operator. $A_{i}$ denotes the ith line of the matrix A.

2 Problem Formulation and Preliminaries

This paper considers the class of plants described by the following continuous-time system with delay:

$$\begin{aligned} {\dot{x}}(t)= & {} Ax(t)+A_{\tau }x(t-\tau (t))+Bsat(u(t))+B_{w}w(t) \nonumber \\ y(t)= & {} C_{y}x(t)\nonumber \\ z(t)= & {} C_{z}x(t) \end{aligned}$$

(1)

where $x(t)\in {\mathbb {R}}^{n}$, $u(t)\in {\mathbb {R}}^{m}$, $w(t)\in {\mathbb {R}}^{q}$, $y(t)\in {\mathbb {R}}^{p}$, $z(t)\in {\mathbb {R}}^{p}$ are the state vector, control vector, disturbance, the measured output and the regulated output, respectively, with $A, A_{\tau }, B, B_{w}, C_{y}$ and $C_{z}$ known constant real matrices.

This continuous-time plant is controlled with a digital device forming a sampled-data control system. By taking this into consideration, the control input takes the following form:

$$\begin{aligned} u(t)=u(t_{k}),~~~~t_{k}\le t<t_{k+1},~~~~(k=0,1,2,\ldots ) \end{aligned}$$

The interval between any two sampling instants is assumed to be bounded by h, which means that for any $k > 0, t_{k+1}-t_{k}=d_{k}\le h,$ where h is the maximum sampling interval. By defining $d(t)=t-t_{k}$ with ${\dot{d}}(t)=1$ for $t\ne t_{k}$, the sampling instant can be written as $t_{k}=t-(t-t_{k})=t-d(t).$ Then, we have $d(t)\le t_{k+1}-t_{k}=d_{k}\le h$; thus, the control law u(t) can be further written as

$$\begin{aligned} u(t)=u(t-d(t)),~~~~t_{k}\le t<t_{k+1},~~~~(k=0,1,2,\ldots ) \end{aligned}$$

(2)

Moreover, u(t) (with m components) is bounded as follows

$$\begin{aligned} -u_{0_{(i)}}\le u_{(i)}\le u_{0_{(i)}}, u_{0_{(i)}}>0, i=1,\ldots ,m \end{aligned}$$

(3)

$\tau (t)$ is the time-varying delay, which satisfies

$$\begin{aligned} 0<\tau _{1}\le \tau (t)\le \tau _{2},~~~~{\dot{\tau }}(t)\le \mu <1 \end{aligned}$$

(4)

where $\mu$ is a constant positive scalar.

The disturbance vector w(t) is assumed to be Lebesgue measurable, that is, $w(t)\in {\mathcal {L}}_{2}$. Hence, the disturbance w(t) is bounded as follows:

$$\begin{aligned} \Vert {w}(t)\Vert ^{2}_{2}=\int _{0}^{\infty }w^{T}(t)w(t)\mathrm{d}t<\infty \end{aligned}$$

(5)

To stabilize the system (1), we consider the following dynamic stabilizing controller

$$\begin{aligned} {\dot{x}}_{c}(t)= & {} A_{c}x_{c}(t)+B_{c}y(t) \nonumber \\ y_{c}(t)= & {} C_{c}x_{c}(t)+D_{c}y(t) \end{aligned}$$

(6)

where $x_{c}(t)$ is the controller state, $u_{c}(t)=y(t)$ is the controller input, and $y_{c}(t)$ is the controller output. $A_{c}, B_{c}, C_{c}$ and $D_{c}$ are known matrices of appropriate dimensions.

In the presence of actuator saturation, the control signal of the system can be described as $u(t)=sat(y_{c}(t))$, where $sat(y_{c_{(i)}}(t))=sign(y_{c_{(i)}}(t))min\{|y_{c_{(i)}}(t)|, u_{0_{(i)}}\}, i=1,\ldots ,m$

To reduce the undesirable effects of the windup caused by the saturation, an anti-windup compensator is added to the controller as follows:

$$\begin{aligned} {\dot{x}}_{c}(t)= & {} A_{c}x_{c}(t)+B_{c}y(t)-E_{c}\psi (y_{c}(t-d(t))) \nonumber \\ y_{c}(t)= & {} C_{c}x_{c}(t)+D_{c}y(t) \end{aligned}$$

(7)

Note that, $\psi (y_{c}(t-d(t)))$ corresponds to a decentralized dead-zone nonlinearity, where $\psi (y_{c}(t-d(t)))=y_{c}(t-d(t))-sat(y_{c}(t-d(t)))$.

Then, the augmented system can be represented as follows

$$\begin{aligned} {\dot{\xi }}(t)= & {} {\mathbb {A}}\xi (t)+{\mathbb {A}}_{\tau }\xi (t-\tau (t))+{\mathbb {A}}_{d}\xi (t-d(t))-({\mathbb {B}}+{\mathbb {R}}E_{c})\psi ({\mathbb {K}}\xi (t-d(t))) \nonumber \\&+\,{\mathbb {B}}_{w}w(t) \nonumber \\ z(t)= & {} {\mathbb {C}}_{z}\xi (t) \end{aligned}$$

(8)

and the augmented system is given by

$$\begin{aligned} \xi (t)= & {} \left[ \begin{array}{c} x(t) \\ x_{c}(t) \end{array} \right] , {\mathbb {A}}=\left[ \begin{array}{cc} A &{}\quad 0 \\ B_{c}C_{y} &{}\quad A_{c} \end{array} \right] , {\mathbb {B}}=\left[ \begin{array}{c} B \\ 0 \end{array} \right] , {\mathbb {A}}_{\tau }=\left[ \begin{array}{cc} A_{\tau } &{}\quad 0 \\ 0 &{}\quad 0 \end{array} \right] \\ {\mathbb {A}}_{d}= & {} \left[ \begin{array}{cc} BD_{c}C_{y} &{}\quad BC_{c} \\ 0 &{}\quad 0 \end{array} \right] , {\mathbb {B}}_{w}=\left[ \begin{array}{c} B_{w} \\ 0 \end{array}\right] , {\mathbb {R}}=\left[ \begin{array}{c} 0 \\ I_{n_{c}} \end{array} \right] , {\mathbb {K}}=\left[ \begin{array}{ccc} D_{c}&\quad C_{y}&\quad C_{c} \end{array} \right] , \\ {\mathbb {C}}_{z}= & {} \left[ \begin{array}{cc} C_{z}&\quad 0 \end{array} \right] . \end{aligned}$$

The initial condition is given by

$$\begin{aligned} \xi (\theta )=\phi _{\xi }, ~~~~~\theta \in [-{\bar{\tau }},0], ~~~~~{\bar{\tau }}=\max (\tau _{2},h) \end{aligned}$$

Consider a matrix $H\in \mathfrak {R}^{m\times (n+n_{c})}$, and define the following polyhedral set

$$\begin{aligned} {\mathcal {S}}=\Big \{\xi (t)\in \mathfrak {R}^{n+n_{c}}; |({\mathbb {K}}_{(i)}-H_{(i)})\xi (t)|\le u_{0_{(i)}}\Big \} \end{aligned}$$

The following useful lemmas will be used in this paper.

Lemma 1

 [34] If $\xi (t)\in {\mathcal {S}}$, then the following relation

$$\begin{aligned} \psi ^{T}({\mathbb {K}}\xi (t))M\Big [\psi ({\mathbb {K}}\xi (t))-H\xi (t)\Big ] \le 0 \end{aligned}$$

is verified for any diagonal positive matrix $M\in \mathfrak {R}^{m\times m}$.

Lemma 2

 [30] For any scalar $b>a$, positive matrix R and function $\xi$, the following inequality holds

$$\begin{aligned} \int _{a}^{b}{\dot{\xi }}^{T}(s)R{\dot{\xi }}(s)\mathrm{d}s\ge & {} \frac{1}{b-a}({\xi }(b)-{\xi }(a)^{T}R({\xi }(b)-{\xi }(a))+\frac{3}{b-a}\theta ^{T}R\theta \end{aligned}$$

where $\theta ={\xi }(b)+{\xi }(a)-\frac{2}{b-a}\int _{a}^{b}{\xi }(s)\mathrm{d}s$

Lemma 3

 [39] (Scaled small gain theorem) Consider the following interconnected feedback system

$$\begin{aligned} (S_{1}) : y_{\vartriangle }(t)={\mathbf {G}} \varpi (t); ~~~~ (S_{2}) :\varpi (t)=\triangle y_{\vartriangle }(t) \end{aligned}$$

(9)

where subsystem $S_{1}$ is a known LTI system with operator ${\mathbf {G}}$ mapping $\varpi (t)$ to $y_{\vartriangle }(t)$, and subsystem $S_{2}$ is an unknown linear time-varying one with operator $\triangle \in {\mathcal {D}} \triangleq \{\triangle :\parallel \triangle \parallel _{\infty }\le 1\}$. Assume that $S_{1}$ is internally stable. The closed-loop system formed by $S_{1}$ and $S_{2}$ is robustly asymptotically stable for all $\triangle \in {\mathcal {D}}$ if there exist matrices $\{T_{\varpi }, T_{y}\} \in T$ with $T\triangleq \{\{T_{\varpi }, T_{y}\} \in {\mathbb {R}}^{\varpi \times \varpi }\times {\mathbb {R}}^{y\times y} : T_{\varpi }, T_{y}$ non-singular, $\Vert T_{\varpi }\circ \triangle \circ T^{-1}_{y}\Vert _{\infty }\le 1\}$ such that the SSG condition holds:

$$\begin{aligned} \Vert T_{y}\circ {\mathbf {G}} \circ T^{-1}_{\varpi }\Vert _{\infty }< 1 \end{aligned}$$

(10)

Finally, for a positive scalar $\kappa$, the ellipsoid $\varepsilon (P,\kappa ^{-1})$ is defined as follows:

$$\begin{aligned} \varepsilon (P,\kappa ^{-1}) = \{\xi (t) \in \mathfrak {R}^{n+n_{c}}; \quad \xi ^{T}(t)P\xi (t)\le \kappa ^{-1}\} \end{aligned}$$

3 Main Results

This section first introduces the transformation of system (8), so then the stability condition is developed by using the SSG theorem.

3.1 Model Transformation

Consider the system (8): following [12], the delayed state is approximated by the following equation:

$$\begin{aligned} \xi (t-\tau (t))=\frac{1}{3}[\xi (t-\tau _{1})+\xi (t-\tau _{a})+\xi (t-\tau _{2})]+\frac{\tau _{12}}{3}\varpi _{r}(t) \end{aligned}$$

(11)

where $\tau _{12}=\tau _{2}-\tau _{1}$, $\tau _{a}=\frac{\tau _{1}+\tau _{2}}{2}$ and $\frac{\tau _{12}}{3}\varpi _{r}(t)$ is the approximation error. From (11), system (8) can be written as a forward interconnection system $(S_{1})$ and as a feedback interconnection system $(S_{2})$.

$$\begin{aligned} {\dot{\xi }}(t)= & {} {\mathbb {A}}\xi (t)+\frac{{\mathbb {A}}_{\tau }}{3}\xi (t-\tau _{1})+\frac{{\mathbb {A}}_{\tau }}{3}\xi (t-\tau _{a})+\frac{{\mathbb {A}}_{\tau }}{3}\xi (t-\tau _{2}) \\ (S_{1}):~~~~~~~~~&+\,\frac{\tau _{12}}{3}{\mathbb {A}}_{\tau }\varpi _{r}(t)+{\mathbb {A}}_{d}\xi (t-d(t))-({\mathbb {B}}+{\mathbb {R}}E_{c})\psi ({\mathbb {K}}\xi (t-d(t))) \\ ~~~~~~~~~&+\,{\mathbb {B}}_{w}w(t) \\ ~~~~~~~~~ z(t)= & {} {\mathbb {C}}_{z}\xi (t)\\ ~~~~~~~~~ y_{\triangle }(t)= & {} {\dot{\xi }}(t) \end{aligned}$$

$~(S_{2})$:     $\varpi (t)=\triangle y_{\triangle }(t)$ with $\varpi _{r}=(3/\sqrt{2})\varpi$

Remark 1

The equation $\varpi _{r}=(3/\sqrt{2})\varpi$ provides the relation between feedback system $(S_2)$ and forward system $(S_1)$, to give a representation of subsystem $(S_1)$ in a compact form, for the IO approach. If we denote the right-hand side of $(S_{1})$ by $f(\xi ,w)$ then we can write $\frac{\mathrm{d} \xi }{d(t)}=f(\xi ,w)$. It is clear that $f(\xi ,w)$ is continuous in some closed and bounded set around the equilibrium point. It follows that $f(\xi ,w)$ is bounded and satisfies Lipschitz conditions in a certain domain. Consequently, $\frac{\mathrm{d} \xi }{d(t)}=f(\xi ,w)$ has at least one solution in that domain, for more details see [23]

The approximation error can be written as follows:

Case 1. If $\tau _{1}\le \tau (t)\le \tau _{a}$, then

$$\begin{aligned} \frac{\tau _{12}}{3}\varpi _{r}= & {} \xi (t-\tau (t))-\frac{1}{3}\bigg \{\xi (t-\tau _{1})+\xi (t-\tau _{a})+\xi (t-\tau _{2}) \bigg \}\\= & {} \frac{1}{3}\bigg [-\int _{t-\tau (t)}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s+2\int _{t-\tau _{a}}^{t-\tau (t)}y_{\triangle }(s)\mathrm{d}s+\int _{t-\tau _{2}}^{t-\tau _{a}}y_{\triangle }(s)\mathrm{d}s\bigg ] \end{aligned}$$

Case 2. If $\tau _{a}\le \tau (t)\le \tau _{2}$, then

$$\begin{aligned} \frac{\tau _{12}}{3}\varpi _{r}= & {} x(t-\tau (t))-\frac{1}{3}\bigg \{x(t-\tau _{1})+x(t-\tau _{a})+x(t-\tau _{2})\bigg \}\\= & {} \frac{1}{3}\bigg [-\int _{t-\tau _{a}}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s+2\int _{t-\tau (t)}^{t-\tau _{a}}y_{\triangle }(s)\mathrm{d}s+\int _{t-\tau _{2}}^{t-\tau (t)}y_{\triangle }(s)\mathrm{d}s\bigg ] \end{aligned}$$

Lemma 4

Operator $\triangle : y_{\triangle } \rightarrow \varpi$, satisfies the SSG condition $\Vert N\circ \triangle \circ N^{-1}\Vert _{\infty }\le 1$, where N is a general invertible matrix.

Proof

If we can prove that $\Vert N\circ \triangle \circ N^{-1}\Vert _{\infty }\le 1\}$ holds for $\tau _{1}\le \tau (t)\le \tau _{a}$ and for $\tau _{a}\le \tau (t)\le \tau _{2}$, then $\Vert N\circ \triangle \circ N^{-1}\Vert _{\infty }\le 1\}$ is true. Let $S=N^{T}N$

Case 1. $\tau _{1}\le \tau (t)\le \tau _{a}$

We have that by Jensen (Cauchy–Schwartz) inequality, for all $t\ge 0$

$$\begin{aligned} \frac{\tau ^{2}_{12}}{9}\varpi ^{T}_{r}(t)\varpi _{r}(t)= & {} \frac{\tau ^{2}_{12}}{9}\Vert \varpi _{r}(t)\Vert ^{2}\\= & {} \frac{1}{9}\bigg \Vert -\int _{t-\tau (t)}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s+2\int _{t-\tau _{a}}^{t-\tau _(t)}y_{\triangle }(s)\mathrm{d}s+\int _{t-\tau _{2}}^{t-\tau _{a}}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\\\le & {} \frac{3}{9}\bigg \{\bigg \Vert \int _{t-\tau (t)}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}+\bigg \Vert 2\int _{t-\tau _{a}}^{t-\tau (t)}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\\&+\,\bigg \Vert \int _{t-\tau _{2}}^{t-\tau _{a}}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\bigg \} \end{aligned}$$

We continue the proof for each term separately. A function $s=p(t)=t-\tau (t)$ is strongly increasing. Hence, the inverse $t=p^{-1}(s)=q(s)$ is well-defined such that $\mid q(s)-(s+\tau _{1})\mid \le \tau _{12}/2$. Then, integrating $\Vert \int _{t-\tau (t)}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s\big \Vert ^{2}$ between 0 and $\infty$, changing the order of the integration and then taking into account that $y_{\triangle }(s)=0$, for $s\le 0$, we find that

$$\begin{aligned} \int _{0}^{\infty } \bigg \Vert \int _{t-\tau (t)}^{t-\tau _{1}}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\mathrm{d}t\le & {} \int _{0}^{\infty }(\tau (t)-\tau _{1})\int _{t-\tau (t)}^{t-\tau _{1}}\Vert y_{\triangle }(s)\Vert ^{2}\mathrm{d}s\mathrm{d}t\\= & {} \bigg | \int _{0}^{\infty }(\tau (q(s))-\tau _{1})\int _{q(s)}^{s+\tau _{1}}\Vert y_{\triangle }(s)\Vert ^{2}\mathrm{d}s\mathrm{d}t\bigg |\\= & {} \bigg | \int _{0}^{\infty }(\tau (q(s))-\tau _{1})(s+\tau _{1}-q(s))\Vert y_{\triangle }(s)\Vert ^{2}\mathrm{d}s\mathrm{d}t \bigg |\\\le & {} \frac{\tau _{12}}{2}\frac{\tau _{12}}{2}\int _{0}^{\infty }\Vert y_{\triangle }(s)\Vert ^{2}\mathrm{d}s\\= & {} \frac{\tau ^{2}_{12}}{4}\Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}} \end{aligned}$$

For the other terms, we follow the same process, to obtain

$$\begin{aligned}&\int _{0}^{\infty } \bigg \Vert 2\int _{t-\tau _{a}}^{t-\tau (t)}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\mathrm{d}t \le 4\frac{\tau ^{2}_{12}}{4}\Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}}\\&\int _{0}^{\infty } \bigg \Vert \int _{t-\tau _{2}}^{t-\tau _{a}}y_{\triangle }(s)\mathrm{d}s\bigg \Vert ^{2}\mathrm{d}t \le \frac{\tau ^{2}_{12}}{4}\Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}} \end{aligned}$$

Then, the summation of the three terms together gives

$$\begin{aligned} \frac{\tau ^{2}_{12}}{9}\Vert \varpi _{r}(t)\Vert ^{2}_{l_{2}}\le & {} \frac{3}{9}\left( \frac{\tau ^{2}_{12}}{4}+4\frac{\tau ^{2}_{12}}{4}+\frac{\tau ^{2}_{12}}{4}\right) \Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}}\\= & {} \frac{\tau ^{2}_{12}}{2}\Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}} \end{aligned}$$

when substituting $\varpi _{r}(t)$ by $(3/\sqrt{2})\varpi (t)$, we obtain $\Vert \varpi (t)\Vert ^{2}_{l_{2}} \le \Vert y_{\triangle }(t)\Vert ^{2}_{l_{2}}$. For case 2, by using similar proof process, we obtain the same results as in case 1. This completes the proof. $\square$

Remark 2

$\{N,N\} \in T$ are the matrices in the SSG theorem given in Lemma 3, to ensure that the system (8) is IO stable, it is necessary to verify that $(S_{1})$ is internally stable and there exists N such that SSG condition $\Vert N\circ G \circ N^{-1}\Vert _{\infty }\le 1$ holds.

3.2 Anti-windup Design

In this subsection, a methodology for computing the anti-windup gain that guarantees asymptotic stability of system (1) is derived.

Theorem 1

For given scalars $h,~\tau _{1},~\tau _{2}, ~\mu$, the closed-loop system (8) is asymptotically stable with a prescribed level $\gamma$, if there exist symmetric positive definite matrices $~X,~X_{j}, (j=1,2,3,4,5),~{\hat{Q}}_{l}, (l=1,2,3,4)$ and appropriately sized matrices $Y_{c}, ~W$ and L such that

$$\begin{aligned} {\hat{\varGamma }}=\left[ \begin{array}{ccccccc} \varPi &{}\quad \tau _{1}\varPi _{1} &{}\quad \tau _{a}\varPi _{1} &{}\quad \tau _{2}\varPi _{1}&{}\quad h\varPi _{1}&{}\quad \varPi _{1}&{}\quad \varPi _{2} \\ *&{}\quad -X_{1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad -X_{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad -X_{3} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad -X_{4} &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -X_{5} &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -\gamma I \\ \end{array} \right]&\quad <&\quad 0 \end{aligned}$$

(12)

$$\begin{aligned} \left[ \begin{array}{cc} X &{}\quad X{\mathbb {K}}_{(i)}^T-W_{(i)}^T \\ *&{}\quad \kappa u_{0_{(i)}}^2 \\ \end{array} \right]&\quad \ge&\quad 0, \end{aligned}$$

(13)

where

$$\begin{aligned} {\varPi }_{1}= & {} \left[ \begin{array}{cccccccccccc} {\mathbb {A}}X &{} \frac{{\mathbb {A}}_{\tau }}{3}X &{} \frac{{\mathbb {A}}_{\tau }}{3}X &{}\frac{{\mathbb {A}}_{\tau }}{3}X &{} {\mathbb {A}}_{d}X &{} \frac{\tau _{12}}{3}{\mathbb {A}}_{\tau }X &{}-{\mathbb {B}}L-{\mathbb {R}}F_{c} &{} {\mathbb {B}}_{w} &{} 0_{4n} \\ \end{array} \right] ^{T}\\ {\varPi }_{2}= & {} \left[ \begin{array}{cc} {\mathbb {C}}_{z}X &{} 0_{11n} \\ \end{array} \right] ^{T} \end{aligned}$$

and the elements of ${\varPi }$ are defined by

$$\begin{aligned} \varPi _{11}= & {} {\mathbb {A}}X+X{\mathbb {A}}^{T}+{\hat{Q}}_{1}+{\hat{Q}}_{2}+{\hat{Q}}_{3}+{\hat{Q}}_{4}+4(X_{1}-2X) \\&+\,4(X_{2}-2X)+4(X_{3}-2X)+4(X_{4}-2X) \\ \varPi _{12}= & {} \frac{{\mathbb {A}}_{\tau }}{3}X+2(X_{1}-2X), \varPi _{13}=\frac{{\mathbb {A}}_{\tau }}{3}X+2(X_{2}-2X)\\ \varPi _{14}= & {} \frac{{\mathbb {A}}_{\tau }}{3}X+2(X_{3}-2X), \varPi _{15}={\mathbb {A}}_{d}X+2(X_{4}-2X)\\ \varPi _{16}= & {} \frac{h_{12}}{3}{\mathbb {A}}_{\tau }X, \varPi _{17}={\mathbb {B}}N-{\mathbb {R}}F_{c}, \varPi _{18}=B_{w}, \varPi _{19}=6(2X-X_{1})\\ \varPi _{110}= & {} 6(2X-X_{2}), \varPi _{111}=6(2X-X_{3}) \varPi _{1112}=6(2X-X_{4}) \\ \varPi _{22}= & {} -{\hat{Q}}_{1}+4(X_{1}-2X)-\frac{(1-\mu )}{9}{\hat{Q}}_{4}, \varPi _{23}=-\frac{(1-\mu )}{9}{\hat{Q}}_{4}\\ \varPi _{24}= & {} -\frac{(1-\mu )}{9}{\hat{Q}}_{4}, \varPi _{26}=-\frac{h_{12}}{9}(1-\mu ){\hat{Q}}_{4}, \varPi _{29}=6(2X-X_{1})\\ \varPi _{33}= & {} -{\hat{Q}}_{2}+4(X_{2}-2X)-\frac{(1-\mu )}{9}{\hat{Q}}_{4}, \varPi _{34}=-\frac{(1-\mu )}{9}{\hat{Q}}_{4}\\ \varPi _{36}= & {} -\frac{\tau _{12}}{9}(1-\mu ){\hat{Q}}_{4}, \varPi _{310}=6(2X-X_{2})\\ \varPi _{44}= & {} -{\hat{Q}}_{3}+4(X_{3}-2X)-\frac{(1-\mu )}{9}{\hat{Q}}_{4}, \varPi _{46}=-\frac{\tau _{12}}{9}(1-\mu ){\hat{Q}}_{4}\\ \varPi _{411}= & {} 6(2X-X_{3}), \varPi _{55}=4(X_{4}-2X), \varPi _{57}=W^{T} \\ \varPi _{512}= & {} 6(2X-X_{4}), \varPi _{66}=\frac{2}{9}(X_{5}-2X)-\frac{h_{12}}{9}(1-\mu ){\hat{Q}}_{4}\\ \varPi _{77}= & {} -L-L^{T}, \varPi _{88}=-I, \varPi _{99}=12({X_{1}-2X})\\ \varPi _{1010}= & {} 12({X_{2}-2X}), \varPi _{1111}=12({X_{3}-2X}), \varPi _{1212}=12(X_{4}-2X) \end{aligned}$$

then, the anti-windup gain matrix $E_{c}=F_{c}L^{-1}$ ensures that:

• 1. the trajectories of the system (8) are bounded for every initial condition satisfying $\beta \le \kappa ^{-1}$;

• 2. Under the zero initial condition,

  $$\begin{aligned} \Vert z(t)\Vert _{2}^2\le \gamma \Vert w(t)\Vert _{2}^2; \end{aligned}$$

• 3. when $w(t)=0$, for all initial conditions belonging to $\beta \le \kappa ^{-1}$, the corresponding trajectories converge asymptotically to the origin, where

  $$\begin{aligned} \beta= & {} \Big ({\overline{\lambda }}(X^{-1})+\tau _{1}{\bar{\lambda }}(X^{-1}{\hat{Q}}_{1}X^{-1})+\tau _{a}{\bar{\lambda }}(X^{-1}{\hat{Q}}_{2}X^{-1})+\tau _{2}{\bar{\lambda }}(X^{-1}{\hat{Q}}_{3}X^{-1})\\&+\,\tau _{2}{\bar{\lambda }}(X^{-1}{\hat{Q}}_{4}X^{-1}) \Big )\Vert \phi _{\xi }\Vert _{c}^{2}+ \Big (\frac{{\tau }^{3}_{1}}{2}{\bar{\lambda }}(X^{-1}_{1})+\frac{{\tau }^{3}_{a}}{2}{\bar{\lambda }}(X^{-1}_{2}) \nonumber \\&+\,\frac{{\tau }^{3}_{2}}{2}{\bar{\lambda }}(X^{-1}_{3})+\frac{h^{3}}{2}{\bar{\lambda }}(X^{-1}_{4})\Big )\Vert {\dot{\phi }}_{\xi }\Vert _{c}^{2} \end{aligned}$$

with ${\overline{\lambda }}$ is the maximal eigenvalue.

Proof

To prove this theorem, let us consider the following Lyapunov functional

$$\begin{aligned} V(t)= & {} \xi ^{T}(t)P\xi (t)+\int _{t- \tau _{1}}^{t}\xi ^{T}(s)Q_{1}\xi (s)\mathrm{d}s +\int _{t-\tau _{a}}^{t}\xi ^{T}(s)Q_{2}\xi (s)\mathrm{d}s \nonumber \\&+\,\int _{t-\tau _{2}}^{t}\xi ^{T}(s)Q_{3}\xi (s)\mathrm{d}s+\int _{t-\tau (t)}^{t}\xi ^{T}(s)Q_{4}\xi (s)\mathrm{d}s \nonumber \\&+\,\tau _{1}\int _{-\tau _{1}}^{0}\int _{t+\theta }^{t}{\dot{\xi }}^{T}(s)R_{1}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta +\tau _{a}\int _{-\tau _{a}}^{0}\int _{t+\theta }^{t}{\dot{\xi }}^{T}(s)R_{2}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta \nonumber \\&+\,\tau _{2}\int _{-\tau _{2}}^{0}\int _{t+\theta }^{t} {\dot{\xi }}^{T}(s)R_{3}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta +h\int _{-h}^{0}\int _{t+\theta }^{t}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta \end{aligned}$$

(14)

Computing the derivative of the functional (14) along the trajectory of the system $(S_{1})$, we get

$$\begin{aligned} \dot{{V}}(t)= & {} 2\xi ^{T}(t)P{\dot{\xi }}(t)+\xi ^{T}(t)[Q_{1}+Q_{2}+Q_{3}+Q_{4}]\xi (t)-\xi ^{T}(t-\tau _{1})Q_{1}\xi (t-\tau _{1}) \nonumber \\&-\,\xi ^{T}(t-\tau _{a})Q_{2}\xi (t-\tau _{a})-\xi ^{T}(t-\tau _{2})Q_{3}\xi (t-\tau _{2})-(1-\mu )\xi ^{T}(t-\tau (t))\nonumber \\&\times Q_{4}\xi (t-\tau (t))+{\dot{\xi }}^{T}(t)[\tau ^{2}_{1}R_{1}+\tau ^{2}_{a}R_{2}+\tau ^{2}_{2}R_{3}+h^{2}R_{4}]{\dot{\xi }}(t)\nonumber \\&-\,\tau _{1}\int _{t-\tau _{1}}^{t}{\dot{\xi }}^{T}(s)R_{1}{\dot{\xi }}(s)\mathrm{d}s-\tau _{a}\int _{t-\tau _{a}}^{t}{\dot{\xi }}^{T}(s)R_{2}{\dot{\xi }}(s)\mathrm{d}s \nonumber \\&-\,\tau _{2}\int _{t-\tau _{2}}^{t}{\dot{\xi }}^{T}(s)R_{3}{\dot{\xi }}(s)\mathrm{d}s-h\int _{t-h}^{t}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s \end{aligned}$$

(15)

with the aid of Lemma 2, we have

$$\begin{aligned} -\tau _{1}\int _{t-\tau _{1}}^{t}{\dot{\xi }}^{T}(s)R_{1}{\dot{\xi }}(s)\mathrm{d}s\le & {} -\Big [{\xi }(t)-{\xi }(t-\tau _{1})\Big ]^{T}R_{1}\Big [{\xi }(t)-{\xi }(t-\tau _{1})\Big ] \nonumber \\&-\,3\varTheta ^{T}_{1}R_{1}\varTheta _{1} \end{aligned}$$

(16)

$$\begin{aligned} -\tau _{a}\int _{t-\tau _{a}}^{t}{\dot{\xi }}^{T}(s)R_{2}{\dot{\xi }}(s)\mathrm{d}s\le & {} -\Big [{\xi }(t)-{\xi }(t-\tau _{a})\Big ]^{T}R_{2}\Big [{\xi }(t)-{\xi }(t-\tau _{a})\Big ] \nonumber \\&-\,3\varTheta ^{T}_{2}R_{2}\varTheta _{2} \end{aligned}$$

(17)

$$\begin{aligned} -\tau _{2}\int _{t-\tau _{2}}^{t}{\dot{\xi }}^{T}(s)R_{3}{\dot{\xi }}(s)\mathrm{d}s\le & {} -\Big [{\xi }(t)-{\xi }(t-\tau _{2})\Big ]^{T}R_{3}\Big [{\xi }(t)-{\xi }(t-\tau _{2})\Big ] \nonumber \\&-\,3\varTheta ^{T}_{3}R_{3}\varTheta _{3} \end{aligned}$$

(18)

where

$$\begin{aligned} \varTheta _{1}= & {} {\xi }(t)+{\xi }(t-\tau _{1})-\frac{2}{\tau _{1}}\int _{t-\tau _{1}}^{t}{\xi }(s)\mathrm{d}s,\,\varTheta _{2}={\xi }(t)+{\xi }(t-\tau _{a})-\frac{2}{\tau _{a}}\int _{t-\tau _{a}}^{t}{\xi }(s)\mathrm{d}s\\ \varTheta _{3}= & {} {\xi }(t)+{\xi }(t-\tau _{2})-\frac{2}{\tau _{2}}\int _{t-\tau _{2}}^{t}{\xi }(s)\mathrm{d}s \end{aligned}$$

It is clear that the following is true

$$\begin{aligned} -\int _{t-h}^{t}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s\le -\int _{t-d(t)}^{t}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s \end{aligned}$$

(19)

Moreover, by applying Lemma 2 to (19) the following inequality is obtained:

$$\begin{aligned} -h\int _{t-d(t)}^{t}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s\le & {} -\Big [{\xi }(t)-{\xi }(t-d(t))\Big ]^{T}R_{4}\Big [{\xi }(t)-{\xi }(t-d(t))\Big ] \nonumber \\&-\,3\varTheta ^{T}_{4}R_{4}\varTheta _{4} \end{aligned}$$

(20)

where $\varTheta _{4}={x}(t)+{\xi }(t-d(t))-\frac{2}{h}\int _{t-d(t)}^{t}{\xi }(s)\mathrm{d}s$

We define the following vectors:

$$\begin{aligned} \alpha ^{T}(t)= & {} \left[ \frac{1}{\tau _{1}}\int _{t-\tau _{1}}^{t}{\xi }^{T}(s)\mathrm{d}s~~\frac{1}{\tau _{a}}\int _{t-\tau _{a}}^{t}{\xi }^{T}(s)\mathrm{d}s~~\frac{1}{\tau _{2}}\int _{t-\tau _{2}}^{t}{\xi }^{T}(s)\mathrm{d}s~~\frac{1}{h}\int _{t-d(t)}^{t}{\xi }^{T}(s)\mathrm{d}s\right] \\ \zeta ^{T}(t)= & {} \left[ \xi ^{T}(t)~~\xi ^{T}(t-\tau _{1})~~\xi ^{T}(t-\tau _{a})~~\xi ^{T}(t-\tau _{2})~~\xi ^{T}(t-d(t))~~\varpi ^{T}_{r}(t)\right. \\&\left. \qquad \qquad \psi ^{T}({\mathbb {K}}\xi (t-d(t)))\right] ,\quad \eta ^{T}=[\zeta ^{T}(t)~~w(t)^{T}~~\alpha ^{T}(t)] \end{aligned}$$

And let

$$\begin{aligned} J=\int _{0}^{\infty } \left[ y^{T}_{\triangle }(s)Sy_{\triangle }(s)-\varpi ^{T}(s)S\varpi (s)-w^{T}(s)w(s)+\frac{1}{\gamma }z^{T}(s)z(s)\right] \mathrm{d}s \end{aligned}$$

(21)

and

$$\begin{aligned} J_{1}= & {} \int _{0}^{\infty } \left[ \dot{{V}}(t)+ y^{T}_{\triangle }(s)Sy_{\triangle }(s)-\varpi ^{T}_{r}(s)\frac{2}{9}S\varpi _{r}(s)-w^{T}(s)w(s)+\frac{1}{\gamma }z^{T}(s)z(s)\right] \mathrm{d}s \\ \end{aligned}$$

By summing Eqs. (15)–(20) and using Lemma 1, we have

$$\begin{aligned} J_{1}\le & {} \int _{0}^{\infty }\eta ^{T}(t)\left[ \varLambda +\varLambda ^{T}_{1}\tau ^{2}_{1}R_{1}\varLambda _{1}+\varLambda ^{T}_{1}\tau ^{2}_{a}R_{2}\varLambda _{1}+\varLambda ^{T}_{1}\tau ^{2}_{2}R_{3}\varLambda _{1}+\varLambda ^{T}_{1}h^{2}R_{4}\varLambda _{1}\nonumber \right. \\&\left. +\varLambda ^{T}_{1}S\varLambda _{1}\right] \eta (t)+\frac{1}{\gamma }({\mathbb {C}}_{z}\xi (t))^{T}({\mathbb {C}}_{z}\xi (t)) \end{aligned}$$

(22)

where

$$\begin{aligned} {\varLambda }_{1}=\left[ \begin{array}{cccccccccccc} {\mathbb {A}} &{} \frac{{\mathbb {A}}_{\tau }}{3} &{} \frac{{\mathbb {A}}_{\tau }}{3} &{}\frac{{\mathbb {A}}_{\tau }}{3} &{} {\mathbb {A}}_{d} &{} \frac{\tau _{12}}{3}{\mathbb {A}}_{\tau } &{}-({\mathbb {B}}+{\mathbb {R}}E_{c}) &{} {\mathbb {B}}_{w} &{} 0_{4n} \\ \end{array} \right] ^{T} \end{aligned}$$

and the elements of ${\varLambda }$ are defined by

$$\begin{aligned} \varLambda _{11}= & {} P{\mathbb {A}}+{\mathbb {A}}^{T}P+Q_{1}+Q_{2}+Q_{3}+Q_{4}-4R_{1}-4R_{2}-4R_{3}-4R_{4} \\ \varLambda _{12}= & {} P\frac{{\mathbb {A}}_{\tau }}{3}-2R_{1},\varLambda _{13}=P\frac{{\mathbb {A}}_{\tau }}{3}-2R_{2}, \varLambda _{14}=P\frac{{\mathbb {A}}_{\tau }}{3}-2R_{3}\\ \varLambda _{15}= & {} P{\mathbb {A}}_{d}-2R_{4},\varLambda _{16}=P\frac{\tau _{12}}{3}{\mathbb {A}}_{\tau }, \varLambda _{17}=-P({\mathbb {B}}+{\mathbb {R}}E_{c})\\ \varLambda _{18}= & {} P{\mathbb {B}}_{w} , \varLambda _{19}=6R_{1} , \varLambda _{110}=6R_{2}, \varLambda _{111}=6R_{3}, \varLambda _{112}=6R_{4}\\ \varLambda _{22}= & {} -Q_{1}-4R_{1}-\frac{(1-\mu )}{9}Q_{4} , \varLambda _{23}=-\frac{(1-\mu )}{9}Q_{4}\\ \varLambda _{24}= & {} -\frac{(1-\mu )}{9}Q_{4}, \varLambda _{26}=-\frac{\tau _{12}}{9}(1-\mu )Q_{4}, \varLambda _{29}=6R_{1}\\ \varLambda _{33}= & {} -Q_{2}-4R_{2}-\frac{(1-\mu )}{9}Q_{4}, \varLambda _{34}=-\frac{(1-\mu )}{9}Q_{4}\\ \varLambda _{36}= & {} -\frac{\tau _{12}}{9}(1-\mu )Q_{4}, \varLambda _{310}=6R_{2}, \varLambda _{44}=-Q_{3}-4R_{3}-\frac{(1-\mu )}{9}Q_{4}\\ \varLambda _{46}= & {} -\frac{\tau _{12}}{9}(1-\mu )Q_{4}, \varLambda _{411}=6R_{3} , \varLambda _{55}=-4R_{4}, \varLambda _{57}=H^{T}T^{T}_{0}\\ \varLambda _{512}= & {} 6R_{4}, \varLambda _{66}=-\frac{2}{9}S-\frac{\tau _{12}}{9}(1-\mu )Q_{4}, \varLambda _{77}= -T_{0}-T^{T}_{0}, \varLambda _{88}=-I \\ \varLambda _{99}= & {} -12R_{1}, \varLambda _{1010}=-12R_{2}, \varLambda _{1111}=-12R_{3}, \varLambda _{1212}=-12R_{4} \end{aligned}$$

By using the Schur complement, it can be easily seen that $J_{1}<0$ if the following condition holds.

$$\begin{aligned} \varXi =\left[ \begin{array}{ccccccc} \varLambda &{}\quad \tau _{1}\varLambda _{1} &{}\quad \tau _{a}\varLambda _{1} &{}\quad \tau _{2}\varLambda _{1}&{}\quad h\varLambda _{1}&{}\quad \varLambda _{1}&{}\quad \varLambda _{2} \\ *&{}\quad -R^{-1}_{1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad -R^{-1}_{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad -R^{-1}_{3} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad -R^{-1}_{4} &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -S^{-1} &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -\gamma I \end{array} \right] <0 \end{aligned}$$

(23)

where $~~\varLambda _{2}=[{\mathbb {C}}z ~~0_{p\times 10n}]^{T}$.

Under zero initial conditions, $V(0)=0$, we have that

$$\begin{aligned} J_{1}=J+V(\infty )-V(0)=J+V(\infty )<0 \end{aligned}$$

which implies that $J<0$

When $w(t)=0$, we obtain

$$\begin{aligned} J_{1}<\int _{0}^{\infty }[\zeta (t)~~\alpha (t)]^{T}{\tilde{\varXi }}[\zeta (t)~~\alpha (t)] \end{aligned}$$

with

$$\begin{aligned} {\tilde{\varXi }}=\left[ \begin{array}{cccccc} {\tilde{\varLambda }} &{}\quad \tau _{1}{\tilde{\varLambda }}_{1} &{}\quad \tau _{a}{\tilde{\varLambda }}_{1} &{}\quad \tau _{2}{\tilde{\varLambda }}_{1}&{}\quad h{\tilde{\varLambda }}_{1}&{}\quad {\tilde{\varLambda }}_{1} \\ *&{}\quad -R^{-1}_{1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad -R^{-1}_{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad -R^{-1}_{3} &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad -R^{-1}_{4} &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad -S^{-1} \end{array} \right] \end{aligned}$$

where

$$\begin{aligned} {\tilde{\varLambda }}= & {} \left[ \begin{array}{ccccccccccc} \varLambda _{11} &{}\quad \varLambda _{12} &{}\quad \varLambda _{13} &{}\quad \varLambda _{14} &{}\quad \varLambda _{15} &{}\quad \varLambda _{16} &{}\quad \varLambda _{17} &{}\quad \varLambda _{19} &{}\quad \varLambda _{110} &{}\quad \varLambda _{111} &{}\quad \varLambda _{112} \\ *&{}\quad \varLambda _{22} &{}\quad \varLambda _{23} &{}\quad \varLambda _{24} &{}\quad 0 &{}\quad \varLambda _{26} &{}\quad 0 &{}\quad \varLambda _{29} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad \varLambda _{33} &{}\quad \varLambda _{34} &{}\quad 0 &{}\quad \varLambda _{36} &{}\quad 0 &{}\quad 0 &{}\quad \varLambda _{310} &{}\quad 0 &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad \varLambda _{44} &{}\quad 0 &{}\quad \varLambda _{46} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varLambda _{411} &{}\quad 0 \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{55} &{}\quad 0 &{}\quad \varLambda _{57} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \varLambda _{512} \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{66} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{77} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{99} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{1010} &{}\quad 0 &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{1111} &{}\quad 0\\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad *&{}\quad \varLambda _{1212} \end{array} \right] \\ \tilde{{\varLambda }}_{1}= & {} \left[ \begin{array}{ccccccccc} {\mathbb {A}}&\quad \frac{{\mathbb {A}}_{\tau }}{3}&\quad \frac{{\mathbb {A}}_{\tau }}{3}&\quad \frac{{\mathbb {A}}_{\tau }}{3}&\quad {\mathbb {A}}_{d}&\quad \frac{\tau _{12}}{3}{\mathbb {A}}_{\tau }&\quad -({\mathbb {B}}+{\mathbb {R}}E_{c})&\quad 0_{4n} \end{array} \right] ^{T} \end{aligned}$$

So ${\tilde{\varXi }}<0$ implies that

$$\begin{aligned} \int _{0}^{\infty } y^{T}_{\triangle }(s)Sy_{\triangle }(s)\mathrm{d}s< \int _{0}^{\infty }\varpi ^{T}(s)S\varpi (s)\mathrm{d}s \end{aligned}$$

(24)

The inequality (24) guarantees that $\Vert N \circ G \circ N^{-1}\Vert <1$.

From Lemma 4, we have the inequality $\Vert N \circ \vartriangle \circ N^{-1}\Vert \le 1$. Also, from, $J_{1}<0$, it can be easily seen that ${\dot{V}}(t)<0$ which implies that the system $(S_{1})$ with $w(t)=0$ is asymptotically stable.

When $w(t)\ne 0$, we multiply the both sides of (23) by $diag \{X,~X,~X,~X,~X,~X, T^{-1}_{0},~I,~X,~X,~X,~X,~X_{1},~X_{2}, ~X_{3},~X_{4},~X_{5},~I\}$ and by letting $X=P^{-1}$, $~X_{1}=R^{-1}_{1},~X_{2}=R^{-1}_{2},~X_{3}=R^{-1}_{3},~X_{4}=R^{-1}_{4},~X_{5}={S}^{-1},~~L=T^{-1}_{0},~~ F_{c}=E_{c}T^{-1}_{0},~~ W=HX^{T},~~{\hat{Q}}_{l}=XQ_{l}X$, $~(l=1,2,3,4)$, and using the relation $-X{X}^{-1}_{j}X \le {X}_{j}-2X$ for $j=1,2,3,4,5$. It is easy to obtain (12). Since (12) holds, it follows that $J<0$. Consequently,

$$\begin{aligned} \frac{1}{\gamma }\int _{0}^{\infty } z^{T}(s)z(s)\mathrm{d}s< \int _{0}^{\infty }\omega ^{T}(s)\omega (s)\mathrm{d}s \end{aligned}$$

On the other hand, the satisfaction of (13) guarantees that $\forall \xi \in \varepsilon (P,\kappa ^{-1}),$$\xi \in {\mathcal {S}}$. In fact, $\varepsilon (P,\kappa ^{-1})\subset {\mathcal {S}}$ is verified by the following conditions

$$\begin{aligned} \left[ \begin{array}{cc} P &{}\quad {\mathbb {K}}_{(i)}^T-H_{(i)}^T \\ *&{}\quad \kappa u_{0_{(i)}}^2\\ \end{array} \right] \ge 0 \end{aligned}$$

(25)

Pre- and post-multiplying (25) by $\varDelta ^{'}=diag\{P^{-1},I\}$, the LMI (13) is obtained.

Moreover, from the L–K functional defined in (14), we have

$$\begin{aligned} V(0)= & {} \xi ^{T}(0)P\xi (0)+\int _{- \tau _{1}}^{0}\xi ^{T}(s)Q_{1}\xi (s)\mathrm{d}s +\int _{-\tau _{a}}^{0}\xi ^{T}(s)Q_{2}\xi (s)\mathrm{d}s \nonumber \\&+\,\int _{-\tau _{2}}^{0}\xi ^{T}(s)Q_{3}\xi (s)\mathrm{d}s+\int _{-\tau (t)}^{0}\xi ^{T}(s)Q_{4}\xi (s)\mathrm{d}s \nonumber \\&+\,\tau _{1}\int _{-\tau _{1}}^{0}\int _{\theta }^{0}{\dot{\xi }}^{T}(s)R_{1}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta +\tau _{a}\int _{-\tau _{a}}^{0}\int _{\theta }^{0}{\dot{\xi }}^{T}(s)R_{2}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta \nonumber \\&+\,\tau _{2}\int _{-\tau _{2}}^{0}\int _{\theta }^{0} {\dot{\xi }}^{T}(s)R_{3}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta +h\int _{-h}^{0}\int _{\theta }^{0}{\dot{\xi }}^{T}(s)R_{4}{\dot{\xi }}(s)\mathrm{d}s\mathrm{d}\theta \\\le & {} \Big \{{\bar{\lambda }}(P)+ \tau _{1}{\bar{\lambda }}(Q_{1})+\tau _{a}{\bar{\lambda }}(Q_{2})+\tau _{2}{\bar{\lambda }}(Q_{3}+\tau _{2}{\bar{\lambda }}(Q_{4})\Big \}\Vert \phi (\theta )\Vert ^{2}\nonumber \\&+\,\Big \{\frac{ \tau _{1}^{3}}{2}{\bar{\lambda }}(R_{1})+\frac{\tau _{a}^{3}}{2}{\bar{\lambda }}(R_{2})+\frac{\tau _{2}^{3}}{2}{\bar{\lambda }}(R_{3})+\frac{h^{3}}{2}{\bar{\lambda }}(R_{4})\Big \}\Vert {\dot{\phi }}(\theta )\Vert ^{2}=\rho \end{aligned}$$

Making the above change of variables, we have $x^{T}(t)Px(t)\le V(t) \le V(0) \le \beta \le \kappa ^{-1}$; that is, for all $t\ge 0$, the trajectories of the system do not leave the set $\varepsilon (P,\kappa ^{-1})$ for any initial condition $\phi (\theta )$ in $\varepsilon (P,\kappa ^{-1})$, which ensures that $x(t)\in {\mathcal {S}}$.

The proof is thus completed. $\square$

4 Optimization Problems

4.1 Minimization of $\gamma$

The problem of minimizing $\gamma$ can be formulated as follows

$$\begin{aligned}&\mathrm{min} ~~\gamma \nonumber \\&\mathrm{subject~~to} ~ (12), (13)\nonumber \\&X>0, X_{j}>0, (j=1,\ldots ,5), {\hat{Q}}_{l}>0, (j=1,\ldots ,4) \end{aligned}$$

(26)

4.2 Maximization of $\rho$

The objective now is to provide (in the disturbance-free case, $w(t)=0$) a methodology to estimate the largest possible domain of initial conditions for which the closed-loop system trajectories remain bounded. This is mathematically complex due to the nonlinearity of $\beta$. The solution proposed is based on solving the optimization problem that is now developed: Let

$$\begin{aligned}&\left[ \begin{array}{cc} \sigma _{1}I &{}\quad I \\ I &{}\quad X\\ \end{array} \right] \ge 0,~~~~\left[ \begin{array}{cc} \sigma _{2}I &{}\quad {\tilde{X}} \\ {\tilde{X}}^{T} &{}\quad {\tilde{Q}}_{1}\\ \end{array} \right] \ge 0, ~~~~\left[ \begin{array}{cc} \sigma _{3}I &{}\quad {\tilde{X}} \\ {\tilde{X}}^{T} &{}\quad {\tilde{Q}}_{2}\\ \end{array} \right] \ge 0 \nonumber \\&\left[ \begin{array}{cc} \sigma _{4}I &{}\quad {\tilde{X}} \\ {\tilde{X}}^{T} &{}\quad {\tilde{Q}}_{3}\\ \end{array} \right] \ge 0, ~~~ \left[ \begin{array}{cc} \sigma _{5}I &{}\quad {\tilde{X}} \\ {\tilde{X}}^{T} &{}\quad {\tilde{Q}}_{4}\\ \end{array} \right] \ge 0, ~~~ \left[ \begin{array}{cc} \sigma _{6}I &{}\quad I \\ I &{}\quad X_{1}\\ \end{array} \right] \ge 0 \nonumber \\&\left[ \begin{array}{cc} \sigma _{7}I &{}\quad I \\ I &{}\quad X_{2}\\ \end{array} \right] \ge 0, ~~~ \left[ \begin{array}{cc} \sigma _{8}I &{}\quad I \\ I &{}\quad X_{3}\\ \end{array} \right] \ge 0,~~~~ \left[ \begin{array}{cc} \sigma _{9}I &{}\quad I \\ I &{}\quad X_{4}\\ \end{array} \right] \ge 0 \end{aligned}$$

(27)

where $~X^{-1}={\tilde{X}}$, $~{\hat{Q}}^{-1}_{i}={\tilde{Q}}$.

It follows that the condition $\beta \le \kappa ^{-1}$ is satisfied if the following condition holds:

$$\begin{aligned} \left[ \sigma _{1}+\tau _{1}\sigma _{2}+\tau _{a} \sigma _{3}+\tau _{2} (\sigma _{4}+\sigma _{5})+\frac{ \tau ^{3}_{1}}{2}\sigma _{6}+\frac{ \tau ^{3}_{a}}{2}\sigma _{7}+\frac{ \tau ^{3}_{2}}{2}\sigma _{8}+\frac{ h^{3}}{2}\sigma _{9}\right] \rho ^{2}\le \kappa ^{-1}\nonumber \\ \end{aligned}$$

(28)

where $\rho ^{2}=max(\Vert \phi _{\xi }\Vert ^{2},\Vert {\dot{\phi }}_{\xi }\Vert ^{2})$, and the stability radius $\rho$ is a scalar to be determined.

Combining the facts derived above, we can construct a feasibility problem for given $\tau _{1}, ~~\tau _{a},~~\tau _{2},~~h, ~~\gamma$, as follows

$$\begin{aligned}&\mathrm{minimize} ~~\varphi = \sigma _{1}+\tau _{1}\sigma _{2}+\tau _{a}\sigma _{3}+\tau _{2}(\sigma _{4}+\sigma _{5}) +\frac{\tau _{1}^{3}}{2}\sigma _{6}+\frac{\tau _{a}^{3}}{2}\sigma _{7}+\frac{\tau _{2}^{3}}{2}\sigma _{8}+\frac{h^{3}}{2}\sigma _{9} \nonumber \\&\mathrm{subject~~to} ~~ (12), (13),~(27),~(28), X>0, X_{j}>0, (j=1,..,5), {\hat{Q}}_{l}>0, (j=1,..,4)\nonumber \\ \end{aligned}$$

(29)

This optimization problem can then be solved using off-the-shelf numerical tools. It must be pointed out that by minimizing $\varphi$, we are, implicitly, maximizing $\rho$.

Remark 3

It is worth mentioning that the computational complexity can be handled by the Matlab LMI toolbox and all designs can be implemented offline, making the LMI method practicable and effective. In order to obtain a simpler form of LMI, no free-weighting matrices are adopted, which leads to small number of decision variables and consequently reduce the computational complexity significantly.

Remark 4

It should be noted that there are few works dealing with sampled-data control in the presence of actuator saturation, time-varying delay and external disturbance. We cite [33], where a dissipative-based controller was developed for a class of time-varying delay systems via sampled-data approach, but no saturation was considered. The robust $H_{\infty }$ sampled-data control problem for uncertain nonlinear time-varying delay systems is considered in [10], but the saturation was not considered either. In this paper, an anti-windup compensator is considered, as it is the most used technique to counterbalance the saturation effects and improve the closed-loop system performance during saturations.

Remark 5

The three-term approximation approach for $x(t-\tau (t))$ that is used here, which includes lower bound, upper bound and mean value of $x(t-\tau (t))$, was first proposed in [12] for continuous-time systems. Then, the same approximation was extended to delta operator systems and discrete time systems in [13] and [40], respectively. It is worth noting that it has been shown in those works that error using the three-term approximation is smaller than the one using two-term [22] and one-term approximation [20]. The three-term approximation is used here for the first time in the context of sampled-data systems subject to input saturation.

Remark 6

From the approaches to handle the saturation nonlinearity, the sector bound approach is used here as there results can be expressed as LMIs, that are easier to solve that those obtained using the polytopic modeling approach [18, 19].

5 Numerical Examples

In the following, two numerical examples are developed to illustrate the effectiveness of the proposed methodology.

Example 1

Consider the system (1) with $w(t)=0$ and the following parameters [9]:

$$\begin{aligned} A=\left[ \begin{array}{cc} 1 &{}\quad 1.5 \\ 0.3 &{}\quad -2\\ \end{array} \right] ,~~~~A_{\tau }=\left[ \begin{array}{cc} 0 &{}\quad -1 \\ 0 &{}\quad 0\\ \end{array} \right] ,~~~~B=\left[ \begin{array}{cc} 10 \\ 0\\ \end{array} \right] ,~~~C_{y}=\left[ \begin{array}{cc} 5 &{}\quad 1 \\ \end{array} \right] .\\ \end{aligned}$$

The dynamic controller is given as:

$$\begin{aligned} A_{c}=\left[ \begin{array}{cc} -20.2042 &{}\quad \quad 2.5216 \\ 2.1415 &{}\quad -4.4821\\ \end{array} \right] ,~B_{c}=\left[ \begin{array}{cc} 1.9516 \\ -0.0649\\ \end{array} \right] ,~C_{c}=\left[ \begin{array}{cc} -0.9165 &{}\quad 0.1091 \\ \end{array} \right] ,~D_{c}=0 \end{aligned}$$

In order to compare with previous results in the literature, that assume constant delays, solving the optimization problem (29), with $h=0.1, \kappa =1$ and $u_{0}=15$, the calculated stability radius $\rho$ for different values of $\tau _{2}$ gives the results in Table 1. It is clear from Table 1 that the obtained stability radius is larger than those obtained by existing works.

Table 1 Comparison of maximum radius $\rho$ for different $\tau _{2}$

Applying Theorem 1 with $h=0.15, \kappa =1$, some bounds of $\rho$ can be obtained for different value of $\tau _{2}~$ . Table 2 shows the comparison between our results and the results in [8] ($\tau _{1}=0.5$ and $\mu =0.5$). It can be seen from Table 2 that the proposed approach provides larger bounds $\rho$ than [8].

Table 2 Bound $\rho$ for different $\tau _{2}$ when $\tau _{1}=0.5$ and $\mu =0.5$

For instance, when $\tau _{2}=2$ and $u_{0}=0.5$ the corresponding anti-windup compensator gain is $E_{c}= 17915$. Figure 1 presents the state trajectories of the closed-loop system, and Fig. 2 shows the control input, simulated from the initial condition $x(0)=[-3.5 ~~4.5]^{T}$. It can be seen that the state trajectories of closed-loop system converge to zero, even when the system saturates, showing the feasibility of the procedure proposed.

Fig. 1

State trajectories of the closed-loop system in Example 1

Fig. 2

Evolution of control signal for Example 1

Example 2

In this example, we adopt the Mach Number in a Wind Tunnel model. As it has been shown in the literature [29], the deviations $\delta M$ of the Mach number induced by small deviations in the guide vane angle actuator $\delta \theta _{a}$ in a driving fan are precisely described at a given operating point (determined by the fan speed, liquid nitrogen injection rate, and gaseous-nitrogen vent rate) by the following dynamic model [29]:

$$\begin{aligned}&\frac{1}{a}\delta {\dot{M}}(t)+\delta M(t)=k\,\delta \theta (t-\tau (t)), \nonumber \\&{\delta \ddot{\theta }(t)+2\xi w\delta {\dot{\theta }}(t)+w^{2}\delta \theta (t)=w^{2}\delta \theta _{a}(t)}, \end{aligned}$$

(30)

where $\delta \theta$ is the guide vane angle, a, k, $\xi$, w are parameters which, at each working point, can be assumed constant if the deviations $\delta M$, $\delta \theta$, $\delta \theta _{a}$ are small. The delay $\tau (t)$ represents the time required by the movement of air between the fan and the test section.

Rewriting (30) in state space form yields the system (1). where

$$\begin{aligned} x= & {} \left[ \begin{array}{c} \delta M(t) \\ \delta \theta (t) \\ \delta {\dot{\theta }}(t) \end{array} \right] , A=\left[ \begin{array}{cccc} -a &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad -w^{2} &{}\quad -2\xi w \\ \end{array} \right] , A_{\tau }=\left[ \begin{array}{ccc} 0 &{} \quad ak &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right] , \\ B= & {} \left[ \begin{array}{c} 0 \\ 0 \\ w^{2} \end{array} \right] , B_{w}=\left[ \begin{array}{c} 0 \\ 0 \\ 10 \end{array} \right] , y(t)=\delta \theta (t), C_{y}=\left[ \begin{array}{ccc} 0&\quad 1&\quad 0 \end{array} \right] , \\ z(t)= & {} \left[ \begin{array}{c} \delta M(t) \\ \delta \theta (t) \end{array} \right] , C_{z}=\left[ \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \end{array} \right] , u(t)=\delta \theta _{a}(t) \end{aligned}$$

The parameters of the wind tunnel are borrowed from [29], and are as follows: $\frac{1}{a}=1.964s$, $k=-0.0117deg^{-1}$, $\xi =0.8$, and $w=6rad/s$.

The dynamic controller of Example 1 is considered again here. For the system with a time-invariant delay with $h=0.9$, applying Theorem 1 it is possible to obtain the optimal $H_{\infty }$ performance $\gamma$ (and the corresponding anti-windup gain matrix) for different values of $\tau _{2}$, as given in Table 3.

Table 3 The minimum allowable $\gamma$ for various $\tau _{2}$ in Example 3

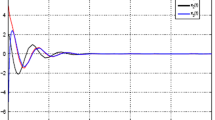
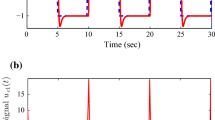
Figure 3 presents the simulation result for state trajectories of the closed-loop system (for the anti-windup gain corresponding to $\tau _{2}=10$), with the initial condition $x(0)=[-5~ 5 ~-5]^{T}$. The disturbance used in simulation is the Gaussian noise presented in Fig. 4.

Fig. 3

The state responses of the closed-loop system

Fig. 4

Disturbance used in the simulation

Figure 3 shows that the anti-windup compensator works well to stabilize the Mach number in wind tunnels.

Example 3

Consider the following system as in [6]:

$$\begin{aligned} A= & {} \left[ \begin{array}{cc} -0.2644 &{}\quad -0.0044 \\ 243.9024 &{}\quad -4.065\\ \end{array} \right] ,~~A_{\tau }=\left[ \begin{array}{cc} -0.2644 &{}\quad -0.0044 \\ 0 &{}\quad 0\\ \end{array} \right] ,\\ B= & {} \left[ \begin{array}{cc} -480.47 \\ 0\\ \end{array} \right] ,~~~B_{w}=\left[ \begin{array}{c} 0 \\ 1\\ \end{array} \right] ,~~~C_{y}=C_{z}=\left[ \begin{array}{cc} 5 &{} 1 \\ \end{array} \right] ,~~~\tau _{2}=0.246\\ \end{aligned}$$

The dynamic controller is given as:

$$\begin{aligned} A_{c}=0,~~~~B_{c}=1,~~~~C_{c}=9.6426\times 10^{-6},~~~~D_{c}=18.194\times 10^{-6} \end{aligned}$$

Applying (26) with $h=0.6$ and $\tau _{1}=0$ gives the anti-windup gain $E_{c}=92782$. The optimal $H_{\infty }$ performance $\gamma$ is listed in Table 4, comparing it with existing results. It is clearly observed from Table 4 that Theorem 1 gives the best $H_{\infty }$ performance index, showing that the method in this paper yields better result than existing methods.

Table 4 Comparison of $\sqrt{\gamma }$

6 Conclusion

This paper has presented a design methodology for anti-windup compensators for a class of systems with time-varying delay and input saturation. By employing the input–output approach, the scaled small gain theorem and a Lyapunov–Krasovskii Functional, compensators can be designed to ensure closed-loop system stability and a given disturbance attenuation. Moreover, the results have been rendered to be potentially less conservative, as illustrated by simulation results.