Introduction

Many applications in the field of electrical, industrial, and mechanical engineering like heat sinks, gas turbines, super heaters, bike heads, vehicle radiators, automobile, and aircraft engines, which deal with the heat transfer phenomenon, will utilize the fin structure to provide additional surface area and thereby enhance the rate of heat transfer. The performance of permeable fin was modeled by Kiwan and Nimr [1], and they explored the significance of porous fin over the solid fin. In addition, the influence of convection on the permeable fin was discussed under different fin tip conditions by Kiwan [2]. The radiation effect along with natural convection on the permeable fin has been examined by Gorla and Bakier [3]. A similar analysis has been carried out via the Homotopy Analysis Method by Darvishi et al. [4]. Additionally, the nonlinear boundary condition and temperature-dependent thermal conductivity were explained by using the Differential Transform Method by Torabi and Yaghoobi [5]. Ghosemi et al. [6] have analytically discussed the significance of solid and permeable convectional fins. Convection and radiation have a significant impact on the heat transmit rate. Hoseinzadeh et al. [7] have considered the numerical and analytical methods and did the comparative study for the temperature field of a porous fin.

Mainly, there are three types of the fin, namely longitudinal, radial, and pin fin. The longitudinal fin has different profiles depending upon the shape due to variation in the thickness. Some of the studies based on the different profiles of fins are as follows: the concave parabolic, trapezoidal, as well as rectangular profiled straight fin under fixed heat flux and fixed temperature boundary condition was presented by Aziz and Fang [8]. Moradi and Ahmadikia [9] considered the longitudinal fin of exponential, convex, and rectangular shapes under varying thermal conductivity conditions by using the Differential Transform Method. Torabi and Zhang [10] also discussed the efficiency of various fin profiles under nonlinear internal heat generation and surface emissivity. Torabi et al. [11] have comprehensively analyzed the performance of trapezoidal, rectangular, and concave parabolic profiled longitudinal fin.

The fully wet condition creates wet nature around the fin and aids in the heat transfer rate. In this regard, the mass and heat transfer study of a circular permeable fin in a fully wet circumstance has been performed by Hatami and Ganji [12]. The comparative study of the efficiency of straight versus exponential permeable fin in a completely wet situation was carried out by Turkyilmazoglu [13]. The thermal performance and efficiency of moving trapezoidal fin were modeled by Turkyilmazoglu [14]. The influence of the occurrence of heat generation internally on the permeable fin has been studied via the Finite Element Method by Sowmya et al. [15]. Baslem et al. [16] scrutinized the behavior of wetted longitudinal fin in the presence of nanofluid. The functionally graded material has been considered by Sowmya et al. [17], and they analyzed the thermal nature of the fin under fully wetted condition and described the significance of the wet nature of a fin.

For some of the applications like high-speed solar energy system, heat exchangers, and aircraft, transient response is also an important aspect to be recognized. Therefore, the unsteady thermal analysis is a significant factor. The longitudinal convecting fin of functionally graded material transient thermal performance was modeled by Khan and Aziz [18]. Darcy’s model was utilized to analyze the thermal behavior in the permeable fin of rectangular shape in the existence of transient effect by Darvishi et al. [19]. The radial fin of diverse profiles was considered, and unsteady temperature response was examined by Mosayebidorcheh et al. [20]. Applying the Differential Transform technique, the heat transfer of longitudinal fin under unsteady conditions along with nonlinear thermal coefficients has been discussed by Pasha et al. [21].

Fins have a wide range of applications in industries that are in the study of heat transfer analysis channels, etc. Xu et al. [22] and Xu [23] carried out a study of the heat transfer of thermal non-equilibrium in a metal-foam-filled solar collector and porous medium included micro heat exchangers, respectively. Hatami [24] studied the nanofluid flow through the wavy walled heated cylinder and discussed the RSM optimization. The heat transfer phenomenon in the micro-vessels and biomicrofluidics channel can be seen in Prakash et al. [25, 26]. MHD effect on the flexible fin in a cavity filled with nanofluid was analyzed by Selimefendigil et al. [27]. Asadollahi et al. [28] have scrutinized the channel with oblique fin coated with evacuating liquid. Some of the recent works can be observed in [29,30,31,32].

Based on all these observations, we intended to scrutinize the unsteady heat transfer through the rectangular, convex, and triangular-shaped longitudinal porous fin in a completely wet circumstance. The natural convection and radiations are also taken into consideration. The governed dimensionless partial differential equation has been solved numerically. The physical significance of the pertinent parameters has been illustrated through graphs and interpreted physically. The fin efficiency of all three profiles under diverse parameters is also plotted and discussed.

Mathematical formulation

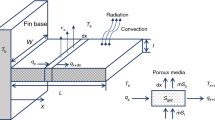
In the present study, we considered the one-dimensional heat transfer in the longitudinal porous fin of length L of diverse profiles like rectangular, triangular, as well as convex, and these are as displayed in Fig. 1. The fin sectional area varies with \(t\left( x \right)\) function, where \(t\left( x \right)\) is nothing but the variation of the thickness of the fin with the length. The surface of the fin is attached to the primary surface maintained at temperature Tb and surrounded by a fully wetted condition with temperature Ta. Initially, the fin is in thermal equilibrium with the surroundings. At time \(t^{*} = 0\), the fin base is subjected to an increase of temperature from Ta to Tb. Fin loses heat to the surrounding due to radiation and natural convection effect. Here, Darcy’s model is imposed to analyze the infiltration of ambient fluid through the pores of the fin. It is assumed that permeable fin is isotropic, homogeneous, and saturated with single-phase fluid. In addition, the radiant exchange through the surface is negligible.

Fig. 1
figure 1

Physical model of different profiles of the longitudinal porous fin

Full size image

The unsteady-state energy balance equation of a longitudinal permeable fin at a small element dx is defined as

$$\begin{aligned} q(x)& - q\left( {x + {\text{d}}x} \right) - 2\dot{m} c_{\text{p}} \left( {T - T_{\text{a}} } \right) - 2(1 - \phi )wh(T - T_{\text{a}} ){\text{d}}x \\ & \quad\quad - 2\varepsilon \sigma w{\text{d}}x\left( {T^{4} - T_{\text{a}}^{4} } \right) - 2h_{\text{D}} w{\text{d}}xi_{\text{fg}} (1 - \phi )(\omega - \omega_{\text{a}} ) \\ & \quad = \rho c_{\text{p}} A_{\text{c}} \frac{\partial T}{{\partial t^{*} }} \\ \end{aligned}$$
(1)

The first two terms in the LHS represent the heat transfer rate due to conduction, the second term stands for energy loss due to mass flow of immersed fluid, the third term is due to convection, the fourth term is the energy loss due to radiation, the fifth term signifies the heat lost because of the wet state, and the RHS is the unsteady term.

Here, \(\omega - \omega_{\text{a}}\) is the difference between the humidity ratio of saturated fluid and surrounding fluid, and it can be expressed as \(\left( {\omega - \omega_{\text{a}} } \right) = b_{2} \left( {T - T_{\text{a}} } \right)\) where \(b_{2}\) is the variable parameter. \(h_{\text{D}}\) is the uniform mass transfer coefficient, \(\phi\) is the porosity, and \(\dot{m}\) is the mass flow rate of fluid through porous fin and is defined as [4]

$$\dot{m} = \rho \upsilon (x)w{\text{d}}x,$$
(2)

where \(\upsilon \left( x \right)\) is the passage velocity, and according to Darcy’s model, it is as shown below [12]:

$$\upsilon (x) = \frac{{gK\beta_{\text{f}} \left( {T - T_{\text{a}} } \right)}}{{\nu_{\text{f}} }}.$$
(3)

Here, Fourier’s law of conduction takes the form as [11]

$$q = - k_{\text{eff}} wt(x) \frac{\partial T}{\partial x},$$
(4)

where \(k_{\text{eff}}\) is the effective thermal conductivity and is represented as [12]

$$k_{\text{eff}} = k_{\text{f}} \phi + k_{\text{s}} \left( {1 - \phi } \right).$$
(5)

The local semi fin thickness t(x) is different for different cases. For case 1: tb for rectangular profile, case 2: \(t_{\text{b}} \left( {\frac{x}{L}} \right)^{1/2}\) for convex profile, case 3: \(t_{\text{b}} \left( {\frac{x}{L}} \right)\) for triangular profile.

The convective heat transfer coefficient (h) is taken as a power function of temperature and is given by

$$h = h_{\text{a}} \left[ {\frac{{T - T_{\text{a}} }}{{T_{\text{b}} - T_{\text{a}} }}} \right]^{\text{p}} = h_{\text{D}} c_{\text{p}} Le^{{\frac{2}{3}}} .$$
(6)

Equation (1) is simplified on applying Eqs. (2)–(6) in it and get reduced as follows

  • Case 1: For rectangular profile

    $$\begin{aligned} & \frac{{\partial^{2} T}}{{\partial x^{2} }} - \frac{{2\rho g\beta_{\text{f}} Kc_{\text{p}} }}{{\nu_{\text{f}} k_{\text{eff}} t_{\text{b}} }}\left( {T - T_{\text{a}} } \right)^{2} \\ & \quad - \frac{2\sigma \varepsilon }{{k_{\text{eff}} t_{\text{b}} }}\left( {T^{4} - T_{\text{a}}^{4} } \right) - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} \left( {T - T_{\text{a}} } \right)^{{\text{p}}+1} }}{{k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} \\ & \quad - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} i_{\text{fg}} b_{2} (T - T_{\text{a}} )^{{\text{p}}+1} }}{{c_{\text{p}} Le^{2/3} k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} = \frac{{\rho c_{\text{p}} }}{{k_{\text{eff}} }}\frac{\partial T}{{\partial t^{*} }}, \\ \end{aligned}$$
    (7a)

  • Case 2: For convex profile

    $$\begin{aligned} & \frac{\partial }{\partial x}\left( {\left( {\frac{x}{L}} \right)^{1/2} \frac{\partial T}{\partial x}} \right) - \frac{{2\rho g\beta_{\text{f}} Kc_{\text{p}} }}{{\nu_{\text{f}} k_{\text{eff}} t_{\text{b}} }}\left( {T - T_{\text{a}} } \right)^{2} \\ & \quad - \frac{2\sigma \varepsilon }{{k_{\text{eff}} t_{\text{b}} }}\left( {T^{4} - T_{\text{a}}^{4} } \right) - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} \left( {T - T_{\text{a}} } \right)^{{\text{p}}+1} }}{{k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} \\ & \quad - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} i_{\text{fg}} b_{2} (T - T_{\text{a}} )^{ {\text{p}}+1} }}{{c_{\text{p}} Le^{2/3} k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} = \frac{{\rho c_{\text{p}} }}{{k_{\text{eff}} }}\frac{\partial T}{{\partial t^{*} }} \\ \end{aligned}$$
    (7b)

  • Case 3: For triangular profile

    $$\begin{aligned} & \frac{\partial }{\partial x}\left( {\frac{x}{L}\frac{\partial T}{\partial x}} \right) - \frac{{2\rho g\beta_{\text{f}} Kc_{\text{p}} }}{{\nu_{\text{f}} k_{\text{eff}} t_{\text{b}} }}\left( {T - T_{\text{a}} } \right)^{2} \\ & \quad - \frac{2\sigma \varepsilon }{{k_{\text{eff}} t_{\text{b}} }}\left( {T^{4} - T_{\text{a}}^{4} } \right) - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} \left( {T - T_{\text{a}} } \right)^{{\text{p}}+1} }}{{k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} \\ & \quad - \frac{{2\left( {1 - \phi } \right)h_{\text{a}} i_{\text{fg}} b_{2} (T - T_{\text{a}} )^{{\text{p}}+1} }}{{c_{\text{p}} Le^{2/3} k_{\text{eff}} t_{\text{b}} \left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }} = \frac{{\rho c_{\text{p}} }}{{k_{\text{eff}} }}\frac{\partial T}{{\partial t^{*} }}. \\ \end{aligned}$$
    (7c)

The following dimensionless terms are introduced to non-dimensionalize the above equations [18].

$$\theta = \frac{T}{{T_{\text{b}} }}, \, \theta_{\text{a}} = \frac{{T_{\text{a}} }}{{T_{\text{b}} }}, X = \frac{x}{L}, \, \tau = \frac{{\alpha t^{*} }}{{L^{2} }}.$$
(8)

On applying Eq. (8) in Eq. (7), it is modified to the dimensionless form as follows:

  • Case 1: For rectangular profile

    $$\begin{aligned} \frac{\partial \theta }{\partial \tau } & = \frac{{\partial^{2} \theta }}{{\partial X^{2} }} - {\text{Nc}}\left( {\theta - \theta_{\text{a}} } \right)^{2} \\ & \quad - {\text{Nr}}\left( {\theta^{4} - \theta_{\text{a}}^{4} } \right) - \frac{{m_{2} \left( {\theta - \theta_{\text{a}} } \right)^{{\text{p}} + 1} }}{{\left( {1 - \theta_{\text{a}} } \right)^{\text{p}} }}. \\ \end{aligned}$$
    (9a)

  • Case 2: For convex profile

    $$\begin{aligned} \frac{\partial \theta }{\partial \tau } & = \frac{\partial }{\partial X}\left( {X^{1/2} \frac{\partial \theta }{\partial X}} \right) - {\text{Nc}}\left( {\theta - \theta_{\text{a}} } \right)^{2} \\ & \quad - {\text{Nr}}\left( {\theta^{4} - \theta_{\text{a}}^{4} } \right) - \frac{{m_{2} \left( {\theta - \theta_{\text{a}} } \right)^{{\text{p}} + 1} }}{{\left( {1 - \theta_{\text{a}} } \right)^{\text{p}} }}. \\ \end{aligned}$$
    (9b)

  • Case 3: For triangular profile

    $$\begin{aligned} \frac{\partial \theta }{\partial \tau } & = \frac{\partial }{\partial X}\left( {X\frac{\partial \theta }{\partial X}} \right) - Nc\left( {\theta - \theta_{a} } \right)^{2} \\ & \quad - {\text{Nr}}\left( {\theta^{4} - \theta_{a}^{4} } \right) - \frac{{m_{2} \left( {\theta - \theta_{a} } \right)^{{\text{p}} + 1} }}{{\left( {1 - \theta_{a} } \right)^{\text{p}} }}. \\ \end{aligned}$$
    (9c)

Corresponding initial and boundary conditions will be

$$\theta (X,0) = 0, \, \theta (1,\tau ) = 1, \, \frac{\partial }{\partial X}\theta (0,\tau ) = 0.$$
(10)

In Eq. (9), \(\theta\) is the dimensionless temperature, X is the dimensionless length, \(\tau\) is the dimensionless time, \({\text{Nc}} = \frac{{2\rho g\beta_{\text{f}} Kc_{\text{p}} T_{\text{b}} L^{2} }}{{\nu_{\text{f}} k_{\text{eff}} t_{\text{b}} }}\) is the convective parameter, \({\text{Nr}} = \frac{{2\varepsilon \sigma L^{2} T_{\text{b}}^{3} }}{{k_{\text{eff}} t_{\text{b}} }}\) is the radiative parameter, p is the power index associated with the convective heat transfer coefficient, \(\theta_{a}\) is the dimensionless ambient temperature, X is the dimensionless length, \(m_{2}\) is the wet porous parameter and is the sum of \(m_{0} = \frac{{2h_{\text{a}} L^{2} \left( {1 - \phi } \right)}}{{k_{\text{eff}} t_{\text{b}} }}\) and \(m_{1} = \frac{{2h_{\text{a}} i_{\text{fg}} \left( {1 - \phi } \right)b_{2} L^{2} }}{{k_{\text{eff}} t_{\text{b}} c_{\text{p}} Le^{{\frac{2}{3}}} }}.\)

Fin efficiency

The total transfer of heat from the fin surface is the sum of heat transfer due to porosity, convection, as well as radiation, and it is expressed as follows:

$$\begin{aligned} Q_{\text{f}} & = \int\limits_{0}^{L} {\left[ {\frac{{2\rho gw\beta_{\text{f}} Kc_{\text{p}} }}{{\nu_{\text{f}} }}\left( {T - T_{\text{a}} } \right)^{2} + 2\sigma \varepsilon w\left( {T^{4} - T_{\text{a}}^{4} } \right)} \right.} \\ & \quad \left. { + \left( {2h_{\text{a}} \left( {1 - \phi } \right)w + \frac{{2h_{\text{a}} i_{\text{fg}} \left( {1 - \phi } \right)b_{2} w}}{{c_{\text{p}} Le^{2/3} }}} \right)\frac{{\left( {T - T_{\text{a}} } \right)^{{\text{p}} + 1} }}{{\left( {T_{\text{b}} - T_{\text{a}} } \right)^{\text{p}} }}} \right]{\text{d}}x \\ \end{aligned}$$
(11)

The ideal transfer of heat from the fin means the heat transfer from the fin surface when it is kept at a base temperature Tb. The ideal case is as follows:

$$\begin{aligned} Q_{\text{ideal}} & = \frac{{2\rho gw\beta_{\text{f}} Kc_{\text{p}} L}}{{\nu_{\text{f}} }}\left( {T_{\text{b}} - T_{\text{a}} } \right)^{2} + 2\sigma \varepsilon wL\left( {T_{\text{b}}^{4} - T_{\text{a}}^{4} } \right) \\ & \quad + \left( {2h_{\text{a}} \left( {1 - \phi } \right)wL + \frac{2{h_{\text{a}} i_{\text{fg}} \left( {1 - \phi } \right)b_{2} wL}}{{c_{\text{p}} Le^{2/3} }}} \right)\left( {T_{\text{b}} - T_{\text{a}} } \right) \\ \end{aligned}$$
(12)

The fin efficiency is described as the ratio of the actual dissipation of heat from the fin to the heat that would be transferred if the entire fin surface is kept at the base temperature. That is

$$\eta = \frac{{Q_{\text{f}} }}{{Q_{\text{ideal}} }}.$$
(13)

The dimensionless form of Eq. (13) is

$$\eta = \frac{{\int\limits_{0}^{1} {\left[ {{\text{Nc}}\left( {\theta - \theta_{\text{a}} } \right)^{2} + {\text{Nr}}\left( {\theta^{4} - \theta_{\text{a}}^{4} } \right) + \frac{{m_{2} \left( {\theta - \theta_{a} } \right)^{{\text{p}} + 1} }}{{\left( {1 - \theta_{\text{a}} } \right)^{\text{p}} }}} \right]} {\text{ d}}X}}{{{\text{Nc}}\left( {1 - \theta_{\text{a}} } \right)^{2} + {\text{Nr}}\left( {1 - \theta_{\text{a}}^{4} } \right) + m_{2} \left( {1 - \theta_{\text{a}} } \right)}}.$$
(14)

Solution procedure

The parabolic partial differential Eq. (9) with initial and boundary conditions (10) was solved numerically via the pdsolve command in MAPLE 18. This is based on the algorithm of the Finite Difference Method (FDM) with the discretization of the differential equation by the center implicit scheme. This command extracts numerical data from the solution obtained in the form of a module. The space step and time step are chosen as \(\Delta x = \Delta t = 0.001\).

The validation of the current solution is done by comparing the obtained solution with the finite element method and is displayed in Fig. 2. The solution found in FDM via Maple is in good agreement and accurate with the FEM solution for rectangular, convex, and triangular profiled fins considered in this study.

Fig. 2
figure 2

Comparison of present solution via FDM with FEM solution

Full size image

Results and discussion

The parametric study of the obtained solution has been conducted to determine the prominence of dimensionless significant constraints on the unsteady thermal distribution as well as efficiency for the longitudinal fin of triangular, convex, and rectangular profiles. The results have been shown in Figs. 3–11 and in Table 1.

Fig. 3
figure 3

Impact of convective parameter on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image
Table 1 Influence of dimensionless time on the unsteady thermal profile of the different profiled fin at \({\text{Nc}} = 1, {\text{Nr}} = 1, p = 1, m_{2} = 1, \theta_{\text{a}} = 0.2\)
Full size table

Figure 3a–c displays the combined effect of variation in convective parameter and different fin profiles on the thermal field along the surface of the porous fin. Here, an increase in convective parameter decreases the temperature profile. This is because, as the convection effect increases, more heat from the fin surface transform to the surrounding. Therefore, the rate of transfer of heat increases and the temperature decreases. The same nature is noticeable in rectangular, convex, as well as triangular profiled fin structure. On the other hand, the thermal drop rate is more for triangular fin followed by convex and rectangular fin.

The significance of the radiative parameter on the temperature behavior of the permeable fin of different profiles is as shown in Fig. 4a–c. The radiation effect positively impacts on the heat transfer purpose. Therefore, the temperature of the fin surface declines with amplification in the radiative parameter because the radiation effect carries away the excess heat from the fin surface. This nature is similar for all the three shaped profiles considered in this study.

Fig. 4
figure 4

Impact of radiative paameter on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image

The wet nature around the fin will aid in absorbing extra heat from the surface of the fin and therefore decreases the fin temperature. This is evident in Fig. 5a–c, where the effect of the wet porous parameter on the different profiles as well as the thermal feature of the fin is plotted. It is seen that, as the wet porous parameter enhances, the temperature profile decreases. The wet porous parameter shows a significant effect on the temperature field of all the three shapes of fin considered in the present analysis. In addition, the temperature decrease rate is faster in the triangular fin compared to the convex and rectangular fins.

Fig. 5
figure 5

Impact of a wet porous parameter on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image

The impact of dimensionless ambient temperature parameter on the temperature attribute of the rectangular, convex, as well as triangular fin is represented in Fig. 6a–c. Here, as \(\theta_{\text{a}}\) rises, the thermal profile is more. This is due to the rise in the ratio of the surrounding temperature to the base temperature of the fin. This implies that when the surrounding temperature amplifies, the thermal variation between the surface of the fin and the surrounding decreases. According to Newton’s law of cooling, the cooling effect decreases due to a reduction in thermal difference between surface and surrounding.

Fig. 6
figure 6

Impact of ambient temperature on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image

The effect of power index p incorporated in a convective heat transfer coefficient on the temperature field of the rectangular, convex, and triangular profiled fin has been captured in Fig. 7a–c. As the power index rises, the temperature profile increases, due to the nonlinearity. Therefore, we notice less heat transfer rate with the rise in the power index in all the three different fin structures.

Fig. 7
figure 7

Impact of power index on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image

The transient effect on the temperature feature of the porous fin of the different profile is displayed in Fig. 8a–c. One can see that as time increases the temperature profile also rises to a certain limit. It is very interesting to note that, after a certain time, the thermal profile becomes constant. The transient effect is visible initially and after some time a steady condition is reached. This is shown in Table 1. Cleary, we saw that the unsteady thermal behavior value increases with time but as time increases it reaches a steady state. On the other hand, the unsteady thermal value of the triangular fin is less than the convex and rectangular profiled fin.

Fig. 8
figure 8

Impact of dimensionless time on the unsteady thermal profile for a rectangular fin, b convex fin, and c triangular fin

Full size image

The efficiency of rectangular, convex, and triangular porous fin versus a convective parameter and radiative parameter for diverse values of ambient temperature and power index is as shown in Figs. 9 and 10, respectively. It is observed that as the convective and radiative parameters rise, efficiency shows decreasing nature. This is because an increase in convection effect reduces the temperature of the fin surface, which leads to the decrease in the ratio of actual heat transport to transfer of heat from the fin surface kept at base temperature. This result can be qualitatively compared with that of Torabi et al. [11].

Fig. 9
figure 9

Fin efficiency versus m2 for diverse Nc

Full size image
Fig. 10
figure 10

Fin efficiency versus Nr for diverse p

Full size image

The transient efficiency of fin of rectangular, convex and triangular profile for different values of Nc, Nr, p, m2 is presented in Fig. 11a–d, respectively. Initially, when there is no heat flow from the base, the fin efficiency is zero and the surface of the fin is in thermal equilibrium with the surrounding but as the heat flow through the fin, the efficiency rises sharply and attains constant value as the steady state is reached. In the transient region, it is noticed that, as the dimensionless time rises, efficiency also enhances. Khan and Aziz [18] attained the same conclusion for unsteady convective fin case. It is observed that steady state is reached earlier for higher Nc, Nr, p, and m2 and as these parameters rise, efficiency decreases. Additionally, it is observed that the efficiency of the rectangular fin is higher and the triangular fin is lower than the convex fin.

Fig. 11
figure 11

Efficiency of fin versus dimensionless time for diverse values of a Nc, b Nr, c p, and d m2

Full size image

Conclusions

The transient thermal performance and efficiency of the longitudinal porous fin of different profiles like rectangular, triangular, and convex shapes under a fully wet circumstance has been scrutinized numerically. The main findings of the present investigation are listed below:

  • The radiative parameter, as well as a convective parameter, induces a pronounced effect on the fin cooling.

  • The higher value of the wet porous parameter is also attributed to the augmentation of the heat dissipation from the fin.

  • The unsteady thermal profile rises for a rise in power index and ambient temperature, which means that it reduces the heat transfer rate.

  • The different profile of the fin surface has a prominent impact on the rate of heat transfer.

  • The efficiency of the fin is affected by the convective and radiative parameters.

  • The efficiency rises with the rise in dimensionless time and becomes constant as a steady state is reached.

  • The temperature drop rate is more for a triangular fin profile compared to rectangular and convex fin profiles.

  • More fin efficiency is observed for a rectangular fin profile followed by convex and triangular fins.