Introduction

Two-phase liquid flow in micro-/mini-channels has several thermal advantages in comparison with single-phase liquid flow, such as heat transfer rate, thermosiphon effect and isothermal heat sinks. Multiphase flows in microfluidic devices are usually used as an effective mode to improve the cooling process, since phase change process can provide high heat transfer coefficient in comparison with single-phase flows. On the other hand, high surface-to-volume ratio of microheat exchangers can intensify the overall heat rejection from the system. To investigate such kinds of flows, numerical analysis is used to solve the problems involving fluid flows. In particular, there is a wide variety of fluid flows in nature, industry, medicine, etc., where numerical simulations, in particular computational fluid dynamics (CFD), are getting extensively evolved in industrial and medical researches [1]. In industry, cooling of electronic equipment using micro-/mini-channel was considered as a practical technique to improve the cooling process. Because of the high value of surface area-to-volume ratio of microcooling systems, these systems are highly advisable as continuous minimization in microdevices requires higher heat waste inside the small and compact systems. Recently, oblique mini-/microchannels are used as a new method for heat transfer augmentation. In this method, a small secondary channel is placed with an angle across the head channels. It is found that the relevant effects of the new development of boundary layer and creation of secondary flows in oblique fins cause more efficient heat transfer performance due to a thinner boundary layer [2]. In a separate study, Lee et al. [3] studied the division of continuous fin into slopping sections which cause the new booting of boundary at the prior borders of slopping fin. This efficiency reduces the boundary layer thickness. They also summarized the following advantages of oblique microchannels for electronics cooling: (a) The oblique frame outstandingly grows the surface area between the refrigerated liquid and the solid matter, (b) the oblique frame is simply usable in applied science, and (c) cutting slopping splits on the continuing fins decreases the heaviness of plate and is economically efficient. It has been emphasized that the unique oblique fin (micro-/mini-channel) design adjusts the flow and as a result makes a new flow field which is eligible for usages especially in heat transfer [4].

The significant role of oblique fins in the structure of microdevices and also electronics cooling makes the research interesting to investigate the phase change process in oblique channels. In some cases, the cooling process leads to condensation of the working fluid. Therefore, several studies have been dedicated to investigating the hydrodynamics of drops through the phase transition using either numerical or experimental method. For instance, Fang et al. [5] investigated the water condensation in a hydrophilic microchannel, experimentally. They found a relation between channel arrangement and condensation across the flow regime visualization and film-thickness evaluations. Hussaini et al. [6] experimentally presented the images of droplet and slug flow inside the operational PEM fuel cells (proton exchange membrane). They presented a novel parameter named wetted area ratio to specify channel flooding. Cho and Wang [7] studied two-phase flows in a microchannel with diverse surface conditions, experimentally and numerically. They observed that liquid water becomes visible in all the quoins of a hydrophilic channel. Carton et al. [8] investigated the droplet coalescence and movement of slug in a mini-channel using imaging techniques and volume of fluid (VOF) two-phase model. They also studied the effect of geometry changes on the flow field. It was found that these changes can interrupt slug motion and eschew blockage of the channel, to some extent. As well as, they found that the excess water formed from collision and coalescence of drops might immediately create slugs in PEM fuel cells. Quan et al. [9] computationally investigated the water operation in PEM fuel cell. They investigated the effect of hydrophilic surfaces of channel, channel arrangement, the air velocity and its pressure decline on the water behavior. They found that pointed edges in the hydrophilic channel influence on water transport. Venkatraman et al. [10] studied the gas flow around a sticky droplet and stagnant drop in a rectangular channel, using both experimental and numerical methods. They found a reverse relationship between channel surface hydrophilicity and pressure drop.

In the computational field of multiphase flows, LBM (the lattice Boltzmann method) as a mesoscopic numerical technique has been successfully implemented. LBM provides several advantages over the usual computational fluid dynamics (CFD) methods. For example, it is not necessary to track the position and the shape of the interface. Furthermore, the wall boundary condition can be set as the bounce-back of the fluid particle at the wall boundary nodes. Therefore, it is relatively simple to simulate flows in complicated geometries by using this method. Pereira [11] numerically studied immiscible flow in a semi-porous medium using LBM. They compared the solution to check states and gained rational understanding as evaluated with analytic solutions. Also they applied the method to porous and regained the capillary and viscous regimes. Leclaire et al. [12] studied the immiscible liquid–liquid interface dynamics via LBM. They figured out that the suggested LBM is in the same direction with the scale methods, and that the related standard error between the results is lower than 1% for multiple values.

There are very few studies in micro-/mini-channel context using LBM, for instance, in the simulation of two-phase flow in a 3D cross-junction microchannels or condensation simulation in a two-dimensional channel with square obstacles [13]. Leclaire et al. [14] studied immiscible multiphase flows. They adjusted the Latva-Kokko and Rothman recoloring algorithms for decreasing the lattice connection problem. Also, they conducted a set of computational tests to display that the compound of the two algorithms causes a betterment in the results’ quality. Fu et al. [15] simulated the nucleation and coalescence of drops on different structured surfaces by using the LBM. They figured out that alongside the surface properties, the topography of structures on surfaces plays a role on the condensation process. Also in the other similar context of drops coalescence (drop to liquid surface), it is indicated that after the inclined drop collision the formed wave in liquid film is stronger in comparison with the normal one [16]. Amara et al. [17] studied the hydrodynamic of the droplet in a PEM fuel cell microchannel via LBM. The results revealed that the microchannel with hydrophobic surfaces is preferable than hydrophilic one for droplet discharge. Also, they presented the theory of the drop hydrodynamic in a cell-channel. Besides the surface type, there are several studies using LBM which investigated the effect of moving and vibrant surfaces on drop evacuation [18]. Huang et al. [19] provided the LBM investigation of drop movement in a hatched channel. The results showed that the drop can move faster on hatched hydrophobic walls than on their hydrophilic counterparts. They also studied the effects of density ratio on the droplet velocity and showed that for walls with coarse surfaces, the wettability and topography are connected together. Few key studies germane to the present investigation can be found in [20,21,22,23,24,25,26,27,28,29,30,31,32,33].

To the best knowledge of the authors, none of the previous studies investigates after the cooling condensation process in oblique micro-/mini-channels. This configuration is widely used in heat pipe devices in which a cooling medium conveys heat from the hot source to the cold source by using gravitational force and thermosiphon effect. Accordingly, in the present study, we utilize a two-dimensional LBM in conjugation with the pseudo-potential multiphase model to simulate the condensation phenomenon in an oblique fin (mini-channel). The aim of this investigation is to study the hydrodynamic of liquid drops in a slopping channel with hydrophilic walls. In this regard, the effect of varying channel angle on the liquid film movement and the liquid evacuation time is analyzed.

Description of the simulation model

Lattice Boltzmann method

LBM is interpreted as particle-based method for simulation of fluid flows. Frisch et al. [34] established the method based on LGA method (lattice gas automata). Regardless of external forces and by using BGK (Bhatnagar–Gross–Krook) approximation, the LB equation is as follows [35]:

$$f_{\text{i}} (x + e_{\text{i}} \delta t,\;t + \delta t) = f_{\text{i}} (x,t) + \frac{{f_{\text{i}}^{\text{eq}} (x,t) - f_{\text{i}} (x,t)}}{\tau } ,$$
(1)

where \(f_{\text{i}} (x,\;t)\) is the distribution function for particles moving with the discrete velocity \(e_{\text{i}}\) at position \(x\) and time \(t\). \(\tau\) is relaxation time, and \(\delta t\) is the dimensionless time step. Also, \(f^{\text{eq}}\) is the equilibrium function that is presented in such a way [36, 37]:

$$f^{\text{eq}} = w_{\text{i}} \rho \left[ {1 + 3\frac{{e_{\text{i}} \cdot u_{\text{eq}} }}{{c^{2} }} + 9\frac{{(e_{\text{i}} \cdot u_{\text{eq}} )^{2} }}{{2c^{4} }} - \frac{{3u_{\text{eq}}^{2} }}{{2c^{2} }}} \right],$$
(2)

where \(w_{\text{i}}\),\(c = \delta x/\delta t\) and \(u_{\text{eq}}\) are mass coefficients, characteristic velocity in LBM and modified velocity of the fluid, respectively. Fluid density \(\rho\) will be [36, 37]:

$$\rho = \sum\limits_{i = 0} {f_{\text{i}} } .$$
(3)

As stated by popular \(D_{2} Q_{9}\) scheme, the discrete velocities \(e_{\text{i}}\) are given as follows [36, 37]:

$$e_{i} = \left\{ {\begin{array}{*{20}l} {(0,0)c,\;\;i = 0,} \hfill \\ {(\cos \left[ {(i - 1)\pi /2} \right],\;\sin \left[ {(i - 1)\pi /2} \right])c,\;\;i = 1 - 4,} \hfill \\ {\sqrt 2 (\cos \left[ {(i - 5)\pi /2 + \pi /4} \right],\;\sin \left[ {(i - 5)\pi /2 + \pi /4} \right])c,\;\;i = 5 - 8.} \hfill \\ \end{array} } \right.$$
(4)

The corresponding mass coefficients \(w_{i}\) are given by [36, 37]:

$$w_{\text{i}} = \left\{ {\begin{array}{*{20}l} {4/9,\;\;i = 0,} \hfill \\ {1/9,\;\;i = 1 - 4,} \hfill \\ {1/36,\;\;i = 5 - 8.} \hfill \\ \end{array} } \right. ,$$
(5)

Furthermore, the kinematic viscosity of LBM is related to relaxation parameter and is calculated by [36, 37]:

$$\upsilon = \left( {\tau - \frac{1}{2}} \right)C_{\text{s}}^{2} \delta t ,$$
(6)

in which \(C_{\text{s}} = c/\sqrt 3\) shows the speed of sound.

Pseudo-potential model

In order to simulate multiphase flow problems, the interaction force \(F_{\text{int}}\) between the particles is defined as follows [38]:

$$F_{\text{int}} (x,t) = - G\psi (x,t)\sum\limits_{i = 1}^{8} {w_{\text{i}} \psi (x + e_{\text{i}} \Delta t,\;t)e_{\text{i}} } ,$$
(7)

where the interaction strength is indicated by \(G\). Also, Shan and Chen [39] propounded one of the widely used forms of the function of interaction potential \(\psi\), as follows:

$$\psi (\rho ) = \psi_{0} \exp ( - \rho_{0} /\rho ) ,$$
(8)

where \(\psi_{0}\) and \(\rho_{0}\) are optional and constant. The negative amount of \(G\) in Eq. (7) signifies the presence of absorption among the particles. It is found that the fluid EOS (equation of state) using the interparticle interaction force \(F_{\text{int}}\) is calculated by [40]:

$$P = \frac{\rho }{3} + \frac{G}{6}(\psi (\rho ))^{2} = \frac{\rho }{3} + \frac{G}{6}(\psi_{0} \exp ( - \rho_{0} /\rho ))^{2} .$$
(9)

Note that by using Eq. (9) for pressures less than critical value, there is coexistence between fluid phases [41]. If the amount of first and second derivatives is considered zero for Eq. (9), it is possible to find the critical parameters in this way:

$$\begin{aligned} \rho_{\text{cr}} & = \rho_{0} \\ G_{\text{ critical}} & = - \frac{{\rho_{0} }}{{\psi_{0}^{2} }}\exp (2) \\ \end{aligned}$$
(10)

In this research, \(\rho_{0} = 200\) is implemented which leads to \(G_{\text{Critical}} = - 92.4\) and \(\psi_{0} = 4\) in \(G \le G_{\text{Critical}}\) phase. The interaction force between the solid surface and fluid particles \(F_{\text{ads}}\) can also be defined as [41]:

$$F_{\text{ads}} (x,t) = - G_{\text{ads}} \psi (x,t)\sum\limits_{i = 1}^{8} {w_{\text{i}} s(x + e_{\text{i}} \Delta t,\;t)e_{\text{i}} } .$$
(11)

where \(G_{\text{ads}}\) is the absorption coefficient and \(s(x + e_{\text{i}} \Delta t,\;t)\) is a switch function (if \((x + e_{\text{i}} \Delta t)\) is a wall node \(s = 1\) and otherwise \(s = 0\)). The hydrophobic and hydrophilic surfaces are distinguished by the absorption coefficient \(G_{\text{ads}}\). Higher values of \(\left| {G_{\text{ads}} } \right|\) will make the surface more hydrophilic. Finally, in order to implement the gravitational force, the following equation is utilized:

$$F_{g} = (\rho (x) - \rho_{v} ) \times g .$$
(12)

where \(g\), \(\rho_{\text{v}}\) and \(\rho (x)\) are the gravitational acceleration, the density of vapor and density of every nodes in the domain, respectively. Then, the amended speed \(u_{\text{eq}}\) can be calculated as follows [38]:

$$u_{\text{eq}} = u + \frac{\tau F}{\rho } .$$
(13)

Here \(F\) is the sum of forces \(F_{\text{int}}\), \(F_{\text{ads}}\) and \(F_{g}\), and \(u\) is the flow speed in macroscopic scale, which is given by [42]:

$$u = \frac{1}{\rho }\sum\limits_{i = 0} {e_{\text{i}} f_{\text{i}} } .$$
(14)

Grid independency

In order to find the appropriate grid resolution for the current study, a grid independence study is adopted. The geometry is illustrated in Fig. 1. Table 1 indicates the effect of grid resolution on the ratio of liquid to vapor (wetness fraction W) which is obtained as follows:

$$W = 100 \times \left( {{\text{Liquid}}\;{\text{volume/Vapour}}\;{\text{volume}}} \right).$$
(15)
Fig. 1
figure 1

Geometry of grid independence study

Full size image
Table 1 The result of resolution on the percent of liquid-to-vapor ratio at time t = 2000
Full size table

The results were introduced for various grid resolutions and lattice time t = 2000. Since it is observable, the difference between case 2 and case 3 is about 0.43% which is satisfactory for the present study. Therefore, grid resolution 2 will be used for the rest of the simulations.

Validation

Based on Laplace law, there is a direct relation between the pressure difference to keep the circular shape of the boundary and the curvature of this boundary, which is given by the following equation:

$$\Delta P = P_{\text{in}} - P_{\text{out}} = \frac{\sigma }{R},$$
(16)

where \(R\) indicates radius and \(\sigma\) denotes the surface tension. “in” and “out” show the inlet and outlet of drop.

By choosing a domain with the grid of 200 × 200, the variation of ∆P with \(1/R\) is shown in Fig. 2. LBM results are indicated by red cycles and fitted line equation as stated by:

$$\Delta P = 14.774\Bigg(\frac{1}{R}\Bigg) - 0.0004,$$
(17)

the incline of the graph specifies the surface tension in Eq. (17), and as it is depicted in Fig. 2, the pressure difference is in a direct relationship with \(1/R\). Hence, it is worth to mention that Laplace law is valid for the current case.

Fig. 2
figure 2

Change of ∆P with 1/R (symbols: LBM, line: fitted line)

Full size image

Boundary conditions

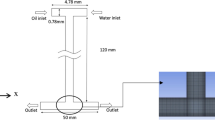
The geometry of the problem is given in Fig. 3. The angle between channel walls with the horizontal surface is defined by \(\theta\). Consequently, the gravitational acceleration \(g\) is decomposed into \(x\) and \(y\) components.

Fig. 3
figure 3

Geometry of the case study with considered boundary conditions

Full size image

In order to apply constant vapor pressure as the channel inlet boundary condition [43, 44]:

$$u_{\text{w}} = 1 - \frac{1}{{\rho_{\text{w}} }}\left[ {f_{0} + f_{2} + f_{4} + 2(f_{3} + f_{6} + f_{7} )} \right],$$
(18)
$$f_{5} = f_{7} - \frac{1}{2}(f_{2} - f_{4} ) + \frac{1}{6}\rho_{\text{w}} u_{\text{w}} + \frac{1}{2}\rho_{\text{w}} v_{\text{w}} ,$$
(19)
$$f_{8} = f_{6} + \frac{1}{2}(f_{2} - f_{4} ) + \frac{1}{6}\rho_{\text{w}} u_{\text{w}} - \frac{1}{2}\rho_{\text{w}} v_{\text{w}} ,$$
(20)
$$f_{1} = f_{3} + \frac{2}{3}\rho_{\text{w}} u_{\text{w}} .$$
(21)

Also, to apply extrapolation boundary condition for the channel outlet:

$$f_{3,x = N} = 2f_{3,x = N - 1} - f_{3,x = N - 2} ,$$
(22)
$$f_{6,x = N} = 2f_{6,x = N - 1} - f_{6,x = N - 2} \text{,}$$
(23)
$$f_{7,x = N} = 2f_{7,x = N - 1} - f_{7,x = N - 2} .$$
(24)

Furthermore, the bounce-back boundary condition is used to specify the surface channel walls. For instance, bounce-back condition applied for the bottom wall is:

$$f_{2} = f_{4} ,\;f_{5} = f_{7} ,\;f_{6} = f_{8} .$$
(25)

Results and discussion

For this part, the computational results for an oblique mini-channel (Fig. 3) with hydrophilic surfaces are presented. The initial density is \(\rho = 150 + \Delta \rho\), where \(\Delta \rho\) is the random perturbation parameter from [0,1]. According to the grid independence study (Grid independency) section, the dimensions of the channel are \(N_{\text{x}} \times N_{\text{y}} = 301 \times 101\). The results are presented for \(\theta = 10\) to \(\theta = 90\) degrees. This inclination angle is chosen to cover a wide range of practical applications.

To investigate the details of dynamics of droplets during the condensation process, a hydrophilic mini-channel with \(\theta = 45^{ \circ }\) is chosen. The time progress of the phase transition process is illustrated in Fig. 4. This process begins with nucleation as shown by step a. Due to the hydrophilic characteristic of surfaces as well as the adhesive interaction between fluid particles and solid walls, a thin liquid film gradually appears on the surfaces. In addition, according to steps b and c, two different phenomena with the opposite effect can be observed. First, if the droplet diameter is less than the critical value, the droplet evaporates. Second, for droplets with diameter beyond the critical limit, the condensation dominates and droplet begins to grow. Furthermore, as time increases (steps d and e), the liquid on the solid surfaces becomes thicker as a result of the droplet coalescence through the liquid film.

Fig. 4
figure 4

Time evolution of condensation process for \(\theta = 45^{ \circ }\), a 50 ts, b 150 ts, c 250 ts, d 550 ts, e 800 ts, f 1250 ts, g 2000 ts, h 3500 ts, i 5000 ts, j 7500 ts

Full size image

In Fig. 5, the effect of channel angle \(\theta\) on the dynamic behavior of the condensed liquid at time t = 7000 ts is presented. Figure 5a shows the results for low channel angles \((\theta = 10^{ \circ } - 40^{ \circ } )\)(while part b presents the results for high angles \((\theta = 50^{ \circ } - 80^{ \circ } )\)). \(\theta\) plays a big part in the ultimate pattern of the liquid phase in the channel. However, as \(\theta\) increases (Fig. 5b), this effect becomes negligible.

Fig. 5
figure 5

Fluid behavior of the condensed liquid for various channel angles at time t = 7000 ts, a from left to right \(\theta = 10^{ \circ } ,20^{ \circ } ,30^{ \circ } ,40^{ \circ }\), respectively, b from left to right, \(\theta = 50^{ \circ } ,60^{ \circ } ,70^{ \circ } ,80^{ \circ }\), respectively

Full size image

Two key parameters associated with evacuation process after cooling in oblique mini-channels are (a) evacuation velocity and (b) evacuation time, which are investigated in this section. The velocity profiles at the outlet of the channel for various angles \((\theta )\) are shown in Fig. 6. For high channel angles \((\theta \ge 50^{ \circ } )\), there is a negligible difference between velocity profiles (maximum 11%), while for low angles \((\theta \le 40^{ \circ } )\) this difference becomes significant (maximum 100%). The logic of this difference can be attached to the fact that for low channel angles, the \(y\) component of the gravitational acceleration is higher than its \(x\) component. Thus, the discharge time of the liquid is the longer in this situation, and the gravitational force has longer time to influence the moving liquid film. Consequently, the top liquid film drops to the bottom surface of the channel. (This can be seen in Fig. 5a.) This liquid movement influences on the vapor velocity at the channel outlet. As a result, the vapor velocity dramatically increases for low angle such as \(\theta = 15^{ \circ }\), as shown in Fig. 6.

Fig. 6
figure 6

Outlet velocity profiles for different channel angles at time t = 7000 ts

Full size image

In this section, the liquid evacuation time is obtained as a function of channel angle \(\theta\). To this respect, the dimensionless time \(t^{ * }\) is defined as follows:

$$t^{ * } = \frac{{{\text{Evacuation}}\;{\text{time}}}}{{t_{\text{b}} }} ,$$
(27)

where \(t_{b}\) is the required time to discharge the liquid from the channel when \(\theta = 90^{ \circ }\). Accordingly, the variation of non-dimensional evacuation time is plotted against the channel angle in Fig. 7.

Fig. 7
figure 7

Variation of non-dimensional discharge time against channel angle

Full size image

It is found that the discrete data in Fig. 7 can be represented by a power law function as follows:

$$t^{ * } = 1.154\theta^{ - 0.6} ,$$
(28)

where \(\theta\) is in radian. In other words, this relation represents the evacuation time based on the \(\theta\). According to Fig. 7, as \(\theta\) increases, the required evacuation time decreases. In other words, as θ increases, the gravitational force increases. This leads to the higher mass flow rate at the channel outlet. It is also evident that for high values of \(\theta\), the effect of channel angle on the evacuation time becomes negligible.

Conclusions

In the current research, the simulation of the drop condensation process in an oblique mini-channel with different angles is investigated by means of LBM. The important detections can be reported as follows:

  • The channel angle plays an important role in the rate of droplet nucleation and evacuation time.

  • The coalescence of droplets and formation of liquid film on the channel walls are investigated during the phase change process. The variation of liquid profile at the channel outlet is negligible at angles higher than 45°.

  • A new expression is introduced to predict the required evacuation time for channel angles of \(\theta = 0 - 90\) degrees.

  • This study reveals that the required time for droplets coalescence and discharging liquid from the mini-channel can be controlled by optimizing the channel angle.

  • In summary, LBM can be considered as an effective tool in order to predict the condensation process and liquid behavior in oblique micro-/mini-channels.