Introduction

Fin is a great engineering component for managing heat transmission over or through a surface, and as such, it is widely used in a variety of sectors. With flexibility in the context of mass, size, and shape fin has gained employment in numerous areas like cooling of a reactor core, electronics, solar collectors, etc. As fin is widely used in industry, researchers are continuously looking for novel ways to improve its performance and forecast its mechanical reaction to expected and unexpected changes in operating circumstances or settings.

The replacement of solid fin structures with porous ones was a milestone in the development of technology using extended surfaces. Kiwan and Al-Nimr [1] were the foremost to develop the porous fin model and they utilized Darcy’s law to study the interaction between solid and fluid particles. It has been inferred that an optimum limit is attained by the thermal conductivity ratio beyond which there is no alteration in the heat transfer rate. Kiwan [2] further studied the convective porous fin by considering structures of different lengths. Gorla and Bakier [3] modelled the energy equation for a convective porous fin exposed to the radiative environment. The affirmative response of radiative heat loss on base heat transfer rate has been conferred in the study. Das and Ooi [4] developed an algorithm by employing inverse analysis technique to predict the range of parameters to achieve a given temperature requirement. The heat transfer rate and efficiency of moving and stationary fin structures have been comparatively analysed by Bhanja et al. [5]. While analytically investigating the optimum fin dimensions it has been concluded that the heat transfer rate elevates with fin volume.

A semi-spherical fin structure was considered by Atouei et al. [6] to analytically compute the spatial distribution of temperature. They have employed the technique of least squares and collocation to analyse the impact of the thermally reliant physical attributes on the heat energy transmission within the fin. The nonlinear porous fin problem was concentrated by Turkyilmazoglu [7] and Das and Kundu [8]. The technique of differential transformation was adopted by Pasha et al. [9] to examine distinct fin structures under unsteady conditions. For the investigation, the convex, triangular, concave, and rectangular profiles of straight fin geometry were considered. The method of solution to analyse the temperature distribution in the different fin structures has attracted the concentration of many researchers. In this regard, the technique of approximating the radial basis function was implemented by Fallah et al. [10] to decipher the moving fin problem. Using this semi-analytical method, the influence of thermal conductivity parameter, radiative and convective parameters and Peclet number on the spatial distribution of fin temperature has been examined. A different approach to mounting the fin structure with a stretching/shrinking mechanism was considered by Gireesha et al. [11], and the numerical analysis was performed by employing the 4–5th ordered Runge Kutta Fehlberg technique. Considering the different thermal attributes to be spatially dependent Turkyilmazoglu [12] recently scrutinized a fin problem and obtained the exact solutions.

Recently, fully wet technology is gaining popularity among researchers in the study of extended surfaces. Hatami and Ganji [13] considered a radial fin under fully wet conditions and employed the techniques of least squares to decipher the solution. They inferred that the presence of humidity enhances the temperature distribution along the fin length. The technique of differential transformation was employed by Kundu et al. [14] in the analysis of exponential wet fin structures. Further, a fully wet porous fin was examined by Darvishi et al. [15] by employing the spectral collocation approach, and it has been concluded that moisture content aids heat dissipation via convection. Furthermore, the works by Wankhade et al. [16] and Das and Kundu [17, 18] are prominent in the field of fully wet extended surfaces. Pirompugd and Wongwises [19] analytically and comparatively examined the hyperbolic circular fin with the rectangular one under partially wet conditions. They have analysed the thermal field and efficiency of both the profiles and found that fin efficiency under partially wet conditions is between that of fully wet and dry ones.

Owing to the application of fin structures, it is necessary to consider the effect of motion on the distribution of temperature within the fin. In this regard, Singla and Das [20] employed the Adomian decomposition approach together with a genetic algorithm for the inverse analysis of a moving fin. It has been concluded that the speed of fin movement has a very strong impact on the fin’s thermal profile than the thermo-physical attributes of the fin. A modified decomposition approach was employed by Roy et al. [21] to investigate a moving triangular fin, and it was deciphered that the Peclet number enhances the local fin temperature. The finite element approach was implemented by Gireesha et al. [22] to scrutinize a moving porous fin of radial outline. One of the major outcomes of the study was that the Peclet number had a negative impact on the base heat transmission rate of the fin. A moving pin fin of parabolic profile was analytically examined by Turkyilmazoglu [23]. The technique of differential transforms embedded with Pade approximant was utilized by Jayaprakash et al. [24] to illustrate the impact of Peclet number and heat absorption on the spatial distribution of temperature along a trapezoidal profiled straight fin structure.

Functionally graded materials (FGMs) are considered to be alternatives to composite materials with their excellent mechanical and thermal characteristics. Aziz et al. [25] have examined the thermal characteristics of FGM fin as compared to homogeneous ones by employing the technique of differential transformation. They have also studied the impact of relevant parameters on the efficiency of the FGM fin structure. FGM fin structures with linear and power law dependent temperature characteristics were investigated by Oguntala et al. [26] by implementing the spectral collocation approach named after Chebyshev. Sowmya et al. [27] illustrated the spatial distribution of temperature in FGM fin structures exposed to fully wet conditions and they further extended the above study by including exponential FGM fin. Analysis of thermal stress on radial fin composed of FGM was undertaken by Yildirim et al. [28] under unsteady conditions and they found that radial fin stress can be minimized with the replacement of homogeneous material with FGM.

Entropy generation denotes the energy degradation during a process and helps estimate the wasted energy. With this, fin optimization has been driven towards a new direction with the assessment of entropy generation in distinct fin structures. Poulikakos and Bejan [29] employed the 1st and 2nd laws of thermodynamics to model the entropy generation in a fin structure. They have analysed the generation of entropy in a pin fin and three distinct fin profiles of longitudinal geometry. An orthotropic pin fin was considered by Aziz and Makinde [30] to investigate entropy generation in it. Further, the effects of radial Biot number, fin aspect ratio, etc. on entropy generation were studied by developing a two-dimensional model. Khatami et al. [31] modelled the entropy generation and average entropy production in a porous longitudinal fin subject to convective heat loss. They have found that the entropy generated is maximum at the base of the fin and minimum at the fin tip. Recently Din et al. [32] investigated the entropy generation in a porous exponential fin exposed to convective-radiative heat dissipation along with thermally reliant heat absorption. Din et al. [33] further extended the study by including the effect of thermal conductivity on the entropy generation and it has been concluded that compared to exponential fin profiles the rectangular one resulted in generating lesser entropy.

The growing realization of the limited supply of energy resources has piqued the scientific community's interest in taking a deeper look at energy conversion devices and developing new strategies to better use the present restricted resources. In the above literature there are numerous studies on fin structures composed of functionally graded materials but entropy generation in an FGM fin has not been considered yet. Also, the comparative study of type I (higher thermal grading towards the fin base) and type II (higher thermal grading towards the fin tip) FGM fin structures with the homogeneous one is novel. For the analysis a porous longitudinal fin with constant thickness exposed to motion and convective-radiative heat exchange has been considered. The derived differential equation has been numerically resolved through the Runge–Kutta Fehlberg 4–5th ordered method. The derived solutions are graphically analysed and discussed.

Modelling of the physical problem

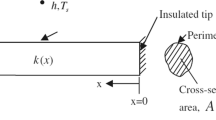
A rectangular profiled longitudinal fin structure with dimensions as depicted in Fig. 1 has been considered for the current study. The fin is composed of functionally graded porous material and is exposed to fully wet conditions. Thus, the fluid is allowed to penetrate through the porous fin matrix and its interaction with the solid surface is modelled by employing the Darcy’s law. Further, the fin is in contact with and receives heat from a prime surface with temperature \({T}_\text{b}\) and undergoes convective-radiative heat transmission with the ambient fluid at temperature \({T}_\text{a}\). The solid fin medium and the surrounding fluid are in local thermodynamic equilibrium and further the surface radiant exchange is neglected. The tip of the fin is assumed adiabatic as there is negligible heat exchange through it when compared to the fin’s lateral surfaces. Further, the temperature is assumed to vary only along the \(x-\) direction as pictured in Fig. 1 and hence the study is one-dimensional.

Fig. 1
figure 1

Pictorial representation of a longitudinal FGM fin

Full size image

Considering a small element \(dx\) in the fin the energy equation of the fin under steady conditions can be modelled as [3, 8, 27],

$$\begin{gathered} q_{{\text{x}}} - q_{{{\text{x}} + {\text{dx}}}} - \rho v_{{\text{w}}} \left( x \right){\text{WC}}_{{\text{p}}} {\text{d}}x\left( {T - T_{{\text{a}}} } \right) - \varepsilon \sigma W{\text{d}}x\left( {T^{4} - T_{{\text{a}}}^{4} } \right) - \rho_{{\text{f}}} C_{{\text{p}}} {\text{UWt}}\frac{{{\text{d}}T}}{{{\text{d}}x}} \hfill \\ - h\left( T \right)W{\text{d}}x\left( {1 - \phi } \right)\left( {T - T_{{\text{a}}} } \right) - h_{{\text{D}}} Wdxi_{{{\text{fg}}}} \left( {1 - \phi } \right)\left( {\omega - \omega_{{\text{a}}} } \right) = 0. \hfill \\ \end{gathered}$$
(1)

According to Fourier’s conduction law, the transfer of heat at distance \(x\) from the base is given by,

$$q = - k\left( x \right)Wt\frac{{{\text{d}}T}}{{{\text{d}}x}},$$
(2)

From Darcy’s law, the fluid flow velocity inside the porous medium can be determined by [2],

$$v_{{\text{w}}} \left( x \right) = \frac{{gK\beta_{{\text{f}}} \left( {T - T_{{\text{a}}} } \right)}}{{\nu_{{\text{f}}} }},$$
(3)

The relation between temperature sensitive convective heat transfer coefficient \(h(T)\) and uniform mass transfer coefficient \({h}_{D}\) is given by [13],

$$h\left(T\right)={h}_{\mathrm{a}}{\left(\frac{T-{T}_{\mathrm{a}}}{{T}_{\mathrm{b}}-{T}_{\mathrm{a}}}\right)}^\text{p}={h}_{\mathrm{D}}{C}_{\mathrm{p}}{\mathrm{Le}}^\frac{2}{3}.$$
(4)

Utilizing Eqs. (2) to (4), Eq. (1) resolves into,

$$\begin{gathered} \hfill t\frac{{\text{d}}}{{{\text{d}}x}}\left[ {k\left( x \right)\frac{{{\text{d}}T}}{{{\text{d}}x}}} \right] - \frac{{\rho_{{\text{f}}} gK\beta_{{\text{f}}} C_{{\text{p}}} }}{{\nu_{{\text{f}}} }}\left( {T - T_{{\text{a}}} } \right)^{2} - \sigma \varepsilon \left( {T^{4} - T_{{\text{a}}}^{4} } \right) - \frac{{\left( {1 - \phi } \right)h_{{\text{a}}} \left( {T - T_{{\text{a}}} } \right)^{\text{p} + 1} }}{{\left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^{\text{p}} }} \\ \hfill - \frac{{h_{{\text{a}}} i_{{{\text{fg}}}} \left( {1 - \phi } \right)\left( {\omega - \omega_{{\text{a}}} } \right)\left( {T - T_{{\text{a}}} } \right)^{\text{p}} }}{{C_{{\text{p}}} {\text{Le}}^{\frac{2}{3}} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} - \rho_{{\text{f}}} C_{{\text{p}}} {\text{Ut}}\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0. \\ \end{gathered}$$
(5)

In Eq. (5), \(k(x)\) is the thermal conductivity of the material dependent on the axial coordinate \(x\). With \({k}_{0}\) being the thermal conductivity of the homogeneous material, three different variations of \(k\) with \(x\) are considered namely:

Case 1 Homogeneous with \(k\left(x\right)={k}_{0}.\)

In this case, the fin material is homogeneous and the substitution of the above condition in Eq. (5) results into,

$$\begin{aligned} & \frac{{{\text{d}}^{2} T}}{{{\text{d}}x^{2} }} - \frac{{\rho_{{\text{f}}} gK\beta_{{\text{f}}} C_{{\text{p}}} }}{{k_{0} t\nu_{{\text{f}}} }}\left( {T - T_{{\text{a}}} } \right)^{2} \\ & \quad - \frac{{\left( {1 - \phi } \right)h_{{\text{a}}} \left( {T - T_{{\text{a}}} } \right)^\text{p + 1} }}{{k_{0} t\left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} - \frac{{h_{{\text{a}}} i_{{{\text{fg}}}} \left( {1 - \phi } \right)\left( {\omega - \omega_{{\text{a}}} } \right)\left( {T - T_{{\text{a}}} } \right)^\text{p} }}{{k_{0} tC_{{\text{p}}} {\text{Le}}^{\frac{2}{3}} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} \\ & \quad - \frac{\sigma \varepsilon }{{k_{0} t}}\left( {T^{4} - T_{{\text{a}}}^{4} } \right) - \frac{{\rho_{{\text{f}}} C_{{\text{p}}} U}}{{k_{0} }}\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0. \\ \end{aligned}$$
(6a)

Case 2 Type I FGM with \(k\left(x\right)={k}_{0}(1+ax)\)

In this case, the thermal conductivity is \({k}_{0}\) at the base of the fin structure and it increases towards the fin tip. The above condition resolves Eq. (5) into,

$$\begin{aligned} & \frac{{{\text{d}}^{2} T}}{{{\text{d}}x^{2} }} + ax\frac{{{\text{d}}^{2} T}}{{{\text{d}}x^{2} }} + a\frac{{{\text{d}}T}}{{{\text{d}}x}} - \frac{{\rho_{{\text{f}}} gK\beta_{{\text{f}}} C_{{\text{p}}} }}{{k_{0} t\nu_{{\text{f}}} }}\left( {T - T_{{\text{a}}} } \right)^{2} - \frac{{\left( {1 - \phi } \right)h_{{\text{a}}} \left( {T - T_{{\text{a}}} } \right)^\text{p + 1} }}{{k_{0} t\left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} \\ & \quad - \frac{{h_{{\text{a}}} i_{{{\text{fg}}}} \left( {1 - \phi } \right)\left( {\omega - \omega_{{\text{a}}} } \right)\left( {T - T_{{\text{a}}} } \right)^\text{p} }}{{k_{0} tC_{{\text{p}}} {\text{Le}}^{\frac{2}{3}} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} - \frac{\sigma \varepsilon }{{k_{0} t}}\left( {T^{4} - T_{{\text{a}}}^{4} } \right) - \frac{{\rho_{{\text{f}}} C_{{\text{p}}} U}}{{k_{0} }}\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0. \\ \end{aligned}$$
(6b)

Case 3 Type II FGM with \(k\left(x\right)={k}_{0}\left(1+a\left(L-x\right)\right)\)

In this case, the thermal conductivity is \({k}_{0}\) at the fin tip and it increases towards the base of the fin. The above condition resolves Eq. (5) into,

$$\begin{aligned} & \frac{{{\text{d}}^{2} T}}{{{\text{d}}x^{2} }} + a\left( {L - x} \right)\frac{{ {\text{d}}^{2} T}}{{{\text{d}}x^{2} }} - a\frac{{{\text{d}}T}}{{{\text{d}}x}} - \frac{{\rho_{{\text{f}}} gK\beta_{{\text{f}}} C_{{\text{p}}} }}{{k_{0} t\nu_{{\text{f}}} }}\left( {T - T_{{\text{a}}} } \right)^{2} - \frac{{\left( {1 - \phi } \right)h_{{\text{a}}} \left( {T - T_{{\text{a}}} } \right)^\text{p + 1} }}{{k_{0} t\left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} \\ & \quad - \frac{{h_{{\text{a}}} i_{{{\text{fg}}}} \left( {1 - \phi } \right)\left( {\omega - \omega_{{\text{a}}} } \right)\left( {T - T_{{\text{a}}} } \right)^\text{p} }}{{k_{0} tC_{{\text{p}}} {\text{Le}}^{\frac{2}{3}} \left( {T_{{\text{b}}} - T_{{\text{a}}} } \right)^\text{p} }} - \frac{\sigma \varepsilon }{{k_{0} t}}\left( {T^{4} - T_{{\text{a}}}^{4} } \right) - \frac{{\rho_{{\text{f}}} C_{{\text{p}}} U}}{{k_{0} }}\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0. \\ \end{aligned}$$
(6c)

The respective boundary conditions are given as follows:

$$T= T_{{\text{b}}} \,{\text{at}}\,x = 0,\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0\,{\text{at}}\,x = L$$
(7)

The following are the dimensionless parameters,

$$\begin{aligned} & \theta = \frac{T}{{T_{{\text{b}}} }}, \theta_{{\text{a}}} = \frac{{T_{{\text{a}}} }}{{T_{{\text{b}}} }}, X = \frac{x}{L}, \alpha = aL, {\text{Nc}} = \frac{{\rho_{{\text{f}}} g\beta_{{\text{f}}} {\text{KC}}_{{\text{p}}} T_{{\text{b}}} L^{2} }}{{\nu_{{\text{f}}} k_{0} t}},{\text{Nr}} = \frac{{\varepsilon \sigma L^{2} T_{{\text{b}}}^{3} }}{{k_{0} t}}, m_{{\text{o}}} = \frac{{h_{{\text{a}}} L^{2} \left( {1 - \phi } \right)}}{{k_{0} t}}, \\ & \quad m_{1} = \frac{{h_{{\text{a}}} i_{{{\text{fg}}}} \left( {1 - \phi } \right)b_{2} L^{2} }}{{k_{0} tC_{{\text{p}}} {\text{Le}}^{\frac{2}{3}} }},m_{2} = m_{0} + m_{1} , \left( {\omega - \omega_{{\text{a}}} } \right) = b_{2} \left( {T - T_{{\text{a}}} } \right),{\text{Pe}} = \frac{{\rho_{{\text{f}}} C_{{\text{p}}} {\text{UL}}}}{{k_{0} }}. \\ \end{aligned}$$
(8)

Equations 6(a)–(c) upon non-dimensionalizing resolve into the following nonlinear ordinary differential equations,

Case 1 Homogeneous\(\frac{{\mathrm{d}}^{2}\theta }{\mathrm{d}{X}^{2}}-\mathrm{Nc}{\left(\theta -{\theta }_{\mathrm{a}}\right)}^{2}-\mathrm{Nr}\left({\theta }^{4}-{\theta }_{\mathrm{a}}^{4}\right)-\frac{{m}_{2}{\left(\theta -{\theta }_{\mathrm{a}}\right)}^{\text p+1}}{{\left(1-{\theta }_{\mathrm{a}}\right)}^{\text p}}-\mathrm{Pe}\frac{\mathrm{d}\theta }{\mathrm{d}X}=0\). (9a)

Case 2 Type I FGM

$$\begin{aligned} & \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}X^{2} }} + \alpha X\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}X^{2} }} + \alpha \frac{{{\text{d}}\theta }}{{{\text{d}}X}} - {\text{Nc}}\left( {\theta - \theta_{{\text{a}}} } \right)^{2} - {\text{Nr}}\left( {\theta^{4} - \theta_{{\text{a}}}^{4} } \right) \\ & \quad - \frac{{m_{2} \left( {\theta - \theta_{{\text{a}}} } \right)^\text{p + 1} }}{{\left( {1 - \theta_{{\text{a}}} } \right)^\text{p} }} - {\text{Pe}}\frac{{{\text{d}}\theta }}{{{\text{d}}X}} = 0. \\ \end{aligned}$$
(9b)

Case 3 Type II FGM

$$\begin{aligned} & \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}X^{2} }} + \alpha \left( {1 - X} \right)\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}X^{2} }} - \alpha \frac{{{\text{d}}\theta }}{{{\text{d}}X}} - {\text{Nc}}\left( {\theta - \theta_{{\text{a}}} } \right)^{2} \\ & \quad - {\text{Nr}}\left( {\theta^{4} - \theta_{{\text{a}}}^{4} } \right) - \frac{{m_{2} \left( {\theta - \theta_{{\text{a}}} } \right)^\text{p + 1} }}{{\left( {1 - \theta_{{\text{a}}} } \right)^\text{p} }} - {\text{Pe}}\frac{{{\text{d}}\theta }}{{{\text{d}}X}} = 0 \\ \end{aligned}$$
(9c)

The respective dimensionless boundary conditions are,

$$\theta \left( 0 \right) = 1,\frac{{{\text{d}}\theta \left( 1 \right)}}{{{\text{d}}X}} = 0.$$
(10)

Entropy generation

Estimating the entropy generation in different fin structures exposed to various circumstances is one of the methods of assessing a fin’s performance. The entropy generation equilibrium as per second law of thermodynamics can be written as [31,32,33],

$$\mathop \sum \limits_{{{\text{i}} = 1}}^{n} \frac{{\dot{Q}}}{T} + \mathop \sum \limits_{{{\text{i}} = 1}}^{n} \left( {\dot{m}_{{\text{i}}} S_{{\text{i}}} - \dot{m}_{0} S_{0} } \right) + \dot{S}_{{{\text{gen}}}} = \frac{{{\text{d}}S}}{{{\text{d}}t^{*} }}$$
(11)

Since the study is conducted under steady conditions, \(\frac{\mathrm{d}S}{\mathrm{d}{t}^{*}}=0\). The above equation can be further simplified by noting the input and output in control volume to get,

$${\dot{m}}_\text{i}\left({S}_\text{i}-{S}_{0}\right)+{\dot{S}}_{\mathrm{gen}}+\frac{{q}_{\mathrm{x}}}{{T}_\text{x}}-\frac{{q}_{\text{x}+\mathrm{d}{\text{x}}}}{{T}_{\mathrm{x}+\mathrm{d}{\text{x}}}}=0$$
(12)

Considering pressure to be constant both in and out of the porous medium and assuming air to be an ideal gas, the following expression can be extracted for \({S}_{\mathrm{i}}-{S}_{0}\) [31,32,33],

$${S}_{\mathrm{i}}-{S}_{0}=-{C}_{\mathrm{p}}\mathrm{ln}\frac{T(x)}{{T}_{\mathrm{a}}}$$

Further it is known that,

$${q}_{\mathrm{x}+\mathrm{dx}}={q}_{\mathrm{x}}-\frac{\partial {q}_{\mathrm{x}}}{\partial x}\mathrm{d}x$$

Assuming \(T\left(x+\mathrm{d}x\right)-T(x)\approx 0\) and substituting the above two equations in Eq. (12) it results in,

$$-\dot{m}{C}_{\mathrm{p}}\mathrm{ln}\frac{T\left(x\right)}{{T}_{\mathrm{a}}}+{\dot{S}}_{\mathrm{gen}}+\frac{{q}_{\mathrm{x}}}{{T}_{\mathrm{x}}}-\frac{{q}_{\mathrm{x}}-\frac{\partial {q}_{\mathrm{x}}}{\partial \mathrm{x}}\mathrm{d}x}{{T}_{\mathrm{x}+\mathrm{dx}}}=0$$

The above equation upon simplifying gives [31,32,33],

$${\dot{S}}_{\mathrm{gen}}=\dot{m}{C}_{\mathrm{p}}\mathrm{ln}\frac{T\left(x\right)}{{T}_{\mathrm{a}}}-\frac{1}{T(x)}\frac{\partial {q}_{\mathrm{x}}}{\partial \mathrm{x}}\mathrm{d}x$$
(13)

After substituting for \({q}_{x}\) and simplifying the above equation reduces to,

$$S_{{{\text{gen}}}}^{\prime \prime \prime } = \frac{{\dot{S}_{{{\text{gen}}}} }}{{Wt{\text{d}}x}} = \frac{{\rho_{{\text{f}}} g\beta_{{\text{f}}} {\text{KC}}_{{\text{p}}} \left( {T - T_{{\text{a}}} } \right)}}{{\nu_{{\text{f}}} t}}\ln \left( {\frac{T}{{T_{{\text{a}}} }}} \right) + \frac{1}{T\left( x \right)}\frac{{\text{d}}}{{{\text{d}}x}}\left( {k\left( x \right)\frac{{{\text{d}}T}}{{{\text{d}}x}}} \right)$$
(14)

Further,

$$\frac{{S_{{{\text{gen}}}}^{\prime \prime \prime } L^{2} }}{{k_{0} }} = \frac{{\rho_{{\text{f}}} g\beta_{{\text{f}}} {\text{KC}}_{{\text{p}}} \left( {T - T_{{\text{a}}} } \right)L^{2} }}{{\nu_{{\text{f}}} tk_{0} }}\ln \left( {\frac{T}{{T_{{\text{a}}} }}} \right) + \frac{{L^{2} }}{{T\left( x \right)k_{0} }}\frac{{\text{d}}}{{{\text{d}}x}}\left( {k\left( x \right)\frac{{{\text{d}}T}}{{{\text{d}}x}}} \right)$$
(15)

On substituting for \(k(x)\) and non-dimensionalizing we get,

Case 1 Homogeneous

$$\mathrm{Ns}=\mathrm{Nc}\left(\theta -{\theta }_{\mathrm{a}}\right)\mathrm{ln}\left(\frac{\theta }{{\theta }_{\mathrm{a}}}\right)+\frac{1}{\theta }\frac{{\mathrm{d}}^{2}\theta }{\mathrm{d}{X}^{2}}$$
(16a)

Case 2 Type I FGM

$$\mathrm{Ns}=\mathrm{Nc}\left(\theta -{\theta }_{\mathrm{a}}\right)\mathrm{ln}\left(\frac{\theta }{{\theta }_{\mathrm{a}}}\right)+\frac{1}{\theta }\left[\left(1+\alpha X\right)\frac{{\mathrm{d}}^{2}\theta }{\mathrm{d}{X}^{2}}+\alpha \frac{\mathrm{d}\theta }{\mathrm{d}X}\right]$$
(16b)

Case 3 Type II FGM

$$\mathrm{Ns}=\mathrm{Nc}\left(\theta -{\theta }_{\mathrm{a}}\right)\mathrm{ln}\left(\frac{\theta }{{\theta }_{\mathrm{a}}}\right)+\frac{1}{\theta }\left[\left(1+\alpha \left(1-X\right)\right)\frac{{\mathrm{d}}^{2}\theta }{\mathrm{d}{X}^{2}}-\alpha \frac{\mathrm{d}\theta }{\mathrm{d}X}\right]$$
(16c)

On substituting Eqs. 9(a)–(c), respectively, in Eqs. 16(a)–(c) all three equations get reduced to Eq. (17) given as follows:

$$\mathrm{Ns}=\mathrm{Nc}\left(\theta -{\theta }_{\mathrm{a}}\right)\left[\mathrm{ln}\left(\frac{\theta }{{\theta }_{\mathrm{a}}}\right)+1-\frac{{\theta }_{\mathrm{a}}}{\theta }\right]+\frac{\mathrm{Nr}}{\theta }\left({\theta }^{4}-{\theta }_{\mathrm{a}}^{4}\right)+\frac{{m}_{2}{\left(\theta -{\theta }_{\mathrm{a}}\right)}^\text{p+1}}{{\theta \left(1-{\theta }_{\mathrm{a}}\right)}^\text{p}}+\frac{\mathrm{Pe}}{\theta }\frac{\mathrm{d}\theta }{\mathrm{d}X}$$
(17)

Average entropy production in the whole fin can be estimated as,

$${\mathrm{Ns}}_{\mathrm{avg}}=\underset{0}{\overset{1}{\int }}\mathrm{Ns}(X)\mathrm{d}X$$
(18)

Numerical procedure

The governing ODEs in Eqs. 9(a)–(c) along with the boundary conditions in Eq. (10) are BVPs which upon conversion into IVPs are numerically evaluated by employing the Runge Kutta Fehlberg (RKF) 45th-order technique in Maple software. The RKF 45th ordered technique proceeds as follows:

\(\begin{gathered} j_{1} = {\text{hf}}\left( {w_{1} ,z_{1} } \right), \hfill \\ j_{2} = {\text{hf}}\left( {w_{1} + \frac{1}{4}h,z_{1} + \frac{1}{4}j_{1} } \right), \hfill \\ j_{3} = {\text{hf}}\left( {w_{1} + \frac{3}{8}h,z_{1} + \frac{3}{{32}}j_{1} + \frac{9}{{32}}j_{2} } \right), \hfill \\ j_{4} = {\text{hf}}\left( {w_{1} + \frac{{12}}{{13}}h,z_{1} + \frac{{1932}}{{2197}}j_{1} - \frac{{7200}}{{2197}}j_{2} + \frac{{7296}}{{2197}}j_{3} } \right), \hfill \\ j_{5} = {\text{hf}}\left( {w_{1} + h,z_{1} + \frac{{439}}{{216}}j_{1} - 8j_{2} + \frac{{3680}}{{513}}j_{3} - \frac{{845}}{{4104}}j_{4} } \right), \hfill \\ j_{6} = {\text{hf}}\left( {w_{1} + \frac{1}{2}h,z_{1} - \frac{8}{{27}}j_{1} + 2j_{2} - \frac{{3544}}{{2565}}j_{3} + \frac{{1859}}{{4104}}j_{4} - \frac{{11}}{{40}}j_{5} } \right). \hfill \\ \end{gathered}\)

The Runge Kutta 4th-order approach is used to get a preliminary solution to the resolved IVP.

$$z_{{{\text{j}} + 1}} = z_\text{j} + \frac{25}{{216}}j_{1} + \frac{1408}{{2565}}j_{3} + \frac{2197}{{4101}}j_{4} - \frac{1}{5}j_{5} .$$

Additionally, the Runge Kutta 5th-order approach is used to enhance the solution's approximated value.

$$y_{{{\text{j}} + 1}} = z_\text{j} + \frac{16}{{135}}j_{1} + \frac{6656}{{12825}}j_{3} + \frac{28561}{{56430}}j_{4} - \frac{9}{50}j_{5} + \frac{2}{55}j_{6} .$$

Here, the error is the difference between the above two terms. If the error term is bigger, we repeat the procedure by reducing the step size. In the current work, a maximum step size of 0.001 is considered and the solutions are derived with a convergence criterion of \({10}^{-6}\). Table 1 records the validation of the results from RKF 45th-order method with those from differential transformation method available in the published literature.

Table 1 \(\theta (X)\) values when all the other parameters are zero except the ones mentioned in the table
Full size table

Results and discussion

The numerical solutions for the ODEs in Eqs. 9(a--c) were derived by utilizing the RKF 45th-order technique. Further these solutions were employed to estimate the entropy generation in a fin given by Eqs. 16(a--c) and average entropy generation in a fin given by Eq. 18. This section has been embedded with the suitable discussions for the results derived by the graphical analysis of the obtained solutions. The values have been extracted by varying relevant parameters and the following are the constant values considered unless mentioned elsewhere: \(\mathrm{Nc}=10,\mathrm{Nr}=5,{\theta }_{\mathrm{a}}=0.2,{m}_{2}=1, m=2,\mathrm{ Pe}=1, a=0.4\).

Figure 2 comparatively depicts the thermal conductivity variation in the fin material composed of different types of FGMs for distinct values of grading parameter \(\alpha\). It can be observed that there is no variation in thermal conductivity for homogeneous material, the thermal conductivity increases with grading towards fin base for type I FGM and the thermal conductivity increases with grading towards fin tip for type II FGM. But the average thermal conductivity for both types of FGMs is found to be equal except that the increase in thermal conductivity with grading differs by direction.

Fig. 2
figure 2

Variation in thermal conductivity ratio for distinct values of grading parameter \(\alpha\) in different fin structures

Full size image

Figures 3 and 4 are of significance as they, respectively, picturize the comparison of the thermal distribution and entropy generation in a fin composed of homogeneous material against those made from type I and type II FGMs. It can be derived that both temperature distribution and entropy generation along the fin length are highest in the case of type II FGM fin and lowest in the case of homogeneous fin, with type I FGM fin assuming a middle place. Even though the average thermal conductivity is same in both the cases of FGMs, the increased thermal conductivity towards the fin tip encourages better distribution of temperature towards the tip of the fin. Further the higher production of entropy in type II FGM can be justified by the increased heat transmission within the fin. On the other hand, entropy production rises with a rise in the thermal gradient of the fin structure and hence justifies the increased entropy towards the fin base.

Fig. 3
figure 3

Thermal profiles of type I FGM, type II FGM and homogeneous material fin structures

Full size image
Fig. 4
figure 4

Entropy generation in type I FGM, type II FGM and homogeneous material fin structures

Full size image

The impact of convective parameter \(\mathrm{Nc}\) on the thermal profile and entropy generation profile of fin structure made up of type I and type II FGMs has been comparatively represented in Figs. 5 and 6, respectively. It can be noted that the fin temperature decreases, and entropy generation increases with an increase in the parameter \(\mathrm{Nc}\). This is because, the parameter \(\mathrm{Nc}\) accounts for convective heat transfer due to buoyancy effect. Thus, as permeability of the fin structure increases, the penetrability of the ambient fluid through the fin pores increases leading to increased convective heat transmission. Further, the increased movement of heat and an increase in the temperature gradient towards the fin base is the reason for higher entropy production towards the base of the fin structure with the values of parameter \(\mathrm{Nc}\).

Fig. 5
figure 5

Thermal profiles of type I and type II FGM fin structures for distinct values of convective parameter \(\mathrm{Nc}\)

Full size image
Fig. 6
figure 6

Entropy generation in type I and type II FGM fin structures for distinct values of convective parameter \(\mathrm{Nc}\)

Full size image

Figures 7 and 8, respectively, illustrate the importance of radiative parameter \(\mathrm{Nr}\) in the thermal and entropy generation analysis of two distinct FGM fin structures. It can be interpreted that fin temperature steeps down towards the fin tip and entropy production elevates towards the fin base with an increase in the parameter \(\mathrm{Nr}\). Here, the parameter \(\mathrm{Nr}\) corresponds to ratio of radiative to conductive heat transfer. Thus, enhancing values of \(\mathrm{Nr}\) result in increased heat transmission via radiative heat transfer as compared to conductive heat transfer. Thus, it results in lower thermal profiles of fin structures. Further, the hike in the temperature difference towards the fin base with escalating values of \(\mathrm{Nr}\) result in increased entropy production at that area.

Fig. 7
figure 7

Thermal profiles of type I and type II FGM fin structures for distinct values of radiative parameter \(\mathrm{Nr}\)

Full size image
Fig. 8
figure 8

Entropy generation in type I and type II FGM fin structures for distinct values of radiative parameter \(\mathrm{Nr}\)

Full size image

The prominence of wet porous parameter \({m}_{2}\) in the variation of thermal field and entropy production of two distinct types of FGM fin structures has been correspondingly represented in Figs. 9 and 10. It can be deciphered that the parameter \({m}_{2}\) has a negative influence on temperature distribution towards the fin tip and positive influence on generation of entropy. This can be interpreted as follows. The parameter \({m}_{2}\) accounts for the porosity and wet nature around the fin structure and hence as it elevates there is increase in the convective heat transmission process resulting in decrease in local fin temperature. Further, this also causes elevation in the temperature gradient towards fin base leading to increased production of entropy.

Fig. 9
figure 9

Thermal profiles of type I and type II FGM fin structures for distinct values of wet porous parameter \({m}_{2}\)

Full size image
Fig. 10
figure 10

Entropy generation in type I and type II FGM fin structures for distinct values of wet porous parameter \({m}_{2}\)

Full size image

Figures 11 and 12 correspondingly capture the effect of Peclet number \(\mathrm{Pe}\) on the thermal and entropy fields of type I and type II FGM fin structures. The figures depict the increase in local fin temperature and decrease in generation of entropy for both kinds of fin structures. Here, Peclet number relates to fin movement and elevation in its values result in faster movement of fin resulting in decrease in time for interaction between ambient fluid and solid fin surface for the process of convective heat transmission. Thus, it results in decreased heat transmission via convection leading to increased local fin temperature. Further, as rise in Peclet number \(Pe\) decreases the thermal gradient values, there is a decrease in the production of entropy.

Fig. 11
figure 11

Thermal profiles of type I and type II FGM fin structures for distinct values of Peclet number \(\mathrm{Pe}\)

Full size image
Fig. 12
figure 12

Entropy generation in type I and type II FGM fin structures for distinct values of Peclet number \(\mathrm{Pe}\)

Full size image

Figures 13 and 14, respectively, picturize the variations in the thermal and entropy generation profiles of distinct FGM longitudinal fin structures for different values of the thermal conductivity grading parameter \(\alpha\). In general, as \(\alpha\) values increase, there is elevation in the local temperature and entropy production in both type I and type II FGM fin structures. This is because the accelerating \(\alpha\) values enhance the fin materials’ average thermal conductivity resulting in better temperature distribution towards the tip of the fin and lead to enhanced values of temperature. Further, the increase in \(\alpha\) values enhances the movement of heat throughout the fin structure leading to increased entropy production.

Fig. 13
figure 13

Thermal profiles of type I and type II FGM fin structures for distinct values of thermal conductivity grading parameter \(\alpha\)

Full size image
Fig. 14
figure 14

Entropy generation in type I and type II FGM fin structures for distinct values of thermal conductivity grading parameter \(\alpha\)

Full size image

The energy field and entropy generation profile of type I and type II FGM fin structures for distinct values of ambient temperature \({\theta }_{\mathrm{a}}\) have been illustrated in Fig. 15 and Fig. 16, respectively. Here, it can be noted that accelerating values of \({\theta }_{\mathrm{a}}\) increase the fin temperature throughout its length and also decrease the production of entropy. This can be explained as follows. The dimensionless ambient temperature \({\theta }_{\mathrm{a}}\) has a significant impact on the convective and radiative heat transmissions as their governing laws depend majorly on the difference in the temperature between the two considered bodies. Thus as \({\theta }_{\mathrm{a}}\) values rise, the temperature difference between the fin structure and the ambient fluid decreases resulting in lesser heat transmission and leads to higher fin temperature. The higher \({\theta }_{\mathrm{a}}\) values also decrease the local thermal gradient resulting in lesser production of entropy.

Fig. 15
figure 15

Thermal profiles of type I and type II FGM fin structures for distinct values of ambient temperature \({\theta }_{\mathrm{a}}\)

Full size image
Fig. 16
figure 16

Entropy generation in type I and type II FGM fin structures for distinct values of ambient temperature \({\theta }_{\mathrm{a}}\)

Full size image

The average entropy generation \({\mathrm{Ns}}_{\mathrm{avg}}\) in type I FGM, type II FGM and homogeneous material fin structures upon variation in radiative parameter \(Nr\) and convective parameter \(\mathrm{Nc}\) has been pictured in Fig. 17. It can be seen that \({\mathrm{Ns}}_{\mathrm{avg}}\) values increase with elevation in the values of \(\mathrm{Nc}\) and \(\mathrm{Nr}\). The observed behaviour is due to the same reasons as discussed before. The variation in \({\mathrm{Ns}}_{\mathrm{avg}}\) values for distinct values of ambient temperature \({\theta }_{\mathrm{a}}\) and wet porous parameter \({m}_{2}\) has been pictured in Fig. 18. There is an elevation in average entropy values with hike in parameter \({m}_{2}\) and there is a dip in average entropy values with rise in parameter \({\theta }_{\mathrm{a}}\). The observed behaviour is similar to the case of entropy production and hence can be explained as before. Additionally, the impact of thermal conductivity grading parameter \(\alpha\) and the Peclet number \(\mathrm{Pe}\) on the average entropy generation \({\mathrm{Ns}}_{\mathrm{avg}}\) in the distinct fin structures has been considered in Fig. 19. There is hike in the \({\mathrm{Ns}}_{\mathrm{avg}}\) values with parameter \(\alpha\) and a dip in \({\mathrm{Ns}}_{\mathrm{avg}}\) values with rise in parameter \(\mathrm{Pe}\). The behaviour is similar to that observed for the case of entropy generation and follows similar reasons as explained earlier.

Fig. 17
figure 17

Average entropy generation in type I and type II FGM fin structures for distinct values of convective parameter \(\mathrm{Nc}\) and radiative parameter \(Nr\)

Full size image
Fig. 18
figure 18

Average entropy generation in type I and type II FGM fin structures for distinct values of wet porous parameter \({m}_{2}\) and ambient temperature \({\theta }_{\mathrm{a}}\)

Full size image
Fig. 19
figure 19

Average entropy generation in type I and type II FGM fin structures for distinct values of Peclet number \(\mathrm{Pe}\) and grading parameter \(\alpha\)

Full size image

Conclusions

The thermal behaviour and entropy generation of a wet porous longitudinal fin made of linear functionally graded material (FGM) that is subject to convective-radiative heat transmission have been studied. When a fin is subject to continuous motion with constant velocity, three different cases of FGM—homogeneous, type I, and type II—have been comparatively explored. The numerically derived solutions are graphically analysed to derive the following key results.

  • Type I FGM fin structures result in lower fin temperatures as compared to type II ones. But fin temperature is lowest in the case of homogeneous ones.

  • The entropy generation along fin length as well as the average entropy generated in a fin are lowest in the case of homogeneous fin structures followed by type I and type II FGM fin structures.

  • The entropy generation towards fin base and the average entropy generation in a fin structure both rise with elevation in the convective, radiative and wet porous parameters.

  • The Peclet number and the ambient temperature result decrease in the entropy generation towards the fin base. Also, average entropy generation faces a dip with the acceleration in these parameters.

  • The fin temperature, entropy generation and average entropy generation all three are prominently affected by the grading parameter as they elevate with its rise.

  • The current work can be extended to distinct fin geometries made of a variety of materials. Also, exact solutions can be attempted for the current model.