1 Introduction

With the advances in material science, functionally graded materials (FGM) with specified continuous variation of properties can now be designed and manufactured for use in thermal components and systems. Such materials are finding increasing use in rocket heat shields, heat exchanger tubes, extended surfaces, thermoelectric generators, heat-engine components, plasma facings for fusion reactors, and electrically insulating metal/ceramic joints [1–3]. The traditional heat conduction theory, including extended surface heat transfer, which applies to conduction in homogeneous materials, must be modified to generate new solutions that are applicable to heat conduction in FGM. This paper embarks upon one such study. The continuous spatial variation of thermophysical properties, such as thermal conductivity, can offer advantages that are not available with the use of homogeneous materials. For example, a thin functionally graded thermal shield can sustain steep temperature gradients without excessive thermal stresses. Similar advantages can be realized with the functionally graded heat exchanger tubes and the heat engine components.

The analysis of heat transfer in a longitudinal fin made of a homogeneous material having a constant area and spatially uniform thermal conductivity is well documented in books [1, 2]. For a fin made of a FGM, the spatial dependence of thermal conductivity must be taken into account to accurately predict the thermal performance of the fin. Aziz and Rahman [3] investigated the steady-state thermal performance of a radial fin of uniform thickness made of a FGM. They considered variable thermal conductivity of the fin and obtained analytical solutions for the temperature distribution, heat transfer rate, fin efficiency, and fin effectiveness. They also presented and discussed numerical results illustrating the effect of the radial dependence of the thermal conductivity on the performance of the fin. Aziz [4] presented new analytical solutions for predicting the steady state performance of a longitudinal fin of uniform thickness with a coordinate dependent thermal conductivity. He assumed boundary conditions of constant base temperature and insulated tip. He considered three types of thermal conductivity variations and obtained analytical solutions for the temperature distribution in the fin, the fin heat transfer and fin efficiency. He also presented numerical results to illustrate the effect of variable thermal conductivity on the thermal performance of the fin.

Several other transient conduction studies in FGM without fins have also been reported. For example, Jin [5] employed a multi-layered material model and obtained a closed form solution for 1-D temperature distribution in a FGM strip having variable properties. He used Laplace transformation, an asymptotic analysis, and an integration technique to obtain interface temperatures for short times. Sladek et al. [6] proposed an advanced computational method for the transient heat conduction analysis of FGM. They used Laplace transform technique to solve the initial-boundary value problem and presented numerical results for a finite strip and a hollow cylinder with an exponential spatial variation of the material properties. Hosseini et al. [7] studied transient heat conduction in a cylindrical shell made of a FGM assuming the thermal properties to be power law functions of the radial coordinate. They obtained temperature distribution in the cylinder in terms of the Bessel functions and validated their results with the available numerical results in the literature. Chen and Tong [8] presented a sensitivity analysis for the steady-state and transient heat conduction in FGM.

Instead of the Fourier model, some studies of transient conduction in FGM have used a hyperbolic heat conduction model. Such a model is more appropriate if the transient process is extremely fast and the temperature profiles manifest wave characteristics such as in applications involving short-pulse laser heating where the transient response time is of the order of picoseconds. Babaei and Chen [9] used such a model to investigate transient heat transfer in a heterogeneous sphere. They allowed the material properties to vary in the radial direction according to a power law and solved the problem using the Laplace transform method. However, the vast majority of research studies such as those by Noda [10], Eslami et al. [11], and Hosseini et al. [7] used the Fourier model which is the approach used in the present work.

For a properly designed longitudinal fin, heat conduction must occur predominantly in the axial direction [12]. To account for the functional grading of the fin material, only the thermal conductivity of the fin is assumed to be a power law function of the axial coordinate. The density and specific heat of the material are assumed to be constant. The exponent in the power law is a measure of the distribution of the nonhomogeneity in the material. Such a power law type of spatial variation of the thermal conductivity was used by Sahin [13] in the study of optimal distribution of insulation on a flat surface and by Babaei and Chen [9] in analyzing 1-D, transient hyperbolic heat conduction in a functionally graded hollow sphere.

This paper models 1-D transient conduction in a longitudinal fin of uniform cross-sectional area A. The shape of the cross-section can be rectangular, circular, elliptical etc. The thermal conductivity of the fin is a prescribed function of the axial coordinate. Three cases of thermal conductivity variations are considered, namely, linear, quadratic, and exponential. For the linear and exponential cases, the steady state solutions are derived in terms of Bessel functions and for the quadratic case, the steady state solution appears in terms of Legendre functions.

2 Analysis

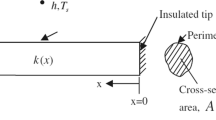
Consider a straight fin of constant cross-sectional area A, perimeter of the cross-section P, and length b as shown in Fig. 1. The thermal conductivity of the fin is a function of the axial coordinate x, but its specific heat and density are taken as constants. The fin has a thermal diffusivity \( \alpha \) based on the thermal conductivity value at x = 0. As indicated in Fig. 1, the axial coordinate x is measured from the tip of the fin. The fin loses heat by surface convection to a sink at temperature \( T_{s} \). The convection heat transfer coefficient h over the surface of the fin is assumed to be constant. The fin is initially in thermal equilibrium with the sink at temperature \( T_{s} \). At time \( t \ge 0 \), the base of the fin is subjected to a step increase in temperature from \( T_{s} \) to \( T_{b} \), while the tip remains adiabatic. The governing partial differential equation for the transient response of a convecting fin with a variable thermal conductivity can be written as

$$ \frac{\partial }{\partial x}\left[ {f(x)\frac{\partial T(x,t)}{\partial x}} \right] - \frac{hP}{{k_{0} A}}\left[ {T(x,t) - T_{s} } \right] = \frac{1}{\alpha }\frac{\partial T(x,t)}{\partial t} $$
(1)

subject to following initial and boundary conditions:

$$ \begin{aligned} T(x,0) & = T_{s} \\ T(b,t) & = T_{b} \\ \frac{\partial T}{\partial x}(0,t) & = 0 \\ \end{aligned} $$
(2a, b, c)
Fig. 1
figure 1

A functionally graded longitudinal fin of constant cross-sectional area

Full size image

with the use of the following dimensionless variables,

$$ \theta (X,\tau ) = \frac{{T - T_{s} }}{{T_{b} - T_{s} }},\,X = \frac{x}{b},\,\tau = \frac{\alpha t}{{b^{2} }},\quad N_{c} = \frac{{hPb^{2} }}{{k_{o} A}} $$
(3)

Equation (1) takes the following form

$$ \frac{\partial }{\partial X}\left[ {f(X)\frac{\partial \theta (X,\tau )}{\partial X}} \right] - N_{c} \theta (X,\tau ) = \frac{\partial \theta (X,\tau )}{\partial t} $$
(4)

The initial and boundary conditions in dimensionless form appear as follows.

$$ \theta (X,0) = 0,\quad \theta (1,\tau ) = 1,\quad \frac{\partial \theta }{\partial X}(0,\tau ) = 0 $$
(5a, b, c)

The following three different cases of variable thermal conductivity are considered in this study, namely

$$ k = k_{0} f(X) $$
(6)

where

$$ f(X) = 1 + aX,\,{\text{linear}} $$
(7)
$$ f(X) = 1 + aX^{2} ,\,{\text{quadratic}} $$
(8)
$$ f(X) = e^{aX} ,\,{\text{exponential}} $$
(9)

These forms of thermal conductivity variations have been used by Sahin [13] in deriving the optimal thickness distribution of a given amount of insulation made of a heterogeneous material. The objective of a nonuniform thickness of insulation was to minimize the heat loss from the surface. It was shown that the insulation with a nonuniform thickness was superior to the insulation with uniform thickness. However, this conclusion is of theoretical interest only because such a nonuniform deposition of insulation on a surface is difficult to achieve in practice, and also expensive. The extra expense may be justified if the energy savings due to reduced heat loss are substantial.

The instantaneous base heat flow is given by

$$ q_{b} = k_{0} f(X = 1)A\frac{\partial T}{\partial x}(b,t) $$
(10)

which may be expressed in dimensionless form as follows:

$$ Q_{b} = \frac{{q_{b} b}}{{k_{0} A(T_{b} - T_{s} )}} = f(X = 1)\frac{\partial \theta }{\partial X}(1,\tau ) $$
(11)

The instantaneous convective heat loss from the fin is given by

$$ q_{c} = P\int\limits_{0}^{b} {h\left( {T - T_{s} } \right){\text{d}}x} $$
(12)

or dimensionless form as

$$ Q_{c} = \frac{{q_{c} b}}{{k_{0} A(T_{b} - T_{s} )}} = N_{c} \int\limits_{0}^{1} {\theta {\text{d}}X} $$
(13)

The instantaneous rate of energy storage in the fin can be determined from the energy balance as follows

$$ q_{\text{stored}} = q_{b} - q_{c} $$
(14)

or in dimensionless form as

$$ Q_{\text{stored}} = Q_{b} - Q_{c} $$
(15)

The instantaneous fin efficiency may be defined as the instantaneous convective heat loss divided by the instantaneous convective heat loss if the entire fin was at the temperature of its base, i.e.

$$ \eta = \frac{{q_{c} }}{{hPb\left( {T_{b} - T_{s} } \right)}} $$
(16)

which may be expressed in terms of the dimensionless quantities as

$$ \eta = \frac{{Q_{c} }}{{N_{c} }}. $$
(17)

3 Transient response

Equation (4) with the initial and boundary conditions (5a, b, c) was solved numerically using the algorithm available in MAPLE 14 [15] for solving parabolic partial differential equations. The procedure can be implemented by calling the command pdsolve. This command with the numeric option specified delivers the numerical solution in the form of a module from which the numerical solution can be extracted in the form of numerical data or as a plot or as an animation. The solutions are generated by using the default method which uses a second order (in space and time) centered implicit finite difference scheme. The space and time steps were chosen as \( \Updelta X = \Updelta \tau = 0.001 \). The procedure also offers the choice of the number of points for plotting the data. Numerical experiments revealed that the use of 1,000 points was sufficient to generate smooth graphs. For each value of dimensionless time \( \tau \), the 1,000 point values of the dimensionless temperature \( \theta \) were used to obtain a least squares fit, fourth-order polynomial which was then used in Eq. (13) to compute the values of \( Q_{c} \). The accuracy of the numerical procedure used by MAPLE 14 and the least squares polynomial fit was tested against the exact analytical solutions developed by Donaldson and Shouman [14] for a constant thermal conductivity. The numerical results agreed with the analytical results [14] to four places of decimal and confirmed the accuracy of the numerical solutions generated by MAPLE 14 [15]. A second check was provided by comparing the numerical results for large times with the steady state solutions which are derived next.

4 Steady state analytical solutions

By ignoring the transient term in Eq. (4) and the initial condition, Eq. (5a, b, c), the steady state energy equation for the fin together with the boundary conditions may be written as

$$ \frac{\text{d}}{{{\text{d}}X}}\left[ {f(X)\frac{{{\text{d}}\theta (X)}}{{{\text{d}}X}}} \right] - N_{c} \theta (X) = 0 $$
(18)
$$ \frac{{{\text{d}}\theta (0)}}{{{\text{d}}X}} = 0,\quad \theta (1) = 1 $$
(19a, b)

The analytical solutions of Eqs. (18, 19a, b) were obtained by inputting these equations in Maple [15] and utilizing its ordinary differential equation solving command dsolve. For all three cases of thermal conductivity variation, namely linear, quadratic, and exponential, Maple delivered exact analytical solutions as shown next.

Linear case:

$$ f(X) = 1 + aX $$

The solution of Eqs. (18) and (19a, b) is found in terms of the Bessel functions and is given by

$$ \theta (X) = \frac{{J_{0} \left[ {g_{1} (X)} \right]Y_{1} (c_{1} ) - Y_{0} \left[ {g_{1} (X)} \right]J_{1} (c_{1} )}}{{J_{0} \left[ {g_{1} (0)} \right]Y_{1} (c_{1} ) - Y_{0} \left[ {g_{1} (0)} \right]J_{1} (c_{1} )}} $$
(20)

where J and Y are the Bessel functions of first and second kind, respectively, with subscripts denoting the order of the function. The function \( g_{1} (X) \) and the constant c 1 are given by

$$ g_{1} (X) = 2\sqrt { - N_{c} (1 + aX)/a^{2} } ,\quad c_{1} = 2{\text{csgn}}(1/a)\sqrt { - N_{c} } /a $$
(21a, b)

where csgn stands for the sign function.

Quadratic case:

$$ f(X) = 1 + aX^{2} $$

In this case, the solution of Eqs. (18) and (19a, b) is found in terms of the Legendre and gamma functions and may be written as

$$ \theta (X) = \frac{{\sqrt \pi Q_{n} (\sqrt { - a} X) - \Upgamma ( - n/2)\Upgamma (p/2)Q_{m} (0)P_{n} (\sqrt { - a} X)}}{{\sqrt \pi Q_{n} (\sqrt { - a} ) - \Upgamma ( - n/2)\Upgamma (p/2)Q_{m} (0)P_{n} (\sqrt { - a} )}} $$
(22)

where P and Q are the Legendre functions of the first and the second kind, respectively, and \( \Upgamma \) is the gamma function. The constants m, n and p are used as shorthand defined as

$$ m = \frac{{\sqrt {a + 4N_{c} } + \sqrt a }}{2\sqrt a },\quad n = \frac{{\sqrt {a + 4N_{c} } - \sqrt a }}{2\sqrt a },\quad p = \frac{{\sqrt {a + 4N_{c} } + 5\sqrt a }}{2\sqrt a }.$$
(23a, b, c)

Exponential case:

$$ f(X) = \exp (aX) $$

In this case, the solution of Eqs. (18) and (19a, b) is found in terms of the modified Bessel functions and may be written as

$$ \theta (X) = \frac{{g_{2} (X)\left\{ {K_{0} \left[ {g_{3} (0)} \right]I_{1} \left[ {g_{3} (X)} \right] + I_{0} \left[ {g_{3} (0)} \right]K_{1} \left[ {g_{3} (X)} \right]} \right\}}}{{K_{0} \left[ {g_{3} (0)} \right]I_{1} \left[ {g_{3} (1)} \right] + I_{0} \left[ {g_{3} (0)} \right]K_{1} \left[ {g_{3} (1)} \right]}} $$
(24)

where I and K are the modified Bessel functions of the first kind and second kind, respectively, and the functions \( g_{2} (X) \) and \( g_{3} (X) \) are defined as follows.

$$ g_{2} (X) = e^{ - a(X - 1)/2} ,\quad g_{3} (X) = 2\sqrt {N_{c} } e^{ - aX/2} /a $$
(25a, b)

The steady state provided by Eqs. (20), (22), and (24) were used to check the transient results for \( \tau = 5 \) (within 0.4 % of steady state) and a match to three places of decimal was verified for all the data generated as illustrated in Table 1 which shows the transient results for \( \tau \) = 2, 3, 4, and 5 along with the steady state analytical results. This exercise provided a second check on the accuracy of the numerical results as mentioned earlier.

Table 1 Comparison of transient results with analytical predictions for the three profiles when Nc = 1, a = 0.5
Full size table

5 Results and discussion

For a better understanding of the thermal conductivity grading parameter a, the effect of a on the dimensionless thermal conductivity for the three selected profiles is illustrated in Fig. 2. It is clear from Fig. 2 that the dimensionless thermal conductivity strong function of the thermal conductivity grading parameter. It decreases for negative values of a and increases for positive values of a, whereas it remains constant when a = 0. To facilitate the interpretation of results, it is convenient to calculate the spatially averaged thermal conductivities for the three variations of k considered. The integration of Eqs. (7), (8), and (9) from \( X = 0 \) to \( X = 1 \) gives the average thermal conductivity \( \bar{k} \) for the linear, quadratic, and exponential cases as \( \bar{k} = k_{0} F \) where

Fig. 2
figure 2

Effect of thermal conductivity grading parameter on dimensionless spatial thermal conductivity variation

Full size image

\( F = \left( {1 + \frac{a}{2}} \right),\,\left( {1 + \frac{a}{3}} \right),\,{\text{and}}\,\frac{1}{a}\left[ {\exp (a) - 1} \right], \) respectively. For a = 0.5, these values are 1.25, 1.17, and 1.30 \( k_{0} \) and for \( a = - 0.5 \), the values are 0.75, 0.83, and 0.79 \( k_{0} \) for the linear, quadratic, and exponential cases, respectively. If one defines the fin parameter \( \bar{N}_{c} \) based on \( \bar{k} \) as \( \bar{N}_{c} = hPb^{2} /\bar{k}A \), then higher values of \( \bar{k} \) give lower values of \( \bar{N}_{c} \) and vice versa.

Equations (4) and (6–9) show that the transient response of the fin depends on two parameters, the classical fin parameter N c and the thermal conductivity grading parameter ra. The effect of these two parameters on fin temperature, base heat flow, convective heat loss, heat stored in the fin and the efficiency will now be presented and discussed. The transient temperature distributions for the linear, quadratic and exponential variations in k for different values of thermal conductivity grading parameter a are shown in Figs. 3, 4 and 5 at different dimensionless times with the fin parameter \( N_{c} \) fixed at 1.0. Following the well known fin behavior, the dimensionless temperature in each case decreases from the base of the fin to the tip. The value a = −0.5 represents a material whose thermal conductivity decreases by 50 % from tip to the base. The value of a = 0 corresponds to a fin of uniform thermal conductivity. Also, the larger the thermal conductivity grading parameter a, the flatter the temperature distribution and consequently higher the fin tip temperature. It is also observed that the dimensionless temperature increases with the dimensionless time in each case as the fin responds to the elevation in its base temperature. The response of the fin temperature to the change in the thermal conductivity grading parameter a can be explained in terms of the spatially averaged thermal conductivity \( \bar{k}. \) For a fin with uniform thermal conductivity \( \bar{k}, \) the steady state temperature distribution is given by the following well known expression.

$$ \theta (X) = \frac{{\cosh \bar{N}_{c} X}}{{\cosh \bar{N}_{c} }} $$
(26)
Fig. 3
figure 3

Transient temperature distribution in a longitudinal fin: linear variation of k with X

Full size image
Fig. 4
figure 4

Transient temperature distribution in a longitudinal fin: quadratic variation of k with X

Full size image
Fig. 5
figure 5

Transient temperature distribution in a longitudinal fin: exponential variation of k with X

Full size image

Consider the temperature distribution for the linear case (Fig. 3). From the preceding paragraph, the values of \( \bar{k} \) for a = −0.5, 0, and 0.5 are 0.75, 1 and 1.25 \( k_{0} \), respectively which means the lowest \( \bar{N}_{c} \) is associated with a = 1 and the highest with a = −0.5. Based on Eq. (20), the fin temperatures should be higher for the case of a = 1 and lower fora = −0.5. Although this is strictly true of the steady state values, the transient curves should also exhibit the same pattern. This is exactly what we see in Fig. 3 for both instances of time. The same argument can be repeated to explain the temperature distributions in Figs. 4 and 5.

The instantaneous dimensionless base heat flow, convective heat loss from the fin and the rate of energy storage in the fin corresponding to the temperature distribution in Figs. 3, 4 and 5 are plotted in Figs. 6, 7 and 8. In each figure, the surface heat loss is small in the early part of the transient, and the bulk of the energy flow from the base of the fin gets stored in the fin. As time passes, the surface heat loss increases and the stored component of the energy decreases. At \( \tau \approx 1.75 \), the fin is virtually at steady state and the storage term vanishes. At this point, the base heat flow equals the surface heat loss. For each case illustrated in Figs. 6, 7 and 8, the base heat flow rate and the surface heat loss increases with the increase in the value of the thermal conductivity parameter a. This can be explained as follows. Consider the steady state base heat flow in terms of the spatially averaged fin parameter which is given by

$$ Q_{b} = F\bar{N}_{c} \tanh \bar{N}_{c} $$
(27)
Fig. 6
figure 6

Heat transfer rates in a longitudinal fin: linear variation of k with X

Full size image
Fig. 7
figure 7

Heat transfer rates in a longitudinal fin: quadratic variation of k with X

Full size image
Fig. 8
figure 8

Heat transfer rates in a longitudinal fin: exponential variation of k with X

Full size image

Equation (27) shows that the base heat flow is a function of F and \( \bar{N}_{c} \). For the linear case, the factor F is 0.75, 1.00, and 1.25 for a = −0.5, 0, 0.5, respectively. For a fixed \( \bar{N}_{c} \), the steady state base heat flow must increase as the thermal conductivity parameter a increases which is what we observe for large values of τ in Fig. 6. The results Figs. 7 and 8 for large values of τ may be similarly explained. The effect of parameter a on base heat flow seen in the steady state results also prevails during the transient response i.e. Q b increases as the parameter a increases.

The transient fin efficiency data for a fin with linear, quadratic and exponential variations in k is plotted Figs. 9, 10 and 11, respectively. Initially, the fin is in thermal equilibrium with its surroundings and the base heat flow and consequently the fin efficiency is zero. As the base temperature is suddenly elevated, heat starts to flow through the fin and its efficiency begins to increase sharply in concert with the sharp increase in base heat flow. As the steady state is approached, each efficiency curve should asymptotically approach the steady value which is given by

$$ \eta = F\frac{{\tanh \bar{N}_{c} }}{{\bar{N}_{c} }} $$
(28)
Fig. 9
figure 9

Efficiency of a functionally graded longitudinal fin: linear variation of k with X

Full size image
Fig. 10
figure 10

Efficiency of a functionally graded longitudinal fin: quadratic variation of k with X

Full size image
Fig. 11
figure 11

Efficiency of a functionally graded longitudinal fin: exponential variation of k with X

Full size image

It is obvious from these figures that, in the transient region, the efficiency increases with the dimensionless time \( \tau \), but attains a constant value as the steady state is approached. The steady state is achieved faster when the convective parameter \( N_{c} \) increases. It is also observed that the efficiency of a functionally graded longitudinal fin increases with the increase in the thermal conductivity grading parameter a, but decreases with the increase in convective parameter \( N_{c} \). This is true of all three cases considered. The efficiency of the fin is compared in Fig. 12 for two values of the convective parameter \( N_{c} \) and three values of the thermal conductivity grading parameter. It is clear that the efficiency is lowest for the linear grading and highest for the exponential grading. Again, the efficiency increases with the decrease in the convective parameter \( N_{c} \) as in the case for a fin made of a homogeneous material.

Fig. 12
figure 12

Efficiency of a functionally graded longitudinal fin having linear, quadratic, and exponential variations of k with X

Full size image

6 Conclusions

A numerical approach has been used to study the transient response of a functionally graded longitudinal fin of constant cross-sectional area. Three cases of spatial variation of thermal conductivity have been investigated, namely linear, quadratic, and exponential. For each case, exact analytical solutions are derived for the steady state temperature distributions in the fin. Of the three types of thermal conductivity grading investigated, the exponentially graded fin yields the highest steady state fin efficiency. A functionally graded fin gives a superior thermal performance when it is operating within an environment which provides low heat transfer coefficient and when the thermal conductivity grading parameter is high. In the early part of the transient, the surface heat loss is small and the energy stored in the fin is large. As time increases, the surface heat loss increases and the stored energy decreases. At steady state, the heat flow from the base equals the surface heat loss. This pattern is observed in all the cases studied in this paper.

The numerical procedure adopted here can be used to study the transient response of a fin for any other form of thermal conductivity grading besides the three cases treated in this paper. The procedure can also be easily adapted to study the transient response of a fin subjected to other types of base and/or environment thermal disturbances.