Bioconvection through interaction of Lorentz force and gyrotactic microorganisms in transverse transportation of rheological fluid

Abstract

Bio-suspensions have been engaged in bio-reactors, bio-petroleum energies, particular drug release, contrast enrichment for magnetic resonance imaging, removal of tumours, synergistic effects in immunology and many more. Bioconvection is created by collective swimming of motile microorganism; these self-propelled motile microorganisms increase the density of base fluid. This article scrutinizes transverse bioconvective flow of Casson magnetic nanofluid with partial slip and role of Newtonian heating. Considering appropriate scaling conversions-governed problem is altered into a set of coupled nonlinear ordinary differential equations and solved via Keller box algorithm. Graphs are plotted for different pertinent physical parameters to analyse behaviour of fluid and heat transfer properties. It is noted that volume fraction of gyrotactic microorganism declines against Prandtl number Pr, bioconvection Lewis number Lb, Peclet number Pe and bioconvection constant σ. Moreover, density of the motile microorganisms rises for bioconvection Peclet number Pe and bioconvection Lewis number Lb. For bioconvection constant, density of motile microorganism rises in free stream and boundary layer density decreases so volume fraction of gyrotactic microorganism also shrinkages.

Introduction

Bioconvection is the spontaneous design structure in suspension of bacteria which are slight thicker in comparison to water. Due to collection of microorganisms, top layer which is much thicker becomes destabilized. This technology is highly beneficial in bio-reactors, petroleum chamber machinery and bio-petroleum energies. Platt [1] practises the term bioconvection that is actually latest secondary category of biology and fluid mechanics. He uses bioconvection themes, used in cultures of free spinning organisms and the high concentrated patterns used in fertilization. Miscellaneous readings have recognized the excellent presentation of magnetic nanofluid suspensions in which nanoparticles are of the same order of magnitude as in chromosome or in proteins. In recent times, magnetic nanoparticles that are based on bio-suspensions have been engaged in particular drug release, contrast enrichment for magnetic resonance imaging (MRI), removal of tumours which are excited through a magnetic field by a frequency identical forfeiture heights, synergistic effects in immunology, cure of asthma by magnetic nano-suspensions where surface tension is acute [2]. Bees et al. [3] study nonlinear arrangement of yawning, stochastic, gyrotactic bioconvection. He used nonlinear equations for fully suspended gyrotactic bioconvective fluid, which are actually developed by Pedley and Kesslar in 1990s, Bees et al. used the assumption of steady state and travelling wave solution for large plume structures. Kuznetsov [4, 5] investigates the effect of cell deposition on bioconvection and negative geotactic microorganisms in a permeable surface. Nield [6] mentioned his problem that bioconvection in a parallel layer over a fully porous sheet. He added Gyrotactic effects he employed the Darcy flow model assuming that bioconvection Peclet number is not greater than one. Waqas et al. [7] studied induction of motile microorganism in stabilized nanoparticles under the influence of magnetohydrodynamic in porous medium. Waqas et al. [8] investigated modified second-grade fluid with suspension of nanoparticles; they also used concept of microorganisms to study heat and mass transfer. Nguyen-Thoai et al. [9] estimated the expedition of the discharging process with the use of aluminium oxide nanoparticles in Y-shaped fins. Tlili et al. [10] interpreted free convective hybrid nanofluid flow with water as base fluid in permeable sheet; finite element method for control volume is used with influence of MHD. Alamri et al. [11] discussed effects of heat transfer with magnetic field and porosity for Buongiorno’s model under the influence of Stefan blowing in a channel. Ellahi et al. [12] developed an original mathematical model for electro-osmotic flow of Couette–Poiseuille nanofluid (with power law fluid as base fluid). They also discussed explicit convergence analysis of all acquired solutions by using recurrence formulae. Khan and Makinde [13] numerically examined the magnetohydrodynamic laminar boundary layer of water-based nanofluid with mixed convection. Mutuku et al. [14] considered MHD flow with bioconvection, in which nanofluid contains water-based nanoparticles and motile microorganisms travelled on a porous vertical moving sheet. They generate bioconvective nanofluid with combination of magnetic field and resistive forces and in the presence of nanoparticles with motile microorganisms. Akbar [15] discussed bioconvective peristaltic flow in an asymmetric channel filled by nanofluid based on gyrotactic microorganism. Raju and Sandeep [16, 17] investigated numerically magnetohydrodynamic Casson fluid and its heat and mass transfer features of gyrotactic microorganisms on a vertical rotating plate in permeable sheet and they established a mathematical programming for analysing all properties of fluid with bioconvective rotating flow on a spinning plate along the assumption of nonlinear thermal radiation and biochemical changes.

A point on surface of any object, where velocity of the fluid becomes zero, is recognized as stagnation point and flow surrounded by this point, is stagnation point flow. Air strikes on an aircraft wing, blood flow at intersection of a blood vessel or a moving cylinder dipped in fluid are examples of this type of flow. 2-D stagnation point flow is most widely investigated in fluid mechanics. Vajravelu and Hadjinicolaou [18] found that flow is under influence by free convective currents and heat generation\absorption with the condition of temperature dependence at an electrically conducted wall. Wu et al. [19] argued the importance of a non-orthogonal plate with heat transmission of mixed convective in a parallel station. Stagnation point flow of Maxwell fluids is computationally investigated by Sadeghy et al. [20]. Ishak et al. [21] mixed convection of the stagnated flow on a stretched vertical porous pane. Yian et al. [22] discussed the mixed convection flow near a non-orthogonal stagnation point on a stretched straight surface. Harris et al. [23] examined the stagnation point boundary layer flow on a non-horizontal wall for mixed convective spongy surface.

Casson fluid is most simple and basic non-Newtonian fluid model, first derived by Casson [24] in 1959, in which he shows that the rate of strain and stress relationship is nonlinear. Casson fluid model is most attracted shear thinning liquid, and many researchers investigated its boundary layer flow with several physical characteristics as homogenous–heterogeneous effects and slip conditions [25,26,27,28,29]; all these studies are related to boundary layer flow on a stretched sheet for Casson fluid without aligned magnetic field. Some applications of Casson fluid, used in industrial pharmacological goods, coal in liquid, china clay, tints, artificial oils, and organic liquids just like synovial liquids, fertilizer slop, gelatin, tomato mush, bee honey, broth, and plasma blood for its fibrinogen and protein.

Heat transmission is used extensively in many industrial and engineering applications like nuclear and space cooling reactors, biomedical presentations and many others. Magyari et al. in [30] examined heat and mass transmission in boundary layers on an exponentially stretched sheet. These types of studies involved uniform heat transfer are discussed by Aziz [31] and Magyari [32]. Ishak [33] reviewed Aziz’s effort, with some addition of suction\injection on levelled sheet. Nadeem et al. [34, 35] conferred oblique stagnation point flow for two types of nanofluid water and kerosene, in which Cu nanoparticles are used, with effects of partial slip. Riaz et al. [36] investigated the influence of bio-heat and mass transfer in peristaltic motion of an Eyring–Powell fluid in 3-D rectangular cross section. Rashidi et al. [37] developed economical efficient system by enhancing rate of heat transfer without dropping the over-all productivity of the conservation systems. This effect has been widely studied [38,39,40,41,42,43,44].

In these days, nanofluid is replaced by microorganisms to study heat transformation. Since nanoparticles have thermophoresis and Brownian motion, there is no movement of microorganisms in nanoparticles. Thus, many researchers are attracted due to its use in health purification ploy skills and bacteriological petroleum cell machinery. Quite a few scientists made an effort to add this type of research with different aspects as mentioned above.

Since bio-microsystems are widely used for improvement of mass transport in industries so in this study oblique bioconvective flow of Casson magnetic nanofluid with partial slip and Newtonian heating effects are considered. Here, it is focused on behavioural physiognomies of gyrotactic microorganisms which depict their character in heat and mass transfer in the presence of magnetohydrodynamic (MHD) forces in Casson nanofluids. Magnetohydrodynamics (MHD) with bioconvection heat transfer flow over a stretched sheet is of significant attention in the practical fields due to its application in manufacturing and engineering technology. These applications contain biological transportation, micro MHD drives, liquid metal fluid and astrophysical problems like sun-spot model, motion of inter-stellar gas, intercontinental ballistic missiles. This study of bioconvection Casson fluid with effects of Lorentz force is applicable in bio-nanopolymer developments and industrial progressions. Using appropriate similarity conversions-governed problem is changed into a set of nonlinear ODEs and solved via Keller box algorithm. Graphs are plotted for different pertinent physical parameters to analyse fluid flow. In order to analyse bioconvective flow features, relevant parameters like bioconvection Lewis number Lb, traditional Lewis number Le, bioconvection Péclet number Pe, Brownian motion parameter Nb, thermophoresis parameter Nt and Hartmann number M were graphically analysed. Major findings additionally show a substantial consequence of Newtonian heating over a stretching sheet by investigating the coefficient values of skin friction, local Nusselt number and the local density number.

Physical modelling of mathematical problem

Casson fluid is one of the simple shear thinning fluids. Mernone and Mazumdar [45] gave tensorial form of the stress strain relationship as $S = - p\delta_{\text{ij}} + 2\mu \left( {J_{2} } \right)U_{\text{ij}}$, where $2\mu \left( {J_{2} } \right) = \left[ {\sqrt \eta + \frac{1}{\sqrt 2 }\frac{{\sqrt {\tau_{\text{y}} } }}{{J_{2}^{1/4} }}} \right]^{2}$ apparent viscosity, S is Cauchy stress tensor, p is pressure term, $\delta_{\text{ij}}$ is the Kronecker delta, $\tau_{\text{y}}$ is yield stress, $\eta$ is known as Casson coefficient of viscosity, $U_{\text{ij}} = \frac{1}{2}\left( {\frac{{\partial u_{\text{i}} }}{{\partial x_{\text{j}} }} + \frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }}} \right)$ is deformation tensor and $J_{2} = \frac{1}{2}U_{\text{ij}} U_{\text{ij}}$ is known as second invariant of a tensor.

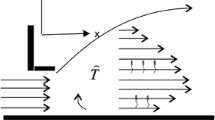
A two-dimensional, steady bioconvective oblique stagnated stream of Casson nanofluid comprising gyrotactic microorganisms’ on mixed convective stretched sheet is taken into account. Magnetic field of uniform strength $B_{0}$ is imposed with partial slip and Newtonian heating. It is assumed that surface is located at x-axis shown in Fig. 1, having velocity in this direction is $u_{\text{w}} = ax + u_{\text{s}}$, where $u_{\text{s}}$ is velocity at slip. Considering couple of balanced forces applied in opposite directions with free stream velocity $u_{\infty } = b_{1} x + b_{2} y$, bioconvection excites the flow by suspending a shrill layer of nanoparticles to avoid suppressing bioconvection. Under these assumptions, the governing model becomes [2]

Fig. 1

Geometrical depiction of model

$$\frac{{\partial u^{*} }}{{\partial x^{*} }} + \frac{{\partial v^{*} }}{{\partial y^{*} }} = 0,$$

(1)

$$u^{*} \frac{{\partial u^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }} + \frac{1}{\rho }\frac{{\partial p^{*} }}{{\partial x^{*} }} = \nu \left( {1 + \frac{1}{\beta }} \right)\nabla^{*2} u^{*} + g_{1} \beta_{\text{T}} \left( {T^{*} - T_{\infty } } \right) - \frac{{\sigma_{\text{e}} B_{0}^{2} }}{\rho }u^{*} ,$$

(2)

$$u^{*} \frac{{\partial v^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial v^{*} }}{{\partial y^{*} }} + \frac{1}{\rho }\frac{{\partial p^{*} }}{{\partial y^{*} }} = \nu \left( {1 + \frac{1}{\beta }} \right)\nabla^{*2} v^{*} ,$$

(3)

$$u^{*} \frac{{\partial T^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial T^{*} }}{{\partial y^{*} }} = \alpha \left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }} + \frac{{\partial^{2} T^{*} }}{{\partial x^{*2} }}} \right) + \frac{{Q_{0} }}{{\rho C_{\text{p}} }}\left( {T^{*} - T_{\infty } } \right) + \tau \left[ {D_{\text{B}} \frac{{\partial T^{*} }}{{\partial y^{*} }}\frac{{\partial c^{*} }}{{\partial y^{*} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial T^{*} }}{{\partial y^{*} }}} \right)^{2} } \right],$$

(4)

$$u^{*} \frac{{\partial c^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial c^{*} }}{{\partial y^{*} }} = D_{\text{B}} \frac{{\partial^{2} c^{*} }}{{\partial y^{*2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }},$$

(5)

$$u^{*} \frac{{\partial n^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial n^{*} }}{{\partial y^{*} }} = D_{\text{n}} \frac{{\partial^{2} n^{*} }}{{\partial y^{*2} }} - \frac{{dw_{\text{c}} }}{{c_{\text{w}} - c_{\infty } }}\frac{\partial }{{\partial y^{*} }}\left( {n^{*} \frac{{\partial c^{*} }}{{\partial y^{*} }}} \right).$$

(6)

The consistent boundary conditions are [35]

$$\left. {\begin{array}{*{20}l} {u^{ *} = ax^{ *} + N_{0} \mu_{\text{B}} \left( {1 + \frac{1}{\beta }} \right)\left( { \frac{{\partial u^{ *} }}{{\partial y^{ *} }} + \frac{{\partial v^{ *} }}{{\partial x^{ *} }}} \right), v^{ *} = 0, } \hfill \\ { \frac{{\partial T^{ *} }}{{\partial y^{ *} }} = - h_{\text{s}} \left( {T^{ *} } \right), \quad c^{ *} = c_{\text{w}} ,\quad n^{ *} = n_{\text{w}} ,} \hfill \\ \end{array} } \right\}\;{\text{when}}\;y^{ *} = 0,$$

(7)

$$u^{*} = b_{1} x^{*} + b_{2} y^{*} , \quad T^{*} = T_{\infty } ,\quad c^{*} \to c_{\infty } , \quad n^{*} \to n_{\infty } ,\;{\text{when}}\;y^{*} \to \infty ,$$

(8)

$$\left. {\begin{array}{*{20}l} {x = x^{*} \sqrt {\frac{a}{\nu }} ,\quad y = y^{*} \sqrt {\frac{a}{\nu }} ,\quad u = u^{*} \frac{1}{{\sqrt {\nu a} }},\quad v = v^{*} \frac{1}{{\sqrt {\nu a} }},} \hfill \\ {p = \frac{{p^{*} }}{\mu a}, \quad T = \frac{{T^{*} - T_{\infty } }}{{T_{\infty } }} ,\quad c = \frac{{c^{*} - c_{\infty } }}{{c_{\text{w}} - c_{\infty } }},\quad n = \frac{{n^{*} - n_{\infty } }}{{n_{\text{w}} - n_{\infty } }}.} \hfill \\ \end{array} } \right\}\;\left[ {35} \right]$$

(9)

Here, above mentioned terms means $u^{*}$ and $v^{*}$ x- and y-component of velocity,

$\nu$ kinematic viscosity, $p^{*}$ pressure, $\rho$ density, $T^{*}$ temperature, $\beta = \mu_{\text{B}} \sqrt {2\pi_{\text{c}} } /p_{\text{y}}$ Casson fluid constraint, $\beta_{\text{T}}$ thermal expansion constant, $\alpha = \frac{k}{{\mu C_{\text{p}} }} + \frac{{16\delta^{*} T_{\infty }^{3} }}{{3\mu C_{\text{p}} K^{*} }}$ thermal diffusivity, $\delta^{*}$ Stefan–Boltzmann constant, $C_{\text{p}}$ specific heat and $T_{\infty }$ temperature of fluid away from the wall.

Putting Eq. (9), into Eqs. (1)–(8), we get

$$\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} = 0,$$

(10)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \left( {1 + \frac{1}{\beta }} \right)\nabla^{2} u + \lambda T - {\text{Mu}} - \frac{\partial p}{\partial x},$$

(11)

$$u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \left( {1 + \frac{1}{\beta }} \right)\nabla^{2} v - \frac{\partial p}{\partial y},$$

(12)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{1}{\Pr }\nabla^{2} T + \gamma T + {\text{Nb}}\frac{\partial T}{\partial y}\frac{\partial C}{\partial y} + {\text{Nt}}\left( {\frac{\partial T}{\partial y}} \right)^{2} ,$$

(13)

$$u\frac{\partial c}{\partial x} + v\frac{\partial c}{\partial y} = \frac{1}{{{\text{Le}}\;\Pr }}\left( {\frac{{\partial^{2} c}}{{\partial y^{2} }} + \frac{\rm{Nt}}{\rm{Nb}}\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right),$$

(14)

$$u\frac{\partial n}{\partial x} + v\frac{\partial n}{\partial y} = \frac{1}{{{\text{Lb}} \;\Pr }}\left[ {\frac{{\partial^{2} n}}{{\partial y^{2} }} - {\text{Pe}}\left( {\frac{\partial n}{\partial y}\frac{\partial c}{\partial y} + \left( {n + \sigma } \right)\frac{{\partial^{2} c}}{{\partial y^{2} }}} \right)} \right],$$

(15)

$$\left. {\begin{array}{*{20}l} {u = x + \delta \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right), \quad v = 0,} \hfill \\ {\frac{\partial T}{\partial y} = - \omega \left( {1 + T} \right), \quad c \to 1,\quad n \to 1} \hfill \\ \end{array} } \right\}\;{\text{at}}\; y \to 0.$$

(16)

$$u = \gamma_{1} x + \gamma_{2} y,\quad T \to 0,\quad c \to 0, \quad n \to 0,\quad {\text{at}}\;y \to \infty ,$$

(17)

where $\lambda = \frac{{g_{1} \beta_{\text{T}} \left( {T_{\text{f}} - T_{\infty } } \right)}}{{a\sqrt {\nu a} }}$ is the mixed convection parameter, $M = \frac{{\sigma_{\text{e}} B_{0}^{2} }}{\rho a}$ is magnetic field parameter, $\gamma = \frac{{Q_{0} }}{{\rho C_{\text{p}} a}}$ is heat generation/absorption parameter, Prandtl number is $\Pr = \frac{\nu }{\alpha }$, Lewis number is ${\text{Le}} = \frac{\alpha }{{D_{\text{B}} }}$, Peclet number is ${\text{Pe}} = \frac{{dW_{\text{c}} }}{{D_{\text{n}} }}$, ${\text{Lb}} = \frac{\alpha }{{D_{\text{n}} }}$ is bioconvection Lewis number $\delta = N_{0} \rho \sqrt {a\nu }$ is velocity slip parameter, $\omega = h_{\text{s}} \sqrt {\frac{\nu }{a}}$ is Newtonian heating parameter, $\gamma_{1} = \frac{{b_{1} }}{a}$ is stretching ratio, and $\gamma_{2} = \frac{{b_{2} }}{a}$ represents obliqueness of the flow. ${\text{Sc}} = {\text{Le}}\;\Pr$ is Schmidt number, ${\text{Nt}} = \frac{{\tau D_{\text{T}} \left( {T_{\text{f}} - T_{\infty } } \right)}}{{T_{\infty } \nu }}$ is thermophoresis parameter, ${\text{Nb}} = \frac{{\tau D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}}{\nu }$ is Brownian motion parameter, and $\sigma = \frac{{n_{\infty } }}{{n_{\text{w}} - n_{\infty } }}$ is bioconvection constant.

Stream function transformation is [35]

$$u = \frac{\partial \psi }{\partial y}, \quad v = - \frac{\partial \psi }{\partial x}.$$

(18)

Substituting Eq. (18) in Eqs. (10)–(17), we get

$$\frac{\partial \psi }{\partial y}\frac{{\partial^{2} \psi }}{\partial x\partial y} - \frac{\partial \psi }{\partial x}\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \frac{\partial p}{\partial x} = \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{3} \psi }}{{\partial y\partial x^{2} }} + \frac{{\partial^{3} \psi }}{{\partial y^{3} }}} \right) + \lambda T - M\frac{\partial \psi }{\partial y},$$

(19)

$$\frac{\partial \psi }{\partial x}\frac{{\partial^{2} \psi }}{\partial y\partial x} - \frac{\partial \psi }{\partial y}\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{\partial p}{\partial y}\left( {1 + \frac{1}{\beta }} \right)\left( { - \frac{{\partial^{3} \psi }}{{\partial x^{3} }} - \frac{{\partial^{3} \psi }}{{\partial y^{2} \partial x}}} \right),$$

(20)

$$\frac{\partial \psi }{\partial y}\frac{\partial T}{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial y} = \frac{1}{\Pr }\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \gamma T + {\text{Nb}}\frac{\partial T}{\partial y}\frac{\partial c}{\partial y} + {\text{Nt}}\left( {\frac{\partial T}{\partial y}} \right)^{2} ,$$

(21)

$$- \frac{\partial \psi }{\partial x}\frac{\partial c}{\partial y} + \frac{\partial \psi }{\partial y}\frac{\partial c}{\partial x} = \frac{1}{\text{Sc}}\left( {\frac{{\partial^{2} c}}{{\partial y^{2} }} + \frac{\rm{Nt}}{\rm{Nb}}\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right),$$

(22)

$$\frac{\partial \psi }{\partial y}\frac{\partial n}{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial n}{\partial y} = \frac{1}{\text{Lb}}\frac{1}{\Pr }\left( {\frac{{\partial^{2} n}}{{\partial y^{2} }} - {\text{Pe}}\left\{ {\frac{\partial c}{\partial y}\frac{\partial n}{\partial y} + \left( {n + \sigma } \right)\frac{{\partial^{2} c}}{{\partial y^{2} }}} \right\}} \right),$$

(23)

$$\left. {\begin{array}{*{20}l} { \frac{\partial \psi }{\partial y} = x + \delta \left( {1 + \frac{1}{\beta }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right),\quad \frac{\partial \psi }{\partial x} = 0,\quad \frac{\partial T}{\partial y} = - \omega \left( {1 + T} \right), } \hfill \\ { c = 1,\quad n = 1,} \hfill \\ \end{array} } \right\}\;{\text{at}}\;y = 0.$$

(24)

$$\frac{\partial \psi }{\partial y} = \gamma_{1} x + \gamma_{2} y,\quad T \to 0,\quad c \to 0,\quad n \to 0,\quad {\text{at}}\;y \to \infty .$$

(25)

Eliminating pressure term from Eqs. (19) and (20),

$$\left( {1 + \frac{1}{\beta }} \right)\nabla^{4} \psi + \frac{{\partial \left( {\psi ,\nabla^{2} \psi } \right)}}{{\partial \left( {x,y} \right)}} + \lambda \frac{\partial T}{\partial y} - M\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0,$$

(26)

Redefining the stream function as [35]

$$\psi \left( {x,y} \right) = xf\left( y \right) + g\left( y \right), \quad T\left( {x,y} \right) = \theta \left( y \right),\quad c\left( {x,y} \right) = \varphi \left( y \right), \quad n\left( {x,y} \right) = \chi \left( y \right).$$

(27)

Putting Eq. (27) in (21)–(26),and on simplifying, we have

$$\left( {1 + \frac{1}{\beta }} \right)f^{{{\prime \prime \prime }}} - Mf^{{\prime }} + ff^{{\prime \prime }} - \left( {f^{{\prime }} } \right)^{2} + B_{1} = 0,$$

(28)

$$\left( {1 + \frac{1}{\beta }} \right)g^{{{\prime \prime \prime }}} - Mg^{{\prime }} - f^{{\prime }} g^{{\prime }} + fg^{{\prime \prime }} + \lambda \theta + B_{2} = 0,$$

(29)

$$\theta^{{\prime \prime }} + \Pr \left( {f\theta^{{\prime }} + \gamma \theta + {\text{Nb}}\theta^{{\prime }} \varphi^{{\prime }} + {\text{Nt}}\theta^{{{\prime 2}}} } \right) = 0,$$

(30)

$$\varphi^{{\prime \prime }} + \frac{\rm{Nt}}{\rm{Nb}}\theta^{{\prime \prime }} + {\text{Sc}}f\varphi^{{\prime }} = 0,$$

(31)

$$\chi^{{\prime \prime }} - {\text{Pe}}\left( {\chi^{{\prime }} \varphi^{{\prime }} + \chi \varphi^{{\prime \prime }} + \sigma \varphi^{{\prime \prime }} } \right) + {\text{Lb}}\Pr f\chi^{{\prime }} = 0,$$

(32)

and boundary conditions become

$$\left. {\begin{array}{*{20}l} {f\left( 0 \right) = 0,\quad f^{{\prime }} \left( 0 \right) = 1 + \delta \left( {1 + \frac{1}{\beta }} \right)f^{{\prime \prime }} \left( 0 \right),\quad g^{{\prime }} \left( 0 \right) = \delta \left( {1 + \frac{1}{\beta }} \right)g^{{\prime \prime }} \left( 0 \right) ,} \hfill \\ {\theta^{{\prime }} \left( 0 \right) = - \omega \left( {1 + \theta \left( 0 \right)} \right), \quad \varphi \left( 0 \right) = 1, \quad \chi \left( 0 \right) = 1 ,} \hfill \\ \end{array} } \right\}$$

(33)

$$\left. {f^{{\prime }} \left( \infty \right) = \gamma_{1} ,\quad g^{{\prime }} \left( y \right) \to \gamma_{2} y,\quad {\text{as}}\; y \to \infty \theta \left( \infty \right) \to 0,\quad \varphi \left( \infty \right) \to 0,\quad \chi \left( \infty \right) \to 0 } \right\}$$

(34)

where $B_{1}$ and $B_{2}$ are constants of integrations,

$$B_{1} = \gamma_{1}^{2} + M\gamma_{1} ,\quad B_{2} = \gamma_{2} \left( {My - A} \right).$$

(35)

Introducing

$$\frac{\text{d}}{{{\text{d}}y}}g\left( y \right) = \gamma_{2} h\left( y \right),$$

(36)

Substituting Eqs. (35)–(36) in Eqs. (28)–(29), we have

$$\left( {1 + \frac{1}{\beta }} \right)f^{{{\prime \prime \prime }}} - Mf^{{\prime }} + ff^{{\prime \prime }} - \left( {f^{{\prime }} } \right)^{2} + \gamma_{1}^{2} + M\gamma_{1} = 0,$$

(37)

$$\left( {1 + \frac{1}{\beta }} \right)h^{{\prime \prime }} - Mh + fh^{{\prime }} - f^{{\prime }} h + \frac{\lambda \theta }{{\gamma_{2} }} + My - A = 0,$$

(38)

$$\theta^{{\prime \prime }} + \Pr \left( {f\theta^{{\prime }} + \gamma \theta + {\text{Nb}}\theta^{{\prime }} \varphi^{{\prime }} + {\text{Nt}}\theta^{{{\prime 2}}} } \right) = 0,$$

(39)

$$\varphi^{{\prime \prime }} + \frac{\rm{Nt}}{\rm{Nb}}\theta^{{\prime \prime }} + {\text{Sc}}f\varphi^{{\prime }} = 0,$$

(40)

$$\chi^{{\prime \prime }} - {\text{Pe}}\left( {\chi^{{\prime }} \varphi^{{\prime }} + \chi \varphi^{{\prime \prime }} + \sigma \varphi^{{\prime \prime }} } \right) + {\text{Lb}}\;\Pr f\chi^{{\prime }} = 0.$$

(41)

Subject to BCs

$$\left. {\begin{array}{*{20}l} {f\left( 0 \right) = 0,\quad f^{{\prime }} \left( 0 \right) = 1 + \delta \left( {1 + \frac{1}{\beta }} \right)f^{{\prime \prime }} \left( 0 \right),\quad h\left( 0 \right) = \delta \left( {1 + \frac{1}{\beta }} \right)h^{{\prime }} \left( 0 \right) ,} \hfill \\ {\theta^{{\prime }} \left( 0 \right) = - \omega \left( {1 + \theta \left( 0 \right)} \right), \quad \varphi \left( 0 \right) = 1, \quad \chi \left( 0 \right) = 1, } \hfill \\ \end{array} } \right\}$$

(42)

$$f^{{\prime }} \left( \infty \right) = \gamma_{1} ,\quad h^{{\prime }} \left( \infty \right) = 1,\quad \theta \left( \infty \right) \to 0,\quad \varphi \left( \infty \right) \to 0,\chi \left( \infty \right) \to 0.$$

(43)

Here, $\left( . \right)^{{\prime }}$ means derivative with respect to $y$.

Physical magnitudes

Practical magnitudes of attention for industrial and engineering purpose are local skin friction coefficients, reduced Nusselt number, motile microorganism’s density number and Sherwood number are

$$\tau_{\text{w}} = \left( {1 + \frac{1}{\beta }} \right)\left[ {xf^{{\prime \prime }} \left( 0 \right) + \gamma_{2} h^{{\prime }} \left( 0 \right)} \right],$$

(44)

$${\text{Nu}}_{\text{x}} = - \left( {{\text{Pe}}_{\text{x}} } \right)^{{\frac{1}{2}}} \theta^{{\prime }} \left( 0 \right),\quad {\text{Sh}}_{\text{x}} = - \left( {{\text{Pe}}_{\text{x}} } \right)^{{\frac{1}{2}}} \varphi^{{\prime }} \left( 0 \right),\quad {\text{Nn}}_{\text{x}} = - \left( {{\text{Pe}}_{\text{x}} } \right)^{{\frac{1}{2}}} \chi^{{\prime }} \left( 0 \right),$$

(45)

where $({\text{Pe}}_{\text{x}} )^{{\frac{1}{2}}}$ is the local Peclet number.

The stagnation point $x_{\text{t}}$ is

$$x_{\text{t}} = \frac{{ - \gamma_{2} h^{{\prime }} \left( 0 \right)}}{{f^{{\prime \prime }} \left( 0 \right)}}.$$

(46)

Computational algorithm

Coupled nonlinear equations presented through (37)–(41) and boundary conditions (42), (43) are solved through Keller box method, the procedure is given below but the detailed calculations of governed problem with Keller box method is presented in the “Appendix” section. The prevailing nonlinear higher-order ODEs are primarily malformed into scheme of ODEs of first order by defining new independent variables. Then, developed a finite difference scheme using central differences, the derivatives involved in governed system have been estimated through central difference gradient scheme, while averages are taken at mid points. Now convert the governed system into discretized form of equations which are nonlinear algebraic equations and linearized through Newton iterations and convert these linearized systems into matrix forms and solved the system by LU factorizations. Numerical solutions and their graphical results are obtained via of Matlab with tolerance of $10^{ - 6} .$

Stability and convergence

The stability of Keller box method can be obtained by reducing nonlinear ODEs (37–41) into linear ODEs by using Newton quasi-linearization technique. By discretizing the quasi-linear first-order system of Eqs. (48–52). To observe stability of set of Eqs. (67–78), Von-Neumann stability scheme is applied. Matrix vector form is obtained as mentioned in Eq. (79), where $\varvec{A}$ is $11 \times 11$ matrix and stability is determined from the eigenvalues of $\varvec{A}$. Condition of stability can be obtained from those nonzero eigenvalues which are less than or equal to one.

A standard KBM (Keller box method) is of order two accuracy so it is reliable with present method as we discretize the present problem by using standard KBM with LU factorization. By using finite difference scheme, approximation of a system becomes convergent if solution of finite difference scheme converges to some value when their increments approaches to zero.

Results and discussion

This segment depicts the results to debate performance of numerous constraints for typical profiles like velocity, temperature, concentration of motile microorganisms. Few are surveyed for heat and mass flux also showed fallouts in tabular arrangement. The macroscopic convective motion of fluid caused by the density gradient is known as bioconvection and is created by collective swimming of motile microorganism.

Figures 2–5 depict velocity contour $f^{{\prime }} \left( y \right)$ and $h^{{\prime }} \left( y \right)$ against velocity slip parameter $\delta$ and magnetic field parameter $M$. We can see that with arise in velocity slip parameter $\delta$, normal velocity as well as momentum boundary layer thickness cuts down; see Fig. 2, because under slip condition the pulling of stretching sheet can only be partially transmitted to fluid so viscous effects dominants and also it is along the direction of the flow so it decreases the flow velocity. Dg force can be determined at very low magnetic field and when magnetic field is increased then magnetic forces among the particles become the main force, also since magnetic field consists of Lorentz force which acts as resisting force towards flow of fluid so similar kind of behaviour is noted for magnetic field parameter $M$ on normal velocity, i.e. decreasing as seen in Fig. 3. It is seen in Fig. 4 that for increasing values of slip parameter $\delta$, transverse velocity declines because it is become the reason for reduction in penetration of stagnation surface through boundary layer. Also, it becomes noticeable that rising vales of magnetic field parameter $M$, transverse component of velocity declines close to wall while rises when gone far away from wall, actually magnetic field parameter grows a resistant force, called Lorentz force which acts in reversed direction to flow field and boosts the thermal boundary layer thickness.

Fig. 2

Normal velocity $f^{{\prime }} \left( y \right)$ for velocity slip parameter $\delta$

Fig. 3

Normal velocity $f^{{\prime }} \left( y \right)$ for magnetic field parameter $M$

Fig. 4

Transverse velocity $h^{{\prime }} \left( y \right)$ for velocity slip parameter $\delta$

Fig. 5

Transverse velocity $h^{{\prime }} \left( y \right)$ for magnetic field parameter $M$

In Fig. 6, temperature profile $\theta \left( y \right)$ increases for Newtonian heating parameter $\omega$, as it is directly proportional to heat transfer coefficient. Figures 7–10 show that profile of volume fraction of gyrotactic microorganism $\chi \left( y \right)$. It is observed in Fig. 7 that volume fraction of gyrotactic microorganism declines for Prandtl number Pr, and Fig. 8 shows that volume fraction of gyrotactic microorganism drops for bioconvection Lewis number Lb, also in Fig. 9 for bioconvection Peclet number Pe volume fraction of gyrotactic microorganism shrinkages since Peclet number is fraction of thermal energy through convection to conduction so when Peclet number rises it means that energy through convection rises which implies that fluid get energized and concentration boundary layer thickness shrinkages. For bioconvection constant $\sigma$, volume fraction of gyrotactic microorganism reduces as shown in Fig. 10 when bioconvection constant rises it implies that density of motile microorganism rises in free stream and boundary layer density decreases which results in volume fraction of gyrotactic microorganism shrinkages. Bioconvection Lewis number Lb decreases the mass diffusivity which implies the decrease in thickness of concentration boundary layer actually, Lewis number is defined as fraction of thermal to mass diffusivity, as it grows thermal diffusivity becomes large and mass diffusivity small, which results in diluent concentration boundary layer. Figures 11–14 give graphical description for surface skin friction, local heat, mass and density number. It is considerably noted in Fig. 11 that both skin friction coefficients, normal as well as transverse decrease for slip parameter $\delta .$ heating source and sink parameter $\gamma$ heat flux $- \theta^{{\prime }} \left( 0 \right)$ at the surface and density number $- \chi^{{\prime }} \left( 0 \right)$ at the surface rises but mass flux $- \phi^{{\prime }} \left( 0 \right)$ at the surface declines, see Fig. 12. The consequence of the parameter replicates that high diffusion of the nanoparticles occurs because of the adding of microorganisms. Figure 13 shows that with an increase in bioconvection Peclet number Pe local density number $- \chi^{{\prime }} \left( 0 \right)$ rises as Peclet number is the ratio of thermal energy through convection to conduction so when it rise it means local density of mile microorganism at surface also rises. Similar kind of result is mentioned in Fig. 14 that local density number $- \chi^{{\prime }} \left( 0 \right)$ rises for an increase in b convection Lewis number Lb.

Fig. 6

Temperature $\theta \left( y \right)$ for Newtonian heating parameter $\omega$

Fig. 7

Microorganism profile $\chi \left( y \right)$ for Prandtl number Pr

Fig. 8

Microorganism profile $\chi \left( y \right)$ for bioconvection Lewis number Lb

Fig. 9

Microorganism profile $\chi \left( y \right)$ for Peclet number Pe

Fig. 10

Microorganism profile $\chi \left( y \right)$ for bioconvection constant $\sigma$

Fig. 11

Surface skin friction coefficients for velocity slip parameter $\delta .$

Fig. 12

Local heat, mass and density for Heating source and sink parameter $\gamma .$

Fig. 13

Local density number for Peclet number Pe

Fig. 14

Local density number for bioconvection Lewis number Lb

Physical outcomes and novelty of the article

Bio-suspensions are highly beneficial in bio-reactors, petroleum cell machinery and bio-petroleum energies. Keeping in view, the present study inspects bioconvective transverse flow of a Casson magnetic nanofluid in influence of partial slip and Newtonian heating effects. The physical problem is transformed via scaling group of transformations which is then tackled using efficient numerical scheme known as Keller box method. The obtained physical results reveal that volume fraction of Gyrotactic microorganism profile declines, while density of motile microorganisms rises with Lb and Pe. Heat flux and density of motile microorganisms’ increase, while mass flux declines for heat generation $\gamma$.

Appendix

The detail calculation of governed problem via Keller box method is described below.

Presenting subsequent replacements in system of Eqs. (37)–(43),

$$\left. {\begin{array}{*{20}l} {f^{{\prime }} = U,\quad f^{{\prime \prime }} = U^{{\prime }} = V,\quad f^{{{\prime \prime \prime }}} = U^{{\prime \prime }} = V^{{\prime }} ,} \hfill \\ {h^{{\prime }} = w,\quad h^{{\prime \prime }} = w^{{\prime }} ,\quad \theta^{{\prime }} = s,\quad \theta^{{\prime \prime }} = s^{{\prime }} ,} \hfill \\ {\phi^{{\prime }} = t,\quad \phi^{{\prime \prime }} = t^{{\prime }} ,\quad \chi^{{\prime }} = z,\quad \chi^{{\prime \prime }} = z^{{\prime }} . } \hfill \\ \end{array} } \right\}$$

(47)

The following scheme of ordinary differential equations of order one with initial conditions,

$$\left( {1 + \frac{1}{\beta }} \right)V^{{\prime }} - MU - U^{2} + fV + \left( {\frac{a}{c}} \right)^{2} + M\gamma_{1} = 0,$$

(48)

$$\left( {1 + \frac{1}{\beta }} \right)w^{{\prime }} - Mh - Uh + fw - \frac{\lambda }{{\gamma_{2} }} + A - My = 0,$$

(49)

$$s^{{\prime }} + \Pr (fs + \gamma \theta + {\text{Nb}}st + {\text{Nt}}s^{2} = 0,$$

(50)

$$t + {\text{Sc}}ft - \frac{\rm{Nt}}{\rm{Nb}}\left( {fs + \gamma \theta + {\text{Nb}}st + {\text{Nt}}s^{2} } \right) = 0,$$

(51)

$$\begin{aligned} & z^{\prime } - {\text{Pe}}zt - {\text{Pe}}\;\Pr \frac{\rm{Nt}}{\rm{Nb}}\left( {\chi + \sigma } \right)\left( {fs + \gamma \theta + {\text{Nb}}st + {\text{Nt}}s^{2} } \right) \\ & \quad + \;{\text{Pe}}\;{\text{Sc}}\left( {\chi + \sigma } \right) + {\text{Lb}}\;{ \Pr }\;fz = 0 .\\ \end{aligned}$$

(52)

Using central difference scheme,

$$\left. {\begin{array}{*{20}l} {\eta_{0} = 0,} \hfill \\ {\eta_{\text{j}} = \eta_{{{\text{j}} - 1}} + d_{\text{j}} , \quad j = 1 < j < \infty ,} \hfill \\ {\eta_{\text{j}} = \eta_{\infty } .} \hfill \\ \end{array} } \right\}$$

(53)

Discretization of Eqs. (48)–(52) takes the following form

$$\frac{{\left( {f_{\text{j}} - f_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = U_{{{\text{j}} - 1/2}} ,$$

(54)

$$\frac{{\left( {U_{\text{j}} - U_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = V_{{{\text{j}} - 1/2}} ,$$

(55)

$$\frac{{\left( {w_{\text{j}} - w_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = h_{{{\text{j}} - 1/2}} ,$$

(56)

$$\frac{{\left( {s_{\text{j}} - s_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = \theta_{{{\text{j}} - 1/2}} ,$$

(57)

$$\frac{{\left( {t_{\text{j}} - t_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = \phi_{{{\text{j}} - 1/2}} ,$$

(58)

$$\frac{{\left( {z_{\text{j}} - z_{{{\text{j}} - 1}} } \right)}}{{d_{\text{j}} }} = \chi_{{{\text{j}} - 1/2}} ,$$

(59)

$$\frac{{A_{1} }}{{d_{\text{j}} }}\left( {V_{{{\text{j}} - }} V_{{{\text{j}} - 1}} } \right) - {\text{MU}}_{{{\text{j}} - \frac{1}{2}}} - U^{2}_{{{\text{j}} - \frac{1}{2}}} + f_{{{\text{j}} - \frac{1}{2}}} V_{{{\text{j}} - \frac{1}{2}}} + A_{2} \left( {A_{2} + M} \right) = 0,$$

(60)

$$\begin{aligned} & \frac{{A_{1} }}{{d_{\text{j}} }}\left( {w_{{{\text{j}} - }} w_{{{\text{j}} - 1}} } \right) - Mh_{{{\text{j}} - \frac{1}{2}}} - U_{{{\text{j}} - \frac{1}{2}}} h_{{{\text{j}} - \frac{1}{2}}} + f_{{{\text{j}} - \frac{1}{2}}} w_{{{\text{j}} - \frac{1}{2}}} \\ & \quad + \;C_{2} \theta_{{{\text{j}} - \frac{1}{2}}} + My_{{{\text{j}} - \frac{1}{2}}} - A = 0, \\ \end{aligned}$$

(61)

$$\left( {s_{{{\text{j}} - }} s_{{{\text{j}} - 1}} } \right) + \Pr \left( {f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} } \right) + \gamma \theta_{{{\text{j}} - \frac{1}{2}}} + {\text{Nb}}s_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} + {\text{Nt}}s^{2}_{{j - \frac{1}{2}}} = 0,$$

(62)

$$\begin{aligned} & \left( {t_{{{\text{j}} - }} t_{{{\text{j}} - 1}} } \right) - \frac{\rm{Nt}}{\rm{Nb}}\left( {f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + \gamma \theta_{{{\text{j}} - \frac{1}{2}}} + {\text{Nb}}s_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} + {\text{Nt}}s^{2}_{{{\text{j}} - \frac{1}{2}}} } \right) \\ & \quad + \;{\text{Sc}}f_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} = 0, \\ \end{aligned}$$

(63)

$$\begin{aligned} & \left( {z_{{{\text{j}} - }} z_{{{\text{j}} - 1}} } \right) - {\text{Pe}}z_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} - {\text{Pe}}\Pr \frac{\rm{Nt}}{\rm{Nb}}\left( {\chi_{{{\text{j}} - \frac{1}{2}}} + \sigma } \right)\left( {f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + \gamma \theta_{{{\text{j}} - \frac{1}{2}}} + {\text{Nb}}s_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} + {\text{Nt}}s^{2}_{{{\text{j}} - \frac{1}{2}}} } \right) \\ & \quad + \;{\text{PeSc}}\left( {\chi_{{{\text{j}} - \frac{1}{2}}} + \sigma } \right)t_{{{\text{j}} - \frac{1}{2}}} + {\text{Lb}}\Pr f_{{{\text{j}} - \frac{1}{2}}} z_{{{\text{j}} - \frac{1}{2}}} = 0, \\ \end{aligned}$$

(64)

where

$$(.)_{{{\text{j}} - \frac{1}{2}}} = \frac{1}{2} \left( {(.)_{\text{j}} + (.)_{{{\text{j}} - \frac{1}{2}}} } \right).$$

(65)

Using Newton iterations defined below, nonlinear Eqs. (60)–(64) can be linearized as:

For $\left( {i + 1} \right){\text{th}}$ iteration,

$$f_{\text{j}}^{i + 1} = f_{\text{j}}^{i} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}}^{i} ,\quad {\text{etc.}}$$

(66)

Using Eqs. (66) in (54)–(64) and ignoring second and above order factors in $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}}^{i}$, we get a linear tri-diagonal system:

$$- a_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{{{\text{j}} - 1}} } \right) + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) = \left( {r_{1} } \right)_{{{\text{j}} - \frac{1}{2} }} ,$$

(67)

$$- a_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{{{\text{j}} - 1}} } \right) + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{{{\text{j}} - 1}} } \right) = \left( {r_{2} } \right)_{{{\text{j}} - \frac{1}{2}}} ,$$

(68)

$$\left( {\zeta_{1} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{\text{j}} + \left( {\zeta_{2} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{{{\text{j}} - 1}} - \left( {\zeta_{3} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{{{\text{j}} - 1}} } \right) + \left( {a_{3} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) = \left( {r_{3} } \right)_{{{\text{j}} - \frac{1}{2} }} ,$$

(69)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } h_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } h_{{{\text{j}} - 1}} } \right) - a_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{{{\text{j}} - 1}} } \right) = \left( {r_{4} } \right)_{\text{j }} ,$$

(70)

$$\begin{aligned} & A_{1} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{{{\text{j}} - 1}} } \right) - \left( {\zeta_{3} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } h_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } h_{{{\text{j}} - 1}} } \right) + \left( {a_{1} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{{{\text{j}} - 1}} } \right) - \left( {a_{4} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{{{\text{j}} - 1}} } \right) \\ & \quad + \;\left( {a_{5} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{4} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \right) = \left( {r_{5} } \right)_{\text{j }} , \\ \end{aligned}$$

(71)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \right) - a_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{{{\text{j}} - 1}} } \right) = \left( {r_{6} } \right)_{{{\text{j}} }} ,$$

(72)

$$\begin{aligned} & \left( {\zeta_{5} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{\text{j}} + \left( {\zeta_{6} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{{{\text{j}} - 1}} + \left( {\zeta_{7} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{8} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \right) \\ & \quad + \;\left( {\zeta_{9} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{{{\text{j}} - 1}} } \right) = \left( {r_{7} } \right)_{\text{j}} , \\ \end{aligned}$$

(73)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \phi_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta \phi_{{{\text{j}} - 1}} } \right) - \left( {a_{1} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{{{\text{j}} - 1}} } \right) = \left( {r_{8} } \right)_{{{\text{j}} }} ,$$

(74)

$$\begin{aligned} & \left( {\zeta_{10} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \phi_{\text{j}} + \left( {\zeta_{11} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \phi_{{{\text{j}} - 1}} + \left( {\zeta_{12} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{13} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) \\ & \quad + \;\left( {\zeta_{14} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \right) = \left( {r_{9} } \right)_{\text{j}} , \\ \end{aligned}$$

(75)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \chi_{\text{j}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \chi_{{{\text{j}} - 1}} } \right) - \left( {a_{1} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{{{\text{j}} - 1}} } \right) = \left( {r_{10} } \right)_{\text{j}} ,$$

(76)

$$\begin{aligned} & \left( {\zeta_{15} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{\text{j}} + \left( {\zeta_{16} } \right)_{\text{j}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{{{\text{j}} - 1}} + \left( {\zeta_{17} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{18} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{{{\text{j}} - 1}} } \right) \\ & \quad + \;\left( {\zeta_{19} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{20} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \chi_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \chi_{{{\text{j}} - 1}} } \right) + \left( {\zeta_{21} } \right)_{\text{j}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{\text{j}} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \right) = \left( {r_{11} } \right)_{\text{j}} , \\ \end{aligned}$$

(77)

$$\left. {\begin{array}{*{20}l} {f\left( 0 \right) = 0, \quad U\left( 0 \right) = 1 + A_{1} V\left( 0 \right), \quad h\left( 0 \right) = A_{1} w\left( 0 \right),} \hfill \\ {\phi \left( 0 \right) = 1, \quad s\left( 0 \right) = - \omega \left( {1 + \theta \left( 0 \right)} \right), \quad \chi \left( 0 \right) = 1, } \hfill \\ {\theta \left( \infty \right) = 0,\quad U\left( \infty \right) = A_{2} ,\quad \phi \left( \infty \right) = 0, \quad h\left( \infty \right) = 1, \chi \left( \infty \right) = 0,} \hfill \\ \end{array} } \right\}$$

(78)

where

$$\left( {r_{1} } \right)_{\text{j}} = f_{{{\text{j}} - 1}} - f_{\text{j}} + d_{\text{j}} U_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {r_{2} } \right)_{\text{j}} = U_{{{\text{j}} - 1}} - U_{\text{j}} + d_{\text{j}} V_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {r_{3} } \right)_{\text{j}} = A_{1} \left( {V_{{{\text{j}} - 1}} - V_{\text{j}} } \right) + Md_{\text{j}} U_{{{\text{j}} - \frac{1}{2}}} + d_{\text{j}} U^{2}_{{{\text{j}} - \frac{1}{2}}} - d_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} V_{{{\text{j}} - \frac{1}{2}}} - C_{1} ,$$

$$\left( {r_{4} } \right)_{\text{j}} = h_{{{\text{j}} - 1}} - h_{\text{j}} + d_{\text{j}} w_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {r_{5} } \right)_{\text{j}} = A_{1} \left( {V_{{{\text{j}} - 1}} - V_{\text{j}} } \right) + Md_{\text{j}} h_{{{\text{j}} - \frac{1}{2}}} + d_{\text{j}} U_{{{\text{j}} - \frac{1}{2}}} h_{{{\text{j}} - \frac{1}{2}}} - d_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} w_{{{\text{j}} - \frac{1}{2}}} - C_{1} d_{\text{j}} \theta_{{{\text{j}} - \frac{1}{2}}} - Md_{\text{j}} y_{{{\text{j}} - \frac{1}{2}}} + A,$$

$$\left( {r_{6} } \right)_{\text{j}} = \theta_{{{\text{j}} - 1}} - \theta_{\text{j}} + d_{\text{j}} s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\begin{aligned} \left( {r_{7} } \right)_{{\text{j}}} & = \left( {t_{{{\text{j}} - 1}} - t_{{\text{j}}} } \right) + \Pr \frac{\rm{Nt}}{\rm{Nb}}d_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + \Pr \gamma \frac{\rm{Nt}}{\rm{Nb}}d_{\text{j}} \theta_{{{\text{j}} - \frac{1}{2}}} + {\text{Nt}}\Pr d_{\text{j}} t_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + \frac{{{\text{Nt}}^{2} }}{\text{Nb}}\Pr d_{\text{j}} s^{2}_{{{\text{j}} - \frac{1}{2}}} \\ & \quad - \;{\text{Sc}}d_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} , \\ \end{aligned}$$

$$\left( {r_{8} } \right)_{\text{j}} = \phi_{{{\text{j}} - 1}} - \phi_{\text{j}} + d_{\text{j}} t_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\begin{aligned} \left( {r_{9} } \right)_{\text{j}} & = \left( {z_{{{\text{j}} - 1}} - z_{\text{j}} } \right) - {\text{Pe}}d_{\text{j}} z_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;\Pr d_{\text{j}} \frac{\rm{Nt}}{\rm{Nb}}\chi_{{{\text{j}} - \frac{1}{2}}} f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} \\ & \quad + \;{\text{Pe}}\;\Pr \;\sigma d_{\text{j}} \frac{\rm{Nt}}{\rm{Nb}}f_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;\Pr \;\gamma d_{\text{j}} \frac{\rm{Nt}}{\rm{Nb}}\chi_{{{\text{j}} - \frac{1}{2}}} \theta_{{{\text{j}} - \frac{1}{2}}} \\ & \quad + \;{\text{Pe}}\;\Pr \;\gamma \sigma d_{\text{j}} \frac{\rm{Nt}}{\rm{Nb}}\theta_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;\Pr \;{\text{Nt}} d_{\text{j}} \chi_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;\Pr \;\sigma d_{\text{j}} \frac{{{\text{Nt}}^{2} }}{\text{Nb}}s^{2}_{{{\text{j}} - \frac{1}{2}}} \\ & \quad - \;{\text{Pe}}\; {\text{Sc}}\; d_{\text{j}} \chi_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} - {\text{Pe }}\;{\text{Sc}}\; \sigma d_{\text{j}} t_{{{\text{j}} - \frac{1}{2}}} - {\text{Lb}}\;{ \Pr }\;d_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} z_{{{\text{j}} - \frac{1}{2}}} , \\ \end{aligned}$$

$$\left( {r_{10} } \right)_{\text{j}} = \chi_{{{\text{j}} - 1}} - \chi_{\text{j}} + d_{\text{j}} z_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{1} } \right)_{\text{j}} = A_{1} + \left( {a_{1} } \right)_{\text{j}} ,$$

$$\left( {\zeta_{2} } \right)_{\text{j}} = - A_{1} + \left( {a_{1} } \right)_{\text{j}} ,$$

$$\left( {\zeta_{3} } \right)_{\text{j}} = M\frac{{d_{\text{j}} }}{2} + \left( {a_{2} } \right)_{\text{j}} ,$$

$$\left( {\zeta_{4} } \right)_{\text{j}} = C_{2} \frac{{d_{\text{j}} }}{2},$$

$$\left( {\zeta_{5} } \right)_{\text{j}} = 1 + \Pr \frac{{d_{\text{j}} }}{2}f_{{{\text{j}} - \frac{1}{2}}} + \Pr \;{\text{Nb}}\frac{{d_{\text{j}} }}{2}t_{{{\text{j}} - \frac{1}{2}}} + \Pr \;{\text{Nt}} d_{\text{j}} s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{6} } \right)_{\text{j}} = - 1 + \Pr \frac{{d_{\text{j}} }}{2}f_{{{\text{j}} - \frac{1}{2}}} + \Pr \;{\text{Nb}}\frac{{d_{\text{j}} }}{2}t_{{{\text{j}} - \frac{1}{2}}} + \Pr \;{\text{Nt}} d_{\text{j}} s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{7} } \right)_{\text{j}} = \Pr \frac{{d_{\text{j}} }}{2}s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{8} } \right)_{\text{j}} = \Pr \frac{{d_{\text{j}} }}{2}\gamma ,$$

$$\left( {\zeta_{9} } \right)_{\text{j}} = \Pr \;{\text{Nb}}\frac{{d_{\text{j}} }}{2}s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{10} } \right)_{\text{j}} = 1 - {\text{Nt}}\;\Pr \frac{{d_{\text{j}} }}{2}s_{{{\text{j}} - \frac{1}{2}}} + {\text{Sc}}\frac{{d_{\text{j}} }}{2}f_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{11} } \right)_{\text{j}} = - 1 - {\text{Nt}}\;\Pr \frac{{d_{\text{j}} }}{2}s_{{{\text{j}} - \frac{1}{2}}} + {\text{Sc}}\frac{{d_{\text{j}} }}{2}f_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{12} } \right)_{{\text{j}}} = - {\text{Nt}}\;\Pr d_{{\text{j}}} \left( {\frac{1}{{2{\text{Nb}}}}f_{{{\text{j}} - \frac{1}{2}}} + \frac{1}{2}h_{{{\text{j}} - \frac{1}{2}}} + {\frac{\rm{Nt}}{\rm{Nb}}s_{{{\text{j}} - \frac{1}{2}}} } } \right),$$

$$\left( {\zeta_{13} } \right)_{\text{j}} = - {\text{Nt}}\;\Pr \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}s_{{{\text{j}} - \frac{1}{2}}} + {\text{Sc}}\frac{{d_{\text{j}} }}{2}t_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{14} } \right)_{\text{j}} = - {\text{Nt}}\;\Pr \gamma \frac{{d_{\text{j}} }}{{2{\text{Nb}}}},$$

$$\left( {\zeta_{15} } \right)_{\text{j}} = 1 + {\text{Pe}}\frac{{d_{\text{j}} }}{2}t_{{{\text{j}} - \frac{1}{2}}} + {\text{Lb}}\;\Pr \left( {a_{1} } \right)_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{16} } \right)_{\text{j}} = - 1 + {\text{Pe}}\left( {a_{1} } \right)_{\text{j}} t_{{{\text{j}} - \frac{1}{2}}} + {\text{Lb}}\;\Pr \left( {a_{1} } \right)_{\text{j}} f_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{17} } \right)_{\text{j}} = {\text{Pe}}\frac{{d_{\text{j}} }}{2}z_{{{\text{j}} - \frac{1}{2}}} - {\text{Pe}}\;\Pr \;{\text{Nt}}\frac{{d_{\text{j}} }}{2}\chi_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;{\text{Sc}}\frac{{d_{\text{j}} }}{2}\chi_{{{\text{j}} - \frac{1}{2}}} + {\text{Pe}}\;{\text{Sc}}\sigma \frac{{d_{\text{j}} }}{2},$$

$$\left( {\zeta_{18} } \right)_{{\text{j}}} = - \frac{{d_{{\text{j}}} }}{{2{\text{Nb\,Pe}}}}\;\Pr \;{\text{Nt}}\chi_{{{\text{j}} - \frac{1}{2}}} f_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{{\text{j}} }}}{{2{\text{Nb\,Pe}}}}\;\Pr \;{\text{Nt}}\sigma f_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{{\text{j}}} }}{2}{\text{Pe}}\;\Pr \;{\text{Nt}}\chi_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{{\text{j}}} }}{\text{Nb\,Pe}}\;\Pr \;{\text{Nt}}^{2} s_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{19} } \right)_{\text{j}} = - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;{ \Pr }\;{\text{Nt}}s_{{{\text{j}} - \frac{1}{2}}} f_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;\Pr \;{\text{Nt}}\gamma \theta_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{\text{j}} }}{2}{\text{Pe}}\;\Pr \;{\text{Nt}}s_{{{\text{j}} - \frac{1}{2}}} t_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{\text{j}} }}{2}{\text{Pe}}\;{\text{Sc}}t_{{{\text{j}} - \frac{1}{2}}} ,$$

$$\left( {\zeta_{20} } \right)_{\text{j}} = - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;\Pr \;{\text{Nt}}\gamma \chi_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;\Pr \;{\text{Nt}}\gamma ,$$

$$\left( {\zeta_{21} } \right)_{\text{j}} = - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;\Pr \;{\text{Nt}}\chi_{{{\text{j}} - \frac{1}{2}}} s_{{{\text{j}} - \frac{1}{2}}} - \frac{{d_{\text{j}} }}{{2{\text{Nb}}}}{\text{Pe}}\;\Pr \;{\text{Nt}}\sigma s_{{{\text{j}} - \frac{1}{2}}} + \frac{{d_{\text{j}} }}{2}{\text{Lb}}\;\Pr z_{{{\text{j}} - \frac{1}{2}}} ,$$

$$A_{1} = 1 + \frac{1}{\beta },$$

$$A_{2} = \gamma_{1} ,$$

$$C_{1} = A_{2}^{2} + MA_{2} ,$$

$$C_{2} = \frac{\lambda }{{\gamma_{2} }}.$$

Linearized equations from (67) to (78) can be written in vector form as:

$$A\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } = r ,$$

(79)

where

$$\varvec{A} = \left[ {\begin{array}{*{20}c} {\left[ {A_{1} } \right]} & {\left[ {E_{1} } \right]} & {} & {} & {} & {} & {} & {} & {} \\ {\left[ {B_{2} } \right]} & {\left[ {A_{2} } \right]} & {\left[ {E_{2} } \right]} & {} & {} & {} & {} & {} & {} \\ {} & {} & {} & \cdot & {} & {} & {} & {} & {} \\ {} & {} & {} & \cdot & \cdot & {} & {} & {} & {} \\ {} & {} & {} & \cdot & \cdot & \cdot & {} & {} & {} \\ {} & {} & {} & {} & \cdot & \cdot & {} & {} & {} \\ {} & {} & {} & {} & {} & \cdot & {\left[ {B_{{{\text{J}} - 1}} } \right]} & {\left[ {A_{{{\text{J}} - 1}} } \right]} & {\left[ {E_{{{\text{J}} - 1}} } \right]} \\ {} & {} & {} & {} & {} & {} & {} & {\left[ {B_{\text{J}} } \right]} & {\left[ {A_{\text{J}} } \right]} \\ \end{array} } \right]$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } = \left[ {\begin{array}{*{20}l} {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{1} } \right]} \hfill \\ {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{2} } \right]} \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \cdot \hfill \\ {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{{{\text{J}} - 1}} } \right]} \hfill \\ {\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{\text{J}} } \right]} \hfill \\ \end{array} } \right],\quad \varvec{ r} = \left[ {\begin{array}{*{20}l} {\left[ {r_{1} } \right]} \hfill \\ {\left[ {r_{2} } \right]} \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \cdot \hfill \\ {\left[ {r_{{{\text{J}} - 1}} } \right]} \hfill \\ {\left[ {r_{\text{J}} } \right]} \hfill \\ \end{array} } \right]$$

$$A_{1} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\left( {\zeta_{2} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {a_{3} } \right)_{1} } \hfill & {\left( {\zeta_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - A_{1} } \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {a_{5} } \right)_{1} } \hfill & {A_{1} } \hfill & {\left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{6} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{7} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{5} } \right)_{1} } \hfill & {\left( {\zeta_{9} } \right)_{1} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{12} } \right)_{1} } \hfill & {\left( {\zeta_{11} } \right)_{1} } \hfill & 0 \hfill & {\left( {\zeta_{13} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{12} } \right)_{1} } \hfill & {\left( {\zeta_{10} } \right)_{1} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \left( {a_{1} } \right)_{1} } \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{15} } \right)_{1} } \hfill & {\left( {\zeta_{17} } \right)_{1} } \hfill & {\left( {\zeta_{16} } \right)_{1} } \hfill & {\left( {\zeta_{19} } \right)_{1} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{18} } \right)_{1} } \hfill & {\left( {\zeta_{17} } \right)_{1} } \hfill & {\left( {\zeta_{15} } \right)_{1} } \hfill \\ \end{array} } \right]$$

$$A_{\text{j}} = \left[ {\begin{array}{*{20}l} { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - \left( {\zeta_{3} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {a_{3} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{1} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - \left( {a_{4} } \right)_{\text{j}} } \hfill & { - \left( {\zeta_{3} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{4} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {a_{5} } \right)_{\text{j}} } \hfill & {A_{1} } \hfill & {\left( {a_{1} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{j} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{8} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{7} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{5} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{9} } \right)_{\text{j}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{j} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & { - \left( {\zeta_{14} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{13} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{12} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{10} } \right)_{\text{j}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill \\ 0 \hfill & 0 \hfill & { - \left( {\zeta_{21} } \right)_{\text{j}} } \hfill & 0 \hfill & {\left( {\zeta_{20} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{19} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{18} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{17} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{15} } \right)_{\text{j}} } \hfill \\ \end{array} } \right]$$

$$2 \le j \le J$$

$$B_{\text{j}} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {a_{3} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{2} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {a_{5} } \right)_{\text{j}} } \hfill & { - A_{1} } \hfill & {\left( {a_{1} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{7} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{6} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{9} } \right)_{\text{j}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{j} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{13} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{12} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{11} } \right)_{\text{j}} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - a_{\text{j}} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{19} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & {\left( {\zeta_{18} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{17} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{16} } \right)_{\text{j}} } \hfill \\ \end{array} } \right]$$

$$2 \le j \le J$$

$$E_{\text{j}} = \left[ {\begin{array}{*{20}l} { - a_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - \left( {\zeta_{3} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ { - \left( {a_{4} } \right)_{\text{j}} } \hfill & { - \left( {\zeta_{3} } \right)_{\text{j}} } \hfill & {\left( {\zeta_{4} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{8} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{14} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\left( {\zeta_{14} } \right)_{\text{j}} } \hfill & 0 \hfill & {\left( {\zeta_{20} } \right)_{\text{j}} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

$$2 \le j \le J$$

$$\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{1} } \right] = \left[ {\begin{array}{*{20}l} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{0} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{0} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{0} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{0} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{0} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{1} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{1} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{1} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{1} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{1} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{1} } \hfill \\ \end{array} } \right],\quad \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{\text{j}} } \right] = \left[ {\begin{array}{*{20}l} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } U_{{{\text{j}} - 1}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } h_{{{\text{j}} - 1}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \theta_{{{\text{j}} - 1}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \phi_{{{\text{j}} - 1}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } \chi_{{{\text{j}} - 1}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } f_{\text{j}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } V_{\text{j}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } w_{\text{j}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } s_{\text{j}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } t_{\text{j}} } \hfill \\ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } z_{\text{j}} } \hfill \\ \end{array} } \right], \quad 2 \le j \le J$$

$$\left[ {r_{\text{j}} } \right] = \left[ {\begin{array}{*{20}l} {\left( {r_{1} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{2} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{3} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{4} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{5} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{6} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{7} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{8} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{9} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{10} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ {\left( {r_{11} } \right)_{{{\text{j}} - 1/2}} } \hfill \\ \end{array} } \right] \cdot 1 \le j \le J$$

Consider

$$A = Lu,$$

(80)

where

$$\varvec{L} = \left[ {\begin{array}{*{20}c} {\left[ {\alpha_{1} } \right]} & {} & {} & {} & {} & {} & {} \\ {\left[ {B_{2} } \right]} & {\left[ {\alpha_{2} } \right]} & {} & {} & {} & {} & {} \\ {} & {} & \cdot & {} & {} & {} & {} \\ {} & {} & \cdot & \cdot & {} & {} & {} \\ {} & {} & {} & \cdot & \cdot & {} & {} \\ {} & {} & {} & {} & \cdot & {\left[ {\alpha_{{{\text{J}} - 1}} } \right]} & {} \\ {} & {} & {} & {} & {} & {\left[ {B_{\text{J}} } \right]} & {\left[ {\alpha_{\text{J}} } \right]} \\ \end{array} } \right],$$

and

$$\varvec{u} = \left[ {\begin{array}{*{20}c} {\left[ I \right]} & {\left[ {\varGamma_{1} } \right]} & {} & {} & {} & {} & {} & {} \\ {} & {\left[ I \right]} & {\left[ {\varGamma_{2} } \right]} & {} & {} & {} & {} & {} \\ {} & {} & {} & \cdot & {} & {} & {} & {} \\ {} & {} & {} & \cdot & \cdot & {} & {} & {} \\ {} & {} & {} & {} & \cdot & \cdot & {} & {} \\ {} & {} & {} & {} & {} & \cdot & {} & {} \\ {} & {} & {} & {} & {} & {} & {\left[ I \right]} & {\left[ {\varGamma_{{{\text{J}} - 1}} } \right]} \\ {} & {} & {} & {} & {} & {} & {} & {\left[ I \right]} \\ \end{array} } \right].$$

Here, $\left[ I \right]$ is the unit matrix and $\left[ {\alpha_{\text{i}} } \right]$, $\left[ {\varGamma_{\text{i}} } \right]$ are square matrices of order 11 whose entries can be found as:

$$\left[ {\alpha_{1} } \right] = \left[ {A_{1} } \right],$$

$$\left[ {A_{1} } \right]\left[ {\varGamma_{1} } \right] = \left[ {C_{1} } \right],$$

$$\left[ {\alpha_{\text{j}} } \right] = \left[ {A_{\text{j}} } \right] - \left[ {B_{\text{j}} } \right]\left[ {\varGamma_{{{\text{j}} - 1}} } \right], \quad j = 2,3, \ldots , J$$

$$\left[ {\alpha_{\text{j}} } \right]\left[ {\varGamma_{\text{j}} } \right] = \left[ {C_{\text{j}} } \right], \quad j = 2,3, \ldots ,J - 1.$$

Incorporating Eq. (80) into Eq. (79) yields

$$LU\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } = r,$$

let

$$U\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta } = W,$$

(81)

so that

$$LW = r ,$$

where

$$\varvec{W} = \left[ {\begin{array}{*{20}l} {\left[ {W_{1} } \right]} \hfill \\ {\left[ {W_{2} } \right]} \hfill \\ {\left[ {W_{3} } \right]} \hfill \\ {\left[ {W_{4} } \right]} \hfill \\ {\left[ {W_{5} } \right]} \hfill \\ {\left[ {W_{6} } \right]} \hfill \\ {\left[ {W_{7} } \right]} \hfill \\ {\left[ {W_{8} } \right]} \hfill \\ {\left[ {W_{9} } \right]} \hfill \\ {\left[ {W_{10} } \right]} \hfill \\ {\left[ {W_{11} } \right]} \hfill \\ \end{array} } \right],$$

and $\left[ {W_{\text{j}} } \right]$ is a $11 \times 1$ column matrix. Elements of $\varvec{W}$ are solved from the following equations

$$\left[ {\alpha_{1} } \right]\left[ {W_{1} } \right] = \left[ {r_{1} } \right],$$

$$\left[ {\alpha_{\text{j}} } \right]\left[ {W_{\text{j}} } \right] = \left[ {r_{\text{j}} } \right] - \left[ {B_{\text{j}} } \right]\left[ {W_{{{\text{j}} - 1}} } \right],$$

$\varGamma_{\text{j}} , \alpha_{\text{j}}$ and $W_{\text{j}}$ are calculated by forward difference scheme; then, using Eq. (35) $\varvec{\delta}$ is obtained whose entries can be found from following equation:

$$\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{\text{J}} } \right] = \left[ {W_{\text{J}} } \right],$$

$$\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{\text{j}} } \right] = \left[ {W_{\text{j}} } \right] - \left[ {\varGamma_{\text{j}} } \right]\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\delta }_{{{\text{j}} + 1}} } \right],\quad j = 2,3, \ldots , J.$$

These calculations are maintained with tolerance of $10^{ - 6}$$.$