1 Introduction

Choi [1] was the first who define the suspension of tiny solid particles of size 1–100 nm in a liquid, as nanofluid. It was the breakthrough in the field of heat transfer. Das et al. [2] presented the detailed research review on nanofluids. Bioconvection is the phenomena through which the microorganisms move upward toward the surface and after increase in their density near surface; the self-propelled microorganism gets unstable and starts moving downward. Pedley et al. [3] was the one who named the said phenomena as bioconvection. They also focused their concentration to get insight of the mechanism of locomotion of the microorganisms in liquid. Wager [4] investigated and presented a detailed study about bioconvection in 1911. According to the exploration of Kuznetsov and Avramenko [5], the favorable condition for the bioconvection process within the nanofluids is that the density of nanoparticles should be so less that it will not affect the movement and direction of the microorganisms.

Separation of different size of molecules in the presence of temperature gradient gives rise to Soret effect. Also, we can observe the Dufour effect in the presence of mass gradient whenever there is heat flux in a chemical system. Soret and Dufour effects are also called as thermal-diffusion and diffusion-thermo effects, respectively. The Soret and Dufour effects on fluid flowing along vertical plate with variable viscosity under free convection were investigated by Elbashbeshy and Ibrahim [6]. The study on boundary layer flow for convection along with Soret and Dufour effects on temperature-based viscosity was conducted by Kafoussias and William [7]. Yih [8] discussed variation in heat and mass transfer due to various parameters by considering the geometry of wedge with changing temperature of the wall. Discussion on heat and mass transfer for non-Newtonian fluid was presented by Jurnah and Mujumdar [9]. Boundary layer flow for thermal-diffusion and diffusion-thermo effects in the presence of suction/injection was studied by Anghel et al. [10].

Wall jet flows have many applications in the industries like electronics, transport and paint spray, especially for cooling/heating systems. Launder [11, 12] explained many applications of laminar/turbulent wall jets. Tetervin [13] was the first one who conducted theoretical study on laminar wall jet flow. Glauert [14] obtained the closed analytical solution of boundary layer equations for incompressible laminar wall jet flow, and the results recorded by him were further used and endorsed by Bajura and Szewezyk [15]. Glauert’s problem [14] was drawn-out by Merkin and Needham [16, 17], considering the cases of moving walls and suction/blowing. They discussed that the similarity solutions obtained by Glauert are possible when the lateral suction is applied through the moving surface. Riley [18] applied the Illingworth–Stewartson transformation to compressible radial wall jet. Chun and Schwarz [19] investigated the stability analysis of wall jet and concluded that the flow remains stable till the value of Reynolds number equals to 57. They also presented second unstable mode named as viscous mode of instability for modest values of Reynolds number. Many eminent researchers recorded remarkable results for heat and mass transfer by considering nanofluids, carbon nanotubes for different geometries [20–22].

In the literature, the research work regarding wall jet flow of nanofluid with bioconvection process with Soret effect has not been presented. Our aim is to investigate bioconvection phenomena with gyrotactic locomotion of microorganism by taking into consideration the Buongiorno [23] model of nanofluid with appropriate boundary conditions. A special concentration will be focused to analyze the Soret effects on temperature and concentration profiles in the presence of normally applied magnetic field. To get insight of the complex problem, the rate of heat and mass transfer will also be taken into account. To best of my knowledge, the results obtained from the present study are new.

2 Problem formulation

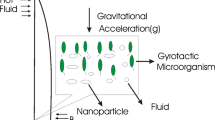
An incompressible Buongiorno [23] model of nanofluid with base fluid water is considered through wall jet. To analyze bioconvection phenomena of gyrotactic microorganisms, it is assumed that suspension of nanoparticles is stable and with concentration of <1 %. It is also assumed that presence of nanoparticles does not alter the swimming direction and velocity of the uniformly shaped microorganisms. Lower horizontal plate parallel to x-axis is at temperature T w, and an ambient temperature of the fluid is taken as T ∞. The experimental results obtained by Sarkar et al. [24] show that microorganism actively survive up to the temperature of 42 °C. To analyze the solute concentration, we have also taken in account Soret effect. Variable magnetic field is applied normal to the flow of the fluid to record the effects on velocity, temperature and concentration profiles with the assumption that induced magnetic field is negligible. The schematic diagram of the problem is given Fig. 1.

Fig. 1
figure 1

Schematic diagram of problem

Full size image

After utilizing boundary layer approximation and said assumptions we obtained the governing equations in the form as follows [25, 26]:

$$\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \frac{{\partial \hat{v}}}{{\partial \hat{y}}} = 0,$$
(1)
$$\begin{aligned} & \hat{u}\frac{{\partial \hat{u}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{u}}}{{\partial \hat{y}}} = \upsilon_{\text{f}} \frac{{\partial^{2} \hat{u}}}{{\partial \hat{y}^{2} }} - \frac{{\sigma B^{2} \left( x \right)}}{{\rho_{\text{f}} }}\hat{u} \\ & \quad + \frac{1}{{\rho_{\text{f}} }}\left( {\left( {1 - C_{\infty } } \right)\rho_{\text{f}} g\left( {\beta_{\text{T}} \left( {\hat{T} - T_{\infty } } \right) + \beta_{\text{s}} \left( {\hat{S} - S_{\infty } } \right)} \right)} \right. \\ & \quad - \left. {\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right)g\left( {\hat{c} - C_{\infty } } \right) - \left( {\hat{n} - n_{\infty } } \right)g\gamma \left( {\rho_{\text{m}} - \rho_{\text{f}} } \right)} \right), \\ \end{aligned}$$
(2)

Velocity components are to be defined as \(\hat{u}\) and \(\hat{v}\) in \(\hat{x}\) and \(\hat{y}\) direction, respectively. Density of nanofluid is denoted as ρ f, υ f is the kinematics viscosity of nanofluid, σ denotes the electric conductivity, and B(x) is used to represent variable magnetic field. \(\hat{C},\hat{T},\hat{S}, \hat{n}\) indicate the concentration of nanofluid, temperature, concentration of solute and microorganism’s concentration, respectively. Thermal expansion coefficient is taken as β T, volumetric solute expansion coefficient is denoted by β s, and the nanoparticle’s density is mentioned by ρ p. The gravitational force and motile microorganism’s average volume fraction are denoted by g and \(\gamma\), respectively.

$$\hat{u}\frac{{\partial \hat{T}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{T}}}{{\partial \hat{y}}} = \alpha \frac{{\partial^{2} \hat{T}}}{{\partial \hat{y}^{2} }} + \tau \left[ {D_{\text{B}} \frac{{\partial \hat{C}}}{{\partial \hat{y}}}\frac{{\partial \hat{T}}}{{\partial \hat{y}}} + \left( {\frac{{D_{\text{T}} }}{{T_{\infty } }}} \right)\left( {\frac{{\partial \hat{T}}}{{\partial \hat{y}}}} \right)^{2} } \right],$$
(3)
$$\hat{u}\frac{{\partial \hat{S}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{S}}}{{\partial \hat{y}}} = D_{\text{s}} \frac{{\partial^{2} \hat{S}}}{{\partial \hat{y}^{2} }} + k_{\text{T}} \left( {\frac{{D_{\text{m}} }}{{T_{\infty } }}} \right)\frac{{\partial^{2} \hat{T}}}{{\partial \hat{y}^{2} }} ,$$
(4)
$$\hat{u}\frac{{\partial \hat{C}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{C}}}{{\partial \hat{y}}} = D_{\text{B}} \frac{{\partial^{2} \hat{C}}}{{\partial \hat{y}^{2} }} + \left( {\frac{{D_{\text{T}} }}{{T_{\infty } }}} \right)\frac{{\partial^{2} \hat{T}}}{{\partial \hat{y}^{2} }} ,$$
(5)
$$\hat{u}\frac{{\partial \hat{n}}}{{\partial \hat{x}}} + \hat{v}\frac{{\partial \hat{n}}}{{\partial \hat{y}}} + \frac{{bW_{\text{c}} }}{{\left( {\hat{C}_{\text{w}} - \hat{C}_{\infty } } \right)}}\left( {\frac{{\partial \hat{n}}}{{\partial \hat{y}}}\frac{{\partial \hat{C}}}{{\partial \hat{y}}} + \hat{n}\frac{{\partial^{2} \hat{C}}}{{\partial \hat{y}^{2} }}} \right) = D_{n} \frac{{\partial^{2} \hat{n}}}{{\partial \hat{y}^{2} }} ,$$
(6)

Thermal diffusivity of nanofluid is taken as α, D B is used for Brownian diffusion coefficient, and D T is the coefficient of thermophoresis diffusion. The ratio of heat capacitance of nanoparticles and base fluid is given by \(\tau = \frac{{\left( {\rho C} \right)_{\text{p}} }}{{\left( {\rho C} \right)_{\text{f}} }} ,\) where \(D_{\text{s}} \,{\text{and}}\,D_{\text{m}}\) represent the coefficients of solute and mass diffusivity, respectively. With the assumption that product of \({\text{b}}\,{\text{and}}\,W_{\text{c}}\) remains constant, we define b as constant of chemo taxis and W c as the maximum speed of microorganisms. We also define D n as coefficient of microorganisms’ diffusion.

The appropriate boundary conditions are:

$$\begin{aligned} \hat{u} & = 0,\,\,\hat{v} = 0,\,\,\hat{T} = T_{\text{w}} ,\,\,\hat{C} = C_{\text{w}} ,\,\,\hat{n} = n_{\text{w}} ,\quad {\text{at}}\quad \hat{y} = 0, \\ \hat{u} & = 0,\,\,\hat{T} \to T_{\infty } ,\,\,\hat{C} \to C_{\infty } ,\,\, \hat{n} \to n_{\infty } \quad {\text{at}}\quad y \to \infty , \\ \end{aligned}$$
(7)

In order to utilize numerical technique, the following similarity transforms [14, 27] are adopted:

$$\begin{aligned} \eta & = \frac{{\hat{y}}}{{\upsilon_{\text{f}}^{1/2} \hat{x}^{3/4} }},\quad \psi = 4\sqrt {\upsilon_{\text{f}} } \hat{x}^{{\frac{1}{4}}} f\left( \eta \right),\quad \theta \left( \eta \right) = \frac{{\hat{T} - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}, \\ \phi \left( \eta \right) & = \frac{{\hat{C} - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }},\quad w\left( \eta \right) = \frac{{\hat{S} - S_{\infty } }}{{S_{\text{w}} - S_{\infty } }},\quad \chi \left( \eta \right) = \frac{{\hat{n} - n_{\infty } }}{{n_{\text{w}} - n_{\infty } }} \\ \end{aligned}$$
(8)

Velocity in stream function form is defined as \(u = \frac{\partial \psi }{{\partial \hat{y}}}\) and \(\hat{v} = - \frac{\partial \psi }{{\partial \hat{x}}}\).

Using Eq. (8) along with stream function into Eqs. (1)–(7), we obtained system of nonlinear differential equations with boundary equations as follows:

$$f^{\prime\prime\prime} + 2\left( {f^{\prime } } \right)^{2} + ff^{\prime \prime } + \frac{1}{4}\lambda \left( {\theta + Nc w - Nr \phi - Rb \chi } \right) - M^{2} f^{\prime } = 0,$$
(9)
$$\theta^{\prime \prime } + Prf\theta^{\prime } + Nb\phi^{\prime } \theta^{\prime } + Nt\theta^{\prime 2} = 0,$$
(10)
$$w^{\prime \prime } + Lnfw^{\prime } + Sr \theta^{\prime \prime } = 0,$$
(11)
$$\phi^{\prime \prime } + Lef\phi^{\prime } + \frac{Nt}{Nb}\theta^{\prime \prime } = 0,$$
(12)
$$\chi^{\prime \prime } + Lb\left( {f\chi^{\prime } } \right) - Pe\left( {\phi^{\prime } \chi^{\prime } + \phi^{\prime \prime } \left( {\Omega + \chi } \right)} \right) = 0.$$
(13)

The boundary conditions also transform to

$$f\left( 0 \right) = 0, \,\,f^{{\prime }} \left( 0 \right) = 0, \,\,\theta \left( 0 \right) = 1,\,\,w\left( 0 \right) = 1, \,\,\phi \left( 0 \right) = 1,\,\, \chi \left( 0 \right) = 1,$$
(14)
$$f\left( \infty \right) = 1,\,\,\theta \left( \infty \right) = 0, \,\,w\left( \infty \right) = \phi \left( \infty \right) = 0, \,\,\chi \left( \infty \right) = 0.$$
(15)

The derivative w.r.t η is represented by primes.

After applying Eq. (8) we obtained following non-dimensional numbers and parameters,

\({\text{M}}^{2} = \frac{{\sigma B_{0}^{2} }}{{\rho_{\text{f}} }}\): Hartmann number

\({\text{Rb}} = \frac{{\gamma \left( {n_{\text{w}} - n_{\infty } } \right)\left( {\rho_{\text{m}} - \rho_{\text{f}} } \right)}}{{\beta_{\text{T}} \rho_{\text{f}} \left( {1 - C_{\infty } } \right)\left( {T_{\text{w}} - T_{\infty } } \right)}}\): Bioconvection Rayleigh number

\(\Pr = \frac{{\nu_{\text{f}} }}{\alpha }\): Prandtl number

\({\text{Nc}} = \frac{{\beta_{\text{s}} }}{{\beta_{\text{T}} }}\frac{{\left( {S_{\text{w}} - S_{\infty } } \right)}}{{\left( {T_{\text{w}} - T_{\infty } } \right)}}\): Regular double-diffusive buoyancy parameter

\({\text{Le}} = \frac{{\nu_{\text{f}} }}{{D_{\text{B}} }}\): Standard Lewis number

\({\text{Sr}} = \frac{{D_{\text{m}} k_{\text{T}} }}{{D_{\text{s}} T_{\infty } }}\frac{{\left( {T_{\text{w}} - T_{\infty } } \right)}}{{\left( {S_{\text{w}} - S_{\infty } } \right)}}\): Soret number

\({\text{Nb}} = \frac{{\tau \,D_{\text{B}} \,(C_{\text{w}} - C_{\infty } )}}{\alpha }\): Brownian motion parameter

\({\text{Ln}} = \frac{{\upsilon_{\text{f}} }}{{D_{\text{s}} }}\): Nanofluid Lewis number

\({\text{Nt}} = \frac{{\tau \,D_{\text{T}} (T_{\text{w}} - T_{\infty } )}}{{T_{\infty } \alpha }}\): Thermophoresis parameter

\({\text{Nr}} = \frac{{\left( {C_{\text{w}} - C_{\infty } } \right)\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right)}}{{\beta_{\text{T}} \rho_{\text{f}} \left( {1 - C_{\infty } } \right)\left( {T_{\text{w}} - T_{\infty } } \right)}}\): Buoyancy ratio parameter

\(\lambda = \frac{{{\text{Gr}}_{x} }}{{{\text{Re}}_{x}^{2} }}\): Ratio of Grashof and Reynolds number

\({\text{Pe}} = \frac{bWc}{Dn}\): Bioconvection Peclet number

\({\text{Gr}}_{x} = \frac{{g \beta_{\text{T}} \left( {1 - C_{\infty } } \right)\left( {T_{\text{w}} - T_{\infty } } \right){\raise0.7ex\hbox{${x^{3} }$} \!\mathord{\left/ {\vphantom {{x^{3} } {\upsilon_{\text{f}}^{ 2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\upsilon_{\text{f}}^{ 2} }$}}}}{{{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {\upsilon_{\text{f}}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\upsilon_{\text{f}}^{2} }$}}}}\): Grashof number

\({\text{Re}}_{x} = \frac{{x^{1/2} }}{{\upsilon_{\text{f}} }}\): Reynolds number

\({\text{Lb}} = \frac{{\upsilon_{\text{f}} }}{{D_{n} }}\): Bioconvection Lewis number

\(\Omega = \frac{{n_{\infty } }}{{\left( {n_{\text{w}} - n_{\infty } } \right)}}\): Microorganisms concentration difference parameter

The physical engineering interest quantities are local Nusselt number Nu x , local Sherwood number Sh x and density number of motile microorganisms Nn x

$$\begin{aligned} & {\text{Nu}}_{x} = \frac{{xq_{\text{w}} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)}}\quad {\text{where}}\quad q_{\text{w}} = - k_{\text{f}} \left( {\frac{{\partial \hat{T}}}{{\partial \hat{y}}}} \right)_{{\hat{y} = 0}} \\ &{\text{Re}}_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{Nu}}_{x} = - \theta^{\prime } \left( 0 \right), \end{aligned}$$
(16)
$$\begin{aligned} & {\text{Sh}}_{x} = \frac{{xq_{\text{m}} }}{{D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}}\quad {\text{where}}\quad q_{\text{m}} = - D_{\text{B}} \left( {\frac{{\partial \hat{C}}}{{\partial \hat{y}}}} \right)_{{\hat{y} = 0}} \\ &{\text{Re}}_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{Sh}}_{x} = - \phi^{\prime } \left( 0 \right), \end{aligned}$$
(17)
$$\begin{aligned} &{\text{Nn}}_{x} = \frac{{xq_{n} }}{{D_{n} \left( {n_{\text{w}} - n_{\infty } } \right)}}\quad {\text{where}}\quad q_{n} = - D_{n} \left( {\frac{{\partial \hat{n}}}{{\partial \hat{y}}}} \right)_{{\hat{y} = 0}}\\ &{\text{Re}}_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{Nn}}_{x} = - \chi^{\prime } \left( 0 \right). \end{aligned}$$
(18)

3 Numerical procedure

To obtain numerical solution of the problem, we have utilized boundary layer approximation and similarity transformation. The obtained solution of set of ordinary differential equations along with boundary conditions we used Runge–Kutta method coupled with shooting method. In order to calculate results in efficient and speedy manner, we extended the support of software like Mathematica 10 in our research work. To obtained the meaningful results and order of convergence at 10−7, we select the interval size Δη = 0.001. To get insight of the problem, the influence of various parameters on velocity, temperature and concentration profiles of nanoparticles and microorganism has also been recorded.

4 Results and discussion

Figures 2, 3, 4, 5 and 6 represent the analysis of velocity distribution under effect of parameters that arise due to nanofluid and bioconvection phenomena. From Figs. 2 and 3, we have observed rise in velocity for increasing values of λ (ratio of Grashof number to Reynolds number) and Nc (regular double-diffusive buoyancy parameter). As we know that double-diffusive means occurrence of heat and mass transfer due to thermal buoyancy, now increasing Nc leads to higher solute volumetric expansion as compared to thermal volumetric expansion. So resistance between fluid layers decreases which in result give rise to velocity distribution. Figure 4 depicted that magnetic field normal to flow produces tendency to resist the flow due to increase in Lorentz drag force. The Hartmann number is taken as controlling parameter because by increasing its value we have observed decrease in velocity profile in normalized manner. Figure 5 shows that increase in buoyancy parameter produces retardation in velocity which in return decreases the momentum boundary layer thickness. Also higher values of bioconvection Rayleigh (Rb) in Fig. 6 show interesting behavior toward velocity distribution. Due to the property of the bioconvection plumes of opposing upward motion of nanofluid because of its downward concentration, the velocity profile decreases along with momentum boundary layer thickness.

Fig. 2
figure 2

Influence of λ on velocity distribution

Full size image
Fig. 3
figure 3

Influence of Nc on velocity distribution

Full size image
Fig. 4
figure 4

Influence of M on velocity distribution

Full size image
Fig. 5
figure 5

Influence of Nr on velocity distribution

Full size image
Fig. 6
figure 6

Influence of Rb on velocity distribution

Full size image

From Fig. 7, it is easy to understand that increased friction between the fluid layers in the presence of Lorentz force tends to raise the temperature profile. Figures 8, 9 and 10 recorded increase in temperature distribution for incremental values of thermophoresis parameter (Nt), Brownian motion parameter (Nb) and buoyancy ratio parameter (Nr). In all of the cases a rapid collision between the molecules increases the kinetic energy which in return increases the overall temperature distribution and thermal boundary layer thickness. For higher value of buoyancy ratio parameter, we have to decrease the value of Reynolds number, which means to increase friction between the fluid layers, as it is known thing that resistance in flow tends to increase in temperature.

Fig. 7
figure 7

Influence of M on temperature distribution

Full size image
Fig. 8
figure 8

Influence of Nt on temperature distribution

Full size image
Fig. 9
figure 9

Influence of Nr on temperature distribution

Full size image
Fig. 10
figure 10

Influence of Nb on temperature distribution

Full size image

Analysis of nanoparticles concentration is given in Figs. 11, 12, 13, 14 and 15. It has been observed that nanoparticles volume fraction decreases for higher value of Lewis number (Le), Brownian motion parameter (Nb) and Soret number (Sr), whereas it increases by considering different incremental values of buoyancy ratio parameter (Nr) and thermophoresis parameter (Nt). When mass diffusion is less than thermal diffusion, then overall Lewis number increases which results decrease in nanoparticle concentration. Similarly, for higher values of Brownian motion parameter the collision among the molecules will be faster which in response reduces the nanoparticle concentration and boundary layer thickness. From Fig. 14, an interesting behavior of nanoparticle concentration has been observed for higher values of buoyancy ratio parameter (Nr). Within the interval 0 ≤ η ≤ 0.7 and η > 3.2, a negligible increase in nanoparticle concentration is obtained, whereas for 0.7 < η ≤ 3.2, a remarkable increase is represented. Also Fig. 15 depicted that for increasing values of thermophoresis parameter, a rapid rise in nanoparticle concentration is recorded near the all due to heated plate.

Fig. 11
figure 11

Influence of Le on nanofluid concentration profile

Full size image
Fig. 12
figure 12

Influence of Nb on nanofluid concentration profile

Full size image
Fig. 13
figure 13

Influence of Sr on nanofluid concentration profile

Full size image
Fig. 14
figure 14

Influence of Nr on nanofluid concentration profile

Full size image
Fig. 15
figure 15

Influence of Nt on nanofluid concentration profile

Full size image

A strong influence of different parameters on motile microorganism’s concentration can be observed in Figs. 16, 17, 18, 19 and 20. Due to high diffusion rate for increasing value of bioconvection Lewis number (Lb), the surface velocity reduces which tends toward decline of the microorganism’s concentration layer thickness, as shown in Fig. 16. From Fig. 17, it is recorded that for higher values of Brownian motion parameter (Nb), the density of microorganisms reduces due to rapid collision of molecules. The speed of the microorganisms is controlled and increases directly with help of bioconvection Peclet number (Pe). Figure 18 represents that by giving increment in the values of Pe we observed reduction in microorganism’s concentration close to the surface.

Fig. 16
figure 16

Influence of Lb on microorganism concentration profile

Full size image
Fig. 17
figure 17

Influence of Nb on microorganism concentration profile

Full size image
Fig. 18
figure 18

Influence of Pe on microorganism concentration profile

Full size image
Fig. 19
figure 19

Influence of Sr on microorganism concentration profile

Full size image
Fig. 20
figure 20

Influence of Nt on microorganism concentration profile

Full size image

The impact of Soret effect can be observed in Fig. 19. The density of the motile microorganism decreases for rising values of Soret number. The low mass diffusion always tends to stronger thermophoresis effects which mean higher values of thermophoresis parameter Fig. 20, helps to increase the concentration profile of motile microorganisms. Figure 21 illustrated decrease in solute concentration for higher values of nanofluid Lewis number (Ln). For Ln = 1, we have observed a rapid increase in solute concentration for interval 0 ≤ η ≤ 1.2 and then gradual decrease. Reduction in mass diffusivity due to higher values of nanofluid Lewis number results in reduction in solute concentration boundary layer thickness. In the presence of Lorentz viscous drag, the velocity of fluid reduces because of friction between the fluid layers which in turn increases the solute concentration, as shown in Fig. 22. Also it is known that Soret effect decreases the temperature gradient which helps in enhancing the solute concentration boundary layer thickness as shown in Fig. 23.

Fig. 21
figure 21

Influence of Ln on solute concentration profile

Full size image
Fig. 22
figure 22

Influence of M on solute concentration profile

Full size image
Fig. 23
figure 23

Influence of Sr on solute concentration profile

Full size image

Influence of various parameters on rate of heat of transfer is presented in Figs. 24, 25, 26 and 27. Since increase in advective transport rate leads to rise in rate of heat transfer, an increasing and converging effect of bioconvection Peclet number in the presence of bioconvection Lewis number on Nusselt number is shown in Fig. 24. With nanofluid Lewis number (Ln), the influence of Soret number (Sr) on Nusselt number is shown in Fig. 25. It has been observed that near the wall the rate of heat transfer is greater. Also with increased Soret number we obtained rise in Nusselt number. Figure 26 depicted that Nusselt number decreases for incremental values of buoyancy ratio parameter (Nr). Actually, increase in Nr along with nanofluid Lewis number (Ln) helps in reducing the thermal boundary layer which in turn decreases the rate of heat transfer near the wall. Figure 27 recorded that for increasing values of bioconvection Rayleigh number (Rb) in the presence of bioconvection Lewis number (Lb), a decrease in Nusselt number in converging manner is observed.

Fig. 24
figure 24

Effect of Pe with Lb on Nusselt number

Full size image
Fig. 25
figure 25

Effect of Sr with Ln on Nusselt number

Full size image
Fig. 26
figure 26

Effect of Nr with Ln on Nusselt number

Full size image
Fig. 27
figure 27

Effect of Rb with Lb on Nusselt number

Full size image

Analysis of rate of mass transfer is recorded through Figs. 28, 29, 30, 31 and 32 under variation of different parameters. In Figs. 28 and 29, an increase in Sherwood number is presented by taking higher values of bioconvection Peclet number (Pe) with bioconvection Lewis number (Lb) and incremental values of Brownian motion parameter (Nb) with thermophoresis parameter (Nt). As for higher Pe, we mean increase in convected thermal energy, which in return increases the rate of mass transfer. Also increase in Brownian motion parameter tends to increase in collision which results in increased Sherwood number. Figures 30 and 31 represent decrease in Sherwood number due to various incremental values of buoyancy ratio parameter (Nr) and Soret number (Sr). Since solute diffusion faces resistance due to higher values of Soret number and in return decreases rate of mass transfer as shown. From Fig. 31, it is recorded that for the interval 0 ≤ η ≤ 0.4, a little rise in Sherwood number has been observed for increasing values of buoyancy ratio parameter with nanofluid Lewis number whereas, after η > 0.4, it decreases.

Fig. 28
figure 28

Effect of Pe with Lb on Sherwood number

Full size image
Fig. 29
figure 29

Effect of Nb with Nt on Sherwood number

Full size image
Fig. 30
figure 30

Effect of Pe with Lb on Sherwood number

Full size image
Fig. 31
figure 31

Effect of Sr with Ln on Sherwood number

Full size image
Fig. 32
figure 32

Effect of Pe with Lb on density number of motile microorganism

Full size image

Influence of various parameters on local density number of motile microorganisms is presented in Figs. 32, 33 and 34. It is known that dependency of density of microorganisms is on the concentration of nanoparticles. From Fig. 32, we have observed that for different incremental values of bioconvection Peclet number (Pe), the density number of gyrotactic microorganisms increases with bioconvection Lewis number due to higher convected thermal energy. Figure 33 reveals that by increasing the bioconvection Rayleigh number in the presence of bioconvection Lewis number the density number of motile microorganisms decreases. A strong buoyancy force in the presence of nanofluid Lewis number leads to decrease in density number of microorganisms as shown in Fig. 34.

Fig. 33
figure 33

Effect of Rb with Lb on density number of motile microorganism

Full size image
Fig. 34
figure 34

Effect of Nr with Ln on density number of motile microorganism

Full size image

5 Conclusion

By considering the wall jet flow of bioconvection gyrotactic microorganisms through incompressible nanofluid under the influence of MHD applied normal to the flow, we have investigated the effects of various parameters on velocity, temperature and concentration profiles. To solve numerically, the governing equations along with appropriate boundary conditions are reduced to ordinary differential equations by utilizing similarity transformation. A graphical representation is used to get more realistic picture of the problem. Following conclusions have been drawn:

  1. 1.

    Regular double-diffusive buoyancy parameter leads to higher solute volumetric expansion as compared to thermal volumetric expansion which results in increase in velocity distribution. Similarly, Hartmann number is used as controlling parameter to normalize the velocity profile.

  2. 2.

    The buoyancy ratio parameter produces retardation in velocity of the flow which in return decreases the momentum boundary layer thickness.

  3. 3.

    Increase in temperature distribution is recorded for incremental values of thermophoresis parameter, Brownian motion parameter and buoyancy ratio parameter. In all of the cases, a rapid collision between the molecules increases the kinetic energy which in return increases the overall temperature distribution and thermal boundary layer thickness.

  4. 4.

    It has been observed that nanoparticles volume fraction decreases for higher value of Lewis number, Brownian motion parameter and Soret number, whereas it increases by considering different incremental values of buoyancy ratio parameter and thermophoresis parameter.

  5. 5.

    For higher values of buoyancy ratio parameter, within the interval 0 ≤ η ≤ 0.7 and η > 3.2, a negligible increase in nanoparticle concentration is obtained, whereas for 0.7 < η ≤ 3.2 a remarkable increase is represented

  6. 6.

    Due to high diffusion rate for increasing value of bioconvection Lewis number, the surface velocity reduces which tends toward decline in the microorganism’s concentration layer thickness. Also we have recorded that for higher values of Brownian motion parameter, the density of microorganisms reduces due to rapid collision of molecules.

  7. 7.

    Decreasing impact of Soret number is observed on density of the motile microorganism. Higher values of thermophoresis parameter help to increase the concentration profile of motile microorganisms.

  8. 8.

    For Ln = 1, we have observed a rapid increase in solute concentration for interval 0 ≤ η ≤ 1.2 and then gradual decrease. Also effect of Soret number decreases the temperature gradient which helps in enhancing the solute concentration boundary layer thickness.

  9. 9.

    Nusselt number rises due to increase in bioconvection Peclet number in the presence of bioconvection Lewis number. With nanofluid Lewis number, the influence of Soret number is observed greater near the wall on Nusselt number. Also for increasing values of bioconvection Rayleigh number in the presence of bioconvection Lewis number, a decrease in Nusselt number in converging manner is observed.

  10. 10.

    Since solute diffusion faces resistance due to higher values of Soret number and in return decreases rate of mass transfer. It is recorded that for the interval 0 ≤ η ≤ 0.4, a little rise in Sherwood number has been observed for increasing values of buoyancy ratio parameter with nanofluid Lewis number, whereas after η > 0.4, it decreases.

  11. 11.

    We have observed that for different incremental values of bioconvection Peclet number (Pe), the density number of gyrotactic microorganisms increases with bioconvection Lewis number due to higher convected thermal energy. A strong buoyancy force in the presence of nanofluid Lewis number leads to decrease in density number of microorganisms.