Introduction

In recent days, the development of the computer age, communication, household appliances, heavy mechanical industries, transportation and the electronics industries have all been running due to some electronics and mechanical devices. To prevent overheating all these devices, a system of cooling or heating is built in which fluid flows over or around the device at a certain temperature threshold.

The improvement in the thermal conductivity of conventional fluids is imperative because many mechanical and electronic devices have retarded their efficiency and working age, as conventional fluids with low thermal conductivity do not occur at the temperature essential. Non-Newtonian fluids have the devotion of engineers and scientists due to their vast applications in the fields of manufacturing, technology and energy. Regular examples of such fluids are fiber technology, rubber sheet manufacturing, plastic, wall paint, polymer processes, lubricants, enhanced oil recovery, plastic, shampoo, greases, blood, mud, food production, toothpaste, ketchup, and drilling. Nanofluid is one of the most important types of non-Newtonian fluids. Nanofluids are the suspension of nanomaterial’s (e.g., nanoparticles, nanosheets, nanofibers, nanotubes, nanowires, nanorods, or droplets) in base fluids.

In the modern era, nanofluids are the center of attention for many researchers due to their wide range of applications. Suspension of nanoparticles in conventional fluids is termed nanofluids, where nanoparticles include metallic and nonmetallic particles of nanosize. For the very first time, Choi [1] introduced the concept of nanofluids. A thin suspension of nanoparticles and base fluids makes nanofluids. Buongiorno [2] developed the numerical study of nanofluids that measure Brownian motion as well as thermophoresis features. Khan and Pop [3] presented a numerical study for nanofluid flow with effects of thermophoresis and Brownian motion via a linearly extending plate. Tiwari and Das [4] studied the mathematical model, which is very important to observe a strong volume fraction of nanomaterials in the regular fluid. Arifin et al. [5] inspected the dynamics of flow suction as well as joule heating and the thermal features of the hybrid (copper and aluminum oxide) nanofluid due to the parallel shrinking and stretching of the film with the combined influence of electrical conducting fluids. Shafiq et al. [6] discussed the flow properties of third-class non-Newtonian nanoliquid over a vertically extending disk. Micro-polar hybrid nanofluid with the impact of slip conditions across the Riga channel has been scrutinized by [7].

An analysis of bioconvection for nanofluid flow in an acoustically dominated source has been investigated by Mansour et al. [8]. Kolsi et al. [9] deliberated the utilization of nanoliquid on a cuboidal surface in occurrence of magnetic flux. The effect of flow rate and buoyancy force with such mass flow features over Sisko nanofluid owing to stretched surfaces in the presence of porous channels has been discovered by Sharma et al. [10].

Due to the various applications of fluid flow over stretching sheets in metallurgy and plastic engineering, it has become a center of research. Crane [11] was the first to deliberate the momentum boundary layer of a linearly extending sheet. Later on, many investigators studied and explored the idea of a stretching sheet [12,13,14,15,16,17,18,19,20,21]. Recently, [22] analyzed the influence of variable viscosity and second-order slip flow on hybrid nanofluids over the porous extending sheet.

The study of magnetohydrodynamics MHD flow plays various roles in different industrial and engineering applications. In industrial applications, the most important roles are liquid metal fluid, metal turning, glass blowing, aerodynamics, and cooling in nuclear plants. In engineering applications used in metal spinning and polymer extrusion, drawing plastic film, paper production and producing cooling when a product is manufacturing. The electrical conducting flow of nanofluids, along with thermophoresis by HAM is studied by [23]. Hayat et al. [24], with the assistance of HAM, inspected the electrical MHD flow of nanofluids due to an extending plate along with buoyancy forces in the occurrence of a magnetic field. Khan et al. [25] examined the magnetohydrodynamics of incompressible flow through a rotating disk using coupled stress fluid. Hayat et al. [26] discovered the magnetohydrodynamic (MHD) consequences of squeezing flow in Jeffery nanofluid.

By witness of above survey of literature current analysis are not preform yet, our attention is to evaluate the magnetohydrodynamic MHD magnetized transport of nanofluid flow with the swimming of gyrotactic microorganisms and variable viscosity due to vertical stretching sheet. The influence of convective boundary conditions along with gravitational body forces is also a segment of this study. The literature survey reveals that such analyses have not been performed yet. The consideration of non-Newtonian viscous nanofluids, swimming motile microorganisms, and the impact of variable viscosity made this analysis quite motivating. The associated boundary value problem is solved numerically by using the shooting technique after converting it into a first-order initial value problem. The physical features of effective parameters are graphically underlined and discussed for involved profiles.

Mathematical Analysis

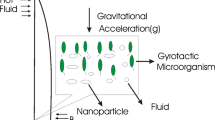
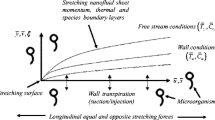
A steady MHD transport of nanofluid toward a stretching sheet with variable viscosity and convective boundary conditions has been under consideration. The theory of microorganisms is used through bioconvection to alleviate the suspended nanoparticles under the influence of buoyancy forces where it is taken as a coordinate system. A magnetic field of strength is induced in the fluid, and it is assumed that the sheet is stretching along the x-direction. In the presence of gravitational body forces, the corresponding governing equations for nanofluid can be described as [27,28,29,30,31] (see Fig. 1).

Fig. 1
figure 1

Geometry of problem

Full size image

The equation of Mass Conservation

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(1)

Equation of Velocity

$$\rho \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = \frac{\partial }{\partial y}\left[ {\mu \left( T \right)\left( {\frac{\partial u}{{\partial y}}} \right)} \right] - \sigma B_{0}^{2} u + g\rho B_{T} \left( {T - T_{\infty } } \right) + \rho gB_{C} \left( {C - C_{\infty } } \right)$$
(2)

Equation of Temperature

$$\rho c_{P} \left( {u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right) = \alpha \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \tau \left\{ {\frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} + D_{B} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}}} \right\}$$
(3)

Equation of Concentration

$$u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }}$$
(4)

Equation of Density of Microorganism

$$u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} + \left[ {\frac{{bW_{c} }}{{C_{W} - C_{\infty } }}} \right]\left( {\frac{\partial N}{{\partial y}}\frac{\partial C}{{\partial y}} + N\frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) = D_{n} \frac{{\partial^{2} N}}{{\partial y^{2} }}$$
(5)

where \(u\) and \(v\) are velocity constituents along \(x-axis\) and \(y-axis,\) respectively, and \({B}_{0}\) represents the strength magnetic field, while \(N\), \(T,\) and \(C\) are density, energy, and concentration of nanofluid, respectively. Equations (2)–(5) are subjected to:

for \(y=0\), \(u={u}_{w}\left(x\right)=bx\), \(v=0\),

$$k_{f} \frac{\partial T}{{\partial y}}h_{f} \left( {T - T_{f} } \right),\;C = C_{w} \;and\;T = T_{w}$$
(6)
$$as\;y \to \infty ,\;u, v \to 0,\;T \to T_{\infty } ,\;C \to C_{\infty } \;and\;N \to N_{\infty }$$
(7)

The similarity transformation and dimensionless variables are described as

$$\psi = (b\nu )^{\frac{1}{2}} xf(\eta ),\; u = bxf^{\prime } (\eta ),\;and\;\eta = \left( {\frac{a}{\nu }} \right)^{\frac{1}{2}} y,\;v = \sqrt {b\upsilon } f(\eta ),\;and$$
(8)
$$\left( {T_{w} - T_{\infty } } \right)\theta (\eta ) = T - T_{\infty } , \;\left( {C_{w} - C_{\infty } } \right) \phi (\eta ) = C - C_{\infty } ,\;\left( {N_{w} - N_{\infty } } \right) \chi (\eta ) = N - N_{\infty } ,$$
(9)

where \(\psi\) is the stream function and \(\eta\) is the similarity variable defined as \(u = \frac{\partial \psi }{{\partial y}}\) and \(v = - \frac{\partial \psi }{{\partial x}},\) which directly satisfies the equation of mass conservation. The viscosity of fluid in momentum equation is temperature-dependent that may vary exponentially [35].

$$\mu \left( T \right) = \mu_{0} e^{{ - H\left( {T - T_{\infty } } \right)}}$$
(10)

where \({\mu }_{0}\) represents the fluid viscosity at \({T}_{\infty }\). The strength dependency between \(\mu \left(T\right)\) and \(T\) are depicted by \(H.\) Utilizing the similarity variables illustrated in Eqs. (8 and 9) and then applying the Maclaurin’s expansion, we obtained the succeeding illustration [32]

$$e^{ - \lambda \theta } = 1 - \lambda \theta + O\left( {\lambda^{2} } \right)$$
(11)

Now, by using the similarity function given in Eqs. (8–9), the subsequent dimensionless coupled equations has been accomplished

$$\begin{gathered} \left( {1 - \left( {\lambda \theta } \right)} \right)f^{\prime \prime \prime } \left( \eta \right) - \lambda \theta^{\prime } \left( \eta \right)f^{\prime \prime } \left( \eta \right) + f\left( \eta \right)f^{\prime \prime } \left( \eta \right) \hfill \\ \;\;\;\;\;\;\;\;\; - f^{\prime 2} - Mf^{\prime } \left( \eta \right) + G_{r} \theta \left( \eta \right) + B_{r} \theta \left( \eta \right) = 0 \hfill \\ \end{gathered}$$
(12)
$$\theta^{\prime \prime } \left( \eta \right) + Prf\left( \eta \right)\theta^{\prime } \left( \eta \right) + Pr\left( {Nb} \right)\theta^{\prime } \left( \eta \right)\phi^{\prime } \left( \eta \right) + Pr(Nt)\theta^{\prime 2} \left( \eta \right) = 0$$
(13)
$$\phi^{^{\prime\prime}(\eta )} + Scf\left( \eta \right)\phi^{^{\prime}(\eta )} + \left( {\frac{Nt}{{Nb}}} \right)\theta^{^{\prime\prime}} \left( \eta \right) = 0$$
(14)
$$\chi^{\prime \prime } \left( \eta \right) + Lbf\left( \eta \right)\chi^{\prime } \left( \eta \right) - Pe\left( {\phi^{\prime \prime } \left( {\chi + \delta } \right) + \chi^{\prime } \left( \eta \right)\phi^{\prime } \left( \eta \right)} \right)$$
(15)

where \(M=\frac{{{B}^{2}}_{0}\sigma }{b\rho }\) is Harman number, \(\lambda =H({T}_{w}-{T}_{\infty })\) is the variable viscosity, \(Pr=\frac{\upsilon }{\alpha }\) is the Prandal number, \({R}_{ex}=\frac{{u}_{w}(x)x}{\upsilon }\) is local Reynoled number, \(\delta =\frac{{N}_{\infty }}{{N}_{w}-{N}_{\infty }}\) is swimming microorganism intensity variation parameter, \(Nt=\frac{\tau \rho {D}_{T}({T}_{w}-{T}_{\infty })}{{\mu }_{0}{T}_{\infty }}\) is thermophoresis parameter, \(Lb=\frac{\upsilon }{{D}_{n}}\) is bioconvection lewis number, \({B}_{T}=\frac{g\rho {B}_{T}({C}_{w}-{C}_{\infty }){X}^{3}}{{\upsilon }^{2}}\) is local concentration Grashof number, \(Nb=\frac{\tau \rho {D}_{B}({C}_{w}-{C}_{\infty })}{{\mu }_{0}}\) is Brownian motion parameter, \(Sc=PrLe\) is Schmidt number, \(Gr=\frac{{G}_{T}}{{{R}^{2}}_{ex}}\) and \(Br=\frac{{B}_{T}}{{{R}^{2}}_{ex}}\) are concentration and thermal Grashof numbers, \(Pe=\frac{bWc}{{D}_{n}}\) is Peclet number, and \({G}_{T}=\frac{g\rho {B}_{T}({T}_{w}-{T}_{\infty }){X}^{3}}{{\upsilon }^{2}}\) is local thermal Grashof number.

The auxiliary conditions in dimensionless form are:

$$At\;\eta = 0,\;f\left( \eta \right) = 0, \;\chi \left( \eta \right) = 1, \;\theta^{\prime } \left( \eta \right) = - B_{i} \left( {1 - \theta \left( \eta \right)} \right),\; f^{\prime } \left( \eta \right) = 0,\;\phi \left( \eta \right) = 1$$
(16)
$$as\;y \to \infty ,\;\phi \left( \eta \right) = \chi \left( \eta \right) = \theta \left( \eta \right) = 0, \; f^{\prime } \left( \eta \right) = 0$$
(17)

Physical quintiles of interest, like microorganism density number, local Sherwood number, local Nusselt number, and skin fraction coefficient, are defined as:

$$C_{f} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }},\;Nu_{x} = \frac{{xq_{w} }}{{k(T_{w} - T_{\infty } )}},\;Sh_{x} = \frac{{xq_{m} }}{{D_{B} (C_{w} - C_{\infty } )}},\;Nn_{x} = \frac{{xq_{m} }}{{D_{n} (N_{w} - N_{\infty } )}}$$
(18)

where

$$\tau_{w} = \mu \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0} ,\;q_{w} = - k\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} ,\;q_{m} = D_{B} \left( {\frac{\partial C}{{\partial y}}} \right)_{y = 0} ,\;q_{n} = - D_{n} \left( {\frac{\partial N}{{\partial y}}} \right)_{y = 0}$$
(19)

So dimensionless form becomes as

$$C_{f} {\text{Re}}_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = (1 - \lambda \theta (0))f^{\prime \prime } (0),\;Nu_{x} {\text{Re}}_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \theta^{\prime}(0),\;Sh_{x} {\text{Re}}_{x}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \phi^{\prime } (0),\;Nn_{x} {\text{Re}}_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = - \chi^{\prime}(0)$$
(20)

Numerical Technique

In daily life, many mathematical models of equations are highly nonlinear differential equations. We know that exact solutions to extremely nonlinear differential equations are not usually possible. In cases of boundary value problems, the shooting method is one of the best and most well-known schemes among all other methods. This procedure is straightforward, sensitive and free from error or complexity. First of all, convert the modeled ODEs into first-order form. Computational software Mathematica is engaged to solve these equation numerically. The steps of shooting method is given below:

Let us use \(f\) by \(y_{1}\), \(\theta\) by \(y_{4}\), \(\phi\) by \(y_{6}\), and \(\chi\) by \(y_{8}\). The subsequent equations are:

$$\left. \begin{gathered} y_{1}^{\prime } = y_{2} \hfill \\ y_{2}^{\prime } = y_{3} \hfill \\ y_{3}^{\prime } = \frac{1}{{1 - \lambda y_{4} }}\left( {y_{2} y_{2} - y_{1} y_{3} + My_{2} - G_{T} y_{4} - B_{r} y_{4} + \lambda y_{5} y_{3} } \right) \hfill \\ y_{4}^{\prime } = y_{5} \hfill \\ y_{5}^{\prime } = - \Pr \left( {y_{1} y_{5} + Nt\left( {y_{5} y_{5} } \right) + Nb(y_{5} y_{6} )} \right) \hfill \\ y_{6}^{\prime } = y_{7} \hfill \\ y_{7}^{\prime } = - \left( {Ley_{1} y_{7} + \left( {Nt/Nb} \right)y_{5}^{\prime } } \right) - Le\gamma y_{6} \hfill \\ y_{8}^{\prime } = y_{9} \hfill \\ y_{9}^{\prime } = Pe\left( {y_{8} y_{7} + y_{7}^{\prime } \left( {y_{9} + \delta } \right)} \right) - Sc\left( {y_{1} y_{9} } \right) \hfill \\ \end{gathered} \right|$$
(21)

Results and Discussions

This section is equipped to explore the act of non-dimensional velocity profile\(f{\prime}(\eta )\), energy profile\(\theta (\eta )\), nanofluid concentration profile \(\phi (\eta )\) and density \(\chi (\eta )\) under the influence of several prominent parameters like Peclet number\(Pe\), the variable viscosity\(\lambda\), Prandtl number\(Pr\), swimming microorganism intensity variation parameter\(\delta\), thermophoresis parameter\(Nt\), bioconvection Lewis number\(Lb\), Brownian motion parameters\(Nb\), Schmidt number\(Sc\), concentration Grashof number\(Gr\), thermal Grashof numbers \(Br,\) and Harman number \(M.\) Figures 3 and 4 are demonstrated to investigate the effect of Hartman number \(M\) on the velocity profile \(f^{\prime}\left( \eta \right)\) and temperature profile \(\theta \left( \eta \right)\). Figure 2 depicts that the supplementing values of \(M\) causes retardation in the velocity profile. Temperature enhanced by increasing values of \(M\) (see Fig. 3). Hartman number includes Lorentz forces that are resistive forces. When M increased, the Lorentz force also increased, which led to a decrease in liquid flow velocity and an increase in temperature. Figure 4 shows that the increment in \(Gr\) increases the fluid speed \(f^{\prime } \left( \eta \right)\); it is due to occurrence of buoyancy forces. A inverse relation between \(Gr\) and \(\theta \left(\eta \right)\) is obtained by Fig. 5, and an increment in values of \(Gr\) decreases the curve of\(\theta \left(\eta \right)\). A straight relation between \(Br\) and \(f^{\prime}\left( \eta \right)\) is obtained by Fig. 6, and an increment in values of \(Br\) as a result increases the curve of velocity component \(f^{\prime}\left( \eta \right).\) Figure 7 show that the increment in \(Br\) decreases the fluid temperature\(\theta \left(\eta \right)\). Figure 8 designates the distinction of \(Bi\) on fluid temperature field \(\theta \left( \eta \right)\). The improvement in Biot number \(Bi\) results in much convective heat transfer and concentration rate. The dimensionless metric Biot number, which is linked to the coefficient of heat transfer, improves the temperature distribution of nanoparticles. Figure 9 shows how the Prandtl number affects the temperature field. Nanoparticle temperatures decrease as \(Pr\) is improved. Prandtl number is defined as the relationship between a fluid’s thermal conductivity and thermal diffusivity. Therefore, the maximum thermal diffusivity results from the smallest Prandtl number, while the temperature and thickness of the boundary layer are reduced. Figures 10 and 11 elucidate the impact of thermophoresis parameter \(Nt\) on non-dimensional energy \(\theta \left( \eta \right)\) field and volumetric concentration profile \(\phi \left( \eta \right)\). These figures depicts that temperature field and volumetric concentration filed are the accumulative functions of \(Nt\) for some rising values of thermophoresis parameter. The increasing value of \(Nt\) results to raise the thermal conductivity of liquid. Tiny fluid particles are moved from a hot surface to a cool one during thermophoresis. The temperature rises as a result of the many microscopic particles leaving the hot surface, and this high temperature indicates an increase in the concentration. When a small change occurs, the concentration profile falls off and rises more quickly. The portrayal for implication of Brownian motion parameter \(Nb\) on temperature field of nanoparticles is explored in Fig. 12. By enhancing the parameter \(Nb\) energy profile improved. Usually, this Brownian parameter \(Nb\) exists because of the participation of nanoparticles. The impact of Schmidt number \(Sc\) on concentration and density profile is shown in Figs. 13 and 14. The curve of concentration distribution as well as density field is decreased as value of \(Sc\) increased. The microorganism profile under the influence of the bioconvection Lewis number is examined in Fig. 15. As the Lewis number rises, the density profile’s inhibiting behavior is seen. The weak diffusivity of microorganisms is what is causing the density profile to behave slowly. Because of the strengthening that occurs as a result of the weaker diffusivity, the density profile is delayed. Figure 16 represents the effects of parameter \(\delta\) called microorganism concentration difference on density profile \(\chi \left( \eta \right)\). By enhancing, the values of \(\delta\) density profile retarded. From Fig. 17, it is demonstrated that within the increment in bioconvection Peclet number \(Pe\), the density \(\chi \left( \eta \right)\) is retarded. Here, the extreme rapidity of cell swimming is enriched by increasing the value of \(Pe\). This advanced rapidity of cell swimming is accountable in the lesser performance of \(\chi \left( \eta \right)\). Comparison of current study with published work is given in Table 1.

Fig. 2
figure 2

Effects of Harman number \(M\) over \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Effects of Harman number \(M\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 4
figure 4

Effects of thermal Grashof number \(Gr\) over \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 5
figure 5

Effects of thermal Grashof number \(Gr\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 6
figure 6

Effects of concentration Grashof number \(Br\) over \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 7
figure 7

Effects of concentration Grashof number \(Br\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 8
figure 8

Effects of Biot number \(Bi\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 9
figure 9

Effects of Prandtl number \(Pr\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 10
figure 10

Effects of thermophoresis parameter \(Nt\) over \(\theta \left( \eta \right)\)

Full size image
Fig. 11
figure 11

Effects of thermophoresis parameter \(Nt\) over \(\phi \left( \eta \right)\)

Full size image
Fig. 12
figure 12

Effects of \(Nb\) over \(\phi \left( \eta \right)\)

Full size image
Fig. 13
figure 13

Effects of Schmidt number \(Sc\) over \(\phi \left( \eta \right)\)

Full size image
Fig. 14
figure 14

Effects of \(Sc\) over \(\chi \left( \eta \right)\)

Full size image
Fig. 15
figure 15

Effects of bioconvection Lewis number \(Lb\) over \(\chi \left( \eta \right)\)

Full size image
Fig. 16
figure 16

Effects of swimming microorganism intensity variation parameter \(\delta\) over \(\chi \left( \eta \right)\)

Full size image
Fig. 17
figure 17

Effects of Peclet number \(Pe\) over \(\chi \left( \eta \right)\)

Full size image
Table 1 Comparison table for different values concentration Grashof number \(Br\), thermal Grashof number \(Gr\), and variable viscosity parameter \(\lambda\) on \(- f^{\prime\prime}(0)\), \(- \theta^{\prime}(0)\), \(- \phi^{\prime}(0).\)
Full size table

Conclusion

Time-independent electrical magnetohydrodynamics nanofluid flow over a vertical stretching surface has been investigated. In addition, the influence of convective boundary condition along with gravitational body forces is considered. The core features of the current investigation are enumerated below:

  • A decreasing act is observed in the velocity function with an increase in the value of \(M\) but enhanced by growing the value of \(Br\) and \(Gr\).

  • The temperature field improved by exaggerating the value of thermophoresis parameter \(Nt\), biot number \(Bi,\) and Brownian motion \(Nb\) deteriorating behavior was observed in the energy distribution as boosted up in the value of \(Pr.\)

  • Concentration profile is decreased for rising value of Brownian motion Nb.

  • The volumetric concentration profile increased as the Brownian motion \(Nt\) value was magnified, but the Schmidt number \(Sc\) exhibited the reverse tendency.

  • The density of gyrotactic motile microorganisms steadily decreases as the Peclet number \(Pe\), Lewis number, and the value of the bioconvection increase.

Reader may read the following interested articles [33,34,35,36,37,38,39,40].

Future Recommendations

In the future, this problem may be extended in many directions, considering the following ideas:

  • The impact of Joule heating.

  • The impact of viscous dissipation.

  • The impact of different nanoparticles.

  • The impact of source and sink.