Local Attractors of Newton-Type Methods for Constrained Equations and Complementarity Problems with Nonisolated Solutions

Abstract

For constrained equations with nonisolated solutions, we show that if the equation mapping is 2-regular at a given solution with respect to a direction in the null space of the Jacobian, and this direction is interior feasible, then there is an associated domain of starting points from which a family of Newton-type methods is well defined and necessarily converges to this specific solution (despite degeneracy, and despite that there are other solutions nearby). We note that unlike the common settings of convergence analyses, our assumptions subsume that a local Lipschitzian error bound does not hold for the solution in question. Our results apply to constrained and projected variants of the Gauss–Newton, Levenberg–Marquardt, and LP-Newton methods. Applications to smooth and piecewise smooth reformulations of complementarity problems are also discussed.

1 Introduction

In this paper, we analyze the local behavior of several Newton-type methods applied to a constrained system of equations. The mapping which defines this system is assumed to be smooth or at least piecewise smooth. The constraints define a closed convex set with nonempty interior. Note that the latter is not that restrictive, as in many applications that lead to constrained equations the constraints are given by simple bounds, or the problem can be reduced to such a setting; see [1, 2].

We are mostly interested in those cases when a given solution of the constrained system might be singular. In the smooth case this means that, at this solution, the Jacobian of the equation mapping is a singular matrix. We are even more interested in the situation when the given solution is not isolated in the solution set of the constrained system, in which case it is necessarily singular. Nevertheless, as we shall show under some reasonable assumptions, a number of Newton-type methods have large domains of starting points from which the iteration sequences are well defined and, moreover, are attracted to that specific given solution. We emphasize that the iterates converge linearly to this solution, despite that there exist other solutions nearby (perhaps even closer to the given starting point). We explain this behavior by the 2-regularity property of the equation mapping, and the resulting lack of the local Lipschitzian error bound near the solution in question. This phenomenon appears related (in part) to critical Lagrange multipliers serving as attractors for optimization algorithms (see [3,4,5, Chapter 7]) and, even more closely, to the corresponding notion of criticality for unconstrained equations [6] and the effect of attraction for Newton-type methods in that setting [7].

Our main result in Sect. 3 shows that if the equation mapping is 2-regular at a given solution with respect to an interior feasible direction which is in the null space of the Jacobian, then there is an associated domain of starting points from which the Newton-type methods in consideration are well defined and converge (to this specific solution). This result can be applied to a variety of Newton-type methods by regarding them as particular perturbations of Newton’s method. Among those Newton-type methods, we particularly consider constrained and projected versions of the Gauss–Newton method and of the Levenberg–Marquardt [8] method, as well as the LP-Newton method [1] and its projected variant. Based on our main result, we derive convergence properties of these methods if applied to piecewise smooth and smooth reformulations of complementarity problems.

The paper is organized as follows. In Sect. 2, we describe the various Newton-type methods under consideration, and briefly review existing convergence results. Moreover, we detail the 2-regularity assumption and some important implications. Section 3 provides our main result as well as illustrations by examples. In Sect. 4, we analyze several Newton-type methods for the case when the equation mapping is associated to complementarity problems and again illustrate the results by examples. Finally, in Sect. 5 we discuss some open questions related to the results obtained.

2 Preliminaries

For a given smooth or at least piecewise smooth mapping $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ and a given closed convex set $P\subset \mathbb {R}^p$ with nonempty interior $\mathrm{int}P$, we consider the constrained equation

$$\begin{aligned} \varPhi (u)=0,\quad u\in P. \end{aligned}$$

(1)

The solution set of (1) is denoted by $\mathcal{S}:=\varPhi ^{-1}(0)\cap P$.

The purpose of this section is threefold. Section 2.1 describes several Newton-type methods for problem (1) whose local convergence can be analyzed by the main result in Sect. 3. For these methods, we also review existing results on local convergence. Section 2.2 will provide some details for the 2-regularity assumption on which our results are based. Finally, most of our notation will be introduced in this section and at the end of Sect. 2.2.

2.1 Newton-Type Methods

Given a current iterate $u^k\in P$, the algorithms considered in this work compute the direction of change $v^k$ as a solution of some Newtonian subproblem and set the next iterate to be $u^{k+1}:=u^k+v^k$. We note that unlike in the unconstrained case ($P=\mathbb {R}^n$), in the current setting of constrained equations it is not quite evident what should be regarded as the basic Newtonian subproblem. Assuming that $\varPhi$ is smooth, one natural possibility is to consider the least-squares solutions of the linearized constrained equation:

$$\begin{aligned} \begin{array}{llll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert ^2&\quad \text{ s.t. }&u^k+v\in P, \end{array} \end{aligned}$$

(2)

what we may call constrained Gauss–Newton method. The objective function of this subproblem is convex quadratic, and if P is polyhedral, (2) always has a solution, due to the Frank-Wolfe theorem [9, Theorem 2.8.1]. Obviously, a solution of this subproblem need not be unique.

Another natural possibility is to consider solving the basic unconstrained Newton equation

$$\begin{aligned} \varPhi (u^k)+\varPhi '(u^k)v = 0 \end{aligned}$$

(3)

for $v_N^k$, and then define $u^{k+1}$ as the projection of $u^k+v_N^k$ onto P. This scheme can be called the projected Newton method. Of course, neither existence nor uniqueness of solutions of (3) can be guaranteed without further assumptions, especially when $u^k$ is close to a singular solution. That said, below we shall provide assumptions on the problem data and on starting points which ensure that along the sequences generated by the methods to be considered, there always exists the unique solution $v^k$ of the unconstrained Newton equation (3), and moreover, it always gives feasible iterates, i.e., $u^k+v^k\in P$. Therefore, and somewhat surprisingly, the peculiarities of the constrained setting will actually play no role in those situations. Our goal is precisely to demonstrate that this is indeed the case: both the constrained Gauss–Newton method and the projected Newton method work in these circumstances exactly as the Newton method for the unconstrained equation

$$\begin{aligned} \varPhi (u)=0, \end{aligned}$$

(4)

and hence, they inherit its behavior near possibly nonisolated solutions, which has been studied in [10, 11].

Furthermore, as we are especially interested in the cases of potentially nonisolated solutions, and following the recent development in [7] for the unconstrained case, it is natural to consider some stabilized versions of the Gauss–Newton method. In the constrained Levenberg–Marquardt method [8, 12, 13], the following subproblems are solved:

$$\begin{aligned} \begin{array}{llll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+\varPhi '(u^k)v \Vert ^2 +\frac{1}{2} \sigma (u^k)\Vert v\Vert ^2&\quad \text{ s.t. }&u^k+v\in P, \end{array} \end{aligned}$$

(5)

where $\sigma :\mathbb {R}^p\rightarrow \mathbb {R}_+$ defines the regularization parameter. If $\sigma (u^k)>0$, the objective function of this subproblem is strongly convex quadratic and, hence, the subproblem has the unique solution.

Another possible alternative is the recently proposed LP-Newton method [1]. The subproblems of this method have the form

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert v \Vert \le \gamma \Vert \varPhi (u^k)\Vert ,\\ &{}u^k+v\in P, \end{array} \end{aligned}$$

(6)

with respect to $(v,\, \gamma )\in \mathbb {R}^p\times \mathbb {R}$. If P is a polyhedral set, and the $l_\infty$-norm is used, then this is a linear programming problem (hence the name).

Along with constrained versions of the methods in question, one can also consider their projected variants. The projected Levenberg–Marquardt method has been proposed in [8]; its iteration consists of finding the solution $v_{LM}^k$ of the unconstrained subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+\varPhi '(u^k)v \Vert ^2 +\frac{1}{2} \sigma (u^k)\Vert v\Vert ^2, \end{array} \end{aligned}$$

(7)

and then defining the next iterate $u^{k+1}$ as the projection of $u^k+v_{LM}^k$ onto P. Note that (7) amounts to solving the linear equation

$$\begin{aligned} \varPhi '(u^k)^{\top }\varPhi (u^k)+(\varPhi '(u^k)^{\top }\varPhi '(u^k)+\sigma (u^k)I)v = 0, \end{aligned}$$

where I is the identity matrix.

Taking $\sigma (u^k):=0$, computing a solution $v_{GN}^k$ of (7), and defining $u^{k+1}$ as the projection of $u^k+v_{GN}^k$ onto P, leads to the projected Gauss–Newton method.

Similarly, one can consider the projected LP-Newton method generating $u^{k+1}$ as the projection of $u^k+v_{LPN}^k$ onto P, where $v_{LPN}^k$ with some $\gamma$ solves the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert v \Vert \le \gamma \Vert \varPhi (u^k)\Vert . \end{array} \end{aligned}$$

We next briefly survey previous convergence results for the methods outlined above. To that end, the following condition is relevant. We say that the constrained local Lipschitzian error bound holds at some solution $\bar{u}$ of (1), if

$$\begin{aligned} \mathrm{dist}(u,\, \mathcal{S})=O(\Vert \varPhi (u)\Vert ) \quad \text{ as } u\in P \text{ tends } \text{ to } \bar{u}. \end{aligned}$$

(8)

If (8) is satisfied, then both the constrained Levenberg–Marquardt method (5) (for $\sigma (\cdot )$ proportional to $\Vert \varPhi (\cdot )\Vert ^\beta$ with $\beta \in [1,\, 2]$) and the LP-Newton method (6) exhibit local quadratic convergence to some solution of (1); see [8, 14] and [1], respectively. For the projected version of the Newton method, convergence cannot be guaranteed under the error bound assumption (8) alone, since the subproblems (3) are not necessarily solvable in that case. Differently from this, the subproblems both of the constrained and of the projected Gauss–Newton methods always have a solution. However, even if we use only the uniquely defined minimum norm solutions of the subproblems, quadratic convergence of these methods can only be expected if a local Lipschitzian error bound stronger than (8) holds, and a condition on the local behavior of the singular values of $\varPhi '(u)$ is satisfied; see Theorem 4.1 in [15]. In addition, Example 4.5 in this thesis shows that the condition on the singular values is crucial for convergence.

As for the projected Levenberg–Marquardt method, quadratic convergence was established in [8], but only under an assumption which is much stronger than (8) and implies, in particular, that locally the solution set of the constrained equation (1) coincides with that of the unconstrained equation (4), see [16]. Moreover, it can be shown (see [17, Example 4]) that superlinear convergence requires more than the error bound (8). However, assuming (8), local R-linear convergence has been established in [18] for $\sigma (\cdot )$ proportional to $\Vert \varPhi (\cdot )\Vert$. To the best of our knowledge, local convergence properties of the projected LP-Newton method have not been studied previously.

In this paper, we are interested in the behavior of the methods described above near solutions violating the error bound (8). In this sense, our results complement those obtained assuming (8). Thus, a more complete understanding of properties of these methods is achieved. It turns out that solutions violating (8), when they exist, may have a strong impact on the behavior of the methods in question. In the unconstrained case, these questions have been recently addressed in [7]. Here, on the one hand, we extend the results from [7] to the constrained setting. On the other hand, Theorem 3.1 itself relies on the main result from [7].

2.2 The Assumption of 2-regularity

Let $\mathrm{im}\varLambda$ and $\ker \varLambda$ stand for the range space and the null space of a linear operator $\varLambda$, respectively. Assuming that $\varPhi$ is twice differentiable at $\bar{u}\in \mathbb {R}^p$, $\varPhi$ is said to be 2-regular at $\bar{u}$ in a direction $v\in \mathbb {R}^p$ if the $p\times p$-matrix $\varPhi '(\bar{u})+\varPi \varPhi ''(\bar{u})[v]$ is nonsingular, where $\varPi$ is the projector onto some complementary subspace L of $\mathrm{im}\varPhi '(\bar{u})$ parallel to $\mathrm{im}\varPhi '(\bar{u})$ (the latter means that $\varPi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ is a linear operator such that $\varPi ^2=\varPi$, $\mathrm{im}\varPi =L$, $\ker \varPi =\mathrm{im}\varPhi '(\bar{u})$). The concept of 2-regularity is useful in nonlinear analysis and optimization theory for a variety of reasons; see, e.g., the book [19] and references therein. It is easy to check that 2-regularity is invariant with respect to the choice of a complementary subspace L and to the length of $\Vert v\Vert$, so it is indeed a directional property. It is also easy to see that this property is further equivalent to saying that there exists no nonzero $u\in \ker \varPhi '(\bar{u})$ such that $\varPhi ''(\bar{u})[v,\, u]\in \mathrm{im}\varPhi '(\bar{u})$.

Theorem 3.1 and the main result of [7] require 2-regularity of $\varPhi$ at $\bar{u}$ in some nonzero direction $\bar{v}\in \ker \varPhi '(\bar{u})$. According to the discussion in [6] (see also [7, Proposition 1]), if $\varPhi '(\bar{u})$ is singular (in particular, if $\bar{u}$ is a nonisolated solution of (4)), the needed $\bar{v}$ can only exist if $\bar{u}$ is a critical solution of (4) as defined in [6]. More precisely, such $\bar{v}$ cannot belong to the contingent cone to $\varPhi ^{-1}(0)$ at $\bar{u}$ (the notion of the contingent cone we refer to is standard, but just for the sake of precision, see [5, p. 3]). Hence, this contingent cone must be a proper subset of $\ker \varPhi '(\bar{u})$. Observe that the latter holds automatically if $\bar{u}$ is a singular but isolated solution of the unconstrained equation (4), as in this case the contingent cone to $\varPhi ^{-1}(0)$ at $\bar{u}$ is trivial, while $\ker \varPhi '(\bar{u})$ is not. Criticality, in turn, is closely related to violation of the Lipschitzian error bound [6].

In Theorem 3.1, we shall assume that $\bar{v}$ belongs to $\ker \varPhi '(\bar{u})$ and also to the radial cone $R_P(\bar{u}):=\{v\in \mathbb {R}^p:\, \exists \, t>0 \text{ such } \text{ that } \bar{u}+tv\in P\}$ to P at $\bar{u}$. If the constrained error bound (8) holds, it evidently follows that any such $\bar{v}$ belongs to the contingent cone to $\mathcal S$, and hence, to the contingent cone to $\varPhi ^{-1}(0)$ at $\bar{u}$. This implies that the assumptions of Theorem 3.1 cannot hold if the error bound (8) does. At the same time, when (8) is violated, Theorem 3.1 can be applicable, and such applications will be discussed below. We note that nearby solutions satisfying (8) give rise to corresponding neighborhoods of convergence; however, these neighborhoods shrink as solutions tend to the one violating the error bound, and the exterior of these neighborhoods might form a large domain of attraction to this special solution. In the sequel, this will be illustrated by examples.

We conclude this subsection by introducing some further notation that will be used in what follows. All the norms are Euclidean, unless explicitly stated otherwise. By $B(u,\, \delta )$ we denote the ball centered at u and of radius $\delta$. The identity matrix is denoted by I, and the elements of the canonical basis by $e^i$. The spaces are always clear from the context. The notation |J| stands for the cardinality of the index set J. By $u_J$ we mean the sub-vector of u formed by the coordinates indexed by J, and by $A_J$ the matrix formed by the rows of the matrix A indexed by J. The notation $\mathrm{diag}z$ refers to the diagonal matrix with coordinates of the vector z on the diagonal.

3 Attraction of Newtonian Sequences to Special Solutions

For a given point $\bar{u}\in \mathbb {R}^p$, a given direction $\bar{v}\in \mathbb {R}^p$, and scalars $\varepsilon >0$ and $\delta >0$, we define the following set:

$$\begin{aligned} K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v}):=\left\{ u\in \mathbb {R}^p{\setminus } \{ \bar{u}\} : \Vert u-\bar{u}\Vert \le \varepsilon ,\; \left\| \frac{u-\bar{u}}{\Vert u-\bar{u}\Vert } -\bar{v}\right\| \le \delta \right\} . \end{aligned}$$

Note that $K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v})$ is a shifted conic neighborhood of the direction $\bar{v}$ intersected with a ball around $\bar{u}$.

The main result of this section relies on [7, Theorem 1], and the following fact, which establishes feasibility of the set defined above (with proper choices of parameters), when the direction $\bar{v}$ is interior feasible for the set P. We note that in Lemma 3.1 closedness of P is not needed; and this also applies to the statement of Theorem 3.1 further below.

Lemma 3.1

Assume that $\bar{v}\in \mathrm{int}R_P(\bar{u})$ for some $\bar{u}\in P$, $\Vert \bar{v}\Vert =1$. Then, there exist $\bar{\varepsilon } >0$ and $\bar{\delta } >0$ such that $K_{\bar{\varepsilon } ,\, \bar{\delta } }(\bar{u},\, \bar{v})\subset P$.

Proof

By assumption, there are nonzero vectors $v^1,\, \ldots ,\, v^r$ in $R_P(\bar{u})$ such that $\bar{v}\in \mathrm{int}K$, where K denotes the convex conic hull of $\{v^1,\,\ldots ,\,v^r\}$. Then, there evidently exists $t>0$ such that $\bar{u}+tv^i\in P$ for all $i\in \{ 1,\, \ldots ,\, r\}$.

Any element $v\in K$ can be written as $v=\sum _{i=1}^r\alpha _iv^i$ with some $\alpha _i\ge 0$, $i\in \{ 1,\, \ldots ,\, r\}$, which can be chosen in such a way that the vectors $v^i$ with $\alpha _i>0$ are linearly independent (see, e.g., [20, Corollary 17.1.2]). Since the number of linearly independent subsystems of $v^1,\, \ldots ,\, v^r$ is finite, it can be easily seen that there exists $c>0$ such that, for every $v\in K$, one can chose $\alpha _1\ge 0,\,\ldots ,\,\alpha _r\ge 0$ in such a way that $\alpha \le c\Vert v\Vert$ with $\alpha :=\sum _{i=1}^r\alpha _i$.

Therefore, assuming that $v\not =0$ (and hence, $\alpha >0$), we obtain that

$$\begin{aligned} \bar{u}+\frac{t}{\alpha } v = \bar{u}+\frac{t}{\alpha }\sum _{i=1}^r\alpha _iv^i = \sum _{i=1}^r\frac{\alpha _i}{\alpha }(\bar{u}+tv^i)\in P, \end{aligned}$$

where the inclusion is by the convexity of P. The latter further implies that

$$\begin{aligned} \bar{u}+\frac{tv}{c\Vert v\Vert } \in P, \end{aligned}$$

and hence, setting $\bar{\varepsilon } :=t/c$, we conclude that $\bar{u}+v\in P$ holds for all $v\in K$ with $\Vert v\Vert \le \bar{\varepsilon }$.

It remains to select $\bar{\delta } >0$ such that $B(\bar{v},\, \bar{\delta } )\subset K$, which is possible since $\bar{v}\in \mathrm{int}K$. With these choices, for any $u\in K_{\bar{\varepsilon } ,\, \bar{\delta } }(\bar{u},\, \bar{v})$ it holds that $v:=u-\bar{u}$ satisfies $v\in K$ and $\Vert v\Vert \le \bar{\varepsilon }$, and hence, $u=\bar{u}+v\in P$. $\square$

We proceed to establish new convergence properties for an iterative framework for constrained equations, which covers the algorithms discussed in Sect. 2.1. Following [7], to handle a variety of methods within a unifying framework, we consider the following perturbed Newton scheme:

$$\begin{aligned} \varPhi (u^k)+(\varPhi '(u^k)+\varOmega (u^k))v = \omega (u^k). \end{aligned}$$

(9)

The requirements on the perturbation terms $\varOmega$ and $\omega$ are specified in Theorem 3.1. As explained in [7], the perturbation terms define specific methods within the general framework (9).

The key discovery is that, if initialized in a certain conic domain associated to an interior feasible direction $\bar{v}\in \ker \varPhi '(\bar{u})$ for which the mapping $\varPhi$ is 2-regular at a solution $\bar{u}$ of (1), the iterates actually remain feasible throughout, and thus the methods behave the same as in the unconstrained case. We remind again that the 2-regularity assumption implies that the error bound (8) does not hold.

In what follows, we use the uniquely defined decomposition of every $u\in \mathbb {R}^p$ into the sum $u=u_1+u_2$, with $u_1\in (\ker \varPhi '(\bar{u}))^\bot$ and $u_2\in \ker \varPhi '(\bar{u})$.

Theorem 3.1

Let $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ be twice differentiable near $\bar{u}\in \mathcal{S}$, with its second derivative being Lipschitz-continuous on P with respect to $\bar{u}$, that is,

$$\begin{aligned} \varPhi ''(u)-\varPhi ''(\bar{u})=O(\Vert u-\bar{u}\Vert ) \end{aligned}$$

as $u\in P$ tends to $\bar{u}$. Assume that $\varPhi$ is 2-regular at $\bar{u}$ in a direction $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathrm{int}R_P(\bar{u})$, $\Vert \bar{v}\Vert =1$. Moreover, let $\varOmega :\mathbb {R}^p\rightarrow \mathbb {R}^{p\times p}$ and $\omega :\mathbb {R}^p\rightarrow \mathbb {R}^p$ satisfy the conditions

$$\begin{aligned}&\varOmega (u)=O(\Vert u-\bar{u}\Vert ), \end{aligned}$$

(10)

$$\begin{aligned}&\omega (u)=O(\Vert u-\bar{u}\Vert ^2), \end{aligned}$$

(11)

$$\begin{aligned}&\varPi \varOmega (u)=O(\Vert u_1-\bar{u}_1\Vert )+O(\Vert u-\bar{u}\Vert ^2), \end{aligned}$$

(12)

and

$$\begin{aligned} \varPi \omega (u)=O(\Vert u-\bar{u}\Vert \Vert u_1-\bar{u}_1\Vert )+O(\Vert u-\bar{u}\Vert ^3) \end{aligned}$$

(13)

as $u\in P$ tends to $\bar{u}$.

Then, for every $\hat{\varepsilon } >0$ and every $\hat{\delta } >0$, there exist $\varepsilon = \varepsilon (\bar{v})>0$ and $\delta = \delta (\bar{v})>0$ such that for any starting point $u^0\in K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v})$ there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^p$ such that for each k the step $v^k:=u^{k+1}-u^k$ satisfies (9), and for this sequence and for each k it holds that $u_2^k\not =\bar{u}_2$, $u^k\in P\cap K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$, $\{ u^k\}$ converges to $\bar{u}$, $\{ \Vert u^k-\bar{u}\Vert \}$ converges to zero monotonically,

$$\begin{aligned} \frac{\Vert u_1^{k+1}-\bar{u}_1\Vert }{\Vert u_2^{k+1}-\bar{u}_2\Vert } = O(\Vert u^k-\bar{u}\Vert ) \end{aligned}$$

as $k\rightarrow \infty$, and

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u_2^k-\bar{u}_2\Vert } = \frac{1}{2} . \end{aligned}$$

Proof

By Lemma 3.1, we conclude that there exist $\bar{\varepsilon } \in ]0,\, \hat{\varepsilon } ]$ and $\bar{\delta } \in ]0,\, \hat{\delta } ]$ such that $K_{\bar{\varepsilon } ,\, \bar{\delta } }(\bar{u},\, \bar{v})\subset P$. The needed result now follows directly from [7, Theorem 1] applied with these $\bar{\varepsilon }$ and $\bar{\delta }$. The key observation is that any sequence generated as specified in [7, Theorem 1] stays within the set $K_{\bar{\varepsilon } ,\, \bar{\delta } }(\bar{u},\, \bar{v})$, and hence, also within P (by Lemma 3.1). Thus the iterates behave as in the unconstrained case of [7, Theorem 1]. $\square$

Taking into account the estimates in [7, Remark 2], the assertions of Theorem 3.1 imply the linear convergence to $\bar{u}$ of sequences generated by the algorithmic framework under consideration, when initialized within $K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v})$. We emphasize that the latter is a “large” set: it is a cone with nonempty interior intersected with a ball centered at zero and shifted by $\bar{u}$. Hence, it is not “asymptotically thin”, i.e., the ratio of its Lebesgue measure to the measure of the ball stays separated from zero as the radius of the ball tends to zero.

In (9), the mappings $\varOmega :\mathbb {R}^p\rightarrow \mathbb {R}^{p\times p}$ and $\omega :\mathbb {R}^p\rightarrow \mathbb {R}^p$ characterize perturbations of various kinds with respect to the basic Newton iteration (i.e., these perturbations define specific methods within the general Newtonian framework). The basic Newton method itself corresponds to $\varOmega \equiv 0$ and $\omega \equiv 0$, and since under the assumptions of Theorem 3.1 it generates feasible iterates, the conclusions of the theorem apply to the projected Newton method mentioned in Sect. 2.1. In [7] it was shown how the unconstrained Levenberg–Marquardt method with $\sigma (\cdot ):=\Vert \varPhi (\cdot )\Vert ^\tau$ for $\tau \ge 2$, and the unconstrained LP-Newton method can be interpreted via (9) with appropriate choices of $\varOmega$ and $\omega$ satisfying (10)–(13). In particular, on the domain of convergence, the Levenberg–Marquardt method corresponds to

$$\begin{aligned} \varOmega (u) := \sigma (u )\left( \varPhi ' (u )^{-1}\right) ^{\top }, \quad \omega (u) := 0, \end{aligned}$$

and the LP-Newton method is characterized by

$$\begin{aligned} \varOmega (u) := 0, \quad \omega (u) \text{ satisfying } \Vert \omega (u)\Vert \le \gamma (u)\Vert \varPhi (u)\Vert ^2, \end{aligned}$$

where $\gamma (u)$ is the optimal value of the LP-Newton subproblem for $u^k =u$. Again, since under the assumptions of Theorem 3.1 feasible iterates are generated, our results cover both the constrained and projected versions of the Levenberg–Marquardt and the LP-Newton methods. As for the Gauss–Newton method, observe that since the basic Newton equation has the unique solution in the domain in question, this is also the unique solution of the Gauss–Newton subproblem. Thus, there, the associated perturbations are zero. Alternatively, the Gauss–Newton method can be interpreted taking $\sigma (u) :=0$ in the perturbation above corresponding to the Levenberg–Marquardt method (thus again resulting in zero perturbations in the domain of convergence).

Before completing this section by an example, we would like to mention that extending the previous result to cases without twice differentiability of $\varPhi$, inspired by [11], is an interesting topic for future research.

Fig. 1

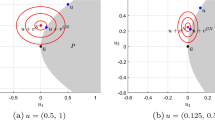
Gauss–Newton method for Example 3.1. a Iterative sequences. b Domain of attraction to solution in question

Fig. 2

Levenberg–Marquardt method for Example 3.1. a Iterative sequences. b Domain of attraction to solution in question

Example 3.1

Let $p:=2$, $\varPhi (u):=((u_1-1)u_2,\, (u_1-1)^2)$, and $P:=\mathbb {R}_+^2$. This yields $\mathcal{S}=\{ u\in \mathbb {R}^2:\, u_1=1, u_2\ge 0\}$. Consider the solution $\bar{u}:=(1,\, 0)$. Then, $R_P(\bar{u})=\mathbb {R}\times \mathbb {R}_+$ and, hence, $\mathrm{int}R_P(\bar{u})$ consists of $v\in \mathbb {R}^2$ such that $v_2>0$. At the same time, we have $\varPhi '(\bar{u})=0$ and

$$\begin{aligned} \varPhi ''(\bar{u})[v]=\left( \begin{array}{cc} v_2&{}v_1\\ 2v_1&{}0 \end{array} \right) , \end{aligned}$$

implying that $\varPhi$ is 2-regular at $\bar{u}$ in any direction $v\in \mathbb {R}^2$ with $v_1\not =0$. Therefore, Theorem 3.1 can be applied for any $\bar{v}\in \mathbb {R}^2$ with $\bar{v}_1\not =0$ and $\bar{v}_2>0$.

In Figs. 1, 2 and 3, the vertical line corresponds to the solution set. These figures show some iterative sequences generated by the Gauss–Newton method, the Levenberg–Marquardt method, and the LP-Newton method, and the domains from which convergence to $\bar{u}$ was detected. From points beyond this domain, all methods converge quadratically to some solutions distinct from $\bar{u}$.

The observed behavior agrees with Theorem 3.1 for solutions when the local Lipschitzian error bound (8) does not hold, as well as with the local convergence theories of these methods under the error bound.

4 Applications to Complementarity Problems

In this section, we apply Theorem 3.1 to the analysis of Newton-type methods for constrained equations arising from reformulations of the nonlinear complementarity problem [21] (NCP)

$$\begin{aligned} z\ge 0,\quad F(z)\ge 0,\quad z^\top F(z) =0, \end{aligned}$$

(14)

with a sufficiently smooth mapping $F:\mathbb {R}^s\rightarrow \mathbb {R}^s$.

Fig. 3

LP-Newton method for Example 3.1. a Iterative sequences. b Domain of attraction to solution in question

Let $\bar{z}$ denote a given solution of the NCP (14). Then, the standard partitioning of the index set $\{1,\, \ldots ,\, s\}$ is defined by

$$\begin{aligned} \begin{array}{ccccl} I_1&{}:=&{}I_1(\bar{z})&{}:=&{}\{ i=1,\, \ldots ,\, s:\, \bar{z}_i>0,\; F_i(\bar{z})=0\} ,\\ I_0&{}:=&{}I_0(\bar{z})&{}:=&{}\{ i=1,\, \ldots ,\, s:\, \bar{z}_i=F_i(\bar{z})=0\} ,\\ I_2&{}:=&{}I_2(\bar{z})&{}:=&{}\{ i=1,\, \ldots ,\, s:\, \bar{z}_i=0,\; F_i(\bar{z})>0\} . \end{array} \end{aligned}$$

Recall that $\bar{z}$ is said to satisfy the strict complementarity condition when $I_0(\bar{z})=\emptyset$. Nonisolated solutions violating strict complementarity are of a certain interest in this context. For example, because they possess special stability properties [22].

In what follows, we shall consider constrained reformulations of the NCP (14), using the slack variable $x\in \mathbb {R}^s$:

$$\begin{aligned} F(z)-x=0,\quad \varPsi (u)=0,\quad u:=(z,\, x)\in \mathbb {R}_+^s\times \mathbb {R}_+^s, \end{aligned}$$

(15)

with some appropriate choices for the mapping $\varPsi :\mathbb {R}^s\times \mathbb {R}^s\rightarrow \mathbb {R}^s$ that enforce complementarity between z and x. Both smooth and piecewise smooth options for $\varPsi$ will be considered.

4.1 Piecewise Smooth Reformulation

Let $\varPsi :\mathbb {R}^s\times \mathbb {R}^s\rightarrow \mathbb {R}^s$ be the complementarity natural residual [21], i.e.,

$$\begin{aligned} \varPsi (u):=\min \{ z,\, x\} , \end{aligned}$$

(16)

with the min-operation applied componentwise. We note that using this min-function, the nonnegativity constraints in (15) are redundant for the reformulation of the NCP itself to be valid. However, the nonnegativity constraints play a role for obtaining stronger convergence properties of Newton-type methods applied to the reformulation; see [1, 2] for detailed discussions.

As is well understood, near a solution $\bar{z}$, locally the solution set of the NCP (14) is the union of solution sets of the branch systems

$$\begin{aligned} F(z)-x=0,\quad z_{I_2}=0,\quad z_{J_2}=0,\quad x_{I_1}=0,\quad x_{J_1}=0,\quad z_{J_1}\ge 0,\quad x_{J_2}\ge 0, \end{aligned}$$

(17)

defined by all the partitions $(J_1,\, J_2)$ of the bi-active index set $I_0$, i.e., all the pairs of index sets satisfying $J_1\cup J_2=I_0$, $J_1\cap J_2=\emptyset$.

Note that a branch system (17) can be considered as a constrained equation (1) with respect to $u:=(z,\, x )$, with $\varPhi :\mathbb {R}^s\times \mathbb {R}^s\rightarrow \mathbb {R}^s\times \mathbb {R}^s$ given by

$$\begin{aligned} \varPhi (u):=(F(z)-x,\, z_{I_2},\, z_{J_2},\, x_{I_1},\, x_{J_1}), \end{aligned}$$

(18)

and

$$\begin{aligned} P:=\{ u:=(z,\, x)\in \mathbb {R}^s\times \mathbb {R}^s:\, z_{J_1}\ge 0,\; x_{J_2}\ge 0\} . \end{aligned}$$

(19)

The solution of interest of this constrained equation is $\bar{u}= (\bar{z},\, \bar{x})$ with $\bar{x}:=F(\bar{z})$.

We next show that Theorem 3.1 is applicable to the constrained equation given by (18) and (19) which corresponds to the branch system (17), for directions $\bar{v}$ satisfying certain assumptions. Then, we show that when initialized in an appropriate domain, Newton-type methods for the original NCP, i.e., the constrained equation (15) with $\varPsi$ defined in (16), behave exactly as their counterparts for the branch system (17). We emphasize that the methods themselves are applied to the original problem, and the set P given by (19) above (which clearly depends on the solution) only plays an auxiliary role for the convergence analysis.

After re-ordering the components of z so that $z=(z^1,\, z^2)$, where $z^1:=(z_{I_1},\, z_{J_1})$, $z^2:=(z_{I_2},\, z_{J_2})$, and similarly for x (and F), we can write

$$\begin{aligned} \varPhi '(\bar{u})=\left( \begin{array}{cccc} M_{11}&{}M_{12}&{}-I&{}0\\ M_{21}&{}M_{22}&{}0&{}-I\\ 0&{}I&{}0&{}0\\ 0&{}0&{}I&{}0 \end{array} \right) , \end{aligned}$$

where the matrices $M_{11}$, $M_{12}$, $M_{21}$, $M_{22}$ (whose dependence of the partition $(J_1,\, J_2)$ is omitted for simplicity) are given by

$$\begin{aligned}&M_{11}:= \left( \begin{array}{cc} \displaystyle \frac{\partial F_{I_1}}{\partial z_{I_1}} (\bar{z})&{} \displaystyle \frac{\partial F_{I_1}}{\partial z_{J_1}} (\bar{z})\\ \displaystyle \frac{\partial F_{J_1}}{\partial z_{I_1}} (\bar{z})&{} \displaystyle \frac{\partial F_{J_1}}{\partial z_{J_1}} (\bar{z}) \end{array} \right) , \quad M_{12}:= \left( \begin{array}{cc} \displaystyle \frac{\partial F_{I_1}}{\partial z_{I_2}} (\bar{z})&{} \displaystyle \frac{\partial F_{I_1}}{\partial z_{J_2}} (\bar{z})\\ \displaystyle \frac{\partial F_{J_1}}{\partial z_{I_2}} (\bar{z})&{} \displaystyle \frac{\partial F_{J_1}}{\partial z_{J_2}} (\bar{z}) \end{array} \right) ,\\&M_{21}:= \left( \begin{array}{cc} \displaystyle \frac{\partial F_{I_2}}{\partial z_{I_1}} (\bar{z})&{} \displaystyle \frac{\partial F_{I_2}}{\partial z_{J_1}} (\bar{z})\\ \displaystyle \frac{\partial F_{J_2}}{\partial z_{I_1}} (\bar{z})&{} \displaystyle \frac{\partial F_{J_2}}{\partial z_{J_1}} (\bar{z}) \end{array} \right) ,\quad M_{22}:= \left( \begin{array}{cc} \displaystyle \frac{\partial F_{I_2}}{\partial z_{I_2}} (\bar{z})&{} \displaystyle \frac{\partial F_{I_2}}{\partial z_{J_2}} (\bar{z})\\ \displaystyle \frac{\partial F_{J_2}}{\partial z_{I_2}} (\bar{z})&{} \displaystyle \frac{\partial F_{J_2}}{\partial z_{J_2}} (\bar{z}) \end{array} \right) . \end{aligned}$$

Therefore,

$$\begin{aligned}&\ker \varPhi '(\bar{u})=\{ v:=(\zeta ,\, \xi ):\, \zeta =(\zeta ^1,\, 0),\; \xi =(0,\, M_{21}\zeta ^1),\; \zeta ^1\in \ker M_{11}\} , \end{aligned}$$

(20)

$$\begin{aligned}&\mathrm{im}\varPhi '(\bar{u})=\left\{ w:=(y,\, \chi ): \begin{array}{l} y=(y^1,\, y^2),\; \chi =(\chi ^1,\, \chi ^2),\\ y^1-M_{12}\chi ^1+\chi ^2\in \mathrm{im}M_{11} \end{array} \right\} . \end{aligned}$$

(21)

In particular, since in the current setting of (19) we have that $R_P(\bar{u})=P$, it follows that

$$\begin{aligned} \ker \varPhi '(\bar{u})\cap \mathrm{int}R_P(\bar{u})=\left\{ \bar{v}:=(\bar{\zeta },\, \bar{\xi }): \begin{array}{l} \bar{\zeta }^1\in \ker M_{11},\; \bar{\zeta }_{J_1}>0,\; \bar{\zeta }^2=0,\\ \bar{\xi }^1=0,\; \bar{\xi }^2=M_{21}\bar{\zeta }^1,\; (M_{21}\bar{\zeta }^1)_{J_2}>0 \end{array} \right\} . \end{aligned}$$

(22)

Employing (20) and (21), it can be seen that for $\bar{v}:=(\bar{\zeta } ,\, \bar{\xi } )$, where $\bar{\zeta } :=(\bar{\zeta } ^1,\, 0)$ with $\bar{\zeta } ^1:=(\bar{\zeta } _{I_1},\, \bar{\zeta } _{J_1})$ and any $\bar{\zeta } _{I_1}$ and $\bar{\zeta } _{J_1}$, and with any $\bar{\xi }$, the 2-regularity of $\varPhi$ at $\bar{u}$ in the direction $\bar{v}$ is equivalent to saying that there exists no $z^1\in \ker M_{11}{\setminus } \{ 0\}$ satisfying

$$\begin{aligned} M(\bar{\zeta } ^1)z^1\in \mathrm{im}M_{11}, \end{aligned}$$

(23)

where the matrix $M(\bar{\zeta } ^1)$ is defined as

$$\begin{aligned} \left( \begin{array}{cc} \displaystyle \frac{\partial ^2F_{I_1}}{\partial z_{I_1}^2} (\bar{z})[\bar{\zeta } _{I_1}] +\frac{\partial ^2F_{I_1}}{\partial z_{I_1}\partial z_{J_1}} (\bar{z})[\bar{\zeta } _{J_1}]&{} \displaystyle \frac{\partial ^2F_{I_1}}{\partial z_{I_1}\partial z_{J_1}} (\bar{z})[\bar{\zeta } _{I_1}] +\frac{\partial ^2F_{I_1}}{\partial z_{J_1}^2} (\bar{z})[\bar{\zeta } _{J_1}]\\ \displaystyle \frac{\partial ^2F_{J_1}}{\partial z_{I_1}^2} (\bar{z})[\bar{\zeta } _{I_1}] +\frac{\partial ^2F_{J_1}}{\partial z_{I_1}\partial z_{J_1}} (\bar{z})[\bar{\zeta } _{J_1}]&{} \displaystyle \frac{\partial ^2F_{J_1}}{\partial z_{I_1}\partial z_{J_1}} (\bar{z})[\bar{\zeta } _{I_1}] +\frac{\partial ^2F_{J_1}}{\partial z_{J_1}^2} (\bar{z})[\bar{\zeta } _{J_1}]\\ \end{array} \right) . \end{aligned}$$

(24)

Therefore, Theorem 3.1 is applicable to the constrained equation in question [corresponding to the branch system (17)] with every $\bar{v}$ satisfying the specified assumptions and $\Vert \bar{v}\Vert =1$.

It remains to show that when initialized in an appropriate domain, the methods we consider for (15) with $\varPsi$ defined in (16), behave exactly as their counterparts for the branch system (17).

To that end, let $G:\mathbb {R}^s\times \mathbb {R}^s\rightarrow \mathbb {R}^{s\times 2s}$ be a mapping such that for each $u:=(z,\, x)\in \mathbb {R}^s\times \mathbb {R}^s$, the rows of the matrix G(u) are given by

$$\begin{aligned} G_i(u):=\left\{ \begin{array}{ll} (e^i,\, 0),&{}\quad \text{ if } z_i<x_i,\\ (e^i,\, 0) \text{ or } (0,\, e^i),&{}\quad \text{ if } z_i=x_i,\\ (0,\, e^i),&{}\quad \text{ if } z_i>x_i, \end{array} \right. \quad i=1,\, \ldots ,\, s. \end{aligned}$$

(25)

Due to the nonsmoothness of $\varPsi$, the matrix G serves as replacement for the possibly non-existing Jacobian of $\varPsi$. Moreover, instead of the constrained Gauss–Newton method (2) we now consider its piecewise version. For a given current iterate $u^k:=(z^k,\, x^k)\in \mathbb {R}_+^s\times \mathbb {R}_+^s$, the constrained piecewise Gauss–Newton method for (15) generates the next iterate as $u^{k+1}:=u^k+v^k$, where $v^k:=(\zeta ^k,\, \xi ^k)$ is a solution of the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \displaystyle \frac{1}{2} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert ^2 +\frac{1}{2} \Vert \varPsi (u^k)+G(u^k)v\Vert ^2\\ \text{ s.t. } &{} u^k+v\ge 0, \end{array} \end{aligned}$$

(26)

with respect to $v:=(\zeta ,\, \xi )$.

For arbitrary fixed $\hat{\varepsilon } >0$, $\hat{\delta } >0$, and $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathrm{int}R_P(\bar{u})$, let $u:=(z,\, x)\in (\mathbb {R}^s\times \mathbb {R}^s) {\setminus } \{ \bar{u}\}$ be such that

$$\begin{aligned} \Vert u-\bar{u}\Vert \le \hat{\varepsilon } ,\quad \left\| \frac{u-\bar{u}}{\Vert u-\bar{u}\Vert } -\bar{v}\right\| \le \hat{\delta } . \end{aligned}$$

(27)

If $\hat{\varepsilon } >0$ is small enough, then from the first inequality in (27), and taking into account (16) and (25), we obtain that

$$\begin{aligned}&z_{I_1}>x_{I_1},\quad \text{ and } \text{ hence, } \varPsi _{I_1}(z)=x_{I_1},\; G_{I_1}(z)=(0\; I_{I_1});\\&z_{I_2}<x_{I_2},\quad \text{ and } \text{ hence, } \varPsi _{I_2}(z)=z_{I_2},\; G_{I_2}(z)=(I_{I_2}\;0). \end{aligned}$$

Furthermore, the second inequality in (27) implies that

$$\begin{aligned} \Vert u-\bar{u}-\Vert u-\bar{u}\Vert \bar{v}\,\Vert \le \hat{\delta } \Vert u-\bar{u}\Vert . \end{aligned}$$

Since $\bar{z}_{I_0}=0$ and $\bar{x}_{I_0}=0$, we then conclude that

$$\begin{aligned} \Vert z_{I_0}-\Vert u-\bar{u}\Vert \bar{\zeta } _{I_0}\,\Vert =\Vert z_{I_0}-\bar{z}_{I_0}-\Vert u-\bar{u}\Vert \bar{\zeta } _{I_0}\,\Vert \le \Vert u-\bar{u}-\Vert u-\bar{u}\Vert \bar{v}\,\Vert \le \hat{\delta } \Vert u-\bar{u}\Vert , \end{aligned}$$

(28)

and similarly,

$$\begin{aligned} \Vert x_{I_0}-\Vert u-\bar{u}\Vert \bar{\xi } _{I_0}\Vert \le \hat{\delta } \Vert u-\bar{u}\Vert . \end{aligned}$$

(29)

For every $i\in J_1$, from (28) it follows that

$$\begin{aligned} z_i\ge (\bar{\zeta } _i -\hat{\delta } )\Vert u-\bar{u}\Vert . \end{aligned}$$

(30)

At the same time, since $\bar{\xi } _{J_1}=0$ holds according to (22), from (29) it follows that

$$\begin{aligned} \Vert x_{J_1}\Vert \le \hat{\delta } \Vert u-\bar{u}\Vert . \end{aligned}$$

(31)

Recalling $\bar{\zeta }_{J_1}>0$ from (22), by (30) and (31) we conclude that if $\hat{\delta } >0$ is small enough, then $z_{J_1}>x_{J_1}$, and hence, taking into account (16) and (25),

$$\begin{aligned} \varPsi _{J_1}(z)=x_{J_1},\quad G_{J_1}(z)=(0\; I_{J_1}). \end{aligned}$$

Similarly, for every $i\in J_2$, from (29) and from the equality $\bar{\xi } ^2=M_{21}\bar{\zeta } ^1$ in (22) it follows that

$$\begin{aligned} x_i\ge (\bar{\xi } _i-\hat{\delta } )\Vert u-\bar{u}\Vert =((M_{21}\bar{\zeta } ^1)_i-\hat{\delta } )\Vert u-\bar{u}\Vert , \end{aligned}$$

(32)

while, since $\bar{\zeta } _{J_2}=0$ holds according to (22), from (28) it follows that

$$\begin{aligned} \Vert z_{J_2}\Vert \le \hat{\delta } \Vert u-\bar{u}\Vert . \end{aligned}$$

(33)

Recalling $(M_{21}\bar{\zeta }^1)_{J_2}>0$ from (22), by (32) and (33) we conclude that if $\hat{\delta } >0$ is small enough, then $z_{J_2}<x_{J_2}$, and hence, taking into account (16) and (25),

$$\begin{aligned} \varPsi _{J_2}(z)=z_{J_2},\quad G_{J_2}(z)=(I_{J_2}\;0). \end{aligned}$$

Summarizing the considerations above, we deduce that if $u:=u^k$ satisfies (27) with sufficiently small $\hat{\varepsilon } >0$ and $\hat{\delta } >0$, then (26) takes the form

$$\begin{aligned} \text{ min }\; \displaystyle \frac{1}{2} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert ^2 \quad \text{ s.t. } \; u^k+v\ge 0, \end{aligned}$$

(34)

where $\varPhi$ is defined in (18).

Note that one cannot apply Theorem 3.1directly to the method defined by the subproblem (34), because the feasible set therein is generally smaller than $P-u^k$ with P given by (19). That said, and as demonstrated above, Theorem 3.1 is in fact applicable for the specified $\varPhi$, and when P is given by (19). This yields the following: for every $\hat{\varepsilon } >0$ and $\hat{\delta } >0$, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0\in K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v})$ there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each iteration index k the step $v^k:=u^{k+1}-u^k$ solves (9) with $\varOmega \equiv 0$ and $\omega \equiv 0$, and for this sequence and for each k it holds that $u_2^k\not =\bar{u}_2$, and $u^k\in P\cap K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$. Observe further that according to (18), equation (9) being solved by $v^k$ implies that for all k

$$\begin{aligned} z_{I_2}^{k+1}=0,\quad z_{J_2}^{k+1}=0,\quad x_{I_1}^{k+1}=0,\quad x_{J_1}^{k+1}=0. \end{aligned}$$

In addition, if $\hat{\varepsilon } >0$ is small enough, then the inclusion $u^k\in K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$ implies that $z_{I_1}^k>0$ and $x_{I_2}^k>0$. Combining these observations with the inclusion $u^k\in P$ and with (19), and assuming that $u^0\ge 0$, we obtain that $u^k\ge 0$ for all k.

Hence, we actually can derive conclusions about the method with the subproblem (34) from Theorem 3.1. This allows to characterize domain of convergence to $\bar{u}$ of the constrained piecewise Gauss–Newton method by means of Theorem 3.1, when the method is applied to the constrained equation corresponding to a proper branch (17) of the solution set of the NCP (14), with the starting point in the proper domain.

Proposition 4.1

Let $F:\mathbb {R}^s\rightarrow \mathbb {R}^s$ be twice differentiable near $\bar{z}\in \mathbb {R}^s$, with its second derivative being Lipschitz-continuous with respect to $\bar{z}$. Let $\bar{z}$ be a solution of the NCP (14), and let $\bar{u}:= (\bar{z},\, \bar{x})$, where $\bar{x}:=F(\bar{z})$. Assume that for some partition $(J_1,\, J_2)$ of $I_0=I_0(\bar{z})$ there exist elements $\bar{\zeta } _{I_1}\in \mathbb {R}^{|I_1|}$$\bar{\zeta } _{J_1}\in \mathbb {R}^{|J_1|}$ such that $\bar{\zeta } ^1:=(\bar{\zeta } _{I_1},\, \bar{\zeta } _{J_1})$ belongs to $\ker M_{11}$ and satisfies $\bar{\zeta }_{J_1}>0$ and $(M_{21}\bar{\zeta }^1)_{J_2}>0$ from (22), there exists no $z^1\in \ker M_{11}{\setminus } \{ 0\}$ satisfying (23), and $\Vert (\bar{\zeta } ^1,\, M_{21}\bar{\zeta } ^1)\Vert =1$. Set $\bar{\zeta } :=(\bar{\zeta } ^1,\, 0)$ with 0 in $\mathbb {R}^{|I_2|}\times \mathbb {R}^{|J_2|}$, $\bar{\xi } :=(0,\, M_{21}\bar{\zeta } ^1)$ with 0 in $\mathbb {R}^{|I_1|}\times \mathbb {R}^{|J_1|}$.

Then, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in (\mathbb {R}^s\times \mathbb {R}^s){\setminus } \{ \bar{u}\}$ satisfying

$$\begin{aligned} \Vert z^0-\bar{z}\Vert \le \varepsilon ,\quad \left\| \frac{z^0-\bar{z}}{\Vert u^0-\bar{u}\Vert } -\bar{\zeta } \right\| \le \delta ,\quad \Vert x^0-\bar{x}\Vert \le \varepsilon ,\quad \left\| \frac{x^0-\bar{x}}{\Vert u^0-\bar{u}\Vert } -\bar{\xi } \right\| \le \delta , \end{aligned}$$

(35)

there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k the step $v^k:=u^{k+1}-u^k$ solves (26) with $\varPsi$ and G defined in (16) and (25), respectively, $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

Remark 4.1

It is natural to choose $x^0$ not independently but in agreement with the choice of $z^0$. For example, if we set $x^0:=\max \{ 0,\, F(z^0)\}$, it can be verified that for given $\varepsilon >0$ and $\delta >0$, the requirements on $x^0$ in (35) are automatically satisfied if the requirement on $z^0$ is satisfied with $\varepsilon >0$ and $\delta >0$ small enough.

Regarding the first requirement on $x^0$, this is obvious. Regarding the second requirement, observe first that the second inequality in (35) implies that

$$\begin{aligned} \Vert z^0-\bar{z}-\Vert u^0-\bar{u}\Vert \bar{\zeta } \Vert \le \delta \Vert u^0-\bar{u}\Vert , \end{aligned}$$

and hence,

$$\begin{aligned} \Vert F(z^0)-F(\bar{z})-\Vert u^0-\bar{u}\Vert F'(\bar{z})\bar{\zeta } \Vert\le & {} \Vert F'(\bar{z})(z^0-\bar{z})-\Vert u^0-\bar{u}\Vert F'(\bar{z})\bar{\zeta } \Vert \nonumber \\&+o(\Vert z^0-\bar{z}\Vert )\nonumber \\\le & {} \Vert F'(\bar{z})\Vert \Vert z^0-\bar{z}-\Vert u^0-\bar{u}\Vert \bar{\zeta } \Vert \nonumber \\&+o(\Vert z^0-\bar{z}\Vert )\nonumber \\\le & {} \delta \Vert F'(\bar{z})\Vert \Vert u^0-\bar{u}\Vert +o(\Vert u^0-\bar{u}\Vert ) \end{aligned}$$

(36)

as $u^0\rightarrow \bar{u}$. For any $i\in I_1\cup J_1$, since $\bar{x}_i=F_i(\bar{z})=0$, $\bar{\xi } _i=0$, and $F_i'(\bar{z})\bar{\zeta } =0$, according to the inclusion $\bar{\zeta } ^1\in \ker M_{11}$ and the definitions of $x^0$ and $\bar{\zeta }$, we then have that

$$\begin{aligned} \left| x_i^0-\bar{x}_i-\Vert u^0-\bar{u}\Vert \bar{\xi } _i \right|= & {} | x_i^0|\\\le & {} |F_i(z^0)|\\= & {} |F_i(z^0)-F_i(\bar{z})-\Vert u^0-\bar{u}\Vert F_i'(\bar{z})\bar{\zeta } |\\\le & {} \delta \Vert F'(\bar{z})\Vert \Vert u^0-\bar{u}\Vert +o(\Vert u^0-\bar{u}\Vert ) \end{aligned}$$

as $u^0\rightarrow \bar{u}$. Furthermore, for $i\in J_2$, since $F_i(\bar{z})=0$, and employing (22), from (36) we derive

$$\begin{aligned} F_i(z^0)\ge F_i'(\bar{z})\bar{\zeta } \Vert u^0-\bar{u}\Vert -\delta \Vert F'(\bar{z})\Vert \Vert u^0-\bar{u}\Vert +o(\Vert u^0-\bar{u}\Vert )>0 \end{aligned}$$

provided $\varepsilon >0$ and $\delta >0$ are small enough. Since $F_{I_2}(\bar{z})>0$, by further reducing $\varepsilon >0$, if necessary, we then obtain that for any $i\in I_2\cup J_2$ it holds that $F_i(z^0)>0$, and hence, employing the definitions of $x^0$ and $\bar{\xi }$,

$$\begin{aligned} \left| x_i^0-\bar{x}_i-\Vert u^0-\bar{u}\Vert \bar{\xi } _i \right|= & {} |F_i(z^0)-F_i(\bar{z})-\Vert u^0-\bar{u}\Vert F_i'(\bar{z})\bar{\zeta } |\\\le & {} \delta \Vert F'(\bar{z})\Vert \Vert u^0-\bar{u}\Vert +o(\Vert u^0-\bar{u}\Vert ) \end{aligned}$$

as $u^0\rightarrow \bar{u}$, where the last inequality is again by (36). The obtained estimates yield the needed conclusion.

Consider now the constrained Levenberg–Marquardt method for (15), in which the step $v^k:=(\zeta ^k,\, \xi ^k)$ is computed as a solution of the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \displaystyle \frac{1}{2} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert ^2 +\frac{1}{2} \Vert \varPsi (u^k)+G(u^k)v\Vert ^2 +\frac{1}{2} \sigma (u^k)\Vert v\Vert ^2\\ \text{ s.t. } &{} u^k+v\ge 0. \end{array} \end{aligned}$$

(37)

As demonstrated above in the context of the constrained piecewise Gauss–Newton method, if $\hat{\varepsilon } >0$ and $\hat{\delta } >0$ are small enough, then the inclusion $u^k\in K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$ implies that solving (37) is equivalent to solving

$$\begin{aligned} \text{ min } \; \displaystyle \frac{1}{2} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert ^2+\frac{1}{2} \sigma (u^k)\Vert v\Vert ^2\; \text{ s.t. } \; u^k+v\ge 0, \end{aligned}$$

(38)

where $\varPhi$ is defined in (18). Furthermore, there exists the unique $v_N^k$ solving (9) with $\varOmega \equiv 0$ and $\omega \equiv 0$, and for this $v_N^k$ it holds that $u^k+v_N^k\ge 0$, i.e., $v_N^k$ is feasible in (38). Therefore, for the unique solution $v^k$ of (38) it holds that

$$\begin{aligned} \Vert \varPhi (u^k)+\varPhi '(u^k)v^k\Vert ^2+\sigma (u^k)\Vert v^k\Vert ^2 \le \sigma (u^k)\Vert v_N^k\Vert ^2, \end{aligned}$$

implying that

$$\begin{aligned} \Vert \varPhi (u^k)+\varPhi '(u^k)v^k\Vert \le \sqrt{\sigma (u^k)} \Vert v_N^k\Vert . \end{aligned}$$

By [7, Lemma 1], it is known that $\Vert v_N^k\Vert =O(\Vert u^k-\bar{u}\Vert )$, and hence, if $\sigma (\cdot )=\Vert \varPhi (\cdot )\Vert ^\tau$ with $\tau \ge 2$, then $v^k$ solves (9) with $\varOmega \equiv 0$ and some $\omega (\cdot )$ satisfying $\omega (u)=O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert )$. As demonstrated in [7], these perturbation mappings $\varOmega$ and $\omega$ satisfy (10)–(13), which allows to apply Theorem 3.1.

Proposition 4.2

Under the assumptions of Proposition 4.1, for any $\tau \ge 2$, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in (\mathbb {R}^s\times \mathbb {R}^s){\setminus } \{ \bar{u}\}$ satisfying (35) there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k the step $v^k:=u^{k+1}-u^k$ solves (37) with $\varPsi$ and G defined in (16) and (25), respectively, $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

Finally, consider the LP-Newton method for (15), in which the step $v^k$ is computed by solving the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ^2,\\ &{}\Vert \varPsi (u^k)+G(u^k)v\Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ^2,\\ &{}\Vert v \Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ,\\ &{}u^k+v\ge 0, \end{array} \end{aligned}$$

(39)

with respect to $(v,\, \gamma ):=((\zeta ,\, \xi ),\, \gamma )\in (\mathbb {R}^s\times \mathbb {R}^s)\times \mathbb {R}$.

Again, as demonstrated above, if $\hat{\varepsilon } >0$ and $\hat{\delta } >0$ are small enough, then the inclusion $u^k\in K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$ implies that solving (39) is equivalent to solving

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert v \Vert \le \gamma \Vert \varPhi (u^k)\Vert ,\\ &{}u^k+v\ge 0, \end{array} \end{aligned}$$

(40)

where $\varPhi$ is defined in (18). Furthermore, there exists the unique $v_N^k$ solving (9) with $\varOmega \equiv 0$ and $\omega \equiv 0$, and for this $v_N^k$ it holds that $u^k+v_N^k\ge 0$. Then, $(v_N^k,\, \Vert v_N^k\Vert /\Vert \varPhi (u^k)\Vert )$ is feasible in (40), and hence for the optimal value $\gamma (u^k)$ of (40) it holds that

$$\begin{aligned} \gamma (u^k)\le \frac{\Vert v_N^k\Vert }{\Vert \varPhi (u^k)\Vert }. \end{aligned}$$

Therefore, for any solution $v^k$ of (38) we have

$$\begin{aligned} \Vert \varPhi (u^k)+\varPhi '(u^k)v^k\Vert \le \Vert v_N^k\Vert \Vert \varPhi (u^k)\Vert , \end{aligned}$$

again implying that $v^k$ solves (9) with $\varOmega \equiv 0$ and some $\omega (\cdot )$ satisfying $\omega (u)=O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert )$. This, once more, allows to apply Theorem 3.1.

Proposition 4.3

Under the assumptions of Proposition 4.1, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in (\mathbb {R}^s\times \mathbb {R}^s){\setminus }\{\bar{u}\}$ satisfying (35) there exists a sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k it holds that $(v^k,\, \gamma _{k+1})$ with $v^k:=u^{k+1}-u^k$ and some $\gamma _{k+1}$ solves (39) with $\varPsi$ and G defined in (16) and (25), respectively; any such sequence $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

Fig. 4

Piecewise Gauss–Newton method for Example 4.1. a Iterative sequences. b Domain of attraction to solution in question

Fig. 5

Piecewise Levenberg–Marquardt method for Example 4.1. a Iterative sequences. b Domain of attraction to solution in question

Example 4.1

Let $s:=2$ and $F(z):=((z_1-1)z_2,\, (z_1-1)^2)$. Then, the solution set of the NCP (14) has the form $\mathcal{S}=\{ z\in \mathbb {R}^2:\, z_1=1,\, z_2\ge 0\} \cup \{ z\in \mathbb {R}^2:\, z_1\ge 0,\, z_2=0\}$, and the two solutions violating strict complementarity are $(0,\, 0)$ and $(1,\, 0)$.

Consider the solution $\bar{z}:=(1,\, 0)$. Then, $I_0=\{ 2\}$, $I_1=\{ 1\}$, $I_2=\emptyset$. We next consider the partitions of $I_0$:

• For $J_1=\emptyset$, $J_2=\{ 2\}$, we have $F_{I_1}(z)=0$ when $z_{J_2}=z_2=0$, implying that $M_{11}=0$, the matrix in (24) is always equal to 0, and hence, 2-regularity cannot hold.

• For $J_1=\{ 2\}$, $J_2=\emptyset$ we have $M_{11}=0$, $M_{21}$ is empty, and hence, the inclusion $\bar{\zeta } ^1\in \ker M_{11}$ and the relations in (22) hold for any $\bar{\zeta } ^1=\bar{\zeta } \in \mathbb {R}^2$ with $\bar{\zeta } _2>0$. Furthermore,

  $$\begin{aligned} M(\bar{\zeta } ^1)=F''(\bar{z})[\bar{\zeta } ]=\left( \begin{array}{cc} \bar{\zeta } _2&{}\bar{\zeta } _1\\ 2\bar{\zeta } _1&{}0 \end{array} \right) , \end{aligned}$$

  which is nonsingular when $\bar{\zeta } _1\not =0$. Therefore, Propositions 4.1–4.3 are applicable with this partition $(J_1,\, J_2)$, and with any $\bar{\zeta } _1\not =0$, $\bar{\zeta } _2>0$.

  Observe that the branch system (17) corresponding to this partition is precisely the constrained equation considered in Example 3.1.

In Figs. 4, 5 and 6, the horizontal and vertical solid lines form the solution set. These figures show the domains from which convergence to $\bar{u}$ was detected, and some iterative sequences generated by the constrained piecewise Gauss–Newton method, the constrained piecewise Levenberg–Marquardt method, and the piecewise LP-Newton method, with the rule for starting values of the slack variable specified in Remark 4.1. The observed behavior agrees with Propositions 4.1–4.3.

Finally, we briefly discuss how the corresponding results can be derived for projected methods. As pointed out above, under the assumptions of Proposition 4.1, and assuming that the starting point $u^0:=(z^0,\, x^0)$ satisfies (35) with sufficiently small $\varepsilon >0$ and $\delta >0$, the iterates generated by the steps of the basic Newton method automatically remain feasible. Therefore, in these circumstances the projected Newton method and the projected Gauss–Newton method will be generating exactly the same sequences as the basic Newton method or the constrained Gauss–Newton method. Thus, the assertion of Proposition 4.1 is valid for all these methods.

Fig. 6

Piecewise LP-Newton method for Example 4.1. a Iterative sequences. b Domain of attraction to solution in question

As for the Levenberg–Marquardt and the LP-Newton methods, for a current iterate $u^k$, let $\tilde{v}^k:=(\tilde{\zeta }^k,\, \tilde{\xi } ^k)$ be a step generated by solving their unconstrained subproblems. According to the discussion above, if $u^k\in K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$ with sufficiently small $\hat{\varepsilon } >0$ and $\hat{\delta } >0$, then $\tilde{v}^k$ satisfies the equation

$$\begin{aligned} \varPhi (u^k)+\varPhi '(u^k)v = \tilde{\omega } (u^k) \end{aligned}$$

(41)

with some $\tilde{\omega } (\cdot )$ such that $\tilde{\omega } (u)=O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert )$ as $u\rightarrow \bar{u}$. Moreover, employing the definition of P in (19), it holds that $(z^k+\tilde{\zeta }^k)_{I_1\cup J_1}\ge 0$ and $(x^k+\tilde{\xi } ^k)_{I_2\cup J_2}\ge 0$. By the definition of $\varPhi$ in (18), we further deduce that

$$\begin{aligned} \Vert (z^k+\tilde{\zeta }^k)_{I_2\cup J_2}\Vert \le \Vert \tilde{\omega } (u^k)\Vert ,\quad \Vert (x^k+\tilde{\xi } ^k)_{I_1\cup J_1}\Vert \le \Vert \tilde{\omega } (u^k)\Vert . \end{aligned}$$

Hence, by Hoffman’s lemma (the error bound for linear systems; see, e.g., [21, Lemma 3.2.3]), for the projection $u^{k+1}$ of $u^k+\tilde{v}^k$ onto $\mathbb {R}^s_+\times \mathbb {R}^s_+$, it holds that

$$\begin{aligned} \Vert u^{k+1}-(u^k+\tilde{v}^k)\Vert =O(\Vert \tilde{\omega } (u^k)\Vert ). \end{aligned}$$

(42)

From (41), (42) we then derive that

$$\begin{aligned} \Vert \varPhi (u^k)+\varPhi '(u^k)(u^{k+1}-u^k)\Vert\le & {} \Vert \varPhi (u^k)+\varPhi '(u^k)\tilde{v}^k\Vert \\&+\Vert \varPhi '(u^k)(u^{k+1}-(u^k+\tilde{v}^k))\Vert \\= & {} O(\Vert \tilde{\omega } (u^k)\Vert ). \end{aligned}$$

The latter estimate again allows to apply Theorem 3.1. Therefore, the counterparts of Proposition 4.2 and 4.3 are valid for the projected Levenberg–Marquardt and LP-Newton methods, respectively.

4.2 Smooth Reformulation

Let $\varPsi$ be now defined by the Hadamard product of the complementarity variables:

$$\begin{aligned} \varPsi (u):=z\circ x , \end{aligned}$$

(43)

where $z\circ x := (z_1x_1,\ldots , z_sx_s)$. With this choice, the equation in (15) is smooth, and the nonnegativity constraints in (15) are necessary for making it an equivalent reformulation of the NCP (14).

Define $\varPhi :\mathbb {R}^s\times \mathbb {R}^s\rightarrow \mathbb {R}^s\times \mathbb {R}^s$,

$$\begin{aligned} \varPhi (u):=(F(z)-x,\, \varPsi (u)). \end{aligned}$$

(44)

It might seem natural to simply take $P:=\mathbb {R}_+^s\times \mathbb {R}_+^s$ in (1). However, as will be seen from the analysis below, this choice would not allow to apply Theorem 3.1 when at least one of the sets $I_1$ or $I_2$ is nonempty. To apply Theorem 3.1, we define

$$\begin{aligned} P:=\{ u:=(z,\, x)\in \mathbb {R}^s\times \mathbb {R}^s:\, z_{I_0}\ge 0,\; x_{I_0}\ge 0\} , \end{aligned}$$

(45)

and consider the constrained equation (1) with these $\varPhi$ and P. The solution of interest is $\bar{u}:= (\bar{z},\, \bar{x})$ with $\bar{x}:=F(\bar{z})$, as before. We emphasize that the set P depends on the solution (via the index set $I_0$), and thus its role here is auxiliary. It will not appear in the iterative schemes, which are as before: those of the constrained Gauss–Newton, Levenberg–Marquardt, and LP-Newton methods applied to the equation $\varPhi (u) =0$ with full nonnegativity constraints, where $\varPhi$ is given by (44). The point is that we show, under certain assumptions, that such iterates can be considered as those for the same $\varPhi$ but P now defined in (45), which allows to apply Theorem 3.1.

The first issue to understand is what the key assumption of 2-regularity of $\varPhi$ in a direction $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathrm{int}R_P (\bar{u})$ means in the current setting. We proceed with this next.

As it is easily seen,

$$\begin{aligned}&\varPhi '(\bar{u})=\left( \begin{array}{cc} F'(\bar{z})&{}-I\\ \mathrm{diag}\bar{x}&{}\mathrm{diag}\bar{z}\end{array} \right) ,\nonumber \\&\quad \ker \varPhi '(\bar{u})=\{ v:=(\zeta ,\, \xi ):\, F'(\bar{z})\zeta -\xi =0,\; \zeta _{I_2}=0,\; \xi _{I_1}=0\} , \end{aligned}$$

(46)

and, after some manipulations,

$$\begin{aligned} \mathrm{im}\varPhi '(\bar{u})=\left\{ w:=(y,\, \chi ):\, \begin{array}{l} y_{I_1}-\frac{\partial F_{I_1}}{\partial z_{I_2}} (\bar{z})(\bar{x}_{I_2}^{-1}\circ \chi _{I_2}) +\bar{z}_{I_1}^{-1}\circ \chi _{I_1}\\ \in \mathrm{im}\frac{\partial F_{I_1}}{\partial z_{I_1\cup I_0}} (\bar{z}),\; \chi _{I_0}=0 \end{array} \right\} , \end{aligned}$$

(47)

where for a vector $\mu$ with positive components, $\mu ^{-1}$ stands for the vector whose components are the inverses of those of $\mu$.

Assuming that the components of all vectors are ordered as above, since $R_P(\bar{u})=(\mathbb {R}^{|I_1|} \times \mathbb {R}_+^{|I_0|}\times \mathbb {R}^{|I_2|})\times (\mathbb {R}^{|I_1|} \times \mathbb {R}_+^{|I_0|}\times \mathbb {R}^{|I_2|})$, we then conclude that $\ker \varPhi '(\bar{u})$ consists of $\bar{v}:=(\bar{\zeta } ,\, \bar{\xi } )$ with $\bar{\zeta }$ and $\bar{\xi }$ satisfying

$$\begin{aligned} \frac{\partial F_{I_1}}{\partial z_{I_1\cup I_0}} (\bar{z})\bar{\zeta } _{I_1\cup I_0}=0,\quad \frac{\partial F_{I_0\cup I_2}}{\partial z_{I_1\cup I_0}} (\bar{z})\bar{\zeta } _{I_1\cup I_0} =\bar{\xi } _{I_0\cup I_2},\quad \bar{\zeta } _{I_2}=0,\quad \bar{\xi } _{I_1}=0, \end{aligned}$$

(48)

while $\bar{v}\in \mathrm{int}R_P(\bar{u})$ means that

$$\begin{aligned} \bar{\zeta } _{I_0}>0,\quad \bar{\xi } _{I_0}>0. \end{aligned}$$

(49)

Employing (47) and (48), it can be seen that for any $\bar{v}:=(\bar{\zeta } ,\, \bar{\xi } )\in \ker \varPhi '(\bar{u})$, 2-regularity of $\varPhi$ at $\bar{u}$ in the direction $\bar{v}$ is equivalent to saying that there exists no nonzero $u:=(z,\, x)$ satisfying

$$\begin{aligned} \frac{\partial F_{I_1}}{\partial z_{I_1\cup I_0}} (\bar{z})z_{I_1\cup I_0}=0,\quad \frac{\partial F_{I_0\cup I_2}}{\partial z_{I_1\cup I_0}} (\bar{z})z_{I_1\cup I_0} =x_{I_0\cup I_2},\quad z_{I_2}=0,\quad x_{I_1}=0, \end{aligned}$$

(50)

and such that

$$\begin{aligned} \frac{\partial ^2F_{I_1}}{\partial z_{I_1\cup I_0}^2} (\bar{z})[\bar{\zeta } _{I_1\cup I_0},\, z_{I_1\cup I_0}] \in \mathrm{im}\frac{\partial F_{I_1}}{\partial z_{I_1\cup I_0}} (\bar{z}),\quad \bar{\xi } _{I_0}\circ z_{I_0}+\bar{\zeta } _{I_0}\circ x_{I_0}=0. \end{aligned}$$

(51)

We therefore conclude that Theorem 3.1 is applicable to the constrained equation in question with every $\bar{v}:=(\bar{\zeta } ,\, \bar{\xi } )$ such that (48), (49), and $\Vert \bar{v}\Vert =1$ hold, and there exists no nonzero $u:=(z,\, x)$ satisfying (50), (51).

Observe that if $F'(\bar{z})=0$, as in Example 4.1, then (48) and (50) imply that $\bar{\xi } _{I_0\cup I_2}=0$, $x_{I_0\cup I_2}=0$, and (51) reduces to the equality

$$\begin{aligned} \frac{\partial ^2F_{I_1}}{\partial z_{I_1\cup I_0}^2} (\bar{z})[\bar{\zeta } _{I_1\cup I_0},\, z_{I_1\cup I_0}]=0. \end{aligned}$$

This is a homogeneous linear system with $|I_1|$ equations and $|I_1|+|I_0|$ variables, and it always has a nontrivial solution unless $I_0=\emptyset$. Therefore, Theorem 3.1 can be applicable in this case only if $I_0=\emptyset$. The latter is not fulfilled for $\bar{z}$ considered in Example 4.1. And indeed, numerical experiments demonstrate the absence of any clear attraction to $\bar{u}$ in this example for the constrained Gauss–Newton method and the other methods, for the smooth NCP reformulation. Some iterative sequences generated by the constrained Levenberg–Marquardt method and the LP-Newton method are shown in Fig. 7. The Gauss–Newton method for this example terminates in one iteration at the orthogonal projection of $z^0$ onto the straight line given by the equation $z_2=0$.

Fig. 7

Iterative sequences for smooth reformulation of NCP from Example 4.1. a Levenberg–Marquardt method. b LP-Newton method

At the same time, in general, the system (50), (51) may reduce to 2s independent linear equations in the same number of variables, as will be demonstrated by examples below.

By Theorem 3.1 (when it is applicable), we obtain that for every $\hat{\varepsilon } >0$ and $\hat{\delta } >0$, there exist $\varepsilon >0$ and $\delta >0$ such that any starting point $u^0\in K_{\varepsilon ,\, \delta }(\bar{u},\, \bar{v})$ uniquely defines the sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k it holds that $v^k:=u^{k+1}-u^k$ solves (9) with $\varOmega \equiv 0$ and $\omega \equiv 0$, and for this sequence and for each k it holds that $u_2^k\not =\bar{u}_2$, and $u^k\in P\cap K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$. Assuming that $\hat{\varepsilon } >0$, and employing (19), this implies that $z_{I_1}^k>0$, $x_{I_2}^k>0$, $z_{I_0}^k\ge 0$, and $x_{I_0}^k\ge 0$.

Observe further that, according to (44) with (43), equation (9) being solved by $v^k$ yields

$$\begin{aligned} z^k\circ x^k+x^k\circ \zeta ^k+z^k\circ \xi ^k=0 \end{aligned}$$

for all k. This implies that, for all $i\in I_2$,

$$\begin{aligned} z_i^{k+1}=z_i^k+\zeta _i^k=-\frac{z_i^k}{x_i^k}\xi _i^k \end{aligned}$$

and, for all $i\in I_1$,

$$\begin{aligned} x_i^{k+1}=x_i^k+\xi _i^k=-\frac{x_i^k}{z_i^k}\zeta _i^k \end{aligned}$$

holds. Therefore, if we show that

$$\begin{aligned} \zeta _{I_1}^k\le 0,\quad \xi _{I_2}^k\le 0, \end{aligned}$$

(52)

then, assuming that $u^0\ge 0$, it would follow that $u^k\ge 0$ for all k. We verify this next.

In order to obtain the needed inequalities, in addition to the assumptions stated above, we require that

$$\begin{aligned} \bar{\zeta } _{I_1}>0,\quad \bar{\xi } _{I_2}>0. \end{aligned}$$

(53)

Then, (52) holds for all $v^k:=(\zeta ^k,\, \xi ^k)$ such that $v^k/\Vert v^k\Vert$ is close enough to $(-\bar{v})$. Therefore, it is sufficient to show that the latter property is automatic provided $\hat{\varepsilon } >0$ and $\hat{\delta } >0$ are small enough. To prove this we first assume without loss of generality that $\bar{u}:=0$. As established above, for each k it holds that both $u^k$ and $u^{k+1}:=u^k+v^k$ belong to $K_{\hat{\varepsilon } ,\, \hat{\delta } }(\bar{u},\, \bar{v})$, and in particular, they are not equal to zero.

As an ingredient of our reasoning, we will reuse a formula from the proof of Theorem 1 in [7]. This formula is displayed there directly after (34) and can be written as

$$\begin{aligned} \left( \frac{1}{2} -\rho (\hat{\varepsilon } ,\, \hat{\delta } )\right) \Vert u^k\Vert \le \Vert u^k+v^k\Vert \le \left( \frac{1}{2} +\rho (\hat{\varepsilon } ,\, \hat{\delta } )\right) \Vert u^k\Vert , \end{aligned}$$

(54)

where $\rho :]0,\, \infty [\times ]0,\, \infty [\rightarrow ]0,\, \infty [$ denotes some function with $\rho (\varepsilon ,\, \delta )\rightarrow 0$ as $(\varepsilon ,\, \delta )\rightarrow (0,\, 0)$. Since

$$\begin{aligned} \left\| \frac{u^k+v^k}{\Vert u^k+v^k\Vert } -\frac{u^k}{\Vert u^k\Vert } \right\| \le \left\| \frac{u^k+v^k}{\Vert u^k+v^k\Vert } -\bar{v}\right\| +\left\| \frac{u^k}{\Vert u^k\Vert } - \bar{v}\right\| \le 2\hat{\delta } , \end{aligned}$$

we obtain

$$\begin{aligned} \left\| u^k+v^k -\frac{\Vert u^k+v^k\Vert }{\Vert u^k\Vert } u^k\right\| \le 2\hat{\delta } \Vert u^k+v^k\Vert . \end{aligned}$$

This implies

$$\begin{aligned} \left\| v^k +\frac{1}{2} u^k\right\|= & {} \left\| u^k+v^k-\frac{1}{2} u^k\right\| \nonumber \\\le & {} \left\| u^k+v^k -\frac{\Vert u^k+v^k\Vert }{\Vert u^k\Vert } u^k\right\| + \left\| \frac{1}{2} u^k-\frac{\Vert u^k+v^k\Vert }{\Vert u^k\Vert } u^k\right\| \nonumber \\\le & {} 2\hat{\delta }\Vert u^k+v^k\Vert +\left| \frac{1}{2} -\frac{\Vert u^k+v^k\Vert }{\Vert u^k\Vert } \right| \Vert u^k\Vert \nonumber \\\le & {} \left( \hat{\delta }+2\hat{\delta }\rho (\hat{\varepsilon },\, \hat{\delta })+\rho (\hat{\varepsilon },\, \hat{\delta })\right) \Vert u^k\Vert , \end{aligned}$$

(55)

where the last inequality is by (54). Therefore, setting $\hat{\rho } (\hat{\varepsilon },\, \hat{\delta }):=\hat{\delta }+2\hat{\delta }\rho (\hat{\varepsilon },\, \hat{\delta })+\rho (\hat{\varepsilon },\, \hat{\delta })$, we have

$$\begin{aligned} \left( \frac{1}{2}-\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })\right) \Vert u^k\Vert \le \Vert v^k\Vert \le \left( \frac{1}{2}+\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })\right) \Vert u^k\Vert , \end{aligned}$$

and, hence,

$$\begin{aligned} 1-2\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })\le \frac{1}{2}\frac{\Vert u^k\Vert }{\Vert v^k\Vert }\le 1+2\hat{\rho }(\hat{\varepsilon },\, \hat{\delta }). \end{aligned}$$

(56)

From (55) and (56), we further derive

$$\begin{aligned} \left\| \frac{u^k}{\Vert u^k\Vert } +\frac{v^k}{\Vert v^k\Vert } \right\|\le & {} \left\| \frac{v^k}{\Vert v^k\Vert } +\frac{1}{2} \frac{u^k}{\Vert v^k\Vert } \right\| +\left\| \frac{u^k}{\Vert u^k\Vert } -\frac{1}{2} \frac{u^k}{\Vert v^k\Vert }\right\| \\\le & {} \hat{\rho }(\hat{\varepsilon },\, \hat{\delta })\frac{\Vert u^k\Vert }{\Vert v^k\Vert } +\left| 1-\frac{1}{2} \frac{\Vert u^k\Vert }{\Vert v^k\Vert } \right| \\\le & {} 4\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })(1+\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })). \end{aligned}$$

This yields

$$\begin{aligned} \left\| \frac{v^k}{\Vert v^k\Vert } +\bar{v}\right\| \le \left\| \frac{u^k}{\Vert u^k\Vert } -\bar{v}\right\| +\left\| \frac{u^k}{\Vert u^k\Vert } +\frac{v^k}{\Vert v^k\Vert } \right\| \le \hat{\delta } +4\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })(1+\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })), \end{aligned}$$

implying that $v^k/\Vert v^k\Vert$ can be made arbitrarily close to $(-\bar{v})$ by taking $\hat{\varepsilon } >0$ and $\hat{\delta } >0$ (and thereby $\rho (\hat{\varepsilon },\hat{\delta })$ and $\hat{\rho }(\hat{\varepsilon },\, \hat{\delta })$) small enough.

The analysis above allows to employ Theorem 3.1 to characterize the domain of convergence to $\bar{u}$ of the constrained Gauss–Newton method for the smooth reformulation of the NCP (14). The method solves the following subproblems:

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \displaystyle \frac{1}{2} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert ^2 +\frac{1}{2} \Vert \varPsi (u^k)+\varPsi '(u^k)v\Vert ^2\\ \text{ s.t. } &{} u^k+v\ge 0, \end{array} \end{aligned}$$

(57)

with respect to $v:=(\zeta ,\, \xi )$. The resulting assertions are as follows.

Proposition 4.4

Let $F:\mathbb {R}^s\rightarrow \mathbb {R}^s$ be twice differentiable near $\bar{z}\in \mathbb {R}^s$, with its second derivative being Lipschitz-continuous with respect to $\bar{z}$. Let $\bar{z}$ be a solution of the NCP (14), and let $\bar{u}:= (\bar{z},\, \bar{x})$, where $\bar{x}:=F(\bar{z})$. Assume that there exist $\bar{v}:=(\bar{\zeta } ,\, \bar{\xi } )\in \mathbb {R}^s\times \mathbb {R}^s$ such that (48), (49), (53), and $\Vert \bar{v}\Vert =1$ hold, and there exists no nonzero $u:=(z,\, x)$ satisfying (50), (51).

Then, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in \mathbb {R}^s\times \mathbb {R}^s$ satisfying (35) there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k the step $v^k:=u^{k+1}-u^k$ solves (57) with $\varPsi$ defined in (43), $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

For the smooth NCP reformulation with $\varPsi$ given by (43), the subproblems of the constrained Levenberg–Marquardt method have the form

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \displaystyle \frac{1}{2} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert ^2 +\frac{1}{2} \Vert \varPsi (u^k)+\varPsi '(u^k)v\Vert ^2 +\frac{1}{2} \sigma (u^k)\Vert v\Vert ^2\\ \text{ s.t. } &{} u^k+v\ge 0, \end{array} \end{aligned}$$

(58)

while the LP-Newton method solves subproblems

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert F(z^k)-x^k+F'(z^k)\zeta -\xi \Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ^2,\\ &{}\Vert \varPsi (u^k)+\varPsi '(u^k)v\Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ^2,\\ &{}\Vert v \Vert \le \gamma \Vert (F(z^k)-x^k,\, \varPsi (u^k))\Vert ,\\ &{}u^k+v\ge 0. \end{array} \end{aligned}$$

(59)

The convergence of the corresponding methods can now be considered literally following the arguments in Sect. 4.1. According to this, we obtain the following.

Proposition 4.5

Under the assumptions of Proposition 4.4, for any $\tau \ge 2$, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in \mathbb {R}^s\times \mathbb {R}^s$ satisfying (35), there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k the step $v^k:=u^{k+1}-u^k$ solves (58) with $\varPsi$ defined in (43), $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

Proposition 4.6

Under the assumptions of Proposition 4.4, there exist $\varepsilon >0$ and $\delta >0$ such that for any starting point $u^0:=(z^0,\, x^0)\in \mathbb {R}^s\times \mathbb {R}^s$ satisfying (35), there exists a sequence $\{ u^k\} \subset \mathbb {R}^s\times \mathbb {R}^s$ such that for each k it holds that $(v^k,\, \gamma _{k+1})$ with $v^k:=u^{k+1}-u^k$ and some $\gamma _{k+1}$ solves (59) with $\varPsi$ defined in (43); any such sequence $\{ u^k\}$ converges to $\bar{u}$, and the rate of convergence is linear.

Next, we give some illustrations.

Fig. 8

Gauss–Newton method for Example 4.2. a Iterative sequences. b Domain of attraction to solution in question

Fig. 9

Levenberg–Marquardt method for Example 4.2. a Iterative sequences. b Domain of attraction to solution in question

Fig. 10

LP-Newton method for Example 4.2. a Iterative sequences. b Domain of attraction to solution in question

Example 4.2

Let $s:=2$, $F(z):=(z_1,\, z_1)$. The solution set of the NCP (14) has the form $\mathcal{S}=\{ z\in \mathbb {R}^2:\, z_1=0,\, z_2\ge 0\}$, and the only solution violating strict complementarity is $\bar{z}:=0$. Then, $I_0=\{ 1,\, 2\}$, $I_1=I_2=\emptyset$, and conditions (48), (49) reduce to

$$\begin{aligned} \bar{\zeta } _1=\bar{\xi } _1=\bar{\xi } _2>0,\quad \bar{\zeta } _2>0, \end{aligned}$$

(60)

while (53) is vacuous. Furthermore, conditions (50) and (51) reduce to

$$\begin{aligned} z_1=x_1=x_2,\quad \bar{\xi } _1z_1+\bar{\zeta } _1x_1=0,\quad \bar{\xi } _2z_2+\bar{\zeta } _2x_2=0, \end{aligned}$$

and taking into account (60), this system with respect to $(z,\, x)$ has only the trivial solution. Therefore, Propositions 4.4–4.6 are applicable with $\bar{v}:=((t,\, \theta ),\, (t,\, t))$, with any $t>0$ and $\theta >0$ such that $3t^2+\theta ^2=1$.

In Figs. 8, 9 and 10, the vertical line along the left side of the square is the solution set. These figures present the same kind of information as Figs. 1, 2 and 3, using the rule for starting values of the slack variable specified in Remark 4.1. The observed behavior agrees with Propositions 4.4–4.6.

Fig. 11

Gauss–Newton method for Example 4.3. a Iterative sequences: main variables. b Iterative sequences: slack variables

Fig. 12

Levenberg–Marquardt method for Example 4.3. a Iterative sequences: main variables. b Iterative sequences: slack variables

Fig. 13

LP-Newton method for Example 4.3. a Iterative sequences: main variables. b Iterative sequences: slack variables

Example 4.3

Let $s:=2$, $F(z):=(z_1,\, z_1+1)$. The NCP (14) has the unique solution $\bar{z}:=0$, at which $\bar{x}=(0,\, 1)$, $I_1=\emptyset$, $I_0=\{ 1\}$, $I_2=\{ 2\}$. Conditions (48), (49) and (53) reduce to

$$\begin{aligned} \bar{\zeta } _1=\bar{\xi } _1=\bar{\xi } _2>0,\quad \bar{\zeta } _2=0, \end{aligned}$$

(61)

whereas conditions (50) and (51) provide

$$\begin{aligned} z_1=x_1=x_2,\quad z_2=0,\quad \bar{\xi } _1z_1+\bar{\zeta } _1x_1=0. \end{aligned}$$

Taking into account (61), this system with respect to $(z,\, x)$ has only the trivial solution. Therefore, Propositions 4.4–4.6 are applicable if we take in them $\bar{v}:=((1/\sqrt{3} ,\, 0),\, (1/\sqrt{3} ,\, 1/\sqrt{3} )$.

Figures 11a, 12a and 13a present some sequences $\{ z^k\}$ generated by the three methods in question, using the rule for starting values of the slack variable specified in Remark 4.1. These figures demonstrate a tendency of the sequences to converge to $\bar{z}$ along the horizontal direction in the boundary of the constraint set. Moreover, the sequences of the Gauss–Newton method actually consist of the basic Newton iterates, and therefore, we observe that the latter never leave the constraint set in this example, even though they are moving along the boundary of this set.

In order to obtain some impression of the behavior of slack sequences, in Figures 11b, 12b and 13b we present some sequences $\{ x^k\}$ generated by the same methods, using $z^0:=(1,\, 1)$. These sequences have a tendency to converge to $\bar{x}$ along the direction with coinciding components.

The observed behavior again fully agrees with Propositions 4.4–4.6.

In addition, we point out that the projected versions of the methods above can be treated similarly to how this is done in Sect. 4.1, giving results for the counterparts of Propositions 4.4–4.6.

Finally, we note that the problems in Examples 4.2 and 4.3 are actually linear complementarity problems, implying that the mapping $\varPhi$ defined in (18) is affine, and hence, it cannot be 2-regular in any direction at any singular solution (as its second derivative is zero). This means that the assumptions of Proposition 4.1 cannot hold in these examples. Recall also that, on the other hand, Proposition 4.4 is not applicable to the problem from Example 4.1. Therefore, the assumptions of Propositions 4.1 and 4.4 are not comparable: neither implies the other.

5 Conclusions

In this paper, we have established local linear convergence for a family of Newton-type methods to certain special solutions of constrained equations, in particular violating the local Lipschitzian error bound. Convergence is shown from large domains of starting points, under the assumption which may hold naturally at such special solutions only, and allows for these solutions to be nonisolated.

One line of further development of these results might be concerned with extensions to the case of equations with Lipschitzian first derivatives, but possibly in the absence of second derivatives, along the lines of [11]. Such extensions might be of interest even in the unconstrained case, with applications to smooth unconstrained reformulations of complementarity problems.

Another promising possibility is an extension to the case of piecewise smooth equations, probably with pieces having Lipschitzian second derivatives. This development might also be of interest even for the unconstrained case, and might allow to cover (unconstrained or constrained) piecewise smooth reformulations of complementarity problems in a unified manner.