1 Introduction

Let us consider the constrained system of equations

$$ H(x)=0,\quad x\in\varOmega, $$
(1)

where \(H:\mathbb {R}^{n}\to \mathbb {R}^{m}\) is continuously differentiable with a locally Lipschitz continuous Jacobian \(J_{H}:\mathbb {R}^{n}\to \mathbb {R}^{m \times n}\). The set \(\varOmega\subseteq \mathbb {R}^{n}\) is closed and convex. Throughout the paper, \(O:=\{x\in \mathbb {R}^{n}\,|\,H(x)=0\}\) denotes the set of zeros of H. Moreover, the solution set X:=O∩Ω of problem (1) is assumed to be nonempty. For later use let x ∗ denote an arbitrary but fixed element of X.

In order to describe the aim and developments of this paper in more detail we need to recall some basic facts and recent work on Levenberg-Marquardt methods. The basic idea of regularizing the Gauss-Newton method goes back to Levenberg [18] and Marquardt [19]. For the unconstrained case (\(\varOmega=\mathbb {R}^{n}\)), in each step of a Levenberg-Marquardt method, the subproblem

$$ \min_{x\in \mathbb {R}^n} \varphi_0(x,s) $$
(2)

has to be solved for some \(s\in \mathbb {R}^{n}\) (current iterate), where \(\varphi_{0}:\mathbb {R}^{n}\times \mathbb {R}^{n}\to \mathbb {R}\) is given by

$$\varphi_0(x,s):=\frac{1}{2}\big\|H(s)+J_H(s) (x-s) \big\|^2+\frac{1}{2}\alpha(s)\|x-s\|^2 $$

with a regularization parameter α(s)>0. Here and throughout the paper, ∥⋅∥ denotes the Euclidean norm. Note that (2) has a strongly convex objective, is equivalent to a system of linear equations, and possesses a unique solution.

In 2001 Yamashita and Fukushima [21] opened a new direction of research for Levenberg-Marquardt methods. In the unconstrained case they showed that the regularization parameter can be chosen in such a way that superlinear convergence to nonisolated solutions is attainable. The main ingredient for obtaining this result is the following error bound condition on a ball

$$\mathcal{B}\bigl(x^*,\delta\bigr):=\bigl\{x\in \mathbb {R}^n\,|\,\big\|x-x^*\big\|\le\delta \bigr\}. $$

By \(\operatorname {dist}[x,W]:=\inf\{\|x-w\|\,|\,w\in W\}\) the distance of \(x\in \mathbb {R}^{n}\) to a nonempty set \(W\subset \mathbb {R}^{n}\) is denoted.

Condition 1

There exist ω>0 and δ>0 such that

$$\omega \operatorname {dist}[x,O]\le\|H(x)\|\quad\mbox{\textit{for all}}\ x\in\mathcal{B}\bigl(x^*,\delta \bigr). $$

This condition is significantly weaker than the classical nonsingularity assumption on J H (x ∗) (for m=n). In particular, Condition 1 does not imply that x ∗ is an isolated solution. If Condition 1 holds then the system H(x)=0 is called calm at x ∗. For other and related notions see [12, 20]. If H is affine (see [16]) or if the rank of J H (x ∗) is full, then H(x)=0 is calm at x ∗. However, Condition 1 encompasses also situations in which J H (x ∗) is not full rank. For example, for the calm system H(x 1,x 2):=(x 2,x 2exp(x 1))⊤=0, the rank of J H is 1 on the solution set and 2 otherwise. For a detailed analysis of consequences of Condition 1 see [1, 3].

In the last decade several works continued the ideas of [21]. Among them are papers on a more robust regularization [11, 12], on inexact Levenberg-Marquardt methods [4, 9, 10, 14], on applications [7, 13], and on constrained Levenberg-Marquardt methods [2, 17, 22]. Instead of (2), the latter methods employ more complex subproblems. In particular,

$$ \min_{x\in\varOmega} \varphi_0(x,s) $$
(3)

was suggested by Kanzow, Yamashita, and Fukushima [17]. They proved local quadratic convergence by means of the following error bound condition.

Condition 2

There exist ω>0 and δ>0 such that

$$ \omega \operatorname {dist}[x,X]\le\|H(x)\|\quad\mbox{\textit{for all}}\ x\in\mathcal{B}\bigl(x^*,\delta \bigr)\cap\varOmega. $$

This condition has the advantage that it is restricted to points in Ω only. It turned out that this error bound condition (together with further assumptions) can be quite useful for dealing with problem (1) if H is nonsmooth; see [6]. Since solving the constrained subproblem (3) can be computationally challenging or, at least, is more expensive than solving the unconstrained minimization problem (2), a projected Levenberg-Marquardt method is suggested in [17] (see also [8, 13]). Per step, the latter method requires the solution of the unconstrained minimization problem (2) plus a projection onto Ω. If the projection is cheap then the computational costs per step compare favorably to the costs of solving (3). However, in order to prove local quadratic convergence, the following quite strong error bound condition is needed.

Condition 3

There exist ω>0 and δ>0 such that

$$\omega \operatorname {dist}[x,X]\le\big\|H(x)\big\|\quad\mbox{\textit{for all}}\ x\in\mathcal{B}\bigl(x^*, \delta\bigr). $$

Obviously, Condition 3 is much stronger than Condition 2. In particular, Condition 3 implies that

$$X\cap \mathcal{B}\bigl(x^*,\delta\bigr)=O\cap \mathcal{B}\bigl(x^*,\delta\bigr) $$

holds for some sufficiently small δ>0, i.e., the set Ω can be disregarded in a neighborhood of x ∗.

The aim of this paper is to design a Levenberg-Marquardt type method that does not need such a strong error bound condition but still employs the simple subproblems (2). Instead, we will use Conditions 1 and 2 as a pair. The price we have to pay is that only local R-linear convergence can be shown, but still to a possibly nonisolated solution of problem (1). To replace the exact projections onto the set Ω the new method allows approximate projections without losing the linear rate. Often, such approximate projections can be done in a computationally cheap way and can be applied even if the set Ω is described by nonsmooth inequalities. Besides approximate projections the new method is able to cope with a certain level of inexactness in solving the subproblem (2).

The paper is organized as follows. In Sect. 2 we formally introduce the Levenberg-Marquardt algorithm with approximate projections. After presenting the assumptions, Sect. 3 is devoted to the convergence analysis of the new algorithm. The paper is completed by final remarks in Sect. 4. They include discussions on the sharpness of the inexactness level and of the convergence rate, as well as a numerical example.

2 Levenberg-Marquardt algorithm with approximate projections

In this section we present a Levenberg-Marquardt method with approximate projections and a possibly inexact solution of the subproblems (2). The next two subsections collect the necessary ingredients for defining the algorithm in Sect. 2.3.

2.1 Inexact subproblems

The Levenberg-Marquardt subproblems we are going to use enable an inexact solution and read as

$$ \min_{x\in \mathbb {R}^n}\varphi(x,s), $$
(4)

where \(\varphi:\mathbb {R}^{n}\times \mathbb {R}^{n}\to \mathbb {R}\) is defined by

$$ \varphi(x,s):= \frac{1}{2} \big\|H(s)+J_H(s) (x-s)\big\|^2+\frac{1}{2}\alpha(s)\|x-s \|^2-\pi(s)^{\top}(x-s) $$
(5)

with \(\alpha:\mathbb {R}^{n}\to \mathbb {R}\) given by

$$ \alpha(s):=\left \{ \begin{array}{l@{\quad}l} \|H(s)\|&\mbox{ if }s\in \mathbb {R}^n\setminus O,\\[3pt] 1&\mbox{ if }s\in O. \end{array} \right . $$
(6)

Moreover, \(\pi:\mathbb {R}^{n}\to \mathbb {R}^{n}\) denotes a function that, for some ϰ,η>0, satisfies

$$ \big\|\pi(s)\big\|\le\varkappa\big\|H(s)\big\|^{2+\eta} $$
(7)

for all \(s\in \mathbb {R}^{n}\). The function π is not explicitly needed within the algorithm but is used to describe and analyze the possible level of inexactness. With the above definition of subproblem (4) we easily see that, for any \(s\in \mathbb {R}^{n}\), this subproblem has a unique solution which we denote by x(s). If s∈O, the definitions of the functions α and π imply x(s)=s. For any \(s\in \mathbb {R}^{n}\), the solution x(s) can be characterized by the necessary and sufficient optimality condition ∇ x φ(x,s)=0, i.e., by a linear system of n equations with n variables. With the definition of the objective φ 0 in the exact Levenberg-Marquardt subproblem (2), we obtain

$$\nabla_x\varphi_0\bigl(x(s),s\bigr)=\pi(s) $$

Thus, π(s) can be regarded as the residual of the optimality condition

$$\nabla_x\varphi_0(x,s)=0$$

for subproblem (2) at x=x(s).

2.2 Approximate projections

Projected Levenberg-Marquardt methods employ a projection step that maps an iterate \(s\in \mathbb {R}^{n}\) onto its nearest point in the set Ω. In order to relax this projection step, we introduce the notion of an approximate projector.

Definition 1

Let \(B\subseteq \mathbb {R}^{n}\) be a nonempty set. A function \(\tilde{P}_{\varOmega}:B\to \mathbb {R}^{n}\) is called an approximate projector defined on B and associated to Ω if the following properties are satisfied:

  1. 1.

    There exists a number γ∈[0,1) such that

    $$ \operatorname {dist}\bigl[\tilde{P}_\varOmega (x),\varOmega \bigr]\le\gamma \operatorname {dist}[x,\varOmega] \quad\mbox{for all}\ x\in B. $$
    (8)
  2. 2.

    For any x∈B, it holds that

    $$ \bigl(x-\tilde{P}_\varOmega (x) \bigr)^{\top} \bigl(y-\tilde{P}_\varOmega (x) \bigr) \le 0\quad \mbox{for all}\ y\in\varOmega. $$
    (9)

The vector \(\tilde{P}_{\varOmega}(x)\) is called an approximate projection of x∈B.

Property 2 in the previous definition means that, for a point x∈B∖Ω, the approximate projection \(\tilde{P}_{\varOmega}(x)\) is the orthogonal projection of x onto some hyperplane h x separating x from Ω.

Of course, the orthogonal projector onto Ω, \(P_{\varOmega}:\mathbb {R}^{n}\to\varOmega\), with P Ω (x) being the unique solution of the minimization problem

$$\min_{w\in\varOmega}\|x-w\|, $$

is an approximate projector defined on \(\mathbb {R}^{n}\) associated to Ω. Indeed, for \(\tilde{P}_{\varOmega}=P_{\varOmega}\), Property 1 in Definition 1 is satisfied with γ=0 and Property 2 is well-known for the orthogonal projector. For some sets Ω, calculating the orthogonal projection of a given point \(x\in \mathbb {R}^{n}\) is not very hard, for instance if Ω is a halfspace, or if it is described by box constraints. However, the projection task can become computationally expensive if Ω is a more general convex set. Fortunately, determining an approximate projection is possible with only little effort in most cases. For example, let us consider the important case in which Ω is described by general convex inequalities, i.e., \(\varOmega:=\{x\in \mathbb {R}^{n}\,|\,g_{i}(x)\le 0,\,i=1,\ldots ,m\}\), where \(g_{1},\ldots,g_{m}:\mathbb {R}^{n}\to \mathbb {R}\) are convex but not necessarily differentiable functions. Then, it is well-known that \(g:\mathbb {R}^{n}\to \mathbb {R}\) defined by g(x):=max{g 1(x),…,g m (x)} is convex and Ω can be written as \(\varOmega:=\{x\in \mathbb {R}^{n}\,|\,g(x)\le 0\}\). Therefore, without loss of generality, only the case m=1 needs to be considered. The following proposition is based on [15] and provides a special approximate projector by means of subgradients of g, i.e., of elements of the subdifferential ∂g(x) of g at x. Moreover, an explicit formula for computing an approximate projection is given. The computational expense of this approximate projection is low, provided that the computation of a subgradient of g is not too expensive.

Proposition 1

Suppose that \(g:\mathbb {R}^{n}\to \mathbb {R}\) is a convex function and that there exists some \(\hat{x}\in \mathbb {R}^{n}\) with \(g(\hat{x})<0\) (Slater condition). Let \(v:\mathbb {R}^{n}\to \mathbb {R}^{n}\) denote a mapping with v(x)∈∂g(x) for any \(x\in \mathbb {R}^{n}\). Moreover, let the mapping \(\tilde{p}:\mathbb {R}^{n}\to \mathbb {R}^{n}\) be defined pointwise, with \(\tilde{p}(x)\) being the unique solution of the problem

$$ \min_p\|p-x\|\quad\mbox{\textit{s.t.}}\quad g(x)+v(x)^{\top}(p-x)\le 0. $$
(10)

Then, the following assertions hold:

  1. (i)

    For any nonempty compact set \(B\subset \mathbb {R}^{n}\), the mapping \(\tilde{p}\) is an approximate projector defined on B associated to the set \(\varOmega:=\{x\in \mathbb {R}^{n}\,|\,g(x)\le 0\}\).

  2. (ii)

    For any \(x\in \mathbb {R}^{n}\), the solution \(\tilde{p}(x)\) of (10) is given by

    $$ \tilde{p}(x)= \begin{cases} x-\frac{g(x)}{\|v(x)\|^2}v(x) & \mbox{\textit{if}\ $g(x)>0$,}\\[3pt] x &\mbox{\textit{if}\ $g(x)\le 0$.} \end{cases} $$
    (11)

Proof

(i) The existence of γ∈[0,1) such that \(\operatorname {dist}[\tilde{p}(x),\varOmega]\le\gamma \operatorname {dist}[x,\varOmega]\) for all x∈B follows from [15, Lemma 4], i.e., (8) holds for \(\tilde{P}_{\varOmega}:=\tilde{p}\). Furthermore, for \(x\in \mathbb {R}^{n}\setminus\varOmega\), the solution \(\tilde{p}(x)\) of (10) is the orthogonal projection of x onto the hyperplane

$$h_x:=\bigl\{w\in \mathbb {R}^n\,|\,g(x)+v(x)^{\top}(w-x)=0 \bigr\}. $$

Since v(x) is a subgradient of g in x, this hyperplane separates x from the convex set Ω and therefore (9) holds. Thus, the mapping \(\tilde{p}\) is an approximate projector defined on B associated to Ω.

(ii) This assertion can be easily verified. □

2.3 The algorithm

Let \(\tilde{P}_{\varOmega}\) denote an approximate projector defined on B associated to Ω.

Since subproblem (4) has always a unique solution, Algorithm 1 is well-defined as long as the approximate projection \(\tilde{P}_{\varOmega}(x(x^{k}))\) is defined. The latter is the case if x(x k) belongs to B, see Definition 1. The restriction to B is only a formal aspect. For example let us consider the mapping \(\tilde{p}\) defined in Proposition 1. Due to assertion (ii) of this proposition, \(\tilde{p}\) is well-defined on \(\mathbb {R}^{n}\) and satisfies Property 2 of Definition 1. Property 1 of this definition holds at least on compact sets B. The latter, however, is sufficient for our local convergence analysis. Note that the iterates of a sequence {x k} generated by Algorithm 1 do not necessarily belong to Ω.

Algorithm 1
figure 1

Levenberg-Marquardt algorithm with approximate projections (LMAP)

Full size image

3 Convergence analysis

In the first subsection we state the assumptions that will be used later on in Sect. 3.2 for analyzing the local convergence properties of Algorithm 1.

3.1 Assumptions

As in Sect. 1, let x ∗∈X denote an arbitrary but fixed solution of (1). Moreover, let δ∈(0,1] denote the arbitrary but fixed radius of the ball \(\mathcal{B}(x^{*},\delta)\).

Assumption 1

The mapping \(H:\mathbb {R}^{n}\to \mathbb {R}^{m}\) is differentiable on \(\mathcal{B}(x^{*},\delta)\) and its Jacobian \(J_{H}:\mathbb {R}^{n}\to \mathbb {R}^{m \times n}\) is Lipschitz continuous on \(\mathcal{B}(x^{*},\delta)\).

To avoid Condition 3 we now present the pair of reasonable error bound conditions.

Assumption 2

There exists ω>0 such that

$$ \omega \operatorname {dist}[x,O]\le\big\|H(x)\big\|\quad\mbox{for all}\ x\in \mathcal{B}\bigl(x^*, \delta\bigr) $$
(12)

and

$$ \omega \operatorname {dist}[x,X]\le\big\|H(x)\big\|\quad\mbox{for all}\ x\in \mathcal{B}\bigl(x^*,\delta\bigr)\cap\varOmega. $$
(13)

Roughly speaking, the error bound (12) (together with the Lipschitz continuity of H around x ∗) implies that ∥H(x)∥ grows locally like \(\operatorname {dist}[x,O]\), while (13) does not allow Ω to be in some sense tangent to O.

The next examples show that the error bounds (12) and (13) do not imply each other.

Example 1

Let \(H:\mathbb {R}^{2}\to \mathbb {R}\) and Ω be given by H(x 1,x 2):=x 2 and

$$\varOmega:=\bigl\{(x_1,x_2)^{\top}\in \mathbb {R}^2\,|\,g(x_1,x_2)\le 0\bigr\}\quad \mbox{with} \ g(x_1,x_2):=\left \{ \begin{array}{l@{\quad}l} x_1^2-x_2&\mbox{if}\ x_1\le 0,\\[3pt] -x_2&\mbox{if}\ x_1>0. \end{array} \right . $$

It is easy to see that the error bound (12) holds for any solution x ∗∈X={(x 1,0)⊤ | x 1≥0} and that (13) is violated for x ∗=0.

Example 2

Let \(H:\mathbb {R}^{3}\to \mathbb {R}^{2}\) and Ω be given by

$$H(x_1,x_2,x_3):=(x_3,x_1x_2)^{\top} \quad\mbox{and}\quad \varOmega:=\bigl\{(x_1,x_2,x_3)^{\top} \in \mathbb {R}^3\,|\,x_3\ge|x_2|\bigr\}. $$

In this example, (13) is satisfied while (12) is violated for x ∗=0.

3.2 Local analysis

In order to prove our main convergence theorem, we need some auxiliary results. Some of them are quite technical, whereas the first lemma is elementary.

Lemma 1

Let Assumption 1 be satisfied. Then, there exists L>0 such that, for all \(x,s\in \mathcal{B}(x^{*},\delta)\), the following inequalities hold:

(14)
(15)

The next lemma lists some properties of an inexact unconstrained Levenberg-Marquardt step. Recall that, for a given point \(s\in \mathbb {R}^{n}\), we denote by x(s) the unique solution of subproblem (4).

Lemma 2

Let Assumptions 1 and 2 be satisfied. Then, there exist δ 1∈(0,δ] and L 1>0 so that the inequalities

$$ \big\|x(s)-s\big\|\le L_1 \operatorname {dist}[s,O], $$
(16)
$$ \operatorname {dist}\bigl[x(s),O\bigr]\le L_1 \operatorname {dist}[s,O]^2, $$
(17)

and

$$ \big\|x(s)-x^*\big\|\le\delta $$
(18)

hold for all \(s\in \mathcal{B}(x^{*},\delta_{1})\). Moreover,

$$ \lim_{\operatorname {dist}[s,O]\to 0} \frac{\|x(s)-s\|}{\operatorname {dist}[s,O]}=1. $$
(19)

Proof

The existence of δ 1∈(0,δ] and L 1>0 so that (16) and (17) hold is a well-known fact, see for example [2, 14]. Furthermore, using (16), we obtain (18) by

$$\big\|x(s)-x^*\big\|\le\big\|x(s)-s\big\| +\big\|s-x^*\big\|\le L_1\operatorname {dist}[s,O]+\big\|s-x^*\big\|\le (L_1+1)\delta_1\le\delta $$

for δ 1>0 sufficiently small. So, only (19) needs a proof. To this end, let \(s\in \mathcal{B}(x^{*},\delta_{1})\setminus O\) be arbitrarily chosen. The set O is closed by continuity of H, and thus there exists s O ∈O with \(\|s_{O}-s\|=\operatorname {dist}[s,O]\). Hence, we get

(20)

using (5) in the first inequality and the first equality, (15), (7) and (16) in the third inequality, and finally (12) and (14) in the fourth one. Dividing (20) by ∥H(s)∥ and extracting the square root, we obtain on the one hand

$$ \big\|x(s)-s\big\|\le\sqrt{\frac{L^2}{\omega} \operatorname {dist}[s,O]+1+2\varkappa L^{1+\eta}(1+L_1)\operatorname {dist}[s,O]^\eta}\,\operatorname {dist}[s,O]. $$
(21)

On the other hand, the triangle inequality and (17) yield

$$\operatorname {dist}[s,O]\le\big\|s-x(s)\big\|+\operatorname {dist}\bigl[x(s),O\bigr]\le\big\|x(s)-s\big\|+L_1 \operatorname {dist}[s,O]^2, $$

which leads to

$$ \operatorname {dist}[s,O]-L_1\operatorname {dist}[s,O]^2\le\big\|x(s)-s\big\|. $$
(22)

Now, dividing the inequalities (21) and (22) by \(\operatorname {dist}[s,O]\), and taking the limit with \(\operatorname {dist}[s,O]\to 0\), (19) follows. □

In order to formulate the following results, we introduce the set-valued map \(P_{X}:\mathbb {R}^{n}\rightrightarrows X\), defined as:

$$P_X(s):=\bigl\{x\in X\,|\,\|x-s\|=\operatorname {dist}[s,X]\bigr\}. $$

Lemma 3

Let Assumptions 1 and 2 be satisfied. Then, for any c∈(0,1), there exists δ(c)>0 such that, for any \(s\in \mathcal{B}(x^{*},\delta(c))\),

$$c\big\|x(s)-s_X\big\|\le\|s-s_X\|\quad\mbox{\textit{for all}}\ s_X\in P_X(s). $$

Proof

Let us assume the contrary. Then there exist c 1∈(0,1) and sequences \(\{s^{k}\}\subset \mathbb {R}^{n}\) and \(\{s_{X}^{k}\}\) with \(s_{X}^{k}\in P_{X}(s^{k})\) for all \(k\in \mathbb {N}\) such that {s k} converges to x ∗ and

$$ \big\|s^k-s^k_X\big\|<c_1\big\|x\bigl(s^k\bigr)-s^k_X\big\| \quad\mbox{for all}\ k\in \mathbb {N}. $$
(23)

Without loss of generality we assume that, for some κ∈(0,δ 1],

$$ \big\|s^k-x^*\big\|\le\kappa \quad\mbox{for all}\ k\in \mathbb {N}. $$
(24)

Later on, κ will be restricted further. Obviously, (23) implies

$$ \big\|x\bigl(s^k\bigr)-s_X^k \big\|>0\quad\mbox{for all}\ k\in \mathbb {N}. $$
(25)

For later use, we define

$$c_2:=\frac{1+c_1}{2}\quad\mbox{and}\quad c_3:=\sqrt{1- \biggl(\frac{1-c_2}{c_2} \biggr)^2}. $$

Since c 1∈(0,1), we easily obtain

$$ \max\biggl\{c_1, \frac{1}{2}\biggr\}<c_2<1<\frac{c_2}{c_1}\quad\mbox{and}\quad 0<c_3<1<\frac{1+c_3}{2c_3}. $$
(26)

Therefore, (19) in Lemma 2 implies, for κ>0 sufficiently small,

$$ \big\|s^k-x \bigl(s^k\bigr)\big\|\le \min\biggl\{\frac{c_2}{c_1},\frac{1+c_3}{2c_3} \biggr\} \operatorname {dist}\bigl[s^k,O\bigr] \quad\mbox{for all}\ k\in \mathbb {N}. $$
(27)

For the sake of simplicity, we now fix \(k\in \mathbb {N}\) and omit this index. Then, from (27) and (23), we obtain

$$\big\|s-x(s)\big\|\le\frac{c_2}{c_1}\operatorname {dist}[s,O] \le\frac{c_2}{c_1}\operatorname {dist}[s,X] < \frac{c_2}{c_1}c_1\big\|x(s)-s_X\big\| =c_2 \big\|x(s)-s_X\big\|. $$

Thus, by (23) and the fact that c 1<c 2, established in (26), we have

$$ \|s-s_X\|<c_2 \big\|x(s)-s_X\big\|\quad\mbox{and}\quad\big\|s-x(s)\big\|<c_2 \big\|x(s)-s_X\big\|. $$
(28)

Now, taking into account (25),

$${\mathcal{L}}(s):=\bigl\{x(s)+\lambda\bigl(s_X-x(s)\bigr)\,|\, \lambda\in \mathbb {R}\bigr\}, $$

defines a straight line. With z(s) denoting the orthogonal projection of s onto this line, we have that

$$ \bigl(s-z(s)\bigr)^{\top} \bigl(x(s)-s_X\bigr)=0 $$
(29)

is valid. Since (s,z(s),s X ) and (s,x(s),z(s)), respectively, are vertices of a right triangle with the right angle at z(s),

$$ \big\|z(s)-s_X\big\|\le \|s-s_X\|\quad\mbox{and}\quad\big\|z(s)-x(s)\big\|\le\big\|s-x(s)\big\| $$
(30)

follow. We conclude from (30) and (28) that the inequalities

$$ \big\|z(s)-s_X\big\|<c_2 \big\|x(s)-s_X\big\|\quad\mbox{and}\quad\big\|z(s)-x(s)\big\| <c_2 \big\|x(s)-s_X\big\| $$
(31)

are satisfied. With \(\lambda(s)\in \mathbb {R}\) given by

$$ z(s)=x(s)+\lambda(s) \bigl(s_X-x(s) \bigr), $$
(32)

(31) implies

$$ \lambda(s)\in(1-c_2,c_2) \subset(0,1), $$
(33)

i.e., z(s) lies on the line \({\mathcal{L}}(s)\) between x(s) and s X . Therefore,

$$\big\|x(s)-z(s)\big\|>(1-c_2)\big\|x(s)-s_X\big\| $$

follows and we get, using (28),

$$ \big\|x(s)-z(s)\big\|>\frac{1-c_2}{c_2} \big\|s-x(s)\big\|. $$
(34)

Moreover, since z(s) belongs to the line \({\mathcal{L}}(s)\) we have, as in (29), that

$$\bigl(s-z(s)\bigr)^{\top}\bigl(x(s)-z(s)\bigr)=0 $$

holds. This and (34) yield

$$ \big\|s-z(s)\big\|^2= \big\|s-x(s)\big\|^2-\big\|x(s)-z(s)\big\|^2< \big\|s-x(s)\big\|^2 - \biggl(\frac{1-c_2}{c_2} \biggr)^2\big\|s-x(s) \big\|^2. $$

With the above definition of c 3, we have

$$ \big\|s-z(s)\big\|<c_3\big\|s-x(s)\big\|. $$
(35)

From (27), we get

$$ \big\|s-x(s)\big\|\le\frac{1+c_3}{2c_3}\operatorname {dist}[s,O], $$

which implies, in view of (35),

$$ \big\|s-z(s)\big\|<c_3\frac{1+c_3}{2c_3} \operatorname {dist}[s,O]=\frac{c_3+1}{2}\operatorname {dist}[s,O]. $$
(36)

The triangle inequality and (36) lead to

$$ \operatorname {dist}[s,O]\le\big\|s-z(s)\big\|+\operatorname {dist}\bigl[z(s),O\bigr]< \frac{c_3+1}{2}\operatorname {dist}[s,O]+\operatorname {dist}\bigl[z(s),O\bigr]. $$
(37)

Since (36) implies \(\operatorname {dist}[s,O]>0\), dividing (37) by \(\operatorname {dist}[s,O]\), we obtain

$$ 1<\frac{c_3+1}{2}+\frac{\operatorname {dist}[z(s),O]}{\operatorname {dist}[s,O]}. $$
(38)

Due to (c 3+1)/2<1 we would get the desired contradiction if the second term on the right hand side of (38) is sufficiently close to 0. We proceed to prove this fact. By (24), we have

$$\big\|s_X-x^*\big\|\le\|s_X-s\|+\big\|s-x^*\big\|\le 2\kappa. $$

Moreover, since \(s\in \mathcal{B}(x^{*},\delta_{1})\), (16) in Lemma 2 yields

$$\big\|x(s)-x^*\big\|\le\big\|x(s)-s\big\|+\big\|s-x^*\big\|\le L_1\operatorname {dist}[s,O]+\kappa \le(L_1+1)\kappa. $$

It follows from (36) and the fact that c 3<1, resulting from (26), that

$$\big\|z(s)-x^*\big\|\le \big\|z(s)-s\big\|+\big\|s-x^*\big\|<\frac{c_3+1}{2}\operatorname {dist}[s,O]+\kappa< 2\kappa. $$

Therefore, for κ∈(0,δ 1] sufficiently small, we have

$$ s, s_X, x(s),z(s)\in \mathcal{B}\bigl(x^*, \delta_1\bigr). $$
(39)

Now, (16) in Lemma 2 and (28) imply that

$$\big\|x(s)-s_X\big\|\le\big\|x(s)-s\big\|+\|s-s_X\|<L_1 \operatorname {dist}[s,O]+c_2\big\|x(s)-s_X\big\| $$

and, using c 2<1 from (26), we obtain

$$ \big\|x(s)-s_X\big\|< \frac{L_1}{1-c_2}\operatorname {dist}[s,O]. $$
(40)

Taking into account (39), we get

(41)

using the error bound (12) in Assumption 2 in the first inequality, (15) in Lemma 1 in the second one, (32) and (33) in the second equality, (15) again in the third inequality, (14) in the fourth one, and (17) in Lemma 2, together with (40), in the fifth one. Dividing (41) by \(\omega \operatorname {dist}[s,O]\), we have

$$\frac{\operatorname {dist}[z(s),O]}{\operatorname {dist}[s,O]}< \biggl( \frac{LL_1}{\omega}+\frac{ 2LL_1^2}{\omega(1-c_2)^2} \biggr) \operatorname {dist}[s,O]. $$

Hence, without loss of generality, we can assume that κ in (24) is sufficiently small so that the right hand side of the previous inequality becomes strictly less than (1−c 3)/2 and, thus, (38) yields a contradiction. □

The following lemma provides the key result for proving local linear convergence of Algorithm 1 since it shows that locally one step of this algorithm provides a linear decrease w.r.t. the distance to the solution set X.

Lemma 4

Let Assumptions 1 and 2 be satisfied and suppose that \(\tilde{P}_{\varOmega}\) is an approximate projector defined on \(B\supseteq \mathcal{B}(x^{*},1)\). Then, there exist δ 2∈(0,δ 1] and τ∈[0,1) such that

$$x(s)\in B\quad\mbox{\textit{and}}\quad \operatorname {dist}\bigl[\tilde{P}_\varOmega\bigl(x(s)\bigr),X \bigr]\le\tau \operatorname {dist}[s,X] $$

hold for all \(s\in \mathcal{B}(x^{*},\delta_{2})\).

Proof

Due to (18), we have \(x(s)\in \mathcal{B}(x^{*},1)\subseteq B\) for all \(s\in \mathcal{B}(x^{*},\delta_{1})\). This implies that \(\tilde{P}_{\varOmega}(x(s))\) is well-defined. By the definitions of x(s) and \(\tilde{P}_{\varOmega}\), we get

$$x(s)=s\quad\mbox{and}\quad\tilde{P}_\varOmega\bigl(x(s)\bigr)= \tilde{P}_\varOmega(s)=s \quad\mbox{for all}\ s\in X. $$

Therefore, the asserted inequality holds for all s∈X for any τ≥0. In order to prove this inequality for s∉X let us now proceed by contradiction, assuming that there exists a sequence \(\{s^{k}\}\subset \mathbb {R}^{n}\setminus X\), converging to x ∗, such that

$$ \liminf_{k\to\infty} \frac{\operatorname {dist}[\tilde{P}_\varOmega(x(s^k)),X]}{\operatorname {dist}[s^k,X]}\ge 1. $$
(42)

Without loss of generality we assume that, for some δ 2∈(0,δ 1],

$$ \big\|s^k-x^*\big\|\le\delta_2\quad \mbox{for all}\ k\in \mathbb {N}. $$
(43)

Later, δ 2 will be further restricted. In order to obtain the desired contradiction, the remainder of the proof will be divided in two parts.

(a) In this part we will show that there exists ρ∈[0,1) such that

$$ \big\|s_X^k-\tilde{P}_\varOmega\bigl(x\bigl(s^k\bigr)\bigr)\big\|\le\rho\big\|x \bigl(s^k\bigr)-s_X^k\big\|\quad \mbox{for all}\ k\in \mathbb {N}, $$
(44)

where \(s_{X}^{k}\) denotes an arbitrary element of P X (s k). For simplicity, we now fix \(k\in \mathbb {N}\) and omit the index k. In order to show (44), we first prove that

$$ x(s)\notin\varOmega\quad\mbox{if } \delta_2\in(0,\delta_1]\mbox{ is sufficiently small.} $$
(45)

Let us assume that (45) does not hold. It follows from (43) and (18), that \(s\in \mathcal{B}(x^{*},\delta_{1})\) and \(x(s)\in \mathcal{B}(x^{*},\delta)\). Therefore, we can apply the error bound (13), (14), and (17) and obtain, for x(s)∈Ω,

$$\begin{array}{rcl} \omega \operatorname {dist}\bigl[\tilde{P}_\varOmega\bigl(x(s)\bigr),X\bigr]&\le& \big\|H\bigl(x(s)\bigr)\big\|\\[6pt] &\le&L\operatorname {dist}\bigl[x(s),O\bigr] \\[6pt] &\le&LL_1\operatorname {dist}[s,O]^2\\[6pt] &\le&LL_1\operatorname {dist}[s,X]^2, \end{array} $$

which contradicts (42) for δ 2>0 sufficiently small. Thus, (45) holds.

Now, we continue with the proof of (44). From the definition of the approximate projector \(\tilde{P}_{\varOmega}\) we have

$$ \bigl(x(s)-\tilde{P}_\varOmega\bigl(x(s)\bigr)\bigr)^{\top}\bigl(s_X- \tilde{P}_\varOmega\bigl(x(s)\bigr)\bigr)\le 0, $$

i.e., the angle at the vertex \(\tilde{P}_{\varOmega}(x(s))\) of the triangle \((x(s),s_{X},\tilde{P}_{\varOmega}(x(s)))\) is obtuse. Therefore, it follows from the cosine rule that

$$ \big\|x(s)-\tilde{P}_\varOmega\bigl(x(s) \bigr)\big\|\le\big\|x(s)-s_X\big\|,\qquad \big\|s_X-\tilde{P}_\varOmega\bigl(x(s)\bigr)\big\|\le\big\|x(s)-s_X\big\|, $$
(46)

and

$$ \big\|x(s)-\tilde{P}_\varOmega\bigl(x(s) \bigr)\big\|^2+\big\|s_X-\tilde{P}_\varOmega\bigl(x(s)\bigr) \big\|^2\le \big\|x(s)-s_X\big\|^2 $$
(47)

hold. Since, by (45), x(s) does not belong to Ω for δ 2>0 small enough, we have

$$ \big\|x(s)-s_X\big\|>0. $$
(48)

Thus, dividing (47) by ∥x(s)−s X ∥2 yields

$$ \frac{\|x(s)-\tilde{P}_\varOmega(x(s))\|^2}{\|x(s)-s_X\|^2} + \frac{\|s_X-\tilde{P}_\varOmega(x(s))\|^2}{\|x(s)-s_X\|^2}\le 1. $$
(49)

From the definition of \(\tilde{P}_{\varOmega}\), we have, for some γ∈(0,1),

Thus, defining \(w(s):=P_{\varOmega}(\tilde{P}_{\varOmega}(x(s)))\), it holds that

$$ \operatorname {dist}\bigl[\tilde{P}_\varOmega\bigl(x(s) \bigr),\varOmega\bigr] =\big\|\tilde{P}_\varOmega\bigl(x(s)\bigr)-w(s)\big\| \le \frac{\gamma}{1-\gamma} \big\|x(s)-\tilde{P}_\varOmega\bigl(x(s)\bigr)\big\|. $$
(50)

In view of Lemma 3, we may assume that

$$ \frac{1}{2}\big\|x(s)-s_X\big\|\le \operatorname {dist}[s,X] $$
(51)

is valid for δ 2>0 sufficiently small. From (51), (42), and (50) we conclude that, for δ 2>0 sufficiently small,

(52)

The next estimate provides an upper bound for \(\operatorname {dist}[w(s),O]\). For δ 2>0 sufficiently small, the triangle inequality, (17), (50), (42), and (46) yield

(53)

Using (46) and (16), we can easily deduce that \(s\in \mathcal{B}(x^{*},\delta_{2})\) implies \(w(s)\in \mathcal{B}(x^{*},\delta)\) for δ 2>0 small enough. Thus, since w(s)∈Ω by definition, we get from the error bound (13) and from (14)

$$ \omega \operatorname {dist}\bigl[w(s),X\bigr]\le\big\|H \bigl(w(s)\bigr)\big\|\le L\operatorname {dist}\bigl[w(s),O\bigr]. $$
(54)

Combining (52), (54), and (53), we obtain

(55)

In view of (48), we can divide (55) by ∥x(s)−s X ∥, yielding

$$ 0<\frac{1}{4}\omega\le 2LL_1 \big\|x(s)-s_X\big\| + \frac{L+\omega\gamma}{1-\gamma} \frac{\|x(s)-\tilde{P}_\varOmega(x(s))\|}{\|x(s)-s_X\|}. $$
(56)

Choosing δ 2≤(32LL 1)−1 ω and taking into account (51), we get

$$2LL_1\big\|x(s)-s_X\big\|\le 4LL_1\operatorname {dist}[s,X]\le 4LL_1\delta_2\le\frac{1}{8}\omega. $$

Hence, by (56), it follows that

$$\frac{\|x(s)-\tilde{P}_\varOmega(x(s))\|}{\|x(s)-s_X\|}\ge\sigma := \min \biggl\{\frac{1}{2},\frac{\omega(1-\gamma)}{8(L+\omega\gamma)} \biggr\} \in(0,1). $$

Therefore, (49) implies (44) with \(\rho:=\sqrt{1-\sigma^{2}}\) completing the proof of (a).

(b) We complete now the proof of the lemma. It follows from (44) that, for δ 2>0 sufficiently small,

$$\operatorname {dist}\bigl[\tilde{P}_\varOmega\bigl(x\bigl(s^k\bigr)\bigr),X\bigr] \le\big\|\tilde{P}_\varOmega\bigl(x\bigl(s^k\bigr) \bigr)-s_X^k\big\|\le \rho\big\|x\bigl(s^k \bigr)-s_X^k\big\|. $$

With c:=2ρ/(1+ρ), Lemma 3 implies

$$\operatorname {dist}\bigl[\tilde{P}_\varOmega\bigl(x\bigl(s^k\bigr)\bigr),X\bigr] \le\frac{\rho}{c}\big\|s^k-s_X^k\big\|= \frac{1+\rho}{2}\operatorname {dist}\bigl[s^k,X\bigr] $$

for δ 2>0 sufficiently small. Since (1+ρ)/2<1, we have a contradiction to (42). □

We show next that Lemma 4 need not hold if the error bound on Ω, given by (13), is violated.

Example 3

Let \(H:\mathbb {R}^{2}\to \mathbb {R}\) and Ω be defined as in Example 1, where we have already noted that the error bound (12) is satisfied for any solution, while the error bound (13) on Ω is violated for x ∗=(0,0)⊤. Now, let us consider the point \(s=(-t,0)^{\top}\in \mathbb {R}^{2}\) with t∈(0,1] arbitrary but fixed. Since s belongs to O, it follows that x(s)=s. Since g (see Example 1) is continuously differentiable, its only subgradient is its gradient, i.e., v(s)=∇g(s)=(−2t,−1)⊤. The approximate projection \(\tilde{p}(s)\) on \(\mathcal{B}(0,1)\) associated to Ω is given by (11) and, since g(s)=t 2>0, we obtain

$$\tilde{p}(s)= \biggl(\frac{2t^3}{4t^2+1} -t , \frac{t^2}{4t^2+1} \biggr)^{\top}. $$

This and \(\operatorname {dist}[s,X]=t\) imply

$$\frac{\operatorname {dist}[\tilde{p}(s),X]^2}{\operatorname {dist}[s,X]^2}= \frac{ (\frac{ 2t^3}{ 4t^2+1}-t )^2+ (\frac{ t^2}{ 4t^2+1} )^2}{t^2} \stackrel{t\to 0}{\longrightarrow}1. $$

Thus, the assertion of Lemma 4 is not satisfied in any neighborhood of x ∗=(0,0)⊤.

Now we are in the position to state and prove the main theorem of this paper.

Theorem 1

Let Assumptions 1 and 2 be satisfied and suppose that Algorithm  1 uses an approximate projector \(\tilde{P}_{\varOmega}\) defined on \(B\supseteq \mathcal{B}(x^{*},1)\). Then, there exists ϵ∈(0,δ 2] such that Algorithm  1 generates a well-defined sequence {x k} for any starting point \(x^{0}\in \mathcal{B}(x^{*},\epsilon)\). This sequence converges R-linearly to a solution \(\hat{x}\in X\) of problem (1).

Proof

Let us first choose ϵ according to

$$ 0<\epsilon\le \biggl(1+\frac{2L_1+1}{1-\tau} \biggr)^{-1}\delta_2 $$
(57)

with τ∈(0,1) from Lemma 4 and L 1>0 from Lemma 2. We first show by induction that Algorithm 1 generates a well-defined sequence \(\{x^{k}\}\subset \mathcal{B}(x^{*},\delta_{2})\) if \(x^{0}\in \mathcal{B}(x^{*},\epsilon)\). To this end we assume that, for some \(k\in \mathbb {N}\), x 0,x 1,…,x k were generated by Algorithm 1 and

$$ \big\|x^\nu-x^*\big\|\le\delta_2 \quad\mbox{for}\ \nu=0,1,\ldots,k. $$
(58)

Using the triangle inequality, we obtain

$$ \big\|x^{k+1}-x^*\big\|\le \big\|x^0-x^* \big\|+\sum_{\nu=0}^{k}\big\|x^{\nu+1}-x^\nu\big\|. $$
(59)

In order to find an upper bound for the second term in the right hand side of (59) note first that \(x^{\nu+1}=\tilde{P}_{\varOmega}(x(x^{\nu}))\) is well-defined for ν=0,1,…,k−1 since x 0,…,x k were successfully generated by Algorithm 1. Moreover, by (58) for ν=k, Lemma 4 with s:=x k implies x(x k)∈B. Thus, \(x^{k+1}=\tilde{P}_{\varOmega}(x(x^{k}))\) is also well-defined and we obtain, for ν=0,…,k,

$$\big\|x^{\nu+1}-x^\nu\big\| \le\big\|\tilde{P}_\varOmega\bigl(x \bigl(x^\nu\bigr)\bigr)-x\bigl(x^\nu\bigr)\big\|+\big\|x \bigl(x^\nu\bigr)-x^\nu\big\|. $$

Moreover, Property 1 of an approximate projector (see Definition 1) and (16) of Lemma 2 applied to s:=x ν yield for ν=0,…,k

(60)

Therefore, (59) leads to

$$\big\|x^{k+1}-x^*\big\|\le\big\|x^0-x^*\big\|+(2L_1+1)\sum _{\nu=0}^k\operatorname {dist}\bigl[x^\nu,X\bigr]. $$

In view of (58), Lemma 4 gives

$$\begin{array}{rcl} \big\|x^{k+1}-x^*\big\|&\le& \big\|x^0-x^*\big\|+(2L_1+1)\operatorname {dist}\bigl[x^0,X\bigr]\displaystyle\sum_{\nu=0}^k\tau^\nu\\[12pt] &\le& \biggl(1+\displaystyle\frac{ 2L_1+1}{ 1-\tau} \biggr)\big\|x^0-x^*\big\|. \end{array} $$

Since \(x^{0}\in \mathcal{B}(x^{*},\epsilon)\), we have from (57) that x k+1 belongs to \(\mathcal{B}(x^{*},\delta_{2})\). Hence, it follows by induction that, for any starting point \(x^{0}\in \mathcal{B}(x^{*},\epsilon)\), Algorithm 1 generates a well-defined infinite sequence \(\{x^{k}\}\subset \mathcal{B}(x^{*},\delta_{2})\).

Next, it will be shown that the sequence {x k} is a Cauchy-sequence. Take \(i,k\in \mathbb {N}\) with k<i. Then, as in (60), we obtain

$$\big\|x^i-x^k\big\|\le\sum_{\nu=k}^{i-1} \big\|x^{\nu+1}-x^\nu\big\|\le (2L_1+1)\sum _{\nu=k}^{i-1}\operatorname {dist}\bigl[x^\nu,X\bigr] $$

and Lemma 4 yields

$$ \big\|x^i-x^k\big\|\le \tau^k(2L_1+1)\operatorname {dist}\bigl[x^0,X\bigr]\sum _{\nu=0}^{i-k-1}\tau^\nu\le \tau^k\frac{2L_1+1}{1-\tau}\epsilon. $$
(61)

Hence, for k→∞ the right hand side of (61) tends to 0. Thus, {x k} is a Cauchy-sequence and converges to some \(\hat{x}\in \mathcal{B}(x^{*},\delta_{2})\). From Lemma 4, we have \(\operatorname {dist}[x^{k+1},X]\le\tau \operatorname {dist}[x^{k},X]\) for all \(k\in \mathbb {N}\) and, thus, \(\lim_{k\to\infty} \operatorname {dist}[x^{k},X]=0\) holds. Since X is a closed set we conclude that \(\hat{x}\) belongs to X. Finally, let us consider (61) and take the limit for i→∞. This yields

$$\big\|\hat{x}-x^k\big\|\le\tau^k\frac{2L_1+1}{\tau-1}\quad \mbox{for all}\ k\in \mathbb {N}. $$

Hence, if \(x^{0}\in \mathcal{B}(x^{*},\epsilon)\) then {x k} converges R-linearly to \(\hat{x}\in X\). □

4 Final remarks

We have shown that the Levenberg-Marquardt algorithm with approximate projections (LMAP) is locally R-linearly convergent under a pair of reasonable error bound conditions. A special case of this algorithm is the projected Levenberg-Marquardt method [17]. Note that in the existing literature local convergence is known only under the very restrictive Condition 3 which we could avoid. Although the Algorithm 1 has no superlinear convergence in general, the approach presented in this paper has some advantages. One is that it allows computationally cheap approximate projections instead of exact ones. This might be helpful when dealing with more complex convex sets Ω, in particular if Ω is described by nonlinear or even nonsmooth functions. A second advantage lies in the fact that the unconstrained Levenberg-Marquardt subproblems of Algorithm 1 are linear systems of equations, in contrast to constrained Levenberg-Marquardt methods (see [2, 17]), where constrained convex programs are used (even if the latter guarantee quadratic convergence). A more hidden benefit of using unconstrained Levenberg-Marquardt subproblems instead of constrained ones is that one can easily control the inexactness of their solution. This is of importance to ensure a certain convergence rate of the whole method. For example, if the linear system of equations of an unconstrained Levenberg-Marquardt subproblem is solved iteratively, then the residual of the corresponding approximate solution is π(s), and so the norm of this residual may be directly used to stop the iterative solver, see [14]. In contrast to this, an appropriate stopping of an iterative solver for constrained Levenberg-Marquardt subproblems seems more difficult.

In the next subsection we show that, in general, the results on the level of inexactness and on the convergence rate cannot be improved. Finally, the last subsection provides numerical results for a test example.

4.1 Sharpness of results

The relation of the regularization parameter α(s) and the inexactness ∥π(s)∥ within Levenberg-Marquardt subproblems and their influence on the convergence rate were investigated in [4, 9, 14] and in [2], where the most general results can be found. In particular, if the regularization parameter α(s) in subproblem (4) is ∥H(s)∥, then a level of inexactness of order \(\mathcal{O}(\|H(s)\|^{2})\), i.e., ∥π(s)∥∼∥H(s)∥2, still maintains the local quadratic convergence of unconstrained or constrained exact Levenberg-Marquardt methods.

In Algorithm 1 we allow only a slightly lower level of inexactness, namely ∥π(s)∥∼∥H(s)∥2+η with some η>0. Interestingly, the following example shows that, for η=0, the algorithm may fail to converge at all.

Example 4

Let \(H:\mathbb {R}^{2}\to \mathbb {R}\) and \(\varOmega\subset \mathbb {R}^{2}\) be given by

$$H(x_1,x_2):=x_2\quad\mbox{and}\quad \varOmega:=\bigl\{x\in \mathbb {R}^2\,|\,x_1+x_2\ge 0 \bigr\}. $$

Assumptions 1 and 2 are satisfied at any solution of problem (1). In particular, the error bounds given by (12) and (13) hold since H is affine and Ω a polyhedron. For some t∈(0,1] let us define

$$s:=(-t,t)^{\top}\in\varOmega\quad\mbox{and}\quad \pi(s):= \biggl( \frac{-t^2}{t+1},0 \biggr)^{\top}. $$

Obviously, we have ∥π(s)∥≤t 2=∥H(s)∥2. For the solution of the Levenberg-Marquardt subproblem (4) we get

$$x(s)=\biggl(-t-\frac{t}{t+1},t-\frac{t}{t+1}\biggr)^{\top}. $$

It is easy to verify that P Ω (x(s))=(−t,t)⊤=s, where P Ω is the orthogonal projector on Ω. Thus, the Algorithm 1 is trapped at s=(−t,t)⊤. No matter how close a starting point is to the solution x ∗:=(0,0)⊤, allowing an inexactness of order \(\mathcal{O}(\|H(s)\|^{2})\), may make Algorithm 1 generate a nonconvergent sequence.

In general, under Assumptions 1 and 2, the convergence rate of Algorithm 1 we can expect even for exact projections is not better than linear. In order to see this, let us again consider the problem in Example 4. For t∈(0,1] define s:=(−t,t)⊤ and π(s):=0. Then, we obtain

$$x(s)= \biggl(-t,t-\frac{t}{1+t} \biggr)^{\top}\quad\mbox{and}\quad P_\varOmega\bigl(x(s)\bigr)= \biggl(-t+\frac{t}{2+2t},t- \frac{t}{2+2t} \biggr)^{\top}. $$

Then,

$$\operatorname {dist}[s,X]=\sqrt{2}t\quad\mbox{and}\quad \operatorname {dist}\bigl[P_\varOmega\bigl(x(s) \bigr),X\bigr]=\sqrt{2}t \biggl(1-\frac{1}{2+2t} \biggr) $$

follow. Hence, in general, Algorithm 1 does not generate a superlinearly convergent sequence.

4.2 A test example

Although the focus of this paper is theoretical, we would like to illustrate how the Levenberg-Marquardt algorithm with approximate projections works to provide a feeling of its behavior.

Example 5

Let \(H:\mathbb {R}^{2}\to \mathbb {R}\) and \(\varOmega\subset \mathbb {R}^{2}\) be defined as

$$H(x):=x_2-x_1 $$

and

$$\varOmega:=\bigl\{x\in \mathbb {R}^2\,|\,g_i(x)\le 0,\ i=1, \ldots,4\bigr\}, $$

with functions \(g_{i}:\mathbb {R}^{2}\to \mathbb {R}\) given by

and

$$g_4(x):=\left \{ \begin{array}{l@{\quad}l} \frac{2}{2x_1+1}-x_2-\frac{3}{2}&\mbox{if}\ x_1\ge 0,\\[6pt] -x_2+\frac{1}{2}&\mbox{if}\ x_1<0. \end{array} \right . $$

One can easily check that Ω is a convex set. Moreover, Ω can be rewritten as

$$\varOmega=\bigl\{x\in \mathbb {R}^2\,|\,g(x)\le 0\bigr\} $$

with

$$g(x):=\max\bigl\{g_1(x),g_2(x),g_3(x),g_4(x) \bigr\}. $$

With H and Ω defined above, the solution set of problem (1) is

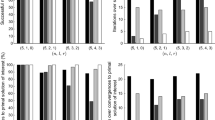
$$X=\biggl\{(t,t)^{\top}\in \mathbb {R}^2\,|\,\frac{\sqrt{5}-2}{2}\le t\le \frac{1}{2}\sqrt{2}\biggr\}. $$

Furthermore, it can be shown that Assumptions 1 and 2 are satisfied at any solution. Algorithm 1 is run with the approximate projector given by (11) and starting point x 0=(−1,1)⊤. The results are shown in Table 1.

Table 1 Numerical results for Example 5
Full size table

If the constrained Levenberg-Marquardt method is used to find a solution of this problem, the subproblems are optimization problems with a convex quadratic objective and the inequality constraints g i (x)≤0 for i=1,…,4. Thus, solving the subproblems might be computationally a harder task. One option for avoiding this situation consists of introducing slack variables y 1,…,y 4 for the inequalities. More precisely, problem (1) could be reformulated as follows

$$\tilde{H}(x,y):=\left ( \begin{array}{c} x_2-x_1\\g_1(x)+y_1\\\ldots\\g_4(x)+y_4 \end{array} \right )=0\quad\mbox{s.t.}\quad(x,y)\in \tilde{\varOmega}:=\mathbb {R}^2\times \mathbb {R}^4_+. $$

If, regardless of the nondifferentiability of g 4, the constrained Levenberg-Marquardt method is applied to this reformulation, the subproblems become quadratic optimization problems with box constraints. However, the number of variables increases and, with it, the cost of solving a subproblem.

Experiments with large scale examples are going to be part of our future research. In this direction, one can consider a differentiable reformulation of Karush-Kuhn-Tucker systems which arise from generalized Nash equilibrium problems as in [5]. In this context, that paper provides a sufficient condition for the pair of error bounds (12) and (13) to hold. Moreover, a hybrid algorithm is described in [5] whose local phase consists of a method with quadratic convergence behavior. Replacing the latter method by Algorithm 1 would lead to local R-linear convergence only, but to significantly less expensive subproblems.