Critical solutions of nonlinear equations: local attraction for Newton-type methods

Abstract

We show that if the equation mapping is 2-regular at a solution in some nonzero direction in the null space of its Jacobian (in which case this solution is critical; in particular, the local Lipschitzian error bound does not hold), then this direction defines a star-like domain with nonempty interior from which the iterates generated by a certain class of Newton-type methods necessarily converge to the solution in question. This is despite the solution being degenerate, and possibly non-isolated (so that there are other solutions nearby). In this sense, Newtonian iterates are attracted to the specific (critical) solution. Those results are related to the ones due to A. Griewank for the basic Newton method but are also applicable, for example, to some methods developed specially for tackling the case of potentially non-isolated solutions, including the Levenberg–Marquardt and the LP-Newton methods for equations, and the stabilized sequential quadratic programming for optimization.

1 Introduction

We consider a nonlinear equation

$$\begin{aligned} \varPhi (u) = 0, \end{aligned}$$

(1)

where the mapping $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ is smooth enough (precise smoothness assumptions will be stated later as needed). This paper is concerned with convergence properties of Newton-type methods for solving the Eq. (1) when it has a singular solution $\bar{u}$ (i.e. the matrix $\varPhi '(\bar{u})$ is singular). Of particular interest is the difficult case when $\bar{u}$ may be a non-isolated solution of (1). Note that if $\bar{u}$ is a non-isolated solution, it is necessarily singular.

To describe the class of methods in question, we define the perturbed Newton method (pNM) framework for Eq. (1) as follows. For the given iterate $u^k\in \mathbb {R}^p$, the next iterate is $u^{k+1}=u^k+v^k$, with $v^k$ satisfying the following linear equation in v:

$$\begin{aligned} \varPhi (u^k)+\left( \varPhi '\left( u^k\right) +\varOmega \left( u^k\right) \right) v = \omega \left( u^k\right) . \end{aligned}$$

(2)

In (2), the mappings $\varOmega :\mathbb {R}^p\rightarrow \mathbb {R}^{p\times p}$ and $\omega :\mathbb {R}^p\rightarrow \mathbb {R}^p$ are certain perturbation terms which may have different roles, and individually or collectively define specific methods within the general pNM framework. In particular, if $\varOmega \equiv 0$ and $\omega \equiv 0$, then (2) reduces to the iteration system of the basic Newton method. The most common setting would be for $\varOmega$ to characterize a perturbation of the iteration matrix of the basic Newton method [i.e. the difference between the matrix a given method actually employs, compared to the exact Jacobian $\varPhi '(u^k)$], and for $\omega$ to account for possible inexactness in solving the corresponding linear system of equations. An example of this setting within this paper, is the stabilized Newton–Lagrange method (stabilized sequential quadratic programming for equality-constrained optimization), considered in Sect. 3.3 below. However, we emphasize that our framework is not restricted to this situation. In particular, subproblems of a given method need not even be systems of linear equations, as long as they can be related to (2) a posteriori. One example is the linear-programming-Newton (LP-Newton) method discussed in Sect. 3.2 below, which solves linear programs, and for which the perturbation term $\omega$ is implicit (i.e. it does not have an explicit analytical formula, but its properties are known). In this respect, we also comment that the way we shall employ the perturbation mappings $\varOmega$ and $\omega$ is somewhat unusual, in the following sense. They may describe a given method not necessarily on the whole neighborhood of a solution of interest, but possibly only in some relevant star-like domain of convergence; see the discussion of the Levenberg–Marquardt method in Sect. 3.1 and of the LP-Newton method in Sect. 3.2. This, however, is exactly what is needed in the presented convergence analysis, as it is shown that the generated iterates do in fact stay within the domain in question and, within this set, $\varOmega$ and $\omega$ that we construct do adequately represent the given algorithms. Finally, we note that the specific methods that we consider in this paper have been designed to tackle the difficult cases when (1) has degenerate/non-isolated solutions, and in this sense the perturbation terms in (2) that describe these methods can be regarded as “structural”, i.e. introduced intentionally for improving convergence properties in the degenerate cases. The assumptions imposed on $\varOmega$ and $\omega$ are only related to their “size”, which allows $\omega$ to cover naturally precision control when the subproblems are solved approximately. However, as already commented, the use of $\omega$ can also be quite different. In the analysis of the LP-Newton method in Sect. 3.2, $\omega$ is implicit and is not related to solving subporoblems approximately.

Our convergence results assume a certain 2-regularity property of the solution of (1), which implies that this solution is “critical” in the sense of [15]. We next state the relevant definitions, and discuss the relations between those concepts.

Recall first that if $\varPhi$ is differentiable at a solution $\bar{u}$ of the Eq. (1), then it holds that

$$\begin{aligned} T_{\varPhi ^{-1}(0)}(\bar{u}) \subset \ker \varPhi '(\bar{u}) , \end{aligned}$$

where $\varPhi ^{-1}(0)$ is the solution set of (1), and by $T_{S}(u)$ we denote the contingent cone to a set $S\subset \mathbb {R}^p$ at $u\in S$, i.e. the tangent cone as defined in [26, Definition 6.1]:

$$\begin{aligned} T_S(u)=\{ v\in \mathbb {R}^p\mid \exists \, \{ t_k\} \subset \mathbb {R}_+:\, \{ t_k\} \rightarrow 0+,\, \mathrm{dist}(u+t_kv,\, S)=o(t_k)\}. \end{aligned}$$

Recall that according to [26, Corollary 6.29] (see also [26, Definition 6.4] and the original definition in [3, Definition 2.4.6]), assuming that a set $S\subset \mathbb {R}^p$ is closed near $u\in S$, this set is Clarke-regular at u if the multifunction $T_S(\cdot )$ is inner semicontinuous at u relative to S (the latter meaning that for any $v\in T_S(u)$ and any sequence $\{ u^k\} \subset S$ convergent to u, there exists a sequence $\{ v^k\}$ convergent to v such that $v^k\in T_S(u^k)$ for all k).

The following notion was introduced in [15].

Definition 1

Assuming that $\varPhi$ is differentiable at a solution $\bar{u}$ of the Eq. (1), this solution is referred to as noncritical if the set $\varPhi ^{-1}(0)$ is Clarke-regular at $\bar{u}$, and

$$\begin{aligned} T_{\varPhi ^{-1}(0)}(\bar{u})=\ker \varPhi '(\bar{u}). \end{aligned}$$

(3)

Otherwise, the solution $\bar{u}$ is referred to as critical.

Observe that according to the above definition, any isolated singular solution is necessarily critical.

As demonstrated in [15], if $\varPhi$ satisfies some mild and natural smoothness assumptions, then noncriticality of $\bar{u}$ is equivalent to the local Lipschitzian error bound on the distance to the solution set in terms of the natural residual of the equation (1):

$$\begin{aligned} \mathrm{dist}\left( u,\, \varPhi ^{-1}(0)\right) =O(\Vert \varPhi (u)\Vert ) \end{aligned}$$

holds as $u\in \mathbb {R}^p$ tends to $\bar{u}$. Moreover, it is also equivalent to the upper-Lipschitzian stability with respect to right-hand side perturbations of (1): any solution u(w) of the perturbed equation

$$\begin{aligned} \varPhi (u)=w, \end{aligned}$$

close enough to $\bar{u}$, satisfies

$$\begin{aligned} \mathrm{dist}(u(w),\, \varPhi ^{-1}(0))=O(\Vert w\Vert ) \end{aligned}$$

as $w\in \mathbb {R}^p$ tends to 0. Accordingly, criticality of $\bar{u}$ means the absence of the properties above.

The interest in critical/noncritical solutions of nonlinear equations originated from the study of special Lagrange multipliers in equality-constrained optimization, also called critical [13, 14, 18, 19, 22], [21, Chapter 7]. For the relations between critical solutions of equations and critical multipliers in optimization, see [15]. It had been demonstrated that critical Lagrange multipliers tend to attract dual sequences generated by a number of Newton-type methods for optimization [18, 19], [21, Chapter 7]. In this paper, we show that critical solutions of nonlinear equations also serve as attractors, in this case for methods described by the pNM framework (2).

For a symmetric bilinear mapping $B:\mathbb {R}^p\times \mathbb {R}^p\rightarrow \mathbb {R}^p$ and an element $v\in \mathbb {R}^p$, we define the linear operator $B[v]: \mathbb {R}^p\rightarrow \mathbb {R}^p$ by $B[v]u= B[v,\, u]$. The notion of 2-regularity is a useful tool in nonlinear analysis and optimization theory; see, e.g. the book [1], as well as [2, 9, 10, 16, 17] for some applications. The essence of the construction is that when a mapping $\varPhi$ is irregular at $\bar{u}$ ($\varPhi '(\bar{u})$ is singular), first-order information is insufficient to adequately represent $\varPhi$ around $\bar{u}$, and so second-order information has to come into play. To this end, we have the following.

Definition 2

Assuming that $\varPhi$ is twice differentiable at $\bar{u}\in \mathbb {R}^p$, $\varPhi$ is said to be 2-regular at the point $\bar{u}$ in the direction $v\in \mathbb {R}^p$ if the $p \times p$-matrix

$$\begin{aligned} \Psi (\bar{u};\, v)= \varPhi '(\bar{u})+\varPi \varPhi ''(\bar{u})[v] \end{aligned}$$

(4)

is nonsingular, where $\varPi$ is the projector in $\mathbb {R}^p$ onto an arbitrary fixed complementary subspace of $\mathrm{im}\,\varPhi '(\bar{u})$, along this subspace.

In our convergence analysis of Newton-type methods described by (2), we shall assume that $\varPhi$ is 2-regular at a solution $\bar{u}$ of (1) in some direction $v\in \ker \varPhi '(\bar{u}){\setminus } \{0\}$. It turns out that this implies that the solution $\bar{u}$ is necessarily critical in the sense of Definition 1. We show this next.

Proposition 1

Let $\varPhi$ be twice differentiable at a solution $\bar{u}$ of the Eq. (1) and 2-regular at this solution in some direction $v\in \ker \varPhi '(\bar{u}){\setminus } \{0\}$.

Then (3) does not hold and, in particular, $\bar{u}$ is a critical solution of (1).

Proof

Let $v\in \ker \varPhi '(\bar{u}){\setminus } \{0\}$. Suppose that (3) holds. Then $v\in T_{\varPhi ^{-1}(0)}(\bar{u})$. Thus, there exist a sequence $\{ t_k\}$ of positive reals and a sequence $\{ r^k\} \subset \mathbb {R}^p$ such that $\{ t_k\} \rightarrow 0$, $r^k=o(t_k)$, and for all k it holds that

$$\begin{aligned} 0=\varPhi \left( \bar{u}+t_kv+r^k\right) = \varPhi '(\bar{u})r^k+\frac{1}{2} t_k^2\varPhi ''(\bar{u})[v,\, v]+o\left( t_k^2\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} t_k^2\varPhi ''(\bar{u})[v,\, v]+o\left( t_k^2\right) \in \mathrm{im}\,\varPhi '(\bar{u}), \end{aligned}$$

which implies that

$$\begin{aligned} \varPhi ''(\bar{u})[v,\, v]\in \mathrm{im}\,\varPhi '(\bar{u}) . \end{aligned}$$

Hence, $\varPi \varPhi ''(\bar{u})[v,\, v] =0$, where $\varPi$ is specified in Definition 2. Since also $\varPhi '(\bar{u})v =0$, from (4) we conclude that $v\in \ker \Psi (\bar{u};\, v)$. As $v\not =0$, this contradicts 2-regularity (specifically, the nonsigularity of $\Psi (\bar{u};\, v)$). Thus, (3) cannot hold, and $\bar{u}$ must be a critical solution. $\square$

In Sect. 2, we shall prove that if $\varPhi$ is 2-regular at a (critical) solution $\bar{u}$ of (1) in some direction $v\in \ker \varPhi '(\bar{u}){\setminus } \{0\}$, then v defines a domain star-like with respect to $\bar{u}$, with nonempty interior, from which the iterates that satisfy the pNM framework (2) necessarily converge to $\bar{u}$. In this sense, the iterates are “attracted” specifically to $\bar{u}$, even though there may be other nearby solutions. These results are related to [11], where the pure Newton method was considered [i.e. (2) with $\varOmega \equiv 0$ and $\omega \equiv 0$]. An interesting extension of the results in [11] to the case when $\varPhi$ is not necessarily twice differentiable, but has a Lipschitz-continuous first derivative, has been proposed in [25]. The latter reference also gives an application to smooth equation reformulations of complementarity problems.

In Sect. 3, we demonstrate how the general results for the pNM framework (2) apply to some specific Newton-type methods. These include the classical Levenberg–Marquardt method [24, Chapter 10.2] and the LP-Newton method [6] for nonlinear equations, and the stabilized Newton–Lagrange method for optimization (or stabilized sequential quadratic programming) [7, 12, 20, 28]; see also [21, Chapter 7].

We finish this section with some words about our notation. Throughout, $\langle \cdot ,\, \cdot \rangle$ is the Euclidian inner product, and unless specified otherwise, $\Vert \cdot \Vert$ is the Euclidian norm, where the space is always clear from the context. Then the unit sphere is $\mathbb {S}= \{ u\mid \Vert u\Vert =1\}$. For a linear operator (a matrix) A, we denote by $\ker A$ its null space, and by $\mathrm{im}\,A$ its image (range) space. The notation I stands for the identity matrix. A set U is called star-like with respect to $u\in U$ if $t\hat{u}+(1-t)u\in U$ for all $\hat{u}\in U$ and all $t\in [0,\, 1]$.

2 Local convergence of pNM iterates to a critical solution

Results of this section are related to those in [11], where the basic Newton method was considered [i.e. pNM (2) with $\varOmega \equiv 0$ and $\omega \equiv 0$]. To the best of our knowledge, this is the only directly related reference, as it also allows for non-isolated solutions. Other literature on the basic Newton method for singular equations uses assumptions that imply that a solution, though possibly singular, must be isolated.

Let $\bar{u}$ be a solution of the Eq. (1). Then every $u\in \mathbb {R}^p$ is uniquely decomposed into the sum $u=u_1+u_2$, with $u_1\in (\ker \varPhi '(\bar{u}))^\bot$ and $u_2\in \ker \varPhi '(\bar{u})$. The corresponding notation will be used throughout the rest of the paper.

We start with the following counterpart of [11, Lemma 4.1], which establishes that, under appropriate assumptions, the pNM subproblem (2) has the unique solution for all $u^k$ close enough to $\bar{u}$, in a certain star-like domain.

Lemma 1

Let $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ be twice differentiable near $\bar{u}\in \mathbb {R}^p$, with its second derivative Lipschitz-continuous with respect to $\bar{u}$, that is,

$$\begin{aligned} \varPhi ''(u)-\varPhi ''(\bar{u})=O(\Vert u-\bar{u}\Vert ) \end{aligned}$$

as $u\rightarrow \bar{u}$. Let $\bar{u}$ be a solution of the Eq. (1), and assume that $\varPhi$ is 2-regular at $\bar{u}$ in a direction $\bar{v}\in \mathbb {R}^p\cap \mathbb {S}$. Let $\varPi$ stand for the orthogonal projector onto $(\mathrm{im}\,\varPhi '(\bar{u}))^\bot$. Let $\varOmega :\mathbb {R}^p\rightarrow \mathbb {R}^{p\times p}$ satisfy the following properties:

$$\begin{aligned} \varOmega (u)=O(\Vert u-\bar{u}\Vert ) \end{aligned}$$

(5)

as $u\rightarrow \bar{u}$, and for every $\varDelta >0$ there exist $\varepsilon >0$ and $\delta >0$ such that for every $u\in \mathbb {R}^p {\setminus } \{ \bar{u}\}$ satisfying

$$\begin{aligned} \Vert u-\bar{u}\Vert \le \varepsilon ,\quad \left\| \frac{u-\bar{u}}{\Vert u-\bar{u}\Vert } -\bar{v}\right\| \le \delta , \end{aligned}$$

(6)

it holds that

$$\begin{aligned} \Vert \varPi \varOmega (u)\Vert \le \varDelta \Vert u-\bar{u}\Vert . \end{aligned}$$

(7)

Let $\omega :\mathbb {R}^p\rightarrow \mathbb {R}^p$ satisfy

$$\begin{aligned} \omega (u)=O\left( \Vert u-\bar{u}\Vert ^2\right) \end{aligned}$$

(8)

as $u\rightarrow \bar{u}$.

Then there exist $\bar{\varepsilon } = \bar{\varepsilon } (\bar{v})>0$ and $\bar{\delta } = \bar{\delta } (\bar{v})>0$ such that for every $u\in \mathbb {R}^p {\setminus } \{ \bar{u}\}$ satisfying

$$\begin{aligned} \Vert u-\bar{u}\Vert \le \bar{\varepsilon } ,\quad \left\| \frac{u-\bar{u}}{\Vert u-\bar{u}\Vert } -\bar{v}\right\| \le \bar{\delta } , \end{aligned}$$

(9)

the Eq. (2) with $u^k=u$ has the unique solution v, satisfying

$$\begin{aligned} u_1+v_1-\bar{u}_1= & {} O\left( \Vert u-\bar{u}\Vert ^2\right) , \end{aligned}$$

(10)

$$\begin{aligned} u_2+v_2-\bar{u}_2= & {} \frac{1}{2} (u_2-\bar{u}_2) +O(\Vert u_1-\bar{u}_1\Vert ) \nonumber \\&+O\left( \Vert u-\bar{u}\Vert ^{-1}\varPi \omega (u)\right) +O\left( \Vert \varPi \varOmega (u)\Vert \right) +O\left( \Vert u-\bar{u}\Vert ^2\right) \nonumber \\ \end{aligned}$$

(11)

as $u\rightarrow \bar{u}$.

Proof

Under the stated smoothness assumptions, without loss of generality we can assume that $\bar{u}=0$ and

$$\begin{aligned} \varPhi (u) = Au+\frac{1}{2} B[u,\, u]+R(u), \end{aligned}$$

(12)

where $A=\varPhi '(0)\in \mathbb {R}^{p\times p}$, $B=\varPhi ''(0)$ is a symmetric bilinear mapping from $\mathbb {R}^p\times \mathbb {R}^p$ to $\mathbb {R}^p$, and the mapping $R:\mathbb {R}^p\rightarrow \mathbb {R}^p$ is differentiable near 0, with

$$\begin{aligned} R(u)=O\left( \Vert u\Vert ^3\right) ,\quad R'(u)=O\left( \Vert u\Vert ^2\right) \end{aligned}$$

(13)

as $u\rightarrow 0$.

Substituting the form of $\varPhi$ stated in (12) into (2), and multiplying (2) be $(I-\varPi )$ and by $\varPi$, we decompose (2) into the following two equations:

$$\begin{aligned}&(A+(I-\varPi )(B[u]+R'(u)+\varOmega (u)))v_1 \nonumber \\&\quad = -Au_1-(I-\varPi )\left( \frac{1}{2} B[u,\, u]+R(u)-\omega (u)\right) \nonumber \\&\quad \quad -(I-\varPi )(B[u]+R'(u)+\varOmega (u))v_2, \end{aligned}$$

(14)

and

$$\begin{aligned} \varPi (B[u]+R'(u)+\varOmega (u))(v_1+v_2)= -\varPi \left( \frac{1}{2} B[u,\, u]+R(u)-\omega (u)\right) . \end{aligned}$$

(15)

Let $\bar{\varepsilon } >0$ and $\bar{\delta } >0$ be arbitrary and fixed for now. From this point on, we consider only those $u\in \mathbb {R}^p {\setminus } \{ 0\}$ that satisfy (9).

Define the family of linear operators ${\mathscr {A}}(u):(\ker A)^\bot \rightarrow \mathrm{im}\,A$ as the restriction of $(A+(I-\varPi )(B[u]+R'(u)+\varOmega (u)))$ to $(\ker A)^\bot$. Let $\bar{\mathscr {A}}:(\ker A)^\bot \rightarrow \mathrm{im}\,A$ be the restriction of A to $(\ker A)^\bot$. Then, taking into account (8) and (13), the equality (14) can be written as

$$\begin{aligned} {\mathscr {A}}(u)v_1 = -\bar{\mathscr {A}}u_1-(I-\varPi )(B[u]+R'(u)+\varOmega (u))v_2+O\left( \Vert u\Vert ^2\right) \end{aligned}$$

(16)

as $u\rightarrow 0$. Evidently, $\bar{\mathscr {A}}$ is invertible, and according to (5) and (13),

$$\begin{aligned} {\mathscr {A}}(u) = \bar{\mathscr {A}}+O(\Vert u\Vert ). \end{aligned}$$

The latter implies that ${\mathscr {A}}(u)$ is invertible, provided $\bar{\varepsilon } >0$ is small enough, and

$$\begin{aligned} \left( {\mathscr {A}}(u)\right) ^{-1} = \left( \bar{\mathscr {A}}\right) ^{-1}+O(\Vert u\Vert ) \end{aligned}$$

as $u\rightarrow 0$ (see, e.g. [21, Lemma A.6]). Therefore, (16) can be written as

$$\begin{aligned} v_1 =-u_1+{\mathscr {M}}\left( u)v_2+O(\Vert u\Vert ^2\right) , \end{aligned}$$

(17)

where ${\mathscr {M}}(u):\ker A\rightarrow (\ker A)^\bot$,

$$\begin{aligned} {\mathscr {M}}(u) = -({\mathscr {A}}(u))^{-1}(I-\varPi )(B[u]+R'(u)+\varOmega (u)) = O(\Vert u\Vert ) \end{aligned}$$

(18)

as $u\rightarrow 0$.

Substituting (17) into (15), and taking into account (13), we obtain that

$$\begin{aligned} \varPi (B[u]+R'(u)+\varOmega (u))(I+{\mathscr {M}}(u))v_2= & {} -\varPi \left( \frac{1}{2} B[u,\, u]-\omega (u)\right) \nonumber \\&+\varPi (B[u]+\varOmega (u))u_1 + O(\Vert u\Vert ^3).\nonumber \\ \end{aligned}$$

(19)

Define the family of linear operators ${\mathscr {B}}(u):\ker A\rightarrow (\mathrm{im}\,A)^\bot$ as the restriction of $\varPi (B[u]+R'(u)+\varOmega (u))(I+{\mathscr {M}}(u))$ to $\ker A$. Let $\bar{\mathscr {B}}(u):\ker A\rightarrow (\mathrm{im}\,A)^\bot$ be the restriction of $\varPi B[u]$ to $\ker A$. Then (19) can be written as

$$\begin{aligned} {\mathscr {B}}(u)v_2=-\frac{1}{2} \bar{\mathscr {B}}(u)u_2 +\varPi \left( \left( \frac{1}{2} B[u]+\varOmega (u)\right) u_1+\omega (u)\right) +O\left( \Vert u\Vert ^3\right) \end{aligned}$$

(20)

as $u\rightarrow 0$.

The 2-regularity of $\varPhi$ at 0 in the direction $\bar{v}$ means precisely that $\bar{\mathscr {B}}(\bar{v})$ is nonsingular. Then, possibly after reducing $\bar{\delta } >0$, by [21, Lemma A.6] we obtain the existence of $C>0$ such that for every $u\in \mathbb {R}^p {\setminus } \{ 0\}$ satisfying the second relation in (9), $\bar{\mathscr {B}}(u/\Vert u\Vert )$ is invertible, and

$$\begin{aligned} \left\| \left( \bar{\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right) \right) ^{-1}\right\| \le C. \end{aligned}$$

(21)

According to (13), (5), (18), it holds that

$$\begin{aligned} {\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right) = \bar{\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right) +\Vert u\Vert ^{-1}\varPi \varOmega (u)+O(\Vert u\Vert ). \end{aligned}$$

Choosing $\varDelta >0$ small enough, and further reducing $\bar{\varepsilon } >0$ and $\bar{\delta } >0$ if necessary, by (7) and (21), and by [21, Lemma A.6], we now obtain that ${\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right)$ is invertible, and

$$\begin{aligned} \left( {\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right) \right) ^{-1} = \left( \bar{\mathscr {B}}\left( \Vert u\Vert ^{-1}u\right) \right) ^{-1} +O\left( \Vert u\Vert ^{-1}\Vert \varPi \varOmega (u)\Vert \right) +O(\Vert u\Vert ) . \end{aligned}$$

Employing again (5), we further conclude that

$$\begin{aligned} \left( {\mathscr {B}}(u)\right) ^{-1} = \left( \bar{\mathscr {B}}(u)\right) ^{-1} +O\left( \Vert u\Vert ^{-2}\Vert \varPi \varOmega (u)\Vert \right) +O(1) =O\left( \Vert u\Vert ^{-1}\right) . \end{aligned}$$

Therefore, (20) is uniquely solvable, and its unique solution has the form

$$\begin{aligned} v_2= & {} -\frac{1}{2} u_2 +(\bar{\mathscr {B}}(u))^{-1}\varPi \left( \frac{1}{2} B[u,\, u_1] + \omega (u)\right) +O(\Vert \varPi \varOmega (u)\Vert )+O(\Vert u\Vert ^2) \nonumber \\= & {} O(\Vert u\Vert ) \end{aligned}$$

(22)

as $u\rightarrow 0$, where the last estimate employs (5) and (8).

Substituting (22) into (17), and employing (18) again, we finally obtain that

$$\begin{aligned} v_1 =-u_1+O\left( \Vert u\Vert ^2\right) \end{aligned}$$

(23)

as $u\rightarrow 0$.

From (22) and (23), we have the needed estimates (10) and (11). $\square$

Remark 1

From the proof of Lemma 1 it can be seen that under the assumptions of this lemma (removing the assumptions on $\omega$ which are not needed for the following), the values $\bar{\varepsilon } = \bar{\varepsilon } (\bar{v})>0$ and $\bar{\delta } = \bar{\delta } (\bar{v})>0$ can be chosen in such a way that for every $u\in \mathbb {R}^p {\setminus } \{ \bar{u}\}$ satisfying (9), the matrix $\varPhi '(u)+\varOmega (u)$ is invertible, and $(\varPhi '(u)+\varOmega (u))^{-1}=O(\Vert u-\bar{u}\Vert ^{-1})$ as $u\rightarrow \bar{u}$. When $\varOmega \equiv 0$, this result is a particular case of [11, Lemma 3.1].

We proceed to establish convergence of the iterates satisfying the pNM framework (2), from any starting point in the relevant domain. This result is a generalization of [11, Lemma 5.1].

Theorem 1

Let $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ be twice differentiable near $\bar{u}\in \mathbb {R}^p$, with its second derivative being Lipschitz-continuous with respect to $\bar{u}$, that is,

$$\begin{aligned} \varPhi ''(u)-\varPhi ''(\bar{u})=O(\Vert u-\bar{u}\Vert ) \end{aligned}$$

as $u\rightarrow \bar{u}$. Let $\bar{u}$ be a solution of the Eq. (1), and assume that $\varPhi$ is 2-regular at $\bar{u}$ in a direction $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathbb {S}$. Let $\varOmega :\mathbb {R}^p\rightarrow \mathbb {R}^{p\times p}$ and $\omega :\mathbb {R}^p\rightarrow \mathbb {R}^p$ satisfy the estimates (5), (8), as well as

$$\begin{aligned} \varPi \varOmega (u)=O(\Vert u_1-\bar{u}_1\Vert )+O\left( \Vert u-\bar{u}\Vert ^2\right) \end{aligned}$$

(24)

and

$$\begin{aligned} \varPi \omega (u)=O(\Vert u-\bar{u}\Vert \Vert u_1-\bar{u}_1\Vert )+O\left( \Vert u-\bar{u}\Vert ^3\right) \end{aligned}$$

(25)

as $u\rightarrow \bar{u}$.

Then for every $\bar{\varepsilon } >0$ and $\bar{\delta } >0$, there exist $\varepsilon = \varepsilon (\bar{v})>0$ and $\delta = \delta (\bar{v})>0$ such that any starting point $u^0\in \mathbb {R}^p{\setminus } \{ \bar{u}\}$ satisfying

$$\begin{aligned} \Vert u^0-\bar{u}\Vert \le \varepsilon ,\quad \left\| \frac{u^0-\bar{u}}{\Vert u^0-\bar{u}\Vert } -\bar{v}\right\| \le \delta \end{aligned}$$

(26)

uniquely defines the sequence $\{ u^k\} \subset \mathbb {R}^p$ such that for each k it holds that $v^k=u^{k+1}-u^k$ solves (2), $u_2^k\not =\bar{u}_2$, the point $u=u^k$ satisfies (9), the sequence $\{ u^k\}$ converges to $\bar{u}$, the sequence $\{ \Vert u^k-\bar{u}\Vert \}$ converges to zero monotonically,

$$\begin{aligned} \frac{\Vert u_1^{k+1}-\bar{u}_1\Vert }{\Vert u_2^{k+1}-\bar{u}_2\Vert } = O\left( \Vert u^k-\bar{u}\Vert \right) \end{aligned}$$

(27)

as $k\rightarrow \infty$, and

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u_2^k-\bar{u}_2\Vert } = \frac{1}{2}. \end{aligned}$$

(28)

Proof

We again assume that $\bar{u}=0$, and $\varPhi$ is given by (12) with R satisfying (13).

Considering that $\bar{v}_1=0$, observe first that if $u\in \mathbb {R}^p {\setminus } \{ 0\}$ satisfies the second condition in (6) with some $\delta \in (0,\, 1)$, then

$$\begin{aligned} \frac{\Vert u_1\Vert }{\Vert u\Vert } =\left\| \frac{u_1}{\Vert u\Vert } -\bar{v}_1\right\| \le \left\| \frac{u}{\Vert u\Vert } -\bar{v}\right\| \le \delta . \end{aligned}$$

This implies that

$$\begin{aligned} \Vert u_1\Vert \le \delta \Vert u\Vert , \end{aligned}$$

(29)

and hence,

$$\begin{aligned} \Vert u\Vert \le \Vert u_1\Vert +\Vert u_2\Vert \le \delta \Vert u\Vert +\Vert u_2\Vert , \end{aligned}$$

so that

$$\begin{aligned} (1-\delta )\Vert u\Vert \le \Vert u _2\Vert . \end{aligned}$$

(30)

Then

$$\begin{aligned} \left\| \frac{u_2}{\Vert u_2\Vert } - \bar{v}\right\|\le & {} \left\| \frac{u_2}{\Vert u\Vert } - \bar{v}_2\right\| +\left\| \frac{u_2}{\Vert u_2\Vert } - \frac{u_2}{\Vert u\Vert } \right\| \nonumber \\\le & {} \left\| \frac{u}{\Vert u\Vert } - \bar{v}\right\| +\frac{\Vert u\Vert -\Vert u_2\Vert }{\Vert u\Vert } \nonumber \\\le & {} \delta +1- \frac{\Vert u_2\Vert }{\Vert u\Vert } \nonumber \\\le & {} 2\delta , \end{aligned}$$

(31)

where the second inequality employs the fact that $u_2/\Vert u\Vert$ is the metric projection of $u/\Vert u\Vert$ onto $\ker A$.

From (24) and (29) it evidently follows that $\varOmega$ satisfies the corresponding assumptions in Lemma 1. Therefore, according to this lemma, there exist $\bar{\varepsilon } >0$ and $\bar{\delta } >0$ such that for every $u\in \mathbb {R}^p {\setminus } \{ \bar{u}\}$ satisfying (9), the Eq. (2) with $u^k=u$ has the unique solution v, and

$$\begin{aligned} u_1+v_1 =O\left( \Vert u\Vert ^2\right) \end{aligned}$$

and

$$\begin{aligned} u_2+v_2=\frac{1}{2} u_2+O(\Vert u_1\Vert )+O\left( \Vert u\Vert ^2\right) \end{aligned}$$

as $u\rightarrow 0$, where (24) and (25) were again taken into account.

In what follows, we use these values $\bar{\varepsilon }$ and $\bar{\delta }$, with the understanding that if we prove the assertion of the theorem for these specific values of $\bar{\varepsilon }$ and $\bar{\delta }$, it will also be valid for any larger values of those constants. At the same time, since Lemma 1 allows for these $\bar{\varepsilon }$ and $\bar{\delta }$, it certainly allows for any smaller values.

Therefore, there exists $C>0$ such that

$$\begin{aligned} \Vert u_1+v_1 \Vert\le & {} C\Vert u\Vert ^2, \end{aligned}$$

(32)

$$\begin{aligned} \left\| u_2+v_2-\frac{1}{2} u_2\right\|\le & {} \left\| u+v-\frac{1}{2} u_2\right\| \le C\left( \Vert u_1\Vert +\Vert u\Vert ^2\right) , \end{aligned}$$

(33)

and hence,

$$\begin{aligned} \frac{1}{2} \Vert u_2\Vert - C\left( \Vert u_1\Vert +\Vert u\Vert ^2\right)\le & {} \Vert u_2+v_2\Vert \le \Vert u+v\Vert \nonumber \\\le & {} \frac{1}{2} \Vert u_2\Vert + C\left( \Vert u_1\Vert +\Vert u\Vert ^2\right) . \end{aligned}$$

(34)

From (9), (29) and (30) with $\delta =\bar{\delta }$, and from (34), we further derive that

$$\begin{aligned} \left( \frac{1-\bar{\delta } }{2} - C(\bar{\delta } +\bar{\varepsilon } )\right) \Vert u\Vert \le \Vert u_2+v_2\Vert \le \Vert u+v\Vert \le \left( \frac{1}{2} + C(\bar{\delta } +\bar{\varepsilon } )\right) \Vert u\Vert . \end{aligned}$$

Reducing $\bar{\varepsilon } >0$ and $\bar{\delta } >0$ if necessary, so that

$$\begin{aligned} \frac{\bar{\delta } }{2} + C(\bar{\delta } +\bar{\varepsilon } )<\frac{1}{2}, \end{aligned}$$

and setting

$$\begin{aligned} q_- = \frac{1-\bar{\delta } }{2} - C(\bar{\delta } +\bar{\varepsilon } ),\quad q_+ = \frac{1}{2} + C(\bar{\delta } +\bar{\varepsilon } ), \end{aligned}$$

we then obtain that

$$\begin{aligned} q_-\Vert u\Vert \le \Vert u_2+v_2\Vert \le \Vert u+v\Vert \le q_+\Vert u\Vert , \end{aligned}$$

(35)

where

$$\begin{aligned} 0< q_-< q_+ <1. \end{aligned}$$

(36)

By (33), the right inequality in (34), and the left inequality in (35), we have that

$$\begin{aligned} \left\| \frac{u+v}{\Vert u+v\Vert } - \frac{u_2}{\Vert u_2\Vert } \right\|= & {} \frac{\Vert (u+v)\Vert u_2\Vert -u_2\Vert u+v\Vert \Vert }{\Vert u_2\Vert \Vert u+v\Vert } \nonumber \\\le & {} \frac{2C\left( \Vert u_1\Vert +\Vert u\Vert ^2\right) }{q_-\Vert u\Vert } \nonumber \\= & {} \frac{2C}{q_-} \left( \frac{\Vert u_1\Vert }{\Vert u\Vert } +\Vert u\Vert \right) , \end{aligned}$$

(37)

$$\begin{aligned} \left\| \frac{u_2+v_2}{\Vert u_2+v_2\Vert } - \frac{u_2}{\Vert u_2\Vert } \right\|= & {} \frac{\Vert (u_2+v_2)\Vert u_2\Vert - u_2\Vert u_2+v_2\Vert \Vert }{\Vert u_2\Vert \Vert u_2+v_2\Vert } \nonumber \\\le & {} \frac{2C\left( \Vert u_1\Vert +\Vert u\Vert ^2\right) }{q_-\Vert u\Vert } \nonumber \\= & {} \frac{2C}{q_-} \left( \frac{\Vert u_1\Vert }{\Vert u\Vert } +\Vert u\Vert \right) . \end{aligned}$$

(38)

Now choose $\varepsilon \in (0,\, \bar{\varepsilon } ]$, $\delta \in (0,\, \bar{\delta } ]$ satisfying

$$\begin{aligned} 2\delta +\frac{2C}{q_-} \left( \delta +\left( \frac{C}{q_-} +1\right) \frac{\varepsilon }{1-q_+}\right) \le \bar{\delta } , \end{aligned}$$

(39)

and assume that (26) holds for $u^0\in \mathbb {R}^p{\setminus } \{ 0\}$. Suppose that $u^j\in \mathbb {R}^p {\setminus } \{ 0\}$, satisfy (2) and (9) with $u=u^j$ for all $j=1,\, \ldots ,\, k$. Then by the choice of $\bar{\varepsilon } >0$ and $\bar{\delta } >0$, there exists the unique $u^{k+1}$ satisfying (2), and by (29), (31), (32), (35), (36), (37), (38), it holds that

$$\begin{aligned} 0<\Vert u^{k+1}\Vert\le & {} q_+\Vert u^k\Vert \le q_+^2\Vert u^{k-1}\Vert \le \cdots \le q_+^{k+1}\Vert u^0\Vert \le q_+^{k+1}\varepsilon \le \varepsilon \le \bar{\varepsilon } ,\\ \left\| \frac{u^{k+1}}{\Vert u^{k+1}\Vert } - \bar{v}\right\|\le & {} \left\| \frac{u_2^k}{\Vert u_2^k\Vert } - \bar{v}\right\| +\left\| \frac{u^{k+1}}{\Vert u^{k+1}\Vert } - \frac{u_2^k}{\Vert u_2^k\Vert } \right\| \\\le & {} \left\| \frac{u_2^{k-1}}{\Vert u_2^{k-1}\Vert } - \bar{v}\right\| +\left\| \frac{u_2^k}{\Vert u_2^k\Vert } - \frac{u_2^{k-1}}{\Vert u_2^{k-1}\Vert } \right\| +\left\| \frac{u^{k+1}}{\Vert u^{k+1}\Vert } - \frac{u_2^k}{\Vert u_2^k\Vert } \right\| \\\le & {} \ldots \\\le & {} \left\| \frac{u_2^0}{\Vert u_2^0\Vert } - \bar{v}\right\| +\sum _{j=1}^k \left\| \frac{u_2^j}{\Vert u_2^j\Vert } - \frac{u_2^{j-1}}{\Vert u_2^{j-1}\Vert } \right\| +\left\| \frac{u^{k+1}}{\Vert u^{k+1}\Vert } - \frac{u_2^k}{\Vert u_2^k\Vert } \right\| \\\le & {} 2\delta +\sum _{j=1}^k\frac{2C}{q_-} \left( \frac{\Vert u_1^{j-1}\Vert }{\Vert u^{j-1}\Vert } +\Vert u^{j-1}\Vert \right) +\frac{2C}{q_-} \left( \frac{\Vert u_1^k\Vert }{\Vert u^k\Vert } +\Vert u^k\Vert \right) \\\le & {} 2\delta +\frac{2C}{q_-} \sum _{j=0}^k\left( \frac{\Vert u_1^j\Vert }{\Vert u^j\Vert } +\Vert u^j\Vert \right) \\\le & {} 2\delta +\frac{2C}{q_-} \left( \frac{\Vert u_1^0\Vert }{\Vert u^0\Vert } +\sum _{j=1}^k\frac{C\Vert u^{j-1}\Vert }{q_-} +\sum _{j=0}^k\Vert u^j\Vert \right) \\\le & {} 2\delta +\frac{2C}{q_-} \left( \delta +\frac{C}{q_-} \sum _{j=1}^kq_+^{j-1}\varepsilon +\sum _{j=0}^kq_+^j\varepsilon \right) \\\le & {} 2\delta +\frac{2C}{q_-} \left( \delta +\frac{C}{q_-} \frac{\varepsilon }{1-q_+} +\frac{\varepsilon }{1-q_+}\right) \\\le & {} 2\delta +\frac{2C}{q_-} \left( \delta +\left( \frac{C}{q_-}+1\right) \frac{\varepsilon }{1-q_+} \right) \\\le & {} \bar{\delta } , \end{aligned}$$

where the last inequality is by (39). Therefore, (9) holds with $u=u^{k+1}$.

We have thus established that there exists the unique sequence $\{ u^k\} \subset \mathbb {R}^p$ such that for each k the point $u^k$ satisfies (2) and (9) with $u=u^k$. By (35) and (36), it then follows that $u^k\not =\bar{u}$ for all k, and $\{ u^k\}$ converges to 0.

According to (32) and (35), it holds that

$$\begin{aligned} \frac{\Vert u_1^{k+1}\Vert }{\Vert u_2^{k+1}\Vert } \le \frac{C}{q_-} \Vert u^k\Vert \end{aligned}$$

for all k. This yields (27).

Furthermore, according to (34),

$$\begin{aligned} \frac{1}{2} - C\frac{\Vert u_1^k\Vert +\Vert u^k\Vert ^2}{\Vert u_2^k\Vert } \le \frac{\Vert u_2^{k+1} \Vert }{\Vert u_2^k\Vert } \le \frac{1}{2} + C\frac{\Vert u_1^k\Vert +\Vert u^k\Vert ^2}{\Vert u_2^k\Vert } , \end{aligned}$$

where by (27) both sides tend to 1 / 2 as $k\rightarrow \infty$. This gives (28). $\square$

Remark 2

In Theorem 1, by the monotonicity of the sequence $\{ \Vert u^k-\bar{u}\Vert \}$, for every k large enough it holds that $\Vert u_2^{k+1}-\bar{u}_2\Vert \le \Vert u^{k+1}-\bar{u}\Vert \le \Vert u^k-\bar{u}\Vert$. Therefore, (27) implies the estimates

$$\begin{aligned} \frac{\Vert u_1^{k+1}-\bar{u}_1\Vert }{\Vert u_{k+1}-\bar{u}\Vert } = O\left( \Vert u^k-\bar{u}\Vert \right) \end{aligned}$$

and

$$\begin{aligned} \Vert u_1^{k+1}-\bar{u}_1\Vert = O\left( \Vert u^k-\bar{u}\Vert ^2\right) \end{aligned}$$

(40)

as $k\rightarrow \infty$.

Furthermore,

$$\begin{aligned} \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u_1^k-\bar{u}_1\Vert +\Vert u_2^k-\bar{u}_2\Vert } \le \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u^k-\bar{u}\Vert } \le \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u_2^k-\bar{u}_2\Vert }, \end{aligned}$$

where by (27) and (28) both sides tend to 1 / 2 as $k\rightarrow \infty$. Therefore,

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u^k-\bar{u}\Vert } = \frac{1}{2}. \end{aligned}$$

(41)

Finally,

$$\begin{aligned} \frac{\Vert u_2^{k+1}-\bar{u}_2\Vert -\Vert u_1^{k+1}-\bar{u}_1\Vert }{\Vert u^k-\bar{u}\Vert } \le \frac{\Vert u^{k+1}-\bar{u}\Vert }{\Vert u^k-\bar{u}\Vert } \le \frac{\Vert u_1^{k+1}-\bar{u}_1\Vert }{\Vert u^k-\bar{u}\Vert } +\frac{\Vert u_2^{k+1}-\bar{u}_2\Vert }{\Vert u^k-\bar{u}\Vert } \end{aligned}$$

where by (40) and (41) both sides tend to 1 / 2 as $k\rightarrow \infty$. Therefore,

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{\Vert u^{k+1}-\bar{u}\Vert }{\Vert u^k-\bar{u}\Vert } = \frac{1}{2}. \end{aligned}$$

Theorem 1 establishes the existence of a set with nonempty interior, which is star-like with respect to $\bar{u}$, and such that any sequence satisfying the pNM relation (2) and initialized from any point of this set, converges linearly to $\bar{u}$. Moreover, if $\varPhi$ is 2-regular at $\bar{u}$ in at least one direction $\bar{v}\in \ker \varPhi '(\bar{u})$, then the set of such $\bar{v}$ is open and dense in $\ker \varPhi '(\bar{u})\cap \mathbb {S}$: its complement is the null set of the nontrivial homogeneous polynomial $\det \bar{\mathscr {B}}(\cdot )$ considered on $\ker \varPhi '(\bar{u})\cap \mathbb {S}$. The union of convergence domains coming with all such $\bar{v}$ is also a star-like convergence domain with nonempty interior. In the case when $\varPhi '(\bar{u})=0$ (full degeneracy), this domain is quite large. In particular, it is “asymptotically dense”: the only excluded directions are those in which $\varPhi$ is not 2-regular at $\bar{u}$, which is the null set of a nontrivial homogeneous polynomial. Beyond the case of full degeneracy, the convergence domain given by Theorem 1 is at least not “asymptotically thin”. Though it is also not “asymptotically dense”.

For the (unperturbed) Newton method, the existence of “asymptotically dense” star-like domain of convergence was established in [11, Theorem 6.1]. Specifically, it was demonstrated that one Newton step from a point $u^0$ in this domain leads to the convergence domain coming with the appropriate $\bar{v}=\pi (u^0)/\Vert \pi (u^0)\Vert$, where

$$\begin{aligned} \pi (u^0)=\frac{1}{2} \left( u_2^0-\bar{u}_2\right) +\frac{1}{2} \left( \bar{\mathscr {B}}(u^0-\bar{u})\right) ^{-1}\varPi B\left[ u^0-\bar{u},\, u_1^0-\bar{u}_1\right] ; \end{aligned}$$

see (22) above. Deriving a result like this for the pNM scheme (2) is hardly possible in general, at least without rather restrictive assumptions on perturbation terms. Perhaps results along those lines can be derived for specific methods, rather than for the general pNM framework, but such developments are not known at this time.

3 Applications to some specific algorithms

In this section we show how our general results for the pNM framework (2) can be applied to some specific methods. In particular, we consider the following algorithms, all developed for tackling the difficult case of non-isolated solutions: the Levenberg–Marquardt method and the LP-Newton method for equations, and the stabilized Newton–Lagrange method for optimization.

We start with observing that the assumptions (5), (8), (24) and (25) on the perturbations terms in Theorem 1 hold automatically if

$$\begin{aligned} \varOmega (u) = O(\Vert \varPhi (u)\Vert ),\quad \omega (u)=O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert ) \end{aligned}$$

(42)

as $u\rightarrow \bar{u}$. Indeed, this readily follows from the relation

$$\begin{aligned} \varPhi (u) = \varPhi '(\bar{u})(u_1-\bar{u}_1)+O\left( \Vert u-\bar{u}\Vert ^2\right) \end{aligned}$$

as $u\rightarrow \bar{u}$.

Thus, to apply Theorem 1, in the part of perturbations properties it is sufficient to verify (42).

3.1 Levenberg–Marquardt method

An iteration of the classical Levenberg–Marquardt method [24, Chapter 10.2] consists in solving the following subproblem:

$$\begin{aligned} \begin{array}{ll} \text{ minimize }&\displaystyle \frac{1}{2} \Vert \varPhi \left( u^k\right) +\varPhi '\left( u^k\right) v \Vert ^2 +\frac{1}{2} \sigma \left( u^k\right) \Vert v\Vert ^2,\quad v\in \mathbb {R}^p, \end{array} \end{aligned}$$

(43)

where $u^k\in \mathbb {R}^p$ is the current iterate and $\sigma :\mathbb {R}^p\rightarrow \mathbb {R}_+$ defines the regularization parameter.

In [29], it was established that under the Lipschitzian error bound condition [i.e. being initialized near a noncritical solution $\bar{u}$ of (1)], the method described by (43) with $\sigma (u)=\Vert \varPhi (u)\Vert ^2$ generates a sequence which is quadratically convergent to a (nearby) solution of (1). For analysis under the Lipschitzian error bound condition of a rather general framework that includes the Levenberg–Marquardt method, see [5, 8]. Our interest here is the case of critical solutions, when the error bound does not hold.

First, note that the unique (if $\sigma (u^k) >0$) minimizer of the convex quadratic function in (43) is characterized by the linear system

$$\begin{aligned} \left( \varPhi '\left( u^k\right) \right) ^\mathrm{T}\varPhi \left( u^k\right) +\left( (\varPhi '\left( u^k\right) )^\mathrm{T}\varPhi '\left( u^k\right) +\sigma \left( u^k\right) I\right) v = 0 . \end{aligned}$$

(44)

We next show how (44) can be embedded into the pNM framework (2). In particular, we construct the perturbation terms for which the conditions (42) hold, and hence Theorem 1 is applicable, and which correspond to (44) on the relevant domain of convergence. As a result, we obtain the following convergence assertions.

Corollary 1

Let $\varPhi :\mathbb {R}^p\rightarrow \mathbb {R}^p$ be twice differentiable near $\bar{u}\in \mathbb {R}^p$, with its second derivative Lipschitz-continuous with respect to $\bar{u}$. Let $\bar{u}$ be a solution of the Eq. (1), and assume that $\varPhi$ is 2-regular at $\bar{u}$ in a direction $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathbb {S}$.

Then for any $\tau \ge 2$, there exist $\varepsilon = \varepsilon (\bar{v})>0$ and $\delta = \delta (\bar{v})>0$ such that any starting point $u^0\in \mathbb {R}^p{\setminus } \{ \bar{u}\}$ satisfying (26) uniquely defines the sequence $\{ u^k\} \subset \mathbb {R}^p$ such that for each k it holds that $v^k=u^{k+1}-u^k$ solves (43) with $\sigma (u) = \Vert \varPhi (u)\Vert ^\tau$, $u_2^k\not =\bar{u}_2$, the sequence $\{ u^k\}$ converges to $\bar{u}$, the sequence $\{ \Vert u^k-\bar{u}\Vert \}$ converges to zero monotonically, and (27) and (28) hold. Moreover, if $\varPhi '(\bar{u}) = 0$, then the same assertion is valid with any $\tau \ge 3/2$.

Proof

Define $\bar{\varepsilon } = \bar{\varepsilon } (\bar{v})>0$ and $\bar{\delta } = \bar{\delta } (\bar{v})>0$ according to Remark 1, where we set $\varOmega \equiv 0$. Define the set

$$\begin{aligned} K= K(\bar{v})=\{ u\in \mathbb {R}^p{\setminus } \{ \bar{u}\} \mid (9) \text{ holds }\} . \end{aligned}$$

(45)

Then $\varPhi '(u)$ is invertible for all $u\in K$, and $(\varPhi '(u))^{-1}=O(\Vert u-\bar{u}\Vert ^{-1})$ as $u\rightarrow \bar{u}$ (this can also be concluded directly from [11, Lemma 3.1], with an appropriate choice of $\bar{\varepsilon } >0$ and $\bar{\delta } >0$).

We next define the mappings $\varOmega$ and $\omega$. First, we set $\varOmega (u) = 0$ and $\omega (u) = 0$ for all $u\in \mathbb {R}^p{\setminus } K$. Of course, those vanishing perturbation terms for $u\not \in K$ have no relation to (44). The point is that we next show that with the appropriate definitions for $u\in K$, we obtain $\varOmega$ and $\omega$ satisfying (42). Then Theorem 1 ensures that if the starting point satisfies (26) with appropriate $\varepsilon >0$ and $\delta >0$, it follows that the subsequent iterates are well defined and remain in the set K. Finally, in K, the constructed $\varOmega$ and $\omega$ do correspond to (44).

Let $u\in K$. Considering (44) with $u^k=u$, and multiplying both sides of this relations by the matrix $(((\varPhi '(u^k))^\mathrm{T})^{-1} = (((\varPhi '(u^k))^{-1})^\mathrm{T}$, we obtain that

$$\begin{aligned} \varPhi \left( u^k\right) +\left( \varPhi '\left( u^k\right) +\sigma \left( u^k\right) \left( \left( \varPhi '\left( u^k\right) \right) ^{-1}\right) ^\mathrm{T}\right) v = 0, \end{aligned}$$

which is the pNM iteration system (2) with the perturbation terms given by

$$\begin{aligned} \varOmega (u) = \sigma (u)\left( (\varPhi '(u))^{-1}\right) ^\mathrm{T},\quad \omega (u)= 0, \quad u\in K. \end{aligned}$$

Then

$$\begin{aligned} \varOmega (u) = O\left( \Vert u-\bar{u}\Vert ^{-1}\sigma (u)\right) . \end{aligned}$$

Therefore, the needed first estimate in (42) would hold if

$$\begin{aligned} \sigma (u) = O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert ) \end{aligned}$$

(46)

as $u\in K$ tends to $\bar{u}$.

Let $\sigma (u) = \Vert \varPhi (u)\Vert ^\tau$ with $\tau >0$. Then (46) takes the form

$$\begin{aligned} \Vert \varPhi (u)\Vert ^{\tau -1} = O(\Vert u-\bar{u}\Vert ), \end{aligned}$$

and since $\varPhi (u) = O(\Vert u-\bar{u}\Vert )$, the last estimate is satisfied as $u\rightarrow \bar{u}$ if $\tau \ge 2$.

Moreover, in the case when $\varPhi '(\bar{u}) = 0$ (full singularity) it holds that $\varPhi (u) = O(\Vert u-\bar{u}\Vert ^2)$ as $u\rightarrow \bar{u}$, and hence, in this case, the appropriate values are all $\tau \ge 3/2$.

The construction is complete. As the exhibited $\varOmega$ and $\omega$ satisfy (42) as $u\rightarrow \bar{u}$ (regardless of whether u stays in K or not), Theorem 1 is applicable. In particular, it guarantees that for appropriate starting points all the iterates stay in K. In this set, the perturbation terms define the Levenberg–Marquardt iterations (44). Thus, the assertions follow from Theorem 1. $\square$

The following example is taken from DEGEN test collection [4].

Example 1

(DEGEN 20101) Consider the equality-constrained optimization problem

$$\begin{aligned} \begin{array}{llll} \text{ minimize } &{}x^2\\ \text{ subject } \text{ to } &{}x^2 = 0. \end{array} \end{aligned}$$

Stationary points and associated Lagrange multipliers of this problem are characterized by the Lagrange optimality system which has the form of the nonlinear equation (1) with

$$\begin{aligned} \varPhi :\mathbb {R}^2\rightarrow \mathbb {R}^2, \quad \varPhi (u)=\left( 2x(1+\lambda ),\, x^2\right) , \quad u=(x,\, \lambda ) . \end{aligned}$$

The unique feasible point (hence, the unique solution, and the unique stationary point) of this problem is $\bar{x}=0$, and the set of associated Lagrange multipliers is the entire $\mathbb {R}$. Therefore, the solution set of the Lagrange system (i.e. the primal–dual solution set) is $\{ \bar{x}\} \times \mathbb {R}$. The unique critical solution is $\bar{u}=(\bar{x},\, \bar{\lambda })$ with $\bar{\lambda }=-1$, the one for which $\varPhi '(\bar{u})=0$ (full singularity).

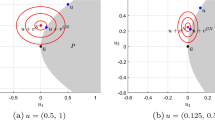
In Figs. 1 and 2, the vertical line corresponds to the primal–dual solution set. These figures show some iterative sequences generated by the Levenberg–Marquardt method, and the domains from which convergence to the critical solution was detected. Using zoom in, and taking smaller areas for starting points, does not significantly change the picture in Fig. 1, corresponding to $\tau =1$. At the same time, such manipulations with Fig. 2a, b put in evidence that for $\tau =3/2$, the domain of convergence is in fact asymptotically dense (see Fig. 2c, d). These observations are in agreement with Theorem 1.

Fig. 1

Levenberg–Marquardt method with $\tau =1$ for Example 1. a Iterative sequences, b Domain of attraction to the critical solution

Fig. 2

Levenberg–Marquardt method with $\tau =3/2$ for Example 1. a Iterative sequences, b Domain of attraction to the critical solution, c Iterative sequences, d Domain of attraction to the critical solution

3.2 LP-Newton method

The LP-Newton method was introduced in [6]. For the Eq. (1), the iteration subproblem of this method has the form

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{} \gamma \\ \text{ subject } \text{ to } &{} \Vert \varPhi (u^k)+\varPhi '(u^k)v\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert v \Vert \le \gamma \Vert \varPhi (u^k)\Vert ,\\ &{}(v,\, \gamma )\in \mathbb {R}^p\times \mathbb {R}. \end{array} \end{aligned}$$

(47)

The subproblem (47) always has a solution if $\varPhi (u^k)\not =0$ (naturally, if $\varPhi (u^k) =0$ the method stops). If the $l_\infty$-norm is used, this is a linear programming problem (hence the name). As demonstrated in [5, 6] (see also [8]), local convergence properties of the LP-Newton method (under the error bound condition, i.e. near noncritical solutions) are the same as for the Levenberg–Marquardt algorithm. Again, our setting is rather that of critical solutions.

The proof of the following result is again by placing (47) within the pNM framework (2). It is interesting that in this case $\varOmega \equiv 0$, while $\omega (\cdot )$ is defined implicitly: there is no analytic expression for it.

Corollary 2

Under the assumptions of Corollary 1, there exist $\varepsilon = \varepsilon (\bar{v})>0$ and $\delta = \delta (\bar{v})>0$ such that for any starting point $u^0\in \mathbb {R}^p{\setminus } \{ \bar{u}\}$ satisfying (26) the following assertions are valid:

• (a) There exists a sequence $\{ u^k\} \subset \mathbb {R}^p$ such that for each k the pair $(v^k,\, \gamma _{k+1})$ with $v^k=u^{k+1}-u^k$ and some $\gamma _{k+1}$ solves (47).

• (b) For any such sequence, $u_2^k\not =\bar{u}_2$ for each k, the sequence $\{ u^k\}$ converges to $\bar{u}$, the sequence $\{ \Vert u^k-\bar{u}\Vert \}$ converges to zero monotonically, and (27) and (28) hold.

Proof

By the second constraint in (47), the equality (2) holds for $\varOmega \equiv 0$ and some $\omega (\cdot )$ satisfying

$$\begin{aligned} \Vert \omega (u)\Vert \le \gamma (u)\Vert \varPhi (u)\Vert ^2, \end{aligned}$$

(48)

where $\gamma (u)$ is the optimal value of the subproblem (47) with $u^k=u$. Note that $\omega (\cdot )$ would satisfy (42), and thus the assumptions of Theorem 1, if

$$\begin{aligned} \gamma (u) = O\left( \Vert \varPhi (u)\Vert ^{-1}\Vert u-\bar{u}\Vert \right) \end{aligned}$$

(49)

as $u\rightarrow \bar{u}$. Indeed, from the first constraint in (47) we then obtain that

$$\begin{aligned} \Vert \varPhi (u)+\varPhi '(u)v\Vert \le \gamma (u)\Vert \varPhi (u)\Vert ^2 = O(\Vert u-\bar{u}\Vert \Vert \varPhi (u)\Vert ), \end{aligned}$$

which implies the second estimate in (42).

We thus have to establish (49) on the relevant set. In this respect, the construction is similar to what had been done in Sect. 3.1 above.

Define $\bar{\varepsilon } = \bar{\varepsilon } (\bar{v})>0$ and $\bar{\delta } = \bar{\delta } (\bar{v})>0$ according to Lemma 1 applied with $\varOmega \equiv 0$ and $\omega \equiv 0$, and define the set K according to (45). Then the step v(u) of the (unperturbed) Newton method from any point $u\in K$ exists, it is uniquely defined, and by (10) and (11), it holds that $v(u)=O(\Vert u-\bar{u}\Vert )$.

We now define the mappings $\varOmega$ and $\omega$. Similarly to the case of the Levenberg–Marquardt method, we first set them identically equal to zero on $\mathbb {R}^p{\setminus } K$. Let $u\in K$. Then the point $(v,\, \gamma )=(v(u),\, \Vert v(u)\Vert /\Vert \varPhi (u)\Vert )$ is feasible in (47), and hence,

$$\begin{aligned} \gamma (u)\le \gamma =\Vert \varPhi (u)\Vert ^{-1}\Vert v(u)\Vert =O\left( \Vert \varPhi (u)\Vert ^{-1}\Vert u-\bar{u}\Vert \right) \end{aligned}$$

as $u\in K$ tends to $\bar{u}$.

As in the proof of Corollary 1, we note that the constructed $\varOmega$ and $\omega$ satisfy (42) as $u\rightarrow \bar{u}$. Therefore, Theorem 1 ensures that for appropriate starting points all the iterates stay in K, and in this set the perturbation terms defined hereby correspond to (47). In particular, the assertions then follow from Theorem 1. $\square$

Observe that for the LP-Newton method, the values of $\omega (\cdot )$ are defined in a posteriori manner, after $v^k$ is computed. For this reason, Theorem 1 cannot yield uniqueness of the iterative sequence: the next iterate can be defined by any $\omega (\cdot )$ satisfying (48) for $u=u^k$, and different choices of appropriate $\omega (\cdot )$ may give rise to different next iterates.

Fig. 3

LP-Newton method for Example 1. a Iterative sequences, b Domain of attraction to the critical solution, c Iterative sequences, d Domain of attraction to the critical solution

Figure 3 shows the same information for the LP-Newton method as Fig. 2 for the Levenberg–Marquardt algorithm, with the same conclusions.

3.3 Equality-constrained optimization and the stabilized Newton–Lagrange method

We next turn our attention to the origin of the critical solutions issues, namely, to the equality-constrained optimization problem

$$\begin{aligned} \begin{array}{llll} \text{ minimize }&f(x)&\text{ subject } \text{ to }&h(x)=0, \end{array} \end{aligned}$$

(50)

where $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $h:\mathbb {R}^{n}\rightarrow \mathbb {R}^{l}$ are smooth. The Lagrangian $L:\mathbb {R}^{n}\times \mathbb {R}^{l}\rightarrow \mathbb {R}$ of this problem is given by

$$\begin{aligned} L(x,\, \lambda )=f(x)+\langle \lambda ,\, h(x)\rangle . \end{aligned}$$

Then stationary points and associated Lagrange multipliers of (50) are characterized by the Lagrange optimality system

$$\begin{aligned} \frac{\partial L}{\partial x} (x,\, \lambda )=0,\quad h(x)=0, \end{aligned}$$

with respect to $x\in \mathbb {R}^{n}$ and $\lambda \in \mathbb {R}^{l}$.

The Lagrange optimality system is a special case of nonlinear equation (1), corresponding to setting $p =q =n+l$, $u=(x,\, \lambda )$,

$$\begin{aligned} \varPhi (u)=\left( \frac{\partial L}{\partial x} (x,\, \lambda ),\, h(x)\right) . \end{aligned}$$

(51)

The stabilized Newton–Lagrange method (or stabilized sequential quadratic programming) was developed for solving the Lagrange optimality system (or optimization problem) when the multipliers associated to a stationary point need not be unique [7, 12, 20, 28]; see also [21, Chapter 7]. For the current iterate $u^k=(x^k,\, \lambda ^k)\in \mathbb {R}^{n}\times \mathbb {R}^{l}$, the iteration subproblem of this method is given by

$$\begin{aligned}\begin{array}{ll} \text{ minimize } &{} \langle f'(x^k), \xi \rangle + \displaystyle \frac{1}{2} \left\langle \displaystyle \frac{\partial ^2L}{\partial x^2}(x^k,\, \lambda ^k)\xi ,\xi \right\rangle +\displaystyle \frac{\sigma (u^k)}{2}\Vert \eta \Vert ^2 \\ \text{ subject } \text{ to } &{} h(x^k)+h'(x^k)\xi - \sigma (u^k)\eta =0 , \end{array} \end{aligned}$$

where the minimization is in the variables $(\xi ,\, \eta )\in \mathbb {R}^{n}\times \mathbb {R}^{l}$, and $\sigma :\mathbb {R}^{n}\times \mathbb {R}^{l}\rightarrow \mathbb {R}_+$ now defines the stabilization parameter. Equivalently, the following linear system (characterizing stationary points and associated Lagrange multipliers of this subproblem) is solved:

$$\begin{aligned}&\frac{\partial L}{\partial x} \left( x^k,\, \lambda ^k\right) +\frac{\partial ^2L}{\partial x^2} \left( x^k,\, \lambda ^k\right) \xi +\left( h'\left( x^k\right) \right) ^\mathrm{T}\eta =0,\nonumber \\&\quad h\left( x^k\right) +h'\left( x^k\right) \xi - \sigma \left( u^k\right) \eta =0. \end{aligned}$$

(52)

With a solution $(\xi ^k,\, \eta ^k)$ of (52) at hand, the next iterate is given by $u^{k+1}=(x^k+\xi ^k,\, \lambda ^k+\eta ^k)$. Note that if $\sigma \equiv 0$, then (52) becomes the usual Newton–Lagrange method, i.e. the basic Newton method applied to the Lagrange optimality system.

For a given Lagrange multiplier $\bar{\lambda }$ associated with a stationary point $\bar{x}$ of problem (50), define the linear subspace

$$\begin{aligned} Q(\bar{x},\, \bar{\lambda })= \left\{ \xi \in \ker h'(\bar{x}) \;\left| \; \frac{\partial ^2L}{\partial x^2} (\bar{x},\, \bar{\lambda })\xi \in \mathrm{im}\,\left( h'(\bar{x})\right) ^\mathrm{T}\right. \right\} . \end{aligned}$$

Recall that the multiplier $\bar{\lambda }$ is called critical if $Q(\bar{x},\, \bar{\lambda })\not =\{ 0\}$; see [13, 18]. Otherwise $\bar{\lambda }$ is noncritical.

As demonstrated in [20], if initialized near a primal–dual solution with a noncritical dual part, the stabilized Newton–Lagrange method with $\sigma (u)=\Vert \varPhi (u)\Vert$, where $\varPhi$ is given by (51), generates a sequence which is superlinearly convergent to a (nearby) solution. Again, of current interest is the critical case.

Evidently, the iteration (52) fits the pNM framework (2) for $\varPhi$ defined in (51), taking

$$\begin{aligned} \varOmega (u) = \left( \begin{array}{cc} 0&{} \; 0\\ 0&{} \; - \sigma (u)I \end{array} \right) ,\quad \omega \equiv 0. \end{aligned}$$

These perturbations satisfy the assumptions in Theorem 1 if, e.g. $\sigma (u)=\Vert \varPhi (u)\Vert ^\tau$, $\tau \ge 1$. We thus conclude the following.

Corollary 3

Let $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $h:\mathbb {R}^{n}\rightarrow \mathbb {R}^{l}$ be three times differentiable near a stationary point $\bar{x}\in \mathbb {R}^{n}$ of problem (50), with their third derivatives Lipschitz-continuous with respect to $\bar{x}$, and let $\bar{\lambda }\in \mathbb {R}^{l}$ be a Lagrange multiplier associated to $\bar{x}$. Assume that the mapping $\varPhi$ defined in (51) is 2-regular at $\bar{u}=(\bar{x},\, \bar{\lambda })$ in a direction $\bar{v}\in \ker \varPhi '(\bar{u})\cap \mathbb {S}$.

Then for any $\tau \ge 1$, there exist $\varepsilon = \varepsilon (\bar{v})>0$ and $\delta = \delta (\bar{v})>0$ such that any starting point $u^0=(x^0,\, \lambda ^0)\in (\mathbb {R}^{n}\times \mathbb {R}^{l}){\setminus } \{ \bar{u}\}$ satisfying (26) uniquely defines a sequence $\{ (x^k,\, \lambda ^k)\} \subset \mathbb {R}^{n}\times \mathbb {R}^{l}$ such that for each k it holds that $(\xi ^k,\, \eta ^k)=(x^{k+1}-x^k,\, \lambda ^{k+1}-\lambda ^k)$ solves (52) with $\sigma (u) = \Vert \varPhi (u)\Vert ^\tau$, $u_2^k\not =\bar{u}_2$, the sequence $\{ u^k\}$ converges to $\bar{u}$, the sequence $\{ \Vert u^k-\bar{u}\Vert \}$ converges to zero monotonically, and (27) and (28) hold.

It is worth to mention that the above results and discussion can be extended to variational problems (of which optimization is a special case), see [7], [21, Chapter 7].

We proceed with some further considerations. A multiplier is said to be critical of order one if $\dim Q(\bar{x},\, \bar{\lambda })=1$. The following was established in [15].

Proposition 2

Let $f:\mathbb {R}^{n}\rightarrow \mathbb {R}$ and $h:\mathbb {R}^{n}\rightarrow \mathbb {R}^{l}$ be three times differentiable at a stationary point $\bar{x}\in \mathbb {R}^{n}$ of problem (50), and let $\bar{\lambda }\in \mathbb {R}^{l}$ be a Lagrange multiplier associated to $\bar{x}$. Let $Q(\bar{x},\, \bar{\lambda })$ be spanned by some $\bar{\xi } \in \mathbb {R}^{n}{\setminus } \{ 0\}$, i.e. $\bar{\lambda }$ is a critical multiplier of order one.

If $\mathrm{rank}\,h'(\bar{x})=l-1$, then $\ker \varPhi '(\bar{u})$ contains elements of the form $v = (\bar{\xi } , \eta )$ with some $\eta \in \mathbb {R}^{l}$, and $\varPhi$ is 2-regular at $\bar{u}$ in every such direction if and only if $h''(\bar{x})[\bar{\xi } , \bar{\xi } ] \not \in \mathrm{im}\,h'(\bar{x})$.

If $\mathrm{rank}\,h'(\bar{x})\le l-2$, then $\varPhi$ cannot be 2-regular at $\bar{u}$ in any direction $v\in \ker \varPhi '(\bar{u})$.

If $h'(\bar{x})=0$, and $l\ge 2$ or $h''(\bar{x})[\bar{\xi } ,\, \bar{\xi } ] =0$, then $\varPhi$ cannot be 2-regular at $\bar{u}$ in any direction $v\in \ker \varPhi '(\bar{u})$.

In the last two cases specified in the proposition above, Theorem 1 is not applicable; these cases require special investigation. In the last case, when $l\ge 2$ but $h''(\bar{x})[\bar{\xi } ,\, \bar{\xi }] \not =0$, allowing for non-isolated critical multipliers, the effect of attraction of the basic Newton–Lagrange method to such multipliers had been studied in [23] for fully quadratic problems.

Table 1 Cases of convergence to $\bar{\lambda }=-1$ in Example 1 (%)

Fig. 4

Critical multipliers in Example 2

On the other hand, if, e.g. $l=1$, $h'(\bar{x})=0$, and $h''(\bar{x})[\bar{\xi } ,\, \bar{\xi } ] \not =0$, then Theorem 1 is applicable with $\bar{v}=(\bar{\xi } ,\, \eta )$ for every $\eta \in \mathbb {R}$. Taking here $\eta =0$ recovers the results in [27] for the basic Newton–Lagrange method and the fully quadratic case. Moreover, this is exactly the situation that we have in Example 1. Table 1 reports on the percentage of detected cases of dual convergence to the unique critical multiplier $\bar{\lambda }=-1$ in Example 1, for the algorithms discussed above, depending on the size $\varepsilon$ of the region for starting points around $(\bar{x},\, \bar{\lambda })$. In the table, L–M refers to the Levenberg–Marquardt method (with different values for the power $\tau$ that defines the regularization parameter), LP-N refers to the LP-Newton method, N–L to the Newton–Lagrange method (i.e. (52) with $\sigma \equiv 0$), and sN–L to the stabilized Newton–Lagrange method.

The case when $\dim Q(\bar{x},\, \bar{\lambda })\ge 2$ (i.e. when $\bar{\lambda }$ is critical of order higher than 1) opens wide possibilities for 2-regularity in the needed directions, and such solutions are often specially attractive for Newton-type iterates.

Table 2 Cases of convergence to $\bar{\lambda }=(1,\, \sqrt{3} )$ in Example 2 (%)

Example 2

(DEGEN 20302) Consider the equality-constrained optimization problem

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{}x_1^2-x_2^2+2x_3^2\\ \text{ subject } \text{ to } &{}\displaystyle -\frac{1}{2} x_1^2+x_2^2-\frac{1}{2} x_3^2=0,\; x_1x_3 = 0. \end{array} \end{aligned}$$

Here, $\bar{x}=0$ is the unique solution, $h'(\bar{x})=0$, and the set of associated Lagrange multipliers is the entire $\mathbb {R}^2$. Critical multipliers are those satisfying $\lambda _1=1$ or $(\lambda _1-3)^2-\lambda _2^2=1$. In Fig. 4, critical multipliers are those forming the vertical straight line and two branches of the hyperbola.

According to Proposition 2, the 2-regularity property cannot hold for $\varPhi$ defined in (51), at $(\bar{x},\, \lambda )$ for any direction $v\in \ker \varPhi '(\bar{u})$, for all critical multipliers $\lambda$, except for $\bar{\lambda }=(1,\, \pm \sqrt{3} )$, which are the two intersection points of the vertical line and the hyperbola. One can directly check that the mapping $\varPhi$ is indeed 2-regular at $\bar{u}=(\bar{x},\, \bar{\lambda })$ in some directions $v\in \ker \varPhi '(\bar{u})$.

Table 2 reports on the percentage of detected cases of dual convergence to $\bar{\lambda }=(1,\, \sqrt{3} )$, for the algorithms discussed above, depending on the size $\varepsilon$ of the region for starting points around $(\bar{x},\, \bar{\lambda })$.