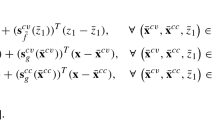Tighter McCormick relaxations through subgradient propagation

Abstract

Tight convex and concave relaxations are of high importance in deterministic global optimization. We present a method to tighten relaxations obtained by the McCormick technique. We use the McCormick subgradient propagation (Mitsos et al. in SIAM J Optim 20(2):573–601, 2009) to construct simple affine under- and overestimators of each factor of the original factorable function. Then, we minimize and maximize these affine relaxations in order to obtain possibly improved range bounds for every factor resulting in possibly tighter final McCormick relaxations. We discuss the method and its limitations, in particular the lack of guarantee for improvement. Subsequently, we provide numerical results for benchmark cases found in the MINLPLib2 library and case studies presented in previous works, where the McCormick technique appears to be advantageous, and discuss computational efficiency. We see that the presented algorithm provides a significant improvement in tightness and decrease in computational time, especially in the case studies using the reduced space formulation presented in (Bongartz and Mitsos in J Glob Optim 69:761–796, 2017).

1 Introduction

Methods based on branch-and-bound (B&B) [34] are the state-of-the art algorithms in deterministic global optimization. In general, B&B methods rely on favorable convergence order of the underlying convex and concave relaxations of all functions involved in a given global optimization problem in order to avoid the so-called cluster effect [16, 22,23,24, 56]. Domain and range reduction techniques are employed within B&B algorithms in order to further increase the quality of the underlying relaxations. These techniques are not necessary to guarantee convergence of the B&B algorithm, however, they are often able to drastically speed up convergence.

Relaxation techniques based on interval arithmetic [33, 41] describe a general way to obtain valid over- and underestimations of a multivariate function $f: Z\rightarrow {\mathbb {R}}$. It is well-known that the simplest interval-based method, called natural interval extensions, often provides very loose estimators. Thus, efforts have been made to improve tightness by introducing improved rigorous arithmetic extensions such as affine reformulations [12, 15, 38] and Taylor models [6, 44].

The method of constructing valid convex and concave relaxations of a continuous factorable function, given by a finite recursion of addition, multiplication and composition via propagation of valid factors, e.g., $F_1\circ f_1 + F_2 \circ f_2 \cdot F_3 \circ f_3$, was presented by McCormick [29, 30] and extended to multivariate outer functions $F_i$ in [52]. McCormick’s idea was used in the development of the well-known auxiliary variable method (AVM) [49,50,51] used in state-of-the-art global optimization solvers such as BARON [51], ANTIGONE [31], SCIP [53], COUENNE [2] and LINDO [26].

In order to further improve the tightness of the relaxations constructed with the AVM, many bound-tightening procedures are used such as Optimality-Based Bound Tightening [27], where additional optimization problems are solved in order to tighten variable bounds; bound propagation techniques [10], where information on a constraint is used to possibly tighten the bounds of a different constraint and finally the variables involved in both constraints; probing [50], where valid constraints are derived from non-active constraints and more. The recent article by Puranik and Sahinidis [40] provides a thorough overview of the field of tightening techniques for AVM. Most of the techniques applicable to the AVM are (at least theoretically) directly applicable to the relaxations obtained via the McCormick technique. Still, there are almost no algorithms developed directly for the improvement of relaxations obtained by the McCormick method. Wechsung et al. [57] present an algorithm for constraint propagation using McCormick relaxations resulting in a reduced variable domain and tighter final McCormick relaxations. They reverse the operations starting with pre-computed McCormick relaxations of a given factorable function g and traverse the factors of g backwards in order to tighten the set of feasible points. Herein, we present a different idea with the same goal of improving the final resulting McCormick relaxations. The presented algorithm uses subgradient propagation [32] in order to possibly improve interval range bounds in each factor of g resulting in a tighter final relaxation. The idea was first shortly discussed in the PhD thesis of Wechsung [55] but has been not elaborated further.

The remainder of the manuscript is structured as follows. In Sect. 2, we provide basic definitions and notation used throughout the article. We present the algorithm in Sect. 3 supported by an example and discuss similarities and differences to methods used in AVM and the limitations of the presented method. Subsequently, we present numerical results in Sect. 4 and examine different adjustments of the presented algorithm. Section 5 concludes the work.

2 Basic definitions

In the following, if not stated otherwise, we consider a continuous function $f:Z\rightarrow {\mathbb {R}}$ with $Z \in {\mathbb {I}}\!{\mathbb {R}}^n$, where ${\mathbb {I}}\!{\mathbb {R}}$ denotes the set of closed bounded intervals of ${\mathbb {R}}$. $Z\in {\mathbb {I}}\!{\mathbb {R}}^n$, also called box, is defined as $Z\equiv [\mathbf {z}^L,\mathbf {z}^U]=[z^L_1,z^U_1]\times \cdots \times [z^L_n,z^U_n]$ with $\mathbf {z}^L,\mathbf {z}^U \in {\mathbb {R}}^n$ where the superscripts L and U always denote a lower and upper bound, respectively. We denote the image of f over Z by $f(Z)\in {\mathbb {I}}\!{\mathbb {R}}$. We denote the estimation of the range bounds of f on Z with the use of natural interval extensions by $I_{f,nat}\supset f(Z)$ and the exact bounds by $I_{f,e}=f(Z)$.

We call a convex function $f^{cv}:Z\rightarrow {\mathbb {R}}$ a convex relaxation (or convex underestimator) of f on Z if $f^{cv}(\mathbf {z})\le f(\mathbf {z})$ for every $\mathbf {z}\in Z$. Similarly, we call a concave function $f^{cc}:Z\rightarrow {\mathbb {R}}$ a concave relaxation (or concave overestimator) of f on Z if $f^{cc}(\mathbf {z})\ge f(\mathbf {z})$ for every $\mathbf {z}\in Z$. We call the tightest convex and concave relaxations of f the convex and concave envelopes $f^{cv}_e, f^{cc}_e$ of f on Z, respectively, i.e., it holds $f^{cv}(\mathbf {z})\le f^{cv}_e(\mathbf {z})\le f(\mathbf {z})$ and $f(\mathbf {z})\le f^{cc}_e(\mathbf {z})\le f^{cc}(\mathbf {z})$ for all $\mathbf {z}\in Z$ and all convex relaxations $f^{cv}$ and concave relaxations $f^{cc}$ of f on Z, respectively.

For a convex and concave function $f^{cv},f^{cc}:Z\rightarrow {\mathbb {R}}$, we call $\mathbf {s}^{cv}(\bar{\mathbf {z}}),\mathbf {s}^{cc}(\bar{\mathbf {z}})\in {\mathbb {R}}^n$ a convex and a concave subgradient of $f^{cv},f^{cc}$ at $\bar{\mathbf {z}}\in Z$, respectively, if

$$\begin{aligned} f^{cv}(\mathbf {z})\ge & {} f^{cv}(\bar{\mathbf {z}}) + (\mathbf {s}^{cv}(\bar{\mathbf {z}}))^T(\mathbf {z}-\bar{\mathbf {z}}), \quad \forall \mathbf {z}\in Z, \end{aligned}$$

(A1)

$$\begin{aligned} f^{cc}(\mathbf {z})\le & {} f^{cc}(\bar{\mathbf {z}}) + (\mathbf {s}^{cc}(\bar{\mathbf {z}}))^T(\mathbf {z}-\bar{\mathbf {z}}), \quad \forall \mathbf {z}\in Z. \end{aligned}$$

(A2)

We denote the affine functions on the right-hand side of inequalities (A1), (A2) constructed with the convex and concave subgradient $\mathbf {s}^{cv}(\bar{\mathbf {z}}),\mathbf {s}^{cc}(\bar{\mathbf {z}})$ by $f^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ and $f^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$, respectively. Note that $f^{cv,sub}$ and $f^{cc,sub}$ are valid under- and overestimators of f on Z, respectively.

2.1 McCormick relaxations and subgradient propagation

We will make use of McCormick propagation rules originally developed by McCormick [29] and extended to multivariate compositions of functions by Tsoukalas and Mitsos [52].

2.2 Computational graph

Fig. 1

Computational graph for $g(z)=(z-z^2)\cdot (z^3-\exp (z))$ on $Z=[-\,0.5,1]$

We assume that a directed acyclic graph (DAG) representation $G=({\mathbb {F}},E)$, described in, e.g., Sects. 2 and 3 in [45], of a (multivariate) factorable function $g:Z\rightarrow {\mathbb {R}}$ with $Z\in {\mathbb {I}}\!{\mathbb {R}}^n$ is given. ${\mathbb {F}}$ is the set of vertices, which we call factors herein, consisting of operations and independent variables, and E the set of edges connecting the factors. For non-commutative operations, e.g., subtraction, the correct order of the previous factors is saved and shown in Fig. 1 from left to right, i.e., the left child of the ’−’ operation is on the left side of the minus sign and the right child is on the right side of it. We assume that for each factor $f_j\in {\mathbb {F}},j\in \{1,\ldots ,|{\mathbb {F}}|\}$ convex $f_j^{cv}(\bar{\mathbf {z}})$ and concave $f_j^{cc}(\bar{\mathbf {z}})$ relaxations, the corresponding convex $\mathbf {s}_j^{cv}(\bar{\mathbf {z}})$ and concave $\mathbf {s}_j^{cc}(\bar{\mathbf {z}})$ subgradients at a point $\bar{\mathbf {z}} \in Z$ and valid upper $f_j^U$ and lower $f_j^L$ bounds on the range of f over Z are calculated, see Example 4.2 and Fig. 4.2 in [32]. The relaxations and subgradients are calculated by the McCormick rules. The upper $f_j^U$ and lower $f_j^L$ bounds on the range of f over Z are obtained via natural interval extension [33, 41] throughout this article, i.e., $I_{j,nat}=[f_j^L,f_j^U]$. In order to evaluate g, its relaxations and its subgradients at a point $\bar{\mathbf {z}} \in Z$ through G, we assume that the corresponding DAG is traversed in a reversed-level-order, i.e., starting at the independent variables $z_i,~i\in \{1,\ldots ,n \}$ and working through all factors up to the root given as $g(\bar{\mathbf {z}})$.

Example 1

Consider the function $g(z)=(z-z^2)(z^3-\exp (z))$ on $Z=[-\,0.5,1]$. It consists of 7 factors, namely the independent variable z and the 6 operations, $\hat{\,}$2, $\hat{\,}$3, $\exp ,-,-$ and $\times$. The corresponding computational graph is shown in Fig. 1.

3 Algorithm for tighter McCormick relaxations

3.1 Basic idea

For a nonlinear factorable function given by a finite recursion of addition, multiplication and composition, $g=f_1 \circ f_2+f_3 \circ f_4 \cdot f_5 \circ f_6$, there are several bound and domain tightening techniques and ideas, found in, e.g., [10, 13, 19, 20, 39, 40]. Many tightening methods use information on constraints within a given problem in order to tighten variable bounds, e.g., [10, 19, 48], while other methods use optimality conditions, reduced costs of variables, and dual multipliers of constraints of the given problem to obtain a tighter relaxation, e.g., [39, 43, 50]. We present an algorithm which uses information on McCormick relaxations and subgradients of each factor of a particular function g within a given optimization problem to possibly improve the resulting final McCormick relaxations of g. In Sect. 2.3 of [37], we have presented that using tighter range bounds for each factor of a McCormick relaxation results in tighter relaxations. Herein, we present an idea for obtaining tighter McCormick relaxations with the use of subgradients for McCormick relaxations, [32] (implemented within MC++(v2.0) [11]). The presented algorithm is not guaranteed to improve the final McCormick relaxations making it a heuristic. We first give the basic idea followed by an example and then formalize the algorithm.

When calculating McCormick relaxations, it is possible to use different interval extensions, e.g., natural interval extensions, the standard centered form or Taylor forms (Sects. 2.2 and 3.7 in [41]). We show that the presented algorithm can still improve the final McCormick relaxations for more sophisticated interval arithmetic and briefly discuss results in Sect. 3.2.2. By solving $\min \nolimits _{\mathbf {z} \in Z} f_j^{cv}(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j^{cc}(\mathbf {z})$ for each factor $f_j, j\in \{1,\ldots , |{\mathbb {F}}|\}$ of a factorable function g, where $f_j^{cv},f_j^{cc}$ are McCormick relaxations of $f_j$, we can obtain valid and possibly tighter range bounds for each factor $f_j$. We can achieve even tighter bounds by solving $\min \nolimits _{\mathbf {z} \in Z} f_j(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j(\mathbf {z})$ resulting in a possible improvement of McCormick relaxations of g (see Examples 2 and 5 in [37]). However, the number of factors in a factorable function can be very large leading to a high computational time. Thus, we want to find a good trade-off between tightness of range bounds of each factor and computational time needed. We could approximately solve $\min \nolimits _{\mathbf {z} \in Z} f_j(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j(\mathbf {z})$ using linear or higher order approximations of $f_j$ in order to simplify the optimization problem but this does not guarantee valid bounds. We could as well approximately solve $\min \nolimits _{\mathbf {z} \in Z} f_j^{cv}(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j^{cc}(\mathbf {z})$ by the use of a solution method for convex (nonsmooth) problems, e.g., bundle-methods [4, 5], and allow only a small number of iteration steps providing valid but possibly extremely loose bounds. In this article, we use range, convex and concave relaxations and subgradients in order to solve $\min \nolimits _{\mathbf {z} \in Z} f_j^{cv}(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j^{cc}(\mathbf {z})$ approximately by solving the simple linear box-constrained problems $\min \nolimits _{\mathbf {z} \in Z} f_j^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$ for every factor $f_j,j\in \{1,\ldots , |{\mathbb {F}}|\}$ resulting in possibly improved range bounds $f_j^L,f_j^U$ and finally tighter convex and concave McCormick relaxations of g.

In Example 4.4 of [32], simple affine relaxations are constructed by using the propagated subgradient at a point $\bar{\mathbf {z}}\in Z$ to construct the affine relaxations $g^{cv,sub}(\bar{\mathbf {z}},\mathbf {z}),g^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$ of the original function g. The lower bound obtained by evaluating the affine functions at their minimum and maximum, respectively, can result in tighter bounds than the underlying (natural) interval extensions, see Fig. 4.4 in [32]. We can exploit this property of the affine estimators when constructing McCormick relaxations by computing the subgradients at a point in the domain, e.g., the middle-point, in each factor $f_j$ of the factorable function g and checking if we can improve the corresponding range bounds for the current factor, i.e., we approximately solve $\min \nolimits _{\mathbf {z} \in Z} f_j^{cv}(\mathbf {z})$ and $\max \nolimits _{\mathbf {z} \in Z} f_j^{cc}(\mathbf {z})$ by solving $\min \nolimits _{\mathbf {z}\in Z} f_j^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ and $\max \nolimits _{\mathbf {z}\in Z} f_j^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$ for every $j\in \{1,\ldots , |{\mathbb {F}}|\}$. We obtain the corresponding values $f_{j,alg}^L,f_{j,alg}^U$ and check if $f_{j,alg}^L>f_j^L,f_{j,alg}^U< f_j^U$, i.e., if we can improve the bounds on the range of $f_j$ for each $j\in \{1,\ldots , |{\mathbb {F}}|\}$. Note that it is not guaranteed that the bounds $f^L_{j,alg},f_{j,alg}^U$ are better than the bounds $f_j^L, f_j^U$ obtained through natural interval extensions. Subsequently, we can compute a next linearization point and repeat the computations if desired. Note that since we cannot provide any guarantee on the new bounds $f^L_{j,alg},f_{j,alg}^U$, it can take many re-computations in order to achieve an improvement for the range bounds $f_j^L, f_j^U$ of a factor $f_j$ and thus, a maximal number of iterations should be predefined.

3.1.1 Connection to existing ideas

The idea can be intuitively described as a specific application of subgradient bundle methods [4, 5]. We use subgradients to approximate the possibly non-smooth convex/concave relaxations of a given factor $f_j$ of the original function g representing our bundle. We then construct a linear approximation of $f_j$ and check if the linearization provides a better range bound than the natural interval extension. If a maximum number of iterations is not reached, we use the subgradient information in order to determine a new point. In contrast to a bundle method, we always work with only one subgradient, i.e., bundle of size 1, making the application easier. We discuss an alternative of the presented method in Sect. 3.6. It is also possible to describe this idea as a modified Sandwich algorithm (4.2 in [50]) where polyhedral approximations are constructed for convex functions. However, the Sandwich algorithm does not work with propagated subgradients and range intervals but rather with the differentials of particular convex functions and its exact range bounds differing from the presented method. Moreover, we try to avoid computing subgradients at all corners, in contrast to what is done in Figs. 4.1–4.8 in [50], since the dimension of $\mathbf {z}$ can be too large to make this algorithm applicable in each factor of g. The idea of the method is presented in the next example.

3.2 Illustrative examples

3.2.1 Natural interval extensions

Example 2

Consider again the function $g(z)=(z-z^2)(z^3-\exp (-z))$ on $Z=[-\,0.5,1]$, Fig. 3, and consider the particular three factors $f_5(z)=z-z^2,~f_6(z)=z^3-\exp (z)$ and $f_7(z)=f_5(z)\cdot f_6(z)$. For factors $f_1,f_2,f_3,f_4$, envelopes are known and natural interval extension provide exact range bounds. The convex and concave McCormick relaxations provide envelopes for $f_5$ on Z given as

$$\begin{aligned} f_5^{cv}(z)=0.5z-0.5 \quad \text {and}\quad f_5^{cc}(z)= z- z^2. \end{aligned}$$

The natural interval extensions are not exact for the range of $f_5$ providing $I_{5,nat}=[-\,1.5,1]$ while the exact range is given as $I_{5,e}=[-\,0.75,0.25]$. The convex and concave subgradient of $f_5^{cv}$ and $f_5^{cc}$, respectively, at the middle point 0.25 of Z are $s^{cv}_5(0.25)=0.5$ and $s^{cc}_5(0.25)=0.5$, respectively. We construct the corresponding affine functions

$$\begin{aligned} f_5^{cv,sub}(0.25,z)&=f_5^{cv}(0.25)+s^{cv}_5(0.25)(z-0.25)\quad \text {and}\\ f_5^{cc,sub}(0.25,z)&=f_5^{cc}(0.25)+s^{cc}_5(0.25)(z-0.25). \end{aligned}$$

Next, we evaluate the affine functions at their respective minimum and maximum in order to obtain

$$\begin{aligned} \begin{aligned} \min _{z\in [-\,0.5,1]} f_5^{cv,sub}(0.25,z)&= f_5^{cv,sub}(0.25,-0.5) = -0.75\quad \text {and } \\ \max _{z\in [-\,0.5,1]} f_5^{cc,sub}(0.25,z)&= f_5^{cc,sub}(0.25,1) = 0.5625. \end{aligned} \end{aligned}$$

(1)

With (1) we can improve the natural interval extensions range bounds $I_{5,nat}$ from $[-\,1.5,1]$ to $I_{5,alg} = [-\,0.75,0.5625]$ for factor $f_5$. The factor $f_5$ together with its convex and concave McCormick relaxations (constructed with natural interval bounds), natural interval bounds $f_5^L,f_5^U$ and the affine functions can be seen in Fig. 2a. This procedure can be rerun for a different point in order to possibly improve the interval bounds even further but to keep this example simple, we do only one iteration. It is possible to rerun the procedure for the same point if we improve a factor before, since the relaxations and the corresponding subgradients change.

Fig. 2

Example 2. a Factor $f_5(z)=z-z^2$ with its convex and concave McCormick relaxations, natural interval extension estimators $f_5^L,f_5^U$ for the range of $f_5$ on $Z=[-\,0.5,1]$ and affine under- and overestimators constructed with the use of subgradients at the middle point 0.25. The affine underestimator equals the convex envelope of $f_5$. b Factor $f_6(z)=z^3-\exp (z)$ with its convex and concave McCormick relaxations, natural interval extension estimators $f_6^L,f_6^U$ for the range of $f_6$ on $Z=[-\,0.5,1]$ and affine under- and overestimators constructed with the use of subgradients at the middle point 0.25

Next, we compute improved range bounds for the factor $f_6(z)=z^3-\exp (z)$. The convex and concave McCormick relaxations of $f_6$ on Z (using the supplementary material of [47]) are given as

$$\begin{aligned} f_6^{cv}(z)&={\left\{ \begin{array}{ll} -\,0.125-\exp (-\,0.5)+\left( 0.1875-\frac{\exp (-\,0.5)-\exp (1)}{-\,0.5-1}\right) (z+0.5), &{}\quad \text {for}\;\; z\le 0.25 \\ z^3 -\exp (-\,0.5) -\frac{\exp (-\,0.5)-\exp (1)}{-\,0.5-1}(z+0.5),&{}\quad \text {else} \end{array}\right. }\\ f_6^{cc}(z)&=0.25+0.75z-\exp (z). \end{aligned}$$

The natural interval extensions provide $I_{6,nat}=[-\,\exp (1)-0.125,1-\exp (-\,0.5)]$$\approx [-\,2.843,0.393]$, while the exact range is given as $I_{6,e}\approx [-\,1.73,-\,0.728]$. The convex and concave subgradients of and , respectively, at the middle point 0.25 of Z are $s_6^{cv}(0.25)=0.1875-\frac{\exp (-\,0.5)-\exp (1)}{-\,0.5-1}$ and $s^{cc}_6(0.25)=0.75-\exp (0.25)$. We construct the corresponding affine functions

$$\begin{aligned} f_6^{cv,sub}(0.25,z)&=f_6^{cv}(0.25)+s^{cv}_6(0.25)(z-0.25)\quad \text {and }\\ f_6^{cc,sub}(0.25,z)&=f_6^{cc}(0.25)+s^{cc}_6(0.25)(z-0.25). \end{aligned}$$

Then, we evaluate the affine functions at their respective minimum and maximum in order to obtain

$$\begin{aligned} \begin{aligned} \min _{z\in [-\,0.5,1]} f_6^{cv,sub}(0.25,z)&= f_6^{cv,sub}(0.25,1) \approx -2.562 \quad \text {and } \\ \max _{z\in [-\,0.5,1]} f_6^{cc,sub}(0.25,z)&= f_6^{cc,sub}(0.25,-0.5) \approx -0.446. \end{aligned} \end{aligned}$$

(2)

With (2) we can improve the natural interval extensions range bounds $I_{6,nat}$ from $\approx [-\,2.843,0.393]$ to $I_{6,alg}\approx [-\,2.562,-\,0.446]$ for factor $f_6$. Factor $f_6$ together with its convex and concave McCormick relaxations (constructed with natural interval bounds), natural interval bounds $f_6^L,f_6^U$ and the affine functions can be seen in Fig. 2b. Once again, this procedure can be rerun for a different point in order to possibly improve the interval bounds even further but to keep this example simple, we do only one iteration.

We can now construct the envelope for the bilinear product $f_7=f_5f_6$ on the improved intervals $I_{5,alg}\times I_{6,alg}$ and finally the convex and concave McCormick relaxations for g. Figure 3 shows function g together with its convex and concave McCormick relaxations constructed with the simple intervals $I_{5,nat},I_{6,nat}$ denoted as $g^{cv}_{nat},g^{cc}_{nat}$ and two improved McCormick relaxations constructed with the new intervals $I_{5,alg},I_{6,alg}$ denoted as $g^{cv}_{alg},g^{cc}_{alg}$. The proposed algorithm drastically improves the relaxations.

The procedure for obtaining improved lower and upper bounds for a factor of g is formally given in Sect. 3.3 and discussed afterwards.

3.2.2 Advanced interval extensions

Although natural interval extensions have the advantage of simplicity, robustness and extremely low computational times, the usage of more sophisticated interval arithmetic is often advisable. If better interval extensions are used for the construction of McCormick relaxations, the resulting under- and overestimators may be much tighter than relaxations constructed with natural interval extensions, cf. Example 5 in [37]. Still, even the more sophisticated interval extensions do not guarantee that the resulting range bounds are exact. This leaves room for improvement of the range bounds by the presented method.

Example 3

Consider $g(z)=(\log (z+1)-z^2)(\log (z+1)-\exp (z-0.5))$ on $Z=[-\,0.5,1]$, Fig. 5, and consider the particular three factors $f_9(z)=\log (z+1)-z^2,f_{10}(z)=\log (z+1)-\exp (z-0.5)$ and $f_{11}(z)=f_9(z)\cdot f_{10}(z)$. For the other factors $z,1,0.5,z+1,z-0.5,z^2,\log (z+1),\exp (z-0.5)$, envelopes are known and simple interval arithmetic provides exact range bounds. In this example, we use the second order Taylor form interval extensions (Sect. 3.7 in [41]) instead of natural interval extension to show that the presented algorithm can provide tighter McCormick relaxations even if more advanced interval arithmetic are used for the construction of McCormick relaxations. In particular, we compute the range bounds for a twice differentiable function $h:Z\rightarrow {\mathbb {R}}$ by calculating $I_{h,T}=[h_T^L,h_T^U]=h(c)+h'(c)(Z-c)+\frac{h''(Z)}{2}(Z-c)^2$, where c is the middle point of Z, $h',h''$ are the first and second derivatives of h and $h''(Z)$ is an interval overestimating the range of $h''$ which we calculated through natural interval extensions in this example.

Fig. 3

Example 2. Function $g(z)=(z-z^2)(z^3-\exp (z))$ on $Z=[-\,0.5,1]$ together with its convex and concave McCormick relaxations $g^{cv}_{nat},g^{cc}_{nat}$ constructed with natural interval extensions and the convex and concave McCormick relaxations $g^{cv}_{alg},g^{cc}_{alg}$ constructed using the range bounds computed Algorithm 1 with only one iteration at each factor

The McCormick relaxations of $f_9$ on Z (using the supplementary material of [47]) are given as

$$\begin{aligned} f_9^{cv}(z)&=f_9(-\,0.5)+\frac{f_9(-\,0.5)-f_9(1)}{-\,0.5-1}(z+0.5)\\ f_9^{cc}(z)&=\log (z+1)-z^2. \end{aligned}$$

Interval extensions obtained by the Taylor form provide $I_{9,T}\approx [-\,1.751,0.385]$ while the exact range is given as $I_{9,e}\approx [-\,0.943,0.177]$. The convex and concave subgradients of $f_9^{cv}$ and $f_9^{cc}$, respectively, at the middle point 0.25 of Z are $s_9^{cv}(0.25)=\frac{f_9^{cv}(-\,0.5)-f_9^{cv}(1)}{-\,0.5-1}$ and $s_9^{cc}(0.25)=0.3$, respectively. We construct the affine functions

$$\begin{aligned} f_9^{cv,sub}(0.25,z)&=f_9^{cv}(0.25)+s^{cv}_9(0.25)(z-0.25)\quad \text {and }\\ f_9^{cc,sub}(0.25,z)&=f_9^{cc}(0.25)+s^{cc}_9(0.25)(z-0.25). \end{aligned}$$

Subsequently, we compute the respective minimum and maximum of the affine functions

$$\begin{aligned} \begin{aligned} \min _{z\in [-\,0.5,1]} f_9^{cv,sub}(0.25,z)&= f_9^{cv,sub}(0.25,-0.5) \approx -0.943\quad \text {and } \\ \max _{z\in [-\,0.5,1]} f_9^{cc,sub}(0.25,z)&= f_9^{cc,sub}(0.25,1) \approx 0.385. \end{aligned} \end{aligned}$$

(3)

With (3) we can improve the interval bounds obtained by the Taylor form from $I_{9,T}=[-\,1.751,0.385]$ to $I_{9,alg}=[-\,0.943,0.385]$ for factor $f_9$. Factor $f_9$ together with its convex and concave relaxations (constructed with Taylor form bounds), Taylor form bounds $f_{9,T}^L, f_{9,T}^U$ and the affine functions can be seen in Fig. 4a. Similar to Example 2, this procedure can be rerun but to keep this example simple, we do only one iteration.

Fig. 4

Example 3. a Factor $f_9(z)=\log (z+1)-z^2$ with its convex and concave McCormick relaxations, Taylor form interval extension estimators $f_{9,T}^L,f_{9,T}^U$ for the range of $f_9$ on $Z=[-\,0.5,1]$ and affine under- and overestimators constructed with the use of subgradients at the middle point 0.25. The affine underestimator equals the convex relaxation of $f_9$. b Factor $f_{10}(z)=\log (z-1)-\exp (z-0.5)$ with its convex and concave McCormick relaxations, Taylor form interval extension estimators $f_{{10},T}^L,f_{{10},T}^U$ for the range of $f_{10}$ on $Z=[-\,0.5,1]$ and affine under- and overestimators constructed with the use of subgradients at the middle point 0.25. The affine underestimator equals the convex relaxation of $f_{10}$

Next, we calculate improved range bounds for factor $f_{10}$. The convex and concave McCormick relaxations of $f_{10}$ on Z (using the supplementary material of [47]) are

$$\begin{aligned} f_{10}^{cv}(z)&=f_{10}(-\,0.5)+\frac{f_{10}(-\,0.5)-f_{10}(1)}{-\,0.5-1}(z+0.5)\\ f_{10}^{cc}(z)&=\log (z+1)-\exp (z-0.5). \end{aligned}$$

The Taylor form interval extensions provide $I_{{10},T}\approx [-\,2.16,-\,0.539]$, while the exact range is given as $I_{{10},e}\approx [-\,1.061,-\,0.555]$. The convex and concave subgradients of ${f_{10}^{cv}}$ and ${f^{cc}_{10}}$, respectively, at the middle point 0.25 of Z are $s_{10}^{cv}(0.25)=\frac{f_{10}(-\,0.5)-f_{10}(1)}{-\,0.5-1}$ and $s_{10}^{cc}(0.25)=0.8-\exp (-\,0.25)$. We construct the corresponding affine functions

$$\begin{aligned} f_{10}^{cv,sub}(0.25,z)&=f_{10}^{cv}(0.25)+s^{cv}_{10}(0.25)(z-0.25)\quad \text {and }\\ f_{10}^{cc,sub}(0.25,z)&=f_{10}^{cc}(0.25)+s^{cc}_{10}(0.25)(z-0.25) \end{aligned}$$

and compute the respective minimum and maximum

$$\begin{aligned} \begin{aligned} \min _{z\in [-\,0.5,1]} f_{10}^{cv,sub}(0.25,z)&= f_{10}^{cv,sub}(0.25,-0.5) \approx -1.061\quad \text {and } \\ \max _{z\in [-\,0.5,1]} f_{10}^{cc,sub}(0.25,z)&= f_{10}^{cc,sub}(0.25,1) \approx -0.539. \end{aligned} \end{aligned}$$

(4)

With (4) we can improve the interval bounds obtained by the Taylor form from $I_{{10},T}$$\approx [-\,2.16,-\,0.539]$ to $I_{{10},alg}=[-\,1.061,-\,0.539]$ for factor $f_{10}$. Factor $f_{10}$ together with its convex and concave McCormick relaxations (constructed with Taylor form bounds), Taylor form bounds $f_{{10},T}^L,f_{{10},T}^U$ and the affine functions can be seen in Fig. 4b. Just as before, these steps can be recalculated but to keep this example simple, we do only one iteration.

Fig. 5

Example 3. Function $g(z)=(\log (z+1)-z^2)(\log (z+1)-\exp (z-0.5))$ on $Z=[-\,0.5,1]$ together with its convex and concave McCormick relaxations $g^{cv}_{T},g^{cc}_{T}$ constructed with Taylor form interval extensions and the convex and concave McCormick relaxation $g^{cv}_{alg},g^{cc}_{alg}$ constructed using the range bounds computed via Algorithm 1 with only one iteration at each factor

Now, we are able to construct the envelope of $f_{11}=f_9f_{10}$ on $I_{9,alg}\times I_{{10},alg}$ and subsequently the McCormick relaxations of g on Z. Figure 5 shows function g together with its convex and concave McCormick relaxations constructed with the intervals $I_{9,T},I_{{10},T}$ obtained with the Taylor form interval extensions denoted as $g_{T}^{cv},g_T^{cc}$ and two improved McCormick relaxations constructed with the intervals $I_{9,alg},I_{{10},alg}$ denoted as $g_{alg}^{cv},g_{alg}^{cc}$. We see that even for the more sophisticated interval extensions, the proposed method is able to significantly improve the final resulting McCormick relaxations.

Example 3 shows that the algorithm is able to improve the McCormick relaxations of a given function g even if more advanced interval arithmetic are used for the computation of range bounds of each factor. Obviously, it holds that the weaker the underlying estimated bounds for each factor, the larger is the potential of the presented heuristic.

3.2.3 Bivariate example

Since univariate functions can often be handled more efficiently, we present a bivariate example to better illustrate the merit of the method.

Fig. 6

Example 4. a Factor $f_6(y)=\log (y)+\exp (-\,y)$ with its convex and concave McCormick relaxations, natural interval extension estimators $f_6^L,f_6^U$ for the range of $f_6$ on $Z=[0.5,1.5]$ and affine under- and overestimators constructed with the use of subgradients at the middle point 1. b Factor $f_{10}(x,y)=x^2\cdot (\log (y)+\exp (-\,y))-x\cdot (\log (y)+\exp (-\,y))$ with its concave McCormick relaxation $f_{10}^{cc}$, concave subgradient $f_{10}^{cc,sub}$ at the middle point (0.375, 1) and the upper bound obtained by natural interval extensions using the improved bounds of factor $f_6$

Fig. 7

Example 4. Function $g(x,y)=(x^2\cdot (\log (y)+\exp (-\,y))-x\cdot (\log (y)+\exp (-\,y)))^3$ on $X\times Y=[-\,0.25,1]\times [0.5,1.5]$ together with its convex and concave McCormick relaxations $g^{cv}_{nat},g^{cc}_{nat}$ constructed with natural interval extensions and the convex and concave McCormick relaxations $g^{cv}_{alg},g^{cc}_{alg}$ constructed using the range bounds computed via Algorithm 1 with only one iteration at each factor

Example 4

Consider the two dimensional function $g:[-\,0.25,1]\times [0.5,1.5]\rightarrow {\mathbb {R}}, (x,y)\mapsto \left( x^2\cdot (\log (y)+\exp (-\,y))-x\cdot (\log (y)+\exp (-\,y))\right) ^3$. First, examine the factor $f_6(y)=\log (y)+\exp (-\,y)$ with its convex and concave McCormick relaxations given as

$$\begin{aligned} f_{6}^{cv}(y)&=\log (0.5)+\frac{\log (1.5)-\log (0.5)}{1.5-0.5}(y-0.5)+\exp (-\,y) \\ f_{6}^{cc}(y)&=\log (y) + \exp (-\,0.5)+\frac{\exp (-1.5)-\exp (-\,0.5)}{1.5-0.5}(y-0.5) \end{aligned}$$

and the (non-exact) natural interval extensions $I_{6,nat}\approx [-\,0.47,1.011]$. The convex and concave subgradient of $f_6^{cv}$ and $f_6^{cc}$, respectively, at the middle point 1 of Y are $s_6^{cv}(1)\approx 0.7307$ and $s_6^{cc}(1)\approx 0.6165$, respectively. We construct the affine functions

$$\begin{aligned} f_6^{cv,sub}(1,y)&=f_6^{cv}(1)+s_6^{cv}(1)(y-1)\quad \text {and }\\ f_6^{cc,sub}(1,y)&=f_6^{cc}(1)+s_6^{cc}(1)(y-1). \end{aligned}$$

Now, we evaluate the affine functions at their respective minimum and maximum and obtain

$$\begin{aligned} \begin{aligned} \min _{y\in [0.5,1.5]}f_6^{cv,sub}(1,y)&=f_6^{cv,sub}(1,0.5)\approx -0.1413 \quad \text {and }\\ \max _{y\in [0.5,1.5]}f_6^{cc,sub}(1,y)&=f_6^{cc,sub}(1,1.5)\approx 0.7231 \end{aligned} \end{aligned}$$

(5)

With (5) we can improve the interval bounds $I_{6,nat}$ from $[-\,0.47,1.011]$ to $[-\,0.1413,0.7231]$ for factor $f_6$. Factor $f_6$ together with its convex and concave McCormick relaxations (constructed with natural interval bounds), natural interval bounds $f_6^L,f_6^U$ and the affine functions are shown in Fig. 6a.

The next factor where an improvement of the interval bounds occurs is $f_{10}(x,y)=x^2\cdot (\log (y)+\exp (-\,y))-x\cdot (\log (y)+\exp (-\,y))$. The concave subgradient of the concave McCormick relaxation $f_{10}^{cc}$ is given by

$$\begin{aligned} f_{10}^{cc,sub}((0.375,1)^T,(x,y)^T) = 0.5452 + 0.5107\cdot (x-0.375). \end{aligned}$$

The concave relaxation of $f_{10}$ was calculated using formulas (5) and (6) in [35] and is not listed herein due to the very large formulas. Natural interval extensions provide $I_{10,nat}\approx [-\,0.8644,0.9039]$, where the improved bounds for factor $f_6$ were used for the computation. The maximum of $f_{10}^{cc,sub}((0.375,1)^T,(x,y)^T)$ is given as

$$\begin{aligned} \begin{aligned}&\max _{x\in [-\,0.25,1],y\in [0.5,1.5]} f_{10}^{cc,sub}((0.375,1)^T,(x,y)^T) \\&\quad = f_{10}^{cc,sub}((0.375,1)^T,(1,y)^T) \approx 0.8644. \end{aligned} \end{aligned}$$

(6)

With (6), we are able to improve $I_{10,nat}$ from $[-\,0.8644,0.9039]$ to $[-\,0.8644,0.8644]$, see Fig. 6b.

Last, we construct the envelopes of $f_{11}=f_{10}^3$ on the improved interval $I_{10,alg}$ and the convex and concave McCormick relaxation of g. Figure 7 shows the two dimensional function g together with its convex and concave McCormick relaxation constructed with the use of simple intervals denoted as $g^{cv}_{nat},g^{cc}_{nat}$ and the improved McCormick relaxations constructed with the use of the presented method denoted as $g^{cv}_{alg},g^{cc}_{alg}$.

3.3 Formal statement of the algorithm

For a given factorable function $g:Z\rightarrow {\mathbb {R}},Z\in {\mathbb {I}}\!{\mathbb {R}}^n$, we traverse the corresponding DAG of g starting at the independent variables $z_i,i\in \{1,\ldots ,n\}$ and working through all factors up to the root given as g (reverse-level-order in Graph Theory terminology). In each factor $f_j,j \in \{1,\ldots , |{\mathbb {F}}| \}$, we execute Algorithm 1 in order to obtain bounds $I_{j,alg}=[f_{j,alg}^L,f_{j,alg}^U]$ on the range of $f_j$ and save these. We use $I_{j,alg}$ then directly when computing $f_{k},k>j$. Note that the computed range bounds for every $f_j$ are valid on whole Z. Thus, after the DAG of g has been completely traversed, we can calculate McCormick relaxations of g and its subgradients at any point $\bar{\mathbf {z}}\in Z$ with the use of the range bounds $I_{j,alg}$ for each factor $f_j,j\in \{1,\ldots ,|{\mathbb {F}}|\}$ instead of using natural interval extensions for the range bounds estimation.

3.4 Algorithm discussion

We now discuss Algorithm 1. First, we check if the factor $f_j$ we currently consider, is a constant function by simply comparing the lower and upper bound (line 4), since if it is the case, we cannot improve any bounds on its range and thus, the algorithm is unnecessary. Obviously this check is only sufficient and not necessary, since it is possible to have different bounds for a constant function due to overestimation. In the for loop (line 7), we solve $\min \nolimits _{\mathbf {z}\in Z} f_j^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ and $\max \nolimits _{\mathbf {z}\in Z} f_j^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$ by simple subgradient comparisons as both problems are box-constrained and linear. The correct corner $\mathbf {z}^c$ of Z is determined by examination of the sign of the subgradient in the particular variable (lines 8–21). Then, we check if we can improve the bounds of factor $f_j$ (lines 23 and 24 ). We update the range bounds $I_j$ of factor $f_j$ (line 25) such that they can be directly used for the computation of relaxations, subgradients and bounds for factors $f_{k},k>j$. Then, we save the improved bounds (line 26). If needed, we compute a new point $\bar{\mathbf {z}}$ (line 28). There are many ways to compute a new point. In our computational studies in Sect. 4, we use the simple bisection in order to obtain a new $\bar{\mathbf {z}} = \text {mid}([\bar{\mathbf {z}},\mathbf {z}^c])$, i.e., the next point is given by the middle point of the interval $[\bar{\mathbf {z}}, \mathbf {z}^c]$, where $\mathbf {z}^c$ is determined before in lines 8–15. Note that the simple bisection method converges to $\min \nolimits _{\mathbf {z}\in Z} f_j^{cv}(\mathbf {z})$ for $N\rightarrow \infty$. A more sophisticated method for the computation of $\bar{\mathbf {z}}_{new}$ may provide better results and represents potential future work. Note that it may also make sense to compute two new separate points in order to independently improve the upper and lower bound within the algorithm but the numerical results for one common new point are very weak (Table 6) and thus, we omit this idea.

We are also interested in the computational complexity of the presented method. The computation of the possibly improved bounds $I_{j,alg}=[f_{j,alg}^L,f_{j,alg}^U]$ (lines 5–26) is linear in the dimension of the optimization variables $\mathbf {z}$, i.e., we have a complexity of ${\mathscr {O}}(n)$ for the computation of $I_{j,alg}$. This is comparable to the computation of McCormick relaxations and propagation of subgradients which have to be computed for each dimension in each factor. If only one iteration is allowed ($N=1$), we can directly use the propagated relaxation and subgradient values at the desired point $\bar{\mathbf {z}}$ and are not forced to re-evaluate McCormick relaxations, subgradients and interval bounds for all the factors on which $f_j$ depends for subsequent points. Therefore, if a function g consists of $|{\mathbb {F}}|$ factors and we allow only one iteration of the algorithm, the computational complexity amounts to ${\mathscr {O}}(|{\mathbb {F}}|\cdot n)$. Regarding the computational time for $N=1$, we can expect that even in cases where the algorithm does not yield any improvement, the additional computational effort is negligible. This observation is also confirmed in the numerical studies in Sect. 4. In contrast, if we allow for more than one iteration ($N>1$) within a factor $f_j$, we have to propagate all required information through all previous factors at the new point. Indeed, if a factor $f_j$ depends on ${\mathscr {J}}$ other factors and we allow N iterations, we need to do ${\mathscr {J}}^N$ computations, which is large for more complicated functions (${\mathscr {J}}\gg 1$) and $N>1$. Moreover, let us assume that each factor depends on all the previous factors, then the complexity for N computations of $f_j$ equals $\sum \nolimits _{k=1}^{j} k^N$, which is a polynomial complexity but still extremely large if a function consists of many factors and $N>1$. The impact of the number of factors for $N>1$ matches the numerical results presented in Sect. 4.

In order to avoid the complexity explosion, it is possible to traverse the DAG at a given point and save the improved intervals $I_{j,new}$ of each factor $f_j$. Then, traverse the DAG again at a different point and improve the lastly computed intervals $I_{j,new}$ until a predefined number of iterations N is reached. Moreover, we could heuristically decide whether it is worth to evaluate a factor again, e.g., by the type of the factor (variable, univariate, known) or if the difference between the McCormick relaxation $f_j^{cv}$ and the natural interval bounds $f_j^L$ is very large. In the computational case studies we use both improvements presented in this paragraph when using the heuristic for $N>1$.

Fig. 8

Example 5. Factor $f(z)=\exp (z)-z^3$ on $Z=[-\,1,1]$. The heuristic does not provide any improvement if the initial point is chosen as ${\bar{z}}=1$ and only 1 iteration ($N=1$) is allowed

3.5 Algorithm properties and limitations

The algorithm cannot deteriorate the bounds, since new bounds $I_{j,alg}$ are given by the maximum and minimum of the originally computed bounds $f_j^L,f_j^U$ and $t^{cv},t^{cc}$ (lines 23 and 24). The best bounds obtained by Algorithm 1 cannot be better than the minimum and maximum of the convex and concave McCormick relaxations of a factor $f_j$, i.e., it holds that

$$\begin{aligned} f^L_{j,alg} \le \min _{\mathbf {z}\in Z} f^{cv}(\mathbf {z}) \quad \text {and}\quad f^U_{j,alg} \ge \max _{\mathbf {z}\in Z} f^{cc}(\mathbf {z}). \end{aligned}$$

Algorithm 1 is able to improve the range bounds of a factor, see Example 2 but is not guaranteed to improve the bounds of a factor $f_j$, e.g., if the underlying interval extensions for the bounds $f_j^L,f_j^U$ are already exact or if the point $\bar{\mathbf {z}}$ is chosen badly as we show in the next example making the method a heuristic.

Example 5

Consider $f(z)=\exp (z)-z^3$ on $Z=[-\,1,1]$. Let us apply Algorithm 1 to f at point ${\bar{z}}=1$. The heuristic does not improve the interval bounds of f, see Fig. 8.

Example 5 shows that the outcome of the method depends on the chosen initial point $\bar{\mathbf {z}}$ and also on the maximum number of iterations. Choosing a corner point $\mathbf {z}^c\in Z$ as initial point for Algorithm 1 is only a good choice if we have some monotonicity information of the convex relaxation. In general, choosing the initial point for the algorithm from the interior of Z seems more intuitive and promising due to the positive curvature of convex underestimators. It was recently shown that if the midpoint is used as initial point, the resulting intervals $I_{j,alg}$ are guaranteed to have quadratic convergence order [25] confirming the intuition. Note that the bounds of f in Example 5 are improved if additional iterations of the heuristic are performed. If we allow for an additional iteration in Example 5, we obtain the middle point $\bar{\mathbf {z}}_{new}=0$ by applying simple bisection of Z for the re-computation of $\bar{\mathbf {z}}$ and the heuristic indeed does improve the range bounds of f, which can be seen in Fig. 9.

Fig. 9

Factor $f(z)=\exp (z)-z^3$ on $Z=[-\,1,1]$. The heuristic provides clear improvement if an additional iteration is allowed or if the initial point is directly set to ${\bar{z}}=0$ in Example 5

3.6 Algorithm alternatives and initial point determination

Instead of solving $\min \nolimits _{\mathbf {z}\in Z} f_j^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ and $\max \nolimits _{\mathbf {z}\in Z} f_j^{cc,sub}(\bar{\mathbf {z}},\mathbf {z})$ for only one point in each factor as described in Sect. 3.4, we could consider multiple points simultaneously in each factor $f_j$. For each point, we compute the subgradient and use it to construct linearizations in each factor $f_j$ resulting in a linear program (LP) for the lower and the upper interval bound each. The resulting LPs would be of the form:

where P is the number of points considered. Note that in general every factor (except for the original variables and trivial cases) has to be inspected, since natural interval extensions do not guarantee exact bounds as soon as a variable occurs more than once or a multivariate operation, e.g., subtraction, is performed. This would result in the solution of twice as many LPs as there are factors for the determination of improved intervals of the whole function g for only one node in the B&B tree. To avoid solving too many LPs, we filter for trivial factors or factors which are not promising such as, e.g., simple univariate operations. Moreover, we track the improvement provided by the heuristic during the B&B and reduce the number of points to 1 in factors where an improvement of at least 1% was not possible in the previous B&B iteration.

Additionally, in order to achieve a worthy improvement through the solution of the high number of linear programs, the multiple points considered simultaneously in each factor $f_j$ have to be chosen properly. In AVM the choice of linearization points for each factor is very simple since each factor has its own auxiliary variables and corresponding bounds. In the McCormick propagation technique, the choice of linearization points is far from simple. Thus, we present an alternative to an optimal choice of linearization points where we determine $(P-1)$ random points for linearization plus the middle point. To not lose any information, we also use the resulting additional linearizations in the final lower bounding problem to further tighten the relaxation of a given node. A comparison of this approach with Algorithm 1 is presented in the next section.

4 Numerical results

In order to test the presented algorithm, we use our in-house deterministic global optimization solver MAiNGO [9]. In particular we use CPLEX v12.8 [14] for linear optimization, the IPOPT v3.12.0 [54] and NLOPT solver 2.5.0 [21] for local nonlinear optimization, the FADBAD++ package for automatic differentiation [3] and the MC++ package v2.0 [11] for McCormick relaxations. All calculations are conducted on an Intel$^{{\textregistered }}$ Core™i3-3240 with 3.4GHz and 8 GB RAM on Windows 7. We solve 7 small problems of varying sizes with up to 14 variables chosen from the MINLPLib2 library; 3 case studies of a combined-cycle power plant presented in Sect. 5 of [7] where we minimize the levelized cost of electricity in the first 2 case studies and maximize the net power output in the third case study, 6 case studies of deep artificial neural networks (ANN) used to learn the well-known peak function with 2-7 hidden layers where i in ANN_i denotes the number of hidden layers in the ANN [46], and 4 case studies of chemical processes presented in Sects. 3.2, 3.3, 3.4 and 4.2.2 of [8]. The McCormick technique was already shown to be advantageous for the case studies from [7, 32, 46] in the respective article, while the case studies from the MINLPLib2 library were not solved with a McCormick based solver before.

We have mainly chosen case studies from our own work, since they are written in the reduced space formulation described in [7]. This is motivated by two reasons. First, the aforementioned applications work particularly well using McCormick relaxations and the reduced space formulation. Second, the presented heuristic is mostly promising for complicated functions, consisting of many complex factors, as is the case in a problem in reduced space formulation. This is because natural interval extensions loose quickly on quality if a function consists of many factors. But the number of factors is not the only key aspect responsible for the success of the heuristic. The factors’ complexity also plays an important role, e.g., for a seemingly complex sum of many univariate factors $f(\mathbf {x})=\sum g_i(\mathbf {x})$ where $g_i$ are univariate functions, the heuristic would most likely provide only little to no improvement. This is due to the fact, that for most univariate functions, natural intervals extensions already provide tight bounds. For f the sum is simultaneously the final and complicating factor w.r.t. to interval extensions and McCormick relaxations, leaving no space for improvement by the presented method.

We solve the nonlinear optimization problems as explained in the following. The upper bounding problems are solved locally with IPOPT in pre-processing and with the SLSQP algorithm provided by the NLOPT package within the B&B in order to obtain a valid upper bound. For the lower bound, we relax the problems using McCormick relaxations and then construct linearizations $g^{cv,sub}(\bar{\mathbf {z}},\mathbf {z})$ at a single point $\bar{\mathbf {z}}\in Z$ with the use of subgradient propagation. The considered problems consist of constrained and box-constrained problems. In both cases we linearize the convex relaxation of the objective function and all constraints (excluding the variable bounds) at a predefined single point to construct a linear program, which is then solved with CPLEX. In the case of box-constraints only, we obtain an extremely simple linear program whose solution can be obtained by simple coefficient analysis. Still, even in this simple case we automatically call CPLEX for the solution. We always use only one linearization point, namely the middle point of the current node in the first and third numerical comparisons (Table 4) and the current incumbent in the second comparison (Table 5). If any of the coordinates of the incumbent is not within a given node, we simply replace it by the corresponding middle point coordinate. For the case of multiple points $P>1$ presented in Table 6, we use P linearization points for the underlying affine relaxation.

Additionally, in some problems, there are no bounds given for the optimization variables. McCormick relaxations need valid bounds and we provide such ensuring containing the global minimum in all problems, see Table 3 in Appendix A for the number of variables, inequalities, equalities and bounds we used. If the bounds are provided in the given optimization problem, we mark it with the keyword given. We use the envelope of the logarithmic mean temperature difference function, presented in [36] for the 3 case studies from [7] explaining the improved computational times for $N=0$, i.e., without the use of Algorithm 1, in this article in comparison to [7].

In the following, we discuss the numerical impact of the method within a B&B framework using McCormick relaxations. The presented algorithm is not applicable to the $\alpha$BB method [1, 28], since the $\alpha$BB method does not depend on tight bounds of intermediate factors of a function g but rather on bounds on the eigenvalues of g. Algorithm 1 is not applicable directly to the AVM, where an auxiliary variable and an auxiliary equation are introduced for each factor, but it can be made applicable with a few modifications. It may be applied to the AVM by computing the subgradient at each factor introduced by an auxiliary equation $e_i$, improving the bounds for the corresponding auxiliary variable $a_i$ and providing this information to all auxiliary equations $e_j$ depending on $a_i$. In $e_j$ the improved bounds on $a_i$ may then provide tighter bounds for further variables $a_j$ which again can be propagated to further auxiliary equations etc. We present a comparison with the state-of-the-art deterministic global optimization solver BARON v18.7.20 [51] which uses the AVM. We are not aware of BARON v18.7.20 implementing such a heuristic. It is worth mentioning that the advantages of the described B&B procedure in the sense of computational time compared to state-of-the-art deterministic global optimization solvers has already been shown in [7, 8, 46] for numerical experiments ANN_i, $i\in \{2,\ldots ,7\}$ [46], Case Studies Henry, NRTL, OME, and Proc [8] and Case studies I,II, and III [7].

In all numerical experiments we set the absolute and relative optimality tolerances to $\epsilon =10^{-4}$ and absolute and relative feasibility tolerances to $\epsilon =10^{-6}$. First, we compare the impact of the algorithm with only one iteration. We allow for a maximum of 3600 s. We consider the computational performance of B&B for four cases: with and without the heuristic, as well as with and without range reduction (RR). Range reduction is performed using Optimization Based Bound Tightening improved by the filtering bounds technique with factor 0.01 described in [17] and also employing bound tightening based on the dual multipliers returned by CPLEX [42]. In the figures the case of no RR and no heuristic is referred to as (MC only), the case of no RR and heuristic used as (MC heur), the case of RR used and no heuristic as (MC RR) and the case of using RR and the heuristic as (MC heur RR).

Fig. 10

Performance plots with time factors and CPU time needed in seconds. The algorithm was always applied at the midpoint with $N=1$. We are comparing the in-house solver MAiNGO [9] with and without additional range reduction and the presented method with the state-of-the-art solver BARON v18.7.20 [51] with default settings

Fig. 11

Performance plots with time factors and CPU time needed in seconds. The algorithm was always applied at the incumbent with $N=1$. We are comparing the in-house solver MAiNGO [9] with and without additional range reduction and the presented method with the state-of-the-art solver BARON v18.7.20 [51] with default settings

Fig. 12

Performance plot comparing the heuristic for $N=P=1,N=3$ and $N=5$ applied at midpoint and solving LP with $P=3$ and $P=5$ linearization points in each factor without additional range reduction

Table 4 in Appendix A summarizes results for only one allowed iteration within Algorithm 1. The heuristic provides an average speed-up of $\approx$7.94 if only McCormick relaxations are used (first row, first column of Table 1). It provides an average speed-up of $\approx$8.18 (first row, second column of Table 1) even if additional range reduction is performed. In addition to performance plots showing all algorithms at once, to ensure reliability, we also present performance plots comparing only two algorithms [18]. Figure 10a–f show performance plots for the heuristic applied at the midpoint. We observe that the algorithm has the potential to drastically decrease the number of iterations and the computational time needed, especially for problems written in the reduced space formulation presented in [8, 46]. In these problems, the objective function and the constraints are composed of many factors and the propagated interval bounds of each factor lose on quality quickly. For the benchmark problems, the maximal number of factors over all participating functions is not very high although the functions itself are complex, see Table 6. Thus, the heuristic does not provide a big improvement compared to the application case studies.

Moreover, in the cases where the heuristic did not improve the relaxations, the number of iterations remained almost the same and the computational time only increased, if at all, by a very marginal amount. This is explained by the fact that if only one iteration of the heuristic is allowed, we can directly integrate the heuristic into the computation of McCormick relaxations and the heuristic only has a constant computational complexity in each propagation step. It is worth noting that the cases where the heuristic did not provide much improvement consist of only a few complicated factors and are solvable within a few seconds with additional range reduction. Still, these case studies present the improvement by the heuristic compared to simple McCormick relaxations, supporting the claims and results of this article. Additionally, we compare the results to the state-of-the-art solver BARON v18.7.20 [51], where we used default settings, see Fig. 10d–f. We also observe that the McCormick-based B&B solver outperforms BARON with and without additional range reduction and the presented heuristic for the hard case studies from [7, 8, 46]. For the application problems NRTL and Proc, we were able to detect spurious behavior of BARON. While BARON converges in only one iteration with default settings, it declares the problem as infeasible if no local searches are allowed (NumLoc 0, DoLocal 0). We still report the result obtained with default settings. For most benchmark problems which are solved within few seconds, the state-of-the-art solver slightly outperforms the methods used herein.

Table 1 The average speed-up factor provided by the presented heuristic for $N=P=1$ with midpoint and incumbent as initial point over the 20 problems considered herein

Table 2 The average slowdown factor provided by the presented heuristic for $N,P>1$ compared to $N=P=1$ with midpoint as initial point over the 20 problems considered herein

Next, we compare the impact of the heuristic with only one iteration but a different initial point. Here the heuristic provides an average speed-up of $\approx$ 7.65 if only McCormick relaxations are used (second row, first column of Table 1). It provides an average speed-up of $\approx$8 if additional range reduction is performed (second row, second column of Table 1). Figure 11d–f show performance plots for the heuristic applied at the incumbent. Again, we allowed for a maximum of 3600 s. This time, instead of the middle point of the node, we use the incumbent found by the local solver in the upper bounding procedure as the initial point and as the only linearization point in order to construct the linear lower bounding problem. If any coordinate of the incumbent is not within the current node, we simply use the appropriate coordinate of the middle point of this node instead. Table 5 in Appendix A summarizes the results for only one allowed iteration within Algorithm 1 with the current incumbent as initial point. Again, especially in the application and ANN case studies from [7, 8, 46], the heuristic improves the solution times drastically. We see again that the computational time only increased, if at all, by a very marginal amount. We observe that the choice of the initial point may have a significant impact on the advantage provided by the heuristic. Again, we compare the results to the state-of-the-art solver BARON v18.7.20 [51], where we used default settings.

Last, we compare the impact of the number of iterations within the heuristic and the solution of LPs in each factor. Table 6 summarizes the numerical results and Fig. 12 shows the performance plot comparing the heuristic for $N=P=1,N=3$ and $N=5$ applied at midpoint and solving LPs with multiple linearization points (Sect. 3.6) for $P=3$ and $P=5$ without any additional range reduction. We allow for a maximum of 3600 s. We see that the number of iterations in the B&B does not increase if we allow more iterations or more points for the LPs within the heuristic but the computational time needed explodes in most cases, especially for problems with many factors. This is the behavior that we already shortly discuss in Sects. 3.4 and 3.6 . Table 2 summerizes the average slowdown if more iterations ($N>1$) or more points ($P>1$) are used. On average increasing the number of iterations slows down the optimization by a factor of $\approx$ 2 while increasing the number of points only slows down the optimization by a factor of $\approx 1.2$. Still, increasing the number of points P may have a positive effect which is explained by the fact that additional linearizations are added to the lower bounding problems for $P>1$. Even if the number of factors within the optimization problems is not very high, the additional time needed for further iterations within each factor or the time needed for the solution of LPs adds up quickly and is clearly visible if many iterations are needed in order to solve a given optimization problem, even after filtering trivial factors and heuristically skipping factors which may have a low improvement. Note that in this work we used a very simple way to compute additional iterations or to choose the linearization points for LPs, so an improved method for computing further iterations could improve the computational times.

5 Conclusion

We present a new heuristic for tightening of the univariate McCormick relaxations [29, 30] and its extension to multivariate outer functions [52] of a factorable function g based on the idea of using tighter interval bounds for the range of each factor of g and obtaining these through subgradients, presented in Sect. 2.3 in [37] and Example 4.4 in [32]. The algorithm possibly improves the range bounds of the factors of g. It uses subgradient propagation for McCormick relaxations [32] in order to construct simple valid affine under- and overestimators of each factor. Then, the affine relaxations are solved with simple function evaluations resulting in improved range bounds for each factor. This results in tighter McCormick relaxations of the original function g.

Subsequently, we provide numerical results confirming the potential of the presented heuristic. We observe that allowing for only one iteration within the heuristic results in the best computational times. Although more iterations give potentially better bounds, this leads to recalculation of a possibly high number of factors of a factorable function g. Moreover, we see that selecting a good initial point may significantly improve the outcome of the algorithm, which remains a potential future work regarding the presented algorithm. Algorithm 1 is especially effective if the underlying interval bounds of the factors are very loose. This is often the case when the well-known dependency problem applies [33, 41]. A combination of the presented method with the reverse propagation of McCormick relaxations presented in [57] appears to be promising, since it works with range bounds of g and could result in an even greater improvement of McCormick relaxations overall, representing a further potential future development for the McCormick technique. As an extension, an automatic reformulation algorithm for variable elimination should make the presented heuristic very viable even for problems consisting of many simple functions, since this would lead to only a few complex functions. This is one of the future works of the authors. One could also think of a combination of the auxiliary variable method [50] and the McCormick technique to isolate problematic factors by introduction of auxiliary variables and then directly applying the presented heuristic to these.

A Appendix

See Tables 3, 4, 5 and 6.

Table 3 The problems for the numerical studies for different numbers of iterations within the heuristic

Table 4 The numerical results. We allowed only 1 iteration within the heuristic and used the middle point of each node as its initial point

Table 5 The numerical results. We allowed only 1 iteration within the heuristic and used the incumbent as its initial point

Table 6 The numerical results for different numbers of iterations and points within the heuristic