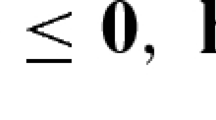Convergence-order analysis of branch-and-bound algorithms for constrained problems

Abstract

The performance of branch-and-bound algorithms for deterministic global optimization is strongly dependent on the ability to construct tight and rapidly convergent schemes of lower bounds. One metric of the efficiency of a branch-and-bound algorithm is the convergence order of its bounding scheme. This article develops a notion of convergence order for lower bounding schemes for constrained problems, and defines the convergence order of convex relaxation-based and Lagrangian dual-based lower bounding schemes. It is shown that full-space convex relaxation-based lower bounding schemes can achieve first-order convergence under mild assumptions. Furthermore, such schemes can achieve second-order convergence at KKT points, at Slater points, and at infeasible points when second-order pointwise convergent schemes of relaxations are used. Lagrangian dual-based full-space lower bounding schemes are shown to have at least as high a convergence order as convex relaxation-based full-space lower bounding schemes. Additionally, it is shown that Lagrangian dual-based full-space lower bounding schemes achieve first-order convergence even when the dual problem is not solved to optimality. The convergence order of some widely-applicable reduced-space lower bounding schemes is also analyzed, and it is shown that such schemes can achieve first-order convergence under suitable assumptions. Furthermore, such schemes can achieve second-order convergence at KKT points, at unconstrained points in the reduced-space, and at infeasible points under suitable assumptions when the problem exhibits a specific separable structure. The importance of constraint propagation techniques in boosting the convergence order of reduced-space lower bounding schemes (and helping mitigate clustering in the process) for problems which do not possess such a structure is demonstrated.

1 Introduction

Global optimization has found widespread applications in various areas of engineering and the sciences [11]. Deterministic global optimization algorithms attempt to determine an approximate optimal solution within a specified tolerance and terminate with a certificate of its optimality in finite time [13]. While efficient algorithms are known for classes of convex optimization problems [4], no such algorithms are currently known for most classes of nonconvex problems. Deterministic global optimization algorithms for nonconvex problems usually involve the concept of partitioning the domain of (‘branching on’) the decision variables [13]. The performance of branch-and-bound algorithms for deterministic global optimization is strongly dependent on the ability to construct tight and rapidly convergent relaxations of nonconvex functions.

Since the worst-case running time of all known branch-and-bound algorithms is exponential in the dimension of the variables partitioned, it may be advantageous to utilize ‘reduced-space’ algorithms which only require branching on a subset of the variables (as opposed to ‘full-space’ branch-and-bound algorithms which may branch on all of the variables) to guarantee convergence. Despite the potential advantages of reduced-space algorithms for nonconvex problems [3, 9, 10, 37], such methods have not been widely adopted in the literature and in commercial software. One potential reason is that most widely-applicable reduced-space branch-and-bound algorithms often do not seem to exhibit favorable convergence rates compared to their full-space counterparts. The convergence properties of reduced-space branch-and-bound algorithms have not been thoroughly investigated, although some progress has been made in this direction [8, 37]. The reader is directed to the work of Epperly and Pistikopoulos [10] for a survey of reduced-space branch-and-bound algorithms.

One metric of the efficiency of a deterministic branch-and-bound algorithm is the order of convergence of its bounding scheme, which, for the case of unconstrained optimization, compares the rate of convergence of an estimated range of a function to its true range [22]. Recently, Bompadre and coworkers [5, 6] developed the notions of Hausdorff and pointwise convergence orders of bounding schemes and established sharp rules for the propagation of convergence orders of bounding schemes constructed using McCormick [20], Taylor [24], and McCormick-Taylor [27] models. In addition, they showed that if a function is twice continuously differentiable, the scheme of relaxations corresponding to its envelopes is at least second-order pointwise convergent which, in turn, implies Hausdorff convergence of at least second-order. Najman and Mitsos [23] used the framework developed in [5, 6] to establish sharp rules for the propagation of convergence orders of multivariate McCormick relaxations [36]. Khan and coworkers [17] developed a continuously differentiable variant of McCormick relaxations [20, 36], and established second-order pointwise convergence of schemes of the differentiable McCormick relaxations for twice continuously differentiable functions. Also note the definition of rate of convergence of bounding schemes for geometric branch-and-bound methods proposed by Schöbel and Scholz [29], and the proof of second-order Hausdorff convergence of centered forms in [18, 30]. Establishing that a scheme of relaxations is at least second-order Hausdorff convergent is important from many viewpoints, notably in mitigating the so-called cluster effect in unconstrained global optimization [7, 38]. Recently, the authors of this work have analyzed the cluster problem for constrained global optimization and determined that, under certain conditions, first-order convergence of the lower bounding scheme may be sufficient to avoid the cluster problem at constrained minima [15]. However, an analysis of convergence order for constrained problems is currently lacking.

In this work, we investigate the convergence orders of some full-space and reduced-space deterministic branch-and-bound algorithms by extending the convergence analysis of Bompadre and coworkers to constrained problems. Specifically, we propose a definition of convergence order for lower bounding schemes, analyze the convergence orders of commonly-used full-space lower bounding schemes, and analyze the convergence orders of some widely-applicable reduced-space lower bounding schemes in the literature. Throughout this work, we tacitly assume that a branch-and-bound algorithm utilizes efficient heuristics for finding feasible points which determine a global optimal solution early on in the branch-and-bound tree (if one exists).

This paper is organized as follows. Section 2 formulates the problem of interest, and provides some background definitions. Section 3 develops the notion of convergence order of a lower bounding scheme, and Sect. 4 provides some results on the convergence orders of commonly-used full-space lower bounding schemes. Section 5 lists some widely-applicable reduced-space lower bounding schemes in the literature, provides some results on their convergence orders, and highlights the importance of constraint propagation in reduced-space branch-and-bound algorithms. Finally, Sect. 6 lists the conclusions and some avenues for future work.

2 Problem formulation and background

Consider the problem

where $X \subset {\mathbb {R}}^{n_x}$ and $Y \subset {\mathbb {R}}^{n_y}$ are nonempty convex sets, $f : X \times Y \rightarrow {\mathbb {R}}$ and ${\mathbf {g}}: X \times Y \rightarrow {\mathbb {R}}^{m_I}$ are partially convex with respect to ${\mathbf {x}}$, i.e., $f(\cdot ,{\mathbf {y}})$ and ${\mathbf {g}}(\cdot ,{\mathbf {y}})$ are convex on X for each ${\mathbf {y}}\in Y, {\mathbf {h}}: X \times Y \rightarrow {\mathbb {R}}^{m_E}$ is affine with respect to ${\mathbf {x}}$, i.e., ${\mathbf {h}}(\cdot ,{\mathbf {y}})$ is affine on X for each ${\mathbf {y}}\in Y$, and ${\mathbf {0}}$ denotes a vector of zeros of appropriate dimension. The following assumption will be made throughout this work.

Assumption 1

The sets X and Y are compact, and the functions $f, {\mathbf {g}}$, and ${\mathbf {h}}$ are continuous on $X \times Y$.

When the dimension $n_y$ of the Y-space corresponding to the nonconvexities in the functions in Problem (P) is significantly smaller than the dimension $n_x$ of the X-space, it may be computationally advantageous to partition only the Y-space during the course of a branch-and-bound algorithm (assuming, of course, that the reduced-space algorithm is guaranteed to converge). However, the convergence rate of a reduced-space branch-and-bound algorithm may be different compared to a similar full-space algorithm, which makes it difficult to judge a priori whether using a reduced-space branch-and-bound approach would be advantageous. Before we analyze the convergence orders of some full-space and reduced-space lower bounding schemes in the literature, we need to define formally the notion of convergence order for constrained problems. For this purpose, we review some relevant definitions [5, 6].

Throughout this work, we use ${\mathbb {I}}Z$ to denote the set of nonempty, closed, and bounded interval subsets of $Z \subset {\mathbb {R}}^n, {\mathbb {R}}_+$ and ${\mathbb {R}}_{-}$ to respectively denote the sets of nonnegative and nonpositive reals, $z_j$ to denote the jth component of a vector ${\mathbf {z}}, (z_1,z_2,\ldots ,z_n)$ to denote a vector ${\mathbf {z}}\in {\mathbb {R}}^n$ with components $z_1,z_2,\ldots ,z_n \in {\mathbb {R}}, ({\mathbf {v}},{\mathbf {w}})$ to denote the column vector ${[{{\mathbf {v}}}^\text{ T } \, {{\mathbf {w}}}^\text{ T }]}^\text{ T }$ corresponding to (column) vectors ${\mathbf {v}}$ and ${\mathbf {w}}, {||}{\mathbf {z}}{||}$ to denote the Euclidean norm of a vector ${\mathbf {z}}\in {\mathbb {R}}^n, \begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}$ to denote a vector-valued function with domain Z and codomain ${\mathbb {R}}^{m + n}$ corresponding to vector-valued functions ${\mathbf {g}}: Z \rightarrow {\mathbb {R}}^m$ and ${\mathbf {h}}: Z \rightarrow {\mathbb {R}}^n$, conv(S) to denote the convex hull of a set $S \subset {\mathbb {R}}^n$, and int(S) to denote the interior of a set $S \subset {\mathbb {R}}^n$.

Definition 1

(Width of an interval) Let $Z = [z^{\text {L}}_1,z^{\text {U}}_1] \times \cdots \times [z^{\text {L}}_n,z^{\text {U}}_n]$ be an element of ${\mathbb {I}}{\mathbb {R}}^{n}$. The width of Z, denoted by w(Z), is given by

$$\begin{aligned} w(Z) := \max _{i = 1,\ldots ,n} \left( z^{\text {U}}_i - z^{\text {L}}_i\right) . \end{aligned}$$

Definition 2

(Distance between two sets) Let $Z, V \subset {\mathbb {R}}^n$. The distance between Z and V, denoted by d(Z, V), is given by

$$\begin{aligned} d(Z,V) := \underset{{\mathbf {v}}\in V}{\inf _{{\mathbf {z}}\in Z,}} \,\, {||}{\mathbf {z}}-{\mathbf {v}}{||}. \end{aligned}$$

Note that the above definition of distance does not define a metric; however, it will prove useful in defining a measure of infeasibility for points in $X \times Y$ for Problem (P). The following result holds.

Lemma 1

Let ${\mathbf {z}}, {\mathbf {v}}\in {\mathbb {R}}^n$, and let $K \subset {\mathbb {R}}^n$ be a convex cone. Then

$$\begin{aligned} d(\{{\mathbf {z}}\},K) - d(\{{\mathbf {v}}\},K) \le d(\{{\mathbf {z}}-{\mathbf {v}}\},K). \end{aligned}$$

Proof

See [31]. $\square$

Corollary 1

Let ${\mathbf {z}}, {\mathbf {v}}\in {\mathbb {R}}^{m+n}$. Then

$$\begin{aligned} d(\{{\mathbf {z}}\},{\mathbb {R}}^m_{-} \times \{{\mathbf {0}}\}) - d(\{{\mathbf {v}}\},{\mathbb {R}}^m_{-} \times \{{\mathbf {0}}\}) \le d(\{{\mathbf {z}}-{\mathbf {v}}\},{\mathbb {R}}^m_{-} \times \{{\mathbf {0}}\}). \end{aligned}$$

Proof

This result is a direct consequence of Lemma 1. $\square$

Lemma 2

All norms on ${\mathbb {R}}^n$ are equivalent. Specifically, if ${||}\cdot {||}_p$ and ${||}\cdot {||}_q$ are two norms in ${\mathbb {R}}^n$ for any $p, q \in {\mathbb {N}} \cup \{+\infty \}$ with $p \ne q$, then there exist constants $c_1, c_2 \in {\mathbb {R}}_+$ such that $c_1 {||}{\mathbf {z}}{||}_p \le {||}{\mathbf {z}}{||}_q \le c_2 {||}{\mathbf {z}}{||}_p, \,\, \forall {\mathbf {z}}\in {\mathbb {R}}^n$. Furthermore, for $(p,q) = (1,2), c_2 = 1$ provides a valid upper bound and for $(p,q) = (+\infty ,2), c_2 = \displaystyle \sqrt{n}$ provides a valid upper bound.

Proof

For the first part of the lemma, see, for instance, [28, Theorem 4.2]. The second part of the lemma follows from the inequalities

$$\begin{aligned} {||}{\mathbf {z}}{||}^2_2 = \displaystyle \sum _{i=1}^{n}{z^2_i} \le \displaystyle \sum _{i=1}^{n}{z^2_i} + \displaystyle \sum _{i=1}^{n}{\displaystyle \sum _{j=i+1}^{n}{2{|}z_i{|}{|}z_j{|}}} = {||}{\mathbf {z}}{||}^2_1 \end{aligned}$$

and

$$\begin{aligned} {||}{\mathbf {z}}{||}^2_2 = \displaystyle \sum _{i=1}^{n}{z^2_i} \le n\underset{i=1,\ldots ,n}{\max }{z^2_i} = n{||}{\mathbf {z}}{||}^2_{\infty } \end{aligned}$$

for any ${\mathbf {z}}\in {\mathbb {R}}^n$. $\square$

Definition 3

(Lipschitz continuous function) Let $Z \subset {\mathbb {R}}^n$. A function $f:Z \rightarrow {\mathbb {R}}$ is said to be Lipschitz continuous with Lipschitz constant $M \ge 0$ if

$$\begin{aligned} {|}f({\mathbf {z}}_1) - f({\mathbf {z}}_2){|} \le M {||}{\mathbf {z}}_1 - {\mathbf {z}}_2{||},\quad \forall {\mathbf {z}}_1,{\mathbf {z}}_2 \in Z. \end{aligned}$$

Remark 1

Locally Lipschitz continuous functions are Lipschitz continuous on compact subsets of their domains. Therefore, the assumption that the functions $f, {\mathbf {g}}$, and ${\mathbf {h}}$ in Problem (P) are Lipschitz continuous on $X \times Y$ is not particularly strong when Assumption 1 is made.

Definition 4

(Hausdorff metric) Let $X = [x^{\text{ L }},x^{\text{ U }}]$ and $Y = [y^{\text{ L }},y^{\text{ U }}]$ be two intervals in ${\mathbb {I}}{\mathbb {R}}$. The Hausdorff metric between X and Y, denoted by $d_H(X,Y)$, is given by

$$\begin{aligned} d_H(X,Y) = \max \{{|}x^{\text{ L }}-y^{\text{ L }}{|},{|}x^{\text{ U }}-y^{\text{ U }}{|}\} = \max \left\{ \max _{x \in X}{\min _{y \in Y} {|}x - y{|}},\max _{y \in Y}{\min _{x \in X}{|}x - y{|}}\right\} . \end{aligned}$$

Definition 5

(Inclusion function) Let $V \subset {\mathbb {R}}^n$ and suppose ${\mathbf {f}}:V \rightarrow {\mathbb {R}}^{m}$ is continuous. For any $Z \subset V$, let $\overline{{\mathbf {f}}}(Z)$ denote the image of Z under ${\mathbf {f}}$. A mapping $F:{\mathbb {I}}V\rightarrow {\mathbb {I}}{\mathbb {R}}^m$ is called an inclusion function for ${\mathbf {f}}$ on ${\mathbb {I}}V$ if, for every $Z \in {\mathbb {I}}V$, we have $\overline{{\mathbf {f}}}(Z) \subset F(Z)$.

Definition 6

(Range order) Let $V \subset {\mathbb {R}}^n$ be a bounded set. Let $f:V \rightarrow {\mathbb {R}}$ be continuous, and let F be an inclusion function for f on ${\mathbb {I}}V$. The inclusion function F is said to have range of order $\alpha > 0$ at a point ${\mathbf {v}}\in V$ if there exists $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}V$ with ${\mathbf {v}}\in Z$,

$$\begin{aligned} w(F(Z)) \le \tau w(Z)^{\alpha }. \end{aligned}$$

The function f itself is said to have a range of order $\alpha > 0$ at ${\mathbf {v}}\in V$ if its image $\overline{f}$ has range of order $\alpha$ at ${\mathbf {v}}$. The functions F and f are said to have ranges of order $\alpha > 0$ on V if they have ranges of order (at least) $\alpha$ at each ${\mathbf {v}}\in V$, with the constant $\tau$ independent of ${\mathbf {v}}$.

The reader is directed to Remark 3 for a discussion on the assumption that the set V in the above definition be bounded. Since the convergence order analysis in this work is asymptotic in nature (see Remark 4 and Lemma 5), we will need the following asymptotic notations.

Definition 7

(Big O and little o notations) Let $Z \subset {\mathbb {R}}, f:Z \rightarrow {\mathbb {R}}$, and $g:Z \rightarrow {\mathbb {R}}$. We say that $f(z) = O(g(z))$ as $z \rightarrow {\bar{z}} \in Z$ if and only if there exist $\delta , M > 0$ such that

$$\begin{aligned} {|}f(z){|} \le M{|}g(z){|}, \quad \forall z \in Z \text { with } {|}z-{\bar{z}}{|} < \delta . \end{aligned}$$

Similarly, we say that $f(z) = o(g(z))$ as $z \rightarrow {\bar{z}} \in Z$ if and only if for all $M' > 0$ there exists $\delta ' > 0$ such that

$$\begin{aligned} {|}f(z){|} \le M'{|}g(z){|}, \quad \forall z \in Z \text { with } {|}z-{\bar{z}}{|} < \delta '. \end{aligned}$$

Note that unless otherwise specified, we consider ${\bar{z}} = 0$ in this work.

The following lemma is from Proposition 11.7 in [14].

Lemma 3

Let $Z \subset {\mathbb {R}}^n$ be nonempty, and $f:Z \rightarrow {\mathbb {R}}$ and $g:Z \rightarrow {\mathbb {R}}$ be bounded on Z. Then

Definition 8

(Convex and concave relaxations) Given a convex set $Z \subset {\mathbb {R}}^n$ and a function $f:Z \rightarrow {\mathbb {R}}$, a convex function $f^{\text{ cv }}_Z: Z \rightarrow {\mathbb {R}}$ is called a convex relaxation of f on Z if $f^{\text{ cv }}_Z({\mathbf {z}}) \le f({\mathbf {z}}), \forall {\mathbf {z}}\in Z$. Similarly, a concave function $f^{\text{ cc }}_Z: Z \rightarrow {\mathbb {R}}$ is called a concave relaxation of f on Z if $f^{\text{ cc }}_Z({\mathbf {z}}) \ge f({\mathbf {z}}), \forall {\mathbf {z}}\in Z$.

Definition 9

(Convex and concave envelopes) Given a convex set $Z \subset {\mathbb {R}}^n$ and a function $f:Z \rightarrow {\mathbb {R}}$, a convex function $f^{\text{ cv,env }}_Z: Z \rightarrow {\mathbb {R}}$ is called the convex envelope of f on Z if $f^{\text{ cv,env }}_Z$ is a convex relaxation of f on Z and for every convex relaxation $f^{\text{ cv }}_Z: Z \rightarrow {\mathbb {R}}$, we have $f^{\text{ cv,env }}_Z({\mathbf {z}}) \ge f^{\text{ cv }}_Z({\mathbf {z}}), \forall {\mathbf {z}}\in Z$. Similarly, a concave function $f^{\text{ cc,env }}_Z: Z \rightarrow {\mathbb {R}}$ is called the concave envelope of f on Z if $f^{\text{ cc,env }}_Z$ is a concave relaxation of f on Z and for every concave relaxation $f^{\text{ cc }}_Z: Z \rightarrow {\mathbb {R}}$, we have $f^{\text{ cc,env }}_Z({\mathbf {z}}) \le f^{\text{ cc }}_Z({\mathbf {z}}), \forall {\mathbf {z}}\in Z$.

The following result establishes sufficient conditions for lower semicontinuity of the convex envelope. Note that a weaker version of this result is presented in [25, Corollary 17.2.1], and stronger versions of this result are stated without proof in [9, p. 349] (where the assumption that the function f is bounded above is relaxed) and in [33, p. 253] (where the assumptions that the function f is bounded above and the set W is bounded are relaxed).

Lemma 4

Let $W \subset {\mathbb {R}}^{n_w}$ be a nonempty compact convex set and $f:W \rightarrow {\mathbb {R}}$ be a lower semicontinuous function on W bounded above by M. Let $f^{\text{ cv,env }}_{W}$ denote the convex envelope of f on W. Then $f^{\text{ cv,env }}_{W}$ is lower semicontinuous on W.

Proof

The function f is lower semicontinuous on the compact set W iff its epigraph $\left\{ ({\mathbf {x}},r) : {\mathbf {x}}\in W, r \ge f({\mathbf {x}}) \right\}$ is closed. Consequently, the set $S := \left\{ ({\mathbf {x}},r) : {\mathbf {x}}\in W, r {\ge } f({\mathbf {x}}), r \le M \right\}$ is compact. Theorem 17.2 in [25] implies that $\text {conv}(S)$ is a compact convex set. Therefore, the set $\text {conv}(S) \cup \left\{ ({\mathbf {x}},r) : {\mathbf {x}}\in W, r \ge f({\mathbf {x}}) \right\}$ is closed, which implies that $\left\{ ({\mathbf {x}},r) : {\mathbf {x}}\in W, r \ge f^{\text{ cv,env }}_{W}({\mathbf {x}}) \right\}$ is closed, which in turn implies that $f^{\text{ cv,env }}_{W}$ is lower semicontinuous on W. $\square$

Remark 2

Although convex and concave relaxations of classes of functions can be constructed on general convex sets, the typical application requires construction of relaxations on bounded intervals. Therefore, we will implicitly assume that the sets X and Y are intervals and that relaxations are constructed on intervals in subsequent sections. The assumption that X and Y are intervals is not restrictive since general convex constraints defining X and Y that are available in factorable form can be equivalently reformulated to appear as part of the constraints ${\mathbf {g}}$ and ${\mathbf {h}}$. The proposed definitions of convergence order in the next section will be based on schemes of relaxations constructed on intervals. Note that similar notions of convergence order can be developed for schemes of relaxations constructed, for instance, on simplices.

3 Definitions of convergence order

This section reviews the definitions of convergence orders of schemes of relaxations [5, 6] and defines the convergence order of a (reduced-space) lower bounding scheme. It is also shown that the convergence order of a convergent scheme of relaxations at a point is governed by the tiny intervals around that point. We begin with the following definition, adapted from [5, Definition 6], that defines schemes of relaxations in a reduced-space.

Definition 10

(Schemes of convex and concave relaxations) Let $V \subset {\mathbb {R}}^{n_v}$ and $W \subset {\mathbb {R}}^{n_w}$ be nonempty convex sets, and let $f:V \times W \rightarrow {\mathbb {R}}$. Suppose, for every $Z \in {\mathbb {I}}W$, we can construct functions $f^{\text{ cv }}_{V \times Z}:V \times Z \rightarrow {\mathbb {R}}$ and $f^{\text{ cc }}_{V \times Z}:V \times Z \rightarrow {\mathbb {R}}$ that are convex and concave relaxations, respectively, of f on $V \times Z$. The sets of functions $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ and $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ define schemes of convex and concave relaxations of f in W, respectively, and the set of pairs of functions $(f^{\text{ cv }}_{V \times Z}, f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ defines a scheme of relaxations of f in W. The schemes of relaxations are said to be continuous when $f^{\text{ cv }}_{V \times Z}$ and $f^{\text{ cc }}_{V \times Z}$ are continuous on $V \times Z$ for each $Z \in {\mathbb {I}}W$.

Bompadre and coworkers [5, 6] define Hausdorff convergence of inclusion functions. Note that an inclusion function can be associated with schemes of relaxations in a natural way (see [5, Definition 7]).

Definition 11

(Hausdorff convergence order of an inclusion function) Let $V \in {\mathbb {I}}{\mathbb {R}}^{n_v}$ and $W \subset {\mathbb {R}}^{n_w}$ be nonempty sets, $h:V \times W \rightarrow {\mathbb {R}}$ be a continuous function, and H be an inclusion function of h on ${\mathbb {I}}(V \times W)$.

The inclusion function H is said to have Hausdorff convergence of order $\beta > 0$ at a point ${\mathbf {w}}\in W$ if for each bounded $Q \subset W$ with ${\mathbf {w}}\in Q$, there exists $\tau \ge 0$ such that

$$\begin{aligned} d_H(\overline{h}(V \times Z),H(V \times Z)) \le \tau {w(Z)}^{\beta }, \quad \forall Z \in {\mathbb {I}}Q\text { with } {\mathbf {w}}\in Z. \end{aligned}$$

Moreover, H is said to have Hausdorff convergence of order $\beta > 0$ on W if it has Hausdorff convergence of order (at least) $\beta$ at each ${\mathbf {w}}\in W$, with the constant $\tau$ independent of ${\mathbf {w}}$.

In the context of (constrained) global optimization, the following definition of convergence of schemes of convex and concave relaxations is more pertinent.

Definition 12

(Convergence order of schemes of convex and concave relaxations) Let $V \subset {\mathbb {R}}^{n_v}, W \subset {\mathbb {R}}^{n_w}$ be nonempty convex sets, and $f:V \times W \rightarrow {\mathbb {R}}$ be a continuous function. Let $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ and $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ respectively denote schemes of convex and concave relaxations of f in W.

The scheme of convex relaxations $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have convergence of order $\beta > 0$ at ${\mathbf {w}}\in W$ if for each bounded $Q \subset W$ with ${\mathbf {w}}\in Q$, there exists $\tau ^{\text {cv}} \ge 0$ such that

$$\begin{aligned} \inf _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f({\mathbf {v}},{\mathbf {z}}) - \inf _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) \le \tau ^{\text {cv}} {w(Z)}^{\beta }, \quad \forall Z \in {\mathbb {I}}Q\text { with } {\mathbf {w}}\in Z. \end{aligned}$$

Similarly, the scheme of concave relaxations $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have convergence of order $\beta > 0$ at ${\mathbf {w}}\in W$ if for each bounded $Q \subset W$ with ${\mathbf {w}}\in Q$, there exists $\tau ^{\text {cc}} \ge 0$ such that

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f^{\text{ cc }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) - \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f({\mathbf {v}},{\mathbf {z}}) \le \tau ^{\text {cc}} {w(Z)}^{\beta }, \quad \forall Z \in {\mathbb {I}}Q\text { with } {\mathbf {w}}\in Z. \end{aligned}$$

The scheme of relaxations $(f^{\text{ cv }}_{V \times Z}, f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have (Hausdorff) convergence of order $\beta > 0$ at ${\mathbf {w}}\in W$ if the corresponding schemes of convex and concave relaxations have convergence of orders (at least) $\beta$ at ${\mathbf {w}}$. The schemes $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ and $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ are said to have convergence of order $\beta > 0$ on W if they have convergence of order (at least) $\beta$ at each ${\mathbf {w}}\in W$, with constants $\tau ^{\text {cv}}$ and $\tau ^{\text {cc}}$ independent of ${\mathbf {w}}$.

Definition 13

(Pointwise convergence order of schemes of convex and concave relaxations) Let $V \subset {\mathbb {R}}^{n_v}, W \subset {\mathbb {R}}^{n_w}$ be nonempty convex sets, and $f:V \times W \rightarrow {\mathbb {R}}$ be a continuous function. Let $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ and $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ respectively denote schemes of convex and concave relaxations of f in W. The scheme of convex relaxations $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have pointwise convergence of order $\gamma > 0$ at ${\mathbf {w}}\in W$ if for each bounded $Q \subset W$ with ${\mathbf {w}}\in Q$, there exists $\tau ^{\text {cv}} \ge 0$ such that

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|} \le \tau ^{\text {cv}} {w(Z)}^{\gamma }, \quad \forall Z \in {\mathbb {I}}Q\text { with } {\mathbf {w}}\in Z. \end{aligned}$$

Similarly, the scheme of concave relaxations $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have pointwise convergence of order $\gamma > 0$ at ${\mathbf {w}}\in W$ if for each bounded $Q \subset W$ with ${\mathbf {w}}\in Q$, there exists $\tau ^{\text {cc}} \ge 0$ such that

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f^{\text{ cc }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) - f({\mathbf {v}},{\mathbf {z}}){|} \le \tau ^{\text {cc}} {w(Z)}^{\gamma }, \quad \forall Z \in {\mathbb {I}}Q\text { with } {\mathbf {w}}\in Z. \end{aligned}$$

The scheme of relaxations $(f^{\text{ cv }}_{V \times Z}, f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ is said to have pointwise convergence of order $\gamma > 0$ at ${\mathbf {w}}\in W$ if the corresponding schemes of convex and concave relaxations have pointwise convergence of orders (at least) $\gamma$ at ${\mathbf {w}}$. Furthermore, the schemes of relaxations are said to have pointwise convergence of order $\gamma > 0$ on W if they have pointwise convergence of order at least $\gamma$ at each ${\mathbf {w}}\in W$, with constants $\tau ^{\text {cv}}$ and $\tau ^{\text {cc}}$ independent of ${\mathbf {w}}$.

Note that we simply say that a scheme of relaxations, $(f^{\text{ cv }}_{V \times Z}, f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$, of a function $f: V \times W \rightarrow {\mathbb {R}}$ in W has (pointwise) convergence order of $\gamma > 0$ if it has (pointwise) convergence of order $\gamma$ on W.

Remark 3

Definitions 11, 12, and 13 are based on a modification (see [16, Definition 9.2.35]) of the definitions of convergence order proposed in [5, 6], which incorporates the set Q. Note that the use of the set Q is necessary when the schemes of relaxations are constructed on unbounded sets, but may be omitted (set to W) when the schemes of relaxations are constructed over bounded sets (which is the typical application). Henceforth, the use of Q shall be omitted for brevity since we are only interested in compact sets V and W (see Assumption 1).

Remark 4

The pointwise convergence order of a convergent scheme of convex and concave relaxations on W is governed by the strength of the relaxations over small intervals in W. This observation is made precise in Lemma 5. Also note that the pointwise convergence order of schemes of either convex, or concave relaxations (as per Definition 13) can be arbitrarily high for nonlinear functions in contrast to the pointwise convergence order of schemes of convex and concave relaxations (see Theorem 2 in [5]). For instance, consider the function $f: [0,1] \times [0,1] =: V \times W \rightarrow {\mathbb {R}}$ with $f(v,w) = v^2-\sqrt{w}$ and a corresponding scheme of convex relaxations $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ defined by $f^{\text{ cv }}_{V \times Z}(v,z) = v^2-\sqrt{w}$ on $[w^{\text{ L }}, w^{\text{ U }}] \subset [0,1]$. The scheme of convex relaxations $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ has arbitrarily high pointwise convergence order on W.

Remark 5

Unlike the pointwise convergence order of a scheme of relaxations, the convergence order of a scheme of convex and concave relaxations can be arbitrarily high for any function. For instance, consider the scheme of constant relaxations of the function $f:[0,1] \times [0,1] =: V \times W \rightarrow {\mathbb {R}}$ with $f(v,w) = w-\sqrt{v}$ defined by $f^{\text{ cv }}_{V \times Z}(v,z) = w^{\text{ L }}-1, f^{\text{ cc }}_{V \times Z}(v,z) = w^{\text{ U }}$ on $[w^{\text{ L }}, w^{\text{ U }}] \subset [0,1]$. The scheme of constant relaxations $(f^{\text{ cv }}_{V \times Z}, f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ has arbitrarily high convergence order on W, but is not pointwise convergent of any order on W.

Lemma 5

Let $V \subset {\mathbb {R}}^{n_v}, W \subset {\mathbb {R}}^{n_w}$ be nonempty compact convex sets and $f:V \times W \rightarrow {\mathbb {R}}$. Let $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ denote a scheme of convex relaxations of f in W with pointwise convergence order $\gamma ^{\text{ cv }} > 0$ and corresponding prefactor $\tau ^{\text{ cv }} \ge 0$ (on W). If there exist constants $\gamma \ge \gamma ^{\text{ cv }}, \tau \ge 0$, and $\delta > 0$ such that for every $Z \in {\mathbb {I}}W$ with $w(Z) \le \delta$,

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|} \le \tau {w(Z)}^{\gamma }, \end{aligned}$$

then $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ converges pointwise with order $\gamma$ to f on W.

Proof

Since $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ converges pointwise with order $\gamma ^{\text{ cv }}$ to f on W which is compact, there exists $M \ge 0$ such that

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|} \le \tau ^{\text{ cv }} {w(Z)}^{\gamma ^{\text{ cv }}} \le M, \quad \forall Z \in {\mathbb {I}}W. \end{aligned}$$

The desired result then follows from the fact that for every $Z \in {\mathbb {I}}W$,

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|} \le \left( \tau + \displaystyle \frac{M}{\delta ^{\gamma }} \right) {w(Z)}^{\gamma }. \end{aligned}$$

$\square$

Results similar to Lemma 5 are applicable to other notions of convergence order presented in this work. Note that if the constant $\delta$ in Lemma 5 is relatively small, then the bound on the prefactor obtained can be relatively large making the result weak on intervals with $w(Z) \gg \delta$.

The next result shows that for schemes of relaxations, the notion of pointwise convergence is stronger than the notion of convergence in Definition 12 (also see [5, Theorem 1]).

Lemma 6

Let $V \subset {\mathbb {R}}^{n_v}, W \subset {\mathbb {R}}^{n_w}$ be nonempty compact convex sets, and $(f^{\text{ cv }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ and $(f^{\text{ cc }}_{V \times Z})_{Z \in {\mathbb {I}}W}$ respectively denote schemes of convex and concave relaxations of a bounded function $f:V \times W \rightarrow {\mathbb {R}}$ in W. If either scheme has pointwise convergence of order $\gamma > 0$, it has convergence of order $\beta \ge \gamma$.

Proof

By noting from Definition 13 that

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|}&\le \tau ^{\text {cv}} w(W)^{\gamma }, \quad \forall Z \in {\mathbb {I}}W, \\ \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f^{\text{ cc }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) - f({\mathbf {v}},{\mathbf {z}}){|}&\le \tau ^{\text {cc}} w(W)^{\gamma }, \quad \forall Z \in {\mathbb {I}}W, \end{aligned}$$

the result follows from Lemma 3 via

$$\begin{aligned} \inf _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f({\mathbf {v}},{\mathbf {z}}) - \inf _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) \le \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f({\mathbf {v}},{\mathbf {z}}) - f^{\text{ cv }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}){|}, \quad \forall Z \in {\mathbb {I}}W, \end{aligned}$$

and

$$\begin{aligned} \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f^{\text{ cc }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) - \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} f({\mathbf {v}},{\mathbf {z}}) \le \sup _{({\mathbf {v}},{\mathbf {z}}) \in V \times Z} {|}f^{\text{ cc }}_{V \times Z}({\mathbf {v}},{\mathbf {z}}) - f({\mathbf {v}},{\mathbf {z}}){|}, \quad \forall Z \in {\mathbb {I}}W. \end{aligned}$$

$\square$

The following lemma establishes mild sufficient conditions under which the scheme of envelopes of a function is first-order pointwise convergent.

Lemma 7

Let $W \subset {\mathbb {R}}^{n_w}$ be a nonempty compact convex set and $f:W \rightarrow {\mathbb {R}}$ be Lipschitz continuous on W. Let $(f^{\text{ cv,env }}_{Z}, f^{\text{ cc,env }}_{Z})_{Z \in {\mathbb {I}}W}$ denote the scheme of envelopes of f in W. Then the scheme $(f^{\text{ cv,env }}_{Z}, f^{\text{ cc,env }}_{Z})_{Z \in {\mathbb {I}}W}$ is at least first-order pointwise convergent on W.

Proof

We wish to show that there exists $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}W$,

$$\begin{aligned}&\sup _{{\mathbf {z}}\in Z} {|}f({\mathbf {z}}) - f^{\text{ cv,env }}_{Z}({\mathbf {z}}){|} \le \tau w(Z), \\&\sup _{{\mathbf {z}}\in Z} {|}f({\mathbf {z}}) - f^{\text{ cc,env }}_{Z}({\mathbf {z}}){|} \le \tau w(Z). \end{aligned}$$

Consider the scheme of relaxations $(f^{\text{ cv }}_{Z}, f^{\text{ cc }}_{Z})_{Z \in {\mathbb {I}}W}$ defined by

$$\begin{aligned} f^{\text{ cv }}_{Z}({\mathbf {z}}) = \underset{{\mathbf {w}}\in Z}{\min } \, f({\mathbf {w}}), \,\, f^{\text{ cc }}_{Z}({\mathbf {z}}) = \underset{{\mathbf {w}}\in Z}{\max } \, f({\mathbf {w}}), \quad \forall Z \in {\mathbb {I}}W. \end{aligned}$$

From the fact that $f^{\text{ cv }}_{Z}$ and $f^{\text{ cc }}_{Z}$ are convex and concave relaxations of f in Z and the assumption that f is Lipschitz continuous, we have that $(f^{\text{ cv }}_{Z}, f^{\text{ cc }}_{Z})_{Z \in {\mathbb {I}}W}$ is at least first-order pointwise convergent on W. The desired result then follows from the definition of $(f^{\text{ cv,env }}_{Z}, f^{\text{ cc,env }}_{Z})_{Z \in {\mathbb {I}}W}$. $\square$

The definitions provided thus far facilitate a theoretical analysis of the (reduced-space) convergence order of a scheme of relaxations to a corresponding scalar function, or, in the context of global optimization, provide a way to analyze theoretically the (reduced-space) convergence order of a (lower) bounding scheme for an unconstrained problem. The subsequent definitions seek to extend naturally the analysis of convergence order to constrained problems.

Definition 14

(Convergence order of a lower bounding scheme) Consider Problem (P) (satisfying Assumption 1). For any $Z \in {\mathbb {I}}Y$, let ${\mathscr {F}}(Z) = \left\{ ({\mathbf {x}},{\mathbf {y}}) \in X \times Z : {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) = {\mathbf {0}} \right\}$ denote the feasible set of Problem (P) with ${\mathbf {y}}$ restricted to Z.

Consider a scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ for Problem (P). We associate with the scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ a scheme of pairs $({\mathscr {O}}(Z),{\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y}$, where $({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y}$ is a scheme of lower bounds on the scheme of problems $\Big (\min \limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}})\Big )_{Z \in {\mathbb {I}}Y}$ and $({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y}$ is a scheme of subsets of ${\mathbb {R}}^{m_I + m_E}$ that indicate the feasibility of the lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$. The schemes $({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y}$ and $({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y}$ (are required to) satisfy

$$\begin{aligned}&\displaystyle {\mathscr {O}}(Z) \le \underset{({\mathbf {x}},{\mathbf {z}}) \in {\mathscr {F}}(Z)}{\min }f({\mathbf {x}},{\mathbf {z}}), \quad \forall Z \in {\mathbb {I}}Y, \\&\displaystyle d({\mathscr {I}}_{C}(Z),{\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\}) \le d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X \times Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) , \quad \forall Z \in {\mathbb {I}}Y, \\&\displaystyle {\mathscr {O}}(Z) = +\infty \iff d({\mathscr {I}}_{C}(Z),{\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\}) > 0, \quad \forall Z \in {\mathbb {I}}Y, \end{aligned}$$

where $\overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X \times Z)$ denotes the image of $X \times Z$ under the vector-valued function $\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}$. The scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is said to have convergence of order $\beta > 0$ at

• 1. A feasible point ${\mathbf {y}}\in Y$ if there exists $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}\in Z$,

  $$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {z}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {z}}) \,\, - {\mathscr {O}}(Z) \le \tau {w(Z)}^{\beta }. \end{aligned}$$

• 2. An infeasible point ${\mathbf {y}}\in Y$ if there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}\in Z$,

  $$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X \times Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }. \end{aligned}$$

The scheme of lower bounding problems is said to have convergence of order $\beta > 0$ on Y if it has convergence of order (at least) $\beta$ at each ${\mathbf {y}}\in Y$, with constants $\tau$ and ${\bar{\tau }}$ independent of ${\mathbf {y}}$.

Remark 6

Definition 14 is motivated by the requirements of a lower bounding scheme to fathom feasible and infeasible regions in a branch-and-bound procedure [13]. The first condition requires that the sequence of lower bounds converges rapidly to the corresponding sequence of minimum objective values on nested sequences of intervals converging to a feasible point of Problem (P). On nested sequences of intervals converging to an infeasible point of Problem (P), the second condition requires that the sequence of lower bounding problems rapidly detect the (eventual) infeasibility of the corresponding sequences of intervals for Problem (P). In simple terms, the first condition can be used to require that feasible points with ‘good objective values’ are fathomed rather easily, while the second condition can be used to require that infeasible points that are ‘close to the feasible region’, as determined by the distance function d, are fathomed with relatively less effort [15]. Note that Definition 14 reduces to the definition of convergence order for unconstrained minimization in [38, Definition 1] when $n_x, m_I$, and $m_E$ are all set to zero.

Definition 14 can be readily applied to analyze the convergence order of a convex relaxation-based lower bounding scheme as follows.

Suppose, for each $Z \in {\mathbb {I}}Y$, we associate a convex set $X(Z)\subset \mathbb {R}^{n_x}$ such that $X \supset X(Z) \supset {\mathscr {F}}_X(Z)$, where ${\mathscr {F}}_X(Z) := \left\{ {\mathbf {x}}\in X : \exists {\mathbf {y}}\in Z \text { s.t. } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) = {\mathbf {0}} \right\}$ denotes the projection of ${\mathscr {F}}(Z)$ on X. The set X(Z) could, for instance, correspond to an interval subset of X that is obtained using bounds tightening techniques [2] when ${\mathbf {y}}$ is restricted to Z (the motivation for considering the set X(Z) in the definition of convergence order below will become clear in Sect. 5). Note that the restriction $X(Z) \supset {\mathscr {F}}_X(Z)$ can be relaxed when optimality-based bounds tightening techniques are employed. Also note that unless otherwise specified, we simply use $X(Z) = X, \forall Z \in {\mathbb {I}}Y$.

By an abuse of Definition 10, let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ and $({\mathbf {g}}^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ denote continuous schemes of convex relaxations of f and ${\mathbf {g}}$, respectively, in Y, and let $({\mathbf {h}}^{\text{ cv }}_{X(Z) \times Z}, {\mathbf {h}}^{\text{ cc }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ denote a continuous scheme of relaxations of ${\mathbf {h}}$ in Y. For any $Z \in {\mathbb {I}}Y$, let

$$\begin{aligned} {\mathscr {F}}^{\text{ cv }}(Z) {=} \left\{ ({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z : {\mathbf {g}}^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}^{\text{ cc }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \ge {\mathbf {0}} \right\} \end{aligned}$$

denote the feasible set of the convex relaxation-based lower bounding scheme. The lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ with

(1)

is said to have convergence of order $\beta > 0$ at

• 1. A feasible point ${\mathbf {y}}\in Y$ if there exists $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}\in Z$,

  $$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {z}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {z}}) - \min _{({\mathbf {x}},{\mathbf {z}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {z}}) \le \tau {w(Z)}^{\beta }. \end{aligned}$$

• 2. An infeasible point ${\mathbf {y}}\in Y$ if there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}\in Z$,

  $$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X(Z) \times Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }, \end{aligned}$$

  where ${\mathscr {I}}_{C}(Z)$ is defined by Eq. (1).

Definition 14 can also be used to analyze the convergence orders of alternative lower bounding schemes such as those based on Lagrangian duality (see Sect. 4.2).

4 Full-space branch-and-bound algorithms

In this section, we present some results on the convergence order of lower bounding schemes for Problem (P) when both the X and Y sets may be partitioned during the course of the branch-and-bound algorithm (we consider schemes of relaxations in $X \times Y$ instead of schemes of relaxations in Y as was considered in Sect. 3). This section is divided into two parts. First, we look at the convergence order of lower bounding schemes which utilize convex and concave relaxations (see, for instance, [1, 17, 20, 35, 36] for techniques to construct relaxations) of the objective and the constraints in its construction. Next, the convergence order of duality-based lower bounding schemes (see, for instance, [9]) is investigated.

4.1 Convex relaxation-based branch-and-bound

This section derives bounds on the convergence order of convex relaxation-based lower bounding schemes by making assumptions on the convergence orders of the schemes of relaxations used by the lower bounding schemes. The reader is directed to [5, 6, 17, 24] for details on how to construct schemes of (convex) relaxations that have the requisite convergence orders.

The following result establishes a lower bound on the convergence order of the lower bounding scheme at infeasible points based on the convergence orders of schemes of convex relaxations of the inequality constraints and schemes of relaxations of the equality constraints. Note that this is the primary result that is used to derive a lower bound on the convergence order of such relaxation-based lower bounding schemes at infeasible points.

Lemma 8

Let $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,$ $m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$, and $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots , m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma _{h,1}> 0, \ldots , \gamma _{h,m_E} > 0$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$

$$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }, \end{aligned}$$

where ${\mathscr {I}}_{C}(Z)$ is defined as

$$\begin{aligned} {\mathscr {I}}_{C}(Z) := \left\{ ({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}= {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z \right\} , \end{aligned}$$

and $\beta$ is defined as

$$\begin{aligned} \beta := \min \left\{ \underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text{ cv }}_{g,j}, \underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k} \right\} . \end{aligned}$$

Proof

Suppose $Z \in {\mathbb {I}}(X \times Y)$. Then for each $j \in \{1,\ldots ,m_I\}, k \in \{1,\ldots ,m_E\}$, we have from Definition 13 that

$$\begin{aligned} \max _{({\mathbf {x}},{\mathbf {y}}) \in Z} {|}g_j({\mathbf {x}},{\mathbf {y}}) - g^{\text {cv}}_{j,Z}({\mathbf {x}},{\mathbf {y}}){|} \le \tau ^{\text {cv}}_{g,j} w(Z)^{\gamma ^{\text {cv}}_{g,j}}, \\ \max _{({\mathbf {x}},{\mathbf {y}}) \in Z} {|}h_k({\mathbf {x}},{\mathbf {y}}) - h^{\text {cv}}_{k,Z}({\mathbf {x}},{\mathbf {y}}){|} \le \tau _{h,k} w(Z)^{\gamma _{h,k}}, \\ \max _{({\mathbf {x}},{\mathbf {y}}) \in Z} {|}h_k({\mathbf {x}},{\mathbf {y}}) - h^{\text {cc}}_{k,Z}({\mathbf {x}},{\mathbf {y}}){|} \le \tau _{h,k} w(Z)^{\gamma _{h,k}}, \end{aligned}$$

since $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}$ and $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}$ converge pointwise to $g_j$ and $h_k$, respectively, on $X \times Y$ with orders $\gamma ^{\text {cv}}_{g,j}$ and $\gamma _{h,k}$. Let $({\mathbf {x}}^{\text {cv}}_{Z},{\mathbf {y}}^{\text {cv}}_{Z}) \in Z$ and $({\mathbf {v}}^{\text {cv}}_Z,{\mathbf {w}}^{\text {cv}}_Z) \in {\mathscr {I}}_{C}(Z)$ such that ${\mathbf {v}}^{\text {cv}}_Z = {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}}^{\text {cv}}_{Z},{\mathbf {y}}^{\text {cv}}_{Z}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}}^{\text {cv}}_{Z},{\mathbf {y}}^{\text {cv}}_{Z}) \le {\mathbf {w}}^{\text {cv}}_Z \le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}}^{\text {cv}}_{Z},{\mathbf {y}}^{\text {cv}}_{Z})$, and $d\left( \left\{ ({\mathbf {v}}^{\text {cv}}_Z,{\mathbf {w}}^{\text {cv}}_Z)\right\} ,{\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\}\right) = d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right)$. The existence of $({\mathbf {x}}^{\text {cv}}_{Z},{\mathbf {y}}^{\text {cv}}_{Z})$ and $({\mathbf {v}}^{\text {cv}}_Z,{\mathbf {w}}^{\text {cv}}_Z)$ follows from the continuity of ${\mathbf {g}}^{\text{ cv }}_Z, {\mathbf {h}}^{\text{ cv }}_Z$, and ${\mathbf {h}}^{\text{ cc }}_Z$ and the compactness of Z. We have

where Corollary 1 is used to derive Step 2, Step 3 follows from the triangle inequality, and Lemma 2 is used to derive Step 6. The desired result follows by choosing ${\bar{\tau }}$ as

$$\begin{aligned} {\bar{\tau }} = \left( \displaystyle \sum _{j=1}^{m_I}{\tau ^{\text {cv}}_{g,j} w(X \times Y)^{\gamma ^{\text {cv}}_{g,j} - \beta }} + \displaystyle \sum _{k=1}^{m_E}{\tau _{h,k} w(X \times Y)^{\gamma _{h,k} - \beta }} \right) . \end{aligned}$$

$\square$

Note that the conclusions of Lemma 8 hold even when the schemes of convex relaxations $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, \forall j \in \{1,\ldots ,m_I\}$, and $(h^{\text{ cv }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, \forall k \in \{1,\ldots ,m_E\}$, are merely lower semicontinuous, and the schemes of concave relaxations $(h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, \forall k \in \{1,\ldots ,m_E\}$, are merely upper semicontinuous.

Remark 7

The analysis in Lemma 8 can be refined under the following assumptions. Let $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,$ $m_I$, denote schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with convergence orders $\beta ^{\text{ cv }}_{g,1}> 0, \ldots , \beta ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$, and let $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots , m_E$, denote schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$ with convergence orders $\beta _{h,1}> 0, \ldots , \beta _{h,m_E} > 0$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Suppose for each interval $Z \in {\mathbb {I}}(X \times Y)$, there exists $({\mathbf {x}}_Z,{\mathbf {y}}_Z) \in Z$ such that

$$\begin{aligned}&\displaystyle d\left( \left\{ ({\mathbf {x}}_Z,{\mathbf {y}}_Z)\right\} , {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) = d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) , \\&\displaystyle \quad ({\mathbf {x}}_Z,{\mathbf {y}}_Z) \in \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\mathop {\mathrm{arg min}}\limits } \, g_j({\mathbf {x}},{\mathbf {y}}), \quad \forall j \in \{1,\ldots ,m_I\}, \\&\displaystyle \quad \text {either } ({\mathbf {x}}_Z,{\mathbf {y}}_Z) \in \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\mathop {\mathrm{arg min}}\limits } \, h_k({\mathbf {x}},{\mathbf {y}}), \text { or } ({\mathbf {x}}_Z,{\mathbf {y}}_Z) \in \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\mathop {\mathrm{arg max}}\limits } \, h_k({\mathbf {x}},{\mathbf {y}}), \quad \forall k \in \{1,\ldots ,m_E\}. \end{aligned}$$

Then, there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$

$$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }, \end{aligned}$$

where $\beta$ is defined as

$$\begin{aligned} \beta := \min \left\{ \underset{j \in \{1,\ldots ,m_I\}}{\min } \beta ^{\text{ cv }}_{g,j}, \underset{k \in \{1,\ldots ,m_E\}}{\min } \beta _{h,k} \right\} . \end{aligned}$$

Note that the above assumptions are trivially satisfied when Problem (P) only has one inequality constraint (cf. Example 1).

The following example demonstrates the importance of a sufficiently high convergence order at nearly-feasible points (also see [15, Example 4]).

Example 1

Let $X = [0,0], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = y$ and $g(x,y) = - y$. For any $[0, 0] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let $f^{\text{ cv }}_Z(x,y) = y, g^{\text {cv}}_Z(x,y) = - y^{\text {U}} - (y^{\text {U}}-y^{\text {L}})^{\alpha }$ for some constant $\alpha > 0$. Note that $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order and arbitrarily high convergence order on $X \times Y$, whereas $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has $\min \{\alpha , 1\}$-order pointwise convergence and $\alpha$-order convergence on $X \times Y$.

Pick $\delta \in (0,1)$ and let $\varepsilon \in (0,\delta )$. Let $y^{\text {L}} = -\delta -\varepsilon , y^{\text {U}} = -\delta +\varepsilon$. The width of Z is $w(Z) = 2\varepsilon$. We have $\overline{g}(Z) = [\delta - \varepsilon , \delta +\varepsilon ]$, which yields $d(\overline{g}(Z),{\mathbb {R}}^{m_I}_{-}) = \delta - \varepsilon$ (this confirms that g is infeasible at each $(x,y) \in Z$). Furthermore, $\overline{g}^{\text {cv}}_Z(Z) = [\delta - \varepsilon - (2\varepsilon )^{\alpha }, \delta - \varepsilon - (2\varepsilon )^{\alpha }]$, which yields $d(\overline{g}^{\text {cv}}_Z(Z),{\mathbb {R}}^{m_I}_{-}) = \max \{0,\delta - \varepsilon - (2\varepsilon )^{\alpha }\}$. Therefore, for $\varepsilon$ sufficiently small, the lower bounding problem detects the infeasibility of Z and we have $d(\overline{g}(Z),{\mathbb {R}}^{m_I}_{-}) - d(\overline{g}^{\text {cv}}_Z(Z),{\mathbb {R}}^{m_I}_{-}) = (2\varepsilon )^{\alpha }$, which implies that convergence of the lower bounding scheme at the infeasible point $(0,-\delta )$ is at most of order $\alpha$.

For $\alpha = 1$, the maximum value of $\varepsilon$ for which the interval Z can be fathomed by infeasibility by the lower bounding scheme is $\varepsilon = \frac{\delta }{3}$, whereas for $\alpha = 0.5$, the maximum value of $\varepsilon$ for which the interval Z can be fathomed by infeasibility by the lower bounding scheme is $\varepsilon = \left( \frac{-\sqrt{2}+\sqrt{2}\sqrt{1+2\delta }}{2}\right) ^2$, which is $O(\delta ^2)$ for $\delta \ll 1$.

Therefore, a lower bounding scheme with a low convergence order at infeasible points may result in a large number of partitions on nearly-feasible points before they are fathomed, thereby resulting in the cluster problem.

The next result shows that under mild assumptions on the objective, the constraints, and the schemes of relaxations, first-order convergence to a global minimum is guaranteed.

Theorem 1

Consider Problem (P). Suppose $f, g_j, j = 1,\ldots ,m_I$, and $h_k, k = 1,\ldots ,m_E$, are Lipschitz continuous on $X \times Y$ with Lipschitz constants $M_{f}, M_{g,1},\ldots ,M_{g,m_I}, M_{h,1}, \ldots , M_{h,m_E}$, respectively. Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}, (g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $f, g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_f \ge 1, \gamma ^{\text{ cv }}_{g,1} \ge 1, \ldots , \gamma ^{\text{ cv }}_{g,m_I} \ge 1$ and corresponding constants $\tau ^{\text{ cv }}_f, \tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$. Let $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k=1,\ldots ,m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma _{h,1} \ge 1, \ldots , \gamma _{h,m_E} \ge 1$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. The scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}(X \times Y)}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \bigl (\big \{({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}= {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \bigr . \\&\displaystyle \quad \bigl . \text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z \big \} \bigr )_{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is at least first-order convergent on $X \times Y$.

Proof

Lemma 8 establishes first-order convergence at infeasible points $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ with the prefactor ${\bar{\tau }}$ independent of $({\mathbf {x}},{\mathbf {y}})$; therefore, it suffices to prove first-order convergence at feasible points $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ with a prefactor independent of $({\mathbf {x}},{\mathbf {y}})$.

In order to do so, suppose ${\mathscr {F}}(X \times Y) \ne \emptyset$ and consider $Z \in {\mathbb {I}}(X \times Y)$ such that $Z \cap {\mathscr {F}}(X \times Y) \ne \emptyset$. Let

$$\begin{aligned} {\mathscr {F}}^{\text{ cv }}(Z) := \left\{ ({\mathbf {x}},{\mathbf {y}}) \in Z : {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}, {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \ge {\mathbf {0}} \right\} \end{aligned}$$

denote the feasible set of the convex relaxation-based lower bounding scheme. Then

$$\begin{aligned}&\qquad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \nonumber \\&= \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) \right) + \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) \nonumber \\&\le \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}})\right) \,\, + \max _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}\left|f({\mathbf {x}},{\mathbf {y}}) - f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right|, \end{aligned}$$

(2)

where the above inequality follows from Lemma 3. The second term in Eq. (2) can be bounded from above as

$$\begin{aligned} \max _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}\left|f({\mathbf {x}},{\mathbf {y}}) - f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right|\le \tau ^{\text {cv}}_f w(Z)^{\gamma ^{\text {cv}}_f}, \end{aligned}$$

since $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ converges pointwise to f on $X \times Y$ with order $\gamma ^{\text {cv}}_f \ge 1$.

Let $({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}} f({\mathbf {x}},{\mathbf {y}})$ and $({\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}} f({\mathbf {x}},{\mathbf {y}})$. The first term in Eq. (2) can be bounded from above as

$$\begin{aligned} \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}})\right) \,\,&= f({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) - f\left( {\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z\right) \\&\le M_f \displaystyle \sqrt{n_x + n_y} \, w(Z), \end{aligned}$$

where the last step follows from the Lipschitz continuity of f on $X \times Y$ and Lemma 2.

Plugging in the above bounds in Eq. (2), we get

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, {-} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \le \left( M_f \displaystyle \sqrt{n_x + n_y} + \tau ^{\text {cv}}_f w(X {\times } Y)^{\gamma ^{\text {cv}}_f-1}\right) w(Z), \end{aligned}$$

which establishes first-order convergence of $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ at feasible points $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ with the prefactor independent of $({\mathbf {x}},{\mathbf {y}})$. $\square$

The following examples show that the convergence order of the lower bounding scheme may be as low as one under the assumptions of Theorem 1.

Example 2

Let $X = [-1,1], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = 2x + 2y$ and $g(x,y) = - x - y$. For any $[x^{\text {L}}, x^{\text {U}}] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let $f^{\text{ cv }}_Z(x,y) = 2x + 2y$ and $g^{\text {cv}}_Z(x,y) = -x^{\text {U}} - y^{\text {U}}$. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$ and the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has first-order pointwise convergence on $X \times Y$. Note that $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

Let $x^{\text {L}} = y^{\text {L}} = -\varepsilon , x^{\text {U}} = y^{\text {U}} = \varepsilon$ with $0 < \varepsilon \le 1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-4\varepsilon$. Convergence at the point (0, 0) is, therefore, at most first-order.

Example 3

Let $X = [-1,1], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = 2x + 2y$ and $g(x,y) = - x - y$. For any $[x^{\text {L}}, x^{\text {U}}] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let $f^{\text{ cv }}_Z(x,y) = 2x^{\text {L}} + 2y^{\text {L}}$ and $g^{\text {cv}}_Z(x,y) = -x-y$. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has first-order pointwise convergence on $X \times Y$ and the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$. Note that $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

Let $x^{\text {L}} = y^{\text {L}} = -\varepsilon , x^{\text {U}} = y^{\text {U}} = \varepsilon$ with $0 < \varepsilon \le 1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-4\varepsilon$. Convergence at the point (0, 0) is, therefore, at most first-order.

Example 4

Let $X = [0,0], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = y$ and $g(x,y) = \min \{-0.5y, -y\}$. For any $[0, 0] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$ with $y^{\text {L}}< 0 < y^{\text {U}}$, let

$$\begin{aligned} f^{\text{ cv }}_Z(x,y) = y, \quad g^{\text {cv}}_Z(x,y) = -\displaystyle \frac{y^{\text {U}} - 0.5y^{\text {L}}}{y^{\text {U}} - y^{\text {L}}} y + \displaystyle \frac{0.5y^{\text {L}}y^{\text {U}}}{y^{\text {U}} - y^{\text {L}}}. \end{aligned}$$

Note that $g^{\text{ cv }}_{Z}$ corresponds to the convex envelope of g on Z. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$ and the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has first-order pointwise convergence on $X \times Y$. Note that $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

Let $y^{\text {L}} = -\varepsilon , y^{\text {U}} = \varepsilon$ with $0 < \varepsilon \le 1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-\frac{\varepsilon }{3}$. Convergence at the point (0, 0) is, therefore, at most first-order.

Example 5

Let $X = [0,0], Y = [-1,1], m_I = 0$, and $m_E = 1$ with $f(x,y) = y$ and $h(x,y) = \min \{-0.5y, -y\}$. For any $[0, 0] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$ with $y^{\text {L}}< 0 < y^{\text {U}}$, let

$$\begin{aligned} f^{\text{ cv }}_Z(x,y) = y, \quad h^{\text {cv}}_Z(x,y) = -\displaystyle \frac{y^{\text {U}} - 0.5y^{\text {L}}}{y^{\text {U}} - y^{\text {L}}} y + \displaystyle \frac{0.5y^{\text {L}}y^{\text {U}}}{y^{\text {U}} - y^{\text {L}}}, \quad h^{\text {cc}}_Z(x,y) = \min \{-0.5y, -y\}. \end{aligned}$$

Note that $h^{\text{ cv }}_{Z}$ and $h^{\text{ cc }}_{Z}$ correspond to the convex and concave envelopes of h on Z, respectively. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$ and the scheme $(h^{\text{ cv }}_{Z},h^{\text{ cc }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has first-order pointwise convergence on $X \times Y$. Note that $(h^{\text{ cv }}_{Z},h^{\text{ cc }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

Let $y^{\text {L}} = -\varepsilon , y^{\text {U}} = \varepsilon$ with $0 < \varepsilon \le 1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-\frac{\varepsilon }{3}$. Convergence at the point (0, 0) is, therefore, at most first-order.

Despite the fact that the schemes of relaxations used in Examples 4 and 5 correspond to the envelopes of the functions involved (unlike those used in Examples 2 and 3), we only have first-order convergence at the global minimizer (0, 0). However, the reader can verify that first-order convergent lower bounding schemes may be sufficient to mitigate the cluster problem in Examples 4 and 5, whereas at least second-order convergent lower bounding schemes are required to mitigate the cluster problem in Examples 2 and 3 [15]. Furthermore, Examples 2–5 illustrate that high convergence orders of schemes of relaxations of the objective and constraints do not guarantee a high convergence order of the lower bounding scheme (cf. Remark 7) at constrained minima (which may be required to mitigate clustering). This is because a high convergence order of a scheme of relaxations of the objective function may only place a restriction on the gap between the minimum value of the relaxation and the minimum value of the objective function without taking the feasible region into account; this restriction may not be sufficient in a constrained setting because the gap between the minimum value of the relaxed problem and the minimum value of the original problem may be relatively large when their respective feasible regions are taken into consideration (see Example 3 for an extreme case). Similarly, a high convergence order of a scheme of relaxations of the constraints may not exclude infeasible regions of the search space in which the objective function value is less than the optimal (constrained) objective value (Example 2 provides an extreme case), potentially leading to relatively large underestimation gaps.

The following result proves second-order convergence at certain points in $X \times Y$.

Theorem 2

Consider Problem (P). Suppose f is Lipschitz continuous on $X \times Y$ with Lipschitz constant $M_{f}$. Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ denote a continuous scheme of convex relaxations of f with pointwise convergence order $\gamma ^{\text{ cv }}_f \ge 2$ and corresponding constant $\tau ^{\text{ cv }}_f$.

Suppose there exists a feasible point $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in {\mathscr {F}}(X \times Y)$, continuous schemes of convex relaxations $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, of $g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$, continuous schemes of relaxations $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots , m_E$, of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$, and a constant $\delta > 0$ such that for each $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in Z$ and $w(Z) \le \delta$, we have

$$\begin{aligned} d\left( {\mathscr {F}}(Z),\underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\mathop {\mathrm{arg min}}\limits } f({\mathbf {x}},{\mathbf {y}})\right)&\le {\hat{\tau }} w(Z)^{\gamma } \end{aligned}$$

(3)

for constants $\gamma \ge 2$ and ${\hat{\tau }} \ge 0$. Then, the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned} ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}(X \times Y)}, \\ \end{aligned}$$

$$\begin{aligned} ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \bigl (\big \{({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}= {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \bigr . \\&\bigl . \text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z \big \} \bigr )_{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is at least $\min \{\gamma ^{\text{ cv }}_f, \gamma \}$-order convergent at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$.

Proof

Suppose $Z \in {\mathbb {I}}(X \times Y)$ such that $({\mathbf {x}}^{\text{ f }}, {\mathbf {y}}^{\text{ f }}) \in Z$ and $w(Z) \le \delta$. From the proof of Theorem 1, we have

$$\begin{aligned}&\quad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \nonumber \\&\le \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\,\right) + \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) \nonumber \\&\le \left( \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\,\right) + \tau ^{\text {cv}}_f w(Z)^{\gamma ^{\text {cv}}_f}. \end{aligned}$$

(4)

Consider $({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}} f({\mathbf {x}},{\mathbf {y}})$. Choose $({\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z) \in {\mathscr {F}}(Z)$ and $({\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}} f({\mathbf {x}},{\mathbf {y}})$ such that $d\left( \{({\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z)\},\{({\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z)\}\right) \le {\hat{\tau }} w(Z)^{\gamma }$ (note that $({\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z)$ and $({\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z)$ exist by assumption). The first term in Eq. (4) can be bounded from above as

$$\begin{aligned} \min _{\left( {\mathbf {x}},{\mathbf {y}}\right) \in {\mathscr {F}}\left( Z\right) }f\left( {\mathbf {x}},{\mathbf {y}}\right) \,\, - \min _{\left( {\mathbf {x}},{\mathbf {y}}\right) \in {\mathscr {F}}^{\text{ cv }}\left( Z\right) }f\left( {\mathbf {x}},{\mathbf {y}}\right)&= f\left( {\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z\right) - f\left( {\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z\right) \\&\le f\left( {\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z\right) - f\left( {\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z\right) \\&\le M_f \, d\left( \left\{ \left( {\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z\right) \right\} ,\left\{ \left( {\mathbf {x}}^{\text{ cv }}_Z,{\mathbf {y}}^{\text{ cv }}_Z\right) \right\} \right) \\&\le M_f {\hat{\tau }} w\left( Z\right) ^{\gamma }, \end{aligned}$$

where Step 3 above follows from the Lipschitz continuity of f. Therefore, from Eq. (4),

$$\begin{aligned}&\quad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \\&\le \left( M_f {\hat{\tau }} w(X \times Y)^{\gamma - \min \left\{ \gamma ^{\text {cv}}_f, \gamma \right\} } + \tau ^{\text {cv}}_f w(X \times Y)^{\gamma ^{\text {cv}}_f - \min \left\{ \gamma ^{\text {cv}}_f, \gamma \right\} } \right) w(Z)^{\min \left\{ \gamma ^{\text {cv}}_f, \gamma \right\} }. \end{aligned}$$

The desired result follows by analogy to Lemma 5 by noting that the lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ has convergence of order at least one at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$ from Theorem 1. $\square$

The key assumption of Theorem 2, Eq. (3), is rather unwieldy since verifying it involves the solution of the optimization problem $\min \limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f({\mathbf {x}},{\mathbf {y}})$ for each $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in Z$ and $w(Z) \le \delta$. The following more restrictive (but potentially more easily verifiable) condition implies Eq. (3):

The following example shows that the convergence order may be as low as two under the assumptions of Theorem 2.

Example 6

Let $X = [-1,1], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = -xy$ and $g(x,y) = x+y-1$. For any $[x^{\text {L}}, x^{\text {U}}] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let

$$\begin{aligned}&f^{\text{ cv }}_Z(x,y) = \max \{-x^{\text {U}} y + (-x) y^{\text {L}} - (-x^{\text {U}}) y^{\text {L}}, -x^{\text {L}} y+ (-x) y^{\text {U}} - (-x^{\text {L}}) y^{\text {U}}\}, \\&\quad g^{\text {cv}}_Z(x,y) = x+y-1. \end{aligned}$$

The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$, which corresponds to the scheme of convex envelopes of f on $X \times Y$, has (at least) second-order pointwise convergence on $X \times Y$ (see [5, Theorem 10]) and the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$. Note that $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

Let $x^{\text {L}} = y^{\text {L}} = 0.5-\varepsilon , x^{\text {U}} = y^{\text {U}} = 0.5+\varepsilon$ with $0 < \varepsilon \le 0.5$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is $-0.25$, while $f^{\text{ cv }}_Z(0.5,0.5) = -0.25 -\varepsilon ^2$ and $g^{\text {cv}}_Z(0.5,0.5) = 0$. Convergence at the point (0.5, 0.5) is, therefore, at most second-order.

Note that the use of feasibility-based bounds tightening techniques is ineffective in boosting the convergence order for the above example. This is in contrast to the similar Example 16 where the use of constraint propagation techniques improves the convergence order of reduced-space branch-and-bound algorithms (also see Examples 17 and 18 in Sect. 5.2).

Remark 8

Theorem 2 requires, at a minimum, second-order pointwise convergence of the scheme of convex relaxations $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$, which cannot be achieved in general by relaxations constructed purely using interval arithmetic [22]. Consequently, lower bounding schemes constructed using interval arithmetic can, in general, only be expected to possess first-order convergence (see Theorem 1). When the functions $f, {\mathbf {g}}$, and ${\mathbf {h}}$ are twice continuously differentiable, references [26] and [34] imply that polyhedral outer-approximation schemes of second-order pointwise convergent schemes of relaxations, that are employed by most state-of-the-art software for nonconvex problems (P) [2, 21, 35], also produce second-order pointwise convergent schemes of relaxations.

The following corollary of Theorem 2 shows that second-order convergence is guaranteed at points $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ such that ${\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) < {\mathbf {0}}$, assuming Problem (P) contains no equality constraints (note the weaker assumption on the pointwise convergence order of the scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$, and the slight abuse of notation in the description of ${\mathscr {I}}_{C}(Z)$ where we simply discard the components corresponding to ${\mathbf {h}}$ since $m_E = 0$). A consequence of the corollary is that second-order convergence to unconstrained minima is guaranteed.

Corollary 2

Consider Problem (P) with $m_E = 0$. Suppose f is Lipschitz continuous on $X \times Y$. Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ denote a continuous scheme of convex relaxations of f in $X \times Y$ with pointwise convergence order $\gamma ^{\text{ cv }}_f \ge 1$, and convergence order $\beta ^{\text{ cv }}_f \ge 2$ with corresponding constant $\tau ^{\text{ cv }}_f$. Furthermore, let $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$.

Suppose $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in X \times Y$ is such that ${\mathbf {g}}({\mathbf {x}}^{\text{ S }}, {\mathbf {y}}^{\text{ S }}) < {\mathbf {0}}$ (i.e. $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ is a Slater point). Then, the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned} ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}(X \times Y)},\\ ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \left( \overline{{\mathbf {g}}}^{\text{ cv }}_Z(Z)\right) _{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is at least $\beta ^{\text{ cv }}_f$-order convergent at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Proof

Since we are interested in the convergence order at the feasible point $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$, it suffices to show that the assumptions of Theorem 2 hold.

Let $g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) = -\varepsilon _j < 0, j = 1,\ldots ,m_I$. Since $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$ by virtue of Assumption 1, there exists $\delta _j > 0, \forall j \in \{1,\ldots , m_I\}$, such that ${||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta _j$ implies ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$ (see Lemma 2).

Define $\delta := \mathop {\min }\limits _{j \in \{1,\ldots ,m_I\}}{\delta _j}$, and note that $\delta > 0$. Consider $Z \in {\mathbb {I}}(X \times Y)$ such that $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in Z$ and $w(Z) \le \delta$. For each $({\mathbf {x}},{\mathbf {y}}) \in Z, j \in \{1,\ldots ,m_I\}$ we have ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$. Consequently, for each $j \in \{1,\ldots ,m_I\}, g_j({\mathbf {x}},{\mathbf {y}}) < -\frac{\varepsilon _j}{2}, \,\forall ({\mathbf {x}},{\mathbf {y}}) \in Z$. Since ${\mathbf {g}}^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) < -\frac{\varepsilon _j}{2}, \forall ({\mathbf {x}},{\mathbf {y}}) \in Z$, we have ${\mathbf {g}}^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) < -\frac{\varepsilon _j}{2}, \forall ({\mathbf {x}},{\mathbf {y}}) \in Z$, i.e. every point in Z is feasible for Problem (P) and the lower bounding problem ${\mathscr {L}}(Z)$.

Therefore, $\delta := {\mathop {\min }\limits _{j \in \{1,\ldots ,m_I\}}{\delta _j}}$, any $({\hat{{\mathbf {x}}}}_Z,{\hat{{\mathbf {y}}}}_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f({\mathbf {x}},{\mathbf {y}}), \gamma = \beta ^{\text {cv}}_f +1}$, and ${\hat{\tau }} = 0$ satisfies the (necessary) assumptions of Theorem 2 which yield an upper bound on the first term in Eq. (4). The second term in Eq. (4) can be bounded from above as

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})&= \min _{({\mathbf {x}},{\mathbf {y}}) \in Z}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in Z} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \\&\le \tau ^{\text {cv}}_f w(Z)^{\beta ^{\text {cv}}_f} \end{aligned}$$

since $f^{\text{ cv }}_Z$ converges with order $\beta ^{\text {cv}}_f$ to f on $X \times Y$, and ${\mathscr {F}}^{\text{ cv }}(Z) = Z$. Substituting the above bounds in Eq. (4), we obtain

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \le \tau ^{\text {cv}}_f w(Z)^{\beta ^{\text {cv}}_f}. \end{aligned}$$

The desired result follows by analogy to Lemma 5 by noting that the lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ is at least first-order convergent at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ from Theorem 1. $\square$

Note that the bound on the prefactor obtained from Corollary 2 for convergence at points where a constraint is ‘nearly active’ can be relatively large (also see the comment after Lemma 5).

Remark 9

Corollary 2 does not apply to Problem (P) with active constraints; however, Theorem 2 can be used to demonstrate second-order convergence when Problem (P) contains active convex constraints (note that this includes affine equality constraints) if the schemes of relaxations of the active constraints are the (convex) functions themselves and the scheme of convex relaxations of the objective function is second-order pointwise convergent. Examples 8 and 9 illustrate cases where the above modification of Corollary 2 does not apply when the schemes of relaxations of active convex constraints are not the constraints themselves (note that if the schemes of relaxations of active convex constraints used are the constraints themselves, then the convergence orders of the lower bounding schemes in these examples would be arbitrarily high at their minimizers), thereby highlighting the importance of convexity detection in boosting the convergence order.

The following example shows that the convergence order of the lower bounding scheme is dictated by the convergence order, $\beta ^{\text {cv}}_f$, of the scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ when the assumptions of Corollary 2 are satisfied.

Example 7

Let $X = [0,0], Y = [0,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = y^4 - y^2$ and $g(x,y) = 1 - 2y$. For any $[0, 0] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let $f^{\text{ cv }}_Z(x,y) = y^4 - (y^{\text {L}} + y^{\text {U}})y + y^{\text {L}}y^{\text {U}}, g^{\text {cv}}_Z(x,y) = 1 - 2y$. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has second-order pointwise convergence and second-order convergence on $X \times Y$, while the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$.

Let $y^{\text {L}} = \frac{1}{\sqrt{2}}-\varepsilon , y^{\text {U}} = \frac{1}{\sqrt{2}}+\varepsilon$ with $0 < \varepsilon \le 0.25$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is $-0.25$, while the optimal objective of the lower bounding problem on Z is $-0.25-\varepsilon ^2$. Convergence at the point $\left( 0,\frac{1}{\sqrt{2}}\right)$ is, therefore, at most second-order.

Example 8

Let $X = [-3,3], Y = [-3,3], m_I = 1$, and $m_E = 0$ with $f(x,y) = x+y$ and $g(x,y) = x^2+y^2-8$. For any $[x^{\text {L}}, x^{\text {U}}] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let $f^{\text{ cv }}_Z(x,y) = x+y, g^{\text {cv}}_Z(x,y) = x^2+y^2-8-(w(Z))^2$. The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$, while the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has second-order pointwise convergence on $X \times Y$.

Let $x^{\text {L}} = y^{\text {L}} = -2-\varepsilon , x^{\text {U}} = y^{\text {U}} = -2+\varepsilon$ with $0 < \varepsilon \le 1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is $-4$, while the optimal objective of the lower bounding problem on Z is $-\sqrt{16+8\varepsilon ^2} = -4 - \varepsilon ^2 + O(\varepsilon ^4)$ for $\varepsilon \ll 1$. Convergence at the point $(-2,-2)$ is, therefore, at most second-order.

Example 9

Let $X = [0,1], Y = [0,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = -x-y$ and $g(x,y) = x^2 + 2xy + y^2 - 1$. For any $[x^{\text {L}}, x^{\text {U}}] \times [y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}(X \times Y)$, let

$$\begin{aligned}&\displaystyle f^{\text{ cv }}_Z(x,y) = -x-y, \\&\displaystyle g^{\text {cv}}_Z(x,y) = x^2 + 2 \max \left\{ x^{\text {L}}y + y^{\text {L}}x - x^{\text {L}}y^{\text {L}}, x^{\text {U}}y + y^{\text {U}}x - x^{\text {U}}y^{\text {U}} \right\} + y^2 - 1. \end{aligned}$$

The scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$, while the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has second-order pointwise convergence on $X \times Y$.

Let $x^{\text {L}} = y^{\text {L}} = 0.5-\varepsilon , x^{\text {U}} = y^{\text {U}} = 0.5+\varepsilon$ with $0 < \varepsilon \le 0.5$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is $-1$, while the point $\left( 0.5-0.25\varepsilon ^2,0.5+0.5\varepsilon ^2\right)$ is feasible for the lower bounding problem on Z with objective value $-1 - 0.25\varepsilon ^2$. Convergence at the point (0.5, 0.5) is, therefore, at most second-order.

The next result provides a slight generalization of Corollary 2 by showing that under the assumptions of Corollary 2, the lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ in fact exhibits (at least) second-order convergence on a neighborhood of $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ (this result is motivated by the assumptions on the convergence order of the lower bounding scheme in the analysis of the cluster problem in [15]).

Corollary 3

Consider Problem (P) with $m_E = 0$. Suppose f is Lipschitz continuous on $X \times Y$. Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ denote a continuous scheme of convex relaxations of f in $X \times Y$ with pointwise convergence order $\gamma ^{\text{ cv }}_f \ge 1$, and convergence order $\beta ^{\text{ cv }}_f \ge 1$ with corresponding constant $\tau ^{\text{ cv }}_f$. Furthermore, let $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$.

Suppose $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in X \times Y$ such that ${\mathbf {g}}({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) < {\mathbf {0}}$ (i.e. $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ is a Slater point). Then, $\exists \delta > 0$ such that the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned} \displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}(X \times Y)},\\ \displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)}&:= \left( \overline{{\mathbf {g}}}^{\text{ cv }}_Z(Z)\right) _{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is at least $\beta ^{\text{ cv }}_f$-order convergent on $\left\{ ({\mathbf {x}},{\mathbf {y}}) : {||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta \right\}$.

Proof

Let $g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) = -\varepsilon _j < 0, j = 1,\ldots ,m_I$. Since $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$, there exists $\delta _j > 0, \forall j \in \{1,\ldots , m_I\}$, such that ${||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta _j$ implies ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \varepsilon _j$ (see Lemma 2). Define ${\bar{\delta }} := {\mathop {\min }\limits _{j \in \{1,\ldots ,m_I\}}{\delta _j}}$, note that ${\bar{\delta }} > 0$, and let $\delta := \frac{{\bar{\delta }}}{2}$.

Consider $Z \in {\mathbb {I}}(X \times Y)$ with $Z \cap \left\{ ({\mathbf {x}},{\mathbf {y}}) : {||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta \right\} \ne \emptyset$ and $w(Z) \le \delta$. Similar to the proof of Corollary 2, it can be shown that

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \le \tau ^{\text {cv}}_f w(Z)^{\beta ^{\text {cv}}_f}. \end{aligned}$$

The desired result follows by analogy to Lemma 5 by noting that the lower bounding scheme $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ has at least first-order convergence on $\left\{ ({\mathbf {x}},{\mathbf {y}}) : {||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta \right\}$ from Theorem 1. $\square$

While it may appear that the neighborhood of a Slater point on which second-order convergence of the lower bounding scheme is guaranteed by Corollary 3 can be unnecessarily small, Example 10 shows that a stronger result cannot be deduced without additional assumptions.

A natural question is whether second-order convergence is guaranteed on $X \times Y$ when second-order pointwise convergent schemes of (convex) relaxations of $f, g_1, \ldots , g_{m_I}, h_1, \ldots , h_{m_E}$ are used by the lower bounding scheme. The following example shows that even when schemes of (convex) envelopes are used to underestimate smooth functions $f, {\mathbf {g}}$, and ${\mathbf {h}}$, at most first-order convergence can be guaranteed at certain points in $X \times Y$.

Example 10

Let $X = [0,0], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = -y$ and $g(x,y) = y^3$. For any $[0, 0] \times [-\varepsilon , \varepsilon ] =: Z \in {\mathbb {I}}(X \times Y)$ with $\varepsilon > 0$, let

$$\begin{aligned} f^{\text{ cv }}_Z(x,y) = -y, \quad g^{\text {cv}}_Z(x,y) = {\left\{ \begin{array}{ll} -0.25\varepsilon ^3 + 0.75\varepsilon ^2 y, &{}\text{ if } y < 0.5\varepsilon \\ y^3, &{} \text{ if } y \ge 0.5\varepsilon \end{array}\right. }. \end{aligned}$$

Note that the scheme $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high pointwise convergence order on $X \times Y$ and the scheme $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$, which is the scheme of convex envelopes of g on $X \times Y$ [19], has (at least) second-order pointwise convergence on $X \times Y$. Also note that $(g^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}$ has arbitrarily high convergence order on $X \times Y$.

The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-\frac{\varepsilon }{3}$. Convergence at the point (0, 0) is, therefore, at most first-order.

Despite the fact that we only have first-order convergence at the global minimizer in Example 10, the reader can verify that the natural interval extension-based lower bounding scheme along with the interval bisection branching rule and lowest lower bound node selection rule is sufficient to mitigate the cluster problem for this case [15].

The following result establishes second-order convergence of a convex relaxation-based lower bounding scheme at a feasible point $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in X \times Y$ when second-order pointwise convergent schemes of relaxations are used and the dual lower bounding scheme (see Sect. 4.2) is second-order convergent at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$. This result will be used to prove second-order convergence of such convex relaxation-based lower bounding schemes at KKT points in Corollary 4.

Theorem 3

Consider Problem (P), and let $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in X \times Y$ be a feasible point. Suppose the dual lower bounding scheme has convergence of order $\beta _d > 0$ at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$ with a corresponding scheme of bounded dual variables $\left( \left( \varvec{\mu }^{({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})}_Z,\varvec{\lambda }^{({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})}_Z\right) \right) _{Z \in {\mathbb {I}}(X \times Y)}$ (not necessarily optimal, but which yield $\beta _d$-order convergence at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$) with and , for some constants ${\bar{\mu }}, {\bar{\lambda }} \ge 0$ (see Sect. 4.2). Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}, (g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $f, g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_f \ge 1, \gamma ^{\text{ cv }}_{g,1} \ge 1, \ldots , \gamma ^{\text{ cv }}_{g,m_I} \ge 1$ and corresponding constants $\tau ^{\text{ cv }}_f, \tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$. Let $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k=1,\ldots ,m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma _{h,1} \ge 1, \ldots , \gamma _{h,m_E} \ge 1$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}(X \times Y)}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \bigl (\big \{({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}= {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \bigr . \\&\displaystyle \bigl . \text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z \big \} \bigr )_{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is at least $\min \left\{ \min \left\{ \gamma ^{\text{ cv }}_f,\underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text{ cv }}_{g,j},\underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k}\right\} ,\beta _d\right\}$-order convergent at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$.

Proof

Let $\beta := \min \left\{ \min \left\{ \gamma ^{\text {cv}}_f,\underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text {cv}}_{g,j},\underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k}\right\} ,\beta _d\right\}$, and let $\varvec{\mu }_Z := \varvec{\mu }^{({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})}_Z, \varvec{\lambda }_Z := \varvec{\lambda }^{({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})}_Z, \forall Z \in {\mathbb {I}}(X \times Y)$, denote the scheme of dual variables corresponding to the dual lower bounding scheme (we omit the dependence of the dual variables on $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$ for ease of exposition). Since we are concerned about the convergence order at the feasible point $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$, it suffices to show the existence of $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in Z$,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \le \tau w(Z)^{\beta }. \end{aligned}$$

Consider $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in Z$. By virtue of the assumption that the dual lower bounding scheme, with the dual variables fixed to $((\varvec{\mu }_Z,\varvec{\lambda }_Z))_{Z \in {\mathbb {I}}(X \times Y)}$, has convergence of order $\beta _d$ at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$, we have

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_Z{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_Z{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right]&\le \tau _d {w(Z)}^{\beta _d}. \end{aligned}$$

(5)

Choose $\varvec{\lambda }_{Z,+}, \varvec{\lambda }_{Z,-} \in {\mathbb {R}}^{m_E}_+$ such that $\varvec{\lambda }_Z = \varvec{\lambda }_{Z,+} - \varvec{\lambda }_{Z,-}, {||}\varvec{\lambda }_{Z,+}{||}_{\infty } \le {\bar{\lambda }}$, and ${||}\varvec{\lambda }_{Z,-}{||}_{\infty } \le {\bar{\lambda }}$.

$$\begin{aligned} \hbox {Let}\,{\bar{\gamma }}&{:}= \min \left\{ \gamma ^{\text {cv}}_f,\underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text {cv}}_{g,j},\underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k}\right\} . \hbox {We}\,\hbox {have}\nonumber \\&\qquad \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_Z{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_Z{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] - \underset{{\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \nonumber \\&\quad \le \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_Z{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_Z{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] \nonumber \\&\quad \quad \quad - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }_1 \ge {\mathbf {0}}, \varvec{\lambda }_2 \le {\mathbf {0}}}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_1{\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_2{\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}})\right] \nonumber \\&\quad \le \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_{Z}{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+ {\varvec{\lambda }}^\text{ T }_{Z,+}{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})-{\varvec{\lambda }}^\text{ T }_{Z,-}{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] \nonumber \\&\quad \quad \quad - \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_{Z}{\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_{Z,+}{\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})-{\varvec{\lambda }}^\text{ T }_{Z,-}{\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}})\right] \nonumber \\&\quad \le \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\max }\Bigl [\left( f({\mathbf {x}},{\mathbf {y}}) - f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) + {\varvec{\mu }}^\text{ T }_{Z} \left( {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})\right) \Bigr . \nonumber \\&\quad \quad \quad + \Bigl . {\varvec{\lambda }}^\text{ T }_{Z,+}\left( {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})\right) + {\varvec{\lambda }}^\text{ T }_{Z,-}\left( {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) \right) \Bigr ] \nonumber \\&\quad \le \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\max }\left( f({\mathbf {x}},{\mathbf {y}}) - f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}})\right) + \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\max }{\varvec{\mu }}^\text{ T }_{Z}\left( {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})\right) \nonumber \\&\quad \quad \quad +\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\max }{\varvec{\lambda }}^\text{ T }_{Z,+}\left( {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})\right) + \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\max }{\varvec{\lambda }}^\text{ T }_{Z,-}\left( {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) - {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) \right) \nonumber \\&\quad \le \tau ^{\text {cv}}_f w(Z)^{\gamma ^{\text {cv}}_f} + \displaystyle \sum _{j=1}^{m_I}{{\bar{\mu }} \tau ^{\text {cv}}_{g,j} w(Z)^{\gamma ^{\text {cv}}_{g,j}}} + 2\displaystyle \sum _{k=1}^{m_E}{{\bar{\lambda }} \tau _{h,k} w(Z)^{\gamma _{h,k}}} \nonumber \\&\quad \le \Biggl ( \tau ^{\text {cv}}_f w(X \times Y)^{\gamma ^{\text {cv}}_f - {\bar{\gamma }}} + \displaystyle \sum _{j=1}^{m_I}{{\bar{\mu }} \tau ^{\text {cv}}_{g,j} w(X \times Y)^{\gamma ^{\text {cv}}_{g,j}-{\bar{\gamma }}}} \nonumber \\&\quad \quad \quad + 2\displaystyle \sum _{k=1}^{m_E}{{\bar{\lambda }} \tau _{h,k} w(X \times Y)^{\gamma _{h,k}-{\bar{\gamma }}}} \Biggr ) w(Z)^{{\bar{\gamma }}}, \end{aligned}$$

(6)

where Step 1 follows from weak duality and Step 3 follows from Lemma 3.

Therefore, from Eqs. (5) and (6), we have

$$\begin{aligned}&\quad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \\&= \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)} f({\mathbf {x}},{\mathbf {y}})\,\, - \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_Z{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_Z{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] \\&\quad \quad + \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }_Z{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }_Z{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_Z({\mathbf {x}},{\mathbf {y}}) \\&\le \tau w(Z)^{\beta }, \end{aligned}$$

where the prefactor $\tau$ is defined as

$$\begin{aligned} \tau:= & {} \Biggl ( \tau ^{\text {cv}}_f w(X \times Y)^{\gamma ^{\text {cv}}_f - \beta } + \displaystyle \sum _{j=1}^{m_I}{{\bar{\mu }} \tau ^{\text {cv}}_{g,j} w(X \times Y)^{\gamma ^{\text {cv}}_{g,j}-\beta }} + 2\displaystyle \sum _{k=1}^{m_E}{{\bar{\lambda }} \tau _{h,k} w(X \times Y)^{\gamma _{h,k}-\beta }} \\&+\, \tau _d w(X \times Y)^{\beta _d-\beta }\Biggr ). \end{aligned}$$

$\square$

4.2 Duality-based branch-and-bound

In this section, we investigate the convergence order of a Lagrangian dual-based lower bounding scheme. Before we define the convergence order of the scheme, the Lagrangian dual problem is introduced and some of its properties are outlined.

The dual problem of Problem (P) that is obtained by dualizing all of the constraints ${\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}$ and ${\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) =~{\mathbf {0}}$ is given by

where $q : {\mathbb {R}}^{m_I}_{+} \times {\mathbb {R}}^{m_E} \rightarrow {\mathbb {R}}$, defined by

$$\begin{aligned} q(\varvec{\mu },\varvec{\lambda }) := \underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Y}{\min } \, {f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {\varvec{\lambda }}^\text{ T } {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) }, \quad \forall (\varvec{\mu },\varvec{\lambda }) \in {\mathbb {R}}^{m_I}_{+} \times {\mathbb {R}}^{m_E}, \end{aligned}$$

is the Lagrangian dual function. Let $\min \mathrm{(P)}$ and $\sup \mathrm{(D)}$ respectively denote the optimal objective values of Problem (P) and Problem (D). From weak duality, we know that $\min \mathrm{(P)} \ge \sup \mathrm{(D)}$, which validates the use of Problem (D) as a lower bounding problem.

The following result shows that the lower bounds obtained by solving the Lagrangian dual Problem (D) are stronger than those obtained by solving any convex relaxation-based lower bounding problem.

Lemma 9

Consider Problem (P), and suppose $Z \in {\mathbb {I}}(X \times Y)$. Let $f^{\text{ cv }}_Z$ and ${\mathbf {g}}^{\text{ cv }}_Z$ denote (continuous) convex relaxations of f and ${\mathbf {g}}$, respectively, on Z, and let ${\mathbf {h}}^{\text{ cv }}_Z$ and ${\mathbf {h}}^{\text{ cc }}_Z$ denote (continuous) convex and concave relaxations, respectively, of ${\mathbf {h}}$ on Z. Furthermore, assume that strong duality holds for the convex relaxation-based lower bounding problem ${\mathop {\min }\limits _{{\mathscr {F}}^{\text{ cv }}(Z)}f^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}})}$. Then the lower bound obtained by solving the Lagrangian dual problem is at least as strong as that obtained by solving the above convex relaxation-based lower bounding problem, i.e.,

$$\begin{aligned} \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] - \underset{{\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \ge 0. \end{aligned}$$

Proof

Since strong duality holds for the convex relaxation-based lower bounding problem, the difference between the lower bounds can be rewritten as

where the last step follows from the fact that $\forall ({\mathbf {x}},{\mathbf {y}}) \in Z, \varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }_1 \ge {\mathbf {0}}, \varvec{\lambda }_2 \le {\mathbf {0}}$,

$\square$

The following result due to Dür [8] establishes the condition under which the dual lower bounding problem detects infeasibility.

Lemma 10

Consider Problem (P) (satisfying Assumption 1). We have

$$\begin{aligned} \sup \mathrm{(D)} = +\infty \iff \text{ conv }\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X \times Y) \right) \cap \left( {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\}\right) = \emptyset . \end{aligned}$$

Proof

The result follows, in part, by replacing ${\mathbf {h}}({\mathbf {x}},{\mathbf {y}})={\mathbf {0}}$ with ${\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}$ and $-{\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {0}}$ and using Theorem 2 in [8]. $\square$

Definition 14 can be applied to analyze the convergence order of the above duality-based lower bounding scheme as follows.

The scheme of dual lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \left( \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})+{\varvec{\lambda }}^\text{ T }{\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] \right) _{Z \in {\mathbb {I}}(X \times Y)}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}(X \times Y)} := \left( \text{ conv }\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z) \right) \right) _{Z \in {\mathbb {I}}(X \times Y)} \end{aligned}$$

is thus said to have convergence of order $\beta > 0$ at

• 1. A feasible point $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ if there exists $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}},{\mathbf {y}}) \in Z$,

  $$\begin{aligned} \min _{({\mathbf {v}},{\mathbf {w}}) \in {\mathscr {F}}(Z)}f({\mathbf {v}},{\mathbf {w}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {v}},{\mathbf {w}}) \in Z}{\min }\left[ f({\mathbf {v}},{\mathbf {w}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}({\mathbf {v}},{\mathbf {w}})+{\varvec{\lambda }}^\text{ T }{\mathbf {h}}({\mathbf {v}},{\mathbf {w}})\right] \le \tau {w(Z)}^{\beta }. \end{aligned}$$

• 2. An infeasible point $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ if there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}},{\mathbf {y}}) \in Z$,

  $$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( \text{ conv }\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z) \right) , {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }. \end{aligned}$$

We associate with the dual lower bounding scheme, $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$, at a feasible point $({\mathbf {x}},{\mathbf {y}})$, a scheme of dual variables $((\varvec{\mu }^{({\mathbf {x}},{\mathbf {y}})}_Z,\varvec{\lambda }^{({\mathbf {x}},{\mathbf {y}})}_Z))_{Z \in {\mathbb {I}}(X \times Y)}$ corresponding to the solution of the scheme of dual lower bounding problems $({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}(X \times Y)}$ with $({\mathbf {x}},{\mathbf {y}}) \in Z$ (note that $\sup \mathrm{(D)}$ may not be attained, in which case we assume that dual variables that yield a dual function value arbitrarily close to the supremum are available). Using Lemma 10, we next show that if the convex relaxation-based lower bounding problem corresponding to Problem (P) that is obtained by replacing the functions in Problem (P) with their envelopes is infeasible, then $\sup \mathrm{(D)} = +\infty$.

Lemma 11

Let $(g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,m_I$, denote (any) schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$ in $X \times Y$ and $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots ,m_E$, denote (any) schemes of relaxations of $h_1,\ldots ,h_{m_E}$ in $X \times Y$. Then for each $Z \in {\mathbb {I}}(X \times Y)$, we have

$$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \ge d\left( \text{ conv }\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z) \right) , {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \ge d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) , \end{aligned}$$

where ${\mathscr {I}}_{C}(Z)$ is defined as

$$\begin{aligned} {\mathscr {I}}_{C}(Z):= & {} \left\{ ({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}} \right\} = {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}})\\&\text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z. \end{aligned}$$

Proof

The first inequality trivially holds. To prove the second inequality, we first notice that

$$\begin{aligned} d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) = d\left( {\bar{{\mathscr {I}}_{C}}}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) , \end{aligned}$$

where ${\bar{{\mathscr {I}}_{C}}}(Z)$ is defined as

$$\begin{aligned} {\bar{{\mathscr {I}}_{C}}}(Z)&{:=}&\left\{ ({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}\ge {\mathbf {g}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{Z}({\mathbf {x}},{\mathbf {y}}) \text { for some } ({\mathbf {x}},{\mathbf {y}}) \in Z \right\} . \end{aligned}$$

Note that ${\bar{{\mathscr {I}}_{C}}}(Z)$ is a convex set since it can be represented as the direct sum of two convex sets. Since $\text{ conv }\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z) \right)$ is the smallest convex set that encloses $\overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (Z)$, the desired result follows. $\square$

Theorem 4

Consider Problem (P). Suppose strong duality holds for the scheme of convex relaxation-based lower bounding problems for Problem (P) obtained by using the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$. If the assumptions of Theorem 1 hold for the functions $f, {\mathbf {g}}, {\mathbf {h}}$, and the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$, then the dual lower bounding scheme is (at least) first-order convergent on $X \times Y$. Furthermore, if the assumptions of Theorem 2 hold for the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$ and $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }}) \in X \times Y$, then the dual lower bounding scheme is (at least) second-order convergent at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$.

Proof

From Lemma 11, we have that the convergence order of the dual lower bounding scheme at an infeasible point $({\mathbf {x}},{\mathbf {y}}) \in X \times Y$ is at least as high as the convergence order at $({\mathbf {x}},{\mathbf {y}})$ of the convex relaxation-based lower bounding scheme obtained by using the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$. Lemma 9 implies that the lower bounds obtained using the dual lower bounding scheme are at least as tight as the lower bounds obtained using the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$. The desired result follows from Definition 14. $\square$

Note that the conclusions of Theorem 4 hold even if the schemes of relaxations of $f, {\mathbf {g}}$, and ${\mathbf {h}}$ do not correspond to their envelopes, so long as the (remaining) assumptions of Theorem 4 are satisfied.

Remark 10

The assumption of strong duality is in fact not required to show first-order convergence of the dual lower bounding scheme when all functions in Problem (P) are Lipschitz continuous. For this case, the proof of first-order convergence at infeasible points follows from Lemmata 7, 8, and 11, and the proof of first-order convergence at feasible points follows from Proposition 1 in [8].

Theorem 4 makes no assumptions on the boundedness of schemes of dual variables. This is reflected in the application of the dual lower bounding scheme to Example 10 where the optimal scheme of dual variables can be unbounded (note, however, that first-order convergence of the dual lower bounding scheme at the global minimizer of Example 10 can be achieved using bounded schemes of dual variables when the dual problem is not solved to optimality). Furthermore, Example 6 shows that the convergence order of the dual lower bounding scheme can be as low as two at $({\mathbf {x}}^{\text{ f }},{\mathbf {y}}^{\text{ f }})$ when the assumptions of Theorem 2 are satisfied for the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$ (see Lemma 14).

The following result shows that in the absence of equality constraints, the dual lower bounding scheme has arbitrarily high convergence order at unconstrained points.

Proposition 1

Consider Problem (P) with $m_E = 0$. Suppose f and $g_j, \forall j \in \{1,\ldots ,m_I\}$, are Lipschitz continuous on $X \times Y$. Furthermore, suppose $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in X \times Y$ such that ${\mathbf {g}}({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) < {\mathbf {0}}$ (i.e. $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ is a Slater point). The dual lower bounding scheme has arbitrarily high convergence order at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Proof

The proof is relegated to Appendix A.1 since it is similar to the proof of Corollary 2. $\square$

Remark 11

Proposition 1 as stated does not apply to Problem (P) with active constraints; however, it can be modified to demonstrate second-order convergence when Problem (P) contains active convex constraints (note that this includes affine equality constraints) if f is twice continuously differentiable, and strong duality holds for the scheme of relaxations of Problem (P) in which only the active (convex) constraints are included and f is replaced by its scheme of convex envelopes (see Remark 9). Proposition 1 can also be extended to demonstrate arbitrarily high convergence order of the dual lower bounding scheme on a neighborhood of $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ in a manner similar to Corollary 3.

The next result shows that the dual lower bounding scheme is second-order convergent at KKT points when the functions $f, {\mathbf {g}}$, and ${\mathbf {h}}$ in Problem (P) are twice continuously differentiable.

Theorem 5

Consider Problem (P). Suppose $\text{ int }(X \times Y)$ is nonempty, and $f, {\mathbf {g}}$, and ${\mathbf {h}}$ are twice continuously differentiable on $\text{ int }(X \times Y)$. Furthermore, suppose there exists $({\mathbf {x}}^*,{\mathbf {y}}^*) \in \text{ int }(X \times Y), \varvec{\mu }^* \in {\mathbb {R}}^{m_I}_+$, and $\varvec{\lambda }^* \in {\mathbb {R}}^{m_E}$ such that $({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is a KKT point for Problem (P). The dual lower bounding scheme is at least second-order convergent at $({\mathbf {x}}^*,{\mathbf {y}}^*)$.

Proof

Let $L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) := f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {\varvec{\lambda }}^\text{ T } {\mathbf {h}}({\mathbf {x}},{\mathbf {y}})$ denote the Lagrangian of Problem (P). Since we are concerned about the convergence order at the feasible point $({\mathbf {x}}^*,{\mathbf {y}}^*)$, it suffices to show the existence of $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^*,{\mathbf {y}}^*) \in Z$,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) \le \tau {w(Z)}^2. \end{aligned}$$

We have

$$\begin{aligned} \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda })&\ge \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu }^*,\varvec{\lambda }^*) \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } \left[ L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) + {\nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*)\right. \\&\left. +\, {\nabla _{{\mathbf {y}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {y}}- {\mathbf {y}}^*) - O(w(Z)^2) \right] \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } \left[ f({\mathbf {x}}^*,{\mathbf {y}}^*) - O(w(Z)^2) \right] \\&\ge f({\mathbf {x}}^*,{\mathbf {y}}^*) - O(w(Z)^2). \end{aligned}$$

Note that Step 3 above uses $L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = f({\mathbf {x}}^*,{\mathbf {y}}^*), \nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = {\mathbf {0}}$, and $\nabla _{{\mathbf {y}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = {\mathbf {0}}$ by virtue of the assumption that $({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is a KKT point for Problem (P). Therefore,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) \le O(w(Z)^2), \end{aligned}$$

which establishes the existence of $\tau$ for all $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^*,{\mathbf {y}}^*) \in Z$ by analogy to Lemma 5 since the dual lower bounding scheme is at least first-order convergent at $({\mathbf {x}}^*,{\mathbf {y}}^*)$. $\square$

A corollary of Theorems 3 and 5 is that second-order convergence at KKT points is guaranteed for convex relaxation-based lower bounding schemes in which second-order pointwise convergent schemes of relaxations are used.

Corollary 4

Consider Problem (P). Suppose $\text{ int }(X \times Y)$ is nonempty and $f, {\mathbf {g}}$, and ${\mathbf {h}}$ are twice continuously differentiable on $\text{ int }(X \times Y)$. Furthermore, suppose there exists $({\mathbf {x}}^*,{\mathbf {y}}^*) \in \text{ int }(X \times Y), \varvec{\mu }^* \in {\mathbb {R}}^{m_I}_+$, and $\varvec{\lambda }^* \in {\mathbb {R}}^{m_E}$ such that $({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is a KKT point for Problem (P). Let $(f^{\text{ cv }}_{Z})_{Z \in {\mathbb {I}}(X \times Y)}, (g^{\text{ cv }}_{j,Z})_{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $f, g_1,\ldots ,g_{m_I}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma ^{\text{ cv }}_f \ge 2, \gamma ^{\text{ cv }}_{g,1} \ge 2, \ldots , \gamma ^{\text{ cv }}_{g,m_I} \ge 2$ and corresponding constants $\tau ^{\text{ cv }}_f, \tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$. Let $(h^{\text{ cv }}_{k,Z}, h^{\text{ cc }}_{k,Z})_{Z \in {\mathbb {I}}(X \times Y)}, k=1,\ldots ,m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in $X \times Y$ with pointwise convergence orders $\gamma _{h,1} \ge 2, \ldots , \gamma _{h,m_E} \ge 2$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, the resulting scheme of convex relaxation-based lower bounding problems for Problem (P) is at least second-order convergent at $({\mathbf {x}}^*,{\mathbf {y}}^*)$.

Proof

The result holds as a consequence of Theorems 3 and 5, by using $\varvec{\mu }_Z = \varvec{\mu }^*, \varvec{\lambda }_Z = \varvec{\lambda }^*, {\bar{\mu }} = {||}\varvec{\mu }^*{||}_{\infty }, {\bar{\lambda }} = {||}\varvec{\lambda }^*{||}_{\infty }$ in Theorem 3. $\square$

The following example shows that the convergence order may be as low as two under the assumptions of Theorem 5.

Example 11

Let $X = [-2,2], Y = [0,3], m_I = 1$, and $m_E = 1$ with $f(x,y) = x+y, g(x,y) = -y^2+y+2$, and $h(x,y) = x$. Consider intervals $[0, 0] \times [2-\varepsilon , 2+\varepsilon ] =: Z \in {\mathbb {I}}(X \times Y)$ with $0 < \varepsilon \le 1$. Note that $w(Z) = 2\varepsilon$, and that $\left( 0,2,\frac{1}{3},-1\right)$ is a KKT point for Problem (P). The optimal objective value of Problem (P) on Z is 2, while the optimal objective value of the Lagrangian dual-based lower bounding problem on Z can be derived as

$$\begin{aligned} {\mathscr {O}}(Z)&= \underset{\mu \ge 0, \lambda }{\sup }\,\,\underset{(x,y) \in Z}{\min }\,\, x + y + \mu \left( -y^2+y+2\right) + \lambda x \\&= \underset{\mu \ge 0}{\sup }\min \left\{ (2-\varepsilon ) + \mu \left( -(2-\varepsilon )^2+(2-\varepsilon )+2 \right) ,\right. \\&\quad \quad \quad \quad \quad \quad \left. (2+\varepsilon )+\, \mu \left( -(2+\varepsilon )^2+(2+\varepsilon )+2\right) \right\} \\&= \underset{\mu \ge 0}{\sup }\min \left\{ (2-\varepsilon ) + \mu \left( 3\varepsilon - \varepsilon ^2 \right) , (2+\varepsilon ) + \mu \left( -3\varepsilon - \varepsilon ^2\right) \right\} \\&= (2-\varepsilon ) + \displaystyle \frac{1}{3} \left( 3\varepsilon - \varepsilon ^2 \right) \\&= 2 - \displaystyle \frac{\varepsilon ^2}{3}, \end{aligned}$$

where Step 2 follows from the fact that the minimum of a concave function on an interval is attained at one of its endpoints, and the value of $\mu$ in Step 4 is obtained by equating the two arguments of the inner $\min$ function in Step 3. Convergence of the dual lower bounding scheme at the point (0, 2) is, therefore, at most second-order.

Finally, we show that the dual lower bounding scheme is (at least) first-order convergent even when the dual problem is not solved to optimality.

Theorem 6

Consider Problem (P). Suppose $f, g_j, j = 1,\ldots ,m_I$, and $h_k, k = 1,\ldots ,m_E$, are Lipschitz continuous on $X \times Y$ with Lipschitz constants $M_f, M_{g,1}, \ldots , M_{g,m_I}, M_{h,1},\ldots ,M_{h,m_E}$, respectively. Furthermore, suppose the dual lower bounding scheme involves at most $n_d \ge 1$ iterations of an algorithm applied to the dual at each node of the branch-and-bound tree. In addition, suppose the branch-and-bound algorithm uses first-order (Hausdorff) convergent schemes of constant relaxations $\left( g^{\text{ L }}_{j,Z}, g^{\text{ U }}_{j,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,m_I$, on $X \times Y$ to overestimate $\left( \overline{g}_j(Z) \right) _{Z \in {\mathbb {I}}(X \times Y)}$ and first-order (Hausdorff) convergent schemes of constant relaxations $\left( h^{\text{ L }}_{k,Z}, h^{\text{ U }}_{k,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots ,m_E$, on $X \times Y$ to overestimate $\left( \overline{h}_k(Z) \right) _{Z \in {\mathbb {I}}(X \times Y)}$ (such schemes of constant relaxations can be obtained, for example, using interval arithmetic [22]), sets $\mu _j = 0$ at each iteration of the algorithm applied to the dual on Z if $g^{\text{ U }}_{j,Z} < 0$ (i.e., when inequality constraint j is determined to be inactive on Z by $g^{\text{ U }}_{j,Z}$), and determines the dual lower bounding problem on Z to be infeasible either when $g^{\text{ L }}_{j,Z} > 0$ for any $j \in \{1,\ldots ,m_I\}$ (i.e., when inequality constraint j is determined to be unsatisfiable on Z by $g^{\text{ L }}_{j,Z}$), or when $0 \not \in \left[ h^{\text{ L }}_{k,Z}, h^{\text{ U }}_{k,Z}\right]$ for any $k \in \{1,\ldots ,m_E\}$ (i.e., when equality constraint k is determined to be unsatisfiable on Z by $(h^{\text{ L }}_{k,Z}, h^{\text{ U }}_{k,Z})$). Assume that the absolute values of the schemes of dual variables generated by the dual lower bounding scheme are bounded from above by $M_{\infty }$. Then the dual lower bounding scheme is at least first-order convergent on $X \times Y$.

Proof

From the assumption that $\left( g^{\text{ L }}_{j,Z}, g^{\text{ U }}_{j,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,m_I$, and $\left( h^{\text{ L }}_{k,Z}, h^{\text{ U }}_{k,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots ,m_E$, are first-order convergent on $X \times Y$, the determination of infeasibility of the dual lower bounding problem on Z if $g^{\text {L}}_{j,Z} > 0$ for any $j \in \{1,\ldots ,m_I\}$, or if $0 \not \in \left[ h^{\text {L}}_{k,Z}, h^{\text {U}}_{k,Z}\right]$ for any $k \in \{1,\ldots ,m_E\}$, Proposition 1 in [6], and Lemma 8, we conclude that the dual lower bounding scheme has at least first-order convergence at infeasible points (although the dual lower bounding scheme detects infeasibility of infeasible points in $X \times Y$ at least as quickly as any convex relaxation-based lower bounding scheme (see Lemma 11), we assume that the schemes $\left( g^{\text{ L }}_{j,Z}, g^{\text{ U }}_{j,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, j = 1,\ldots ,m_I$, and $\left( h^{\text{ L }}_{k,Z}, h^{\text{ U }}_{k,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}, k = 1,\ldots ,m_E$, are available to detect infeasibility since we are only allowed to use at most $n_d$ iterations of an algorithm applied to the dual).

Next, suppose ${\mathscr {F}}(X \times Y) \ne \emptyset$ and $Z \in {\mathbb {I}}(X \times Y)$ with $Z \cap {\mathscr {F}}(X \times Y) \ne \emptyset$. Let $J_Z$ denote the set of inequality constraints that are potentially active at some point in Z as determined by $\left( g^{\text{ L }}_{j,Z}, g^{\text{ U }}_{j,Z} \right)$, i.e. $J_Z := \left\{ j \in \{1,\ldots ,m_I\} : g^{\text {U}}_{j,Z} \ge 0 \right\}$. Let $({\bar{\varvec{\mu }}}_Z,{\bar{\varvec{\lambda }}}_Z) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}$ denote the pair of dual variables corresponding to the dual lower bound on Z after at most $n_d$ iterations of an algorithm applied to the dual with ${\bar{\mu }}_{j,Z} = 0, \forall j \in \{1,\ldots ,m_I\} \backslash J_Z$, and let $({\bar{{\mathbf {x}}}}_Z,{\bar{{\mathbf {y}}}}_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in Z}} \, {f({\mathbf {x}},{\mathbf {y}}) + {{\bar{\varvec{\mu }}}}^\text{ T }_Z {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {{\bar{\varvec{\lambda }}}}^\text{ T }_Z {\mathbf {h}}({\mathbf {x}},{\mathbf {y}}) }$. Note that the condition ${\bar{\mu }}_{j,Z} = 0, \forall j \in \{1,\ldots ,m_I\} \backslash J_Z$ can be guaranteed by a suitable initialization of the dual variables and by suitably modifying the dual variables generated by the algorithm applied to the dual (this modification of the dual lower bounding scheme is once again necessitated by the assumption that at most $n_d$ iterations of an algorithm applied to the dual are used). For each $j \in J_Z$, we have

$$\begin{aligned} g^{\text{ U }}_{j,Z} - \max _{({\mathbf {x}},{\mathbf {y}}) \in Z} g_j({\mathbf {x}},{\mathbf {y}}) \le \tau _j w(Z) \end{aligned}$$

for some constant $\tau _j \ge 0$ by virtue of the fact that the scheme of constant concave relaxations $\left( g^{\text{ U }}_{j,Z} \right) _{Z \in {\mathbb {I}}(X \times Y)}$ has first-order convergence on $X \times Y$. Since $g^{\text {U}}_{j,Z} \ge 0, \forall j \in J_Z$, and $g_j$ is Lipschitz continuous on $X \times Y$, this implies

$$\begin{aligned} g_j({\mathbf {x}},{\mathbf {y}}) \ge - \left( \tau _j + M_{g,j} \sqrt{n_x + n_y} \right) w(Z), \quad \forall ({\mathbf {x}},{\mathbf {y}}) \in Z, \,\,\forall j \in J_Z. \end{aligned}$$

Let $({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}} \, f({\mathbf {x}},{\mathbf {y}})$. We have

which establishes the desired result. $\square$

5 Reduced-space branch-and-bound algorithms

In this section, we present some results on the convergence orders of some widely-applicable reduced-space lower bounding schemes in the literature [9, 10] for Problem (P) when only the set Y may be partitioned during the course of the algorithm. This section is divided into two parts. First, we consider a convex relaxation-based reduced-space lower bounding scheme for a subclass of Problem (P) [10] and investigate its convergence order. Next, we look at the convergence order of a duality-based reduced-space lower bounding scheme [9, Section 3.3] for Problem (P). Algorithm 1 outlines a generic reduced-space branch-and-bound algorithm for Problem (P). It should be noted that Algorithm 1 merely provides the backbone of a generic reduced-space branch-and-bound algorithm. In practice, the order in which the subproblems are solved may vary and additional subproblems may be solved to speed up the convergence of the algorithm. The reader is directed to references [9] and [10] for two widely-applicable instances of Algorithm 1, and for examples of their application. In the remainder of this section, we investigate the convergence orders of the reduced-space lower bounding schemes described in [9] and [10].

5.1 Convex relaxation-based branch-and-bound for problems with special structure

Epperly and Pistikopoulos [10] proposed a reduced-space branch-and-bound algorithm for Problem (P) when $m_E = 0$ (note that this condition can be relaxed as detailed below), and the functions f and $g_j, \forall j \in \{1,\ldots ,m_I\}$, in Problem (P) are each of the form

$$\begin{aligned} w({\mathbf {x}},{\mathbf {y}})&= w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}})} + w^{D}({\mathbf {y}}), \end{aligned}$$

(W)

where Q is a finite set of indices, and the functions $w^{A}, {\mathbf {w}}^{B}, {\mathbf {w}}^{C}$, and $w^{D}$ satisfy:

• 1. $w^{A}$ and ${\mathbf {w}}^{B}$ are convex on X.

• 2. ${\mathbf {w}}^{C}$ and $w^{D}$ are continuous on Y.

• 3. Strongly consistent convex and concave relaxations are available for ${\mathbf {w}}^{C}$ and $w^{D}$ on Y.

• 4. ${\mathbf {w}}^{B}$ and ${\mathbf {w}}^{C}$ have continuous tight bounds.

• 5. For each $i \in Q$, at least one of the following two conditions must hold:

  • a. $w^{B}_i({\mathbf {x}}) = {{\mathbf {c}}}^\text{ T }_{i}{\mathbf {x}}$ for some constant ${\mathbf {c}}_{i} \in {\mathbb {R}}^{n_x}$,

  • b. $w^{C}_i({\mathbf {y}}) \ge 0$ for all ${\mathbf {y}}\in Y$.

Epperly and Pistikopoulos [10] state that equality constraints can be equivalently reformulated using pairs of inequalities; however, the above assumptions restrict the functional forms of the equality constraints $h_k, k = 1,\ldots ,m_E$, to

Suppose for each $Z \in {\mathbb {I}}Y$, we associate an interval X(Z) such that $\square X \supset X(Z) \supset {\mathscr {F}}_X(Z)$, where $\square X$ denotes the interval hull of X (note that we make the implicit assumption (see Remark 2) that X is an interval in this section). Assumption 3 can be restated as follows: there exists a continuous scheme, $(w^{C,\text{ cv }}_{i,Z}, w^{C,\text{ cc }}_{i,Z})_{Z \in {\mathbb {I}}Y}$, of relaxations of $w^C_i, i \in Q$, in Y with pointwise convergence order $\gamma ^C_i > 0$, and there exists a continuous scheme of convex relaxations, $(w^{D,\text{ cv }}_{Z})_{Z \in {\mathbb {I}}Y}$, of $w^D$ in Y with pointwise convergence order $\gamma ^{D, \text {cv}} > 0$. Assumption 4 can be replaced by the following: there exist schemes of constant relaxations $(w^{B,\text{ L }}_{i,Z}, w^{B,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}\square {X}}$ and $(w^{C,\text{ L }}_{i,Z}, w^{C,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}Y}, i \in Q$, of $w^B_i$ and $w^C_i$ in X and Y, respectively, with (Hausdorff) convergence orders $\beta ^{B,\text {c}}_i > 0$ and $\beta ^{C,\text {c}}_i > 0$. In addition, we assume that the range order of $w^C_i, \forall i \in Q$, is greater than zero on Y (cf. Lemma 12).

Under the above assumptions, Epperly and Pistikopoulos [10] show that underestimating each function $w({\mathbf {x}},{\mathbf {y}})$ of the form (W) using the scheme $(w^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ of convex relaxations defined by

where, for each $i \in Q$, the scheme of convex relaxations $(w^{BC,\text{ cv }}_{i,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ is obtained using McCormick’s product rule [20] as

yields a convergent reduced-space lower bounding scheme with any accumulation point of the sequence of lower bounding solutions solving Problem (P) when the subdivision process is exhaustive on Y and the selection procedure is bound improving.

Before we investigate the convergence order of the reduced-space lower bounding scheme in [10], we look at the propagation of the convergence orders of the relaxation schemes $(w^{B,\text{ L }}_{i,Z}, w^{B,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}\square {X}}, (w^{C,\text{ cv }}_{i,Z}, w^{C,\text{ cc }}_{i,Z})_{Z \in {\mathbb {I}}Y}, (w^{C,\text{ L }}_{i,Z}, w^{C,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}Y}, \forall i \in Q$, and $(w^{D,\text{ cv }}_{Z})_{Z \in {\mathbb {I}}Y}$ to the convergence order of the reduced-space scheme of convex relaxations $(w^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$. Note that unless otherwise specified, we simply use $X(Z) = \square X (= X), \forall Z \in {\mathbb {I}}Y$. The following result provides sufficient conditions for the scheme of convex relaxations defined by  $(\text {W}^{\text {cv}})$ to have pointwise convergence of a given order on Y.

Lemma 12

Let $X \subset {\mathbb {R}}^{n_x}, Y \subset {\mathbb {R}}^{n_y}$ be nonempty compact convex sets and $f: X \times Y \rightarrow {\mathbb {R}}$ be a function of the form (W) such that

$$\begin{aligned} f: X \times Y \ni ({\mathbf {x}},{\mathbf {y}}) \longmapsto w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}})} + w^{D}({\mathbf {y}}). \end{aligned}$$

Assume that $w^A, w^{B}_i, \forall i \in Q$, and $w^{D}$ are continuous, and for each $i \in Q, w^{C}_i$ has range of order $\alpha ^C_i \ge 1$ on Y with corresponding constant $\tau ^{C,\text{ r }}_i$. Let $(w^{C,\text{ cv }}_{i,Z}, w^{C,\text{ cc }}_{i,Z})_{Z \in {\mathbb {I}}Y}$ and $(w^{D,\text{ cv }}_{Z})_{Z \in {\mathbb {I}}Y}$ respectively denote continuous schemes of relaxations of $w^{C}_i, i \in Q$, and $w^{D}$ in Y with pointwise convergence orders $\gamma ^{C}_i \ge 1$ and $\gamma ^{D,\text{ cv }} \ge 1$ and corresponding constants $\tau ^{C}_i$ and $\tau ^{D,\text{ cv }}$. Let $(w^{B,\text{ L }}_{i,Z}, w^{B,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}\square {X}}$ and $(w^{C,\text{ L }}_{i,Z}, w^{C,\text{ U }}_{i,Z})_{Z \in {\mathbb {I}}Y}$ respectively denote schemes of constant relaxations of $w^B_i$ in $\square X$ and $w^C_i$ in $Y, \forall i \in Q$, with (Hausdorff) convergence orders $\beta ^{B,\text{ c }}_i > 0$ and $\beta ^{C,\text{ c }}_i \ge 1$ and corresponding constants $\tau ^{B,\text{ c }}_i$ and $\tau ^{C,\text{ c }}_i$. Then the continuous scheme of convex relaxations $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ of the form  $(\text {W}^{\text {cv}})$ defined by

$$\begin{aligned} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) := w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{BC,\text{ cv }}_{i,X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})} + w^{D,\text{ cv }}_Z({\mathbf {y}}), \quad \forall ({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z, \end{aligned}$$

has pointwise convergence of order at least $\min \left\{ \underset{i \in Q}{\min } \left\{ \, \min \left\{ \alpha ^C_i, \beta ^{C,\text{ c }}_i,\gamma ^{C}_i \right\} \right\} , \gamma ^{D,\text{ cv }} \right\}$ on Y.

Proof

From Eq. $(\text {W}^{\text {cv}})$, we have for each $({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z$:

$$\begin{aligned} f({\mathbf {x}},{\mathbf {y}}) - f^{\text {cv}}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})&=\left( w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}})} + w^{D}({\mathbf {y}}) \right) \\&\quad \quad \quad - \left( w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{BC,\text {cv}}_{i,X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})} + w^{D,\text {cv}}_Z({\mathbf {y}}) \right) \\&= \displaystyle \sum _{i \in Q}{\left( w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}}) - w^{BC,\text {cv}}_{i,X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \right) } \\&\quad \quad \quad + \left( w^{D}({\mathbf {y}}) - w^{D,\text {cv}}_Z({\mathbf {y}})\right) . \end{aligned}$$

Depending on whether $w^{B,\text {L}}_{i,X(Z)} \ge 0, w^{B,\text {U}}_{i,X(Z)} < 0$, or $0 \in \left( w^{B,\text {L}}_{i,X(Z)}, w^{B,\text {U}}_{i,X(Z)}\right]$ for each $i \in Q$, we have that $\left( w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}}) - w^{BC,\text {cv}}_{i,X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})\right)$ is bounded from above either by

$$\begin{aligned} \left[ w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}}) - \left( {w^{B,\text {U}}_{i,X(Z)} w^{C,\text {cv}}_{i,Z}({\mathbf {y}}) + w^{B}_i({\mathbf {x}}) w^{C,\text {U}}_{i,Z} - w^{B,\text {U}}_{i,X(Z)} w^{C,\text {U}}_{i,Z}}\right) \right] , \end{aligned}$$

or by

$$\begin{aligned} \left[ w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}}) - \left( {w^{B,\text {U}}_{i,X(Z)} w^{C,\text {cc}}_{i,Z}({\mathbf {y}}) + w^{B}_i({\mathbf {x}}) w^{C,\text {U}}_{i,Z} - w^{B,\text {U}}_{i,X(Z)} w^{C,\text {U}}_{i,Z}}\right) \right] \end{aligned}$$

for each $({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z$. Consequently, it is sufficient to show the existence of constants $\tau _1, \tau _2 \ge 0$ such that

and

where $\gamma := \min \left\{ \underset{i \in Q}{\min } \left\{ \, \min \left\{ \alpha ^C_i, \beta ^{C,\text {c}}_i,\gamma ^{C}_i \right\} \right\} , \gamma ^{D,\text {cv}} \right\}$, to prove that $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ converges pointwise to f with order $\gamma$ on Y. The ensuing arguments prove the existence of $\tau _1$; the existence of $\tau _2$ can be proven analogously.

We have $\forall ({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z$:

$$\begin{aligned}&\quad \quad \quad \!\left( \left( w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}{w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}})} + w^{D}({\mathbf {y}}) \right) \right. \nonumber \\&\quad \quad \quad - \left. \left( w^{A}({\mathbf {x}}) + \displaystyle \sum _{i \in Q}\left( {w^{B,\text {U}}_{i,X(Z)} w^{C,\text {cv}}_{i,Z}({\mathbf {y}}) + w^{B}_i({\mathbf {x}}) w^{C,\text {U}}_{i,Z} - w^{B,\text {U}}_{i,X(Z)} w^{C,\text {U}}_{i,Z}}\right) + w^{D,\text {cv}}_Z({\mathbf {y}}) \right) \right) \nonumber \\&\quad = \left( \displaystyle \sum _{i \in Q}{ w^{B}_i({\mathbf {x}}) w^{C}_i({\mathbf {y}}) - \left( {w^{B,\text {U}}_{i,X(Z)} w^{C,\text {cv}}_{i,Z}({\mathbf {y}}) + w^{B}_i({\mathbf {x}}) w^{C,\text {U}}_{i,Z} - w^{B,\text {U}}_{i,X(Z)} w^{C,\text {U}}_{i,Z}}\right) } \right) \nonumber \\&\quad \qquad + \left( w^{D}({\mathbf {y}}) - w^{D,\text {cv}}_Z({\mathbf {y}})\right) . \end{aligned}$$

(7)

Note that can be bounded from above as

with $M^C_i := \tau ^{C,\text {r}}_i w(Y)^{\alpha ^C_i - \beta ^{C,\text {r}}_i} + \tau ^{C,\text {c}}_i w(Y)^{\beta ^{C,\text {c}}_i - \beta ^{C,\text {r}}_i}$ and $\beta ^{C,\text {r}}_i := \min \left\{ \alpha ^C_i, \beta ^{C,\text {c}}_i \right\}$.

The first term in Eq. (7) can be bounded as

where the constants $M^{BC}, \gamma ^{BC}$, and $M^{BC}_i, \gamma ^{BC}_i, \forall i \in Q$, can be computed as

$$\begin{aligned} M^{BC}&:= \displaystyle \sum _{i \in Q}{M^{BC}_i w(Y)^{\gamma ^{BC}_i - \gamma ^{BC}}}, \quad \gamma ^{BC} := \underset{i \in Q}{\min } \, \gamma ^{BC}_i, \quad \gamma ^{BC}_i := \min \left\{ \beta ^{C,\text {r}}_i,\gamma ^{C}_i \right\} , \\ M^{BC}_i&:= \left[ M^{B,1}_i M^C_i w(Y)^{\beta ^{C,\text {r}}_i - \gamma ^{BC}_i} + M^{B,2}_{i} \tau ^{C}_i w(Y)^{\gamma ^{C}_i - \gamma ^{BC}_i} \right] , \\ M^{B,1}_i&:= \underset{{\mathbf {x}}\in X}{\max } \, w^B_i({\mathbf {x}}) - \underset{{\mathbf {x}}\in X}{\min } \, w^B_i({\mathbf {x}}) + \tau ^{B,\text {c}}_i w(X)^{\beta ^{B,\text {c}}_i}, \\ M^{B,2}_{i}&:= \underset{{\mathbf {x}}\in X}{\max } \, w^B_i({\mathbf {x}}) + \tau ^{B,\text {c}}_i w(X)^{\beta ^{B,\text {c}}_i}. \end{aligned}$$

The second term in Eq. (7) is simply bounded as

$$\begin{aligned}&w^{D}({\mathbf {y}}) - w^{D,\text {cv}}_Z({\mathbf {y}}) \le \tau ^{D,\text {cv}} w(Z)^{\gamma ^{D,\text {cv}}}, \quad \forall {\mathbf {y}}\in Z. \end{aligned}$$

(9)

From Eqs. (8) and (9), we have

which proves the existence of $\tau _1$. $\square$

The following remark is in order.

Remark 12

• 1. Suppose $w^C_i$ is Lipschitz continuous on Y for each $i \in Q$. We then have $\alpha ^{C}_i \ge 1, \forall i \in Q$. If $\gamma ^{C}_i \ge 1$ and $\beta ^{C,\text {c}}_i \ge 1, \forall i \in Q$, and $\gamma ^{D,\text {cv}} \ge 1$, we have from Lemma 12 that $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ has at least first-order convergence on Y.

• 2. Let $X = [1,2], Y = [-1,1]$, and $f(x,y) = xy$. For any $[-\varepsilon ,\varepsilon ] =: Z \in {\mathbb {I}}Y$ with $\varepsilon > 0$, consider the scheme of convex relaxations $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ of f in Y with

  $$\begin{aligned} f^{\text {cv}}_{X(Z) \times Z}(x,y) = \max \{y - \varepsilon x + \varepsilon , 2y + \varepsilon x - 2\varepsilon \}. \end{aligned}$$

  The above scheme corresponds to the tightest possible scheme of convex relaxations in the reduced-space, but has at most first-order pointwise convergence on Y. This is in contrast to Theorem 10 in [5] where the scheme of convex envelopes of any twice continuously differentiable function was shown to have pointwise convergence order of at least two on $X \times Y$. Note that if $Q = \emptyset$, the pointwise convergence order of the scheme of convex relaxations $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ is dictated by the pointwise convergence order of the scheme $(w^{D,\text{ cv }}_{Z})_{Z \in {\mathbb {I}}Y}$, and second-order pointwise convergence of $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ can be achieved by using the scheme of convex envelopes of $w^{D}$ if $w^{D}$ is twice continuously differentiable. Also note that Theorem 2 in [5], which states that the pointwise convergence order of a scheme of relaxations of a nonlinear twice continuously differentiable function can be at most two on $X \times Y$, naturally holds over Y as well.

The following result establishes a lower bound on the convergence order of the reduced-space lower bounding scheme proposed in [10] at infeasible points.

Lemma 13

Consider Problem (P), and suppose functions $g_j, j = 1,\ldots ,m_I$, are each of the form (W) and functions $h_k, k = 1,\ldots ,m_E$, are each of the form $(\text {W}_{\text {eq}})$. Let $(g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$, and let $(h^{\text{ cv }}_{k,X(Z) \times Z}, h^{\text{ cc }}_{k,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, k = 1,\ldots , m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in Y with pointwise convergence orders $\gamma _{h,1}> 0, \ldots , \gamma _{h,m_E} > 0$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, there exists ${\bar{\tau }} \ge 0$ such that for every $Z \in {\mathbb {I}}Y$

$$\begin{aligned} d\left( \overline{\begin{bmatrix} {\mathbf {g}}\\ {\mathbf {h}}\end{bmatrix}} (X(Z) \times Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) - d\left( {\mathscr {I}}_{C}(Z), {\mathbb {R}}^{m_I}_{-} \times \{{\mathbf {0}}\} \right) \le {\bar{\tau }} {w(Z)}^{\beta }, \end{aligned}$$

where ${\mathscr {I}}_{C}(Z)$ is defined as

$$\begin{aligned} {\mathscr {I}}_{C}(Z)&:= \Big \{({\mathbf {v}},{\mathbf {w}}) \in {\mathbb {R}}^{m_I} \times {\mathbb {R}}^{m_E} : {\mathbf {v}}= {\mathbf {g}}^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}), {\mathbf {h}}^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \le {\mathbf {w}}\le {\mathbf {h}}^{\text{ cc }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})\\&\text { for some } ({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z \Big \} \end{aligned}$$

and $\beta$ is defined as

$$\begin{aligned} \beta := \min \left\{ \underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text{ cv }}_{g,j}, \underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k} \right\} . \end{aligned}$$

Proof

The proof is similar to that of Lemma 8 and is therefore omitted. $\square$

Definition 15

(Feasible point in the reduced-space) Consider Problem (P). A point ${\mathbf {y}}\in Y$ is said to be feasible (in the reduced-space) if there exists ${\mathbf {x}}\in X$ such that $({\mathbf {x}},{\mathbf {y}})$ is feasible for Problem (P).

The following result establishes first-order convergence of the reduced-space lower bounding scheme proposed in [10] at a feasible point in the reduced-space when first-order pointwise convergent schemes of relaxations are used and the reduced-space dual lower bounding scheme (see Sect. 5.2) is first-order convergent.

Theorem 7

Consider Problem (P). Suppose the functions f and $g_j, j = 1,\ldots ,m_I$, are each of the form (W) and functions $h_k, k = 1,\ldots ,m_E$, are each of the form $\text {W}_{\text {eq}}$). Let ${\mathbf {y}}^{\text{ f }} \in Y$ be a feasible point in the reduced-space for Problem (P). Suppose the reduced-space dual lower bounding scheme (see Sect. 5.2) has convergence of order $\beta _d$ at ${\mathbf {y}}^{\text{ f }}$ and a corresponding scheme of dual variables $\left( \left( \varvec{\mu }^{{\mathbf {y}}^{\text{ f }}}_Z,\varvec{\lambda }^{{\mathbf {y}}^{\text{ f }}}_Z\right) \right) _{Z \in {\mathbb {I}}Y}$ (not necessarily optimal, but which yield $\beta _d$-order convergence at ${\mathbf {y}}^{\text{ f }}$) with and , for some constants ${\bar{\mu }}, {\bar{\lambda }} \ge 0$. Let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, (g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $f, g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_f \ge 1, \gamma ^{\text{ cv }}_{g,1} \ge 1, \ldots , \gamma ^{\text{ cv }}_{g,m_I} \ge 1$ and corresponding constants $\tau ^{\text{ cv }}_f, \tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$. Let $(h^{\text{ cv }}_{k,X(Z) \times Z}, h^{\text{ cc }}_{k,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, k=1,\ldots ,m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in Y with pointwise convergence orders $\gamma _{h,1} \ge 1, \ldots , \gamma _{h,m_E} \ge 1$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ with

is at least $\min \left\{ \min \left\{ \gamma ^{\text{ cv }}_f,\underset{j \in \{1,\ldots ,m_I\}}{\min } \gamma ^{\text{ cv }}_{g,j},\underset{k \in \{1,\ldots ,m_E\}}{\min } \gamma _{h,k}\right\} ,\beta _d\right\}$-order convergent at ${\mathbf {y}}^{\text{ f }}$.

Proof

The proof is similar to that of Theorem 3 and is therefore omitted. $\square$

Definition 16

(Unconstrained point in the reduced-space) Consider Problem (P) with $m_E = 0$. A point ${\mathbf {y}}\in Y$ is said to be unconstrained (in the reduced-space) if there exists $\delta > 0$ such that $\forall {\mathbf {z}}\in Y$ with ${||}{\mathbf {z}}- {\mathbf {y}}{||} < \delta$, we have ${\mathbf {g}}({\mathbf {x}},{\mathbf {z}}) < {\mathbf {0}}, \forall {\mathbf {x}}\in X$.

The next result establishes first-order convergence of the reduced-space lower bounding scheme proposed in [10] at unconstrained points in the reduced-space when a first-order convergent scheme of relaxations of the objective is used by the (convergent) lower bounding scheme.

Proposition 2

Consider Problem (P) with $m_E = 0$. Suppose the functions f and $g_j, j = 1,\ldots ,m_I$, are each of the form (W). Let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ denote a continuous scheme of convex relaxations of f in Y with convergence order $\beta ^{\text{ cv }}_f > 0$ and corresponding constant $\tau ^{\text{ cv }}_f, \text {and}\, (g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$.

Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space, and the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y} := \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}Y}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y} := \left( \overline{{\mathbf {g}}}^{\text{ cv }}_{X(Z) \times Z}(X(Z) \times Z)\right) _{Z \in {\mathbb {I}}Y} \end{aligned}$$

has convergence of order $\beta \in (0,\beta ^{\text{ cv }}_f]$ at ${\mathbf {y}}^{\text{ S }}$. Then the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is at least $\beta ^{\text{ cv }}_f$-order convergent at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is relegated to Appendix A.2 since it is similar to the proof of Corollary 2. $\square$

Note that Proposition 2 can be generalized in a manner similar to Corollary 3 to show that the above lower bounding scheme has $\beta ^{\text{ cv }}_f$-order convergence on a neighborhood of ${\mathbf {y}}^{\text{ S }}$.

The following example shows that the convergence order of the reduced-space lower bounding scheme is dictated by the convergence order, $\beta ^{\text {cv}}_f$, of the scheme $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ under the assumptions of Proposition 2.

Example 12

Let $X = [-1,0.1], Y = [-1,1], m_I = 1$, and $m_E = 0$ with $f(x,y) = x^2 + y^2$ and $g(x,y) = x + y - 0.5$. For any $[y^{\text {L}}, y^{\text {U}}] =: Z \in {\mathbb {I}}Y$, let

$$\begin{aligned} f^{\text{ cv }}_{X(Z) \times Z}(x,y)&= {\left\{ \begin{array}{ll} x^2 - (y^{\text {U}} - y^{\text {L}})^3, &{}\text{ if } 0 \in [y^{\text {L}}, y^{\text {U}}] \\ x^2 + \min \left\{ (y^{\text {L}})^2, (y^{\text {U}})^2 \right\} - (y^{\text {U}} - y^{\text {L}})^3, &{} \text{ otherwise } \end{array}\right. }, \\ g^{\text {cv}}_{X(Z) \times Z}(x,y)&= x+y-0.5. \end{aligned}$$

The scheme $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ has first-order pointwise convergence on Y and third-order convergence on Y, while the scheme $(g^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ has arbitrarily high pointwise convergence order on Y.

Let $y^{\text {L}} = -\varepsilon , y^{\text {U}} = \varepsilon$ with $0 < \varepsilon \le 0.1$. The width of Z is $w(Z) = 2\varepsilon$. The optimal objective value of Problem (P) on Z is 0, while the optimal objective of the lower bounding problem on Z is $-8\varepsilon ^3$. Convergence at the point $y = 0$ is, therefore, at most third-order.

It is natural to wonder at this stage whether the reduced-space lower bounding scheme in [10] has ‘similar convergence properties’ to the full-space lower bounding scheme that was analyzed in Sect. 4.1. Example 16 presents a case where the reduced-space lower bounding scheme in [10] only has first-order convergence at a constrained minimizer that is a KKT point (cf. Example 6, Theorem 2 and Corollary 4). The following example shows that the reduced-space lower bounding scheme in [10] may have a convergence order as low as one even for unconstrained problems with smooth objective functions.

Example 13

Consider the following instance of Problem (P):

$$\begin{aligned} \underset{x,y}{\min }&\,\, 2x^2 + x^2y - xy^2 + (y-0.5)^2 \\ \text {s.t.}&\,\, x \in [-1,1], y \in [0,1]. \end{aligned}$$

The global minimum, $(x^{*},y^{*})$, of the above ‘unconstrained problem’ is $x^{*} = \frac{2\sqrt{21}}{3} - 3, y^{*} = \frac{\sqrt{21}}{3} - 1$ with optimal objective value $\nu ^* = 2(x^*)^2 + (x^*)^2y^* - x^*(y^*)^2 + (y^*-0.5)^2$.

Consider $[y^* - \varepsilon , y^* + \varepsilon ] =: Z \in {\mathbb {I}}Y$ with $\varepsilon \in (0,0.25]$. The reduced-space lower bounding scheme in [10] yields

Note that the point $(x^{\text{ f }}_Z,y^{\text{ f }}_Z,w^{\text{ f }}_{1,Z},w^{\text{ f }}_{2,Z}) = (x^*,y^*,(x^*)^2(y^* - \varepsilon ),-(y^*)^2 - \varepsilon ^2 - x^*(y^*-\varepsilon )^2 + (y^* - \varepsilon )^2)$ is feasible for the lower bounding scheme with objective value $2(x^*)^2 + w^{\text{ f }}_{1,Z} + w^{\text{ f }}_{2,Z} + (y^*-0.5)^2 = \nu ^* + 2x^*y^*\varepsilon - (x^*)^2\varepsilon - x^*\varepsilon ^2 - 2y^*\varepsilon$. Therefore, we have

which establishes that the reduced-space lower bounding scheme in [10] has at most first-order convergence at (the reduced-space minimizer) $y^*$.

Remark 13

Example 13 provides an instance of Problem (P) for which the minimum is unconstrained but the reduced-space lower bounding scheme in [10] is only first-order convergent at the reduced-space minimizer. Therefore, the lower bounding scheme in [10] could face severe clustering for this example [7, 38]. Note that this is in contrast to the full-space lower bounding schemes in Sect. 4 which can achieve at least second-order convergence at the above minimizer and thereby mitigate clustering.

The presence of the terms $x^2 y$ and $-x y^2$ in the objective function in Example 13 plays a crucial role in limiting the convergence order of the reduced-space lower bounding scheme in [10] (see Remark 12). Additionally, the analysis in Example 13 implies that the scheme of relaxations of its objective function has at most first-order Hausdorff convergence on Y. Theorem 10 in Sect. 5.2 implies that the reduced-space lower bounding scheme in [10] has second-order convergence at KKT points when all of the functions in Problem (P) are twice continuously differentiable and separable in ${\mathbf {x}}$ and ${\mathbf {y}}$.

5.2 Duality-based branch-and-bound

Dür and Horst [9, Section 3.3] outlined a reduced-space branch-and-bound algorithm in which they used Lagrangian duality to obtain lower bounds (also see [3, 8]). Dür and Horst [9] prove that when a constraint qualification holds for the reduced-space convex relaxation-based lower bounding scheme with each function in Problem (P) replaced by its (convex) envelope on $X \times Z$ (for each $Z \in {\mathbb {I}}Y$), the subdivision process is exhaustive on Y, and the selection procedure is bound improving, then any accumulation point of the sequence of reduced-space dual lower bounding solutions solves Problem (P).

The reduced-space Lagrangian dual lower bounding problem is in essence the same as its full-space counterpart Problem (D), with the major difference being that we only branch on the Y-space in the reduced-space dual lower bounding scheme to converge. We associate with the reduced-space dual lower bounding scheme, $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$, at a feasible point in the reduced-space ${\mathbf {y}}$, a scheme of dual variables $((\varvec{\mu }^{{\mathbf {y}}}_Z,\varvec{\lambda }^{{\mathbf {y}}}_Z))_{Z \in {\mathbb {I}}Y}$ corresponding to the solution of the scheme of dual lower bounding problems $({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y}$ with ${\mathbf {y}}\in Z$. Dür and Horst [9, Section 4] also outlined classes of problems for which the reduced-space dual lower bounding problem can be solved to optimality. The following result, analogous to Theorem 4, holds.

Theorem 8

Consider Problem (P). Suppose strong duality holds for the reduced-space convex relaxation-based lower bounding scheme for Problem (P) obtained by using the schemes of (convex) envelopes of $f, {\mathbf {g}}$, and ${\mathbf {h}}$. Then, the reduced-space dual lower bounding scheme has at least as high a convergence order as the reduced-space convex relaxation-based lower bounding scheme obtained by using schemes of (convex) envelopes.

Proof

The proof is similar to that of Theorem 4 and is therefore omitted. $\square$

The following result from [9] states that when the constraints in Problem (P) are affine on $X \times Y$, the lower bounding scheme corresponding to schemes of (convex) envelopes provides the same scheme of lower bounds as that obtained using the dual lower bounding scheme.

Lemma 14

Consider Problem (P), and suppose the constraints in Problem (P) are affine in ${\mathbf {x}}$ and ${\mathbf {y}}$, i.e. ${\mathbf {g}}: X \times Y \ni ({\mathbf {x}},{\mathbf {y}}) \mapsto {\mathbf {A}}_g{\mathbf {x}}+ {\mathbf {B}}_g{\mathbf {y}}- {\mathbf {c}}_g$ and ${\mathbf {h}}: X \times Y \ni ({\mathbf {x}},{\mathbf {y}}) \mapsto {\mathbf {A}}_h{\mathbf {x}}+ {\mathbf {B}}_h{\mathbf {y}}- {\mathbf {c}}_h$. In addition, suppose Problem (P) is feasible and strong duality holds for Problem (P) for ${\mathbf {y}}$ restricted to any feasible point in Y. Then the lower bound obtained by solving the dual problem on $Z \in {\mathbb {I}}Y$ is the same as the lower bound obtained by solving the relaxation of the original problem on Z with the objective function f replaced by its convex envelope on $X \times Z$.

Proof

See Proposition 2.1 in [9]. $\square$

Lemma 13 (in conjunction with Lemma 11) guarantees that the reduced-space dual lower bounding scheme has at least first-order convergence at infeasible points for the subclass of Problem (P) for which the algorithm of Epperly and Pistikopoulos is applicable when the functions $w^C_i, \forall i \in Q$, and $w^D$ corresponding to each of the constraints are Lipschitz continuous. The following result shows that first-order convergence at infeasible points is guaranteed for a more general class of problems in the form of Problem (P) even when constraint propagation techniques are not used.

Lemma 15

Let $X \subset {\mathbb {R}}^{n_x}, Y \subset {\mathbb {R}}^{n_y}$ be nonempty compact convex sets, $f: X \times Y \rightarrow {\mathbb {R}}$ be Lipschitz continuous on $X \times Y$ with Lipschitz constant $M_f$. Suppose f is partially convex with respect to ${\mathbf {x}}$, i.e. $f(\cdot ,{\mathbf {y}})$ is convex on X for each ${\mathbf {y}}\in Y$. For any $Z \in {\mathbb {I}}Y$, let $f^{\text{ cv,env }}_{X \times Z}: X \times Z \rightarrow {\mathbb {R}}$ denote the convex envelope of f on $X \times Z$. Assume that for each ${\bar{{\mathbf {x}}}} \in X$, there exists a subgradient ${\mathbf {s}}({\mathbf {y}};{\bar{{\mathbf {x}}}}) \in \partial _{{\mathbf {x}}} f({\mathbf {x}},{\mathbf {y}})|_{{\mathbf {x}}={\bar{{\mathbf {x}}}}}$ such that each $s_i({\mathbf {y}};{\bar{{\mathbf {x}}}}), i = 1,\ldots ,n_x$, is Lipschitz continuous on Y with Lipschitz constant $M_s$. Then, the reduced-space scheme of convex envelopes $\left( f^{\text{ cv,env }}_{X \times Z} \right) _{Z \in {\mathbb {I}}Y}$ has pointwise convergence of order at least one on Y.

Proof

We wish to prove the existence of a constant $\tau \ge 0$ such that

$$\begin{aligned} \max _{({\mathbf {x}},{\mathbf {y}}) \in X \times Z} {|}f({\mathbf {x}},{\mathbf {y}}) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}},{\mathbf {y}}){|} \le \tau w(Z), \quad \forall Z \in {\mathbb {I}}Y. \end{aligned}$$

Note that the existence of the maximum in the above expression follows from the (Lipschitz) continuity of f, Lemma 4, and the compactness of $X \times Y$. Consider $Z \in {\mathbb {I}}Y$, and let $({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) \in {\mathop {\mathop {\mathrm{arg max}}\limits }\limits _{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}} \, {|}f({\mathbf {x}},{\mathbf {y}}) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}},{\mathbf {y}}){|}$. We have

$$\begin{aligned} \max _{({\mathbf {x}},{\mathbf {y}}) \in X \times Z} {|}f({\mathbf {x}},{\mathbf {y}}) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}},{\mathbf {y}}){|}&= f({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}}^*_Z,{\mathbf {y}}^*_Z) \nonumber \\&= \max _{{\mathbf {y}}\in Z} {|}f({\mathbf {x}}^*_Z,{\mathbf {y}}) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}}^*_Z,{\mathbf {y}}){|}. \end{aligned}$$

(10)

Since $f(\cdot ,{\mathbf {y}})$ is convex on X for each ${\mathbf {y}}\in Y$, we have

$$\begin{aligned} f({\mathbf {x}},{\mathbf {y}})&\ge f({\mathbf {x}}^*_Z,{\mathbf {y}}) +{{\mathbf {s}}({\mathbf {y}};{\mathbf {x}}^*_Z)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*_Z) \\&= f({\mathbf {x}}^*_Z,{\mathbf {y}}) + w_Z({\mathbf {x}},{\mathbf {y}}) \\&\ge f^{\text {cv,env}}_{Z}({\mathbf {x}}^*_Z,{\mathbf {y}}) + w^{\text {cv}}_{X \times Z}({\mathbf {x}},{\mathbf {y}}), \quad \forall ({\mathbf {x}},{\mathbf {y}}) \in X \times Z, \end{aligned}$$

where ${\mathbf {s}}({\mathbf {y}};{\mathbf {x}}^*_Z) \in \partial _{{\mathbf {x}}} f({\mathbf {x}},{\mathbf {y}})|_{{\mathbf {x}}={\mathbf {x}}^*_Z}$ is a subgradient of $f(\cdot ,{\mathbf {y}})$ at ${\mathbf {x}}^*_Z$ such that $s_i({\mathbf {y}};{\mathbf {x}}^*_Z), \forall i \in \{1,\ldots ,n_x\}$, is Lipschitz continuous on Z with Lipschitz constant $M_s, f^{\text {cv,env}}_Z({\mathbf {x}}^*_Z,\cdot )$ denotes the convex envelope of $f({\mathbf {x}}^*_Z,\cdot )$ on $Z, w_Z({\mathbf {x}},{\mathbf {y}}) := {{\mathbf {s}}({\mathbf {y}};{\mathbf {x}}^*_Z)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*_Z)$ is a function of the form (W), and $w^{\text {cv}}_{X \times Z}$ is a convex relaxation of $w_Z$ on $X \times Z$ of the form $(\text {W}^{\text {cv}})$ with first-order (pointwise) convergent schemes of estimators of ${\mathbf {s}}({\mathbf {y}};{\mathbf {x}}^*_Z)$ used in its construction.

Since f is Lipschitz continuous on $X \times Y$ and $f^{\text {cv,env}}_Z({\mathbf {x}}^*_Z,\cdot )$ is the convex envelope of $f({\mathbf {x}}^*_Z,\cdot )$ on Z, we have from Lemma 7 that

$$\begin{aligned} \max _{{\mathbf {y}}\in Z} {|}f({\mathbf {x}}^*_Z,{\mathbf {y}}) - f^{\text {cv,env}}_{Z}({\mathbf {x}}^*_Z,{\mathbf {y}}){|} \le M_f w(Z). \end{aligned}$$

Using Lemma 12 with $w^B_i({\mathbf {x}}) = (x_i - x^*_{i,Z}), w^C_i({\mathbf {y}}) = s_i({\mathbf {y}};{\mathbf {x}}^*_Z), w^{B,\text {L}}_{i,X} = {\mathop {\min }\limits _{{\mathbf {x}}\in X}} \, (x_i - x^*_{i,Z}), w^{B,\text {U}}_{i,X} = {\mathop {\max }\limits _{{\mathbf {x}}\in X}} \, (x_i - x^*_{i,Z}), w^{C,\text {cv}}_{i,Z}({\mathbf {y}}) = w^{C,\text {L}}_{i,Z} = {\mathop {\min }\limits _{{\mathbf {y}}\in Z}} \, s_i({\mathbf {y}};{\mathbf {x}}^*_Z)$, and $w^{C,\text {cc}}_{i,Z}({\mathbf {y}}) = w^{C,\text {U}}_{i,Z} = \underset{{\mathbf {y}}\in Z}{\max } \, s_i({\mathbf {y}};{\mathbf {x}}^*_Z)$, we can show the existence of a constant ${\bar{\tau }} \ge 0$ such that

From the above two inequalities, we have

Using $w_Z({\mathbf {x}}^*_Z,{\mathbf {y}}) = 0$, we obtain

Since the convex envelope of f on $X \times Z, f^{\text {cv,env}}_{X \times Z}$, is, by definition, tighter than the convex relaxation $f^{\text {cv,env}}_{Z}({\mathbf {x}}^*_Z,\cdot ) + w^{\text {cv}}_{X \times Z}$ at ${\mathbf {x}}^*_Z$, we have from Eq. (10) that

$$\begin{aligned}&\max _{{\mathbf {y}}\in Z} {|}f({\mathbf {x}}^*_Z,{\mathbf {y}}) - f^{\text {cv,env}}_{X \times Z}({\mathbf {x}}^*_Z,{\mathbf {y}}){|} \le \left( M_f + {\bar{\tau }} \right) w(Z), \end{aligned}$$

which proves the existence of $\tau$. $\square$

Note that the assumptions of Lemma 15 are readily satisfied if f is a Lipschitz continuous function of the form (W) that is composed of continuous functions $w^A, w^{B}_i, \forall i \in Q$, and $w^{D}$ and Lipschitz continuous functions $w^{C}_i, \forall i \in Q$. An instance for which the assumptions of Lemma 15 are not satisfied is $f(x,y) = {|}y{|}{|}x+y+1{|}$ with $X = [-1,1]$ and $Y = [-1,1]$. The following examples provide instances for which the assumptions of Lemma 15 are satisfied, but where the functions involved are not in the form (W).

Example 14

Let $X = [-1,1], Y = [-1,1]$, and $f(x,y) = \exp (xy)$. We have $M_f = \sqrt{2}\exp (1), s(y;x) = y \exp (xy)$, and $M_s = 2\exp (1)$ satisfying the assumptions of Lemma 15.

Example 15

Let $X = [-1,1], Y = [-1,1]$, and $f(x,y) = -{|}y{|}\sqrt{x+y+3}$. We have $M_f = 4, s(y;x) = -\frac{{|}y{|}}{2\sqrt{x+y+3}}$, and $M_s = 1$ satisfying the assumptions of Lemma 15.

The next result shows that the reduced-space dual lower bounding scheme has arbitrarily high convergence order at unconstrained points in the reduced-space.

Proposition 3

Consider Problem (P) with $m_E = 0$. Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space. Furthermore, suppose the reduced-space dual lower bounding scheme has convergence of order $\beta > 0$ at ${\mathbf {y}}^{\text{ S }}$. Then the reduced-space dual lower bounding scheme has arbitrarily high convergence order at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is relegated to Appendix A.3 since it is similar to the proof of Proposition 1. $\square$

The following result establishes first-order convergence of the reduced-space dual lower bounding scheme even in the absence of constraint propagation.

Theorem 9

Consider Problem (P). Suppose $f, g_j, j = 1,\ldots ,m_I$, and $h_k, k = 1,\ldots ,m_E$, are Lipschitz continuous on $X \times Y$ with Lipschitz constants $M_f, M_{g,1}, \ldots , M_{g,m_I}, M_{h,1}, \ldots , M_{h,m_E}$, respectively, and assume that the assumptions of Lemma 15 hold for ${\mathbf {g}}$ and ${\mathbf {h}}$. Assume, in addition, that Problem (P) is feasible, and that strong duality holds for Problem (P) for ${\mathbf {y}}$ restricted to any feasible point in Y. Furthermore, suppose the set of optimal dual variables for Problem (P) restricted to any feasible ${\mathbf {y}}\in Y$ is bounded (with the bound independent of ${\mathbf {y}}$). Then the reduced-space dual lower bounding scheme is at least first-order convergent on Y.

Proof

Lemma 11, 13, and 15 imply that the dual lower bounding scheme is at least first-order convergent at any infeasible point ${\mathbf {y}}\in Y$ with the prefactor independent of ${\mathbf {y}}$ (note that the conclusion of Lemma 13 does not depend on the schemes of relaxations of the constraints being in the form $(\text {W}^{\text {cv}})$).

Define $F({\mathbf {y}},\varvec{\mu },\varvec{\lambda }) := {\mathop {\min }\limits _{{\mathbf {x}}\in X}}\,\, f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {\varvec{\lambda }}^\text{ T } {\mathbf {h}}({\mathbf {x}},{\mathbf {y}})$. We first show that $F(\cdot ,\varvec{\mu },\varvec{\lambda })$ is Lipschitz continuous on Y for any $(\varvec{\mu }, \varvec{\lambda }) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}$. Consider $(\varvec{\mu }, \varvec{\lambda }) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}$ and ${\mathbf {y}}_1, {\mathbf {y}}_2 \in Y$. We have

where Step 2 follows from Lemma 3, and Step 4 follows from the Lipschitz continuity of the functions involved.

Suppose ${\mathscr {F}}(Y) \ne \emptyset$ and $Z \in {\mathbb {I}}Y$ such that $Z \cap {\mathscr {F}}(Y) \ne \emptyset$. Since strong duality holds for Problem (P) with ${\mathbf {y}}$ restricted to any feasible point in Y, Problem (P) can be equivalently expressed on Z as

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) = \underset{{\mathbf {y}}\in Z}{\min }\,\, \underset{(\varvec{\mu }, \varvec{\lambda }) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}}{\sup }\,\, F({\mathbf {y}},\varvec{\mu },\varvec{\lambda }). \end{aligned}$$

By strong duality and $Z \cap {\mathscr {F}}(Y) \ne \emptyset$, there exists a minimizer $({\mathbf {y}}^*_Z,\varvec{\mu }^*_Z,\varvec{\lambda }^*_Z)$ of the above ‘dual form’ of Problem (P) when ${\mathbf {y}}$ is restricted to Z. We have

where ${\bar{{\mathbf {y}}}}_Z \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{{\mathbf {y}}\in Z}} \,\, F({\mathbf {y}},\varvec{\mu }^*_Z,\varvec{\lambda }^*_Z), M_{\infty } := \underset{{\mathbf {y}}\in Y}{\sup } \, \max \left\{ {||}\varvec{\mu }^*({\mathbf {y}}){||}_{\infty }, {||}\varvec{\lambda }^*({\mathbf {y}}){||}_{\infty } \right\}$ is an upper bound on the norm of pairs of optimal dual variables $(\varvec{\mu }^*({\mathbf {y}}),\varvec{\lambda }^*({\mathbf {y}})) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}} \,\, F({\mathbf {y}},\varvec{\mu },\varvec{\lambda })$, and the penultimate step follows from the Lipschitz continuity of $F(\cdot ,\varvec{\mu },\varvec{\lambda })$ on Y. $\square$

The assumption that the set of optimal dual variables for Problem (P) restricted to any feasible ${\mathbf {y}}\in Y$ is bounded can be replaced with the less restrictive assumption that there exists an optimal dual variable pair $(\varvec{\mu }^*({\mathbf {y}}),\varvec{\lambda }^*({\mathbf {y}})) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}} \,\, F({\mathbf {y}},\varvec{\mu },\varvec{\lambda })$ for each ${\mathbf {y}}\in Y$ such that ${\mathop {\sup }\limits _{{\mathbf {y}}\in Y}} \, \max \left\{ {||}\varvec{\mu }^*({\mathbf {y}}){||}_{\infty }, {||}\varvec{\lambda }^*({\mathbf {y}}){||}_{\infty } \right\} \le M_{\infty }$.

A corollary of Theorems 7 and 9 is that first-order convergence is guaranteed for the convex relaxation-based reduced-space lower bounding scheme in [10] when first-order pointwise convergent schemes of relaxations on Y are used in its construction. Instead of proving first-order convergence of the lower bounding scheme in [10] at feasible points under the assumption that schemes of bounded optimal dual variables exist, we show that the reduced-space lower bounding scheme in [10] enjoys first-order convergence at any feasible point in the reduced-space under the (less restrictive) assumption that strong duality holds for Problem (P) with ${\mathbf {y}}$ fixed to the feasible point.

Corollary 5

Consider Problem (P). Suppose the functions f and $g_j, \forall j \in \{1,\ldots ,m_I\}$, are Lipschitz continuous on $X \times Y$ with Lipschitz constants $M_f, M_{g,1},\ldots ,M_{g,m_I}$, respectively, and are each of the form (W). Furthermore, suppose functions $h_k, k = 1,\ldots ,m_E$, are Lipschitz continuous on $X \times Y$ with Lipschitz constants $M_{h,1},\ldots ,M_{h,m_E}$, respectively, and are each of the form $(\text {W}_{\text {eq}})$. Suppose ${\mathbf {y}}^{\text{ f }} \in Y$ is a feasible point in the reduced-space and strong duality holds for Problem (P) when ${\mathbf {y}}$ is fixed to ${\mathbf {y}}^{\text{ f }}$. Let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, (g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $f, g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_f \ge 1, \gamma ^{\text{ cv }}_{g,1} \ge 1, \ldots , \gamma ^{\text{ cv }}_{g,m_I} \ge 1$ and corresponding constants $\tau ^{\text{ cv }}_f, \tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$. Let $(h^{\text{ cv }}_{k,X(Z) \times Z}, h^{\text{ cc }}_{k,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, k=1,\ldots ,m_E$, denote continuous schemes of relaxations of $h_1,\ldots ,h_{m_E}$, respectively, in Y with pointwise convergence orders $\gamma _{h,1} \ge 1, \ldots , \gamma _{h,m_E} \ge 1$ and corresponding constants $\tau _{h,1}, \ldots , \tau _{h,m_E}$. Then, the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ proposed in [10] is at least first-order convergent at ${\mathbf {y}}^{\text{ f }}$.

Proof

Let $\left( \varvec{\mu }^{{\mathbf {y}}^{\text{ f }}},\varvec{\lambda }^{{\mathbf {y}}^{\text{ f }}}\right) \in \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\mathop {\mathrm{arg max}}\limits } \,\, F({\mathbf {y}}^{\text{ f }},\varvec{\mu },\varvec{\lambda })$ be an optimal pair of dual variables for ${\mathbf {y}}$ fixed to ${\mathbf {y}}^{\text{ f }}$ in Problem (P). Suppose $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}^{\text{ f }} \in Z$. Similar to the proof of Theorem 9, we have

$$\begin{aligned}&\quad \quad \left|\min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \sup _{(\varvec{\mu }, \varvec{\lambda }) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}}\min _{({\mathbf {x}},{\mathbf {y}}) \in X \times Z} \left[ f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {\varvec{\lambda }}^\text{ T } {\mathbf {h}}({\mathbf {x}},{\mathbf {y}})\right] \right|\\&\le \, \left|F\left( {\mathbf {y}}^{\text{ f }},\varvec{\mu }^{{\mathbf {y}}^{\text{ f }}},\varvec{\lambda }^{{\mathbf {y}}^{\text{ f }}}\right) - \sup _{(\varvec{\mu }, \varvec{\lambda }) \in {\mathbb {R}}^{m_I}_+ \times {\mathbb {R}}^{m_E}} \,\, \min _{{\mathbf {y}}\in Z} \, F({\mathbf {y}},\varvec{\mu },\varvec{\lambda }) \right|\\&\le \, \left|F\left( {\mathbf {y}}^{\text{ f }},\varvec{\mu }^{{\mathbf {y}}^{\text{ f }}},\varvec{\lambda }^{{\mathbf {y}}^{\text{ f }}}\right) - \min _{{\mathbf {y}}\in Z} \, F\left( {\mathbf {y}},\varvec{\mu }^{{\mathbf {y}}^{\text{ f }}},\varvec{\lambda }^{{\mathbf {y}}^{\text{ f }}}\right) \right|\\&\le \, \tau ^{\text{ f }} w(Z), \end{aligned}$$

for some constant $\tau ^{\text{ f }} \ge 0$. The result then holds as a consequence of Theorem 7 by using , and in Theorem 7. $\square$

The following example shows that the convergence order of the reduced-space dual lower bounding scheme may be as low as one at constrained minima.

Example 16

Consider the following instance of Problem (P):

$$\begin{aligned} \underset{x,y}{\min }&\,\, -xy \\ \text {s.t.}&\,\, x + y \le 1, \\&\,\, x \in [-1,1], y \in [0,1]. \end{aligned}$$

The optimal solution is $(x^*,y^*) = (0.5,0.5)$ with optimal objective value $-0.25$. When the inequality constraint is dualized, the following dual function is obtained:

$$\begin{aligned} q(\mu ) = \underset{x,y}{\min }&\, -xy + \mu \left( x+y-1 \right) \\ \text {s.t.}&\,\, x \in [-1,1], y \in [0,1]. \end{aligned}$$

Consider $[y^{\text {L}},y^{\text {U}}] = [0.5-\varepsilon ,0.5+\varepsilon ] =: Z \in {\mathbb {I}}Y$ with $\varepsilon \in (0,0.5]$. In order to derive the dual function

$$\begin{aligned} q(\mu ) = \underset{y \in [y^{\text {L}},y^{\text {U}}]}{\min _{x \in [-1,1]}} -xy + \mu (x+y-1) \end{aligned}$$

as an explicit function of $\mu$, we partition the domain of $\mu$ to obtain

$$\begin{aligned} q(\mu ) = {\left\{ \begin{array}{ll} (\mu - 1) y^{\text {U}}, &{}\text{ if } \mu \le y^{\text {L}} \\ \min \{(\mu - 1) y^{\text {U}},(\mu +1)y^{\text {L}} - 2\mu \}, &{}\text{ if } y^{\text {L}} \le \mu \le y^{\text {U}} \\ (\mu + 1)y^{\text {L}} - 2\mu , &{} \text{ if } \mu \ge y^{\text {U}} \end{array}\right. } \end{aligned}$$

when the bounds on x are taken to be $[-1,1]$ irrespective of the bounds on y. The dual lower bound can therefore be derived as:

$$\begin{aligned} \underset{\mu \ge 0}{\sup }\,\, q(\mu ) = \displaystyle \frac{(y^{\text {L}}-1)y^{\text {U}}}{1 + 0.5(y^{\text {U}} - y^{\text {L}})}. \end{aligned}$$

Therefore, for $[y^{\text {L}},y^{\text {U}}] = [0.5-\varepsilon ,0.5+\varepsilon ]$, the dual lower bound can be derived as

$$\begin{aligned} \underset{\mu \ge 0}{\sup }\,\, q(\mu ) = \displaystyle \frac{(-0.5-\varepsilon )(0.5+\varepsilon )}{1+\varepsilon } = -\displaystyle \frac{(0.5+\varepsilon )^2}{1+\varepsilon }. \end{aligned}$$

Consequently,

$$\begin{aligned} \underset{(x,y) \in {\mathscr {F}}(Z)}{\min } -xy \,\,-\,\, \underset{\mu \ge 0}{\sup }\,\, q(\mu ) = -0.25 + \displaystyle \frac{(0.5+\varepsilon )^2}{1+\varepsilon } = \displaystyle \frac{0.75\varepsilon + \varepsilon ^2}{1 + \varepsilon } \ge 0.75\varepsilon , \end{aligned}$$

which implies that the dual lower bounding scheme is at most first-order convergent at $y^*$.

Remark 14

Example 16 provides an instance of Problem (P) for which both the reduced-space dual lower bounding scheme [9] and the reduced-space lower bounding scheme in [10] (this follows from Lemma 14) are only first-order convergent at the minimizer. Furthermore, for each $y \in [0,1]$, the reduced-space objective function $v:[0,1] \rightarrow {\mathbb {R}}$ can be derived as

$$\begin{aligned} v(y) = \underset{x}{\min }&\,\, -xy \\ \text {s.t.}&\,\, x + y \le 1, \\&\,\, x \in [-1,1], \end{aligned}$$

which reduces to $v(y) = y^2 - y$. It can be seen that $y^* = 0.5$ is an unconstrained minimum of the reduced-space objective v(y), which implies that at least second-order convergence of the reduced-space lower bounding scheme is typically required at $y^*$ to mitigate clustering [7, 38].

Therefore, neither reduced-space lower bounding scheme can be expected to avoid clustering for this example. Note that this is in contrast to the full-space lower bounding schemes in Sect. 4 which can achieve at least second-order convergence at $(x^*,y^*)$ and thereby mitigate clustering [15].

Note, however, that the use of constraint propagation techniques by reduced-space lower bounding schemes can potentially increase their convergence order as demonstrated by Examples 17 and 18. This demonstrates the importance of constraint propagation techniques in reduced-space lower bounding schemes, which has not been emphasized in [9, 10].

Example 17

Consider the instance of Problem (P) in Example 16 with $Z = [y^{\text {L}},y^{\text {U}}] \subset [0,1], y^{\text {L}} \le 0.5, y^{\text {U}} \ge 0.5$. Suppose we use constraint propagation to derive $X(Z) = [-1,1-y^{\text {L}}]$. The dual function can be derived as

$$\begin{aligned} q(\mu ) = {\left\{ \begin{array}{ll} \mu (y^{\text {U}} - y^{\text {L}}) + y^{\text {U}}(y^{\text {L}} - 1), &{}\text{ if } \mu \le y^{\text {L}} \\ \min \{\mu (y^{\text {U}} - y^{\text {L}}) + y^{\text {U}}(y^{\text {L}} - 1),(\mu +1)y^{\text {L}} - 2\mu \}, &{}\text{ if } y^{\text {L}} \le \mu \le y^{\text {U}} \\ (\mu + 1)y^{\text {L}} - 2\mu , &{} \text{ if } \mu \ge y^{\text {U}} \end{array}\right. }, \end{aligned}$$

which yields the dual lower bound

$$\begin{aligned} \underset{\mu \ge 0}{\sup }\,\, q(\mu ) = \displaystyle \frac{(y^{\text {L}} + y^{\text {U}} - y^{\text {L}}y^{\text {U}})(y^{\text {L}}-2)}{2 + y^{\text {U}} - 2y^{\text {L}}} + y^{\text {L}}. \end{aligned}$$

Consider $y^{\text {L}} = 0.5 - \varepsilon , y^{\text {U}} = 0.5 + \varepsilon$ for some $\varepsilon \in (0,0.5)$. The dual lower bound reduces to

$$\begin{aligned} \underset{\mu \ge 0}{\sup }\,\, q(\mu ) = \displaystyle \frac{-\varepsilon ^3 - 4.5\varepsilon ^2 - 0.75\varepsilon - 0.375}{1.5 + 3\varepsilon }. \end{aligned}$$

Consequently,

for some constant $\tau > 0$ (where we may assume that the above inequality holds for $\varepsilon = 0.5$ as well).

Consider any nondegenerate interval $Z = [y^{\text {L}},y^{\text {U}}] \subset [0,1]$ with $0.5 \in Z$ and construct ${\bar{Z}} \supset Z$ such that ${\bar{Z}} = [y^* - \varepsilon , y^* + \varepsilon ]$ with $\varepsilon = \max \{ y^{\text {U}} - y^*, y^* - y^{\text {L}} \}$. We have

$$\begin{aligned}&\quad \underset{(x,y) \in {\mathscr {F}}(Z)}{\min } -xy \,\, - \,\, \sup _{\mu \ge 0}\min _{(x,y) \in X(Z) \times Z} \left[ -xy + \mu g(x,y)\right] \\&\le \underset{(x,y) \in {\mathscr {F}}({\bar{Z}})}{\min } -xy \,\, - \,\, \sup _{\mu \ge 0}\min _{(x,y) \in X({\bar{Z}}) \times {\bar{Z}}} \left[ -xy + \mu g(x,y)\right] \\&\le \tau \varepsilon ^2 \\&\le \tau w(Z)^2, \end{aligned}$$

which implies that the reduced-space dual lower bounding scheme with constraint propagation is second-order convergent at $y^*$.

Fig. 1

(a) Comparison of the number of branch-and-bound iterations between the different lower bounding schemes considered in this work for different absolute termination tolerances for Example 16. The solid line indicates the number of iterations of the full-space lower bounding schemes, the dashed line indicates the number of iterations of the reduced-space lower bounding schemes without constraint propagation, and the dash-dotted line indicates the number of iterations of the reduced-space lower bounding schemes with constraint propagation. (b) Comparison of the number of branch-and-bound iterations of the reduced-space lower bounding schemes without constraint propagation with the predictions from the cluster problem model for different absolute termination tolerances for Example 16. The dashed line indicates the number of iterations of the reduced-space lower bounding schemes without constraint propagation, and the dash-dotted line indicates the predicted number of iterations from the cluster problem model

Figure 1 illustrates the performance of the lower bounding schemes considered in this work in a bare-bones branch-and-bound framework for Examples 16 and 17. The branch-and-bound framework was implemented in MATLAB^®, and the (convex) lower bounding problems were solved using the CVX [12] package. The lowest lower bound node selection rule and the interval bisection branching rule (which bisects the domain of the variable whose interval has the largest width) were used by the branch-and-bound algorithm. Since Example 16 is not particularly challenging, it is assumed that a local solver finds its global solution at the root node of the branch-and-bound tree (i.e., the upper bound is set to the optimal objective value at the root node). In addition, the bounds on x and y were modified to $\left[ -1,1-\frac{\sqrt{3}}{100}\right]$ and $\left[ \frac{\sqrt{2}}{100},1\right]$, respectively, to prevent the full-space lower bounding schemes from branching at the optimal solution and (fortuitously) converging early (this modification enables a truer characterization of the convergence rates of the lower bounding schemes).

Figure 1a plots the number of iterations of the branch-and-bound algorithm versus the (absolute) termination tolerance for the full-space lower bounding schemes, the reduced-space lower bounding schemes without constraint propagation (see Example 16), and the reduced-space lower bounding schemes with constraint propagation (see Example 17). Note that both full-space (reduced-space) lower bounding schemes considered in this work result in the same lower bound for this problem (see Lemma 14). It can be seen that the full-space lower bounding schemes and the reduced-space lower bounding schemes with constraint propagation perform significantly better than the reduced-space lower bounding schemes without constraint propagation for small tolerances, and that they exhibit a much more favorable scaling with a decrease in the termination tolerance as well. Furthermore, the advantage of using constraint propagation techniques in the reduced-space lower bounding schemes is evident, and its use puts the reduced-space lower bounding schemes at an advantage compared to the full-space lower bounding schemes. Figure 1b illustrates that the dependence of the number of iterations on the termination tolerance for the reduced-space lower bounding schemes without constraint propagation is in good agreement with their associated cluster problem models (see [15, Theorem 3] for the details of the cluster problem model). Note that the prediction of the number of iterations from the cluster problem model in Fig. 1b is obtained by fitting the prefactor in the cluster model (i.e., intercept of the line in the plot; the slope of the line is determined by the cluster model using the estimate of the convergence order of the lower bounding scheme obtained from this work) against the number of iterations obtained from the computational experiments. It is worth mentioning at this stage that only basic versions of the lower bounding schemes considered in this work have been used to generate Fig. 1; the performance of the lower bounding schemes may be significantly different if they are implemented within a state-of-the-art branch-and-bound framework that solves additional subproblems to speed up their convergence.

The following example illustrates another instance of Problem (P) for which constraint propagation plays a crucial rule in boosting the convergence order of the convex relaxation-based reduced-space lower bounding scheme in [10].

Example 18

Consider the following instance of Problem (P):

$$\begin{aligned} \underset{x,y}{\min }&\,\, \exp (x) - 4x + y \\ \text {s.t.}&\,\, x^2 + x \exp (3-y) \le 10, \\&\,\, x \in [0.5,2], y \in [-1,1]. \end{aligned}$$

The optimal solution of the above problem, which is a constrained minimum, is $(x^*,y^*) \approx (1.029,0.838)$ $\Bigg ($the ‘exact’ optimal solution can be determined as follows: $x^*$ is the (unique real) root of the function $(4 - \exp (x))(10x - x^3) - x^2 - 10$ in [0.5, 2], and $y^* := 3 - \ln \left( \frac{10 - \left( x^*\right) ^2}{x^*}\right) \Bigg )$ with optimal objective value approximately equal to $-0.480$. The reader can verify that $(x^*,y^*,\mu ^*)$ is a KKT point for Problem (P), where $\mu ^* := \frac{1}{x^* \exp (3-y^*)}$. This implies, in particular, that the full-space lower bounding schemes in Sect. 4 can be designed to be at least second-order convergent at $(x^*,y^*)$ (see Theorem 5 and Corollary 4). The reader can also verify that second-order convergence of the lower bounding scheme may be sufficient to mitigate the cluster problem around $(x^*,y^*)$ [15].

Since all of the functions in the above instance of Problem (P) are in the form (W), both the reduced-space lower bounding schemes considered in this section can be employed to solve it. The ensuing arguments show that the convex relaxation-based reduced-space lower bounding scheme in [10] is only first-order convergent at $y^*$ when constraint propagation techniques are not used.

Consider $[y^{\text{ L }}, y^{\text{ U }}] := [y^* - \varepsilon , y^* + \varepsilon ] =: Z \in {\mathbb {I}}Y$ with $0 < \varepsilon \le 0.1$. The reduced-space lower bounding scheme in [10] yields

$$\begin{aligned} {\mathscr {O}}(Z) = \underset{x,y}{\min }&\,\, \exp (x) - 4x + y \\ \text {s.t.}&\,\, x^2 + 2 \exp (3-y) + x \exp (3 - y^{\text{ L }}) - 2 \exp (3 - y^{\text{ L }}) \le 10, \\&\,\, x^2 + 0.5 \exp (3-y) + x \exp (3 - y^{\text{ U }}) - 0.5 \exp (3 - y^{\text{ U }}) \le 10, \\&\,\, x \in [0.5,2], y \in [y^{\text{ L }}, y^{\text{ U }}]. \end{aligned}$$

Note that the point

$$\begin{aligned} (x^{\text{ f }}_Z,y^{\text{ f }}_Z) := \left( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } - \exp (3 - y^{\text{ U }})}{2}, y^* \right) \end{aligned}$$

is feasible for the above lower bounding scheme with objective value $\exp (x^{\text{ f }}_Z) - 4x^{\text{ f }}_Z + y^{\text{ f }}_Z$. Furthermore,

$$\begin{aligned} x^{\text{ f }}_Z - x^*&= \, \Bigg ( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } - \exp (3 - y^{\text{ U }})}{2} \\&\qquad \,\, - \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} - \exp (3 - y^*)}{2} \Bigg ) \\&\ge \, 0.2\varepsilon + o\left( \varepsilon \right) , \end{aligned}$$

where the details pertaining to the derivation of the above inequality are presented in Appendix A.4. Therefore, we have

for $\varepsilon \ll 1$, which establishes that the reduced-space lower bounding scheme in [10] has at most first-order convergence at $y^*$ (note that first-order convergence of the scheme follows from Corollary 5). This is rather unfortunate because $y^*$ can be seen to be an unconstrained minimizer of the reduced-space objective function $v : [-1,1] \rightarrow {\mathbb {R}}$, which can be derived (around $y = y^*$) to be

$$\begin{aligned} v(y) = \exp \left( x^*(y) \right) - 4x^*(y) + y, \quad \forall y \in [0.5,1], \end{aligned}$$

where $x^*: [0.5,1] \ni y \longmapsto [0.5,2]$ is now given by

$$\begin{aligned} x^*(y) := \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} - \exp (3-y)}{2}, \end{aligned}$$

which implies that at least second-order convergence of the reduced-space lower bounding scheme at $y^*$ is typically required to mitigate clustering [7, 38].

We next show that when constraint propagation is used to infer (exact) bounds for x on Z, second-order convergence of the reduced-space lower bounding scheme in [10] can be achieved. Note that for $[y^{\text{ L }}, y^{\text{ U }}] := [y^* - \varepsilon , y^* + \varepsilon ] =: Z \in {\mathbb {I}}Y$ with $0 < \varepsilon \le 0.1$, the best possible (interval) bounds that can be obtained for x are $x \in X(Z) := [x^{\text{ L }}_Z,x^{\text{ U }}_Z]$ with

$$\begin{aligned} x^{\text{ L }}_Z = 0.5, \quad x^{\text{ U }}_Z = \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40} - \exp (3 - y^{\text{ U }})}{2}. \end{aligned}$$

The reduced-space lower bounding scheme in [10] with constraint propagation yields

By noticing that the first constraint in the above relaxation of Problem (P) is always active at the solution of the relaxed problem, we can reformulate the reduced-space lower bounding problem as

$$\begin{aligned} {\mathscr {O}}(Z) = \underset{y \in [y^{\text{ L }}, y^{\text{ U }}]}{\min }&\,\exp \left( {\bar{x}}_Z(y) \right) - 4\left( {\bar{x}}_Z(y) \right) + y, \end{aligned}$$

where ${\bar{x}}_Z: Z \ni y \longmapsto [0.5,x^{\text{ U }}_Z]$ is given by

$$\begin{aligned} {\bar{x}}_Z(y) := \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } - \exp (3 - y^{\text{ L }})}{2}. \end{aligned}$$

We have (see Appendix A.4 for details)

$$\begin{aligned}&{\bar{x}}_Z(y) - x^*(y) \\&\quad = \, \displaystyle \frac{ \left( \exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z \right) \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \\&\quad \quad \quad - \displaystyle \frac{\left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2} \\&\quad = \displaystyle \frac{ \alpha \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) }, \end{aligned}$$

with $0 \le \alpha \le {\hat{\tau }} \varepsilon + O(\varepsilon ^2)$ for some ${\hat{\tau }} \ge 0$. Consequently, we have $\forall y \in Z$ that

$$\begin{aligned}&\qquad {\bar{x}}_Z(y) - x^*(y) \\&\le \, \displaystyle \frac{ \left( {\hat{\tau }} \varepsilon + O(\varepsilon ^2) \right) \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \\&\le \, {\bar{\tau }} \varepsilon ^2 + O(\varepsilon ^3) \end{aligned}$$

for some ${\bar{\tau }} \ge 0$, since $\exp (3 - y^{\text{ L }}) - \exp (3 - y)$ is $O(\varepsilon )$. Note that ${\bar{x}}_Z(y) \ge x^*(y), \forall y \in Z, \forall Z$. Therefore, on intervals $[y^* - \varepsilon , y^* + \varepsilon ] =: Z \in {\mathbb {I}}Y$ with $0 < \varepsilon \le 0.1$, we have

for $\varepsilon \ll 1$, which establishes second-order convergence of the scheme at $y^*$ when restricted to symmetric intervals around $y^*$.

Consider any nondegenerate interval $Z = [y^{\text {L}},y^{\text {U}}] \in {\mathbb {I}}Y$ with $y^* \in Z$ and $w(Z) \le 0.1$, and construct ${\bar{Z}} \supset Z$ such that ${\bar{Z}} = [y^* - \varepsilon , y^* + \varepsilon ]$ with $\varepsilon = \max \{ y^{\text {U}} - y^*, y^* - y^{\text {L}} \}$. We have

$$\begin{aligned}&\quad \min _{(x,y) \in {\mathscr {F}}(Z)}f(x,y) \,\, - \min _{(x,y) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_{X(Z) \times Z}(x,y) \\&\le \underset{(x,y) \in {\mathscr {F}}({\bar{Z}})}{\min } f(x,y) \,\, - \min _{(x,y) \in {\mathscr {F}}^{\text{ cv }}({\bar{Z}})} f^{\text{ cv }}_{X(Z) \times Z}(x,y) \\&\le {\bar{\tau }} w({\bar{Z}})^2 \\&\le 4 {\bar{\tau }} w(Z)^2, \end{aligned}$$

which implies that the convex relaxation-based reduced-space dual lower bounding scheme with constraint propagation is second-order convergent at $y^*$.

Finally, we show that the reduced-space dual lower bounding scheme in [9] has at least second-order convergence at $y^*$ even when constraint propagation is not used to infer bounds on x. Consider $[y^{\text{ L }}, y^{\text{ U }}] =: Z \in {\mathbb {I}}Y$ with $w(Z) \le 0.1$. The feasible region of the original problem on Z is given by

$$\begin{aligned} {\mathscr {F}}(Z) = \left\{ (x,y) \in [0.5,2] \times [y^{\text{ L }}, y^{\text{ U }}] : x \le x^*(y) \right\} . \end{aligned}$$

The convex hull of the feasible region on Z is given by

$$\begin{aligned} \text {conv}({\mathscr {F}}(Z)) = \left\{ (x,y) \in [0.5,2] \times [y^{\text{ L }}, y^{\text{ U }}] : x \le x^{*,\text{ cc }}_Z(y) \right\} , \end{aligned}$$

where $x^{*,\text{ cc }}_Z$ denotes the concave envelope of $x^*$ on Z. It is not hard to see that $d_H \left( {\mathscr {F}}(Z),\text {conv}({\mathscr {F}}(Z)) \right) \le {\tilde{\tau }} w(Z)^2$ for some ${\tilde{\tau }} \ge 0$ (this partly follows from the fact that $x^*$ is twice continuously differentiable on $[y^*-0.1,y^*+0.1]$ and the fact that $\left( x^{*,\text{ cc }}_Z \right) _{Z \in {\mathbb {I}}Y}$ converges pointwise to $x^*$ with order at least two on $[y^*-0.1,y^*+0.1]$). Since the dual lower bounding scheme produces a lower bound that is at least as tight as any convex relaxation-based scheme, we have

where $({\tilde{x}}_Z,{\tilde{y}}_Z) \in {\mathop {\mathop {\mathrm{arg min}}\limits }\limits _{(x,y) \in \text {conv}({\mathscr {F}}(Z))}} f(x,y), ({\hat{x}}_Z,{\hat{y}}_Z) \in {\mathscr {F}}(Z)$ is chosen such that ${||}({\hat{x}}_Z,{\hat{y}}_Z) - ({\tilde{x}}_Z,{\tilde{y}}_Z){||} \le {\tilde{\tau }} w(Z)^2$, and $M_f$ denotes the Lipschitz constant of f on $[0.5,2] \times [-1,1]$. Since the Lagrangian dual-based reduced-space lower bounding scheme is at least first-order convergent at $y^*$ from Theorem 9, it is at least second-order convergent at $y^*$ by analogy to Lemma 5.

Fig. 2

(a) Comparison of the number of branch-and-bound iterations between the full-space and reduced-space convex relaxation-based lower bounding schemes considered in this work for different absolute termination tolerances for Example 18. The solid line indicates the number of iterations of the convex relaxation-based full-space lower bounding scheme, the dashed line indicates the number of iterations of the convex relaxation-based reduced-space lower bounding scheme without constraint propagation, and the dash-dotted line indicates the number of iterations of the convex relaxation-based reduced-space lower bounding scheme with constraint propagation. (b) Comparison of the number of branch-and-bound iterations of the convex relaxation-based reduced-space lower bounding scheme without constraint propagation with the predictions from the cluster problem model for different absolute termination tolerances for Example 18. The dashed line indicates the number of iterations of the convex relaxation-based reduced-space lower bounding scheme without constraint propagation, and the dash-dotted line indicates the predicted number of iterations from the cluster problem model

Figure 2 illustrates the performance of the convex relaxation-based full-space and reduced-space lower bounding schemes in the bare-bones branch-and-bound implementation for Example 18 (note that we do not consider the Lagrangian dual-based full-space and reduced-space lower bounding schemes for the numerical experiments for this example because we do not have closed-form expressions for the lower bounds obtained using those schemes). Once again, the convex lower bounding problems were solved using the CVX [12] package, and the lowest lower bound node selection rule and the interval bisection branching rule were used by the branch-and-bound algorithm. Since Example 18 is not particularly challenging, we assume that a local solver finds its global solution at the root node of the branch-and-bound tree (i.e., the upper bound is set to the optimal objective value of the problem at the root node).

Figure 2a plots the number of iterations of the branch-and-bound algorithm versus the (absolute) termination tolerance for the full-space convex relaxation-based lower bounding scheme, the reduced-space convex relaxation-based lower bounding scheme without constraint propagation, and the reduced-space convex relaxation-based lower bounding scheme with constraint propagation. It can be seen that the full-space lower bounding scheme and the reduced-space lower bounding scheme with constraint propagation perform significantly better (for small tolerances) and exhibit a much more favorable scaling with a decrease in the termination tolerance compared to the reduced-space lower bounding scheme without constraint propagation. Furthermore, there is a clear advantage in using constraint propagation techniques in the reduced-space lower bounding scheme, and its use makes the performance of the reduced-space lower bounding scheme superior to that of the full-space lower bounding scheme for this example. Figure 2b shows that the number of iterations versus the termination tolerance for the reduced-space lower bounding scheme without constraint propagation closely follows the prediction from its associated cluster problem model (see [15] for the details of the cluster problem model). Note, once again, that the prediction of the number of iterations from the cluster problem model in Fig. 2b is obtained by fitting the prefactor in the cluster model against the number of iterations obtained from the computational experiments. We wish to reiterate that only basic versions of the convex relaxation-based lower bounding schemes have been used to generate Fig. 2; the performance of the lower bounding schemes may be significantly different if they are implemented within a state-of-the-art branch-and-bound framework that solves additional subproblems to speed up their convergence.

The following result shows that the reduced-space dual lower bounding scheme is second-order convergent at KKT points even in the absence of constraint propagation when all of the functions in Problem (P) are twice continuously differentiable and separable in ${\mathbf {x}}$ and ${\mathbf {y}}$.

Theorem 10

Consider Problem (P), and suppose $f, g_j, j = 1,\ldots ,m_I$, and $h_k, k = 1,\ldots ,m_E$, are separable in ${\mathbf {x}}$ and ${\mathbf {y}}$. Suppose $\text{ int }(X \times Y)$ is nonempty, and $f, {\mathbf {g}}$, and ${\mathbf {h}}$ are twice continuously differentiable on $\text{ int }(X \times Y)$. Furthermore, suppose there exists $({\mathbf {x}}^*,{\mathbf {y}}^*) \in \text{ int }(X \times Y), \varvec{\mu }^* \in {\mathbb {R}}^{m_I}_+, \varvec{\lambda }^* \in {\mathbb {R}}^{m_E}$ such that $({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is a KKT point for Problem (P). The reduced-space dual lower bounding scheme is at least second-order convergent at ${\mathbf {y}}^*$.

Proof

Let $L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) := f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}}) + {\varvec{\lambda }}^\text{ T } {\mathbf {h}}({\mathbf {x}},{\mathbf {y}})$ denote the Lagrangian of Problem (P). Since we are concerned about the convergence order at the reduced-space feasible point ${\mathbf {y}}^*$, it suffices to show the existence of $\tau \ge 0$ such that for every $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}^* \in Z$,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) \le \tau {w(Z)}^2. \end{aligned}$$

We have

$$\begin{aligned} \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda })&\ge \underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu }^*,\varvec{\lambda }^*) \\&\ge \underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } \left[ L({\mathbf {x}}^*,{\mathbf {y}},\varvec{\mu }^*,\varvec{\lambda }^*) + {\nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}},\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*)\right] \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } \left[ L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) + {\nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*)\right. \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \left. +\, {\left( \nabla _{{\mathbf {y}}} \left( {\nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*) \right) \right) }^\text{ T } ({\mathbf {y}}- {\mathbf {y}}^*) \right. \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \left. +\, {\nabla _{{\mathbf {y}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {y}}- {\mathbf {y}}^*) - O(w(Z)^2) \right] \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } \left[ f({\mathbf {x}}^*,{\mathbf {y}}^*) - O(w(Z)^2) \right] \\&\ge f({\mathbf {x}}^*,{\mathbf {y}}^*) - O(w(Z)^2). \end{aligned}$$

Note that we have used the fact that L is partly convex with respect to ${\mathbf {x}}$ in Step 2, that $L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = f({\mathbf {x}}^*,{\mathbf {y}}^*), \nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = {\mathbf {0}}, \nabla _{{\mathbf {y}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*) = {\mathbf {0}}$ in Step 4 since it is assumed that $({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is a KKT point for Problem (P), and that $\nabla _{{\mathbf {y}}} \Big ({\nabla _{{\mathbf {x}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)}^\text{ T } ({\mathbf {x}}- {\mathbf {x}}^*) \Big ) = {\mathbf {0}}$ in Step 4 by virtue of the assumption that the Lagrangian is separable in ${\mathbf {x}}$ and ${\mathbf {y}}$. Therefore,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}, \varvec{\lambda }}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in X \times Z}{\min } L({\mathbf {x}},{\mathbf {y}},\varvec{\mu },\varvec{\lambda }) \le O(w(Z)^2), \end{aligned}$$

which establishes the existence of $\tau$ for all $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}^* \in Z$ by analogy to Lemma 5. $\square$

Note that the assumption of separability in Theorem 10 can be replaced with the weaker assumption that $\nabla ^2_{{\mathbf {x}}{\mathbf {y}}} L({\mathbf {x}}^*,{\mathbf {y}}^*,\varvec{\mu }^*,\varvec{\lambda }^*)$ is the zero matrix.

Remark 15

Similar to Corollary 5, it can be shown that the reduced-space lower bounding scheme in [10] has second-order convergence at KKT points even in the absence of constraint propagation when all of the functions in Problem (P) are separable in ${\mathbf {x}}$ and ${\mathbf {y}}$ and second-order pointwise convergent schemes of relaxations are used. Furthermore, under the above assumption of separability, the reduced-space lower bounding schemes in [10] and [9] can be shown to possess second-order convergence at infeasible points and unconstrained points in the reduced-space under suitable assumptions on the lower bounding schemes (see Remark 12). Consequently, the convergence properties of the reduced-space lower bounding schemes considered in this section are similar to their counterpart full-space lower bounding schemes in Sect. 4 when all of the functions in Problem (P) are twice continuously differentiable and separable in ${\mathbf {x}}$ and ${\mathbf {y}}$. Example 11 provides an instance wherein the convergence order is exactly two at ${\mathbf {y}}^*$ under the assumptions of Theorem 10.

6 Conclusion

A definition of convergence order for constrained problems has been introduced. The definition reduces to previously developed notions of convergence order for the case of unconstrained problems. An analysis of the convergence order of some full-space and reduced-space branch-and-bound algorithms has been performed.

It has been shown that convex relaxation-based full-space lower bounding schemes enjoy first-order convergence under mild assumptions and second-order convergence at KKT points when second-order pointwise convergent schemes of relaxations of the objective and the constraints are used. Furthermore, the importance of a sufficiently high convergence order at nearly-feasible points has been demonstrated. Lagrangian dual-based full-space lower bounding schemes have been shown to have at least as large a convergence order as convex relaxation-based lower bounding schemes. In addition, it has been shown that Lagrangian dual-based lower bounding schemes where the dual function is not exactly optimized still enjoy first-order convergence.

The convergence order of the reduced-space convex relaxation-based lower bounding scheme of Epperly and Pistikopoulos has been investigated, and it has been shown that the scheme enjoys first-order convergence under certain assumptions. However, their scheme can have as low as first-order convergence even at unconstrained points which can lead to clustering. It has also been shown that the reduced-space dual lower bounding scheme enjoys first-order convergence and that its convergence order may be as low as one for constrained problems. In that regard, the importance of constraint propagation in boosting the convergence order of reduced-space lower bounding schemes has been demonstrated. Furthermore, it has been shown that when all of the functions in Problem (P) are twice continuously differentiable and separable in ${\mathbf {x}}$ and ${\mathbf {y}}$, the above reduced-space lower bounding schemes can achieve second-order convergence at KKT points, at unconstrained points in the reduced-space, and at infeasible points.

Future work involves determining whether full-space lower bounding schemes can achieve second-order convergence on a neighborhood of constrained minima that are KKT points (such a result may be required to mitigate the cluster problem at such constrained minima - see [15, Proposition 2], for instance), analyzing the convergence orders of some other widely-applicable reduced-space lower bounding schemes in the literature (see, for example, [32]), and determining sufficient conditions on the constraint propagation scheme to ensure second-order convergence of reduced-space lower bounding schemes at constrained minima that satisfy certain regularity conditions.

Proofs

1.1 Proof of Proposition 1

Proposition 1

Consider Problem (P) with $m_E = 0$. Suppose f and $g_j, \forall j \in \{1,\ldots ,m_I\}$, are Lipschitz continuous on $X \times Y$. Furthermore, suppose $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in X \times Y$ such that ${\mathbf {g}}({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) < {\mathbf {0}}$ (i.e. $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ is a Slater point). The dual lower bounding scheme has arbitrarily high convergence order at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Proof

The arguments below are closely related to the proof of Corollary 2.

Since we wish to prove that the dual lower bounding scheme has arbitrarily high convergence order at the feasible point $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$, it suffices to show that for each $\beta > 0$, there exists $\tau \ge 0, \delta > 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in Z$ and $w(Z) \le \delta$,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] \le \tau {w(Z)}^{\beta }, \end{aligned}$$

and the desired result follows by analogy to Lemma 5 by observing that the dual lower bounding scheme is at least first-order convergent at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Let $g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) = -\varepsilon _j < 0, \forall j \in \{1,\ldots ,m_I\}$. Since $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$, there exists $\delta _j > 0, \forall j \in \{1,\ldots ,m_I\}$, such that ${||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta _j$ implies ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$ (see Lemma 2).

Define $\delta := {\mathop {\min }\limits _{j \in \{1,\ldots ,m_I\}}}{\delta _j}$, and note that $\delta > 0$. Consider $Z \in {\mathbb {I}}(X \times Y)$ such that $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in Z$ and $w(Z) \le \delta$. For each $({\mathbf {x}},{\mathbf {y}}) \in Z, j \in \{1,\ldots ,m_I\}$ we have ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$. Therefore, for each $j \in \{1,\ldots ,m_I\}, g_j({\mathbf {x}},{\mathbf {y}})< -\frac{\varepsilon _j}{2} < 0, \,\forall ({\mathbf {x}},{\mathbf {y}}) \in Z$. Consequently,

$$\begin{aligned} \underset{\varvec{\mu }\ge {\mathbf {0}}}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } {\left[ f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] }&\ge \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } f({\mathbf {x}},{\mathbf {y}}) \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}{\min } f({\mathbf {x}},{\mathbf {y}}) \end{aligned}$$

since Problem (P) is effectively unconstrained over the small intervals Z around $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$, which implies $\tau = 0$ and $\delta = \underset{j \in \{1,\ldots ,m_I\}}{\min }{\delta _j}$ satisfy the requirements. $\square$

1.2 Proof of Proposition 2

Proposition 2

Consider Problem (P) with $m_E = 0$. Suppose the functions f and $g_j, j = 1,\ldots ,m_I$, are each of the form (W). Let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ denote a continuous scheme of convex relaxations of f in Y with convergence order $\beta ^{\text{ cv }}_f > 0$ and corresponding constant $\tau ^{\text{ cv }}_f, (g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$.

Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space, and the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y} := \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}Y}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y} := \left( \overline{{\mathbf {g}}}^{\text{ cv }}_{X(Z) \times Z}(X(Z) \times Z)\right) _{Z \in {\mathbb {I}}Y} \end{aligned}$$

has convergence of order $\beta \in (0,\beta ^{\text{ cv }}_f]$ at ${\mathbf {y}}^{\text{ S }}$. Then the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is at least $\beta ^{\text{ cv }}_f$-order convergent at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is similar to the proof of Corollary 2.

Since ${\mathbf {y}}^{\text{ S }}$ is an unconstrained point in the reduced-space and $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$ by virtue of Assumption 1, $\exists \delta > 0$ such that $\forall {\mathbf {z}}\in Y$ with ${||}{\mathbf {z}}- {\mathbf {y}}^{\text{ S }}{||}_{\infty } \le \delta$ (see Lemma 2), we have ${\mathbf {g}}({\mathbf {x}},{\mathbf {z}}) < {\mathbf {0}}, \forall {\mathbf {x}}\in X$.

Consider $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}^{\text{ S }} \in Z$ and $w(Z) \le \delta$. We have $\overline{{\mathbf {g}}}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$ and $\overline{{\mathbf {g}}}^{\text {cv}}_{X(Z) \times Z}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$. Consequently,

$$\begin{aligned}&\quad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \\&= \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \\&\le \tau ^{\text {cv}}_f w(Z)^{\beta ^{\text {cv}}_f}. \end{aligned}$$

The desired result follows by analogy to Lemma 5 based on the assumption that $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is at least $\beta$-order convergent at ${\mathbf {y}}^{\text{ S }}$. $\square$

1.3 Proof of Proposition 3

Proposition 3

Consider Problem (P) with $m_E = 0$. Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space. Furthermore, suppose the reduced-space dual lower bounding scheme has convergence of order $\beta > 0$ at ${\mathbf {y}}^{\text{ S }}$. Then the reduced-space dual lower bounding scheme has arbitrarily high convergence order at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is closely related to the proof of Proposition 1.

Since ${\mathbf {y}}^{\text{ S }}$ is an unconstrained point in the reduced-space and $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$ by virtue of Assumption 1, there exists $\delta > 0$ such that $\forall {\mathbf {z}}\in Y$ satisfying ${||}{\mathbf {z}}- {\mathbf {y}}^{\text{ S }}{||}_{\infty } \le \delta$ (see Lemma 2), we have ${\mathbf {g}}({\mathbf {x}},{\mathbf {z}}) < 0, \forall {\mathbf {x}}\in X$.

Consider $Z \in {\mathbb {I}}Y$ with $w(Z) \le \delta$. Since $\overline{{\mathbf {g}}}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$, Problem (P) can be reformulated as

$$\begin{aligned} \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}{\min } f({\mathbf {x}},{\mathbf {y}}) = \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f({\mathbf {x}},{\mathbf {y}}). \end{aligned}$$

The dual lower bound can be bounded from below as

$$\begin{aligned} \sup _{\varvec{\mu }\ge {\mathbf {0}}}\min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} \left[ f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] \ge \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f({\mathbf {x}},{\mathbf {y}}). \end{aligned}$$

The desired result follows by analogy to Lemma 5 and the assumption that the dual lower bounding scheme is at least $\beta$-order convergent at ${\mathbf {y}}^{\text{ S }}$. $\square$

1.4 Proof of arguments in Example 18

Proof

We first show that $x^{\text{ f }}_Z - x^* \ge 0.2\varepsilon + o\left( \varepsilon \right)$.

$$\begin{aligned}&x^{\text{ f }}_Z - x^*\\ {}&\quad = \, \Bigg ( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } - \exp (3 - y^{\text{ U }})}{2} \\&\quad \quad \quad - \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} - \exp (3 - y^*)}{2} \Bigg ) \\&\quad = \, \displaystyle \frac{ \left( \left( \exp (3 - y^{\text{ U }}) \right) ^2 - \left( \exp (3 - y^*) \right) ^2 \right) + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad = \, \displaystyle \frac{ \left( \exp (3 - y^{\text{ U }}) + \exp (3 - y^*) + 2 \right) \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad \ge \displaystyle \frac{ \left( \exp (3 - y^*) + \exp (3 - y^*) + 2 \right) \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^* - 0.1) \right) ^2 + 40 + 2 \left( \exp (3 - y^* - 0.1) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad \ge \, 0.025 \left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) \\&\quad = \, 0.025 \exp (3 - y^*) \varepsilon + o\left( \varepsilon \right) \\&\quad \ge \, 0.2\varepsilon + o\left( \varepsilon \right) . \end{aligned}$$

Next, we derive an expression for ${\bar{x}}_Z(y) - x^*(y)$.

$$\begin{aligned} {\bar{x}}_Z(y) - x^*(y)&= \, \Bigg ( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } - \exp (3 - y^{\text{ L }})}{2} \nonumber \\&\quad \quad \quad - \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} - \exp (3 - y)}{2} \Bigg ) \nonumber \\&= \, \displaystyle \frac{ \left( \left( \exp (3 - y^{\text{ L }}) \right) ^2 - \left( \exp (3 - y) \right) ^2 \right) + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \nonumber \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y) - \exp (3 - y^{\text{ L }}) \right) }{2} \nonumber \\&= \, \displaystyle \frac{ \left( \exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z \right) \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \nonumber \\&\quad \quad \quad - \displaystyle \frac{\left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2}. \end{aligned}$$

(11)

We next establish the dependence of the different terms in Eq. (11) on $\varepsilon$. We first derive an expression for $\exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z$.

$$\begin{aligned}&\qquad \! \exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z \\&= \, \exp (3-y^*+\varepsilon ) + \exp (3-y) + 2\displaystyle \sqrt{\left( \exp (3-y^*-\varepsilon \right) ^2 + 40} - 2\exp (3-y^*-\varepsilon ) \\&= \, \exp (3-y^*) + \exp (3-y) + \varepsilon \exp (3-y^*) + O(\varepsilon ^2) \\&\quad \quad + 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 \left[ 1 - 2\varepsilon + O(\varepsilon ^2) \right] + 40}-2\exp (3-y^*)\left[ 1 - \varepsilon + O(\varepsilon ^2) \right] \\&= \, 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \exp (3-y) - \exp (3-y^*) + 3\exp (3-y^*)\varepsilon \\&\quad \quad - \displaystyle \frac{2\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2). \end{aligned}$$

Next, we derive an expression for $4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right)$.

$$\begin{aligned}&4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*-\varepsilon \right) ^2 + 40} - 2\exp (3-y^*-\varepsilon ) \right) \left( \exp (3-y^*+\varepsilon ) - \exp (3-y) \right) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - 2\exp (3-y^*) \right) \left( \exp (3-y^*+\varepsilon )- \exp (3-y) \right) + O(\varepsilon ^2) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - 2\exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) +\exp (3-y^*)\varepsilon \right) \\ {}&\quad \quad \quad + O(\varepsilon ^2). \end{aligned}$$

Finally, we consider $\sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40}$.

$$\begin{aligned}&\, \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \, \displaystyle \sqrt{\left( \exp (3-y^*+\varepsilon )\right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \, \displaystyle \sqrt{\left( \exp (3-y^*)\right) ^2 + 40} \displaystyle \sqrt{1 + \displaystyle \frac{4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) + 2\left( \exp (3-y^*)\right) ^2 \varepsilon + O(\varepsilon ^2)}{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} + \displaystyle \frac{\left( \exp (3-y^*)\right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad {+} \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 {+} 40} {-} \exp (3-y^*) \right) \left( \exp (3-y^*) {-} \exp (3-y) {+} \exp (3-y^*) \varepsilon \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 {+} 40}} {+} O(\varepsilon ^2). \end{aligned}$$

Substituting the above expressions in Eq. (11), we get

$$\begin{aligned}&\qquad {\bar{x}}_Z(y) - x^*(y) \\&= \, \displaystyle \frac{ \alpha \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 {+} 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) {-} \exp (3 - y) \right) } {+} \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) }, \end{aligned}$$

with

$$\begin{aligned} \alpha&:= \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} + \exp (3-y) - \exp (3-y^*) \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + 3\exp (3-y^*) \varepsilon - \displaystyle \frac{3\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \exp (3-y^*) \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2) \\&\quad = \left( \displaystyle \frac{\exp (3-y^*) + \exp (3-y)}{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40}} - 1 \right) \left( \exp (3-y^*) - \exp (3-y) \right) \\&\quad \quad \quad -\displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + 3\exp (3-y^*) \varepsilon - \displaystyle \frac{3\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \exp (3-y^*) \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2) \\&\quad \le {\hat{\tau }} \varepsilon + O(\varepsilon ^2) \end{aligned}$$

for some ${\hat{\tau }} \ge 0$ since $y \in Z = [y^{\text{ L }}, y^{\text{ U }}]$ with $w(Z) = O(\varepsilon )$ and each term in the expression for $\alpha$ is $O(\varepsilon )$. Note that $\alpha \ge 0$ (since $\bar{x}_Z(y) \ge x^*(y), \, \forall y \in Z$). $\square$