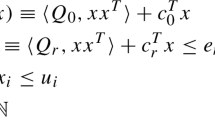A reliable affine relaxation method for global optimization

Abstract

An automatic method for constructing linear relaxations of constrained global optimization problems is proposed. Such a construction is based on affine and interval arithmetics and uses operator overloading. These linear programs have exactly the same numbers of variables and inequality constraints as the given problems. Each equality constraint is replaced by two inequalities. This new procedure for computing reliable bounds and certificates of infeasibility is inserted into a classical branch and bound algorithm based on interval analysis. Extensive computation experiments were made on 74 problems from the COCONUT database with up to 24 variables or 17 constraints; 61 of these were solved, and 30 of them for the first time, with a guaranteed upper bound on the relative error equal to $10^{-8}$. Moreover, this sample comprises 39 examples to which the GlobSol algorithm was recently applied finding reliable solutions in 32 cases. The proposed method allows solving 31 of these, and 5 more with a CPU-time not exceeding 2 min.

1 Introduction

For about thirty years, interval branch and bound algorithms are increasingly used to solve global optimization problems in a deterministic way (Hansen and Walster 2004; Kearfott 1996; Markot et al. 2006; Ratschek and Rokne 1988). Such algorithms are reliable, i.e., they provide an optimal solution and its value with a guaranteed bound on the error, or a proof that the problem under study is infeasible. Other approaches of global optimization (e.g. Androulakis et al. 1995; Audet et al. 2000; Horst and Tuy 1996; Lasserre 2001; Lebbah et al. 2005; Maranas and Floudas 1997; Mitsos et al. 2009; Sherali and Adams 1999; Tawarmalani and Sahinidis 2004), while useful and often less time-consuming than interval methods, do not provide such a guarantee. Recently, the second author adapted and improved standard interval branch and bound algorithms to solve design problems of electromechanical actuators (Fitan et al. 2004; Fontchastagner et al. 2007; Messine 2005; Messine et al. 1998). This work showed that interval propagation techniques based on constructions of computation trees (Messine 2004; Hentenryck et al. 1997; Vu et al. 2009) and on linearization techniques (Hansen and Walster 2004; Kearfott 1996; Lebbah et al. 2005) improved considerably the speed of convergence of the algorithm.

Another way to solve global optimization problems, initially outside the interval branch and bound framework, is the reformulation-linearization technique developed by Sherali and Adams (1999), see also Audet et al. (2000), Perron (2004) for methods dedicated to quadratic non-convex problems. The main idea is to reformulate a global optimization problem as a larger linear one, by adding new variables as powers or products of the given variables and linear constraints on their values. Notice that in Schichl and Neumaier (2005), Schichl and Neumaier proposed another linearization technique based on the slopes of functions. This technique has the advantage of keeping the same number of variables as the original optimization problem.

Kearfott (2006), Kearfott and Hongthong (2005) and Lebbah et al. (2005) embedded the reformulation-linearization technique in interval branch and bound algorithms, showing their efficiency on some numerical examples. However, it is not uncommon that the relaxed linear programs are time-consuming to solve exactly at each iteration owing to their large size. Indeed, if the problem has highly nonlinear terms, fractional exponents or many quadratic terms, these methods will require many new variables and constraints.

In this paper, the main idea is to use affine arithmetic (Comba and Stolfi 1993; de Figueiredo 1996; Figueiredo and Stolfi 2004; Stolfi and de Figueiredo 1997) to generate linear relaxations. This arithmetic can be considered as an extension of interval arithmetic (Moore 1966) by converting intervals into affine forms. This has several advantages: (i) keeping affine information on the dependencies among the variables during the computations reduces the dependency problem which occurs when the same variable has many occurrences in the expression of a function; (ii) as with interval arithmetic, affine arithmetic can be implemented in an automated way by using computation trees and operator overloading (Mitsos et al. 2009) which are available in some languages such as C++, Fortran 90/95/2000 and Java; (iii) the linear programs have exactly the same numbers of variables and of inequality constraints as the given constrained global optimization problem. The equality constraints are replaced by two inequality constraints. This is due to the use of two affine forms introduced by the second author in a previous work (Messine 2002). The linear relaxations have to be solved by specialized codes such as CPLEX. Techniques for obtaining reliable results with such non reliable codes have been proposed by Neumaier and Shcherbina (2004), and are used in some of the algorithms proposed below; (iv) compared with previous, often specialized, works on the interval branch and bound approach (Kearfott 2006; Lebbah et al. 2005), or which could be embedded into such an approach (Audet et al. 2000; Sherali and Adams 1999), the proposed method is fairly general and can deal with many usual functions such as logarithm, exponential, inverse, square root.

The paper is organized as follows. Section 2 specifies notations and recalls basic definitions about affine arithmetic and affine forms. Section 3 is dedicated to the proposed reformulation methods and their properties. Section 4 describes the reliable version of these methods. In Sect. 5, their embedding in an interval Branch and Bound algorithm is discussed. Section 6 validates the efficiency of this approach by performing extensive numerical experiments on a sample of 74 test problems from the COCONUT website. Section 7 concludes.

2 Affine arithmetic and affine forms

Interval arithmetic extends usual functions of arithmetic to intervals, see Moore (1966). The set of intervals will be denoted by ${\mathbb {I}}{\mathbb {R}}$, and the set of n-dimensional interval vectors, also called boxes, will be denoted by ${\mathbb {I}}{\mathbb {R}}^n$. The four standard operations of arithmetic are defined by the following equations, where ${ {\varvec{x}}= [\underline{x},\overline{x}]}$ and ${ {\varvec{y}}= [\underline{y},\overline{y}]}$ are intervals:

$$\begin{aligned} {\varvec{x}}\oplus {\varvec{y}}&= [\underline{x}+\underline{y},\overline{x}+\overline{y}],\qquad {\varvec{x}}\odot {\varvec{y}}=[\min (\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y}),\max ( \underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\overline{y})],\\ {\varvec{x}}\ominus {\varvec{y}}&= [\underline{x}-\overline{y}, \overline{x}-\underline{y}],\qquad {\varvec{x}}\oslash {\varvec{y}}=[\underline{x},\overline{x}]\odot [1/\overline{y}, 1/\underline{y}], \qquad \text { if } 0 \not \in {\varvec{y}}. \end{aligned}$$

These operators are the basis of interval arithmetic, and its principle can be extended to many unary functions, such as $\cos$, $\sin$, $\exp$, $\log$, ${\sqrt{.}}$Kearfott (1996), Stolfi and de Figueiredo (1997). We can also write $\text {inf}({\varvec{x}})=\underline{x}$ for the lower bound, $\text {sup}({\varvec{x}})=\overline{x}$ for the upper bound and $\text {mid}({\varvec{x}})= \frac{\underline{x}+\overline{x}}{2}$ for the midpoint of the interval ${\varvec{x}}$.

Given a function $f$ of one or several variables $x_1, \dots , x_n$ and the corresponding intervals for the variables ${\varvec{x}}_1, \dots ,{\varvec{x}}_n$, the natural interval extension $\mathsf f$ of $f$ is an interval obtained by substituting variables by their corresponding intervals and applying the interval arithmetic operations. This provides an inclusion function, i.e., $\mathsf f:{\mathbb {D}}\subseteq {\mathbb {I}}{\mathbb {R}}^n \rightarrow {\mathbb {I}}{\mathbb {R}}$ such that $\forall {\varvec{x}}\in {\mathbb {D}},\, \mathtt{range}(f,{\varvec{x}})=\{f(x): x\in {\varvec{x}}\}\subseteq \mathsf f({\varvec{x}})$, for details see (Ratschek and Rokne (1988), Sect. 2.6).

Example 1

Using the rounded interval arithmetic in Fortran double precision, such as defined in (Moore (1966), Chap. 3),

$$\begin{aligned} {\varvec{x}}&= [1,2]\times [2,6],~~ f(x) = x_1\cdot x_2^2-\exp (x_1+x_2),\\ {\mathsf f}({\varvec{x}})&= [1,2]\odot [2,6]^2\ominus \exp ([1,2]\oplus [2,6])=[-2976.957987041728,\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad 51.914463076812], \end{aligned}$$

We obtain that: $\forall x\in {\varvec{x}},\, f(x)\in [-2976.957987041728,51.914463076812]$.

Affine arithmetic was introduced in 1993 by Comba and Stolfi (1993) and developed by De Figueiredo and Stolfi in de Figueiredo (1996), Figueiredo and Stolfi (2004), Stolfi and de Figueiredo (1997). This technique is an extension of interval arithmetic obtained by replacing intervals with affine forms. The main idea is to keep linear dependency information during the computations. This makes it possible to efficiently deal with a difficulty of interval arithmetic: the dependency problem, which occurs when the same variable appears several times in an expression of a function (each occurrence of the same variable is treated as an independent variable). To illustrate that, the natural interval extension of $f(x)=x-x$, where $x \in {\varvec{x}}=[\underline{x},\overline{x}]$, is equal to $[\underline{x}-\overline{x},\overline{x}-\underline{x}]$ instead of $0$.

A standard affine form is written as follows, where $x$ is a partially unknown quantity, the coefficients $x_i$ are finite floating-point numbers (we denote this with a slight abuse of notation as ${\mathbb {R}}$) and $\epsilon _i$ are symbolic real variables whose values are unknown but assumed to lie in the interval ${\varvec{\epsilon }}_i=[-1,1]$, see Stolfi and de Figueiredo (1997):

$$\begin{aligned} \widehat{x}= x_0 + \displaystyle \sum _{i=1}^{n} x_i \epsilon _i, \end{aligned}$$

(1)

with $\forall i \in \{0,1,\dots ,n\}, x_i \in {\mathbb {R}}$ and $\forall i \in \{1,2,\dots ,n\}, \epsilon _i\in {\varvec{\epsilon }}_i = [-1, 1]$.

An affine form can also be defined by a vector of all its components: $(x_0, x_1, \dots , x_n)$.

As in interval arithmetic, usual operations and functions are extended to deal with affine forms. For example, the addition between two affine forms, latter denoted by $\widehat{x}$ and $\widehat{y}$, is simply the term-wise addition of their coefficients $x_i$ and $y_i$. The algorithm for the other operations and some transcendental functions, such as the square root, the logarithm, the inverse and the exponential, can be found in Stolfi and de Figueiredo (1997). Conversions between affine forms and intervals are done as follows:

Indeed, using these conversions, it is possible to construct an affine inclusion function; all the intervals are converted into affine forms, the computations are performed using affine arithmetic and the resulting affine form is then converted into an interval; this generates bounds on values of a function over a box (Messine 2002; Stolfi and de Figueiredo 1997). These inclusion functions cannot be proved to be equivalent or better than natural interval extensions. However, empirical studies done by Stolfi and de Figueiredo (1997), Messine (2002) and Messine and Touhami (2006) show that when applied to global optimization problems, affine arithmetic is, in general, significantly more efficient for computing bounds than the direct use of interval arithmetic.

Nevertheless, standard affine arithmetic such as described in Stolfi and de Figueiredo (1997) introduces a new variable each time a non-affine operation is done. Thus, the size of the affine forms is not fixed and its growth may slow down the solution process. To cope with this problem, one of the authors proposed two extensions of the standard affine form which are denoted by AF1 and AF2 (Messine 2002). These extended affine forms make it possible to fix the number of variables and to keep track of errors generated by approximation of non-affine operations or functions.

• The first form AF1 is based on the same principle as the standard affine arithmetics but all the new symbolic terms generated by approximations are accumulated in a single term. Therefore, the number of variables does not increase. Thus:

  $$\begin{aligned} \widehat{x}= x_0 + \displaystyle \sum _{i=1}^{n} x_i \epsilon _i + x_{n+1} \epsilon _{\pm }, \end{aligned}$$

  (2)

  with $\forall i \in \{0,1,\dots ,n\}, x_i \in {\mathbb {R}}$, $x_{n+1} \in {\mathbb {R}}^+$, $\epsilon _i\in {\varvec{\epsilon }}_i = [-1, 1]$ and $\epsilon _{\pm }\in {\varvec{\epsilon }}_{\pm } = [-1, 1]$.

• The second form AF2 is based on AF1. Again the number of variables is fixed but the errors are stacked in three terms, separating the positive, negative and unsigned errors. Thus:

  $$\begin{aligned} \widehat{x}= x_0 + \displaystyle \sum _{i=1}^{n} x_i \epsilon _i + x_{n+1} \epsilon _{\pm } + x_{n+2} \epsilon _{+} + x_{n+3} \epsilon _{-}, \end{aligned}$$

  (3)

  with $\forall i \in \{0,1,\dots ,n\}, x_i \in {\mathbb {R}}$ and $\forall i \in \{1,2,\dots ,n\}$, $\epsilon _i\in {\varvec{\epsilon }}_i = [-1, 1]$, and $(x_{n+1}, x_{n+2}, x_{n+3}) \in {\mathbb {R}}_+^3$, $\epsilon _{\pm }\in {\varvec{\epsilon }}_{\pm } = [-1,1], \epsilon _{+}\in {\varvec{\epsilon }}_{+} = [0,1], \epsilon _{-}\in {\varvec{\epsilon }}_{-} = [-1, 0]$.

In this paper, we use mainly the affine form AF2. Note that a small mistake was recently found in the computation of the error of the multiplication between two AF2 forms in Messine (2002), see Vu et al. (2009).

Usual operations and functions are defined by extension of affine arithmetic, see Messine (2002) for details. For example, the multiplication between two affine forms of type AF1 is performed as follows:

$$\begin{aligned} \widehat{x}\cdot \widehat{y}= x_0 y_0 + \displaystyle \sum _{i=1}^n (x_0 y_i + x_i y_0) \epsilon _i + \displaystyle \left( x_0 y_{n+1} + x_{n+1} y_0 + \left( \sum _{i=1}^{n+1} |x_i| \cdot \displaystyle \sum _{i=1}^{n+1} |y_i| \right) \right) \epsilon _{\pm }. \end{aligned}$$

For computing unary functions in affine arithmetic, Stolfi and de Figueiredo (1997) proposed two linear approximations: the Chebyshev and the min-range approximations, see Fig. 1. The Chebyshev approximation is the reformulation which minimizes the maximal absolute error. The min-range approximation is that one which minimizes the range of the approximation. These affine approximations are denoted as follows:

$$\begin{aligned} \begin{aligned} \widehat{\mathsf f}(\widehat{x})&= \zeta +\alpha \widehat{x}+ \delta \epsilon _{\pm },\\ \mathrm{with}\ \widehat{x}\ \mathrm{given\ by\ Eq}.~&(4)\ \mathrm{or}\ (5)\ \mathrm{and}\ \zeta \in {\mathbb {R}}, \alpha \in {\mathbb {R}}^+, \delta \in {\mathbb {R}}^+. \end{aligned} \end{aligned}$$

(4)

Fig. 1

Affine approximations by min-range methods and Chebyshev

Thus on the one hand, the Chebyshev linearization gives the affine approximation which minimizes the error $\delta$ but the lower bound is worse than the actual minimum of the range, see Fig. 1. On the other hand, the min-range linearization is less efficient in estimating linear dependency among variables, while the lower bound is equal to the actual minimum of the range. In our affine arithmetic code, as in De Figueiredo et al.’s one (1997), we choose to implement the min-range linearization technique. Indeed, in experiments with monotonic functions, bounds were found to be better than those calculated by the Chebyshev approximation when basic functions were combined (because the Chebyshev approximations increase the range).

A representation of the computation of AF1 is shown in Fig. 2 (numbers are truncated with 6 digits after the decimal point). In our implementation, the computation tree is implicitly built by operator overloading (Mitsos et al. 2009). Hence, its form depends on how the equation is written. The leaves contain constants or variables which are initialized with the affine form generated by the conversion of the initial interval. Then, the affine form of each internal node is computed from the affine form of its sons by applying the corresponding operation of AF1. The root gives the affine form for the entire expression. Lower and upper bounds are obtained by replacing the $\epsilon _i$ variables by $[-1,1]$ and applying interval arithmetic.

Fig. 2

Visualization of AF1 by computation tree: $f(x) = x_1 \cdot x_2^2 - \exp (x_1+x_2) \text { in } [1,2]\times [2,6]$

Example 2

Consider the following function:

$$\begin{aligned} f(x) = x_1\cdot x_2^2 - \exp (x_1+x_2) \text { in } [1,2]\times [2,6]. \end{aligned}$$

First, using Eq. (2), we transform the intervals $[1,2]$ and $[2,6]$ into the following affine forms (at this stage it is equivalent to use AF1 or AF2):

$$\begin{aligned} \displaystyle {\varvec{x}}_1 =[1,2]\rightarrow \widehat{x}_1 = 1.5 + 0.5 \epsilon _{ 1} \text { and } \displaystyle {\varvec{x}}_2 = [2,6] \rightarrow \widehat{x}_2 = 4 + 2 \epsilon _2. \end{aligned}$$

Computing with the extended operators of AF1 and of AF2, we obtain the following affine forms:

$$\begin{aligned} {\widehat{\mathsf f}_{AF1}({\varvec{x}})}&= -1476.521761 -2.042768\epsilon _1 -16.171073\epsilon _2 + 1446.222382\epsilon _{\pm },\\ {\widehat{\mathsf f}_{AF2} ({\varvec{x}})}&= -1476.521761 -2.042768\epsilon _1 -16.171073\epsilon _2 + 1440.222382\epsilon _{\pm } + 6\epsilon _+ + 0\epsilon _-. \end{aligned}$$

The details of the computation by AF1 are represented in Fig. 2. The variable $\epsilon _1$ corresponds to ${\varvec{x}}_1$, $\epsilon _2$ to ${\varvec{x}}_2$ and using AF1, $\epsilon _{\pm }$ contains all the errors generated by non-affine operations. Using AF2, $\epsilon _{\pm }$ contains the errors generated by the multiplication and the exponential, and $\epsilon _+$ the errors generated by the square.

To conclude, using Eq. (3), we convert these affine forms into intervals to have the following bounds:

Using interval arithmetic directly, we obtain

$$\begin{aligned} \begin{array}{ll} &{}\forall x \in [1,2]\times [2,6], f(x) \in [-2976.9579870417284,51.91446307681234],\\ \text {using AF1: }&{}\forall x \in [1,2]\times [2,6], f(x) \in [-2940.9579870417297,-12.085536923186737],\\ \text {using AF2:} &{}\forall x \in [1,2]\times [2,6], f(x) \in [-2934.9579870417297,-12.085536923186737], \end{array} \end{aligned}$$

and the exact range with 12 digits after comma is

$$\begin{aligned} \mathtt{range} (f,[1,2]\times [2,6]) = [-2908.957987041728,-16.085536923187668]. \end{aligned}$$

In this example, the enclosure computed by interval arithmetic contains $0$. This introduces an ambiguity on the sign of $f$ over $[1,2]\times [2,6]$ while it is clearly negative. This example shows why AF1 and AF2 are interesting.

An empirical comparison among interval arithmetic, AF1 and AF2 affine forms has been done on several randomly generated polynomial functions (Messine 2002), and the proof of the following proposition is given there.

Proposition 1

Consider a polynomial function $f$ of ${\varvec{x}}\subset {\mathbb {R}}^n$ to ${\mathbb {R}}$ and $\mathsf f_{AF}$, $\mathsf f_{AF1}$ and $\mathsf f_{AF2}$ the reformulations of $f$ respectively with AF, AF1 and AF2. Then one has:

$$\begin{aligned} \displaystyle \mathtt{range}(f,{\varvec{x}}) \subseteq \widehat{\mathsf f}_{AF2}({\varvec{x}}) \subseteq \widehat{\mathsf f}_{AF1}({\varvec{x}}) = \widehat{\mathsf f}_{AF}({\varvec{x}}). \end{aligned}$$

3 Affine reformulation technique based on affine arithmetic

Since many years, reformulation techniques have been used for global optimization (Androulakis et al. 1995; Audet et al. 2000; Horst and Tuy 1996; Kearfott and Hongthong 2005; Lebbah et al. 2005; Maranas and Floudas 1997; Perron 2004; Sherali and Adams 1999; Tawarmalani and Sahinidis 2004). In most cases, the main idea is to approximate a mathematical program by a linear relaxation. Thus, solving the linear program yields bounds on this optimal value or a certificate of infeasibility of the original problem. The originality of our approach lies in how the linear relaxation is constructed.

In our approach, named Affine Reformulation Technique $(ART_\mathrm{AF})$, we have kept the computation tree and relied on the extended affine arithmetics (AF1 and AF2). Indeed, the extended affine arithmetics handle affine forms on the computation tree. But until now, this technique has been only used to compute bounds. Now, our approach uses the extended affine arithmetics not only as a simple way to compute bounds but also as a way to automatically linearize every factorable function (Tawarmalani and Sahinidis 2004). This becomes possible by fixing the number of $\epsilon _i$ variables in the extended affine arithmetics. Thus, an affine transformation ${\mathcal {T}}$ between the original set ${\varvec{x}}\subset {\mathbb {R}}^n$ and ${\varvec{\epsilon }}= [-1,1]^n$ is introduced, see Eq. (2); notice that ${\mathcal {T}}$ is bijective. Now, we can identify the linear part of AF1 and AF2 as a linear approximation of the original function. Thus, this leads to the following propositions:

Proposition 2

Consider $(\mathsf f_0, \dots , \mathsf f_{n+1})$, the components of the affine form AF1 of a function $f$ over ${\varvec{x}}$.

If $\forall x\in {\varvec{x}}, f(x) \le 0$, then $\forall y \in [-1,1]^n, ~\displaystyle \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}-\mathsf f_0$.

If $\forall x\in {\varvec{x}}, f(x) = 0$, then $\forall y \in [-1,1]^n$, $\left\{ \begin{array}{l} \displaystyle \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}-\mathsf f_0,\\ - \displaystyle \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}+\mathsf f_0. \end{array}\right.$

Proof

Denote the affine form AF1 of $f$ over ${\varvec{x}}$ by $\widehat{\mathsf f}({\varvec{x}})$. Here the components $\mathsf f_i$ in the formulation depend also on ${\varvec{x}}$:

$$\begin{aligned} \begin{array}{c} \widehat{\mathsf f}({\varvec{x}}) = \mathsf f_0 +\displaystyle \sum ^n_{i=1}\mathsf f_i \epsilon _i + \mathsf f_{n+1} \epsilon _{\pm }, \\ \text { with } \forall i \in \{0,1,\dots ,n\}, \mathsf f_i \in {\mathbb {R}}, \mathsf f_{n+1} \in {\mathbb {R}}^+ ,\\ \forall i \in \{1,2,\dots ,n\} , \epsilon _i\in {\varvec{\epsilon }}_i = [-1, 1] \text { and } \epsilon _{\pm }\in {\varvec{\epsilon }}_{\pm }= [-1, 1]. \end{array} \end{aligned}$$

By definition, the affine form AF1 is an inclusion function:

$$\begin{aligned} \forall x\in {\varvec{x}}, f(x) \in \mathsf f_0 \oplus \displaystyle \sum ^n_{i=1}\mathsf f_i {\varvec{\epsilon }}_i \oplus \mathsf f_{n+1} {\varvec{\epsilon }}_{\pm }. \end{aligned}$$

But $\forall y \in {\varvec{\epsilon }}=[-1,1]^n, \exists x \in {\varvec{x}}, y = {\mathcal {T}}(x)$ where ${\mathcal {T}}$ is an affine function, then:

$$\begin{aligned} \begin{aligned} \forall x \in {\varvec{x}},&f(x) \in \left( \displaystyle \sum ^n_{i=1}\mathsf f_i {\mathcal {T}}_i(x_i) \oplus \mathsf f_0 \oplus \mathsf f_{n+1} [-1,1]\right) ,\\ \forall x\in {\varvec{x}},&f(x) - \displaystyle \sum ^n_{i=1}\mathsf f_i {\mathcal {T}}_i(x_i) \in [\mathsf f_0 - \mathsf f_{n+1} ,\mathsf f_0 + \mathsf f_{n+1}],\\&\mathrm{where}\ {\mathcal {T}}_i\ \mathrm{are\ the\ components\ of} {\mathcal {T}}. \end{aligned} \end{aligned}$$

(5)

Thus the result follows. $\square$

Proposition 3

Consider $(\mathsf f_0, \dots , \mathsf f_{n+1}, \mathsf f_{n+2}, \mathsf f_{n+3})$, the components of the affine form AF2 of a function $f$ over ${\varvec{x}}$. .

If  $\forall x\in {\varvec{x}}, f(x) \le 0$ then $\forall y \in [-1,1]^n , ~\displaystyle \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}+\mathsf f_{n+3}-\mathsf f_0$.

If  $\forall x\in {\varvec{x}}, f(x) = 0$ then $\forall y \in [-1,1]^n$, $\left\{ \begin{array}{l} \displaystyle \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}+\mathsf f_{n+3}-f_0,\\ \displaystyle - \sum ^n_{i=1}\mathsf f_i y_i \le \mathsf f_{n+1}+\mathsf f_{n+2}+\mathsf f_0. \end{array}\right.$

Proof

If we replace AF1 with AF2 in Eq. (7), we have the following inclusion:

$$\begin{aligned} \forall x\in {\varvec{x}}, f(x) - \displaystyle \sum ^n_{i=1}\mathsf f_i {\mathcal {T}}_i(x_i) \in [\mathsf f_0 - \mathsf f_{n+1}-\mathsf f_{n+3} ,\mathsf f_0 + \mathsf f_{n+1}+\mathsf f_{n+2}]. \end{aligned}$$

$\square$

Consider a constrained global optimization problem (8), defined below, a linear approximation of each of the expressions for $f$, $g_i$ and $h_j$ is obtained using AF1 or AF2. Each inequality constraint is relaxed by one linear inequality and each equality constraint by two linear inequalities. Thus, the linear program (9) is automatically generated.

The linear objective function $c$ of the linear program (9) is obtained from the linear part of the affine form of the objective function $f$ of the original problem (8): i.e. $c= (\mathsf f_1,\mathsf f_2,\dots ,\mathsf f_n)^T$. The linear constraints ($A y \le b$) are composed using Proposition 2 or 3 over each constraints $g_k$ and $h_l$ of the original problem (8).

Remark 1

The size of the linear program (9) still remains small. The number of variables is the same as in the general problem (8) and the number of inequality constraints cannot exceed twice its number of constraints.

Let us denote by $S_1$ the set of feasible solutions of the initial problem (8), $S_2$ the set of feasible solutions of the linear program (9), ${\mathcal {T}}$ the bijective affine transformation between ${\varvec{x}}$ and ${\varvec{\epsilon }}=[-1, 1]^n$, and $E_f$ the lower bound of the error of the affine form of $f$. Using AF1, $E_f = \text {inf}(\mathsf f_0 \oplus \mathsf f_{n+1} {\varvec{\epsilon }}_{\pm }) = \mathsf f_0 -\mathsf f_{n+1}$ and using AF2, $E_f = \text {inf}(\mathsf f_0 \oplus \mathsf f_{n+1} {\varvec{\epsilon }}_{\pm }\oplus \mathsf f_{n+2} {\varvec{\epsilon }}_{+}\oplus \mathsf f_{n+3} {\varvec{\epsilon }}_{-}) = \mathsf f_0 - \mathsf f_{n+1}-\mathsf f_{n+3}$.

Proposition 4

Assume that $x$ is a feasible solution of the original problem (8), hence $y = {\mathcal {T}}(x)$ is a feasible solution of the linear program (9) and therefore, one has ${\mathcal {T}}(S_1) \subseteq S_2$.

Proof

The proposition is a simple consequence of Propositions 2 and 3. $\square$

Corollary 1

If the relaxed linear program (9) of a problem (8) does not have any feasible solution then the problem (8) does not have any feasible solution.

Proof

Using directly Proposition 4, $S_2 =\emptyset \text { implies }S_1 = \emptyset$ and the result follows. $\square$

Proposition 5

If $y_{sol }$ is a solution which minimizes the linear program (9), then

$$\begin{aligned} \forall x \in S_1 , f(x) \ge (\mathsf f_1,...,\mathsf f_n)^T y_{sol} + {E}_f, \end{aligned}$$

with $E_f = \mathsf f_0 - \mathsf f_{n+1}$ if AF1 has been used to generate the linear program (9), and $E_f= \mathsf f_0-\mathsf f_{n+1}-\mathsf f_{n+3}$ if AF2 has been used.

Proof

Using Proposition 4, one has $\forall x \in S_1, y = {\mathcal {T}}(x) \in S_2$. Moreover, $y_{sol }$ denotes by assumption the solution which minimizes the linear program (9), hence one obtains $\forall y \in S_2, c^T y \ge c^T y_{sol}$. Using Proposition 2 and Proposition 3, we have $\forall x \in S_1, \exists y \in [-1,1], f(x)-c^T y \ge {E}_f$ and therefore $\forall x \in S_1, f(x)\ge c^T y_{sol}+ {E}_f$.

$\square$

We remark that equality occurs when the problem (8) is linear, because, in this case, AF1 and AF2 are just a rewriting of program (8) on $[-1,1]^n$, instead of ${\varvec{x}}$.

Proposition 6

Let us consider a polynomial program; i.e., $f$ and all $g_i$, $h_j$ are polynomial functions. Denote a minimizer point of a relaxed linear program (9) using AF1 form by $y_{_{AF1}}$, and another one using AF2 form by $y_{_{AF2}}$. Moreover, using the notations $c_{_{AF1}}$, $E_{f_{AF1}}$ and $c_{_{AF2}}$, $E_{f_{AF2}}$ for the reformulations of $f$ using AF1 and AF2 forms respectively, we have:

$$\begin{aligned} \forall x \in S_1,f(x) \ge c_{_{AF2}}^T y_{_{AF2}} +{E}_{f _{AF2}} \ge c_{_{AF1}}^T y_{_{AF1}} + {E}_{f _{AF1}}. \end{aligned}$$

Proof

By construction of the arithmetics defined in Messine (2002) (with corrections as in Vu et al. (2009)) and mentioned in Proposition 1, if $y \in S_2$, we have:

$$\begin{aligned} \begin{array}{c} c_{_{AF2}}^T y + {E}_{f _{AF2}} \ge c_{_{AF1}}^T y + {E}_{f _{AF1}},\\ \\ c_{_{AF2}}^T y \ge c_{_{AF2}}^T y_{_{AF2}} \text { and } c_{_{AF1}}^T y \ge c_{_{AF1}}^T y_{_{AF1}}. \end{array} \end{aligned}$$

But Proposition 4 yields $\forall x \in S_1$, $y={\mathcal {T}}(x) \in S_2$ and then,

$$\begin{aligned} \forall x \in S_1, f(x) \ge c_{_{AF2}}^T y_{_{AF2}} + {E}_{f _{AF2}} \ge c_{_{AF1}}^T y_{_{AF2}} + {E}_{f _{AF1}} \ge c_{_{AF1}}^T y_{_{AF1}} + {E}_{f _{AF1}}. \end{aligned}$$

$\square$

Remark 2

Proposition 6 could be generalized to factorable functions depending on the definition of transcendental functions in AF1 and AF2 corresponding arithmetic. In Messine (2002), only affine operations and the multiplication between two affine forms were taken into account.

Proposition 7

If a constraint of the problem (8) is proved to be satisfied by interval analysis, then the associated linear constraint can be removed from the linear program (9) and the solution does not change.

Proof

If a constraint of the original problem (8) is satisfied on ${\varvec{x}}$ (which is guaranteed by interval arithmetic based computation), then the corresponding linear constraint is always satisfied for all the values of $y\in [-1,1]$ and it is not necessary to have it in (9). $\square$

Example 3

Let us consider the following problem with ${\varvec{x}}= [1, 1.5]\times [4.5, 5]\times [3.5, 4]\times [1, 1.5]$:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{x \in {\varvec{x}}} &{}x_3+(x_1+x_2+x_3) x_1 x_4\\ s.t. &{} x_1 x_2 x_3 x_4\ge 25,\\ ~ &{} x_1^2+x_2^2+x_3^2+x_4^2 =40,\\ ~ &{} 5 x_1^4 -2 x_2^3 +11 x_3^2 +6 e^{x_4} \le 50. \end{array}\right. \end{aligned}$$

We denote the first constraint by $c_1$, the second one by $c_2$ and the last one by $c_3$.

First we compute an enclosure of each constraint by interval arithmetic:

$$\begin{aligned} \mathsf c_1({\varvec{x}}) = [15.75,45.0], \mathsf c_2({\varvec{x}})= [34.5,45.5]\,\, \hbox {and }\mathsf c_3({\varvec{x}})= [-93.940309,45.952635]. \end{aligned}$$

So, $\forall x\in {\varvec{x}}$, $c_3(x)\le 50$. Thus we do not need to linearize the last constraint.

This example is constructed numerically by using the double precision floating point representation. To simplify the notations, the floating point numbers are rounded to rational ones with two decimals. The aim is to illustrate how the technique ART is used. By using the affine form AF1, the linear reformulations of the above equations provide:

$$\begin{aligned} \begin{array}{ r l} x_3+(x_1+x_2+x_3) x_1 x_4 \longrightarrow &{}18.98 + 3.43\epsilon _{1} + 0.39\epsilon _{2} + 0.64\epsilon _{3} + 3.04\epsilon _{4} + 1.12\epsilon _{\pm }, \\ 25 - x_1 x_2 x_3 x_4 \longrightarrow &{} -2.83 -5.56\epsilon _{1} -1.46\epsilon _{2} -1.85\epsilon _{3} -5.56\epsilon _{4} + 2.71\epsilon _{\pm },\\ x_1^2+x_2^2+x_3^2+x_4^2 -40 \longrightarrow &{} -0.25 + 0.62\epsilon _{1} + 2.37\epsilon _{2} + 1.87\epsilon _{3} + 0.62\epsilon _{4} + 0.25\epsilon _{\pm }. \end{array} \end{aligned}$$

We have now to consider the following linear program:

$$\begin{aligned} \left\{ \begin{array}{crl } \displaystyle \min _{ y \in [-1, 1]^{4} } &{} 3.43 y_{1} + 0.39 y_{2} + 0.64 y_{3} + 3.04 y_{4} &{}~ \\ s. t. &{} -5.56 y_{1} -1.46 y_{2} -1.85 y_{3} -5.56 y_{4} &{}\le 5.54,\\ ~ &{} 0.62 y_{1} + 2.37 y_{2} + 1.87 y_{3} + 0.62 y_{4} &{}\le 0.5,\\ ~ &{} -0.62 y_{1} - 2.37 y_{2} - 1.87 y_{3} - 0.62 y_{4} &{}\le 0. \end{array}\right. \end{aligned}$$

After having solved the linear program, we obtain the following optimal solution:

$$\begin{aligned} y_{sol} = (-1,-0.24,1,-0.26), ~c^T y_{sol} = -3.70, c^T y_{sol}+E_f =14.15. \end{aligned}$$

Hence, using Proposition 5, we obtain a lower bound ${14.15}$. By comparison, the lower bound computed directly with interval arithmetic is $12.5$ and $10.34$ using directly only AF1 on the objective function, respectively. This is due to the fact that we do not consider only the objective function to find a lower bound but we use the constraints and the set of feasible solutions as well.

Remark 3

This section defines a methodology for constructing relaxed linear programs using different affine forms and their corresponding arithmetic evaluations. These results could be extended to the use of other forms such as those defined in Messine (2002) and in Messine and Touhami (2006), which are based on quadratic formulations.

Remark 4

The expression of the linear program (9) depends on the box ${\varvec{x}}$. Thus, if ${\varvec{x}}$ changes, the linear program (9) must be generated again to have a better approximation of the original problem (8).

4 Reliable affine reformulation technique: ${rART}_\mathrm{rAF}$

The methodology explained in the previous section has some interests in itself; (i) the constraints are applied to compute a better lower bound on the objective function, (ii) the size of the linear program is not much larger than the original and (iii) the dependence links among the variables are exploited. But the method is not reliable in the presence of numerical errors due to the approximations provided by using some floating point representations and computations. In the present section, we explain how to make our methodology completely reliable.

First, we need to use a reliable affine arithmetic. The first version of affine arithmetic defined by Comba and Stolfi (1993), was not reliable. In Stolfi and de Figueiredo (1997), De Figueiredo and Stolfi proposed a self-validated version for standard affine arithmetic; i.e., all the basic operations are done three times (including the computations of the value of the scalar, the positive and the negative numerical errors). Another possibility is to use the Reliable Affine Arithmetic such as defined by Messine and Touhami in Messine and Touhami (2006). This affine arithmetic replaces all the floating numbers of the affine form by an interval, see Eq. (10), where the variables in bold indicate the interval variables.

$$\begin{aligned} \mathbf{\widehat{x}} = \mathbf{x_0} + \displaystyle \sum _{i=1}^{n}\mathbf{x_i } \epsilon _i, \end{aligned}$$

(6)

with $\forall i \in \{0,1,\dots ,n\}, \mathbf{x_i} = [\underline{x_i}, \overline{x_i}] \in {\mathbb {I}}{\mathbb {R}}$ and $\forall i \in \{1,\dots ,n\},\epsilon _i\in {\varvec{\epsilon }}_i = [-1,1]$.

The conversions between interval arithmetic, affine arithmetic and reliable affine arithmetic are performed as follows:

In this Reliable Affine Arithmetic, all the affine operations are done as for the standard affine arithmetic but using properly rounded interval arithmetic (Moore 1966) to ensure its reliability. In Messine and Touhami (2006), the multiplication was explicitly given, and the same principle is used in this paper to define other nonlinear operations.

Algorithm 1 is a generalization of the min-range linearization introduced by Stolfi and de Figueiredo (1997), for finding that linearization, which minimizes the range of a monotonic continuous convex or concave function in reliable affine arithmetic. Such as in the algorithm of De Figueiredo and Stolfi, Algorithm 1 consists of finding, in a reliable way, the three scalars $\alpha , \zeta$ and $\delta$, see Eq. (6) and Fig. 1.

Remark 5

The arithmetic in Algorithm 1 is a particular case of the generalized interval arithmetic introduced by E. Hansen in Hansen (1975). Hansen’s generalized arithmetic is equivalent to an affine form with interval coefficients. The multiplication has the same definition as in reliable affine arithmetic. However, the division is not generalizable and the affine information is lost. Furthermore, for nonlinear functions, such as the logarithm, exponential, and square root, nothing is defined in Hansen (1975). In our particular case of a reliable affine arithmetic, these difficulties to compute the division and nonlinear functions are avoided.

Indeed, using the principle of this reliable affine arithmetic, we obtain reliable versions for the affine forms AF1 and AF2, denoted by rAF1 and rAF2. Moreover, as in Sect. 3, we apply Proposition 2 and 3 to rAF1 and rAF2 to provide a reliable affine reformulation for every factorable function; i.e., we obtain a linear relaxation in which all variables are intervals. Consequently, using the reformulation methodology described in Sect. 3 for rAF1 or rAF2, we produce automatically a reliable linear program, i.e. all the variables of the linear program (9) are intervals, and the feasibility of a solution $x$ in Proposition 4 can exactly be verified.

When the reliable linear program is generated, two approaches can be used to solve it; (i) the first one relies on the use of an interval linear solver such as LURUPA (Jansson 2003; Keil 2006) to obtain a reliable lower bound on the objective function or a certificate of infeasibility. Thus, these properties are extended to the general problem (8) using Proposition 5 and Corollary 1; (ii) the second one is based on generating a reliable linear reformulation of each function of the general problem (8). Then, we use the conversion between rAF1/AF1 or rAF2/AF2 (see Eq. (12)) to obtain a linear reformulation in which all variables are scalar numbers, but, in this case, all numerical errors are taken into account as intervals, and moved to the error variables of the affine form by the conversion. Indeed, we have a linear program which satisfies the conditions of Proposition 4 in a reliable way. Then, we use a result from Neumaier and Shcherbina (2004) to compute a reliable lower bound of our linear program or a reliable certificate of infeasibility. This method applied to our case yields:

$$\begin{aligned} \left\{ \begin{array}{cl} \displaystyle \min _{\lambda \in {\mathbb {R}}_+^{m}, u, l \in {\mathbb {R}}_+^{n} } &{} b^T \lambda + \displaystyle \sum _{i=1}^{n}\left( l_i + u_i\right) \\ {s.t.} &{}A^T \lambda - l +u = -c. \end{array}\right. \end{aligned}$$

(7)

The linear program (13) corresponds to the dual formulation of the linear program (9). Let $(\lambda _S, l_S, u_S)$ be an approximate dual solution given by a linear solver, the bold variables indicate the interval variables and $(\varvec{\Lambda }_\mathbf{S}, \mathbf{L_S}, \mathbf{U_S})$ is the extension of $(\lambda _S, l_S, u_S)$ into interval arithmetic, i.e. $\varvec{\Lambda }_\mathbf{S}=[\lambda _S]$, $\mathbf{L_S}=[l_S]$ and $\mathbf{U_S}=[u_S]$. This conversion makes it possible to perform all computations using rounded interval arithmetic. Then, we can compute the residual of the dual (13) by interval arithmetic, such as:

$$\begin{aligned} r \in \mathbf{R} = c \oplus A^T \varvec{\Lambda }_\mathbf{S} \ominus \mathbf{L_S} \oplus \mathbf{U_S}. \end{aligned}$$

(8)

Hence, using the bounds calculated in Neumaier and Shcherbina (2004), we have:

$$\begin{aligned} \forall y \in S_2 , c^T y \in \left( \mathbf{R}^T {\varvec{\epsilon }}\ominus {{\varvec{\Lambda }}_\mathbf{S}}^T [-\infty , b] \oplus \mathbf{L_S}^T {\varvec{\epsilon }}\ominus \mathbf{U_S}^T {\varvec{\epsilon }}\right) , \end{aligned}$$

(9)

where ${\varvec{\epsilon }}=([-1,1], \dots , [-1,1])^T$ and $[-\infty , b] = ([-\infty , b_1], \dots , [-\infty , b_m])^T$.

Proposition 8

Let $(\lambda _S, l_S, u_S)$ be an approximate solution which minimizes (13), the dual of the linear program (9). Let $\varvec{\Lambda }_\mathbf{S}=[\lambda _S]$, $\mathbf{L_S}=[l_S]$ and $\mathbf{U_S}=[u_S]$. Then,

$$\begin{aligned} \forall x \in S_1 , f(x) \ge \text {inf}\left( \mathbf{R}^T {\varvec{\epsilon }}\ominus {{\varvec{\Lambda }}_\mathbf{S}}^T [-\infty , b] \oplus \mathbf{L_S}^T {\varvec{\epsilon }}\ominus \mathbf{U_S}^T {\varvec{\epsilon }}\oplus E_f\right) . \end{aligned}$$

Proof

The result is obtained by applying Eqs. (14), (15) and Proposition 5. $\square$

When the bounds cannot be computed, the dual program (13) can be unbounded or infeasible. If it is the case, the primal (9) must be infeasible or unbounded. Since the feasible set of the primal (9) is included in the bounded set $[-1,1]^n$, it must be infeasible. Indeed, to prove that the dual (13) is unbounded, we look for a feasible solution of the constraint satisfaction problem (16) (it is a well-known method directly adapted from Neumaier and Shcherbina 2004), since such a solution provides an unbounded direction:

$$\begin{aligned} \left\{ \begin{array}{l} b^T \lambda + \displaystyle \sum _{i=1}^{n}\left( l_i + u_i\right) \ne 0\\ A^T \lambda - l +u = 0,\\ \lambda \in {\mathbb {R}}_+^{m}, u, l \in {\mathbb {R}}_+^{n}. \end{array}\right. \end{aligned}$$

(10)

Proposition 9

Let $(\lambda _c, l_c, u_c)$ be the approximate solution of the constraint satisfaction problem (16). Let $\varvec{\Lambda }_\mathbf{c}=[\lambda _c]$, $\mathbf{L_c}=[l_c]$ and $\mathbf{U_c}=[u_c]$.

If $0 \not \in {\left( { \left( A^T \varvec{\Lambda }_\mathbf{c} \ominus \mathbf{L_c} \oplus \mathbf{U_c} \right) }^T{\varvec{\epsilon }}\ominus {{\varvec{\Lambda }}_\mathbf{c}}^T [-\infty , b] \oplus \mathbf{L_c}^T {\varvec{\epsilon }}\ominus \mathbf{U_c}^T {\varvec{\epsilon }}\right) }$ then the general problem (8) is guaranteed to be infeasible.

Proof

By applying the previous calculation with the dual residual $r \in \mathbf{R} = A^T \varvec{\Lambda }_\mathbf{c} - \mathbf{L_c} + \mathbf{U_c}$, we obtain that:

if $0 \not \in {\left( { \left( A^T \varvec{\Lambda }_\mathbf{c} \ominus \mathbf{L_c} \oplus \mathbf{U_c} \right) }^T {\varvec{\epsilon }}\ominus {{\varvec{\Lambda }}_\mathbf{c}}^T [-\infty , b] \oplus \mathbf{L_c}^T {\varvec{\epsilon }}\ominus \mathbf{U_c}^T {\varvec{\epsilon }}\right) }$, then the primal program (9) is guaranteed to be infeasible. Thus by applying Corollary 1, Proposition 9 is proven. $\square$

Indeed, using Propositions 8 and 9, we have a reliable way to compute a lower bound on the objective function and a certificate of infeasibility by taking into account the constraints. In the next section, we will explain how to integrate this technique into an interval branch and bound algorithm.

5 Application within an interval branch and bound algorithm

In order to prove the efficiency of the reformulation method described previously, we apply it in an Interval Branch and Bound Algorithm named IBBA, previously developed by two of the authors (Messine 2005; Ninin 2010). The general principle is described in Algorithm 2. Note that there exist other algorithms based on interval arithmetic such as for example GlobSol, developed by Kearfott (1996). The fundamental principle is still the same, except that different acceleration techniques are used.

In Algorithm 2, at each iteration, the domain under study is chosen and bisected to improve the computation of bounds. In Line 11 of Algorithm 2, boxes are eliminated if and only if it is certified that at least one constraint cannot be satisfied by any point in such a box, or that no point in the box can produce a solution better than the current best solution minus the required relative accuracy. The criterion $\displaystyle \left( \tilde{f}- \varepsilon _f \max (|\tilde{f}~|, 1)\ge {f_z}_j\right)$ has the advantage of reducing both the cluster problem (Du and Kearfott 1994; Schichl et al. 2014) and the excess processing that occurs when an infinity of equivalent non-isolated solutions exists.

At the end of the execution, Algorithm 2 is able to provide only one global minimizer $\tilde{x}$, if a feasible solution exists.

$\tilde{x}$ is reliably proven to be a global minimizer with a relative guaranteed error $\varepsilon _f$ which depends on the magnitude of $\tilde{f}$. If Algorithm 2 does not provide a solution, this proves that the problem is infeasible (case when $(\tilde{f}==\infty )$ and $({\mathcal {L}}==\emptyset )$). For more details about this kind of interval branch and bound algorithms, please refer to (Hansen and Walster 2004, Kearfott 1996; Messine 2005; Ninin 2010, Ratschek and Rokne 1988).

Remark 6

On a computer, each real number is represented by a flaoting point number. This approximation introduces numerous difficulties to certify numerical solutions provided by an algorithm. Denote the set of floating point numbers by $\mathbb {F}$ and the expressions of $f, g_k$ and $h_l$ in floating point arithmetic by $f^{\mathbb {F}}, g_k^{\mathbb {F}}$ and $h_l^{\mathbb {F}}$ respectively. Notice that in Problem (8), if we replace $\mathbb {R}$ by $\mathbb {F}$, in many cases, there will be no floating point number satisfying the equality constraints. That is why the constraints must be relaxed. Hence, optimization codes have to deal with the following problem:

$$\begin{aligned} \left\{ \begin{array}{cll} \displaystyle \min _{x \in {\varvec{x}}^{\mathbb {F}} \subset \mathbb {F}^n } &{}f^{\mathbb {F}}(x) \\ \text {s.t.} &{}\quad g^{\mathbb {F}}_k(x) \le \varepsilon _g , &{}\quad \forall k\in \{1,\dots , p\}, \\ &{}\quad h^{\mathbb {F}}_l(x) \in [-\varepsilon _h,\varepsilon _h] , &{}\quad \forall l\in \{1,\dots ,q\}. \end{array}\right. \end{aligned}$$

(11)

where $\varepsilon _g$ and $\varepsilon _h$ are small positive floating point numbers, and the box ${\varvec{x}}^{\mathbb {F}}$ is the smaller box such that ${\varvec{x}}$ is included in its convex hull. Thus, by considering Problem (17) over $\mathbb {R}^n$ in place of $\mathbb {F}^n$, we obtain a relaxation of Problem (8). Therefore, at the end of Algorithm 2, it is proven that there is no real vector $x$ satisfying the relaxed constraints such that: $f(x) < \tilde{f}-\varepsilon _f \max (|\tilde{f}~|,1)$. Hence, the returning floating point vector $\tilde{x}$ is certified to be a $\varepsilon _f-$global optimum of Problem (17). Notice that Algorithm 2 could not find such a point $\tilde{x}$ if the set defined by the constraints is too small or does not contain any floating point vector. Moreover, using our upper bounding technique, we can find a solution of Problem (17) better and also different from the real one of Problem (8). Nevertheless, notice that the solutions of Problem (17) depend directly on $\varepsilon _g$ and $\varepsilon _h$ given by the user.

One of the main advantages of Algorithm 2 is its modularity. Indeed, acceleration techniques can be inserted or removed from IBBA. For example at Line 8, an interval constraint propagation technique is included to reduce the width of boxes ${\varvec{z}}_j$; for more details refer to Messine (2004). Another implementation of this method is included in the code RealPaver (Granvilliers and Benhamou 2006), the code Couenne of the project COIN-OR (Belotti et al. 2009), the code IBEX (2014) and the code GlobSol (Kearfott Jan 2009). This additional technique improves the speed of the convergence of such a Branch and Bound algorithm.

Affine reformulation techniques described in the previous sections can also be introduced in Algorithm 2. This routine must be inserted between Lines 8 and 9. At each iteration, as described in Section 3, for each ${\varvec{z}}_1$ and ${\varvec{z}}_2$, the associated linear program (9) is automatically generated and a linear solver (such as CPLEX) is applied. If the linear program is proved to be infeasible, the element is eliminated. Otherwise the solution of the linear program is used to compute a lower bound of the general problem over the boxes ${\varvec{z}}_1$ and ${\varvec{z}}_2$.

Remark 7

In order to take into account the value of the current minimum in the affine reformulation technique, the equation $f(x) \le \tilde{f}~$ is added to the constraints when $\tilde{f}\ne \infty$.

Algorithm 3 describes all the steps of the affine reformulation technique $ART_\mathrm{AF}$. The purpose of this method is to accelerate the solution by reducing the number of iterations and the computation time of Algorithm 2. At Line 11 of Algorithm 3, Proposition 7 is used to reduce the number of constraints; this limits the size of the linear program without losing any information. The computation performed in Line 18 provides a lower bound for the general problem over a particular box by using Proposition 5. Corollary 1 involves the elimination part which corresponds to Line 20. If the linear solver cannot produce a solution in an imposed time or within a given number of iterations, the bound is not modified and Algorithm 2 continues.

Remark 8

Affine arithmetic cannot be used when in an intermediate node of the computation tree, the resulting interval is unbounded. For example {$\min _{x\in [-1,1]} \frac{1}{x}$ s.t. $x^2\ge 1/4$}, it is impossible to construct a linearization of the objective function with our method. Therefore, if the objective function corresponds to this case, the bound is not modified and Algorithm 2 continues without using the affine reformulation technique at the current iteration. More generally, if it is impossible to linearize a constraint, the method continues without including this constraint into the linear program. Thus, the linear program is more relaxed, and the computation of the lower bound and the elimination property are still correct.

In Sect. 4, we have explained how the affine reformulation technique can be reliable and rigorous. Algorithm 4 summarizes this method named $rART_\mathrm{rAF}$ and adapts Algorithm 3. We first use rAF1 or rAF2 with the conversion between rAF1/AF1 or rAF2/AF2 to produce the linear program (9), using Eq. (12), Propositions 2 and 3. Then, Proposition 7 is used in Line 11 of Algorithm 4 to reduce the number of constraints. Thus, in most cases, the number of added constraints is small, and the dual solution is improved. Moreover, we do not need to explicitly give the primal solution, thus we advise generating the dual (13) directly and solving it with a primal solver. If a dual solution is found, Proposition 8 guarantees a lower bound of the objective function, Line 20 of Algorithm 4. Otherwise, if the solver returns that the dual is unbounded or infeasible, Proposition 9 produces a certificate of infeasibility for the original problem (8).

In this section, we have described two new acceleration methods, which can be added to an interval branch and bound algorithm. $rART_\mathrm{rAF}$ (Algorithm 4) included in IBBA (Algorithm 2) allows us to take rounding errors into account everywhere in the interval branch and bound codes. In the next section, this method will be tested to several numerical tests to prove its efficiency concerning CPU-times and the number of iterations.

6 Numerical tests

In this section, 74 non-linear and non-convex constrained global optimization problems are considered. These test problems come from Library 1 of the COCONUT website (Neumaier Neumaier; Neumaier et al. 2005). We take into account all the problems with constraints, having less than 25 variables and without the cosine and sine functions which are not yet implemented in our affine arithmetic code (Messine 2002; Ninin 2010); however square root, inverse, logarithm and exponential functions are included, using Algorithm 1. For all 74 test problems, no symbolic reformulation has been done. The expressions of the equations are exactly the same as those provided in the COCONUT format. No modification has been done on the expressions of those functions and constraints, even when some of them are clearly unadapted to the computation of bounds with interval and affine arithmetic.

The code is written in Fortran 90/95 and compiled using the f90 ORACLE compiler which includes a library for interval arithmetic. In order to solve the linear programming relaxation, CPLEX version 11.0 is used. All tests are performed on a Intel-Xeon based 3 GHz computer with 2 GB of RAM and using a 64-bit Linux system (the standard time unit (STU) is 13 seconds which corresponds to $10^8$ evaluations of the Shekel-5 function at the point $(4,4,4,4)^T$). The termination condition is based on the precision of the value of the global minimum: $\tilde{f}-\min _{({\varvec{z}},{f_z})\in {\mathcal {L}}} {f_z}\le \varepsilon _f \max (|\tilde{f}~|,1)$. This relative accuracy of the objective function is fixed to $\varepsilon _f=10^{-8}$ for all the problems and the accuracies of the constraints are $\varepsilon _g = 10^{-8}$ and $\varepsilon _h=10^{-8}$. The accuracy to solve the linear program by CPLEX is fixed to $10^{-8}$ and we limit the number of iterations of a run of CPLEX to 15. Furthermore, two limits are imposed: (a) on the CPU-time which must be less than 60 minutes and (b) on the maximum number of elements in $\mathcal {L}$ which must be less than two millions (corresponding approximately to the limit of the RAM of our computer for the largest problem). When the code terminates normally the values corresponding to (i) whether the problem is solved or not, (ii) the number of iterations of the main loop of Algorithm 2, and (iii) the CPU-time in seconds (s) or in minutes (min), are respectively given in columns ‘ok?’, ‘iter’ and ‘t’ of Tables 1, 2 and 3.

Table 1 Numerical results for reliable IBBA based methods

Table 2 Comparison with GlobSol approach Kearfott 2006 and our approach

Table 3 Numerical results for non reliable but exact global optimization methods

The names of the COCONUT problems are in the first column of the tables; in the COCONUT website, all problems and best known solutions are given. Columns $N$ and $M$ represent the number of variables and the number of constraints for each problem. Test problem hs071 from Library 2 of COCONUT corresponds to Example 3 when the box is ${\varvec{x}}=[1,5]^4$ and the constraints are only $c_1$ and $c_2$.

For all tables and performance profiles, IBBA+CP indicates results obtained with Algorithm 2 (IBBA) and the constraint propagation technique (CP) described in Messine (2004). $IBBA+rART_\mathrm{rAF2}$ represents results obtained with Algorithm 2 and the reliable affine reformulation technique based on the rAF2 affine form (Algorithm 4) and the corresponding affine arithmetic (Messine 2002;Ninin 2010; Messine and Touhami 2006). $IBBA+rART_\mathrm{rAF2}$ +CP represents results obtained with Algorithm 2 and both acceleration techniques. GlobSol+LR and GlobSol represent the results extracted from Kearfott (2006) and obtained using (or not) the linear relaxation based on RLT (Kearfott and Hongthong 2005).

The performance profiles, defined by Dolan and Moré (2002), are visual tools to benchmark algorithms. Thus, Tables 1, 2 and 3 are summarized in Fig. 3 accordingly. The percentage of solved problems is represented as a function of the performance ratio; the latter depending itself on the CPU-time. More precisely, for each test problem, one compares the ratio of the CPU-time of each algorithm to the minimum of those CPU-times. Then the performance profiles, i.e. the cumulative distribution functions for the ratio, are computed.

Remark 9

Algorithm 2 was also tested alone. The results are not in Table 1 because Algorithm 2 does not work efficiently without one of the two acceleration techniques. In this case, only 24 of the 74 test problems were solved.

6.1 Validation of the reliable approach

In Table 1, a comparison is made among the basic algorithm IBBA with constraint propagation CP, with the new relaxation technique rART and with both. It appears that:

• IBBA+CP solved 37 test problems, $IBBA+rART_\mathrm{rAF2}$ 52 test problems and $IBBA+rART_\mathrm{rAF2}$ +CP 61 test problems.

• The solved cases are not the same using the two distinct techniques (CP or $rART_\mathrm{rAF2}$). Generally, IBBA+CP finished when the limit on the number of elements in the list is reached (corresponding to the limitation of the RAM). In contrast, the $IBBA+rART_\mathrm{rAF2}$ code stopped when the limit on the CPU-time was reached.

• All problems solved with one of the acceleration techniques are solved also when both are combined. Moreover, this is achieved in a moderate computing time of about 1 min 9 s on average.

• Considering only the 33 cases solved by all three methods (in the tables), in the line ‘Average when T for all’ of Table 1, we obtain that average computing time of IBBA+CP is three times the one of $IBBA+rART_\mathrm{rAF2}$, but is divided by a factor of about $10$ when those two techniques are combined. Considering the number of iterations, the gain of $IBBA+rART_\mathrm{rAF2}$ +CP is a factor of about $200$ compared to IBBA+CP, and about $3.5$ compared to $IBBA+rART_\mathrm{rAF2}$.

The performance profiles of Fig. 3 confirm that $IBBA+rART_\mathrm{rAF2}$ +CP is the most efficient and effective of the three first studied algorithms. Considering the curve of the algorithms $IBBA+rART_\mathrm{rAF2}$ and IBBA+CP shows that IBBA+CP is in general faster than the other but $IBBA+rART_\mathrm{rAF2}$ solves more problems, which implies a crossing of the two curves.

Fig. 3

Performance profile comparing the results of various versions of algorithms

By observing how the acceleration techniques work on a box, the reformulation $rART_\mathrm{rAF2}$ is more precise when the box under study is small. This technique is slow at the beginning and becomes very efficient after a while. In contrast, CP enhances the convergence when the box is large, but since it considers the constraints one by one, this technique is less useful at the end. That is why the combination of CP and $rART_\mathrm{rAF2}$ is so efficient: CP reduces quickly the size of boxes and then $rART_\mathrm{rAF2}$ considerably improves the lower bound on each box and eliminates boxes which do not contain the global minimum.

In Table 2, column ‘our guaranteed UB’ corresponds to the upper bound found by our algorithm and column ‘UB of COCONUT’ corresponds to the upper bound listed in Neumaier and found by the algorithm of the column ‘Algorithm’. We remark that all our bounds are close to those of COCONUT. These small differences appear to be due to the accuracy guaranteed on the constraint satisfactions.

6.2 Comparison with GlobSol

Kearfott and Hongthong (2005) have developed another technique based on the same principle such as Reformulation Linearization Technique (RLT), by replacing each nonlinear term by linear overestimators and underestimators. This technique was well-known and already embedded without interval and affine arithmetics in the software package BARON (Tawarmalani and Sahinidis 2004). Another paper by Kearfott (2006) studies its integration into an interval branch and bound algorithm named GlobSol. In Kearfott (2006), the termination criteria of the branch and bound code are not exactly the same for GlobSol and $IBBA+rART_\mathrm{rAF2}$ +CP. The stopping criterion of GlobSol ensures enclosures of all exactly optimizing points. This difference leads to favor IBBA. Thus, this empirical comparison between GlobSol and $IBBA+rART_\mathrm{rAF2}$ +CP should be considered as a first approximation. Moreover, (i) the CPU-times in Table 2 depend on the performances of the two different computers (Kearfott used GlobSol with the Compaq Visual Fortran version 6.6, on a Dell Inspiron 8200 notebook with a mobile Pentium 4 processor running at 1.60 GHz), (ii) the version of GlobSol used in Kearfott (2006) is not the last one, and (iii) it is the first version of $IBBA+rART_\mathrm{rAF2}$ +CP which does not include classical accelerating techniques as the use of a local solver to improve the upper bounds. However, this does not modify our conclusions. It appears that:

• GlobSol+LR solves 26 among the subset of 39 test problems attempted, GlobSol without LR solves 32 of them, and $IBBA+rART_\mathrm{rAF2}$ +CP solves 36.

• Kearfott limited his algorithm to problems with 10 variables at most. Indeed problems solved by GlobSol without LR have at most 8 variables and 9 constraints. Problems solved by $IBBA+rART_\mathrm{rAF2}$ +CP have at most 24 variables and 17 constraints.

• GlobSol without LR solved 1 problem in 53 minutes that $IBBA+rART_\mathrm{rAF2}$ +CP does not solve in 60 minutes (ex6_1_1). $IBBA+rART_\mathrm{rAF2}$ +CP solved 5 problems that GlobSol without LR does not solve and 10 that GlobSol+LR does not solve.

Turning now to the performance profile of Fig. 3, we observe that: (i) the linear relaxation of Kearfott and Hongthong slows down their algorithm on this set of test problems; (ii) the performance of $IBBA+rART_\mathrm{rAF2}$ +CP dominates those of GlobSol with and without LR, it still remains true if we multiply the computation time by $2$ to overestimate the difference between the computers.

6.3 Comparison with the non-reliable methods

In Table 3, results for non-rigorous global optimization algorithms are presented to evaluate the cost of the reliability in our algorithm combining CP and $ART_\mathrm{AF2}$ techniques. Thus, we test for all three cases an IBBA algorithm associated with the CP and $ART_\mathrm{AF2}$ techniques (Algorithm 3) when the affine arithmetic corresponding to the affine form AF2 is not strictly reliable (the rounding errors are not taken into account). In the first and second main data column, Algorithm 3 is used and the associated linear programs for computing bounds are solved by using the primal formulation of program (9) for the column $IBBA+ART_\mathrm{AF2\_primal}$ +CP and the dual formulation for the column $IBBA+ART_\mathrm{AF2\_dual}$ +CP. In the third columns $IBBA+rART_\mathrm{AF2}$ +CP, we use Algorithm 4 but the linear program is generated directly with AF2 instead of rAF2, thus the linear program is not completely reliable. It appears that:

• Comparing to the reliable code $IBBA+rART_\mathrm{rAF2}$ +CP, two new test problems, ex6_1_1 and ex7_2_3 of COCONUT, are now solved by all the three non-reliable algorithms, see Table 3. However, this is only due to the stopping criterion on the CPU-time which is fixed to one hour.

• Analyzing the performance profiles on Fig. 3, the primal formulation seems to be more efficient. Indeed up to a ratio of about 2, we note that the largest part of the tests are most rapidly solved by the version using the primal formulation for solving the linear programs $IBBA+ART_\mathrm{AF2\_primal}$ +CP. Nevertheless, we also note that some cases are more difficult to solve using the primal formulation (see ex2_1_9 and ex7_3_1 of Table 3) than using the dual formulation. This provides the worst CPU-time average for $IBBA+ART_\mathrm{AF2\_primal}$ +CP even if it is generally the most efficient (see Fig. 3). In fact, it appears that $IBBA+ART_\mathrm{AF2\_primal}$ +CP spends more time to reach the fixed precision of $10^{-8}$ than the dual versions; solutions with an accuracy of about $10^{-6}$ are rapidly obtained with the primal version, but sometimes, this code spends a huge part of the time to improve the precision until $10^{-8}$ is reached (as for example ex2_1_9 in Table 3).

• The increasing CPU-time to obtain reliable computations is about a factor of 2, see last line of Tables 3 and 1 where the averages are done for the 61 cases which the reliable code find the global solution in less than one hour. Indeed, the CPU-time average for the reliable method is $69.3$ seconds for the 61 results solved in Table 1, compared to about $35$ seconds obtained by the two non-reliable dual versions of the code. Similar results are obtained concerning the number of iterations of reliable and non-reliable dual versions of the code which confirms that each iteration of the reliable method is about $2$ times more consuming compared to the corresponding non-reliable one.

• All methods presented in Table 3 are efficient: the algorithms are not exactly reliable, but no numerical error results in a wrong optimal solution.

7 Conclusion

In this paper, we present a new reliable affine reformulation technique based on affine forms and their associated arithmetics. These methods construct a linear relaxation of continuous constrained optimization problems in an automatic way. In this study, we integrate these new reliable affine relaxation techniques into our own interval branch and bound algorithm for computing lower bounds and for eliminating boxes which do not contain the global minimizer point. The efficiency of this technique has been validated on 74 problems from the COCONUT database. The main advantage of this method is that the number of variables in the linear programs generated is the same as in the original optimization problem. Indeed, the linear programs require short times to be solved. Moreover, when the width of the boxes under study becomes small, the errors generated by the relaxation are reduced and the computed bounds are more precise.

Furthermore, inserting this new affine relaxation technique with constraint propagation into an interval branch and bound algorithm results in a relatively simple and efficient algorithm.