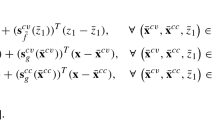Reverse propagation of McCormick relaxations

Abstract

Constraint propagation techniques have heavily utilized interval arithmetic while the application of convex and concave relaxations has been mostly restricted to the domain of global optimization. Here, reverse McCormick propagation, a method to construct and improve McCormick relaxations using a directed acyclic graph representation of the constraints, is proposed. In particular, this allows the interpretation of constraints as implicitly defining set-valued mappings between variables, and allows the construction and improvement of relaxations of these mappings. Reverse McCormick propagation yields potentially tighter enclosures of the solutions of constraint satisfaction problems than reverse interval propagation. Ultimately, the relaxations of the objective of a non-convex program can be improved by incorporating information about the constraints.

1 Introduction

A constraint satisfaction problem (CSP) consists of a finite set of variables, domains and constraints. A solution of a CSP is an assignment of elements of the domains to the variables so that all constraints are satisfied. In general, these problems are NP-hard and hence it is desirable to compute an enclosure of the solution set. Constraint propagation routines, or, more generally, contractors, are numerical methods that assist in this task. Using the information about the relationship between variables that is contained in a single constraint or in a set of constraints, they attempt to shrink an initial enclosure of the domains. Typically, intervals are used to enclose the solution sets whereas a constraint propagation technique for McCormick relaxations [39, 52] is proposed in this contribution that is applicable to factorable functions.

1.1 Review of constraint propagation methods

Constraint propagation was first developed for logic constraints on discrete domains [35]. Different notions of consistency, which describes the degree to which the remaining elements of the domain satisfy the constraints, have been introduced for this case [2, 9]. Constraint propagation has also been applied to connected sets that appear in so-called numerical CSPs [8, 13] and a large number of techniques have been proposed in the literature.

Many constraint propagation methods use ideas from interval analysis: they consider interval domains and use interval arithmetic. Cleary [12] and Davis [13] presented the first algorithms for constraint propagation with interval domains. Hyvönen [26] considered cases where exact numbers are insufficient and studied how interval arithmetic can be utilized in CSPs. Lhomme [33] proposed an extension of arc-consistency to numeric CSPs. Benhamou et al. [6] introduced the notion of box-consistency. Sam-Haroud and Faltings [49] approximated feasible regions by $2^n$-trees and presented algorithms to label leaves consistently. Benhamou and Older [5] proposed the notion of hull-consistency. Van Hentenryck et al. [59] showed how interval extensions can be used to calculate box-consistent labels, see also [60]. Benhamou et al. [7] proposed an algorithm for hull-consistency that does not require decomposing constraints into primitives. Vu et al. [61] proposed a method to construct inner and outer approximations of the feasible set using unions of intervals. Lebbah et al. [32] discussed how the reformulation-linearization technique can be used to relax nonlinear constraints and to aid in pruning the search space. Granvilliers and Benhamou [19] proposed an algorithm that prunes boxes using both constraint propagation techniques and the interval Newton method. Recently, Domes and Neumaier [15] proposed a constraint propagation method for linear and quadratic constraints and constraints and Jaulin [27] studied set-valued CSPs.

Jaulin et al. [28] discussed contractors based on interval analysis, many of which were also the subject of Neumaier’s book, though it focused on solving systems of equations in the presence of data uncertainty [43]. Recently, Schichl and Neumaier [50] studied directed acyclic graphs (DAG) to represent functions for interval evaluation. Vu et al. [62] used this representation and extended the contractor proposed in [7], which propagates interval information forward and backward along the DAG. Recently, Stuber et al. [55] extended contractors based on interval analysis to compute convex and concave relaxations of implicit functions. However, their methods require existence and uniqueness of the implicit function on the full domain.

1.2 Connection to global optimization

Continuous optimization problems are often solved to guaranteed global optimality using continuous branch-and-bound algorithms [17, 25]. It is well-known that the efficiency of these algorithms can be improved by discarding parts of the search space that are infeasible or that are known not to contain optimal solutions [56]. These tasks are often referred to as domain reduction. Obviously, global optimization is an important application of CSPs [44] and ideas originally developed for CSPs are routinely utilized in global optimization: logic-based methods can enhance and expedite optimization routines [24], constraint propagation is often used to discard parts of the domain where the solution is known not to exist (e.g., [21, 22, 47]). For example, constraint propagation routines are part of BARON’s pre-processing step [48]. It is also not coincidental that many constraint satisfaction tools use branch-and-prune frameworks inspired by global optimization algorithms to identify a set of boxes that contains all solutions (e.g., [19, 32, 59]). Also, see the recent discussion of feasibility-based bounds-tightening procedures in [3, 4]. Thus, borrowing and embracing ideas from the other field has been very beneficial for both fields.

As indicated by the “bound” keyword, branch-and-bound algorithms also require computable bounds on the range of the objective function and non-convex constraints. Interval methods have been used to provide such bounds [42, 43, 45, 56]. However, their slow convergence results in long computational times when the number of variables is large, which led to the development of several nonlinear convex relaxation techniques [1, 39, 41, 52, 56, 57] that are more accurate and have higher convergence order [10]. Methods for domain reduction, and CSPs in general, however, still rely almost exclusively on interval arithmetic.

1.3 Replacing intervals with relaxations in constraint propagation

Schichl and Neumaier [50] demonstrated that factorable functions can be represented alternatively as a DAG¹ and discussed how this representation can be used for calculations in interval analysis. Vu et al. [62] detailed how to propagate interval information on DAGs to improve interval bounds. Their method can utilize the information from equality and inequality constraints. We will refer to this idea as reverse interval propagation. In this paper, the idea is extended to convex and concave relaxations.

The remainder of the paper is organized as follows. In Sect. 2, the proposed method will be described briefly. In Sect. 3, the notion of a factorable function is defined and concepts from interval and McCormick analysis are reviewed. Section 4 recapitulates the important results for reverse interval propagation from [62], which are extended to McCormick objects in Sect. 5. Section 6 discusses how the theoretical results from the previous section can be applied to construct, improve and utilize relaxations in the context of CSPs and global optimization. Section 7 describes how the method can be implemented and some small illustrative examples are given in Sect. 8. The results of applying the method to a set of more complicated global optimization test problems are shown in Sect. 9. Section 10 summarizes the contributions and concludes the paper.

2 Method description

In this section, we summarize the proposed method and describe how it can be applied in the context of solving constraint satisfaction problems and optimization problems globally.

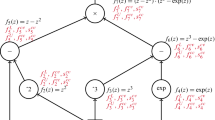
The class of factorable functions encompasses most functions that can be implemented as computer programs without conditional statements. It is well-known that relaxations of factorable functions can be computed using McCormick’s composition rule [39, 52]; the obtained relaxations are often referred to as McCormick relaxations. Here, it is proposed to use the DAG representation of the constraints to also propagate McCormick relaxations backward. For the benefit of the reader we provide an interpretation of relaxations in the context of constraint propagation. Suppose we partition the variables into $p$ and $x$. Whereas reverse interval propagation yields a constant interval bound that all feasible $(x,p)$ must satisfy, reverse McCormick propagation yields bounds that are (convex and concave) functions of $p$. For a given $p$ in the domain, all $x$ so that $(p,x)$ is feasible are bounded. Figure 1 illustrates this interpretation. It shows that a domain (dash-dotted box) can be shrunk by interval constraint propagation to find an outer approximation of the feasible region (dotted box). However, the relaxations (solid and dashed lines) can provide a tighter approximation that is a function of $p$. For example, consider $p_1$, for which a thick solid line shows all feasible $x$. Given $p_1$, the relaxations restrict $x$ to the interval (curly brace in Fig. 1) whereas the interval bounds only constrain them to the larger interval (square bracket). Furthermore, since the bounds are convex and concave functions of $p$, it is tractable, for example, to calculate a reduced interval domain using affine relaxations based on the subgradients of the relaxations [41] or by minimizing and maximizing the relaxations of each $x_i$ on the $p$ domain.

Fig. 1

Illustration of domain reduction by reverse interval and McCormick propagation. The gray area is the set of all feasible points, the dash-dotted line is the original domain, the dotted line is the reduced domain using reverse interval propagation. The solid and dashed lines are relaxations of the feasible region that are functions of $p$

When solving global optimization problems, the improved domains for $x$ and $p$ can be used as input to the calculation of the relaxations of the objective function. By taking advantage of the information about the feasible region, it is possible to improve the tightness of the objective function relaxations, a very desirable feature in global optimization.

The method can be described as follows: First, a particular partitioning of the variables is selected and initial interval bounds $({{{\varvec{p}}}},{{{\varvec{x}}}})$ on the variables are specified. For each variable suitable initial values are then derived from these bounds. Next, for each factor of the function ${F}$ bounds and McCormick relaxations are computed. After this forward pass, bounds as well as convex and concave relaxations of the reachable set $\{{F}(x,p):(x,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}\}$ have been constructed. Now, known restrictions of this reachable set, i.e., equality or inequality constraints are used to tighten these bounds and relaxations. Lastly, this information is propagated back to the variables $x$ and $p$ by “inverting”, in some sense, the operation related to each factor of the function. This yields the relaxations of the feasible space described above.

3 Preliminary definitions and results

In this section, factorable functions will be formally defined with the following development in mind. The notation follows [51], Chapter 2] closely. Also, some concepts from interval and McCormick analysis are reviewed. In particular, Sect. 3.3 utilizes many definitions introduced in [51], Chapter 2].

3.1 Factorable functions

Loosely speaking, a function is factorable if it can be represented as a finite sequence of simple binary operations and univariate functions.

Herein, a function will be denoted as a triple $(o,B,R)$ where $B$ is the domain, $R$ is the range, and $o$ is a mapping from $B$ into $R$, $o:B\rightarrow R$. Permissible functions shall include binary addition $(+,{\mathbb {R}}^2,{\mathbb {R}})$ and multiplication $(\times ,{\mathbb {R}}^2,{\mathbb {R}})$ as well as a collection of univariate functions, cf. Definition 1.

Definition 1

Let ${{\fancyscript{L}}}$ denote a set of functions $(u,B,{\mathbb {R}})$ where $B\subset {\mathbb {R}}$. ${{\fancyscript{L}}}$ will be referred to as a library of univariate functions.

It will be required that, for each $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$, $u(x)$ can be evaluated on a computer for any $x\in B$. Additional assumptions will be introduced when necessary.

Factorable functions will be defined in terms of computational sequences, which are ordered sequences of the permissible basic operations defined above. Every such sequence of computations defines a sequence of intermediate quantities called factors. In the following definition, the factors are denoted by $v_k$, and the functions $\pi _k$ are used to select one or two previous factors to be the operand(s) of the next operation. Note that a computational sequence is a specialization of a DAG because it allows binary and unary operations only.

Definition 2

Let $n_i,n_o\ge 1$. A ${{\fancyscript{L}}}$-computational sequence with $n_i$ inputs and $n_o$ outputs is a pair $({{\fancyscript{S}}},\pi _o)$, where:

• 1. ${{\fancyscript{S}}}$ is a finite sequence of pairs $\{((o_k,B_k,{\mathbb {R}}),(\pi _k,{\mathbb {R}}^{k-1},{\mathbb {R}}^{d_k}))\}_{k={n_i+1}}^{n_f}$ with every element defined by one of the following options:

  • (a) $(o_k,B_k,{\mathbb {R}})$ is either $(+,{\mathbb {R}}^2,{\mathbb {R}})$ or $(\times ,{\mathbb {R}}^2,{\mathbb {R}})$ and $\pi _k:{\mathbb {R}}^{k-1}\rightarrow {\mathbb {R}}^2$ is defined by $\pi _k(v)=(v_i,v_j)$ for some integers $i,j\in \{1,\ldots ,k-1\}$.

  • (b) $(o_k,B_k,{\mathbb {R}})\in {{\fancyscript{L}}}$ and $\pi _k:{\mathbb {R}}^{k-1}\rightarrow {\mathbb {R}}$ is defined by $\pi _k(v)=v_i$ for some integer $i\in \{1,\ldots ,k-1\}$.

• 2. $\pi _o:{\mathbb {R}}^{n_f}\rightarrow {\mathbb {R}}^{n_o}$ is defined by $\pi _o(v)=(v_{i(1)},\ldots ,v_{i(n_o)})$ for some integers $i(1),\ldots ,i(n_o)\in \{1,\ldots ,n_f\}$.

A computational sequence defines a function ${F}_{{\fancyscript{S}}}:D_{{\fancyscript{S}}}\subset {\mathbb {R}}^{n_i} \rightarrow {\mathbb {R}}^{n_o}$ by the following construction.

Definition 3

Let $({{\fancyscript{S}}},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence with $n_i$ inputs and $n_o$ outputs. Define the sequence of factors $\{(v_k,D_k,{\mathbb {R}})\}_{k=1}^{n_f}$ with $D_k\subset {\mathbb {R}}^{n_i}$, where

• 1. for $k=1,\ldots ,n_i$, $D_k={\mathbb {R}}^{n_i}$ and $v_k(x)=x_k$, $\forall x\in D_k$,

• 2. for $k=n_i+1,\ldots ,n_f$, $D_k=\{x\in D_{k-1}:\pi _k(v_1(x),\ldots ,v_{k-1}(x))\in B_k\}$ and $v_k(x)=o_k(\pi _k(v_1(x),\ldots ,v_{k-1}(x)))$, $\forall x\in D_k$.

The set $D_{{\fancyscript{S}}}\equiv D_{n_f}$ is the natural domain of $({{\fancyscript{S}}},\pi _o)$, and the natural function $({F}_{{\fancyscript{S}}},D_{{\fancyscript{S}}},{\mathbb {R}}^{n_o})$ is defined by ${F}_{{\fancyscript{S}}}(x)=\pi _o(v_1(x),\ldots ,v_{n_f}(x))$, $\forall x\in D_{{\fancyscript{S}}}$.

Definition 4

A function ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$ is ${{\fancyscript{L}}}$-factorable if there exists a ${{\fancyscript{L}}}$-computational sequence $({{\fancyscript{S}}},\pi _o)$ with $n$ inputs and $m$ outputs such that the natural function $({F}_{{\fancyscript{S}}},D_{{\fancyscript{S}}},{\mathbb {R}}^m)$ satisfies $D\subset D_{{\fancyscript{S}}}$ and ${F}={F}_{{\fancyscript{S}}}|_D$.

3.2 Interval analysis

Definition 5

We conform to the standardized interval notation outlined in [30]. For $a,b\in {\mathbb {R}}$, $a\le b$ define the interval $[a,b]$ as the compact, connected set $\{x\in {\mathbb {R}}:a\le x\le b\}$. The set of all nonempty intervals is denoted as ${\mathbb {I\! R}}$, and intervals are denoted by bold face letters, ${{{\varvec{x}}}}\in {\mathbb {I\! R}}$. The set of $n$-dimensional boxes (Cartesian products of $n$ intervals) is denoted by ${\mathbb {I\! R}}^n$. The “interval vector” notation $({{{\varvec{x}}}}_1, {{{\varvec{x}}}}_2, \ldots , {{{\varvec{x}}}}_n)$ will often be used for ${{{\varvec{x}}}}_1 \times {{{\varvec{x}}}}_2 \times \cdots \times {{{\varvec{x}}}}_n$. Suppose ${{{\varvec{x}}}}\in {\mathbb {I\! R}}^n$. Then, the lower and upper bounds of ${{{\varvec{x}}}}$ are denoted as $\underline{x}$ and $\overline{x}$, respectively. Suppose $Z\subset {\mathbb {R}}^n$. The set of all interval subsets of $Z$ is denoted by ${\mathbb {I}}\! Z\subset {\mathbb {I\! R}}^n$. Lastly, if $Z$ is nonempty and bounded, then $\Box Z$ with $(\Box {Z})_i=[\inf _{z\in Z} z_i,\sup _{z\in Z} z_i]$, $i=1,\ldots ,n$ denotes the interval hull of $Z$, the tightest box enclosing $Z$. Note that $(\cdot )^L$ and $(\cdot )^U$ will be used for more complex expressions to denote the respective lower and upper bound vectors of a box.

We will encounter functions that either return a vector of reals or the symbol $\mathrm {NaN}$, or “not a number”, which can be thought of as undefined or unspecified. It is convenient to define ${\mathbb {R}}_\emptyset ={\mathbb {R}}\cup \{\mathrm {NaN}\}$. We also define ${}^*\mathbb {R}\! = {\mathbb {R}}\cup \{-\infty ,+\infty \}$ to denote the extended reals. For the purposes of this paper it is also necessary to extend the definition of an interval to include unbounded intervals and empty intervals, which are commonly excluded in the definition of ${\mathbb {I\! R}}$ (e.g, [30]). Here, $\emptyset$ is used to denote the empty interval.

Definition 6

Let ${\mathbb {I}}_\emptyset {\mathbb {R}}\equiv {\mathbb {I\! R}}\cup \{\emptyset \}$, and let the set of all interval subsets of $Z\subset {\mathbb {R}}^n$ including the empty interval be denoted by ${\mathbb {I}}_\emptyset Z\subset {\mathbb {I}}_\emptyset {\mathbb {R}}^n$. Similarly to Definition 5, define the set of all extended intervals as ${}^*\mathbb {I}\! {\mathbb {R}}=\{[a,b]:a \in {\mathbb {R}}\cup \{-\infty \},b \in {\mathbb {R}}\cup \{+\infty \}, a\le b\}\cup \{\emptyset \}$, which includes all unbounded intervals and also the empty interval. Lastly, the set of all extended interval subsets of $Z\subset {\mathbb {R}}^n$ is denoted by ${}^*\mathbb {I}\! Z\subset {}^*\mathbb {I}\! {\mathbb {R}}^n$.

We will follow the conventions that real-valued operations involving $\mathrm {NaN}$ result in $\mathrm {NaN}$, that $[\mathrm {NaN},\mathrm {NaN}]=\emptyset$, that $\mathrm {NaN}$ is an element of any interval, that every interval ${{{\varvec{x}}}}\in {\mathbb {I}}_\emptyset {\mathbb {R}}$ or ${{{\varvec{x}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}$ contains the empty interval and that any interval operation involving the empty interval will again result in the empty interval with the exception of the construction of the interval hull where $\Box \{{{{\varvec{x}}}},\emptyset \}={{{\varvec{x}}}}$ for any ${{{\varvec{x}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}^n$. Note that ${{{\varvec{x}}}}=\emptyset$ for ${{{\varvec{x}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}^n$ if ${{{\varvec{x}}}}_i=\emptyset$ for some $i=1,\ldots ,n$. Otherwise, the operations of interval arithmetic extend naturally. For any $x\in {\mathbb {R}}$ and $\circ \in \{+,-,\cdot ,/\}$, define $x\circ \pm \infty =\lim _{a\rightarrow \pm \infty }x\circ a$.

As described in detail in Sect. 6.1 one benefit of this definition is the ease with which potential domain violations occurring during an evaluation of the natural function can be handled. If we let points outside the natural domain evaluate to $\mathrm {NaN}$ which, by our convention, is an element of any interval then the all-important inclusion property of interval functions, which we will define below, can be maintained.

Definition 7

Let ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}_\emptyset ^m$, and for any ${{{\varvec{x}}}}\subset D$, let $\mathrm{range}({F},{{{\varvec{x}}}})$ denote the image of the box ${{{\varvec{x}}}}$ under ${F}$. A mapping ${{{\varvec{F}}}}:{{\mathfrak {D}}}\subset {}^*\mathbb {I}\! D\rightarrow {}^*\mathbb {I}\! {\mathbb {R}}^m$ is an inclusion function for ${F}$ on ${{\mathfrak {D}}}$ if $\mathrm{range}({F},{{{\varvec{x}}}})\subset {{{\varvec{F}}}}({{{\varvec{x}}}})$, $\forall {{{\varvec{x}}}}\in {{\mathfrak {D}}}$.

Definition 8

Let $D\subset {\mathbb {R}}^n$. A set ${{\mathfrak {D}}}\subset {}^*\mathbb {I}\! {\mathbb {R}}^n$ is an interval extension of $D$ if ${{\mathfrak {D}}}\subset {}^*\mathbb {I}\! D$ and every $x\in D$ satisfies $[x,x]\in {{\mathfrak {D}}}$. Let ${F}:D\rightarrow {\mathbb {R}}_\emptyset ^m$. A function ${{{\varvec{F}}}}:{{\mathfrak {D}}}\subset {}^*\mathbb {I}\! D\rightarrow {}^*\mathbb {I}\! {\mathbb {R}}^m$ is an interval extension of ${F}$ on $D$ if ${{\mathfrak {D}}}$ is an interval extension of $D$ and ${{{\varvec{F}}}}([x,x])=[{F}(x),{F}(x)]$ for every $x\in D$.

Definition 9

Let ${{{\varvec{F}}}}:{{\mathfrak {D}}}\subset {}^*\mathbb {I}\! {\mathbb {R}}^n\rightarrow {}^*\mathbb {I}\! {\mathbb {R}}^m$. ${{{\varvec{F}}}}$ is inclusion monotonic on ${{\mathfrak {D}}}$ if ${{{\varvec{x}}}}_1\subset {{{\varvec{x}}}}_2$ implies that ${{{\varvec{F}}}}({{{\varvec{x}}}}_1)\subset {{{\varvec{F}}}}({{{\varvec{x}}}}_2)$, $\forall {{{\varvec{x}}}}_1,{{{\varvec{x}}}}_2\in {{\mathfrak {D}}}$.

Theorem 1

Let ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}_\emptyset ^m$ and let ${{{\varvec{F}}}}:{{\mathfrak {D}}}\rightarrow {}^*\mathbb {I}\! {\mathbb {R}}^m$ be an interval extension of ${F}$. If ${{{\varvec{F}}}}$ is inclusion monotonic on ${{\mathfrak {D}}}$, then ${{{\varvec{F}}}}$ is an inclusion function for ${F}$ on ${{\mathfrak {D}}}$.

Proof

Choose any ${{{\varvec{x}}}}\in {{\mathfrak {D}}}$ and any $x\in {{{\varvec{x}}}}$. Since $x\in D$, it follows that $[x,x]\in {{\mathfrak {D}}}$. Since $\emptyset \in {{{\varvec{F}}}}({{{\varvec{x}}}})$ is always true, if $f_i(x)=\mathrm {NaN}$ for some $i\in \{1,\ldots ,m\}$ then ${F}(x)\in {{{\varvec{F}}}}({{{\varvec{x}}}})$. Otherwise, the result follows from [51], Theorem 2.3.4]. $\square$

Define the typical inclusion functions for addition and multiplication: let the functions $(+,{\mathbb {I}}_\emptyset {\mathbb {R}}^2,{\mathbb {I}}_\emptyset {\mathbb {R}})$ and $(\times ,{\mathbb {I}}_\emptyset {\mathbb {R}}^2,{\mathbb {I}}_\emptyset {\mathbb {R}})$ be defined by $+({{{\varvec{x}}}},{{{\varvec{y}}}})\equiv [\underline{x}+\underline{y},\overline{x}+\overline{y}]$ and $\times ({{{\varvec{x}}}},{{{\varvec{y}}}})\equiv [\min (\underline{x}\underline{y}, \underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\,\overline{y}), \max (\underline{x}\underline{y},\underline{x}\overline{y},\overline{x}\underline{y},\overline{x}\,\overline{y})]$ and recall our convention² that any operation involving the empty interval results in an empty interval, i.e., $+({{{\varvec{x}}}},\emptyset )=+(\emptyset ,{{{\varvec{x}}}})=\emptyset$ or $\times ({{{\varvec{x}}}},\emptyset )=\times (\emptyset ,{{{\varvec{x}}}})=\emptyset$ for any ${{{\varvec{x}}}}\in {\mathbb {I}}_\emptyset {\mathbb {R}}$.

Assumption 1

Assume that for every $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$, an interval extension $(u,{\mathbb {I}}_\emptyset B,{\mathbb {I}}_\emptyset {\mathbb {R}})$ is known. Furthermore, this interval extension is inclusion monotonic on ${\mathbb {I}}_\emptyset B$.

Suppose that Assumption 1 holds and that $({{\fancyscript{S}}},\pi _o)$ is a ${{\fancyscript{L}}}$-computational sequence. Then, to any element $(o_k,\pi _k)$ of ${{\fancyscript{S}}}$ a corresponding $(o_k,{\mathbb {I}}_\emptyset B_k,{\mathbb {I}}_\emptyset {\mathbb {R}})$ exists. Also, the functions $(\pi _k,{\mathbb {I}}_\emptyset {\mathbb {R}}^{k-1},{\mathbb {I}}_\emptyset {\mathbb {R}})$ or $(\pi _k,{\mathbb {I}}_\emptyset {\mathbb {R}}^{k-1},{\mathbb {I}}_\emptyset {\mathbb {R}}^2)$ with $\pi _k({{{\varvec{v}}}})=({{{\varvec{v}}}}_i)$ or $\pi _k({{{\varvec{v}}}})=({{{\varvec{v}}}}_i,{{{\varvec{v}}}}_j)$ extend $(\pi _k,{\mathbb {R}}^{k-1},{\mathbb {R}})$ or $(\pi _k,{\mathbb {R}}^{k-1},{\mathbb {R}}^2)$ naturally. Note that we do not distinguish notationally between the real and interval versions of the elementary operations and functions $u, \pi _k,$ and $o_k$. Rather, they are assumed to always act on the class of the object in their argument(s).

Definition 10

For every ${{\fancyscript{L}}}$-computational sequence $({{\fancyscript{S}}},\pi _o)$ with $n_i$ inputs and $n_o$ outputs, define the sequence of inclusion factors $\{({{{\varvec{v}}}}_k,{{\mathfrak {D}}}_k,{\mathbb {I}}_\emptyset {\mathbb {R}})\}_{k=1}^{n_f}$ where

• 1. for all $k=1,\ldots ,n_i$, ${{\mathfrak {D}}}_k={\mathbb {I}}_\emptyset {\mathbb {R}}^{n_i}$ and ${{{\varvec{v}}}}_k({{{\varvec{x}}}})={{{\varvec{x}}}}_k$, $\forall {{{\varvec{x}}}}\in {{\mathfrak {D}}}_k$,

• 2. for all $k=n_i+1,\ldots ,n_f$, ${{\mathfrak {D}}}_k=\{{{{\varvec{x}}}}\in {{\mathfrak {D}}}_{k-1}:\pi _k({{{\varvec{v}}}}_1({{{\varvec{x}}}}), \ldots ,{{{\varvec{v}}}}_{k-1}({{{\varvec{x}}}}))\in {\mathbb {I}}_\emptyset B_k\}$ and ${{{\varvec{v}}}}_k({{{\varvec{x}}}})=o_k(\pi _k({{{\varvec{v}}}}_1({{{\varvec{x}}}}),\ldots ,{{{\varvec{v}}}}_{k-1}({{{\varvec{x}}}})))$, $\forall {{{\varvec{x}}}}\in {\mathfrak {D}}_k$.

The natural interval extension of $({{\fancyscript{S}}},\pi _o)$ is the function $({{{\varvec{F}}}}_{{\fancyscript{S}}},{{\mathfrak {D}}}_{{\fancyscript{S}}},{\mathbb {I}}_\emptyset {\mathbb {R}}^{n_o})$ defined by ${{\mathfrak {D}}}_{{\fancyscript{S}}}\equiv {{\mathfrak {D}}}_{n_f}$ and ${{{\varvec{F}}}}_{{\fancyscript{S}}}({{{\varvec{x}}}})=\pi _o({{{\varvec{v}}}}_1({{{\varvec{x}}}}),\ldots ,{{{\varvec{v}}}}_{n_f}({{{\varvec{x}}}}))$, $\forall {{{\varvec{x}}}}\in {{\mathfrak {D}}}_{{\fancyscript{S}}}$.

Theorem 2

Let $({{\fancyscript{S}}},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence with associated natural function $({F}_{{\fancyscript{S}}},D_{{\fancyscript{S}}},{\mathbb {R}}^{n_o})$. The natural interval extension $({{{\varvec{F}}}}_{{\fancyscript{S}}},{{\mathfrak {D}}}_{{\fancyscript{S}}},{\mathbb {I}}_\emptyset {\mathbb {R}}^{n_o})$ is an inclusion monotonic interval extension of $({F}_{{\fancyscript{S}}},D_{{\fancyscript{S}}},{\mathbb {R}}^{n_o})$ on ${{\mathfrak {D}}}_{{\fancyscript{S}}}$ and an inclusion function for ${F}_{{\fancyscript{S}}}$ on ${{\mathfrak {D}}}_{{\fancyscript{S}}}$. In particular, each inclusion factor ${{{\varvec{v}}}}_k$ of $({{\fancyscript{S}}},\pi _o)$ is an inclusion monotonic interval extension of $v_k$ on ${{\mathfrak {D}}}_{{\fancyscript{S}}}$ for all $k=1,\ldots ,n_f$.

Proof

See [51], Theorem 2.3.11] together with Theorem 1. $\square$

3.3 McCormick analysis

Let $D\subset {\mathbb {R}}^n$ be convex. A vector-valued function ${G}:D\rightarrow {\mathbb {R}}^m$ is convex on $D$ if each component is convex on $D$. Similarly, it is concave on $D$ if each component is concave on $D$. For any set $A$, let ${\mathbb {P}}(A)$ denote the power set, or set of all subsets, including the empty set, of $A$.

Definition 11

Let $D\subset {\mathbb {R}}^n$ be a convex set and ${F}:D \rightarrow {\mathbb {P}}({\mathbb {R}}^m)$. A function is a convex relaxation, or convex underestimator, of ${F}$ on $D$ if is convex on $D$ and , $\forall x\in D$ and $i=1,\ldots ,m$. A convex relaxation ${G}:D\rightarrow {\mathbb {R}}^m$ is called the convex envelope of ${F}$ on $D$ if for all convex relaxations of ${F}$, $\forall x\in D$ and $i=1,\ldots ,m$. A function $\hat{{F}}:D\rightarrow {\mathbb {R}}^m$ is a concave relaxation, or concave overestimator, of ${F}$ on $D$ if $\hat{{F}}$ is concave on $D$ and $\hat{f}_i(x)\ge \sup \{f_i(x)\}$, $\forall x\in D$ and $i=1,\ldots ,m$. A concave relaxation ${G}:D\rightarrow {\mathbb {R}}^m$ is called the concave envelope of ${F}$ on $D$ if $g_i(x)\le \hat{f}_i(x)$ for all concave relaxations of ${F}$, $\forall x\in D$ and $i=1,\ldots ,m$.

Remark 1

Definition 11 allows that $f_i(x)=\mathrm {NaN}$ for some $i\in \{1,\ldots ,m\}$ and $x\in D$. In this case, the inequality defining a relaxation will hold for any function. However, the convexity and concavity requirement must still be met by and $\hat{{F}}$, respectively, and this requirement constrains the set of functions that satisfy the definition, as exemplified in Fig. 7.

The following notation was introduced in [51]. While it differs from the previously used notation for McCormick relaxations, it is more compact and very useful for the proposed operations on computational sequences, and it also makes the relationship with interval arithmetic more apparent. In the latter, information is passed from one operation in the sequence of factors to the next in the form of intervals. McCormick’s procedure to construct relaxations [39], on the other hand, requires a box ${{{\varvec{x}}}}$ and a point $x\in {{{\varvec{x}}}}$ as input and returns three values: a box ${{{\varvec{v}}}}_k({{{\varvec{x}}}})$, which encloses the image of ${{{\varvec{x}}}}$ under $v_k$, and two additional values and $\hat{v}_k({{{\varvec{x}}}},x)$, which represent the value of the convex and concave relaxation of $v_k$ on ${{{\varvec{x}}}}$ evaluated at $x$. After a recent generalization, one can also consider mappings that take a box and two relaxation values as input and return a box and two relaxation values; these are called generalized McCormick relaxations [52]. One advantage of this generalization is that it yields mappings with conformable inputs and outputs, which are hence composable.

Definition 12

Let ${\mathbb {M\! R}}^n\equiv \{({{{\varvec{z}}}}^B,{{{\varvec{z}}}}^C)\in {\mathbb {I\! R}}^n\times {\mathbb {I\! R}}^n:{{{\varvec{z}}}}^B\cap {{{\varvec{z}}}}^C\ne \emptyset \}$. Elements of ${\mathbb {M\! R}}^n$ are denoted by script capitals, ${{\fancyscript{Z}}}\in {\mathbb {M\! R}}^n$. For any ${{\fancyscript{Z}}}\in {\mathbb {M\! R}}^n$, the notations ${{{\varvec{z}}}}^{B},{{{\varvec{z}}}}^{C}\in {\mathbb {I\! R}}^n$ and will be commonly used to denote the boxes and vectors satisfying . For any $D\subset {\mathbb {R}}^n$, let ${\mathbb {M}}\! D$ denote the set $\{{{\fancyscript{Z}}}\in {\mathbb {M\! R}}^n:{{{\varvec{z}}}}^B\subset D\}$. Note that for more complex expressions, $(\cdot )^{C}$ will be used to denote the relaxation box, and $(\cdot )^{cv}$ and $(\cdot )^{cc}$ will be used to denote the convex and concave relaxation vectors, respectively, of a McCormick object.

In this paper, it is also necessary to consider unbounded and empty McCormick objects. Analogous to Definition 6, define the sets ${\mathbb {M}}_\emptyset {\mathbb {R}}^n\equiv \{({{{\varvec{z}}}}^B,{{{\varvec{z}}}}^C)\in {\mathbb {I}}_\emptyset {\mathbb {R}}^n\times {\mathbb {I}}_\emptyset {\mathbb {R}}^n:{{{\varvec{z}}}}^B\cap {{{\varvec{z}}}}^C\ne \emptyset \vee {{{\varvec{z}}}}^C=\emptyset \}$ and ${}^*{\mathbb {M}}\! {\mathbb {R}}^n\equiv \{({{{\varvec{z}}}}^B,{{{\varvec{z}}}}^C)\in {}^*\mathbb {I}\! {\mathbb {R}}^n\times {}^*\mathbb {I}\! {\mathbb {R}}^n:{{{\varvec{z}}}}^B\cap {{{\varvec{z}}}}^C\ne \emptyset \vee {{{\varvec{z}}}}^C=\emptyset \}$, which are extensions of ${\mathbb {M\! R}}^n$. Also, define ${\mathbb {M}}_\emptyset D$ and ${}^*{\mathbb {M}}\! D$ for any $D\in {\mathbb {R}}^n$ analogous to ${\mathbb {I}}_\emptyset D$ and ${}^*\mathbb {I}\! D$. Introduce ${{\mathrm{Enc}}}:{}^*{\mathbb {M}}\! {\mathbb {R}}^n\rightarrow {}^*\mathbb {I}\! {\mathbb {R}}^n$ defined by ${{\mathrm{Enc}}}({{\fancyscript{Z}}})={{{\varvec{z}}}}^B\cap {{{\varvec{z}}}}^C$ for all ${{\fancyscript{Z}}}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^n$. This function is necessary since for $z\in {\mathbb {R}}_\emptyset ^n$, $z\in {{\fancyscript{Z}}}$ is not well-defined whereas $z\in {{\mathrm{Enc}}}({{\fancyscript{Z}}})$ is.

Next, we formalize McCormick’s technique by defining operations on ${\mathbb {M}}_\emptyset {\mathbb {R}}^n$. We introduce the concept of a relaxation function, which is analogous to the notion of an inclusion function in interval analysis, and is the fundamental object that we want to compute for a given real-valued function. Then, we show how relaxation functions can be obtained through a simpler construction, just as inclusion functions can be constructed from inclusion monotonic interval extensions. First, however, some preliminary concepts are necessary.

Definition 13

Let ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^n$. ${{\fancyscript{X}}}$ and ${{\fancyscript{Y}}}$ are coherent if ${{{\varvec{x}}}}^B={{{\varvec{y}}}}^B$. A set ${{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! {\mathbb {R}}^n$ is coherent if every pair of elements is coherent. A set ${{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! {\mathbb {R}}^n$ is closed under coherence if, for any coherent ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^n$, ${{\fancyscript{X}}}\in {\fancyscript{D}}$ implies ${{\fancyscript{Y}}}\in {{\fancyscript{D}}}$.

For any coherent ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}^n$ with a common box part ${{{\varvec{q}}}}$ and for all $\lambda \in [0,1]$, define

$$\begin{aligned} \text {Conv}(\lambda ,{{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2)\equiv ({{{\varvec{q}}}}, \lambda {{{\varvec{x}}}}^C_1+(1-\lambda ){{{\varvec{x}}}}^C_2) \end{aligned}$$

where the rules of interval arithmetic are used to evaluate $\lambda {{{\varvec{x}}}}^C_1+(1-\lambda ){{{\varvec{x}}}}^C_2$. For any ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}^n$, the inclusion ${{\fancyscript{X}}}_1\subset {{\fancyscript{X}}}_2$ holds iff ${{{\varvec{x}}}}_1^B\subset {{{\varvec{x}}}}_2^B$ and ${{{\varvec{x}}}}_1^C\subset {{{\varvec{x}}}}_2^C$. Likewise, ${{\fancyscript{X}}}_1\supset {{\fancyscript{X}}}_2$ iff ${{\fancyscript{X}}}_2\subset {{\fancyscript{X}}}_1$. Also, define ${{\fancyscript{X}}}_1\cap {{\fancyscript{X}}}_2\equiv ({{{\varvec{x}}}}_1^B\cap {{{\varvec{x}}}}_2^B,{{{\varvec{x}}}}_1^C\cap {{{\varvec{x}}}}_2^C)$.

Definition 14

Suppose ${{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! {\mathbb {R}}^n$ is closed under coherence. A function ${{\fancyscript{F}}}:{{\fancyscript{D}}}\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ is coherently concave on ${{\fancyscript{D}}}$ if for every coherent ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {{\fancyscript{D}}}$, i.e., ${{{\varvec{q}}}}={{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$, ${{\fancyscript{F}}}({{\fancyscript{X}}}_1)$ and ${{\fancyscript{F}}}({{\fancyscript{X}}}_2)$ are coherent, and ${{\fancyscript{F}}}(\text {Conv}(\lambda ,{{\fancyscript{X}}}_1, {{\fancyscript{X}}}_2))\supset \text {Conv}(\lambda , {{\fancyscript{F}}}({{\fancyscript{X}}}_1),{{\fancyscript{F}}}({{\fancyscript{X}}}_2))$ for every $\lambda \in [0,1]$.

Definition 15

Let ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}_\emptyset ^m$. A mapping ${{\fancyscript{F}}}:{{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! D\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ is a relaxation function for ${F}$ on ${{\fancyscript{D}}}$ if ${{\fancyscript{D}}}$ is closed under coherence, ${{\fancyscript{F}}}$ is coherently concave on ${{\fancyscript{D}}}$, and ${F}(x)\in {{\mathrm{Enc}}}({{\fancyscript{F}}}({{\fancyscript{X}}}))$ is satisfied for every ${{\fancyscript{X}}}\in {{\fancyscript{D}}}$ and $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$.

Remark 2

Definition 14 is a generalization of convexity and concavity, and Definition 15 is a generalization of the notion of convex and concave relaxations. Convex and concave relaxations of ${F}$ can be recovered from a relaxation function of ${F}$ as follows. Let ${{{\varvec{x}}}}\in {\mathbb {I}}\! D$ so that there exists ${{\fancyscript{Y}}}\in {{\fancyscript{D}}}$ with ${{{\varvec{x}}}}={{{\varvec{y}}}}^B$. Define the functions ${{\fancyscript{U}}},{{\fancyscript{O}}}:{{{\varvec{x}}}}\rightarrow {\mathbb {R}}_\emptyset ^m$ for all $x\in {{{\varvec{x}}}}$ by . Then, ${{\fancyscript{U}}}$ and ${{\fancyscript{O}}}$ are convex and concave relaxations of ${F}$ on ${{{\varvec{x}}}}$, respectively, as shown in [51], Lemma 2.4.11].

Definition 16

Let $D\subset {\mathbb {R}}^n$. A set ${{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! {\mathbb {R}}^n$ is a McCormick extension of $D$ if ${{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! D$ and every $x\in D$ satisfies $([x,x],[x,x])\in {{\fancyscript{D}}}$. Let ${F}:D\rightarrow {\mathbb {R}}_\emptyset ^m$. A function ${{\fancyscript{F}}}:{{\fancyscript{D}}}\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ is a McCormick extension of ${F}$ if ${{\fancyscript{D}}}$ is a McCormick extension of $D$ and ${{\fancyscript{F}}}([x,x],[x,x])=([{F}(x),{F}(x)],[{F}(x), {F}(x)])$, $\forall x\in D$.

Definition 17

Let ${{\fancyscript{F}}}:{{\fancyscript{D}}}\subset {}^*{\mathbb {M}}\! {\mathbb {R}}^n\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}^m$. ${{\fancyscript{F}}}$ is inclusion monotonic on ${\fancyscript{D}}$ if ${{\fancyscript{X}}}_1\subset {{\fancyscript{X}}}_2$ implies that $\fancyscript{F}({{\fancyscript{X}}}_1)\subset \fancyscript{F}({{\fancyscript{X}}}_2)$ for all ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {{\fancyscript{D}}}$.

Theorem 3

Let ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}_\emptyset ^m$ and let ${{\fancyscript{F}}}:{{\fancyscript{D}}}\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ be a McCormick extension of ${F}$. If ${{\fancyscript{F}}}$ is inclusion monotonic on ${{\fancyscript{D}}}$, then every ${{\fancyscript{X}}}\in {{\fancyscript{D}}}$ satisfies ${F}(x)\in {{\mathrm{Enc}}}({{\fancyscript{F}}}({{\fancyscript{X}}}))$ for all $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$.

Proof

See [51], Theorem 2.4.14]. $\square$

We conclude that an inclusion monotonic McCormick extension that is also coherently concave is a relaxation function. Hence, it suffices to derive an inclusion monotonic, coherently concave McCormick extension. As shown in [51], Lemmas 2.4.15,2.4.17] the composition of inclusion monotonic, coherently concave McCormick extensions yields an inclusion monotonic, coherently concave McCormick extension. This motivates the derivations of inclusion monotonic, coherently concave McCormick extensions of the basic operations below.

Define the following relaxation functions for addition and multiplication: let the functions $(+,{\mathbb {M}}_\emptyset {\mathbb {R}}^2,{\mathbb {M}}_\emptyset {\mathbb {R}})$ and $(\times ,{\mathbb {M}}_\emptyset {\mathbb {R}}^2,{\mathbb {M}}_\emptyset {\mathbb {R}})$ be given by $+({{\fancyscript{X}}},{{\fancyscript{Y}}})=({{{\varvec{x}}}}^B+{{{\varvec{x}}}}^B,{{{\varvec{x}}}}^C+{{{\varvec{x}}}}^C)$ and $\times ({{\fancyscript{X}}},{{\fancyscript{Y}}})=({{{\varvec{x}}}}^B{{{\varvec{y}}}}^B,[,\hat{z}])$ where

Note that this definition of multiplication ensures that [51], Theorems 2.4.22, 2.4.23]. Furthermore, the standard rules for addition and multiplication of McCormick relaxations are implied by these definitions, see [51], p. 69f], with the addition of the intersection with the bounds from interval arithmetic in the case of the multiplication rule. These functions are indeed relaxation functions and also inclusion monotonic as shown in [51], Section 2.4.2].

The following assumption is needed to construct relaxation functions for the elements of $\fancyscript{L}$. For many univariate functions, objects satisfying these assumptions are known and readily available [51], Section 2.8].

Assumption 2

Assume that for every $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$, functions where $\tilde{B}\equiv \{({{{\varvec{x}}}},x)\in {\mathbb {I}}\! B\times B:x\in {{{\varvec{x}}}}\}$ and $x^{\min },x^{\max }:{\mathbb {I}}\! B\rightarrow {\mathbb {R}}$ are known such that and $\hat{u}({{{\varvec{x}}}},\cdot )$ are convex and concave relaxations of $u$ on ${{{\varvec{x}}}}\in {\mathbb {I}}\! B$, respectively, and $x^{\min }({{{\varvec{x}}}})$ and $x^{\max }({{{\varvec{x}}}})$ are a minimum of and a maximum of $\hat{u}({{{\varvec{x}}}},\cdot )$ on ${{{\varvec{x}}}}$, respectively. Furthermore, assume that for any ${{{\varvec{x}}}}_1,{{{\varvec{x}}}}_2\in {\mathbb {I}}\! B$ with ${{{\varvec{x}}}}_1\subset {{{\varvec{x}}}}_2$, and $\hat{u}({{{\varvec{x}}}}_1,x)\le \hat{u}({{{\varvec{x}}}}_2,x)$ for all $x\in {{{\varvec{x}}}}_1$ and that for all $x\in B$.

Let ${{\mathrm{mid}}}:{\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ return the middle value of its arguments. It can be shown (cf. [51], p. 76f) that a relaxation function of $(u,B,R)\in {{\fancyscript{L}}}$ is given by $(u,{\mathbb {M}}\! B,{\mathbb {M\! R}})$ with

(1)

Note that if the convex and concave envelopes of $u$ are known and used, then the intersection with $u({{{\varvec{x}}}}^B)$ in (1) is redundant.

Suppose that Assumption 2 holds and that $({{\fancyscript{S}}},\pi _o)$ is a ${{\fancyscript{L}}}$-computational sequence. Then, for any element $(o_k,\pi _k)$ of ${\fancyscript{S}}$, the preceding developments provide an inclusion monotonic McCormick extension $(o_k,{\mathbb {M}}_\emptyset B_k,{\mathbb {M}}_\emptyset {\mathbb {R}})$. Also, the functions $(\pi _k,{\mathbb {M}}_\emptyset {\mathbb {R}}^{k-1},{\mathbb {M}}_\emptyset {\mathbb {R}})$ or $(\pi _k,{\mathbb {M}}_\emptyset {\mathbb {R}}^{k-1},{\mathbb {M}}_\emptyset {\mathbb {R}}^2)$ with $\pi _k({{\fancyscript{V}}})=({{\fancyscript{V}}}_i)$ or $\pi _k({{\fancyscript{V}}})=({{\fancyscript{V}}}_i,{{\fancyscript{V}}}_j)$ extend $(\pi _k,{\mathbb {R}}^{k-1},{\mathbb {R}})$ or $(\pi _k,{\mathbb {R}}^{k-1},{\mathbb {R}}^2)$ naturally.

Definition 18

For every ${{\fancyscript{L}}}$-computational sequence $({{\fancyscript{S}}},\pi _o)$ with $n_i$ inputs and $n_o$ outputs, define the sequence of relaxation factors $\{({{\fancyscript{V}}}_k,{{\fancyscript{D}}}_k,{\mathbb {M}}_\emptyset {\mathbb {R}})\}_{k=1}^{n_f}$ where

• 1. for all $k=1,\ldots ,n_i$, ${{\fancyscript{D}}}_k={\mathbb {M}}_\emptyset {\mathbb {R}}^{n_i}$ and ${{\fancyscript{V}}}_k({{\fancyscript{X}}})={{\fancyscript{X}}}_k$, $\forall {{\fancyscript{X}}}\in {{\fancyscript{D}}}_k$,

• 2. for all $k=n_i+1,\ldots ,n_f$, ${{\fancyscript{D}}}_k=\{{{\fancyscript{X}}}\in {{\fancyscript{D}}}_{k-1}:\pi _k({{\fancyscript{V}}}_1 ({{\fancyscript{X}}}),\ldots ,{{\fancyscript{V}}}_{k-1}({{\fancyscript{X}}}))\in {\mathbb {M}}_\emptyset B_k\}$ and ${{\fancyscript{V}}}_k({{\fancyscript{X}}})=o_k(\pi _k({{\fancyscript{V}}}_1({{\fancyscript{X}}}), \ldots ,{{\fancyscript{V}}}_{k-1}({{\fancyscript{X}}})))$, $\forall {{\fancyscript{X}}}\in {{\fancyscript{D}}}_k$.

The natural McCormick extension of $(\fancyscript{S},\pi _o)$ is the function $({{\fancyscript{F}}}_{\fancyscript{S}},{{\fancyscript{D}}}_{{\fancyscript{S}}},{\mathbb {M\! R}}^{n_o})$ defined by ${{\fancyscript{D}}}_{{\fancyscript{S}}}\equiv {{\fancyscript{D}}}_{n_f}$ and ${{\fancyscript{F}}}_{{\fancyscript{S}}}({{\fancyscript{X}}})=\pi _o({{\fancyscript{V}}}_1({{\fancyscript{X}}}), \ldots ,{{\fancyscript{V}}}_{n_f}({{\fancyscript{X}}}))$, $\forall {{\fancyscript{X}}}\in {{\fancyscript{D}}}_{{\fancyscript{S}}}$.

Theorem 4

Let $({{\fancyscript{S}}},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence with associated natural function $({F}_{\fancyscript{S}},D_{{\fancyscript{S}}},{\mathbb {R}}^{n_o})$. The natural McCormick extension $({{\fancyscript{F}}}_{{\fancyscript{S}}},{{\fancyscript{D}}}_{{\fancyscript{S}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^{n_o})$ is a McCormick extension of $({F}_{\fancyscript{S}},D_{{\fancyscript{S}}},{\mathbb {R}}^{n_o})$ and coherently concave and inclusion monotonic on ${{\fancyscript{D}}}_{{\fancyscript{S}}}$. Thus, it is a relaxation function for ${F}_{{\fancyscript{S}}}$ on ${{\fancyscript{D}}}_{{\fancyscript{S}}}$. In particular, each relaxation factor $\fancyscript{V}_k$ of $(\fancyscript{S},\pi _o)$ is a inclusion monotonic, coherently concave McCormick extension of $v_k$ on $\mathfrak {D}_{\fancyscript{S}}$ for all $k=1,\ldots ,n_f$.

Proof

See [51], Theorem 2.4.32] together with Theorem 3. $\square$

Thus, so far we have described forward propagation of intervals and McCormick objects, as is commonly done to compute natural interval extensions and standard McCormick relaxations. Next, we consider reverse propagation of intervals and describe its use in CSPs. The formal development of forward McCormick propagation in this section as an analogous process to forward interval propagation allows us to then extend the reverse interval propagation ideas to McCormick objects in Sect. 5.

4 Reverse interval propagation

In this section, we will focus on propagating interval bounds backwards through the computational sequence, which is a particular form of a DAG. Since the reverse McCormick propagation is similar in spirit, it is very instructive to first revisit the interval case. The results, which are stated below, have been adapted from [62], though the notation is introduced here.

Definition 19

Consider ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$. Let ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}:{\mathbb {I}}_\emptyset D\times {}^*\mathbb {I}\! {\mathbb {R}}^m\rightarrow {\mathbb {I}}_\emptyset {\mathbb {R}}^n$. If for all ${{{\varvec{x}}}}\in {\mathbb {I}}_\emptyset D$ and ${{{\varvec{r}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}^m$ it holds that

$$\begin{aligned} \{x\in {{{\varvec{x}}}}:{F}(x)\in {{{\varvec{r}}}}\} \subset \{x\in {{{\varvec{F}}}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}},{{{\varvec{r}}}})\} \subset {{{\varvec{x}}}}, \end{aligned}$$

(2)

then ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}$ is called a reverse interval update of ${F}$.

Definition 20

Let $(\fancyscript{S},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence with $n_i$ inputs and $n_o$ outputs with natural interval extension $({{{\varvec{F}}}}_\fancyscript{S},\mathfrak {D}_\fancyscript{S},{\mathbb {R}}^{n_o})$. Let ${{{\varvec{x}}}}\in \mathfrak {D}_\fancyscript{S}$. Suppose that ${{{\varvec{v}}}}_1({{{\varvec{x}}}}),\ldots ,{{{\varvec{v}}}}_{n_f}({{{\varvec{x}}}})$ have been calculated according to Definition 10. Let $o_k^{{{\mathrm{rev}}}}:{\mathbb {I}}_\emptyset B_k\times {}^*\mathbb {I}\! {\mathbb {R}}\rightarrow {\mathbb {I}}_\emptyset B_k$ be a reverse interval update of $o_k$ for each $k=n_i+1,\ldots ,n_f$. Suppose $\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}\in {\mathbb {I}}_\emptyset {\mathbb {R}}$ are calculated for any ${{{\varvec{x}}}}\in \mathfrak {D}_\fancyscript{S}$ and ${{{\varvec{r}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}$ by the following procedure:

$$\begin{aligned}&(\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}):=({{{\varvec{v}}}}_1({{{\varvec{x}}}}),\ldots , {{{\varvec{v}}}}_{n_f}({{{\varvec{x}}}}))\\&\pi _o(\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}):=\pi _o(\tilde{{{{\varvec{v}}}}}_1, \ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}) \cap {{{\varvec{r}}}}\\&\mathtt {for} \;l:=1,\ldots ,n_f-n_i \; \mathtt {do}\\&\qquad \pi _{n_f-l+1}(\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f-l}):= o_{n_f-l+1}^{{{\mathrm{rev}}}}(\pi _{n_f-l+1}(\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_ {n_f-l}),\tilde{{{{\varvec{v}}}}}_{n_f-l+1})\\&\mathtt {end} \end{aligned}$$

The reverse interval propagation of $(\fancyscript{S},\pi _o)$ is the function $({{{\varvec{F}}}}_\fancyscript{S}^{{{\mathrm{rev}}}},\mathfrak {D}_\fancyscript{S}\times {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}, {\mathbb {I}}\! D_\fancyscript{S})$ defined by ${{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}},{{{\varvec{r}}}})\equiv \tilde{{{{\varvec{v}}}}}_1 \times \cdots \times \tilde{{{{\varvec{v}}}}}_{n_i}$.

Theorem 5

The reverse interval propagation of $(\fancyscript{S},\pi _o)$ as given by Definition 20 is a reverse interval update of $({F}_\fancyscript{S},D_\fancyscript{S},{\mathbb {R}}^{n_o})$. If the reverse update of $o_k$ is inclusion monotonic for each $k=n_i+1,\ldots ,n_f$ then the reverse interval propagation of $(\fancyscript{S},\pi _o)$ is inclusion monotonic.

Proof

Finite induction yields immediately that the second inclusion in (2) holds.

Let ${{{\varvec{r}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}$ and ${{{\varvec{x}}}}\in \mathfrak {D}_{\fancyscript{S}}$. If there does not exist a $x\in {{{\varvec{x}}}}$ such that ${F}_{\fancyscript{S}}(x)\in {{{\varvec{r}}}}$, then the first inclusion in (2) holds trivially.

Let $x\in {{{\varvec{x}}}}$ such that ${F}_{\fancyscript{S}}(x)\in {{{\varvec{r}}}}$. Then, there exists a sequence of factor values $\{v_k(x)\}_{k=1}^{n_f}$ with $v_1(x)=x_1$, $\ldots$, $v_{n_i}(x)=x_{n_i}$ and $\pi _o(v_1(x),\ldots ,v_{n_f}(x))\in {{{\varvec{r}}}}$. Also, since ${{{\varvec{v}}}}_1,\ldots ,{{{\varvec{v}}}}_{n_f}$ are inclusion functions (see Theorem 2), $(v_1(x),\ldots ,v_{n_f}(x))\in ({{{\varvec{v}}}}_1({{{\varvec{x}}}}),\ldots ,{{{\varvec{v}}}}_{n_f}({{{\varvec{x}}}}))$ so that $(v_1(x),\ldots ,v_{n_f}(x))\in (\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f})$ prior to entering the loop. In the following, let $\tilde{{{{\varvec{v}}}}}_k^l$ denote the value of $\tilde{{{{\varvec{v}}}}}_k$ for the given ${{{\varvec{x}}}}$ and ${{{\varvec{r}}}}$ after the $l$th reverse update, $l=1,\ldots ,n_f-n_i$. Since $o_{n_f}^{{{\mathrm{rev}}}}$ is a reverse interval update, it follows that $(v_1(x),\ldots ,v_{n_f-1}(x))\in (\tilde{{{{\varvec{v}}}}}_1^1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f-1}^1)$. Finite induction yields that $(v_1(x),\ldots ,v_{n_i}(x))\in (\tilde{{{{\varvec{v}}}}}_1^{n_f-n_i},\ldots ,\tilde{{{{\varvec{v}}}}}_{n_i}^{n_f-n_i})\equiv {{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}},{{{\varvec{r}}}})$. Thus, $x\in {{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}},{{{\varvec{r}}}})$ and the first inclusion in (2) holds.

Assume now that $o_k^{{{\mathrm{rev}}}}$ is inclusion monotonic for each $k=n_i+1,\ldots ,n_f$. Let ${{{\varvec{x}}}}^1,{{{\varvec{x}}}}^2\in \mathfrak {D}_\fancyscript{S}$ with ${{{\varvec{x}}}}^1\subset {{{\varvec{x}}}}^2$ and ${{{\varvec{r}}}}^1,{{{\varvec{r}}}}^2\in {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}$ with ${{{\varvec{r}}}}^1\subset {{{\varvec{r}}}}^2$. Then, $(\tilde{{{{\varvec{v}}}}}_1({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1))\subset (\tilde{{{{\varvec{v}}}}}_1({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2))$ prior to entering the loop. Since $o_{n_f}^{{{\mathrm{rev}}}}$ is inclusion monotonic, $(\tilde{{{{\varvec{v}}}}}_1^1({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}^1({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1)) \subset (\tilde{{{{\varvec{v}}}}}_1^1({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}^1({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2))$. Using finite induction over $l$ yields that $(\tilde{{{{\varvec{v}}}}}_1^{n_f-n_i}({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_i}^{n_f-n_i} ({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1))\subset (\tilde{{{{\varvec{v}}}}}_1^{n_f-n_i}({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2),\ldots ,\tilde{{{{\varvec{v}}}}}_{n_i}^{n_f-n_i} ({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2))$. Thus, it follows that ${{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^1,{{{\varvec{r}}}}^1)\subset {{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^2,{{{\varvec{r}}}}^2)$. $\square$

Next, we will present a result very closely related to Theorem 5 that relies more on standard concepts from interval analysis.

Theorem 6

Consider $(\fancyscript{S},\pi _o)$ and assume that for each $k=n_i+1,\ldots ,n_f$, the reverse interval update of $o_k$ is inclusion monotonic. Define ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}:D\times {\mathbb {R}}^{n_o}\rightarrow {\mathbb {R}}_\emptyset ^{n_i}$ for each $x\in D$ and $r\in {\mathbb {R}}^{n_o}$ by

$$\begin{aligned} {F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}(x,r)= \left\{ \begin{array}{l@{\quad }l} x &{}\quad \text {if}~{F}_{\fancyscript{S}}(x)=r, \\ \mathrm {NaN}&{}\quad \text {otherwise}. \end{array} \right. \end{aligned}$$

(3)

Then, ${{{\varvec{F}}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ is an inclusion function of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ on $\mathfrak {D}_{\fancyscript{S}}\times {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}$.

Proof

Let $r\in {}^*\mathbb {R}\! ^{n_o}$. First, consider $x\in D$ so that ${F}_{\fancyscript{S}}(x)=r$. Since ${{{\varvec{F}}}}_\fancyscript{S}$ is an interval extension of ${F}_{\fancyscript{S}}$, each factor is a degenerate interval after the forward evaluation with ${{{\varvec{v}}}}_k([x,x])=[v_k(x),v_k(x)]$. Since ${F}_{\fancyscript{S}}(x)=r$, the intersections during the reverse interval propagation return degenerate intervals so that it is clear that ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is an interval extension of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ for such $[x,x]$. If $x\in D$ such that ${F}_{\fancyscript{S}}(x)\ne r$ then $\pi _o(\tilde{{{{\varvec{v}}}}}_1,\ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}):=\pi _o(\tilde{{{{\varvec{v}}}}}_1, \ldots ,\tilde{{{{\varvec{v}}}}}_{n_f}) \cap {{{\varvec{r}}}}$ results in $\tilde{{{{\varvec{v}}}}}_k = \emptyset$ for at least one $k \in \{1, \ldots , n_f\}$. For each $k \in \{1, \ldots , n_f\}$, $\tilde{{{{\varvec{v}}}}}_k$ influences at least one $\tilde{{{{\varvec{v}}}}}_j$ with $j \in \{1, \ldots , n_i\}$ through a sequence of reverse interval updates. Any reverse interval update involving empty intervals yields empty intervals because it is an interval operation. Hence, once the loop is executed, $\tilde{{{{\varvec{v}}}}}_1 \times \cdots \times \tilde{{{{\varvec{v}}}}}_{n_i} = \emptyset$ so that ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}_\fancyscript{S}([x,x],[r,r])=\emptyset =[\mathrm {NaN},\mathrm {NaN}]=[{F}_ {\fancyscript{S}}^{{{\mathrm{rev}}}}(x,r),{F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}(x,r)]$. Thus, ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is an interval extension of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$. Inclusion monotonicity of ${{{\varvec{F}}}}^{{{\mathrm{rev}}}}_\fancyscript{S}$ has been established in Theorem 5. The assertion follows then from Theorem 1. $\square$

Here, we will demonstrate how to obtain inclusion monotonic reverse interval updates for the case of addition. Similar constructions are possible for multiplication and univariate operations [62].

Lemma 1

Consider $(+,{\mathbb {R}}^2,{\mathbb {R}})$. The function $(+^{{{\mathrm{rev}}}},{\mathbb {I}}_\emptyset {\mathbb {R}}^2\times {}^*\mathbb {I}\! {\mathbb {R}},{\mathbb {I}}_\emptyset {\mathbb {R}}^2)$ defined for all ${{{\varvec{x}}}},{{{\varvec{y}}}}\in {\mathbb {I}}_\emptyset {\mathbb {R}}$ and ${{{\varvec{r}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}$ by

$$\begin{aligned} +^{{{\mathrm{rev}}}}(({{{\varvec{x}}}},{{{\varvec{y}}}}),{{{\varvec{r}}}}) = ({{{\varvec{r}}}}-{{{\varvec{y}}}},{{{\varvec{r}}}}-{{{\varvec{x}}}})\cap ({{{\varvec{x}}}},{{{\varvec{y}}}}) \end{aligned}$$

is an inclusion monotonic reverse interval update of $(+,{\mathbb {R}}^2,{\mathbb {R}})$.

5 Reverse McCormick propagation

In this section, the ideas for reverse interval propagation are extended to McCormick objects. Again, the enclosure property will be established, but also coherent concavity and inclusion monotonicity of the resulting relaxations will be proved.

Definition 21

Suppose ${F}:D\subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$. Consider ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}:{\mathbb {M}}_\emptyset D\times {}^*{\mathbb {M}}\! {\mathbb {R}}^m\rightarrow {\mathbb {M}}_\emptyset {\mathbb {R}}^n$. If for all ${{\fancyscript{X}}}\in {\mathbb {M}}_\emptyset D$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ it holds that

$$\begin{aligned} \{x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}):{F}(x)\in {{\mathrm{Enc}}}(\fancyscript{R})\} \subset \{x\in {{\mathrm{Enc}}}({{\fancyscript{F}}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R}))\} \end{aligned}$$

(4)

and ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R})\subset {{\fancyscript{X}}}$, then ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}$ is called a reverse McCormick update of ${F}$.

Definition 22

Let $(\fancyscript{S},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence with $n_i$ inputs and $n_o$ outputs with natural McCormick extension $({{\fancyscript{F}}}_\fancyscript{S},{{\fancyscript{D}}}_\fancyscript{S},{\mathbb {R}}^{n_o})$. Let ${{\fancyscript{X}}}\in {{\fancyscript{D}}}_\fancyscript{S}$. Suppose $\fancyscript{V}_1({{\fancyscript{X}}}),\ldots ,$ $\fancyscript{V}_{n_f}({{\fancyscript{X}}})$ have been calculated according to Definition 18. Let  $o_k^{{{\mathrm{rev}}}}:{\mathbb {M}}_\emptyset B_k\times {}^*{\mathbb {M}}\! {\mathbb {R}}\rightarrow {\mathbb {M}}_\emptyset B_k$ be a reverse McCormick update of $o_k$ for each $k=n_i+1,\ldots ,n_f$. Suppose $\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ are calculated for any ${{\fancyscript{X}}}\in {{\fancyscript{D}}}_\fancyscript{S}$ and $\fancyscript{R}\in {}^*\mathbb {I}\! {\mathbb {R}}^{n_o}$ by the following procedure:

$$\begin{aligned}&(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}):= (\fancyscript{V}_1({{\fancyscript{X}}}),\ldots ,\fancyscript{V}_{n_f}({{\fancyscript{X}}}))\\&\pi _o(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}):= \pi _o(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}) \cap \fancyscript{R}\\&\mathtt {for} \;l:=1,\ldots ,n_f-n_i \; \mathtt {do}\\&\qquad \pi _{n_f-l+1}(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_ {n_f-l}):= o_{n_f-l+1}^{{{\mathrm{rev}}}}(\pi _{n_f-l+1}(\tilde{\fancyscript{V}}_1, \ldots ,\tilde{\fancyscript{V}}_{n_f-l}),\tilde{\fancyscript{V}}_{n_f-l+1})\\&\mathtt {end} \end{aligned}$$

The reverse McCormick propagation of $(\fancyscript{S},\pi _o)$ is the function $({{\fancyscript{F}}}_\fancyscript{S}^{{{\mathrm{rev}}}},{{\fancyscript{D}}}_\fancyscript{S}\times {}^*{\mathbb {M}}\! {\mathbb {R}}^ {n_o},{\mathbb {M}}_\emptyset D_\fancyscript{S})$ defined for any ${{\fancyscript{X}}}\in {{\fancyscript{D}}}_\fancyscript{S}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_o}$ by ${{\fancyscript{F}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R})\equiv \tilde{\fancyscript{V}}_1 \times \cdots \times \tilde{\fancyscript{V}}_{n_i}$.

Theorem 7

The reverse McCormick propagation of $(\fancyscript{S},\pi _o)$ as given by Definition 22 is a reverse McCormick update of $({F}_\fancyscript{S},D_\fancyscript{S},{\mathbb {R}}^{n_o})$.

Proof

Let $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^m$ and ${{\fancyscript{X}}}\in {{\fancyscript{D}}}_{\fancyscript{S}}$. Finite induction yields immediately that ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R})\subset {{\fancyscript{X}}}$. If there does not exist $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$ such that ${F}_{\fancyscript{S}}(x)\in {{\mathrm{Enc}}}(\fancyscript{R})$, then (4) holds trivially.

Let $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$ satisfy ${F}_{\fancyscript{S}}(x)\in {{\mathrm{Enc}}}(\fancyscript{R})$. Then, there exists a sequence of factor values $\{v_k(x)\}_{k=1}^{n_f}$ with $v_1(x)=x_1$, $\ldots$, $v_{n_i}(x)=x_{n_i}$ and $\pi _o(v_1(x),\ldots ,v_{n_f}(x))\in {{\mathrm{Enc}}}(\fancyscript{R})$. Also, since $\fancyscript{V}_1,\ldots ,\fancyscript{V}_{n_f}$ are relaxation functions, $(v_1(x),\ldots ,v_{n_f}(x))\in {{\mathrm{Enc}}}((\fancyscript{V}_1({{\fancyscript{X}}}),\ldots ,\fancyscript{V}_{n_f}({{\fancyscript{X}}})))$ so that $(v_1(x),\ldots ,v_{n_f}(x))\in {{\mathrm{Enc}}}((\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}))$ prior to entering the loop.

In the following, let $\tilde{\fancyscript{V}}_k^l$ denote the value of $\tilde{\fancyscript{V}}_k$ for the given ${{\fancyscript{X}}}$ and $\fancyscript{R}$ after the $l$th reverse update, $l=1,\ldots ,n_f-n_i$. Since $o_{n_f}^{{{\mathrm{rev}}}}$ is a reverse McCormick update, it follows that $(v_1(x),\ldots ,v_{n_f-1}(x))\in {{\mathrm{Enc}}}(\tilde{\fancyscript{V}}_1^1,\ldots ,\tilde{\fancyscript{V}}_{n_f-1}^1)$. Finite induction yields that $(v_1(x),\ldots ,v_{n_i}(x))\in {{\mathrm{Enc}}}((\tilde{\fancyscript{V}}_1^{n_f-n_i},\ldots ,\tilde{\fancyscript{V}}_{n_i} ^{n_f-n_i}))\equiv {{\mathrm{Enc}}}({{\fancyscript{F}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R}))$. Thus, $x\in {{\mathrm{Enc}}}({{\fancyscript{F}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R}))$ and (4) holds. $\square$

Lemma 2

Consider $(\fancyscript{S},\pi _o)$ and assume that for each $k=n_i+1,\ldots ,n_f$, the reverse McCormick update of $o_k$ is coherently concave and inclusion monotonic on ${\mathbb {M}}_\emptyset B_k\times {}^*{\mathbb {M}}\! {\mathbb {R}}$. Then, ${{\fancyscript{F}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ is coherently concave and inclusion monotonic on ${{\fancyscript{D}}}_{\fancyscript{S}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_o}$.

Proof

Compositions of coherently concave and inclusion monotonic functions are coherently concave and inclusion monotonic [51], Lemma 2.4.15]. The result thus follows from finite induction, analogous to the proof of Theorem 7. $\square$

Theorem 8

Consider $(\fancyscript{S},\pi _o)$ and assume that for each $k=n_i+1,\ldots ,n_f$, the reverse McCormick update of $o_k$ is coherently concave and inclusion monotonic. Then, ${{\fancyscript{F}}}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ is a relaxation function of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ on ${{\fancyscript{D}}}_{\fancyscript{S}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_o}$.

Proof

Let $r\in {}^*\mathbb {R}\! ^{n_o}$. First, consider $x\in D$ so that ${F}_{\fancyscript{S}}(x)=r$. It is clear that ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is a McCormick extension of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ for such $([x,x],[x,x])$ since ${{\fancyscript{F}}}_\fancyscript{S}$ is a McCormick extension of ${F}_{\fancyscript{S}}$ and $o_k^{{{\mathrm{rev}}}}(\fancyscript{B},\fancyscript{R})\subset \fancyscript{B}$ for all $(\fancyscript{B},\fancyscript{R})\in {\mathbb {M}}_\emptyset B_k\times {}^*{\mathbb {M}}\! {\mathbb {R}}$ by definition. If $x\in D$ such that ${F}_{\fancyscript{S}}(x)\ne r$ then $\pi _o(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}):= \pi _o(\tilde{\fancyscript{V}}_1,\ldots ,\tilde{\fancyscript{V}}_{n_f}) \cap ([r,r],[r,r])$ results in $\tilde{\fancyscript{V}}_k = \emptyset$ for at least one $k \in \{1, \ldots , n_f\}$. For each $k \in \{1, \ldots , n_f\}$, $\tilde{\fancyscript{V}}_k$ influences at least one $\tilde{\fancyscript{V}}_j$ with $j \in \{1, \ldots , n_i\}$ through a sequence of reverse McCormick updates. Any reverse McCormick update involving empty McCormick objects yields empty McCormick objects because it is a McCormick operation. Hence, once the loop is executed, $\tilde{\fancyscript{V}}_1 \times \cdots \times \tilde{\fancyscript{V}}_{n_i} = \emptyset$ so that ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}_\fancyscript{S}(([x,x],[x,x]),([r,r],[r,r]))=\emptyset$. Thus, ${{\fancyscript{F}}}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is a McCormick extension of ${F}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$. The assertion follows from Lemma 2 in conjunction with Theorem 3. $\square$

5.1 Reverse McCormick updates of binary operations

Lemma 3

Consider $(+,{\mathbb {R}}^2,{\mathbb {R}})$ and its relaxation function $(+,{\mathbb {M\! R}}^2,{\mathbb {M\! R}})$. The function $(+^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2)$ defined for all ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ by

$$\begin{aligned} +^{{{\mathrm{rev}}}}(({{\fancyscript{X}}},\fancyscript{Y}),\fancyscript{R}) = (\fancyscript{R}-{{\fancyscript{Y}}},\fancyscript{R}-{{\fancyscript{X}}})\cap ({{\fancyscript{X}}}, {{\fancyscript{Y}}}) \end{aligned}$$

is a reverse McCormick update of $(+,{\mathbb {R}}^2,{\mathbb {R}})$.

Proof

Let ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$. If ${{\mathrm{Enc}}}(+({{\fancyscript{X}}},{{\fancyscript{Y}}})\cap \fancyscript{R})=\emptyset$, then $\not \exists (x,y,r)\in {{\mathrm{Enc}}}(({{\fancyscript{X}}},{{\fancyscript{Y}}},\fancyscript{R})):r-y=x$. Thus, $r-y\not \in {{\mathrm{Enc}}}({{\fancyscript{X}}})$ for all $(y,r)\in {{\mathrm{Enc}}}(({{\fancyscript{Y}}},\fancyscript{R}))$ so that ${{\mathrm{Enc}}}(\fancyscript{R}-{{\fancyscript{Y}}})\cap {{\mathrm{Enc}}}({{\fancyscript{X}}})=\emptyset$. Similarly, ${{\mathrm{Enc}}}(\fancyscript{R}-{{\fancyscript{X}}})\cap {{\mathrm{Enc}}}({{\fancyscript{Y}}})=\emptyset$ so that (4) holds trivially.

Otherwise, pick $(x,y)\in {{\mathrm{Enc}}}({{\fancyscript{X}}})\times {{\mathrm{Enc}}}({{\fancyscript{Y}}})$ so that $x+y\in {{\mathrm{Enc}}}(\fancyscript{R})$. Since and , it follows that and and that and so that $(x,y)\in {{\mathrm{Enc}}}(+^{{{\mathrm{rev}}}}(({{\fancyscript{X}}},{{\fancyscript{Y}}}),\fancyscript{R}))$. Thus, (4) holds. $\square$

Let $(\varGamma ,{\mathbb {I}}_\emptyset {\mathbb {R}}\times {}^*\mathbb {I}\! {\mathbb {R}}\times {\mathbb {I}}_\emptyset {\mathbb {R}},{\mathbb {I}}_\emptyset {\mathbb {R}})$ denote the Gauss–Seidel operator for all ${{{\varvec{x}}}},{{{\varvec{y}}}}\in {\mathbb {I}}_\emptyset {\mathbb {R}}$ and ${{{\varvec{r}}}}\in {}^*\mathbb {I}\! {\mathbb {R}}$, see [43], Proposition 4.2.1] for its description.

Definition 23

Define an extension of the Gauss–Seidel operator to ${\mathbb {M\! R}}$, denoted as $\fancyscript{G}:{\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}\rightarrow {\mathbb {M}}_\emptyset {\mathbb {R}}$, for all ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ by $(\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}}))^B= \varGamma ({{{\varvec{x}}}}^B,{{{\varvec{r}}}}^B,{{{\varvec{y}}}}^B)$ and

$$\begin{aligned} \left( \fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\right) ^C = \left\{ \begin{array}{ll} (\fancyscript{R}'\times \frac{1}{{{\fancyscript{X}}}'})^C\cap ({{{\varvec{y}}}}')^C &{}\quad \text {if}\,\, 0\notin {{{\varvec{x}}}}^B,\\ \varGamma ({{{\varvec{x}}}}^B,{{{\varvec{r}}}}^B,{{{\varvec{y}}}}^B)\cap ({{{\varvec{y}}}}')^C &{}\quad \text {if}\,\, 0\in {{{\varvec{x}}}}^B,0\notin {{{\varvec{r}}}}^B, \\ ({{{\varvec{y}}}}')^C &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

where ${{\fancyscript{X}}}'=({{{\varvec{x}}}}^B,{{{\varvec{x}}}}^B\cap {{{\varvec{x}}}}^C)$, ${{\fancyscript{Y}}}'=({{{\varvec{y}}}}^B,{{{\varvec{y}}}}^B\cap {{{\varvec{y}}}}^C)$ and $\fancyscript{R}'=({{{\varvec{r}}}}^B,{{{\varvec{r}}}}^B\cap {{{\varvec{r}}}}^C)$.

Lemma 4

Suppose ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$, $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$. Then, $\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\subset \fancyscript{B}$ and

$$\begin{aligned} {{\mathrm{Enc}}}(\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}}))\supset \{y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\exists x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}), r\in {{\mathrm{Enc}}}(\fancyscript{R}): xy=r\}. \end{aligned}$$

(5)

Proof

$\varGamma ({{{\varvec{x}}}}^B,{{{\varvec{r}}}}^B,{{{\varvec{b}}}}^B)\subset {{{\varvec{b}}}}^B$ follows from [43], 4.3.2] and it is also clear that $\left( \fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\right) ^C\subset ({{{\varvec{y}}}}')^C$, hence $\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\subset {{\fancyscript{Y}}}' \subset {{\fancyscript{Y}}}$. It has already been established  [43], Proposition 4.2.1] that

$$\begin{aligned} \varGamma ({{{\varvec{x}}}}^B,{{{\varvec{r}}}}^B,{{{\varvec{y}}}}^B)=\Box \{y\in {{{\varvec{b}}}}^B:\exists a\in {{{\varvec{x}}}}^B, r\in {{{\varvec{r}}}}^B: xy=r\}. \end{aligned}$$

Next, note that

$$\begin{aligned}&\Box \{y\in {{{\varvec{y}}}}^B:\exists x\in {{{\varvec{x}}}}^B, r\in {{{\varvec{r}}}}^B: xy=r\} \supset \left\{ y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\right. \\&\quad \left. \exists x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}), r\in {{\mathrm{Enc}}}(\fancyscript{R}): xy=r\right\} \end{aligned}$$

since ${{\mathrm{Enc}}}({{\fancyscript{X}}})\subset {{{\varvec{x}}}}^B$, ${{\mathrm{Enc}}}({{\fancyscript{Y}}})\subset {{{\varvec{y}}}}^B$, and ${{\mathrm{Enc}}}(\fancyscript{R})\subset {{{\varvec{r}}}}^B$. Therefore, (5) holds for the second and third case. Establishing $\left( \fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\right) ^C\supset \Box \{y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\exists x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}), r\in {{\mathrm{Enc}}}(\fancyscript{R}): xy=r\}$ is sufficient to show that (5) holds in the first case.

Suppose that $0\notin {{{\varvec{x}}}}^B$. Consider $y\in {{{\varvec{y}}}}^C$ such that $\exists x\in ({{{\varvec{x}}}}')^C,r\in ({{{\varvec{r}}}}')^C$ with $xy=r$, noting that $x\ne 0$ by assumption. If such $y$ does not exist then $\{y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\exists x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}), r\in {{\mathrm{Enc}}}(\fancyscript{R}): xy=r\}=\emptyset$ and (5) holds trivially. If such $y$ exists, then $y=r\times \frac{1}{x}$. Also, $\frac{1}{{{\fancyscript{X}}}'}$ exists and $\frac{1}{x}\in {{\mathrm{Enc}}}(\frac{1}{\fancyscript{X'}})$. Since $r\times \frac{1}{x}\in (\fancyscript{R}'\times \frac{1}{{{\fancyscript{X}}}'})^C$, $\left( \fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}})\right) ^C\supset \{y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\exists x\in {{\mathrm{Enc}}}({{\fancyscript{X}}}), r\in {{\mathrm{Enc}}}(\fancyscript{R}): xy=r\}$. $\square$

Lemma 5

Consider $(\times ,{\mathbb {R}}^2,{\mathbb {R}})$ and its relaxation function $(\times ,{\mathbb {M\! R}}^2,{\mathbb {M\! R}})$. The function $(\times ^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2)$ defined for all ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ by

$$\begin{aligned} \times ^{{{\mathrm{rev}}}}(({{\fancyscript{X}}},{{\fancyscript{Y}}}),\fancyscript{R}) = \left( \fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}),\fancyscript{G} (\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}),\fancyscript{R}, {{\fancyscript{Y}}})\right) \end{aligned}$$

is a reverse McCormick update of $(\times ,{\mathbb {R}}^2,{\mathbb {R}})$.

Proof

Let ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$, $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$. If $\times ({{\fancyscript{X}}},{{\fancyscript{Y}}})\cap \fancyscript{R}=\emptyset$, there does not exist $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$, $y\in {{\mathrm{Enc}}}({{\fancyscript{Y}}})$ so that $xy\in {{\mathrm{Enc}}}(\fancyscript{R})$. Thus, (4) holds trivially. Otherwise, pick $(x,y)\in {{\mathrm{Enc}}}({{\fancyscript{X}}})\times {{\mathrm{Enc}}}({{\fancyscript{Y}}})$ so that $xy\in {{\mathrm{Enc}}}(\fancyscript{R})$. By Lemma 4, ${{\mathrm{Enc}}}(\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}))\supset \{\tilde{x}\in {{\mathrm{Enc}}}({{\fancyscript{X}}}):\exists \tilde{y}\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}),z\in {{\mathrm{Enc}}}(\fancyscript{R}):\tilde{x}\tilde{y}=z\}$, and hence $x\in {{\mathrm{Enc}}}(\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}))$. Likewise, $\{\tilde{y}\in {{\mathrm{Enc}}}({{\fancyscript{Y}}}):\exists \tilde{x}\in {{\mathrm{Enc}}}(\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}})),z\in {{\mathrm{Enc}}}(\fancyscript{R}):\tilde{x}\tilde{y}=z\}\subset {{\mathrm{Enc}}}(\fancyscript{G}(\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}), \fancyscript{R},{{\fancyscript{Y}}}))$, hence $y\in {{\mathrm{Enc}}}(\fancyscript{G}(\fancyscript{G}({{\fancyscript{Y}}},\fancyscript{R},{{\fancyscript{X}}}), \fancyscript{R},{{\fancyscript{Y}}}))$. Thus, $(x,y)\in {{\mathrm{Enc}}}(\times ^{{{\mathrm{rev}}}}(({{\fancyscript{X}}},{{\fancyscript{Y}}}),\fancyscript{R}))$ and (4) holds. $\square$

Note that $\times ^{{{\mathrm{rev}}}}(({{\fancyscript{X}}},{{\fancyscript{Y}}}),\fancyscript{R}) = \left( \fancyscript{G}(\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R},{{\fancyscript{Y}}}), \fancyscript{R},{{\fancyscript{X}}}),\fancyscript{G}({{\fancyscript{X}}},\fancyscript{R}, {{\fancyscript{Y}}})\right)$ is an alternative reverse McCormick update of $(\times ,{\mathbb {R}}^2,{\mathbb {R}})$.

5.2 Reverse McCormick updates of univariate functions

Lemma 6

Let $B\subset {\mathbb {R}}$ and consider an injective continuous function $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$. Furthermore, assume that $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$ where $\mathrm{range}(u,B)$ refers to the image of $B$ under the real-valued function $u$. The function $(u^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset B\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ defined for all ${{\fancyscript{X}}}\in {\mathbb {M}}_\emptyset B$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ by

$$\begin{aligned} u^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R})= u^{-1}(\fancyscript{T}) \cap {{\fancyscript{X}}} \end{aligned}$$

where $\fancyscript{T}=({{{\varvec{r}}}}^B\cap u({{{\varvec{x}}}}^B),{{\mathrm{Enc}}}(\fancyscript{R}\cap u({{\fancyscript{X}}})))$ is a reverse McCormick update of $(u,B,{\mathbb {R}})$.

Proof

Let ${{\fancyscript{X}}}\in {\mathbb {M}}_\emptyset B$. Suppose that ${{\mathrm{Enc}}}(\fancyscript{T})=\emptyset$. Since $(u,{\mathbb {M}}_\emptyset B,{\mathbb {M\! R}})$ is a relaxation function, there does not exist an $x\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$ so that $u(x)\in {{\mathrm{Enc}}}(\fancyscript{R})$. Otherwise, since $(u,B,{\mathbb {R}})$ is continuous and injective, it is invertible on $\mathrm{range}(u,B)$ and $u^{-1}$ is continuous [46], Thm. 4.17]. Since $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$, $u(x)\in {{\mathrm{Enc}}}(\fancyscript{T})$ implies $x=u^{-1}(u(x))\in {{\mathrm{Enc}}}(u^{-1}(\fancyscript{T}))$. $\square$

Remark 3

Lemma 6 can be used to define the reverse McCormick update of $-(\cdot )$, $(\cdot )^n$ for odd $n\in \mathbb {N}$, $\exp$, $\log$, $\sqrt{\cdot }$, etc. It is also applicable to $\frac{1}{(\cdot )}$ if $B$ is restricted to either the negative or positive reals.

Lemma 7

Let $n\in \mathbb {N}$ be even. Consider $(u,{\mathbb {R}},{\mathbb {R}})\in {{\fancyscript{L}}}$ where $u(x)=x^n$ and assume that $(\root n \of {\cdot },[0,+\infty ),{\mathbb {R}})\in {{\fancyscript{L}}}$. The function $(u^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ defined for all ${{\fancyscript{X}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ by

$$\begin{aligned} u^{{{\mathrm{rev}}}}({{\fancyscript{X}}},\fancyscript{R})=\left\{ \begin{array}{l@{\quad }l} \emptyset &{}\quad \text {if}\,\, {{{\varvec{r}}}}^B\cap u({{{\varvec{x}}}}^B)=\emptyset , \\ \root n \of {\fancyscript{T}}\cap {{\fancyscript{X}}} &{}\quad \text {if} \,\, \underline{x}\ge 0, \\ -\root n \of {\fancyscript{T}}\cap {{\fancyscript{X}}} &{}\quad \text {if} \,\, \overline{x}\le 0, \\ \left( u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^B,{{{\varvec{t}}}}^B),\left[ -\root n \of {\hat{t}},\root n \of {\hat{t}}\, \right] \cap u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^B,{{{\varvec{t}}}}^B)\right) \cap {{\fancyscript{X}}} &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

where $\fancyscript{T}=({{{\varvec{t}}}}^B, {{{\varvec{t}}}}^C) = ({{{\varvec{r}}}}^B\cap u({{{\varvec{x}}}}^B)\cap [0,+\infty ),{{\mathrm{Enc}}}(\fancyscript{R})\cap {{\mathrm{Enc}}}(u({{\fancyscript{X}}}))\cap [0,+\infty ))$ is a reverse McCormick update of $(u,{\mathbb {R}},{\mathbb {R}})$, and $u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^B,{{{\varvec{t}}}}^B)$ denotes the reverse interval update for the operation.

Proof

Let ${{\fancyscript{X}}}\in {\mathbb {M}}_\emptyset {\mathbb {R}}$. Suppose that ${{{\varvec{r}}}}^B\cap u({{{\varvec{x}}}}^B)=\emptyset$. Since $(u,{\mathbb {I}}_\emptyset {\mathbb {R}},{\mathbb {I\! R}})$ is an inclusion function, there does not exist an $x\in {{{\varvec{x}}}}^B$ so that $u(x)\in {{{\varvec{r}}}}^B$.

In the following, assume that ${{{\varvec{r}}}}^B\cap u({{{\varvec{x}}}}^B)\ne \emptyset$. Note that intersecting $\fancyscript{R}$ with the non-negative half space only ensures that no domain violation occurs. Let $\tilde{x}\in {{\mathrm{Enc}}}({{\fancyscript{X}}})$ so that $u(\tilde{x})\in {{\mathrm{Enc}}}(\fancyscript{R})\}$. If $\underline{x}\ge 0$ then $\tilde{x}\ge 0$. By definition of the relaxation function of $\root n \of {\cdot }$, it follows that $\{x\in {\mathbb {R}}:x\ge 0 \wedge u(x)\in {{\mathrm{Enc}}}(\fancyscript{R})\} \subset {{\mathrm{Enc}}}(\root n \of {\fancyscript{T}})$. Similarly, if $\overline{x}\le 0$ then $\tilde{x}\le 0$. Since $u(-\tilde{x})=u(\tilde{x})\ge 0$ and $u(-\tilde{x})\in {{\mathrm{Enc}}}(\fancyscript{R})$, $u(-\tilde{x})\in {{\mathrm{Enc}}}(\fancyscript{T})$ so that $\tilde{x}=-(-\tilde{x})=-\root n \of {u(-\tilde{x})}\in {{\mathrm{Enc}}}(-\root n \of {\fancyscript{T}})$. Hence, $\{x\in {\mathbb {R}}:x\le 0 \wedge u(x)\in {{\mathrm{Enc}}}(\fancyscript{R})\} \subset {{\mathrm{Enc}}}(-\root n \of {\fancyscript{T}})$. Otherwise, if $0\not \in {{{\varvec{x}}}}^B$, it is easy to see that

$$\begin{aligned} \{x\in {\mathbb {R}}:u(x)\in {{\mathrm{Enc}}}(\fancyscript{R})\}=\{x\in {\mathbb {R}}:\exists y\in {{\mathrm{Enc}}}(\fancyscript{R}),{{{\varvec{x}}}}=-\root n \of {y}\vee {{{\varvec{x}}}}=\root n \of {y}\}\subset \left[ -\root n \of {\hat{t}},\root n \of {\hat{t}}\,\right] . \end{aligned}$$

Intersecting with the reverse interval update does not discard any $\tilde{x}$ for which $u(\tilde{x})\in {{\mathrm{Enc}}}(\fancyscript{R})$ holds. $\square$

Note that a similar construction is possible to find the reverse McCormick update of the absolute value function.

5.3 Inclusion monotonicity of the reverse McCormick updates

Next, it will be shown that reverse McCormick updates are inclusion monotonic while the next subsection focuses on establishing coherent concavity. Note that [51], Lemma 2.4.15] will be referenced multiple times hereafter to establish inclusion monotonicity of a finite composition of inclusion monotonic functions. Though coherent concavity was also assumed in that result, it is not necessary in order to establish inclusion monotonicity of a finite composition of inclusion monotonic functions.

First, note that the intersection update is inclusion monotonic.

Lemma 8

The mapping $\cap :{}^*{\mathbb {M}}\! {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}$ defined by $\cap ({{\fancyscript{X}}},{{\fancyscript{Y}}})={{\fancyscript{X}}}\cap {{\fancyscript{Y}}}$ for all ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ is inclusion monotonic on ${}^*{\mathbb {M}}\! {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Let ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2,{{\fancyscript{Y}}}_1,{{\fancyscript{Y}}}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$. Then, ${{\fancyscript{X}}}_1\subset {{\fancyscript{X}}}_2$ and ${{\fancyscript{Y}}}_1\subset {{\fancyscript{Y}}}_2$ imply ${{\fancyscript{X}}}_1\cap {{\fancyscript{Y}}}_1\subset {{\fancyscript{X}}}_2 \cap {{\fancyscript{Y}}}_2$. $\square$

Next, the binary operations are considered.

Lemma 9

$(+^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ is inclusion monotonic on ${\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

This follows immediately since the negative univariate function [51], Theorem 2.4.29 together with Section 2.8], addition [51], Theorem 2.4.20], the intersection operator (Lemma 8) as well as finite composition of inclusion monotonic mappings [51], cf. Lemma 2.4.15] are inclusion monotonic. $\square$

It is helpful to study the extended Gauss–Seidel operator prior to looking at the reverse update of multiplication.

Lemma 10

$\fancyscript{G}$ is inclusion monotonic on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}$.

Proof

It was already shown that multiplication [51], Theorem 2.4.23] and the reciprocal function [51], Theorem 2.4.29 together with Section 2.8] as well as finite composition [51], Lemma 2.4.15] are inclusion monotonic. Also note that $\varGamma$ is inclusion monotonic [43], 4.3.2]. Let $({{\fancyscript{X}}}_1,\fancyscript{R}_1,{{\fancyscript{Y}}}_1), ({{\fancyscript{X}}}_2,\fancyscript{R}_2,{{\fancyscript{Y}}}_2)\in {\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}$ so that $({{\fancyscript{X}}}_1,\fancyscript{R}_1,{{\fancyscript{Y}}}_1)\subset ({{\fancyscript{X}}}_2,\fancyscript{R}_2,{{\fancyscript{Y}}}_2)$. If $0\not \in {{{\varvec{x}}}}_2^B$ then $(\fancyscript{R}_1'\times \frac{1}{{{\fancyscript{X}}}_1'})^C\cap ({{{\varvec{y}}}}_1')^C\subset (\fancyscript{R}_2'\times \frac{1}{{{\fancyscript{X}}}_2'})^C\cap ({{{\varvec{y}}}}_2')^C$. Otherwise, if $0\not \in {{{\varvec{x}}}}_1^B$ then $(\fancyscript{R}_1'\times \frac{1}{{{\fancyscript{X}}}_1'})^C\cap ({{{\varvec{y}}}}_1')^C\subset \varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)\cap ({{{\varvec{y}}}}_1')^C\subset \varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)\cap ({{{\varvec{y}}}}_2')^C$. Otherwise, if $0\in {{{\varvec{x}}}}_1^B$ and $0\not \in {{{\varvec{r}}}}_2^B$ then $\varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)\cap ({{{\varvec{y}}}}_1')^C\subset \varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)\cap ({{{\varvec{y}}}}_2')^C$. Otherwise, if $0\in {{{\varvec{x}}}}_1^B$ and $0\in {{{\varvec{r}}}}_2^B$ then $\varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)\cap ({{{\varvec{y}}}}_1')^C\subset ({{{\varvec{y}}}}_1')^C\subset ({{{\varvec{y}}}}_2')^C$ Thus, $\fancyscript{G}$ is inclusion monotonic. $\square$

Lemma 11

$(\times ^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ is inclusion monotonic on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Since $\fancyscript{G}$ and finite composition [51], Lemma 2.4.15] are inclusion monotonic, the result is immediate. $\square$

Next, the reverse updates of univariate functions are considered.

Lemma 12

Let $B\subset {\mathbb {R}}$ and consider an injective continuous function $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$. Assume that $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$. Then, $u^{{{\mathrm{rev}}}}$ as defined in Lemma 6 is inclusion monotonic on ${\mathbb {M}}_\emptyset B\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Since $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$, it follows that $u^{-1}$ is inclusion monotonic [51], Theorem 2.4.29]. $\square$

Lemma 13

Let $n\in \mathbb {N}$ be even. Consider $(u,{\mathbb {R}},{\mathbb {R}})\in {{\fancyscript{L}}}$ where $u(x)=x^n$. Assume that $(\root n \of {\cdot },[0,+\infty ),{\mathbb {R}})\in {{\fancyscript{L}}}$. Suppose that the convex and concave envelopes of $\root n \of {\cdot }$ are used in calculating relaxations. Then, $u^{{{\mathrm{rev}}}}$ as defined in Lemma 7 is inclusion monotonic on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Note that the relaxation function of $\root n \of {\cdot }$ and of the negative operator, the intersection operator and finite composition is inclusion monotonic. Note that $\fancyscript{T}$ is inclusion monotonic by construction and so is $u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}^B,{{{\varvec{t}}}}^B)$. Let $({{\fancyscript{X}}}_1,\fancyscript{R}_1),({{\fancyscript{X}}}_2,\fancyscript{R}_2)\in {\mathbb {M}}_\emptyset B \times {}^*{\mathbb {M}}\! {\mathbb {R}}$ so that $({{\fancyscript{X}}}_1,\fancyscript{R}_1)\subset ({{\fancyscript{X}}}_2,\fancyscript{R}_2)$. If ${{{\varvec{r}}}}_1^B\cap u({{{\varvec{x}}}}_1^B)=\emptyset$ or if $\underline{x}_2\ge 0$ or $\overline{x}_2\le 0$ then $u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_1,\fancyscript{R}_1)\subset u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_2,\fancyscript{R}_2)$. Otherwise, suppose $\underline{x}_1\ge 0$. Then $\root n \of {\fancyscript{T}_1}\cap {{\fancyscript{X}}}_1\subset (u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}_1^B,{{{\varvec{t}}}}_1^B),[-\root n \of {\hat{t}_1},\root n \of {\hat{t}_1}]\cap u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}_1^B,{{{\varvec{t}}}}_1^B))\cap {{\fancyscript{X}}}_1\subset (u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}_2^B,{{{\varvec{t}}}}_2^B),[-\root n \of {\hat{t}_2},\root n \of {\hat{t}_2}]\cap u^{{{\mathrm{rev}}}}({{{\varvec{x}}}}_2^B,{{{\varvec{t}}}}_2^B))\cap {{\fancyscript{X}}}_2$. A similar argument applies when $\overline{x}_1\le 0$. In any other case, inclusion monotonicity follows directly from the properties referenced above and the monotonicity of $\root n \of {\cdot }$, i.e., $\hat{t}_1\le \hat{t}_2$ implies that $[-\root n \of {\hat{t}_1},\root n \of {\hat{t}_1}]\subset [-\root n \of {\hat{t}_2},\root n \of {\hat{t}_2}]$. $\square$

5.4 Coherent concavity of the reverse McCormick updates

Next, it will be shown that reverse McCormick updates are coherently concave. Note that if either ${{\mathrm{Enc}}}({{\fancyscript{F}}}({{\fancyscript{X}}}_1))=\emptyset$ or ${{\mathrm{Enc}}}({{\fancyscript{F}}}({{\fancyscript{X}}}_2))=\emptyset$, then the subset condition for coherent concavity holds trivially. Thus, in the proofs below, this case is never considered explicitly.

First, note that the intersection update is coherently concave.

Lemma 14

The mapping $\cap :{}^*{\mathbb {M}}\! {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\rightarrow {}^*{\mathbb {M}}\! {\mathbb {R}}$ defined by $\cap ({{\fancyscript{X}}},{{\fancyscript{Y}}})={{\fancyscript{X}}}\cap {{\fancyscript{Y}}}$ for all ${{\fancyscript{X}}},{{\fancyscript{Y}}}\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ is coherently concave on ${}^*{\mathbb {M}}\! {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Suppose ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ and ${{\fancyscript{Y}}}_1,{{\fancyscript{Y}}}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ are coherent. Let $\lambda \in [0,1]$. Since ${{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$ and ${{{\varvec{y}}}}_1^B={{{\varvec{y}}}}_2^B$, it follows that ${{{\varvec{x}}}}_1^B \cap {{{\varvec{y}}}}_1^B={{{\varvec{x}}}}_2^B \cap {{{\varvec{y}}}}_2^B=(\lambda {{{\varvec{x}}}}_1^B+(1-\lambda ){{{\varvec{x}}}}_2^B)\cap (\lambda {{{\varvec{y}}}}_1^B+(1-\lambda ){{{\varvec{y}}}}_2^B)$. Thus, $\cap ({{\fancyscript{X}}}_1,{{\fancyscript{Y}}}_1)$ and $\cap ({{\fancyscript{X}}}_2,{{\fancyscript{Y}}}_2)$ are coherent.

We will show that $\cap (\text {Conv}(\lambda ,({{\fancyscript{X}}}_1,{{\fancyscript{Y}}}_1),({{\fancyscript{X}}}_2, {{\fancyscript{Y}}}_2)))\supset \text {Conv}(\lambda ,\cap ({{\fancyscript{X}}}_1,{{\fancyscript{Y}}}_1),\cap ({{\fancyscript{X}}}_2,{{\fancyscript{Y}}}_2))$. Let $z_1\in {{{\varvec{x}}}}_1^C\cap {{{\varvec{y}}}}_1^C$ and $z_2\in {{{\varvec{x}}}}_2^C\cap {{{\varvec{y}}}}_2^C$. Denote $z=\lambda z_1+(1-\lambda )z_2$. By construction, $z_1\in {{{\varvec{x}}}}_1^C$, $z_1\in {{{\varvec{y}}}}_1^C$ and $z_2\in {{{\varvec{x}}}}_2^C$, $z_2\in {{{\varvec{y}}}}_2^C$ so that $z\in \lambda {{{\varvec{x}}}}_1^C+(1-\lambda ){{{\varvec{x}}}}_2^C$ and $z\in \lambda {{{\varvec{y}}}}_1^C+(1-\lambda ) {{{\varvec{y}}}}_2^C$. Thus, $z \in (\lambda {{{\varvec{x}}}}_1^C+(1-\lambda ){{{\varvec{x}}}}_2^C)\cap (\lambda {{{\varvec{y}}}}_1^C+(1-\lambda ){{{\varvec{y}}}}_2^C)$ so that $\lambda ({{{\varvec{x}}}}_1^C\cap {{{\varvec{y}}}}_1^C)+(1-\lambda )({{{\varvec{x}}}}_2^C\cap {{{\varvec{y}}}}_2^C)\subset ((\lambda {{{\varvec{x}}}}_1^C+(1-\lambda ){{{\varvec{x}}}}_2^C)\cap (\lambda {{{\varvec{y}}}}_1^C+(1-\lambda ){{{\varvec{y}}}}_2^C))$. $\square$

In particular, note that the proof indicates that $\cap ({{\fancyscript{X}}}_1,{{\fancyscript{Y}}}_1)\ne \emptyset$ and $\cap ({{\fancyscript{X}}}_2,{{\fancyscript{Y}}}_2)\ne \emptyset$ imply that $\cap (\text {Conv}(\lambda , ({{\fancyscript{X}}}_1,{{\fancyscript{Y}}}_1), ({{\fancyscript{X}}}_2,{{\fancyscript{Y}}}_2))) \ne \emptyset$.

Next, the binary operations are considered.

Lemma 15

$(+^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ is coherently concave on ${\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Note that negative univariate function [51], Theorems 2.4.29 and 2.4.30 together with Section 2.8], addition [51], Theorem 2.4.20] and the intersection operator (Lemmas 8 and 14) are inclusion monotonic and coherently concave, $(+^{{{\mathrm{rev}}}},{\mathbb {I}}_\emptyset {\mathbb {R}}^2\times {}^*\mathbb {I}\! {\mathbb {R}},{\mathbb {I}}_\emptyset {\mathbb {R}})$ is inclusion monotonic and finite composition [51], Lemma 2.4.15] is coherently concave. Thus, the result follows. $\square$

It is helpful to study the extended Gauss–Seidel operator prior to looking at the reverse update of multiplication.

Lemma 16

$\fancyscript{G}$ is coherently concave on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}$.

Proof

Let ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {\mathbb {M}}_\emptyset {\mathbb {R}}$, $\fancyscript{R}_1,\fancyscript{R}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ and ${{\fancyscript{Y}}}_1,{{\fancyscript{Y}}}_2\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ be coherent. Since ${{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$, ${{{\varvec{y}}}}_1^B={{{\varvec{y}}}}_2^B$ and ${{{\varvec{r}}}}_1^B={{{\varvec{r}}}}_2^B$, it follows that $\varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)=\varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)$ so that $\fancyscript{G}({{\fancyscript{X}}}_1,\fancyscript{R}_1,{{\fancyscript{Y}}}_1)$ and $\fancyscript{G}({{\fancyscript{X}}}_2,\fancyscript{R}_2,{{\fancyscript{Y}}}_2)$ are coherent.

Suppose $0\not \in {{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$. It was already shown that multiplication [51], Theorems 2.4.23 and 2.4.24] and the reciprocal function [51], Theorems 2.4.29 and  2.4.30 together with Section 2.8] are inclusion monotonic and coherently concave and finite compositions of inclusion monotonic, coherently concave functions are coherently concave [51], Lemma 2.4.15]. Also, Lemmas 8 and 14 show that the intersection operation is coherently concave and inclusion monotonic. Thus, $\fancyscript{G}$ is coherently concave in this case.

Next, suppose $0\in {{{\varvec{x}}}}_1^B$ and $\underline{r}_1=\underline{r}_2>0$ or $\overline{r}_1=\overline{r}_2<0$. Pick $\lambda \in [0,1]$ and let $z_1\in \varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)\cap {{{\varvec{y}}}}_1^C$, $z_2\in \varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)\cap {{{\varvec{y}}}}_2^C$. Consider $z=\lambda z_1+(1-\lambda )z_2$. Since $z_1\in {{{\varvec{y}}}}_1^C$ and $z_2\in {{{\varvec{y}}}}_2^C$, $z\in \lambda {{{\varvec{y}}}}_1^C+(1-\lambda ){{{\varvec{y}}}}_2^C$. Note that $z\in \varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)=\varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)$. Thus, $z\in \lambda (\varGamma ({{{\varvec{x}}}}_1^B,{{{\varvec{r}}}}_1^B,{{{\varvec{y}}}}_1^B)\cap {{{\varvec{y}}}}_1^C)+(1-\lambda )(\varGamma ({{{\varvec{x}}}}_2^B,{{{\varvec{r}}}}_2^B,{{{\varvec{y}}}}_2^B)\cap {{{\varvec{y}}}}_2^C)$ and $\fancyscript{G}$ is coherently concave in this case.

In the last case, coherent concavity is immediate. $\square$

Lemma 17

$(\times ^{{{\mathrm{rev}}}},{\mathbb {M}}_\emptyset {\mathbb {R}}^2\times {}^*{\mathbb {M}}\! {\mathbb {R}},{\mathbb {M}}_\emptyset {\mathbb {R}})$ is coherently concave on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Since $\fancyscript{G}$ is inclusion monotonic and coherently concave and finite compositions of inclusion monotonic, coherently concave functions are coherently concave [51], Lemma 2.4.15], the result is immediate. $\square$

Next, the reverse updates of univariate functions are considered.

Lemma 18

Let $B\subset {\mathbb {R}}$ and consider an injective continuous function $(u,B,{\mathbb {R}})\in {{\fancyscript{L}}}$. Assume that $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$. Then, $u^{{{\mathrm{rev}}}}$ as defined in Lemma 6 is coherently concave on ${\mathbb {M}}_\emptyset B\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Let ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}_1,\fancyscript{R}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ be coherent, i.e., ${{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$ and ${{{\varvec{r}}}}_1^B={{{\varvec{r}}}}_2^B$. Note that $u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_1,\fancyscript{R}_1)$ and $u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_2,\fancyscript{R}_2)$ are coherent. Since $(u^{-1},\mathrm{range}(u,B),{\mathbb {R}})\in {{\fancyscript{L}}}$, it follows that $u^{-1}$ is coherently concave [51], Theorem 2.4.30]. $\square$

Lemma 19

Let $n\in \mathbb {N}$ be even. Consider $(u,{\mathbb {R}},{\mathbb {R}})\in {{\fancyscript{L}}}$ where $u(x)=x^n$. Assume that $(\root n \of {\cdot },[0,+\infty ),{\mathbb {R}})\in {{\fancyscript{L}}}$. Then, $u^{{{\mathrm{rev}}}}$ as defined in Lemma 7 is coherently concave on ${\mathbb {M}}_\emptyset {\mathbb {R}}\times {}^*{\mathbb {M}}\! {\mathbb {R}}$.

Proof

Let ${{\fancyscript{X}}}_1,{{\fancyscript{X}}}_2\in {\mathbb {M}}_\emptyset {\mathbb {R}}$ and $\fancyscript{R}_1,\fancyscript{R}_2\in {}^*{\mathbb {M}}\! {\mathbb {R}}$ be coherent, i.e., ${{{\varvec{x}}}}_1^B={{{\varvec{x}}}}_2^B$ and ${{{\varvec{r}}}}_1^B={{{\varvec{r}}}}_2^B$. Note that $u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_1,\fancyscript{R}_1)$ and $u^{{{\mathrm{rev}}}}({{\fancyscript{X}}}_2,\fancyscript{R}_2)$ are coherent.

By assumption, the relaxation function of $\root n \of {\cdot }$ is coherently concave. Likewise, $-\root n \of {\cdot }$ is coherently concave which follows from coherent concavity of the negative operator and the composition theorem [51], Lemma 2.4.15]. It follows that $\root n \of {\cdot }$ and $-\root n \of {\cdot }$ are relaxation functions. As the intersection operator is coherently concave (Lemma 14), coherent concavity for the cases $\underline{x}\ge 0$ and $\overline{x}\le 0$ follows. Otherwise, we must consider two potential roots. Define $(\tilde{u}^{-1},[0,+\infty ),{\mathbb {P}}({\mathbb {R}}))$ for each $x\in [0,+\infty )$ by $\tilde{u}^{-1}(x)=\{-\root n \of {x},\root n \of {x}\}$ and note that $u(y)=x$ for each $y\in \tilde{u}^{-1}(x)$ and $x\in \tilde{u}^{-1}(u(x))$. It is easy to see that $-\root n \of {\cdot }$ and $\root n \of {\cdot }$ are the convex and concave envelopes of $\tilde{u}^{-1}$ so that we can use the construction of the relaxation function of $\tilde{u}^{-1}$ in Eq. (1). Furthermore, $t^{\min }({{{\varvec{t}}}}^B)=t^{\max }({{{\varvec{t}}}}^B)=\overline{t}$ and $\overline{t}\ge \hat{t}$ in this case so that ${{\mathrm{mid}}}(,\hat{t},t^{\min }({{{\varvec{t}}}}^B))={{\mathrm{mid}}}(,\hat{t},t^{\max }({{{\varvec{t}}}}^B))=\hat{t}$. This is equivalent to the relaxation we obtain by using Eq. (1). It has already been established that Eq. (1) provides for a coherently concave relaxation function [51], Theorem 2.4.30] so that, together with Lemma 14, coherent concavity of the last case follows. $\square$

6 Using reverse McCormick propagation in CSPs and in global optimization

Consider a CSP with variables $y=(y_1,\ldots ,y_n)$, domains ${{{\varvec{d}}}}\in {\mathbb {I\! R}}^n$ and constraints

$$\begin{aligned} {G}(y)&\le 0, \end{aligned}$$

(6)

$$\begin{aligned} {H}(y)&=0, \end{aligned}$$

(7)

where ${G}:{{{\varvec{d}}}}\rightarrow {\mathbb {R}}^{n_g}$ and ${H}:{{{\varvec{d}}}}\rightarrow {\mathbb {R}}^{n_h}$ are ${{\fancyscript{L}}}$-factorable functions.

Suppose that the variables $y\in {{{\varvec{d}}}}$ can be partitioned into independent and dependent variables, $p\in {{{\varvec{p}}}}\in {\mathbb {I\! R}}^{n-m}$ and $z\in {{{\varvec{x}}}}\in {\mathbb {I\! R}}^m$, respectively, where ${{{\varvec{p}}}}\times {{{\varvec{x}}}}={{{\varvec{d}}}}$. Consider the set-valued map ${X}:{{{\varvec{p}}}}\rightarrow {\mathbb {P}}({{{\varvec{x}}}})$ defined by: $p\mapsto \{\xi \in {{{\varvec{x}}}}:{G}(\xi ,p)\le 0, {H}(\xi ,p)=0 \}$. In words, this mapping returns for each $p\in {{{\varvec{p}}}}$ all points in ${{{\varvec{x}}}}$ that are feasible in the constraints (6) and (7) and thus are solutions of the CSP.

Remark 4

It is not assumed that $m=n_h$. The proposed method will work for any choice of $m$. In particular note that is often not possible to find a closed form for $x$ nor is nonempty ${X}(p)$ or ${X}(p)$ a singleton immediate in many cases.

In this section, we will first discuss how reverse McCormick propagation can be applied to utilize equality and inequality constraints. Next, we will compare different full-space and reduced-space relaxations of nonlinear programs and we will conclude with a discussion on how to partition the variables into independent and dependent ones.

6.1 Solving CSPs with equality and inequality constraints

For easier notation, define ${C}:{{{\varvec{d}}}}\rightarrow {\mathbb {R}}^{n_g+n_h}$ with $c_i(y)=g_i(y)$ for $i=1,\ldots ,n_g$ and $c_{i+n_g}(y)=h_i(y)$ for $i=1,\ldots ,n_h$ and introduce $\fancyscript{N}\in {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_g+n_h}$ with $\fancyscript{N}_i=((-\infty ,0],(-\infty ,0])$, $i=1,\ldots ,n_g$ and $\fancyscript{N}_{i+n_g}=([0,0],[0,0])$, $i=1,\ldots ,n_h$. Let ${{\fancyscript{Y}}}^0:{{{\varvec{p}}}}\rightarrow {\mathbb {M\! R}}^n$ where ${{\fancyscript{Y}}}^0_i=({{{\varvec{x}}}}_i,[\underline{x}_i,\overline{x}_i])$ for $i=1,\ldots ,m$ and ${{\fancyscript{Y}}}^0_{i+m}=({{{\varvec{p}}}}_i,[p_i,p_i])$ for $i=1,\ldots ,n-m$.

${{\fancyscript{Y}}}^0$ can be interpreted as an a priori enclosure of the solution set of the CSP when $y_{i+m}=p_i$, $i=1,\ldots ,n-m$. Using the idea of constraint propagation on the DAG of ${C}$, several avenues to tighten ${{\fancyscript{Y}}}^0$ exist. First, it is possible to discard parts of ${{{\varvec{d}}}}$ for which it can be guaranteed that no $y$ exists that satisfies Eqs. (6) and (7). Most easily, this can be achieved by reverse interval propagation [62], which considers the bounds only. Second, reverse McCormick propagation provides a means to improve the original bounds and relaxations to find new bounds and relaxations that are at least as tight as the original relaxations and possibly nonconstant.

Let $(\fancyscript{S},\pi _o)$ be a ${{\fancyscript{L}}}$-computational sequence corresponding to ${C}$. Recall the definition of ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}$, cf. Eq. (3), and note that for each $p\in {{{\varvec{p}}}}$ and $\xi \in {X}(p)$ there exists a $\phi \in {{\mathrm{Enc}}}(\fancyscript{N})$ so that ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}((\xi ,p),\phi )=(\xi ,p)$. Consider the reverse McCormick propagation of ${C}$:

(8)

Note that $\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is a relaxation function of ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}$ by Theorem 8. As the following theorem shows, one interpretation of Equation 8 is that it defines , which are convex and concave relaxations of ${X}$ on ${{{\varvec{p}}}}$, respectively, (and, less interestingly, , which are convex and concave relaxations of the identity function ${P}$ on ${{{\varvec{p}}}}$).

Theorem 9

Consider $\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}$, a relaxation function of ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}$ on $(({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p,p]))\times {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_g+n_h}$. Let be as defined by Equation 8. Then, are convex and concave relaxations of ${X}$ on ${{{\varvec{p}}}}$, respectively.

Proof

Let $x\in {{{\varvec{x}}}}$, $p\in {{{\varvec{p}}}}$ and $\phi \in {{\mathrm{Enc}}}(\fancyscript{N})$. Note that ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}((x,p),\phi )=(x,p)$ if ${C}_\fancyscript{S}(x,p)=\phi$. Since $\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is a relaxation function of ${C}^{{{\mathrm{rev}}}}_\fancyscript{S}$, it follows for such $(x,p)$ that

$$\begin{aligned}&{{\mathrm{Enc}}}(\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}((({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p,p])),\fancyscript{N})) \supset {{\mathrm{Enc}}}(\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}((({{{\varvec{x}}}},[x,x]),({{{\varvec{p}}}},[p,p])),\fancyscript{N}))\\&\quad \supset ([x,x],[p,p]). \end{aligned}$$

In particular, .

Pick $p_1,p_2\in {{{\varvec{p}}}}$ and $\lambda \in (0,1)$. Consider ${{\fancyscript{Y}}}_1=(({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p_1,p_1]))\times \fancyscript{N}$ and ${{\fancyscript{Y}}}_2=(({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p_2,p_2]))\times \fancyscript{N}$. $\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}$ is coherently concave on $(({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p,p]))\times {}^*{\mathbb {M}}\! {\mathbb {R}}^{n_g+n_h}$, so it follows that

$$\begin{aligned} \fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}(\text {Conv}(\lambda ,{{\fancyscript{Y}}}_1, {{\fancyscript{Y}}}_2))\supset \text {Conv}(\lambda ,\fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}({{\fancyscript{Y}}}_1), \fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}({{\fancyscript{Y}}}_2)), \end{aligned}$$

which implies that

Thus, are convex and concave relaxations of ${X}$ on ${{{\varvec{p}}}}$, respectively. $\square$

In other words, given $p\in {{{\varvec{p}}}}$ and $\xi \in {X}(p)$, it holds that . Also note that a particular possible outcome of the reverse McCormick propagation is

$$\begin{aligned} \fancyscript{C}^{{{\mathrm{rev}}}}_\fancyscript{S}((({{{\varvec{x}}}},{{{\varvec{x}}}}),({{{\varvec{p}}}},[p,p])),\fancyscript{N})= ((\tilde{{{{\varvec{x}}}}},\emptyset ),(\tilde{{{{\varvec{p}}}}},\emptyset ))), \end{aligned}$$

in which case ${X}(p)=\emptyset$.

Fig. 2

Principle of forward–reverse McCormick update to construct relaxations of the implicit set-valued mapping ${X}(\cdot )$: forward evaluation of relaxation functions [52] to obtain a particular kind of relaxations of ${G}$ and ${H}$ on $\varvec{p}$ (1), intersection with constraint information (2), and reverse propagation of additional information (3). This procedure can be iterated on if desired (4)

The sequence of the calculations for the reverse update $\fancyscript{C}_{\fancyscript{S}}^{{{\mathrm{rev}}}}$ is outlined in Fig. 2. In contrast to the evaluation of natural McCormick extensions, the forward evaluation of the relaxation functions in Step (1) is initialized differently. The results of this evaluation are interval bounds on the range of ${G}$ and ${H}$ on ${{{\varvec{x}}}}\times {{{\varvec{p}}}}$, as well as a particular kind of relaxations of ${G}$ and ${H}$ on ${{{\varvec{p}}}}$, here denoted by , etc. From the properties of the relaxation function it follows that is convex on ${{{\varvec{p}}}}$ and that , $\forall (x,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$ and $i=1,\ldots ,n_g$. Similarly, $\hat{{G}}({{{\varvec{x}}}},p)$ denotes an analogue concave relaxation of ${G}$. In Step (2), the constraint information is intersected with the relaxation functions of the constraints. This tightens the relaxations without losing the convexity and concavity properties. Step (3) propagates this information back to the variables so that we obtain relaxations of ${X}$ evaluated at $p$ or the information that ${X}(p)=\emptyset$. It is also shown that the procedure can be repeated in order to further improve the computed relaxations (Step (4)).

Let ${{\fancyscript{Y}}}^{k+1}=\fancyscript{C}_{\fancyscript{S}}^{{{\mathrm{rev}}}}({{\fancyscript{Y}}}^k,\fancyscript{N})$, $k=0,1,\ldots$. Note that the coherent concavity property of ${{\fancyscript{Y}}}^k$ is guaranteed only for a fixed $k$ so that it is important that the number of reverse updates is equal for all $p\in {{{\varvec{p}}}}$.

Avoiding domain violations Definition 3 ensures that the natural function ${F}_\fancyscript{S}$ of a computational sequence $(\fancyscript{S},\pi _o)$, and, in particular, each participating univariate function, is defined at each point of its natural domain $D_\fancyscript{S}$ and hence can be safely evaluated there. However, the natural domain of a complicated computational sequence is not easily obtained. If the natural function is evaluated at a point outside its domain, which is possible due to difficulty in practically establishing the exact natural domain, the domain of at least one univariate function will be violated. Additionally, Definition 10 further restricts the natural domains of the natural interval and McCormick extensions. Due to the inherent conservatism of the interval and McCormick techniques, domain violations are also potentially possible for ${{{\varvec{x}}}}\in {\mathbb {I}}\! D_\fancyscript{S}$ or ${{\fancyscript{X}}}\in {\mathbb {M}}\! D_\fancyscript{S}$. In order to avoid either problem, the following convention is implemented. Consider $(u,{{{\varvec{b}}}},{\mathbb {R}})\in {{\fancyscript{L}}}$ with ${{{\varvec{b}}}}\in {\mathbb {I\! R}}$, as is the case for many common univariate functions. If $x\not \in {{{\varvec{b}}}}$ then set $u(x)=\mathrm {NaN}$. For ${{{\varvec{x}}}}\in {\mathbb {I\! R}}$ or ${{\fancyscript{X}}}\in {\mathbb {M\! R}}$ with ${{{\varvec{x}}}}\not \subset {{{\varvec{b}}}}$ or ${{{\varvec{x}}}}^B\not \subset {{{\varvec{b}}}}$, the evaluation of $u({{{\varvec{x}}}})$ or $u({{\fancyscript{X}}})$ is undefined whereas $u({{{\varvec{x}}}}\cap {{{\varvec{b}}}})$ or $u({{\fancyscript{X}}}\cap ({{{\varvec{b}}}},{{{\varvec{b}}}}))$ is always defined due to the convention used herein that $u(\emptyset )=\emptyset$. Given any ${{{\varvec{x}}}}\in {\mathbb {I\! R}}^{n_i}$ or ${{\fancyscript{X}}}\in {\mathbb {M\! R}}^{n_i}$, this approach continues to construct valid enclosures and relaxations of $\tilde{{F}}:{\mathbb {R}}^{n_i}\rightarrow {\mathbb {R}}_\emptyset ^{n_o}$ defined by

$$\begin{aligned} \tilde{{F}}(x)=\left\{ \begin{array}{ll} {F}_\fancyscript{S}(x) &{}\quad \text {if}\,\, x\in D_\fancyscript{S},\\ \mathrm {NaN}&{}\quad \text {otherwise.}\\ \end{array} \right. \end{aligned}$$

Points outside the natural domain evaluate to $\mathrm {NaN}$ and, by our convention, $\mathrm {NaN}$ is an element of any interval so that any interval-valued or McCormick-valued function satisfies the inclusion property for such $x$. On the other hand, the natural interval or McCormick extensions bound or relax the natural function at each point that is contained in the natural domain by its usual properties. Overall, this convention allows us to circumvent difficulties with domain violations without losing the inclusion or relaxation function properties. In particular, it provides more directly useful information than throwing a flag indicating that a domain violation occurred.

6.2 Constructing relaxations for reduced-space optimization problems

Consider

$$\begin{aligned} \begin{array}{lll} f^*=&{}\min \limits _{z\in {{{\varvec{x}}}},p\in {{{\varvec{p}}}}} \; &{} f(z,p) \\ &{}\text {s.t.} &{} {G}(z,p)\le 0, \\ &{}&{}{H}(z,p)= 0, \end{array} \end{aligned}$$

(P)

where $f:{{{\varvec{x}}}}\times {{{\varvec{p}}}}\rightarrow {\mathbb {R}}$, ${G}:{{{\varvec{x}}}}\times {{{\varvec{p}}}}\rightarrow {\mathbb {R}}^{n_g}$ and ${H}:{{{\varvec{x}}}}\times {{{\varvec{p}}}}\rightarrow {\mathbb {R}}^{n_h}$ are ${{\fancyscript{L}}}$-factorable.

Define the set-valued mapping $\phi :{{{\varvec{p}}}}\rightarrow {\mathbb {P}}({\mathbb {R}})$ for each $p\in {{{\varvec{p}}}}$ by $\phi (p)=\{f(z,p):z\in {{{\varvec{x}}}},{G}(z,p)\le 0, {H}(z,p)= 0\}$. It is obvious that $f^*=\min _{p\in {{{\varvec{p}}}}} \inf \phi (p)$.

Let $\tilde{{{{\varvec{x}}}}}$ and $\tilde{{{{\varvec{p}}}}}$ denote the results of a reverse interval update as outlined above and illustrated in Fig. 2. First, note that $\tilde{{{{\varvec{x}}}}}\times \tilde{{{{\varvec{p}}}}}$ is a superset of the feasible region by construction of the reverse interval update. Recall that the procedure described in the previous section provides valid relaxations of the set-valued mapping ${X}$, and $\hat{{X}}$. These can be used to calculate generalized relaxation functions of $f$. To this extent, let ${{\fancyscript{F}}}$ denote the natural McCormick extension of $f$ and we will define

Proposition 1

Consider

$$\begin{aligned} \phi ^*=\min _{p\in \tilde{{{{\varvec{p}}}}}} \;&(p). \end{aligned}$$

(R1)

Then, (R1) is a convex program and $f^*\ge \phi ^*$.

Proof

(R1) is a convex program since $\tilde{{{{\varvec{p}}}}}$ is a convex set and is convex on $\tilde{{{{\varvec{p}}}}}$. $f^*\ge \phi ^*$ follows immediately from  [51], Theorem 2.7.13]. $\square$

Proposition 2

Let , and denote the standard convex McCormick relaxations of $f$, ${G}$ and ${H}$, respectively, on $\tilde{{{{\varvec{x}}}}}\times \tilde{{{{\varvec{p}}}}}$ and let $\hat{{H}}$ denote the standard concave McCormick relaxation of ${H}$ on $\tilde{{{{\varvec{x}}}}}\times \tilde{{{{\varvec{p}}}}}$. Consider

Then, $f^*\ge f_1\ge \phi ^*$.

Proof

It is clear that (R2) is a relaxation of (P) so that $f^*\ge f_1$. Note that holds for the standard McCormick relaxation of $f$ on $\tilde{{{{\varvec{x}}}}}\times \tilde{{{{\varvec{p}}}}}$. Inclusion monotonicity of the natural McCormick extensions implies that for any $p\in \tilde{{{{\varvec{p}}}}}$ and , and thus $(z,p)\ge (p)$ so that $f_1\ge \phi ^*$. $\square$

Remark 5

(R1) and (R2) are valid relaxations of (P). It is known that McCormick relaxations can be nonsmooth functions [41]. Thus, while (R2) is a tighter relaxation of (P), it potentially requires the solution of a convex nonsmooth program with nonlinear nonsmooth constraints. While several methods to solve such programs have been proposed (e.g.,[23, 31, 37]), and some software is available (e.g., [29, 36]), this remains a challenging class of problems to solve robustly. The constraints in (R2) can also be linearized using subgradients [41] to construct an outer-approximation. In this case, the consequence of Proposition 2 is no longer guaranteed to hold. On the other hand, convex nonsmooth programs with box-constraints such as (R1) can be solved more readily using methods such as that provided in [34]. Furthermore, (R1) only requires the solution of a $n-m$-dimensional optimization problem whereas (R2) is $n$-dimensional.

Remark 6

An alternative method to obtain a relaxation of (P) is the auxiliary variable method which introduces additional variables and constraints for each factor that appears in the DAG [54, 56–58]. Its relaxations, prior to linearization, are at least as tight as McCormick relaxations [56], p. 127f] and are differentiable functions. However, the dimension of the resulting nonlinear convex optimization problem is (much) larger. It is typically linearized so that the more robust and more efficient linear programming algorithms can be used. Again, no general comparison of the tightness of different relaxations is possible once the linearization is performed. Also, this approach does not include the constraint in the relaxation so no direct comparison with (R1) and (R2) in terms of tightness is possible.

Suppose it is known that ${ UBD}$ is a valid upper bound on the optimal objective function value of (P), e.g., there exists a $(z^\dagger ,p^\dagger )$ feasible in (P) with $f(z^\dagger ,p^\dagger )={ UBD}$. Similarly, suppose that ${ LBD}$ is a valid lower bound on the optimal objective function value, e.g., there does not exists a $(z^\dagger ,p^\dagger )$ feasible in (P) with $f(z^\dagger ,p^\dagger )<{ LBD}$. Both cases are very common in the context of a branch-and-bound algorithm. Consider

$$\begin{aligned} f^\ddagger =\min _{z\in {{{\varvec{x}}}},p\in {{{\varvec{p}}}}} \;&f(z,p) \\ \text {s.t.} \quad&{G}(z,p)\le 0, \\&{H}(z,p)= 0,\\&f(z,p)-{ UBD}\le 0,\\&{ LBD}-f(z,p)\le 0. \end{aligned}$$

It is clear that $f^\ddagger =f^*$ since $(z^\dagger ,p^\dagger )$ is feasible in (P). However, we can potentially strengthen the relaxations , $\hat{{X}}$ and thus also $\phi ^*$ or $f^1$ by including $f(z,p)-{ UBD}\le 0$ and ${ LBD}-f(z,p)\le 0$ in the reverse propagation outlined in Sect. 6.1.

6.3 Partitioning variables

A discussion on how to partition the variables into ${{{\varvec{x}}}}$ and ${{{\varvec{p}}}}$ concludes this section. We begin by analyzing the two extreme cases: $m=0$ and $m=n$.

First consider $m=0$. Here, ${{\fancyscript{Y}}}$ is initialized using a point, i.e., ${{\fancyscript{Y}}}^0_i=({{{\varvec{p}}}}_i,[p_i,p_i])$ for each $i=1,\ldots ,n$, constructing the tightest relaxations of ${C}(p)$ after the forward evaluation. However, only two outcomes are possible after the reverse propagation, either ${{\fancyscript{Y}}}^1_i=(\tilde{{{{\varvec{p}}}}}_i,[p_i,p_i])$ or ${{\fancyscript{Y}}}^1_i=(\tilde{{{{\varvec{p}}}}}_i,\emptyset )$. While the latter case indicates that $p$ violates at least one of the constraints, it is not clear how this information can be exploited numerically. For example, it is not clear how to obtain a hyperplane separating infeasible from potentially feasible points.

Next consider $m=n$. In this case, ${{\fancyscript{Y}}}$ is initialized using the interval bounds, i.e., ${{\fancyscript{Y}}}^0_i=({{{\varvec{p}}}}_i,{{{\varvec{p}}}}_i)$ for each $i=1,\ldots ,n$. This will yield looser relaxations of ${C}$ after the forward evaluation and since ${{\fancyscript{Y}}}$ is constant, we will obtain ${{\fancyscript{Y}}}^1=(\tilde{{{{\varvec{p}}}}},\breve{{{{\varvec{p}}}}})$ after the reverse propagation where $\breve{{{{\varvec{p}}}}}\in {\mathbb {I}}_\emptyset P$ is a box. Actually, in this case the reverse McCormick propagation yields the same information as the reverse interval propagation given that the exact image for each univariate function is used as the interval extension and the envelopes are used as the relaxations.

The advantages of the proposed method over interval methods are obtained for partitions between the two extremes listed above. A partitioning with $m=n_h$ such that there exists a unique implicit function ${X}:{{{\varvec{p}}}}\rightarrow {{{\varvec{x}}}}$ with ${H}({X}(p),p)= 0$ for all $p\in {{{\varvec{p}}}}$ is more favorable. In our numerical experience, this partitioning gave results that were better compared to interval reverse propagation. Interval Newton methods can be used to verify the existence and uniqueness of ${X}$, see [43], Ch. 5]. Additional inequality constraints can be used to reduce ${{{\varvec{x}}}}$ and ${{{\varvec{p}}}}$ further.

Another effective strategy is to partition the variables such that $m=n_h$, and that the resulting occurrence matrix corresponding to the equality constraint system is structurally nonsingular. Note that in general such a partitioning will not be unique. This approach was used in the majority of the test problems described in Sect. 9. One means of finding such a partition is given by the Dulmage–Mendelsohn decomposition [16]. Dulmage and Mendelsohn showed that any occurrence matrix can be transformed to a block structure consisting of up to three parts: an over-determined part, a fully-determined part and an under-determined part. In the types of problems considered here, the over-determined block should never exist, and by specifying $p$ as the variables in the under-determined block, the equation system will become structurally nonsingular, as desired. An automatic implementation of this algorithm is available in MATLAB [38]. This procedure could also be combined with interval Newton methods to further screen the possible choices for good partitions.

7 Implementation

In this section, an implementation of the reverse interval and McCormick propagation in C++ is presented. First, it is briefly discussed how the DAG of a factorable function can be easily constructed. Next, it is shown how forward and reverse interval and McCormick calculations can be performed on this DAG. Lastly, an outward rounding method for McCormick arithmetic is given, which is necessary for the practical application of reverse McCormick propagation. Consider a factorable function ${F}:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$. In this section, independent and dependent variables will refer to $y$ and ${F}(y)$, respectively. The boost interval library is used for the interval calculations [40] and MC++ provides the necessary routines for McCormick objects [11].

7.1 Algorithm implementation

The first step is the parsing of the factorable function to construct the DAG. In C++ this can be easily achieved using function and operator overloading. The DAG is stored as an array. Each element of the array corresponds to one factor of the factorable function including factors for the assignment of independent variables. Each element stores the operation type as well as pointers to its parent element(s), an interval and a McCormick object (as defined by MC++). Optionally, a constant parameter can be stored, which is used to keep track of, for example, constant exponents or factors. While the first $n$ array elements correspond to the independent variables, pointers to the dependent variables must be stored. Note that after the DAG has been constructed, all remaining operations are performed on this DAG object.

Prior to a forward interval/McCormick pass, the interval/McCormick objects of the independent variables are initialized. During the forward pass each factor is visited in sequence and the factor’s interval/McCormick object is updated according to the operation type using the pointers to parents’ values. After the forward pass, the interval/McCormick objects of the dependent variables store the values, which could have been alternatively calculated using traditional methods.

Prior to a reverse pass, the interval/McCormick objects of the dependent variables are updated based on the information supplied by the constraints. Then, each factor is visited in reverse order. A reverse interval/McCormick update is performed and the parents’ interval/McCormick objects are updated accordingly. After the reverse pass, the independent variables now store the updated interval/McCormick values. If during the reverse pass one of the intervals or McCormick objects of a factor is set to the empty set then the calculation can be aborted and the result of the reverse propagation is the empty set.

Note that MC++ also provides functionality to calculate subgradients of the convex and concave relaxations [41]. This functionality is essential when the relaxations are to be used in convex optimization algorithms. The present implementation also provides routines to update the subgradients during the reverse pass accordingly.

Additionally, the implementation allows the user to provide constraints on the domains of intermediate factors. These can avoid domain violations as outlined at the end of Sect. 6.1 and they are already taken into account during the forward interval or McCormick pass.

Lastly, it is possible to generate code automatically, in any programming language, that implements any combination of the discussed computations. Similar to source code transformation in automatic differentiation [20], the produced code can be executed to efficiently evaluate and $\hat{{X}}(\cdot )$, for example.

7.2 Outward rounding

A major cornerstone of interval arithmetic is the idea that interval extensions of expressions and functions must provide a valid, rigorous enclosure of the range of all real-valued results on the domain of interest. Due to the finite precision of floating-point arithmetic, a rigorous computer implementation of interval arithmetic must use directed rounding to achieve this. In the case of intervals, if a calculation produces an interval ${{{\varvec{x}}}}\in {\mathbb {I\! R}}$ whose upper bound and lower bound may not be exactly representable as floating-point numbers, the lower bound must be rounded downward (towards $-\infty$) and the upper bound must be rounded upward (towards $+\infty$) in order for all real numbers $x \in {{{\varvec{x}}}}$ to be validly enclosed [43]. With the rounding performed in this way, the interval result is said to be outward rounded.

Analogously, the convex and concave relaxations calculated using reverse McCormick propagation must also provide this rigorous enclosure property. In initial attempts to apply reverse McCormick propagation to large problems, allowing the results of floating-point operations to all be rounded in the default manner (i.e. to the nearest floating-point) caused two types of failures in the procedure. The first occurred when the value of the convex underestimator of the McCormick object exceeded that of its concave overestimator. This behavior was often observed in the backward pass when the result of the calculation should have been an equal convex and concave relaxation, but the value was not exactly representable as a floating-point. The other major issue arose from the incorrect assertion of empty intersections, which most often occurred at the start of the backward pass when the results of the forward pass were intersected with constraint information. Simple fixes, such as adding a small error tolerance to the intersection operation, allowed the algorithm to run without failing, but led to erroneous results.

As a result, it was necessary to implement an outward rounding scheme for McCormick arithmetic. For the operations in McCormick arithmetic that only involve a single floating-point operation to define either the convex or concave relaxation at a point, the outward rounding is easily implemented. These operations include addition or subtraction of two McCormick objects, as well as any operation involving a scalar and a McCormick object (note that taking the negative of a number is an exact operation, and so it is not counted as an second operation in this sense). For example, the outward rounded result of the addition of two McCormick objects can be defined as:

(9)

with ${\scriptstyle \, \updownarrow \!(+) \,}$ as shorthand for outward rounded addition, and ${\scriptstyle \, \downarrow \!(+) \,}$ and ${\scriptstyle \, \uparrow \!(+) \,}$ denoting downward and upward rounded addition, respectively. This can be easily implemented in C++ by calling the function $\mathtt{fesetround }$ provided by the standard library header $\mathtt{fenv.h }$ with appropriate argument before each of the operations involving the values of the relaxations, and then allowing the interval operations to be performed with a rigorous interval library. Subtraction of McCormick objects and the operations involving scalars are handled analogously.

For operations such as taking the reciprocal or square root of a McCormick object, as well as for binary multiplication, a different procedure is needed. For instance, the definition for the convex underestimator in the reciprocal operation is as follows:

Here, in the case where $\underline{x} > 0$, the correctly rounded result can be obtained as before by first calling $\mathtt{fesetround(FE\_DOWNWARD) }$ to invoke downward rounding, and then performing the division operation. In the case where $\overline{x} <0$ however, it is not necessarily true that performing each of the individual calculations with downward rounding will lead to a final result that is less than or equal to the true real-valued result. Instead, it is necessary to use outward rounded interval arithmetic for the individual operations, which will be guaranteed to give a valid result, as in [43], Theorem 1.4.1].

This is implemented in MC++ as follows. First, the double precision variables corresponding to $\underline{x}$, $\overline{x}$, and are copied into a rigorous interval type. Then, all calculations are performed using outward rounded interval arithmetic, which will potentially widen the intervals if the results of the individual calculations are not floating-point numbers. Finally, the value of the convex underestimator is set to the value of the lower bound of the final interval result. For the reciprocal, this series of operations can be written out somewhat obtusely as:

where ${{{\varvec{x}}}}_L$, ${{{\varvec{x}}}}_U$, and ${{{\varvec{x}}}}_M$ are the interval objects corresponding to the lower bound, upper bound, and result of the mid operation, respectively, and the operations adjacent to the up/down arrows represent the corresponding outward rounded interval arithmetic operations. The concave overestimator is defined similarly, and formulas can also be written using the exactly the same approach for outward rounded binary multiplication and other univariate operations such as the square root, exponential, and logarithm. These modified operations were added to the MC++ source code and used to generate the numerical results found in the following sections.

8 Illustrative examples

In this section, we will present illustrative case studies that show how enclosures of the solution sets can be obtained from the reverse McCormick propagation and that these compare favorably to the enclosures computed with reverse interval propagation. In the first case study, the constraints define a unique implicit function on ${{{\varvec{p}}}}$. It is taken from [55] and the results are compared. The second case study compares the feasible region of the relaxed program obtained using reverse McCormick propagation to the feasible region of the standard McCormick relaxation. The third case study focuses on constraints defining a non-unique implicit mapping. The fourth case study shows the effect of a reverse interval propagation pre-processing step when there is no feasible $z$ for some $p$. The fifth case study shows that relaxations can be sensibly calculated even when there are no feasible $z$ for some $p$ in the interior of ${{{\varvec{p}}}}$. The sixth case study demonstrates how information from inequality constraints can be incorporated. The last case study illustrates how relaxations of the objective function can be significantly improved by incorporating information from the constraints.

We only consider univariate functions from the library ${{\fancyscript{L}}}=\{(\cdot )^l,\root l \of {\cdot },\log ,\exp \}$, $l\in \mathbb {N}$. However, the method can be applied to any other univariate functions that satisfy Assumptions 1 and 2.

8.1 Equality constraints

Example 1

Let ${{{\varvec{x}}}}=[-0.8,-0.3]$ and ${{{\varvec{p}}}}=[6,9]$. Consider $h(z,p)=z^2+zp+4$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ implicitly defines a set-valued mapping $x:{{{\varvec{p}}}}\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{-\frac{p}{2}+\sqrt{\left( \frac{p}{2}\right) ^2-4}\}$ so that $h(\xi ,p)=0$ for all $p\in {{{\varvec{p}}}}$ and $\xi \in x(p)$. While Fig. 3a shows the result after one iteration of the reverse McCormick propagation, Fig. 3b depicts the effect of 10 reverse propagation iterations. In both figures the relaxations are compared to those calculated using the method presented in [55]. Note that the calculations for 60 different values of $p$ take a total of 0.0021, 0.0039 and 0.014 s in the case of one reverse propagation, ten reverse propagations and one iteration of the parametric Gauss–Seidel method given in [55] with $\lambda =0.5$, respectively. Thus, the new method is faster and provides tighter relaxations.

Fig. 3

Result of reverse McCormick propagation for Example 1 showing the original bounds (dashed-dotted lines), the improved bounds (gray box), the convex and concave relaxations (solid line, respectively) as well as results of the set-valued mapping $x(p)$ (asterisks). In a one iteration of the reverse McCormick propagation was performed while in b the reverse propagation iterations was repeated ten times. The dashed lines show convex and concave relaxations calculated using one iteration of the more expensive method in [55]

Example 2

Let ${{{\varvec{x}}}}=[-3,5]$ and ${{{\varvec{p}}}}=[-3,4]$. Consider $h(z,p)=(\sqrt{p+4}-3)(\log (p^2+1)-z)$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ implicitly defines a set-valued mapping $x:{{{\varvec{p}}}}\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{\log (1+p^2)\}$ so that $h(\xi ,p)=0$ for all $p\in {{{\varvec{p}}}}$ and $\xi \in x(p)$. The results of a single reverse McCormick propagation are shown in Fig. 4a. Additionally, we also show two different relaxations of the non-convex feasible space $\{(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}:h(z,p)=0)\}$ (shown in asterisks). A common way to relax constraints is the construction of a convex outer-approximation of the feasible space by considering where are standard McCormick relaxations of $h$ on ${{{\varvec{x}}}}\times {{{\varvec{p}}}}$. This set can be traced by plotting the zero level sets of , i.e., and $\hat{h}(z,p)=0$. An alternative, tighter outer-approximation can be found by computing on $\tilde{{{{\varvec{x}}}}}\times \tilde{{{{\varvec{p}}}}}=[0,2.834]\times [-3,4]$ instead. In Fig. 4b, the same information is shown for smaller original intervals, ${{{\varvec{x}}}}=[-3,3]$ and ${{{\varvec{p}}}}=[-1,1]$.

Fig. 4

Result of reverse McCormick propagation for Example 2 showing the original bounds (dashed-dotted lines), the improved bounds (gray box), the convex and concave relaxations (solid lines) as well as results of the set-valued mapping $x(p)$ (asterisks). Additionally, zero level sets of the McCormick relaxations of $h(z,p)$ constructed on ${\varvec{x}}\times {\varvec{p}}$ (short dashed lines) as well as $\tilde{{\varvec{x}}}\times \tilde{{\varvec{p}}}$ (dashed lines) are shown except where they are outside the interval bounds. Here, the results for different ${\varvec{x}} \times {\varvec{p}}$ are shown in a and b

Example 3

Let ${{{\varvec{x}}}}=[-10,10]$ and ${{{\varvec{p}}}}=[0,3]$. Consider $h(z,p)=z^2-p$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ implicitly defines a set-valued mapping $x:{{{\varvec{p}}}}\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{\sqrt{p},-\sqrt{p}\}$ so that $h(\xi ,p)=0$ for all $p\in {{{\varvec{p}}}}$ and $\xi \in x(p)$. The results of the reverse McCormick propagation are shown in Fig. 5. Here, no comparison with [55] is possible due to non-uniqueness of $x$.

Fig. 5

Result of reverse McCormick propagation for Example 3 showing the original bounds (dashed-dotted lines), the improved bounds (gray box), the convex and concave relaxations (solid lines) as well as results of the set-valued mapping $x(p)$ (asterisks)

Example 4

Let ${{{\varvec{x}}}}=[-10,10]$ and ${{{\varvec{p}}}}=[0,3]$. Consider $h(z,p)=z^4-p^2+1$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ implicitly defines a set-valued mapping $x:[1,3]\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{\root 4 \of {p^2-1},-\root 4 \of {p^2-1}\}$ so that $h(\xi ,p)=0$ for all $p\in [1,3]$ and $\xi \in x(p)$. While Fig. 6a shows the result using the original bounds, Fig. 6b depicts the effect of using bounds obtained from reverse interval propagation. In the latter case, the reverse interval propagation reduces both ${{{\varvec{x}}}}$ and ${{{\varvec{p}}}}$ to obtain $\tilde{{{{\varvec{x}}}}}$ and $\tilde{{{{\varvec{p}}}}}$. Then, the reverse McCormick propagation is performed using the reduced intervals $\tilde{{{{\varvec{x}}}}}$ and $\tilde{{{{\varvec{p}}}}}$.

Fig. 6

Result of reverse McCormick propagation for Example 4 showing the original bounds (dashed-dotted lines), the improved bounds (gray box), the convex and concave relaxations (solid lines) as well as results of the set-valued mapping $x(p)$ (asterisks). While in a the original bounds are used, in b the result of the bounds obtained from reverse interval propagation is shown

Example 5

Let ${{{\varvec{x}}}}=[-10,10]$ and ${{{\varvec{p}}}}=[-3,3]$. Consider $h(z,p)=z^2-(\sqrt{p^2-p}-2)^4$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ implicitly defines a set-valued mapping $x:[-3,0]\cap [1,3]\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{(\sqrt{p^2-p}-2)^2,-(\sqrt{p^2-p}-2)^2\}$ so that $h(\xi ,p)=0$ for all $p\in [-3,0]\cap [1,3]$ and $\xi \in x(p)$. On the other hand, if $p\in (0,1)$ no feasible $z$ exists that satisfies $h(z,p)=0$. The results of the reverse McCormick propagation are shown in Fig. 7. Here, the algorithm was supplied with the information that the argument of the square root cannot be negative.

Fig. 7

Result of reverse McCormick propagation for Example 5 showing the original bounds (dotted lines), the improved bounds (dashed lines), the convex and concave relaxations (solid lines) as well as results of the set-valued mapping $x(p)$ (asterisks)

8.2 Inequality constraints

Example 6

Let ${{{\varvec{x}}}}=[-10,10]$ and ${{{\varvec{p}}}}=[0,3]$. Consider $h(z,p)=z^2-p$ and $g(z,p)=(p-1)^2-z-2.5$ with $(z,p)\in {{{\varvec{x}}}}\times {{{\varvec{p}}}}$. Note that $h(z,p)=0$ and $g(z,p)\le 0$ implicitly defines set-valued mappings $x:[0,2.03593]\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{\sqrt{p},-\sqrt{p}\}$ and $x:(2.03593,3]\rightarrow {\mathbb {P}}({{{\varvec{x}}}}):p\mapsto \{\sqrt{p}\}$ so that $h(\xi ,p)=0$ for all $p\in {{{\varvec{p}}}}$ and $\xi \in x(p)$. However, we are only interested in those $(z,p)$ for which $g(z,p)\le 0$. The results of the reverse McCormick propagation are shown in Fig. 8.

Fig. 8

Result of reverse McCormick propagation for Example 6 showing the original bounds (dotted lines), the improved bounds (gray box), the convex and concave relaxations (solid lines) as well as results of the set-valued mapping $x(p)$ (asterisks)

8.3 Objective function

Example 7

Let ${{{\varvec{y}}}}=[-3,3]\times [-2,2]^2$ and consider the optimization of the six-hump camel back function [14]

$$\begin{aligned} \min _{y\in {{{\varvec{y}}}}}\quad&f(y)=\left( 4-2.1y_1^2+\frac{1}{3}y_1^4\right) y_1^2+y_1y_2+\left( -4+4y_2^2\right) y_2^2\\ \text {s.t.}\quad&g(y)=y_1^2+(y_2-0.5)^2-0.5\le 0 \end{aligned}$$

where an inequality constraint has been added. We are interested in constructing relaxations of $f(y)$ which take the information from the constraint $g(y)\le 0$ into account. Here, let $y_1$ take the role of the independent and $y_2$ the role of the dependent variable. The reverse McCormick update will proceed as outlined in Sect. 6.1. Then, one last forward evaluation will be performed to obtain improved relaxations of $f$. Fig. 9 shows the obtained relaxations. Clearly, the McCormick relaxations can be improved substantially by incorporating the information from the constraint.

Fig. 9

Result of reverse McCormick propagation for Example 7. In a the original bounds (dashed-dotted line), the improved bounds (gray box), the objective function $f$ (asterisks) and the convex relaxations (solid line) are shown as well as standard convex McCormick relaxations constructed on ${\varvec{y}}$ (short dashed line) and $\tilde{{\varvec{y}}}$ (dashed line) in a section. In b $f$ is shown as a mesh and relaxations are shown as surfaces

9 Global optimization test problems

A set of standard global optimization problems from the COCONUT Benchmark [53] were solved with the reverse McCormick propagation technique to demonstrate its effectiveness. Twenty representative problems involving twenty or less variables, for which the number of variables exceeded the number of equality constraints, were solved from Library 1 of this collection. A basic branch-and-bound framework was used to solve the problems to global optimality, with three different strategies for obtaining lower bounding values for each test case.

As a baseline method, lower bounds on the optimal objective value were found by constructing standard McCormick relaxations of the objective function and constraints on each node, and then solving the resulting nonsmooth convex program. For comparison, reverse McCormick propagation was applied in two different ways to the lower bounding problem: the full-space formulation R2 and the reduced-space formulation R1. In all three cases, a reverse interval propagation step was performed on each node before the relaxations were constructed. This was done both to improve the strength of the lower bound, and in order to most directly show the advantage of applying reverse McCormick propagation beyond that afforded by use of reverse interval propagation. The set of parameters $p$ for each problem was chosen such that the number of remaining dependent variables was equal to the number of equality constraints, and that the resulting square equation system defined by these constraints was structurally nonsingular. Since such a partitioning is non-unique in general, different parameter sets may exist for each test problem that could perform either more or less favorably than those explored in this work. Table 1 shows the variables chosen as parameters for each of the test problems.

In practice, solving the convex lower bounding problems was found to be highly nontrivial due to the nonsmooth nature of the McCormick relaxations and the presence of constraints in two of the formulations. Two freely-available nonsmooth local optimization algorithms were used in this work: MPBNGC, an implementation of the proximal bundle method [36], and SolvOpt, an implementation of Shor’s r-algorithm with an exact penalty formulation for handling constraints [29]. It was observed that neither of these algorithms could be used on all problems in the test set, either due to the assumptions of the method or numerical difficulties. However, for each problem, at least one of the two algorithms was suitable, and the same solver was used for all three formulations for consistency. The solver used for each problem is also noted in Table 1. It was noted that MPBNGC generally required fewer but more expensive iterations than SolvOpt to solve the lower bounding problems. Improved methods for constrained nonsmooth optimization using reverse McCormick propagation will be a topic of future research.

Table 1 Set of variables chosen as parameters and the nonsmooth solver used for each of the test problems

The SQP algorithm SNOPT [18] was used to obtain upper bounds and find feasible points required for initialization of the MPBNGC method. No range reduction techniques were employed in this branch-and-bound implementation, and the relative and absolute tolerances used to terminate the algorithm were $10^{-3}$ and $10^{-8}$, respectively. Branching was performed such that the current box was bisected along the largest current width relative to the original box dimensions. Nodes were selected according to the lowest lower bound heuristic. The results of the numerical tests can be found in Table 2.

Table 2 Results of applying reverse propagation of McCormick relaxations to a set of standard global optimization test problems

The results indicate the use of reverse McCormick propagation significantly improves solution speed (in both elapsed time and iteration count) on the majority of the test problems. The full-space (R2) formulation seems to be most effective in reducing the number of branch-and-bound iterations required for convergence, however, since it requires the solution of a difficult nonsmooth local optimization problem at each iteration, the cost per iteration is high. The reduced-space (R1) formulation was generally the fastest to converge in terms of elapsed time, although sometimes required more branch-and-bound iterations than either the full-space reverse mode or standard formulations. This is likely due to the fact that the two full-space formulations are guaranteed to be quadratically convergent methods, whereas the reduced-space formulation is not [10]. However, the reduced number of decision variables in the problem offsets the effect of the lower convergence order in most cases. Furthermore, we note that there is no reason to even expect that the reduced-space formulation will converge for an arbitrary partition $(x, p)$. It appears necessary that for all $p \in {{{\varvec{p}}}}$ either ${X}(p)$ is a singleton or ${X}(p) = \emptyset$, but a derivation of a convergence result for reverse interval propagation would also be required. These conditions were not checked a priori for these test cases, and Table 1 shows the results from those problems which did successfully converge in the (R1) formulation. We note that other problems from the library were tested for which the (R2) formulation converged but the (R1) formulation did not, although numerical difficulties with the nonsmooth solvers were also observed in some of these cases.

In a few cases, the reverse McCormick propagation was observed to be less effective than using the Standard McCormick relaxations (e.g. problems process and alkyl). These exceptions occur when the reverse McCormick update fails and returns the empty set during the lower bounding procedure on a large number of iterations, which can happen when the local optimization routine picks a value of $p$ for which no ${X}(p)$ exists and no relaxations can be calculated (see Fig. 6a when $p \le \frac{1}{3}$ for a graphical example). In the current implementation, this is handled by using the information from the reverse interval pass to calculate the lower bounding value, and then immediately branching on the node. Handling this case more effectively is the topic of ongoing research, and will further improve the performance of this promising constraint propagation method.

10 Conclusion

Reverse McCormick propagation, a new method to construct and improve McCormick relaxations of implicitly defined set-valued mappings has been presented. It takes advantage of the directed acyclic graph representation of a factorable function, which has been previously used for interval calculations [50, 62]. Bounds and relaxations of factors can often be improved by using information about the permissible range of a factorable function and propagating it backwards through the graph. In particular, this allows the construction and improvement of relaxations of mappings that are only implicitly defined. This is useful in the context of CSPs since it allows to construct convex relaxations of non-convex solution sets defined by nonlinear equality constraints and non-convex inequality constraints. Furthermore, McCormick relaxations of the objective function of an NLP can be improved using information contained in the constraints. While Stuber et al. [55] also put forward methods to construct relaxations of implicit functions, the method presented here does not require existence nor uniqueness of the implicit function on all or parts of the domain. Furthermore, it is less computationally intensive and does not require a pre-processing step. It also provides a reduced-space relaxation for nonconvex programs that can take constraints into account, but does not require convex optimizers that can cope with general nonsmooth nonlinear constraints. When used as a constraint propagation method in the context of global optimization, the reverse McCormick approach proved to be effective at improving solution rate compared to the standard McCormick relaxation approach and reverse interval propagation over a set of representative test problems.