Different Correlations in a System of Two Entangled Atoms Interacting with the Pólya State Field

Abstract

In this paper, we discuss four measures for the quantum and classical correlations of two atoms in a system of two entangled atoms interacting with the Pólya field state. In five different initial states of the two atoms, we compare and analyze the influence of the atomic and optical field parameters on the time evolution of the quantum correlation and the classical correlation between two entangled atoms in the considered system. The results show that though the atomic state is initially in a separate one, the time evolution of geometrical quantum discord (GQD), concurrence (C), quantum discord (QD) can still exhibit non zero quantum correlation behavior. The results also show that the time evolution of the three measures of quantum correlation has obvious consistency but the time evolution of classical correlation (CC) is different from that of quantum correlation in the mentioned cases. In addition, the two atoms always remain in the maximum entangled state during the evolution as the two atoms are initially in a maximum entangled state $\left |{\varPsi }_{4}\right \rangle$.

1 Introduction

Quantum information processing has the advantages that classical information processing doesn’t, usually because there is a correlation beyond the classical between two subsystems. This correlation is called quantum correlation, and one can obtain the possibility of the measured results information of another subsystem by statistical measurement for a subsystem [1]. Owing to being a basic resource in information processing, so it becomes a very important issue to study the properties of quantum correlation in the quantum system [2]. In recent years, as a non-local quantum correlation, quantum entanglement is widely investigated and used in quantum information processing [3,4,5]. However, it has been found that non-classical correlations can also exist in separable states [6,7,8]. These researches show that quantum entanglement is just one form of quantum correlation and cannot describe all the quantum correlation of a quantum system [9,10,11]. It is imperative and desirable to introduce the physical quantity measuring general nonlocal correlations. Therefore, Ollivier et al. proposed the concept of quantum discord (QD) by which the more general nonclassical correlations in a system can be expressed [12, 13].The observations suggest that QD has more unique advantages than quantum entanglement in some aspects of quantum information processing. For instance, a nonzero quantum discord may be responsible for the efficiency of deterministic one-pure-qubit quantum computation and that of the quantum Carnot engine [14]. Since the concept of QD was proposed, many works have been devoted to the research of the quantum discord both theoretically and experimentally [15,16,17,18,19,20,21]. In practical application, since QD needs to be maximized in the calculation process, it is difficult to obtain an analytical expression. In order to get around this difficulty, Dakić et al. put forward a new method, geometrical quantum discord (GQD), which can be more convenient to measure quantum correlation [22]. The GQD is defined as the smallest Hilbert-Schmidt distance between the given state and the zero-discord states [23]. Recently, the quantum correlation and the entanglement in a system of two atoms interacting with a single-mode cavity field, such as the Fock state, the coherent field state and thermal field state etc., have been intensively investigated [24,25,26,27,28,29,30,31,32]. The Pólya state is a typically constructed state superimposed by the binomial state and the negative binomial state [33]. By adjusting some parameters in this model, the Pólya field state can easily describe the varying process of the optical field from the binomial state through the intermediate state to the negative binomial state. So the Pólya state optical field can easily present binomial state, negative binomial state and intermediate state with their unique quantum properties. In this work, we investigate the quantum and classical correlations in a system of two two-level entangled atoms interacting with the Pólya field state. Our goal will try to understand how the various correlations in the system evolve with time. We use the three criteria of GQD, concurrence(C) and QD to measure the quantum correlation between two atoms by the means of numerical calculations, and then compare them with the classical correlation. The content of the article is organized as follows. In Section 2, we give the theoretical model and its solution. In Section 3, we present a brief overview of four correlation quantities and then study quantum and classical correlations between two atoms. In Section 4, we give numerical results and discussion. Finally, the conclusion is drawn in Section 5.

2 The Theoretical Model and its Solution

Here, we consider the system of two two-level atoms labeled A and B resonantly interacting with a single-mode cavity field. Assume that there is the dipole-dipole interaction between atoms, and the values of the coupling strength between either of two atoms and a cavity field are the equals. In this case, the Hamiltonian of the system under the rotating wave approximation ($\hbar =1$)is

$$ \begin{array}{@{}rcl@{}} H&=&{\varOmega} a^{+} a+\frac{1}{2} \omega\left( {\sigma_{A}^{z}}+{\sigma_{B}^{z}}\right)+\mathrm{g}\left[\left( a^{+} \sigma_{A}^{-}+a \sigma_{A}^{+}\right)+\left( a^{+} \sigma_{B}^{-}+a \sigma_{B}^{+}\right)\right]\\ &&+\mathrm{g}_{a}\left( \sigma_{A}^{-} \sigma_{B}^{+}+\sigma_{B}^{-} \sigma_{A}^{+}\right). \end{array} $$

(1)

Where a⁺ and a are the creation and annihilation operators, Ω and ω are the frequency of the cavity field and the atomic transition frequency, ${\sigma _{i}^{z}}=|e_{i}\rangle \langle e_{i}|, \sigma _{i}^{+}$$\left .\left .=\right | e_{i}\right \rangle \left \langle \mathrm {g}_{i}\right |$, $\sigma _{i}^{-}=\left |\mathrm {g}_{i}\right \rangle \left \langle e_{i}\right |$ are the inversion, rising and lowing operators of the i-th atom(i=A,B), respectively. $\left |e_{i}\right \rangle$ denotes an excited state of an atom, $\left |\mathrm {g}_{i}\right \rangle$ denotes a ground state of an atom, g is the atom-field coupling constant, g_a is the atomic dipole-dipole coupling constant. For simplicity, we consider the resonance case (Ω = ω).

Assume that at t = 0 the two atoms are in an arbitrarily entangled state

$$ \left|{\varPsi}_{a}(0)\right\rangle=\cos \frac{\theta}{2}\left|e_{A},\mathrm{g}_{B}\right\rangle-\sin \frac{\theta}{2} e^{i \phi}\left|\mathrm{g}_{A},e_{B}\right\rangle, 0 \leq \theta \leq \pi, -\pi \leq \phi \leq \pi, $$

(2)

the field is in a single-mode Pólya State

$$ \left| {{{\varPsi}_{f}}(0)} \right\rangle = {\sum}_{n = 0}^{M} {{{\left[ {{P_{n}^{M}}(l,\eta )} \right]}^{\frac{1}{2}}}} |n\rangle, $$

(3)

here the probability parameter of the light field, the maximum number of photons,

$$ {P_{n}^{M}}(l,\eta)=\left( \begin{array}{c} M \\ n \end{array}\right) \frac{\eta(\eta+l) \cdots[\eta+(n-1) l] \bar{\eta}(\bar{\eta}+l) \cdots[\bar{\eta}+(M-n-1) l]}{(1+l)(1+2 l) \cdots[1+(M-1) l]}, $$

$$ (\eta \in[0,1], \bar{\eta}=1-\eta, l \geq 0, M \geq n, n=0,1,2, \dots). $$

(4)

In (4), M is the maximum number of photons, η is the probability parameter of the light field and l is the distribution parameter of the light field. When $l \rightarrow 0$, the Pólya state is reduced to a binomial state. And when $M \rightarrow \infty$, $l \rightarrow 0$, $\eta \rightarrow 0$ with Mη = λ, Ml = ρ^− 1, the Pólya state goes to a negative binomial state [33]. In the interaction picture, the evolution of the state vector of the system obeys the Schrödinger equation

$$ i \frac{\partial}{\partial t}\left|{\varPsi}_{s}(t)\right\rangle= H_{I}\left|{\varPsi}_{s}(t)\right\rangle. $$

(5)

It can be obtained by solving the Schrödinger equation

$$ \begin{array}{@{}rcl@{}} \left|{\varPsi}_{s}(t)\right\rangle&=&{\sum}_{n=0}^{M} N_{1}(t, n)\left|e_{A}, e_{B}, n-1\right\rangle+{\sum}_{n=0}^{M} N_{2}(t, n)\left|e_{A}, \mathrm{g}_{B}, n\right\rangle\\ &&+{\sum}_{n=0}^{M} N_{3}(t, n)\left|\mathrm{g}_{A}, e_{B}, n\right\rangle+{\sum}_{n=0}^{M} N_{4}(t, n)\left|\mathrm{g}_{A}, \mathrm{g}_{B}, n+1\right\rangle. \end{array} $$

(6)

Here the coefficients [34]

$$ \begin{array}{@{}rcl@{}} N_{1}(t,n)&=&\frac{\left( \cos \frac{\theta}{2}-\sin \frac{\theta}{2} e^{i \phi}\right)\left[{P_{n}^{M}}(l, \eta)\right]^{\frac{1}{2}} \sqrt{n}\left( 1-e^{i \mathrm{g} {\varDelta} t}\right) e^{-i \mathrm{g} k t}}{{\varDelta}},\\ {N_{2}}(t,n) &=& \frac{1}{4}{\left[ {{P_{n}^{M}}(l,\eta )} \right]^{\frac{1}{2}}}{e^{- i{\text{g}}kt}}\begin{array}{*{20}{c}} {\left[\left( {a + \frac{{\left( {1 - {e^{i{\text{g}}{\varDelta} t}}} \right)G}}{{\varDelta} }} \right)\cos \frac{\theta }{2}- \right.} \\ {\left.{\left( {b + \frac{{\left( {1 - {e^{i{\text{g}}{\varDelta} t}}} \right)G}}{{\varDelta} }} \right)\sin \frac{\theta }{2}{e^{i\phi }}} \right]} \end{array},\\ {N_{3}}(t,n) &= &\frac{1}{4}{\left[ {{P_{n}^{M}}(l,\eta )} \right]^{\frac{1}{2}}}{e^{- i{\text{g}}kt}}\begin{array}{*{20}{c}} {\left[ {\left( {b + \frac{{\left( {1 - {e^{i{\text{g}}{\varDelta} t}}} \right)G}}{{\varDelta} }} \right)\cos \frac{\theta }{2} - } \right.} \\ {\left. {\left( {a + \frac{{\left( {1 - {e^{i{\text{g}}{\varDelta} t}}} \right)G}}{{\varDelta} }} \right)\sin \frac{\theta }{2}{e^{i\phi }}} \right]} \end{array},\\ N_{4}(t,n)&=&\frac{\left( \cos \frac{\theta}{2}-\sin \frac{\theta}{2} e^{i \phi}\right)\left[{P_{n}^{M}}(l, \eta)\right]^{\frac{1}{2}} \sqrt{n+1}\left( 1-e^{i \mathrm{g} {\varDelta} t}\right) e^{-i \mathrm{g} k t}}{{\varDelta}}, \end{array} $$

(7)

with

$$ G=\frac{\mathrm{g} a}{\mathrm{g}}, k=\frac{G+{\varDelta}}{2}, {\varDelta}=\sqrt{8(1+2 n)+G^{2}}, $$

$$ a=1+e^{i \mathrm{g} {\varDelta} t}+2 e^{i \frac{1}{2}(3 G+{\varDelta}) \mathrm{g} t}, b=1+e^{i \mathrm{g} {\varDelta} t}-2 e^{i \frac{1}{2}(3 G+{\varDelta}) \mathrm{g} t}. $$

(8)

The density matrix of the system can be expressed as $\rho (t)=\left |{\varPsi }_{s}(t)\right \rangle \left \langle {\varPsi }_{s}(t)\right |$, the reduced density matrix ρ_AB of the subsystem consisting of two atoms can be obtained by tracing over the field variables. In the atom-atom bases $\left \{\left |e_{A} e_{B}\right \rangle ,\left |e_{A} \mathrm {g}_{B}\right \rangle \right .,$$\left .\left |\mathrm {g}_{A} e_{B}\right \rangle ,\left |\mathrm {g}_{A} \mathrm {g}_{B}\right \rangle \right \}$, the reduced density matrix ρ_AB is obtained in the following form

$$ \rho_{A B}=\text{Tr}_{\text {field}}[\rho(t)]=\left( \begin{array}{llll} \rho_{11} & \rho_{12} & \rho_{13} & \rho_{14} \\ \rho_{21} & \rho_{22} & \rho_{23} & \rho_{24} \\ \rho_{31} & \rho_{32} & \rho_{33} & \rho_{34} \\ \rho_{41} & \rho_{42} & \rho_{43} & \rho_{44} \end{array}\right), $$

(9)

where

$$ \begin{array}{@{}rcl@{}} \rho_{11}&=&{\sum}_{n=1}^{M}\left|N_{1}(t, n)\right|^{2}, \rho_{12}={\sum}_{n=0}^{M} N_{1}(t, n+1) N_{2}^{*}(t, n),\\ \rho_{13}&=&{\sum}_{n=0}^{M} N_{1}(t, n+1) N_{3}^{*}(t, n), \rho_{14}={\sum}_{n=0}^{M} N_{1}(t, n+2) N_{4}^{*}(t, n),\\ \rho_{21}&=&{\sum}_{n=0}^{M} N_{2}(t, n) N_{1}^{*}(t, n+1), \rho_{22}={\sum}_{n=0}^{M}\left|N_{2}(t, n)\right|^{2},\\ \rho_{23}&=&{\sum}_{n=0}^{M} N_{2}(t, n) N_{3}^{*}(t, n), \rho_{24}={\sum}_{n=0}^{M} N_{2}(t, n+1) N_{4}^{*}(t, n),\\ \rho_{31}&=&{\sum}_{n=0}^{M} N_{3}(t, n) N_{1}^{*}(t, n+1), \rho_{32}={\sum}_{n=0}^{M} N_{3}(t, n) N_{2}^{*}(t, n),\\ \rho_{33}&=&{\sum}_{n=0}^{M}\left|N_{3}(t, n)\right|^{2}, \rho_{34}={\sum}_{n=0}^{M} N_{3}(t, n+1) N_{4}^{*}(t, n),\\ \rho_{41}&=&{\sum}_{n=0}^{M} N_{4}(t, n) N_{1}^{*}(t, n+2), \rho_{42}={\sum}_{n=0}^{M} N_{4}(t, n) N_{2}^{*}(t, n+1),\\ \rho_{43}&=&{\sum}_{n=0}^{M} N_{4}(t, n) N_{3}^{*}(t, n+1), \rho_{44}={\sum}_{n=0}^{M}\left|N_{4}(t, n)\right|^{2}. \end{array} $$

(10)

3 Quantum Correlations Between the Two Atoms

In this section, we will study the quantum correlations between two entangled atoms by using the three criteria of the geometrical quantum discord, the concurrence and the quantum discord.

We use the geometrical quantum discord (GQD) to measure the correlation between the two bodies. The density matrix of two-body system can be expressed as

$$ \rho_{A B}=\frac{1}{4}\left[I \otimes I+\sum\limits_{i=1}^{3}\left( A_{i} \sigma_{i} \otimes I+B_{i} I \otimes \sigma_{i}\right)+\sum\limits_{i, j=1}^{3}\left( P_{i j} \sigma_{i} \otimes \sigma_{j}\right)\right], $$

(11)

where I is an identity matrix, $A_{i}=\text {Tr}\left [\rho _{A B}\left (\sigma _{i} \otimes I\right )\right ], B_{i}=\text {Tr}\left [\rho _{A B}\left (I \otimes \sigma _{i}\right )\right ]$ are components of the local Bloch vectors, σ_i, σ_j(i, j = x, y, z) are three Pauli matrices, and $P_{i j}=\text {Tr}\left [\rho _{A B}\left (\sigma _{i} \otimes \sigma _{j}\right )\right ]$.

Therefore, GQD for two-body systems is [22]

$$ D(t)=\frac{1}{4}\left( \|A\|^{2}+\|P\|^{2}-\kappa_{\max }\right), $$

(12)

here $\|A\|^{2}={\sum }_{i=1}^{3} {A_{i}^{2}}, P=P_{i j}$ is a matrix, $\|P\|^{2}=\text {Tr}\left (P^{T} P\right ), \kappa _{{\max \limits } }$ is the largest eigenvalue of the matrix K = AA^T + PP^T, superscript T denotes transpose of vector A or matrix P.

According to the above theory, we can conveniently obtain the following results,

$$ \begin{array}{@{}rcl@{}} A_{1}&=&\rho_{13}+\rho_{24}+\rho_{31}+\rho_{42}, P_{11}=\rho_{14}+\rho_{23}+\rho_{32}+\rho_{41},\\ A_{2}&=&i\left( \rho_{13}+\rho_{24}-\rho_{31}-\rho_{42}\right), P_{12}=i\left( \rho_{14}-\rho_{23}+\rho_{32}-\rho_{41}\right),\\ A_{3}&=&\rho_{11}+\rho_{22}-\rho_{33}-\rho_{44}, P_{13}=\rho_{13}-\rho_{24}+\rho_{31}-\rho_{42},\\ P_{21}&=&i\left( \rho_{14}+\rho_{23}-\rho_{32}-\rho_{41}\right), P_{31}=\rho_{12}+\rho_{21}-\rho_{34}-\rho_{43},\\ P_{22}&=&-\rho_{14}+\rho_{23}+\rho_{32}-\rho_{41}, P_{32}=i\left( \rho_{12}-\rho_{21}-\rho_{34}+\rho_{43}\right),\\ P_{23}&=&i\left( \rho_{13}-\rho_{24}-\rho_{31}-\rho_{42}\right), P_{33}=\rho_{11}-\rho_{22}-\rho_{33}+\rho_{44}. \end{array} $$

(13)

$$ \|A\|^{2}={A_{1}^{2}}+{A_{2}^{2}}+{A_{3}^{2}}, $$

(14)

$$ \|P\|^{2}=P_{11}^{2}+P_{21}^{2}+P_{31}^{2}+P_{12}^{2}+P_{22}^{2}+P_{32}^{2}+P_{13}^{2}+P_{23}^{2}+P_{33}^{2}. $$

(15)

Accordingly, three eigenvalues of the matrix K are

$$ \begin{array}{@{}rcl@{}} \kappa_{1}&=&-\frac{1}{3} X_{1}-\frac{2}{3}\left( {X_{1}^{2}}-3 X_{2}\right)^{1 / 2} \cos \frac{\gamma}{3},\\ \kappa_{2}&=&-\frac{1}{3} X_{1}+\frac{1}{3}\left( {X_{1}^{2}}-3 X_{2}\right)^{1 / 2}\left( \cos \frac{\gamma}{3}+\sqrt{3} \sin \frac{\gamma}{3}\right),\\ \kappa_{3}&=&-\frac{1}{3} X_{1}+\frac{1}{3}\left( {X_{1}^{2}}-3 X_{2}\right)^{1 / 2}\left( \cos \frac{\gamma}{3}-\sqrt{3} \sin \frac{\gamma}{3}\right), \end{array} $$

(16)

with

$$ \gamma=\arccos L, L=\frac{2 {X_{1}^{3}}+27 X_{3}-9 X_{1} X_{2}}{2\left( {X_{1}^{2}}-3 X_{2}\right)^{3 / 2}}, $$

(17)

and

$$ \begin{array}{@{}rcl@{}} X_{1}&=&-\left( Y_{1}+Y_{2}+Y_{3}\right),\\ X_{2}&=&Y_{1} Y_{2}+Y_{2} Y_{3}+Y_{1} Y_{3}-Y_{4} Y_{5}-Y_{6} Y_{7}-Y_{8} Y_{9},\\ X_{3}&=&-Y_{1} Y_{2} Y_{3}-Y_{4} Y_{7} Y_{8}-Y_{5} Y_{6} Y_{9}+Y_{2} Y_{6} Y_{7}+Y_{3} Y_{4} Y_{5}+Y_{1} Y_{8} Y_{9},\\ Y_{1}&=&{A_{1}^{2}}+P_{11}^{2}+P_{12}^{2}+P_{13}^{2},\\ Y_{2}&=&{A_{2}^{2}}+P_{21}^{2}+P_{22}^{2}+P_{23}^{2},\\ Y_{3}&=&{A_{3}^{2}}+P_{31}^{2}+P_{32}^{2}+P_{33}^{2},\\ Y_{4}&=&A_{1} A_{2}+P_{11} P_{21}+P_{12} P_{22}+P_{13} P_{23},\\ Y_{5}&=&A_{1} A_{2}+P_{21} P_{11}+P_{22} P_{12}+P_{23} P_{13},\\ Y_{6}&=&A_{1} A_{3}+P_{11} P_{31}+P_{12} P_{32}+P_{13} P_{33},\\ Y_{7}&=&A_{1} A_{3}+P_{31} P_{11}+P_{32} P_{12}+P_{33} P_{13},\\ Y_{8}&=&A_{2} A_{3}+P_{21} P_{31}+P_{22} P_{32}+P_{23} P_{33},\\ Y_{9}&=&A_{2} A_{3}+P_{31} P_{21}+P_{32} P_{22}+P_{33} P_{23}. \end{array} $$

(18)

It follows from (9–18), we get the GQD to measure the correlation between two atoms

$$ D(t)=-\frac{1}{4}\left[X_{1}+\max \left( \kappa_{1}, \kappa_{2}, \kappa_{3}\right)\right]. $$

(19)

Generally, we have two measurement methods, which are called by negativity [35, 36] and concurrence [37], to quantify the quantum entanglement between two atoms in a system. In this paper, the concurrence is adopted to measure the entanglement between two atoms. It is defined as

$$ C(t)=\max \left\{0, \lambda_{1}-\lambda_{2}-\lambda_{3}-\lambda_{4}\right\}, $$

(20)

where λ₁ ≥ λ₂ ≥ λ₃ ≥ λ₄ is the eigenvalue of the Hermitian matrix R.

$$ R \equiv \sqrt{\sqrt{\rho_{A B}} \tilde{\rho}_{A B} \sqrt{\rho_{A B}}}. $$

(21)

Here $\tilde {\rho }_{A B}=\left (\sigma _{y} \otimes \sigma _{y}\right ) \rho _{A B}^{*}\left (\sigma _{y} \otimes \sigma _{y}\right )$, in which σ_y is the Pauli matrix and $\rho _{A B}^{*}$ denotes the complex conjugate of the density matrix ρ_AB.The range of concurrence is from 0 to 1. The larger the concurrence, the stronger the entanglement. For the unentangled state, C = 0, whereas C = 1 for the maximally entangled state.

The quantum discord (QD) of a bipartite system AB is defined as the difference between the total correlation and classical correlation (CC) [13],

$$ Q D\left( \rho_{A B}\right)=I\left( \rho_{A B}\right)-C C\left( \rho_{A B}\right). $$

(22)

Here the total correlation is measured by their quantum mutual information

$$ I\left( \rho_{A B}\right)=S\left( \rho_{A}\right)+S\left( \rho_{B}\right)-S\left( \rho_{A B}\right), $$

(23)

and the classical correlation can be expressed as [11]

$$ C C\left( \rho_{A B}\right)=S\left( \rho_{A}\right)-\min_{\left\{{{\varPi}_{k}^{B}}\right\}}\left[S\left( \rho_{A B} |\left\{{{\varPi}_{k}^{B}}\right\}\right)\right]. $$

(24)

In which $S\left (\rho _{j}\right )=-T r_{j}\left (\rho _{j} \log _{2} \rho _{j}\right )=-{\sum }_{i} {\lambda _{j}^{i}} \log _{2} {\lambda _{j}^{i}}$ is the von Neumann entropy with $\left \{{\lambda _{j}^{i}}\right \}$ being the nonzero eigenvalues of the quantum state ρ_j, and the subscript j indicates either the subsystem A(B) or the total system AB, and the reduced density matrix of A(B) defined as

$$ \rho_{A(B)}=\text{Tr}_{B(A)}\left( \rho_{A B}\right), $$

(25)

and $\left \{ {{{\varPi }_{k}^{B}}} \right \}$ denotes a complete set of projective measurements performed on the subsystem B, and $S\left (\rho _{A B} |\left \{{{\varPi }_{k}^{B}}\right \}\right )={\sum }_{k} p_{k} S\left ({\rho _{k}^{A}}\right )$ is the quantum conditional entropy, with

$$ p_{k}=T r_{A B}\left[\left( I_{A} \otimes {{\varPi}_{k}^{B}}\right) \rho_{A B}\left( I_{A} \otimes {{\varPi}_{k}^{B}}\right)\right] $$

(26)

being the corresponding probability of measurement outcome k(k = 1,2), and

$$ {\rho_{k}^{A}}=\frac{1}{p_{k}} \text{Tr}_{B}\left[\left( I_{A} \otimes {{\varPi}_{k}^{B}}\right) \rho_{A B}\left( I_{A} \otimes {{\varPi}_{k}^{B}}\right)\right] $$

(27)

is the corresponding conditional density matrix.

Substituting (23) and (24) into (22), the quantum discord of the system is finally determined to be

$$ Q D\left( \rho_{A B}\right)=S\left( \rho_{B}\right)-S\left( \rho_{A B}\right)+\min_{\left\{{{\varPi}_{k}^{B}}\right\}}\left[{\Sigma}_{k} p_{k} S\left( {\rho_{k}^{A}}\right)\right]. $$

(28)

The calculation of quantum discord is not so easy due to its definition. It is difficult to obtain an analytical expression. According to the proposed scheme in [12], we choose the method of von Neumann measurement:

$$ {{\varPi}_{1}^{B}}=\left|\vartheta_{\|}\right\rangle\left\langle\vartheta_{\|}\right|, {{\varPi}_{2}^{B}}=\left| \vartheta_{\perp}\right\rangle\left\langle\vartheta_{\perp}\right|, $$

(29)

with

$$ \left|\vartheta_{\|}\right\rangle=\cos \vartheta\left|\mathrm{g}_{B}\right\rangle+ e^{i \varphi} \sin \vartheta\left|e_{B}\right\rangle,\left|\vartheta_{\perp}\right\rangle=-\cos \vartheta\left|e_{B}\right\rangle+ e^{-i \varphi} \sin \vartheta\left|\mathrm{g}_{B}\right\rangle, $$

(30)

where 0 ≤ 𝜗 ≤ 2π,0 ≤ φ ≤ 2π.

Combining (9), (25), (26), (27), (29) and (30), we can obtain

$$ \begin{array}{@{}rcl@{}} p_{1}&=&\sin^{2} \vartheta\left( \rho_{11}+\rho_{33}\right)+\cos^{2} \vartheta\left( \rho_{22}+\rho_{44}\right)\\ &&+e^{i \varphi} \sin \vartheta \cos \vartheta\left( \rho_{21}+\rho_{43}\right)+e^{-i \varphi} \sin \vartheta \cos \vartheta\left( \rho_{12}+\rho_{34}\right),\\ p_{2}&=&\sin^{2} \vartheta\left( \rho_{22}+\rho_{44}\right)+\cos^{2} \vartheta\left( \rho_{11}+\rho_{33}\right)\\ &&-e^{i \varphi} \sin \vartheta \cos \vartheta\left( \rho_{21}+\rho_{43}\right)-e^{-i \varphi} \sin \vartheta \cos \vartheta\left( \rho_{12}+\rho_{34}\right), \end{array} $$

(31)

and

$$ {\rho_{1}^{A}}=\frac{1}{p_{1}}\left( \begin{array}{ll} E_{11} & E_{12} \\ E_{21} & E_{22} \end{array}\right), \quad {\rho_{2}^{A}}=\frac{1}{p_{2}}\left( \begin{array}{ll} F_{11} & F_{12} \\ F_{21} & F_{22} \end{array}\right), $$

(32)

with

$$ \begin{array}{ll} E_{11}=&\sin^{2} \vartheta \rho_{11}+\cos^{2} \vartheta \rho_{22}+e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{21}+e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{12},\\ E_{12}=&\sin^{2} \vartheta \rho_{13}+\cos^{2} \vartheta \rho_{24}+e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{23}+e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{14},\\ E_{21}=&\sin^{2} \vartheta \rho_{31}+\cos^{2} \vartheta \rho_{42}+e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{41}+e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{32},\\ E_{22}=&\sin^{2} \vartheta \rho_{33}+\cos^{2} \vartheta \rho_{44}+e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{43}+e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{34},\\ F_{11}=&\sin^{2} \vartheta \rho_{22}+\cos^{2} \vartheta \rho_{11}-e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{21}-e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{12},\\ F_{12}=&\sin^{2} \vartheta \rho_{24}+\cos^{2} \vartheta \rho_{13}-e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{23}-e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{14},\\ F_{21}=&\sin^{2} \vartheta \rho_{42}+\cos^{2} \vartheta \rho_{31}-e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{41}-e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{32},\\ F_{22}=&\sin^{2} \vartheta \rho_{44}+\cos^{2} \vartheta \rho_{33}-e^{i \varphi} \sin \vartheta \cos \vartheta \rho_{43}-e^{-i \varphi} \sin \vartheta \cos \vartheta \rho_{34}. \end{array} $$

(33)

By use of the above obtained results, we can discuss the dynamics behavior of the quantum correlation and classical one in the considered system.

4 Numerical Results and Discussion

In this section, we will focus on the numerical calculation and then analyze the obtained results. When the atoms are initially in different states (parameters θ, ϕ corresponding to several fixed values) and the parameters of the field states for G, M and η take some fixed values, the evolution behavior of GQD, C, QD and CC are analyzed in the four situations respectively.

Case 1. We assume θ = π, and ϕ = −π, the two atoms are initially in a separate state $\left |{\varPsi }_{1}\right \rangle =\left |{\varPsi }_{a}(0)\right \rangle =\left |\mathrm {g}_{A}, e_{B}\right \rangle$.

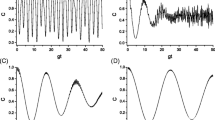
In Fig. 1, the time evolution of GQD, C, QD and CC is plotted as a function of gt with θ = π, ϕ = −π, G = 1, M = 10, l = 0 for different values η = 0.3, 0.6, 0.9. For G = 1, it means that the atomic dipole-dipole coupling strength is equal to the atom-field one, and l = 0 indicates that Pólya state field reduces to binomial state field. These evolution curves of GQD, C, QD and CC change in non-monotonous oscillating manner respectively. It has been shown that the amount of the correlation (GQD, QD and CC) or the quantum entanglement (C) is enhanced if we increase the value of the light field parameter η, and the changing trend for GQD, QD or C is similar. However, the time behavior of the classical correlation (CC) is different from that of the correlation (GQD, QD or C). The intense oscillations of CC occur in certain time intervals in which the smaller fluctuations of GQD, QD or C appear with the increasing η.

Fig. 1

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with θ = π, ϕ = −π, G = 1, M = 10, l = 0 for a η = 0.3, bη = 0.6, cη = 0.9

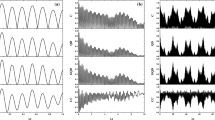
In Fig. 2, the time evolution of GQD, C, QD and CC is plotted as a function of gt with θ = π, ϕ = −π, G = 1, η = 0.5, l = 0.5 for different values M = 1, 10, 20. For l = 0.5, the light field state is in an intermediate one. In Fig. 2a, it can be seen that the evolution behavior of the four quantities is periodical with period 2π. For the moments $t=2 n \pi (n=1,2, \dots )$, the values of GQD, C, QD and CC reach zero, which means that two atoms are in the states of existing neither quantum correlation nor classical one. The Fig. 2b and c indicate that the periodicity of GQD, C, QD or CC disappears and the oscillations of GQD, C, QD or CC in time tend to become smaller irregular fluctuations, and the ranges of these quantities shift down gradually as M increases.

Fig. 2

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with θ = π, ϕ = −π, G = 1, η = 0.5, l = 0.5 for a M = 1, bM = 10, cM = 20

In Fig. 3, the time evolution of GQD, C, QD and CC is plotted as a function of gt with θ = π, ϕ = −π, M = 15, η = 0.5, l = 0 for different values G = 0, 1, 5. In Fig. 3a, for the case that there is no interaction between the atoms, the time behavior of GQD, C, QD and CC has been shown. In Fig. 3b and c, the time evolutions of GQD, C, QD and CC are displayed with different coupling strength for G = 1 (both of the coupling strength are equal) and G = 5 (the coupling strength between two atoms is stronger than that between two atoms and field) respectively. Comparing Fig. 3a with Fig. 3b and c, it can be observed that the ranges for the oscillating values of GQD, C, QD and CC become wider, and these curves oscillate intensely at higher frequencies within the certain time intervals with the increased parameter G. In addition, we can also see from Figs. 1, 2 and 3 that though two atoms are initially in the unentangled state, in which the initial values of four quantities are zero, both the quantum correlations and entanglement between two atoms interacting with the Pólya field state exist during their evolutions.

Fig. 3

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with θ = π, ϕ = −π, M = 15, η = 0.5, l = 0 for a G = 0, bG = 1, cG = 5

Case 2. In case of $\theta =\frac {\pi }{3}$, and ϕ = 0, the two atoms are initially in an entangled state of the form $\left |{\varPsi }_{2}\right \rangle =\left |{\varPsi }_{a}(0)\right \rangle =\frac {\sqrt {3}}{2}\left |e_{A}, \mathrm {g}_{B}\right \rangle -\frac {1}{2}\left |\mathrm {g}_{A}, e_{B}\right \rangle$.

In case 2, all the chosen parameters are the same as in case 1 except $\theta =\frac {\pi }{3}, \phi =0$. The time evolution of GQD, C, QD and CC are shown in Figs. 4, 5 and 6. In Fig. 4, it is shown that the evolution curves of QD are between 0.65 and 1, those of C from 0.85 to near 1, the values of GQD are about 0.35 to 0.5, the range of CC is from 0.75 to near 1. They are the irregular oscillating curves and vary slightly with the increased η. The evolution behavior of GQD, C, QD or CC indicates that in these situations there exist the stronger quantum correlations and classical ones between atoms during the time evolution.

Fig. 4

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with $\theta =\frac {\pi }{3}, \phi =0$, G = 1, M = 10, l = 0 for a η = 0.3, bη = 0.6, cη = 0.9

Fig. 5

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with $\theta =\frac {\pi }{3}, \phi =0$, G = 1, η = 0.5, l = 0.5 for a M = 1, bM = 10, cM = 20

Fig. 6

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with $\theta =\frac {\pi }{3}, \phi =0$, M = 15, η = 0.5, l = 0 for a G = 0, bG = 1, cG = 5

Compared with Fig. 2a, one can see in Fig. 5a that the period of GQD, C, QD and CC still keep at the fixed value 2π, the time evolution curves of them shift up and the oscillations of the temporal evolution become flat. In Fig. 5b and c, it is observed that the values of C are about 0.9, those of GQD are about 0.4. The temporal evolution curves of QD and CC tend to fluctuate in the vicinity of 0.8. The oscillations of QD, C, and CC decay gradually to the ones which have smaller fluctuations but the oscillating amplitude of GQD goes to a stable value 0.4 with the enhanced M.

In Fig. 6, we can see that the evolution curves of GQD, C, QD and CC keep almost in a similar pattern such as Fig. 4, except when in the beginning time-interval and the middle one the curves of them oscillate intensely with the increasing G during the observed time.

Case 3. In case of $\theta =\frac {\pi }{3}, \phi =\frac {\pi }{2}$, the two atoms are also initially in an entangled state $\left |{\varPsi }_{3}\right \rangle =\left |{\varPsi }_{a}(0)\right \rangle =\frac {\sqrt {3}}{2}\left |e_{A}, \mathrm {g}_{B}\right \rangle -\frac {i}{2}\left |\mathrm {g}_{A}, e_{B}\right \rangle$.

In case 3, all the chosen parameters are the same as in case 1 except $\theta =\frac {\pi }{3}, \phi =\frac {\pi }{2}$. In Fig. 7, it can be seen that the maximums of GQD, C, QD or CC appear almost at the initial time t = 0 and then the maximums of these quantities shift to the right slightly with the increasing η. We can also observe that some local maximums of four quantities occur in the fixed time intervals and they can be enhanced with the increasing η. The oscillation and amplitudes of CC enhance within certain time intervals.

Fig. 7

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{3}, \phi =\frac {\pi }{2}, G=1, M=10, l=0$ for a η = 0.3, bη = 0.6, cη = 0.9

In Fig. 8, the periodic phenomena for the time evolution of GQD, C, QD and CC can be still observed. It is worth noting that the maximum values of C, QD or CC reach close to 1 while those of GQD are close to 0.5 at the moments t = 2nπ(n = 1,2,…) and the amplitudes of each oscillation decrease with the increasing parameter M.

Fig. 8

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{3}, \phi =\frac {\pi }{2}, G=1, \eta =0.5, l=0$ for a M = 1, b M = 10, c M = 20

In Fig. 9, one can find that each curve of GQD, C, QD or CC evolves in a non-monotonic manner and all the evolution curves exhibit the different oscillations, moreover, the larger the value of parameter G is, the more intensely the evolution curves oscillate within some time intervals.

Fig. 9

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{3}, \phi =\frac {\pi }{2}, M=15, \eta =0.5, l=0$ for a G = 0, b G = 1, c G = 5

Case 4. Suppose $\theta =\frac {\pi }{2}$, and ϕ = 0 or ϕ = π, the initial states of the two atoms are $\left |{\varPsi }_{4}\right \rangle =\left |{\varPsi }_{a}(0)\right \rangle =\frac {\sqrt {2}}{2}\left (\left |e_{A},\mathrm {g}_{B}\right \rangle -\left |\mathrm {g}_{A}, e_{B}\right \rangle \right )$ or $\left |{\varPsi }_{5}\right \rangle =\left |{\varPsi }_{a}(0)\right \rangle =\frac {\sqrt {2}}{2}\left (\left |e_{A}, \mathrm {g}_{B}\right \rangle +\left |\mathrm {g}_{A}, e_{B}\right \rangle \right )$.

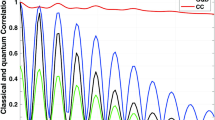
In case 4, all the chosen parameters are the same as in case 1 except $\theta =\frac {\pi }{2}, \phi =0$ or ϕ = π. Firstly, the time evolution of GQD, C, QD and CC is investigated as ϕ = 0. The numerical results show that the values of QD, C and CC are always equal to 1, those of GQD stay in 0.5, therefore, the time evolution of the four quantities is independent of the atomic and field state parameters. It means that the two atoms always remain in the maximum entangled state during the evolution. Secondly, the time evolutions of GQD, C, QD and CC are considered as ϕ = π. From Fig. 10 it has been observed that the evolution curves of GQD, C, QD and CC tend gradually to display the quasi-periodic behavior and the oscillations of the evolution curves become more intense as η increases respectively. In Fig. 11a, one can see that the time behavior of C, QD and CC is still periodical with 2π, the values of QD, C and CC are equal to 1 and these of GQD are 0.5 for the moments t = 2nπ(n = 1,2,…), which indicates that the states of two atoms are in the maximum entangled state at the above-mentioned moments. Furthermore, Fig. 11b and c depict that the amplitudes of the time evolution of GQD, C, QD and CC decay gradually to the smaller values and there are the similar varying manners for these quantities with the increase of M. In addition, we can see in Fig. 12 that the evolution curves of GQD, C, QD and CC also display more intense oscillating behavior with the increasing G. Compared the differences as ϕ = 0 and ϕ = π, in spite of $\left |{\varPsi }_{4}\right \rangle$ and $\left |{\varPsi }_{5}\right \rangle$ being all initially in maximum entangled states, the time evolution of the four quantities starting from the two initial states exhibit quite distinct behavior during the wholly evolution process.

Fig. 10

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{2}, \phi =\pi , G=1, M=10, l=0$ for a η = 0.3, bη = 0.6, cη = 0.9

Fig. 11

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{2}, \phi =\pi , G=1, \eta =0.5, l=0$ for a M = 1, b M = 10, c M = 20

Fig. 12

Time evolution of C (solid line), QD (solid line) and GQD (dot-dashed line), and CC (solid line) versus gt with fixed values $\theta =\frac {\pi }{2}, \phi =\pi , M=15, \eta =0.5, l=0$ for a G = 0, b G = 1, c G = 5

5 Conclusions

In conclusion, we explore the time evolution of the different correlations measured by the geometrical quantum discord (GQD), concurrence (C), quantum discord (QD) and classical correlation (CC) in a system of two entangled atoms interacting with a single-mode Pólya field state. The effects of the probability parameter of the light field η, the maximum photon number M, the relative coupling strength G on the time evolution of GQD, C, QD and CC between two atoms in five atomic initial states are investigated respectively. It is shown that though the atomic initial state is in a separate one, the time evolution of GQD, C and QD can exhibit non zero quantum correlation behavior. For M = 1, the time evolution curves of four quantities oscillate with the same period 2π for five atomic initial states and the considered states reach the maximum entangled ones at some fixed moments. Particularly, as the two atoms are initially in the $\left |{\varPsi }_{4}\right \rangle$, the atomic states will always stay in the maximum entangled ones during the whole evolution process. In addition, the evolution curves of CC are generally different from these of GQD, C and QD, but the time evolution of GQD, C and QD have the similar trends.