1 Introduction

Quantum entanglement is just a special kind of quantum correlation, it cannot depict all the quantum correlation of a quantum system. Even when entanglement is zero in a system, quantum correlation can still be finite. Whereupon, Olliver et al proposed the concept of quantum discord in 2001 [1]. The quantum discord is different from the quantum entanglement in the quantum correlation, it is another measure of quantum correlations. The quantum discord characterizes non-classical of correlations in quantum mechanics, similar to the entanglement, quantum discord can also capture the fundamental features of quantum states. Since the quantum discord is put forward, and soon it has been found the non-classical correlations are more widespread than the entanglement. Only under the status that the discord is equal to zero, the state is a pure classic state. The existence of the non-classical correlation means there is a positive value of discord. The concept of quantum discord was investigated quite intensively in recent years, for example: two body system of more general situation [2, 3], the time-dependent evolution, and pattern of manifestation for dynamic quantity [4, 5], change the way of measurement, research symmetry of a system [6], even try to multibody system [7–9]. Due to the quantum discord maximize involved in the process of calculation, and it is difficult to get the analytic expression. In order to overcome this difficulty, Dakic et al [10] put forward a new method of measuring quantum correlations, namely the geometrical quantum discord(GQD). GQD is the use of between a given state and quantum discord for zero state the smallest Hilbert - schmidt distance of the definition. So far, some new research progress has been made for GQD in different quantum system [11–13]. This not entangled quantum correlation can be used to implement quantum communication and quantum computing. In this paper, we study the GQD of a quantum system which is consist of two two-level entangled atoms and the binomial optical field. For our purpose, we use GQD to measure the correlation between the two bodies by the means of numerical calculations. This paper is organized as follows. In Section 2, we give our theoretical model and time-dependence wave function. In Section 3, the GQD of between two atoms are investigated. Finally, our results are summarized in Section 4.

2 Theoretical Model and Time-Dependence Wave Function

Consider a well-known cavity QED system, which contains two two-level atoms resonantly interacting with a single-mode binomial optical cavity simultaneously. Assume that the distance between atoms are smaller than the wavelength of the cavity field, the dipole-dipole interaction should not be neglected, and there are same couplings of the two atoms interacting with a binomial optical field. Under these conditions, the Hamiltonian of the system in the rotating wave approximation can be written as \((\hbar = 1)\)

$$\begin{array}{@{}rcl@{}} H={\Omega} a^{+}a+\frac{1}{2}\omega\sum\limits_{i=1}^{2}{\sigma_{i}^{z}}+g\sum\limits_{i=1}^{2}(a^{+}\sigma_{i}^{-}+a\sigma_{i}^{+})+g_{a}\sum\limits_{i\neq j=1}^{2}(\sigma_{i}^{-}\sigma_{j}^{+}). \end{array} $$
(1)

Where a + and a are the creation and annihilation operators of the field mode of frequency Ω, ω is the atomic transition frequency, \({{\sigma _{i}^{z}}=|e_{i}\rangle \langle e_{i}|}\), \({\sigma _{i}^{+}=|e_{i}\rangle \langle g_{i}|}\), \({\sigma _{i}^{-}=|g_{i}\rangle \langle e_{i}|}\) are the inversion, rise and drop operators of i t h atom (i = 1,2), respectively. |e〉 denotes an excited state of atom, |g〉 denotes a ground state of atom, g is the atom-field coupling constant, g a is the atomic dipole-dipole coupling constant. For simplicity, we consider the resonant case (Ω = ω).

Assume that at t = 0 the two atoms is in a arbitrarily entangled state

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\cos{\frac{\theta}{2}}|e_{1}, g_{2}\rangle-\sin{\frac{\theta}{2}} e^{i \phi}|g_{1}, e_{2}\rangle, \theta\in[0,\pi],\phi\in[-\pi,\pi] \end{array} $$
(2)

the field is in a single-mode binomial state

$$\begin{array}{@{}rcl@{}} |{\Psi}_{f}(0)\rangle=|\sigma,M\rangle=\sum\limits_{n=0}^{M}{\beta_{M}^{n}}|n\rangle,& &\left( 0\leq\sigma\leq1, M\geq n, n=0,1,2,...\right), \end{array} $$
(3)

here

$$\begin{array}{@{}rcl@{}} {\beta_{M}^{n}}=\left[\left( \begin{array}{cc} M\\ n \end{array} \right) \left( \sigma\right)^{n}\left( 1-\sigma \right)^{M-n}\right]^{1/2}. \end{array} $$
(4)

In Eq. 3, |n〉 is the number state of the field mode, σ and (1−σ) are the probabilities of the two possible outcomes of a the Bernoulli trial, M is the largest number of photon in the Fock state. In interacting picture, at any time t>0, the evolution of the state vector of the system obeys the Schrödinger equation

$$\begin{array}{@{}rcl@{}} i\frac{\partial}{\partial t}|{\Psi}_{s}(t)\rangle=H_{I}|{\Psi}_{s}(t)\rangle. \end{array} $$
(5)

It can be obtained by solving the Schrödinger equation

$$\begin{array}{@{}rcl@{}} |{\Psi}_{s}(t)\rangle=\sum\limits_{n=0}^{M}C_{1}(t,n)|e_{1}, e_{2},n-1\rangle +\sum\limits_{n=0}^{M}C_{2}(t,n)|e_{1}, g_{2},n\rangle\\ +\sum\limits_{n=0}^{M}C_{3}(t,n)|g_{1}, e_{2},n\rangle +\sum\limits_{n=0}^{M}C_{4}(t,n)|g_{1}, g_{2},n+1\rangle. \end{array} $$
(6)

Here the coefficients

$$\begin{array}{@{}rcl@{}} C_{1}(t,n)&=&\frac{\left( \cos\frac{\theta}{2}-\sin\frac{\theta}{2} e^{i \phi}\right){\beta_{M}^{n}}\sqrt{n}(1-e^{i{\Delta} gt})e^{-iagt}}{\Delta},\\ C_{2}(t,n)&=&\frac{1}{4}{\beta_{M}^{n}}e^{-iagt}[(c+\frac{(1-e^{i{\Delta} gt})G}{\Delta})\cos\frac{\theta}{2}-(d+\frac{(1-e^{i{\Delta} gt})G}{\Delta})\sin\frac{\theta}{2} e^{i \phi}],\\ C_{3}(t,n)&=&\frac{1}{4}{\beta_{M}^{n}}e^{-iagt}[(d+\frac{(1-e^{i{\Delta} gt})G}{\Delta})\cos\frac{\theta}{2}-(c+\frac{(1-e^{i{\Delta} gt})G}{\Delta})\sin\frac{\theta}{2} e^{i \phi}],\\ C_{4}(t,n)&=&\frac{\left( \cos\frac{\theta}{2}-\sin\frac{\theta}{2} e^{i \phi}\right){\beta_{M}^{n}}\sqrt{n+1}(1-e^{i{\Delta} gt})e^{-iagt}}{\Delta}. \end{array} $$
(7)

With

$$\begin{array}{@{}rcl@{}} G&=&\frac{g_{a}}{g}, a=\frac{G+{\Delta}}{2}, {\Delta}=\sqrt{8(1+2n)+G^{2}},\\ c&=&1+e^{i{\Delta} gt}+2e^{i\frac{1}{2}(3G+{\Delta})g t}, d=1+e^{i{\Delta} gt}-2e^{i\frac{1}{2}(3G+{\Delta})g t}. \end{array} $$
(8)

The density matrix of the system is ρ(t)=|Ψ s (t)〉〈Ψ s (t)|.

By tracing over the variable of field for the density matrix of the system, the reduced density matrix of two atoms is obtained. In the atom-atom bases |e e〉, |e g〉, |g e〉, |g g〉, the reduced density matrix of the subsystem composed of two atoms is

$$\begin{array}{@{}rcl@{}} \rho_{atoms}=Tr_{field}(|{\Psi}_{s}(t)\rangle \langle{\Psi}_{s}(t)|)= \left( \begin{array}{cccc} \rho_{11} & \rho_{12} & \rho_{13} & \rho_{14}\\ \rho_{21} & \rho_{22} & \rho_{23} & \rho_{24}\\ \rho_{31} & \rho_{32} & \rho_{33} & \rho_{34}\\ \rho_{41} & \rho_{42} & \rho_{43} & \rho_{44}\\ \end{array} \right) \end{array} $$
(9)

where

$$\begin{array}{@{}rcl@{}} \rho_{11}&=&\sum\limits_{n=1}^{M}|C_{1}(t,n)|^{2}, \rho_{12}=\sum\limits_{n=0}^{M}C_{1}(t,n+1)C_{2}^{*}(t,n),\\ \rho_{13}&=&\sum\limits_{n=0}^{M}C_{1}(t,n+1)C_{3}^{*}(t,n), \rho_{14}=\sum\limits_{n=0}^{M}C_{1}(t,n+2)C_{4}^{*}(t,n),\\ \rho_{21}&=&\sum\limits_{n=0}^{M}C_{2}(t,n)C_{1}^{*}(t,n+1), \rho_{22}=\sum\limits_{n=0}^{M}|C_{2}(t,n)|^{2},\\ \rho_{23}&=&\sum\limits_{n=0}^{M}C_{2}(t,n)C_{3}^{*}(t,n), \rho_{24}=\sum\limits_{n=0}^{M}C_{2}(t,n+1)C_{4}^{*}(t,n),\\ \rho_{31}&=&\sum\limits_{n=0}^{M}C_{3}(t,n)C_{1}^{*}(t,n+1), \rho_{32}=\sum\limits_{n=0}^{M}C_{3}(t,n)C_{2}^{*}(t,n),\\ \rho_{33}&=&\sum\limits_{n=0}^{M}|C_{3}(t,n)|^{2}, \rho_{34}=\sum\limits_{n=0}^{M}C_{3}(t,n+1)C_{4}^{*}(t,n),\\ \rho_{41}&=&\sum\limits_{n=0}^{M}C_{4}(t,n)C_{1}^{*}(t,n+2), \rho_{42}=\sum\limits_{n=0}^{M}C_{4}(t,n)C_{2}^{*}(t,n+1),\\ \rho_{43}&=&\sum\limits_{n=0}^{M}C_{4}(t,n)C_{3}^{*}(t,n+1), \rho_{44}=\sum\limits_{n=0}^{M}|C_{4}(t,n)|^{2}. \end{array} $$
(10)

3 The GQD of Between Two Atoms

We use the GQD to measure the correlation between the two bodies. The density matrix of two body system can be expressed as

$$\begin{array}{@{}rcl@{}} \rho=\frac{1}{4}[I\otimes I+\sum\limits_{i=1}^{3}(A_{i}\sigma_{i}\otimes I+B_{i}I\otimes \sigma_{i})+\sum\limits_{i,j=1}^{3}P_{ij}\sigma_{i}\otimes \sigma_{j}], \end{array} $$
(11)

where I is an identity matrix, A i = T r ρ(σ i ⊗I), B i = T r ρ(I⊗σ i ) are components of the local Bloch vectors, σ i , σ j (i, j = x, y, z) are three Pauli matrices, and P i j = T r ρ(σ i ⊗σ j ).

Therefore GQD for two body systems is [10]

$$\begin{array}{@{}rcl@{}} D(\rho)=\frac{1}{4}(\parallel A \parallel^{2}+\parallel P \parallel^{2}-K_{max}), \end{array} $$
(12)

here \(\parallel A \parallel ^{2}={\sum }_{i=1}^{3}{A_{i}^{2}}\), P = P i j is a matrix, ∥P∥2 = T r(P T P), K m a x is the largest eigenvalue of the matrix K = A A T + P P T, superscript T denotes transpose of vector A or matrix P.

According to the above theory, we can conveniently obtain the following results,

$$\begin{array}{@{}rcl@{}} A_{1}&=&\rho_{13}+\rho_{24}+\rho_{31}+\rho_{42},\\ A_{2}&=&i(\rho_{13}+\rho_{24}-\rho_{31}-\rho_{42}),\\ A_{3}&=&\rho_{11}+\rho_{22}-\rho_{33}-\rho_{44}, \\ P_{11}&=&\rho_{14}+\rho_{23}+\rho_{32}+\rho_{41},\\ P_{12}&=&i(\rho_{14}-\rho_{23}+\rho_{32}-\rho_{41}),\\ P_{13}&=&\rho_{13}-\rho_{24}+\rho_{31}-\rho_{42}, \\ P_{21}&=&i(\rho_{14}+\rho_{23}-\rho_{32}-\rho_{41}),\\ P_{22}&=&-\rho_{14}+\rho_{23}+\rho_{32}-\rho_{41},\\ P_{23}&=&i(\rho_{13}-\rho_{24}-\rho_{31}+\rho_{42}),\\ P_{31}&=&\rho_{12}+\rho_{21}-\rho_{34}-\rho_{43},\\ P_{32}&=&i(\rho_{12}-\rho_{21}-\rho_{34}+\rho_{43}),\\ P_{33}&=&\rho_{11}-\rho_{22}-\rho_{33}+\rho_{44}. \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \parallel A \parallel^{2}=\sum\limits_{i=1}^{3}{A_{i}^{2}}=4(\rho_{13}\rho_{31}+\rho_{13}\rho_{42}+\rho_{24}\rho_{31}\!+\rho_{24}\rho_{42})+(\rho_{11}+\rho_{22}\!-\rho_{33}-\rho_{44})^{2}, \\\end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} \parallel P \parallel^{2}=P_{11}^{2}+P_{21}^{2}+P_{31}^{2}+P_{12}^{2}+P_{22}^{2}+P_{32}^{2}+P_{13}^{2}+P_{23}^{2}+P_{33}^{2}. \end{array} $$
(15)

Accordingly, three eigenvalues of the matrix K are

$$\begin{array}{@{}rcl@{}} K_{1}&=&\frac{1}{3}\theta_{1}-\frac{2}{3}({\theta_{1}^{2}}-3\theta_{2})^{1/2}cos{\Psi},\\ K_{2}&=&\frac{1}{3}\theta_{1}+\frac{2}{3}({\theta_{1}^{2}}-3\theta_{2})^{1/2}(cos{\Psi}+\sqrt{3}sin{\Psi}),\\ K_{3}&=&\frac{1}{3}\theta_{1}+\frac{2}{3}({\theta_{1}^{2}}-3\theta_{2})^{1/2}(cos{\Psi}-\sqrt{3}sin{\Psi}), \end{array} $$
(16)

respectively. In Eq. 16

$$\begin{array}{@{}rcl@{}} {\Psi}&=&\frac{1}{3}arccos(\frac{\xi}{\zeta}), \\ \xi&=&9\theta_{1}\theta_{2}-2{\theta_{1}^{2}}-27\theta_{3}, \\ \zeta&=&2({\theta_{1}^{2}}-3\theta_{2})^{3/2}, \end{array} $$
(17)

and

$$\begin{array}{@{}rcl@{}} \theta_{1}&=&-({\Gamma}_{1}+{\Gamma}_{2}+{\Gamma}_{3}), \\ \theta_{2}&=&{\Gamma}_{1}{\Gamma}_{2}+{\Gamma}_{1}{\Gamma}_{3}+{\Gamma}_{2}{\Gamma}_{3}-{\Gamma}_{4}{\Gamma}_{5}-{\Gamma}_{6}{\Gamma}_{8}-{\Gamma}_{7}{\Gamma}_{9}, \\ \theta_{3}&=&-{\Gamma}_{1}{\Gamma}_{2}{\Gamma}_{3}+{\Gamma}_{1}{\Gamma}_{7}{\Gamma}_{9}+{\Gamma}_{2}{\Gamma}_{6}{\Gamma}_{8}+{\Gamma}_{3}{\Gamma}_{4}{\Gamma}_{5}-{\Gamma}_{4}{\Gamma}_{7}{\Gamma}_{8}-{\Gamma}_{5}{\Gamma}_{6}{\Gamma}_{9}, \\ {\Gamma}_{1}&=&P_{11}^{2}+P_{12}^{2}+P_{13}^{2}+{A_{1}^{2}}+{A_{2}^{2}}+{A_{3}^{2}},\\ {\Gamma}_{2}&=&P_{21}^{2}+P_{22}^{2}+P_{23}^{2}+{A_{1}^{2}}+{A_{2}^{2}}+{A_{3}^{2}},\\ {\Gamma}_{3}&=&P_{31}^{2}+P_{32}^{2}+P_{33}^{2}+{A_{1}^{2}}+{A_{2}^{2}}+{A_{3}^{2}},\\ {\Gamma}_{4}&=&P_{11}P_{21}+P_{12}P_{22}+P_{13}P_{23},\\ {\Gamma}_{5}&=&P_{21}P_{11}+P_{22}P_{12}+P_{23}P_{13},\\ {\Gamma}_{6}&=&P_{11}P_{31}+P_{12}P_{32}+P_{13}P_{33},\\ {\Gamma}_{7}&=&P_{21}P_{31}+P_{22}P_{32}+P_{23}P_{33},\\ {\Gamma}_{8}&=&P_{31}P_{11}+P_{32}P_{12}+P_{33}P_{13},\\ {\Gamma}_{9}&=&P_{31}P_{21}+P_{32}P_{22}+P_{33}P_{23}. \end{array} $$
(18)

Combining Eqs. 9–18, we get the GQD to measure the correlation of the two atoms

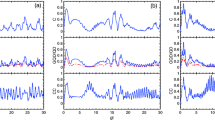
$$\begin{array}{@{}rcl@{}} D_=\frac{1}{4}\left[{\Gamma}_{1}+{\Gamma}_{2}+{\Gamma}_{3}+\frac{1}{3}({A_{1}^{2}}+{A_{2}^{2}}+{A_{3}^{2}})-max(K_{1},K_{2},K_{3})\right]. \end{array} $$
(19)

In order to discuss the influence of the parameters on GQD, Figs. 1–10, correspond to eight different atomic initial entangled states and parameters, respectively.

Fig. 1
figure 1

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different G. The parameters ϕ = 0, M = 5, and σ = 0.5. From (a) to (d): G = 0;G = 1;G = 5;G = 10

Full size image

Case 1

We assume \({\theta =\frac {\pi }{3}}\) or \({\theta =\frac {2 \pi }{3}}\), and ϕ = 0, the two atoms are initially in

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{\sqrt{3}}{2}|e_{1}, g_{2}\rangle-\frac{1}{2}|g_{1}, e_{2}\rangle, \end{array} $$
(20)

or

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{2}|e_{1}, g_{2}\rangle-\frac{\sqrt{3}}{2}|g_{1}, e_{2}\rangle. \end{array} $$
(21)

By Eqs. 20–21 it can be seen that two two-level atoms is initially in non-maximum entangled state, the temporal evolution of GQD is shown as Figs. 1–3. The temporal evolution curves of GQD between two atoms is much alike, under the condition of the above two atomic initial state.

In Fig. 1, M and σ are in a fixed values, respectively. Firstly, we set G = 0, that is to say, in the absence of the dipole-dipole interaction of two atoms, the time evolution of the GQD as a function of gt is shown in Fig. 1a, while evolution of GQD are depicted in Fig. 1b, c and d with atomic coupling increasing. Figure. 1a shows that the oscillation of the temporal evolution of GQD has smaller range and irregularity compared with Fig. 1b, c and d, and initial value of GQD is 0.5. With atomic coupling enhancing, the evolution of GQD is in the range between 0.35 and 0.5. The greater the atomic coupling, the more fast the oscillation frequency of GQD, which is shown in Fig. 1c-d. In Fig. 2, the parameter G and σ are in a fixed values, respectively. In the single photon process(M = 1), Fig. 2a shows that the oscillation of the time evolution of GQD appears cyclical, With particle number enhancing, the evolution of GQD is that the oscillation is ruleless (see Fig. 2b-d). In Fig. 3, G and M are in a fixed values, respectively. When the probabilities of a Bernoulli trial increases (see Fig. 3a-d), the features of the oscillation of the evolution of GQD has irregularity.

Fig. 2
figure 2

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different M. The parameters ϕ = 0, G = 1, and σ = 0.5. From (a) to (d): M = 1;M = 5;M = 10;M = 15

Full size image
Fig. 3
figure 3

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different σ. The parameters ϕ = 0, M = 5, and G = 1. From (a) to (d): σ = 0.1;σ = 0.3;σ = 0.6;σ = 0.9

Full size image

Case 2

In case of \({\theta =\frac {\pi }{3}}\) or \({\theta =\frac {2 \pi }{3}}\), and ϕ = π, the initial states of the two atoms are

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{\sqrt{3}}{2}|e_{1}, g_{2}\rangle+\frac{1}{2}|g_{1}, e_{2}\rangle, \end{array} $$
(22)

or

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{2}|e_{1}, g_{2}\rangle+\frac{\sqrt{3}}{2}|g_{1}, e_{2}\rangle. \end{array} $$
(23)

Similarly, we can be seen that at initially two two-level atoms is in non-maximum entangled state by Eqs. 22–23, the temporal evolution curves of GQD between two atoms is very similar. The temporal evolution of GQD is shown in Figs. 4–6.

Fig. 4
figure 4

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different G. The parameters ϕ = π, M = 5, and σ = 0.5. From (a) to (d): G = 0;G = 1;G = 5;G = 10

Full size image
Fig. 5
figure 5

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different M. The parameters ϕ = π, G = 1, and σ = 0.5. From (a) to (d): M = 1;M = 5;M = 10;M = 15

Full size image
Fig. 6
figure 6

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different σ. The parameters ϕ = π, M = 5, and G = 1. From (a) to (d): σ = 0.1;σ = 0.3;σ = 0.6;σ = 0.9

Full size image

In Fig. 4, the choosed parameters of M and σ are the same as Fig. 1. Compared with Fig. 1, the same character is that the temporal evolution of GQD has the initial value and emerge the oscillation of collapse-and-revival, the different one is evolution curve and in the range between 0 and 0.5. Homologous, the parameters of G and σ chosen in Fig. 5 are the same as Fig. 2, the parameters of G and M chosen in Fig. 6 are the same as Fig. 3, respectively. Compared with Figs. 2 and 3, separately, it is observed that the temporal evolution of GQD has the same initial value and expression characteristics, but evolution curve is different and the entanglement is in the range between 0 and 1.

Case 3

Suppose \({\theta =\frac {\pi }{2}}\), ϕ = 0 or ϕ = π, the initial states of the two atoms are

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{\sqrt{2}}(|e_{1}, g_{2}\rangle-|g_{1}, e_{2}\rangle), \end{array} $$
(24)

or

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{\sqrt{2}}(|e_{1}, g_{2}\rangle+|g_{1}, e_{2}\rangle). \end{array} $$
(25)

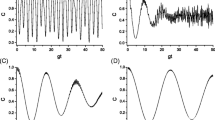
That is the two atoms are initially in maximal entangled states. The temporal evolution of GQD shown as Fig. 7.

Fig. 7
figure 7

Time evolution of GQD versus \(\theta =\frac {\pi }{2}\) for different σ. The parameters ϕ = 0 or ϕ = π, M = 5, and G = 1. From (a) to (d): σ = 0.1;σ = 0.3;σ = 0.6;σ = 0.9

Full size image

In Case 3, although chose certain parameters, obtained Fig. 7 of the temporal evolution of GQD. However, under the condition that two two-level atoms is initially in maximum entangled state, the temporal evolution of GQD between the two atoms always stays in 0.5, independent of the change of the parameter.

Case 4

In case of 𝜃 = 0 or 𝜃 = π, the initial states of the two atoms are

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=|e_{1}, g_{2}\rangle, \end{array} $$
(26)

or

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=|g_{1}, e_{2}\rangle. \end{array} $$
(27)

Eqs. 26 and 27 denotes two atoms is initially in a separate state. The temporal evolution of GQD is shown in Figs. 8–10.

Fig. 8
figure 8

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different G. The parameters ϕ = π, M = 5, and σ = 0.5. From (a) to (d): G = 0;G = 1;G = 5;G = 10

Full size image

From Figs. 8, 9 and 10, we can draw a conclusion that two atoms initially in a non-entangled state interacting with the binomial light field still exist quantum correlation.

Fig. 9
figure 9

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different M. The parameters ϕ = π, G = 1, and σ = 0.5. From (a) to (d): M = 1;M = 5;M = 10;M = 15

Full size image
Fig. 10
figure 10

Time evolution of GQD versus \(\theta =\frac {\pi }{3}\), or \({\theta =\frac {2 \pi }{3}}\) for different σ. The parameters ϕ = π, M = 5, and G = 1. From (a) to (d): σ = 0.1;σ = 0.3;σ = 0.6;σ = 0.9

Full size image

4 Conclusions

In this paper, by using a measurement method of the geometric quantum discord, the properties of the quantum correlation between two atoms have been investigated based on atom-cavity system. The influence of the strength of the dipole-dipole interaction of between two atoms, probabilities of a the Bernoulli trial and particle number of the binomial optical field on the temporal evolution of the geometrical quantum discord between two atoms are discussed, respectively. The result shows that two atoms always exist the correlation for different parameters. In addition, if and only if the two atoms are initially in the maximally entangled state, the temporal evolution of GQD between the two atoms always stays in 0.5, independent of the change of the parameter. Our results will be helpful to the quantum information and the quantum computation.