1 Introduction

There is usually the quantum correlation between two subsystems in a quantum system such as entanglement. Quantum correlation has the special characteristics to be quite different from the classical. Quantum information processing has the advantages over the corresponding classical one for performing various intriguing tasks in some information technologies. Owing to this reason, the quantum entanglement has been regarded as a core resource [1, 2] in quantum information, quantum computation and so on. Many researches focus on the quantum entanglement phenomena in the quantum system and the numerous interesting results have been reported in the past decades. It has been observed that quantum entanglement can suddenly disappear and suddenly revive due to spontaneous emission within a limited time interval under certain conditions, which are called “sudden death” (ESD) [3, 4] and “sudden birth” (ESB) [5,6,7] of quantum entanglement. With the advances of the experimental and theoretical investigation into quantum correlation, it is also found that the non-classical correlation can also exist in the separable states [8,9,10], which indicates that the non-classical correlation in these states is a kind of the quantum correlation beyond entanglement. The results show that quantum entanglement may not include all the quantum correlation in the quantum systems [11]. To depict the properties of quantum correlations more generally, the concepts of quantum discord (QD) [12,13,14,15] and geometrical quantum discord (GQD) [16] has been introduced. The quantum correlations in some physical systems have been investigated under the several conditions [17,18,19,20,21,22,23,24,25,26,27,28,29]. The system interacting two atoms with a single-mode field is a well-known simplest quantum one in which quantum effects, such as quantum coherence and quantum entanglement, can be observed clearly. The time evolution behavior of these quantities has been intensively investigated [30]. However, the evolution process of quantum system cannot get out of the influence of the external environment practically, which is often responsible for the effects such as quantum decoherence and the loss of the quantum correlation. Many researchers pay much attention to the subject that is concerned with the time evolution of quantum correlation of the system exposed to its external environment [31,32,33,34,35,36,37,38,39,40]. Recently, it is manifested that sudden death and birth of entanglement in a system of two coupled atoms interacting with a very small environment take place under the certain conditions [41]. In this paper, we consider the system consisting of two coupled atoms plus a single-mode thermal field in which one of the coupled atoms interacts with a single-mode thermal field (termed a very small environment) under intensity-dependent coupling. Our aims are to study the properties of the quantum and classical correlations in the above system and to grasp how the different correlations evolve with time under various conditions of the external field. The three criteria of concurrence (C), quantum discord (QD) and geometrical quantum discord (GQD) are employed to measure the quantum correlation between two atoms. We have compared the evolution properties of C, QD, GQD with that of the classical correlation (CC) in detail. The article is organized as follows: in Sect. 2, the theoretical model and its solution are given. In Sect. 3, we present the definitions and expressions of various correlations. In Sect. 4, we discuss the obtained results by means of numerical way. Finally, the conclusion is drawn in Sect. 5.

2 The model

2.1 The theoretical model

Here we consider the system which consists of two two-level atoms labeled 1 and 2 plus a single mode quantized field in the rotating wave approximation. Assume that the atoms are themselves coupled, and only the second atom interacts with a single-mode thermal field in the form of the intensity-dependent coupling. Let the transition frequencies of atoms be same as the resonance between the second atom and the field \(\left( \omega _{1}=\omega _{2}=\omega _{3}\right)\). \(\lambda\) is the coupling constant between the two atoms, and g is the effective coupling strength between the second atom and a single-mode thermal field. So the interaction Hamiltonian of the system \((\hbar =1)\) may be written as

$$\begin{aligned} \begin{aligned} H=&H_{0}+H_{1}, \\ H_{0}=&\frac{1}{2} \omega \sigma _{1 z}+\frac{1}{2} \omega \sigma _{2 z}+\omega a^{+} a, \\ H_{1}=&\lambda \left( \sigma _{1}^{+} \sigma _{2}^{-}+\sigma _{1}^{-} \sigma _{2}^{+}\right) +g\left( a f(n) \sigma _{2}^{+}+a^{+} f(n) \sigma _{2}^{-}\right) , \end{aligned} \end{aligned}$$
(1)

where \(H_{0}\) and \(H_{1}\) denote the unperturbed and interaction parts of the Hamiltonian, respectively. \(a^{+}\) and a are the usual creation and annihilation field operators. f(n) represents an arbitrary function of intensity-dependent coupling [42, 43]. The rising and lowing operators are \(\sigma _{i}^{+}=\left. \left| e_{i}\right. \right\rangle \left\langle \left. g_{i}\right| \right.\), \(\sigma _{i}^{-}=\left. \left| g_{i}\right. \right\rangle \left\langle \left. e_{i}\right| \right.\), respectively, and \(\sigma _{i z}=\left. \left| e_{i}\right. \right\rangle \left\langle \left. e_{i}\right| \right. -\left. \left| g_{i}\right. \right\rangle \left\langle \left. g_{i}\right| \right.\) \((i=1,2)\). Let \(\left. \left| e_{i}\right. \right\rangle\) and \(\left. \left| g_{i}\right. \right\rangle\) denote the upper and lower level states of the atoms. We can work conveniently in the interaction picture. So the interaction Hamiltonian of the system (interaction picture) is given by

$$\begin{aligned} V=e^{i H_{0} t / \hbar } H_{1} e^{-i H_{0} t / \hbar }. \end{aligned}$$
(2)

Combining (1) and (2), we have

$$\begin{aligned} V=\lambda \left( \sigma _{1}^{+} \sigma _{2}^{-}+\sigma _{1}^{-} \sigma _{2}^{+}\right) +a g f(n) \sigma _{2}^{+}+a^{+} g f(n) \sigma _{2}^{-}. \end{aligned}$$
(3)

The density operator of time-evolved joint system (interaction picture)

$$\begin{aligned} \rho _{I}(t)=e^{-i H_{1} t} \rho (0) e^{i H_{1} t}, \end{aligned}$$
(4)

with

$$\begin{aligned} \begin{aligned} \rho (0)=&\rho _{q 1}(0) \otimes \rho _{q 2}(0) \otimes \rho _{f}(0) \\ =&\left. \left| e_{1}\right. \right\rangle \left\langle \left. e_{1}\right| \right. \otimes \left. \left| g_{2}\right. \right\rangle \left\langle \left. g_{2}\right| \right. \otimes \sum _{n=0}^{\infty } P_{n}\left. \left| n\right. \right\rangle \left\langle \left. n\right| \right. \\ \equiv&\sum _{n=0}^{\infty } P_{n}\left. \left| {e}_{1},{g}_{2},{n}\right. \right\rangle \left\langle \left. {e}_{1},{g}_{2},{n}\right| \right. , \end{aligned} \end{aligned}$$
(5)

here

$$\begin{aligned} \begin{aligned} P_{n}=\frac{\bar{n}^{n}}{(1+\bar{n})^{n+1}}, \bar{n}=\frac{1}{e^{\frac{\omega }{k_{B} T}}-1}, \end{aligned} \end{aligned}$$
(6)

where \(P_{n}\) denotes the photon number distribution of the single mode thermal field, and \(\bar{n}\) is mean photon number in the thermal equilibrium (frequency \(\omega\)) at the effective temperature T.

2.2 Solution of the model

The Schrödinger equation of the system is

$$\begin{aligned} i \frac{\partial }{\partial t}\left. \left| \Psi _{I} (t)\right. \right\rangle =V\left. \left| \Psi _{I} (t)\right. \right\rangle . \end{aligned}$$
(7)

The state vector of two interacting two-level atoms can be written in the form

$$\begin{aligned} \begin{aligned} \left. \left| \Psi _{I}(t)\right. \right\rangle = C_{1, n}(t) \left. \left| {e}_{1},{e}_{2},{n-1}\right. \right\rangle +C_{2, n}(t)\left. \left| {e}_{1},{g}_{2},{n}\right. \right\rangle \\ +C_{3, n}(t)\left. \left| {g}_{1},{e}_{2},{n}\right. \right\rangle +C_{4, n}(t)\left. \left| {g}_{1},{g}_{2},{n+1}\right. \right\rangle . \end{aligned} \end{aligned}$$
(8)

Here \(\left. \left| e_{1},{g}_{2},{n}\right. \right\rangle\) means that atom 1 is in an excited state, atom 2 is in a ground state and the single mode field has n photons. There are similar descriptions for the states \(\left. \left| e_{1},{e}_{2},{n-1}\right. \right\rangle\), \(\left. \left| g_{1},e_{2},{n}\right. \right\rangle\) and \(\left. \left| g_{1},{g}_{2},{n+1}\right. \right\rangle\). The coefficients \(C_{j, n}(t)\) are the probability amplitudes of finding two atoms in these four states with \(j=1,2,3,4\), respectively. Substitute (3) and (8) into (7), we get the following differential equations

$$\begin{aligned} \begin{aligned} i \dot{C}_{1, n}=&g f(n) \sqrt{n} C_{2, n}, \\ i \dot{C}_{2, n}=&g f(n) \sqrt{n} C_{1, n}+\lambda C_{3, n}, \\ i \dot{C}_{3, n}=&\lambda C_{2, n}+g f(n) \sqrt{n+1} C_{4, n}, \\ i \dot{C}_{4, n}=&g f(n) \sqrt{n+1} C_{3, n}. \end{aligned} \end{aligned}$$
(9)

The solution can be expressed as

$$\begin{aligned} C_{j, n}(t)=\sum _{m=1}^{4} A_{j m}^{(n)}(t) c_{m}(0), j=1,2,3,4, \end{aligned}$$
(10)

with \(A_{j m}^{(n)}=A_{m j}^{(n)}\), the dimensionality of the Fock state basis is expressed as n \((n=0,1,2, \ldots )\). The relevant matrix elements can therefore be written as

$$\begin{aligned} \begin{aligned} A_{11}^{(n)}(t)=&\frac{1}{r_{n}}\left[ \begin{array}{l} \left( \omega _{+, n}^{2}-b_{n}^{2}-\lambda ^{2}\right) \cos \left( \omega _{+, n} t\right) -\\ \left( \omega _{-, n}^{2}-b_{n}^{2}-\lambda ^{2}\right) \cos \left( \omega _{-, n} t\right) \end{array}\right] ,\\ A_{12}^{(n)}(t)=&\frac{i a_{n}}{r_{n}}\left[ \frac{\left( b_{n}^{2}-\omega _{+, n}^{2}\right) \sin \left( \omega _{+, n} t\right) }{\omega _{+, n}}-\frac{\left( b_{n}^{2}-\omega _{-, n}^{2}\right) \sin \left( \omega _{-,n} t\right) }{\omega _{-, n}}\right] , \\ A_{13}^{(n)}(t)=&\frac{\lambda a_{n}}{r_{n}}\left[ \cos \left( \omega _{+, n} t\right) -\cos \left( \omega _{-, n} t\right) \right] , \\ A_{14}^{(n)}(t)=&-\frac{i \lambda a_{n} b_{n}}{r_{n}}\left[ \frac{\sin \left( \omega _{+,n} t\right) }{\omega _{+, n}}-\frac{\sin \left( \omega _{-, n} t\right) }{\omega _{-, n}}\right] , \\ A_{22}^{(n)}(t)=&\frac{1}{r_{n}}\left[ \left( \omega _{+, n}^{2}-b_{n}^{2}\right) \cos \left( \omega _{+, n} t\right) -\left( \omega _{-, n}^{2}-b_{n}^{2}\right) \cos \left( \omega _{-, n} t\right) \right] , \\ A_{23}^{(n)}(t)=&\frac{-i \lambda }{r_{n}}\left[ \omega _{+, n} \sin \left( \omega _{+, n} t\right) -\omega _{-, n} \sin \left( \omega _{-, n} t\right) \right] , \\ A_{24}^{(n)}(t)=&\frac{\lambda b_{n}}{r_{n}}\left[ \cos \left( \omega _{+, n} t\right) -\cos \left( \omega _{-,n} t\right) \right] , \\ A_{33}^{(n)}(t)=&\frac{1}{r_{n}}\left[ \left( \omega _{+, n}^{2}-a_{n}^{2}\right) \cos \left( \omega _{+, n} t\right) -\left( \omega _{-, n}^{2}-a_{n}^{2}\right) \cos \left( \omega _{-, n} t\right) \right] , \\ A_{34}^{(n)}(t)=&\frac{i b_{n}}{r_{n}}\left[ \frac{\left( a_{n}^{2}-\omega _{+, n}^{2}\right) \sin \left( \omega _{+, n} t\right) }{\omega _{+, n}}-\frac{\left( a_{n}^{2}-\omega _{-, n}^{2}\right) \sin \left( \omega _{-, n} t\right) }{\omega _{-, n}}\right] , \\ A_{44}^{(n)}(t)=&\frac{1}{r_{n}}\left[ \begin{array}{l} \left( \omega _{+, n}^{2}-a_{n}^{2}-\lambda ^{2}\right) \cos \left( \omega _{+, n} t\right) - \left( \omega _{-, n}^{2}-a_{n}^{2}-\lambda ^{2}\right) \cos \left( \omega _{-, n} t\right) \end{array}\right] , \end{aligned} \end{aligned}$$
(11)

with

$$\begin{aligned} \begin{aligned} a_{n}=&g f(n) \sqrt{n}, b_{n}=g f(n) \sqrt{n+1}, \\ r_{n}=&\sqrt{\left( g^{2} f^{2}(n)+\lambda ^{2}\right) ^{2}+4 n g^{2} f^{2}(n) \lambda ^{2}}, \\ \omega _{\pm , n}=&\frac{1}{\sqrt{2}} \sqrt{(2 n+1) g^{2} f^{2}(n)+\lambda ^{2} \pm r_{n}}. \end{aligned} \end{aligned}$$
(12)

Assume that the system is initially in a separated state

$$\begin{aligned} \left. \left| \Psi (0)\right. \right\rangle =\left. \left| {e}_{1},{g}_{2},{n}\right. \right\rangle . \end{aligned}$$
(13)

The coefficients \(C_{j, n}(t)\) become

$$\begin{aligned} \begin{aligned} C_{1, n}(t)=&\frac{i a_{n}}{r_{n}}\left[ \frac{\left( b_{n}^{2}-\omega _{+, n}^{2}\right) \sin \left( \omega _{+, n} t\right) }{\omega _{+, n}}-\frac{\left( b_{n}^{2}-\omega _{-, n}^{2}\right) \sin \left( \omega _{-, n} t\right) }{\omega _{-, n}}\right] , \\ C_{2, n}(t)=&\frac{1}{r_{n}}\left[ \left( \omega _{+, n}^{2}-b_{n}^{2}\right) \cos \left( \omega _{+, n} t\right) -\left( \omega _{-, n}^{2}-b_{n}^{2}\right) \cos \left( \omega _{-, n} t\right) \right] , \\ C_{3, n}(t)=&\frac{-i \lambda }{r_{n}}\left[ \omega _{+, n} \sin \left( \omega _{+, n} t\right) -\omega _{-, n} \sin \left( \omega _{-, n} t\right) \right] , \\ C_{4, n}(t)=&\frac{\lambda b_{n}}{r_{n}}\left[ \cos \left( \omega _{+, n} t\right) -\cos \left( \omega _{-, n} t\right) \right] . \end{aligned} \end{aligned}$$
(14)

Thus the joint density operator of the system can be expressed as

$$\begin{aligned} \begin{aligned} \rho _{\mathrm {I}}(t)=&\sum _{n=0}^{\infty } P_{n}\left[ \begin{array}{l} C_{1, n}(t) \left. \left| {e}_{1},{e}_{2},{n-1}\right. \right\rangle +C_{2, n}(t) \left. \left| {e}_{1},{g}_{2},{n}\right. \right\rangle \\ +C_{3, n}(t) \left. \left| {g}_{1},{e}_{2},{n}\right. \right\rangle +C_{4, n}(t)\left. \left| {g}_{1},{g}_{2},{n+1}\right. \right\rangle \end{array}\right] \\ \times&\left[ \begin{array}{l} C_{1, n}^{*}(t) \left\langle \left. {e}_{1},{e}_{2},{n-1}\right| \right. +C_{2, n}^{*}(t) \left\langle \left. {e}_{1},{g}_{2},{n}\right| \right. \\ +C_{3, n}^{*}(t) \left\langle \left. {g}_{1},{e}_{2},{n}\right| \right. +C_{4, n}^{*}(t) \left\langle \left. {g}_{1},{g}_{2},{n+1}\right| \right. \end{array}\right] . \end{aligned} \end{aligned}$$
(15)

By tracing the field variables, we get the following operator

$$\begin{aligned} \begin{aligned}&\rho _{q 1, q 2}(t)={\text {Tr}}_{f}\left[ \rho _{I}(t)\right] \\&=\sum _{n=0}^{\infty } P_{n+1} \left| C_{1, n+1}\right| ^{2} \left. \left| {e}_{1},{e}_{2}\right. \right\rangle \left\langle \left. {e}_{1},{e}_{2}\right| \right. \\&+\sum _{n=0}^{\infty } P_{n} \left| C_{2, n}\right| ^{2} \left. \left| {e}_{1},{g}_{2}\right. \right\rangle \left\langle \left. {e}_{1},{g}_{2}\right| \right. \\&+\sum _{n=0}^{\infty } P_{n} \left| C_{3, n}\right| ^{2} \left. \left| {g}_{1},{e}_{2}\right. \right\rangle \left\langle \left. {g}_{1},{e}_{2}\right| \right. \\&+\sum _{n=0}^{\infty } P_{n-1} \left| C_{4, n-1}\right| ^{2} \left. \left| {g}_{1},{g}_{2}\right. \right\rangle \left\langle \left. {g}_{1},{g}_{2}\right| \right. \\&+\sum _{n=0}^{\infty } P_{n} C_{2, n} C_{3, n}^{*}\left. \left| {e}_{1},{g}_{2}\right. \right\rangle \left\langle \left. {g}_{1},{e}_{2}\right| \right. \\&+\sum _{n=0}^{\infty } P_{n} C_{3, n} C_{2, n}^{*}\left. \left| {g}_{1},{e}_{2}\right. \right\rangle \left\langle \left. {e}_{1},{g}_{2}\right| \right. , \end{aligned} \end{aligned}$$
(16)

which is a peculiar type of bipartite state called X-form state [44].

$$\begin{aligned} \rho _{q 1, q 2}(t)=\left( \begin{array}{llll} \rho _{11} &{} \rho _{12} &{} \rho _{13} &{} \rho _{14} \\ \rho _{21} &{} \rho _{22} &{} \rho _{23} &{} \rho _{24} \\ \rho _{31} &{} \rho _{32} &{} \rho _{33} &{} \rho _{34} \\ \rho _{41} &{} \rho _{42} &{} \rho _{43} &{} \rho _{44} \end{array}\right) =\left( \begin{array}{cccc} \rho _{11} &{} 0 &{} 0 &{} 0 \\ 0 &{} \rho _{22} &{} \rho _{23} &{} 0 \\ 0 &{} \rho _{23}^{*} &{} \rho _{33} &{} 0 \\ 0 &{} 0 &{} 0 &{} \rho _{44} \end{array}\right) , \end{aligned}$$
(17)

where

$$\begin{aligned} \begin{aligned} \rho _{11}=&\sum _{n=0}^{\infty } P_{n+1}\left| C_{1, n+1}\right| ^{2}, \rho _{22}=\sum _{n=0}^{\infty } P_{n}\left| C_{2, n}\right| ^{2}, \rho _{23}\\&=\sum _{n=0}^{\infty } P_{n} C_{2, n} C_{3, n}^{*}, \\ \rho _{23}^{*}=&\sum _{n=0}^{\infty } P_{n} C_{3, n} C_{2, n}^{*}, \rho _{33}=\sum _{n=0}^{\infty } P_{n}\left| C_{3, n}\right| ^{2}, \rho _{44}\\&=\sum _{n=0}^{\infty } P_{n-1}\left| C_{4, n-1}\right| ^{2}. \end{aligned} \end{aligned}$$
(18)

3 Entanglement, classical and quantum correlations

In this section, the quantum correlations between two subsystems will be measured by introducing the concurrence (C), the quantum discord (QD) and the geometrical quantum discord (GQD).

3.1 Quantum entanglement

The atom-atom interactions usually result in bipartite entanglement. There are usually two ways to measure quantum entanglement between two subsystems: concurrence (C) [45] and negativity [46,47,48]. We adopt the concurrence as a function of time here

$$\begin{aligned} C(\mathrm {t})=\max [0, \Lambda (t)], \end{aligned}$$
(19)

with

$$\begin{aligned} \begin{aligned} \Lambda (t)=&\sqrt{\xi _{1}(t)}-\sqrt{\xi _{2}(t)}-\sqrt{\xi _{3}(t)}-\sqrt{\xi _{4}(t)},\\&\left( \xi _{1}(t) \ge \xi _{2}(t) \ge \xi _{3}(t) \ge \xi _{4}(t)\right) , \end{aligned} \end{aligned}$$
(20)

where \(\xi _{i}\) \((i=1,2,3,4)\) are the eigenvalues of the Hermitian matrix M(t)

$$\begin{aligned} M(t)=\rho _{q 1, q 2}(t)\left( \sigma _{y}^{(1)} \otimes \sigma _{y}^{(2)}\right) \rho _{q 1, q 2}^{*}(t)\left( \sigma _{y}^{(1)} \otimes \sigma _{y}^{(2)}\right) , \end{aligned}$$
(21)

\(\sigma _{y}\) is the Pauli Y matrix and \(\rho _{q 1, q 2}^{*}\) is the complex conjugate of the two atoms density operator \(\rho _{q 1, q 2}\). The value of concurrence ranges from 0 to 1. The larger the value of the function, the stronger the corresponding entanglement. In particular, it is straightforward to derive the expression for the concurrence in a system of two two-level interacting atoms with a single mode thermal field [49]

$$\begin{aligned} \Lambda (t)=2\mid \rho _{23}\mid -2 \sqrt{\rho _{11} \rho _{44}}. \end{aligned}$$
(22)

3.2 Quantum discord and classical correlation

Quantum entanglement is the core resource for realizing quantum information processing and quantum computing. It has recently been discovered that quantum entanglement can not contain all types of quantum correlation and there are still some quantum correlations in the quantum system without quantum entanglement. The results show that these quantum correlations can improve the efficiency of the quantum communication and realize the quantum speedup algorithm in the absence of quantum entanglement. In order to describe and measure the general quantum correlations between two subsystems of a quantum system, Ollivier and Zurek introduced the concept of quantum discord [12]. It is defined by the difference between two equivalent expressions of classical mutual information during quantum generalization, that is, the difference between quantum mutual information and classical correlation

$$\begin{aligned} Q D\left( \rho _{q 1, q 2}\right) =I\left( \rho _{q 1, q 2}\right) -CC\left( \rho _{q 1, q 2}\right) . \end{aligned}$$
(23)

Here \(I\left( \rho _{q 1, q 2}\right)\) and \(CC\left( \rho _{q 1, q 2}\right)\) are equal in the classical case, but not equal in quantum physics. Therefore, it is necessary to measure the quantum difference between the two quantities. The quantum mutual information of the two-body system can be expressed by the total correlation of quantum states

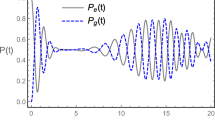
$$\begin{aligned} I\left( \rho _{\mathrm {q} 1, q 2}\right) =S\left( \rho _{\mathrm {q} 1}\right) +S\left( \rho _{q 2}\right) -S\left( \rho _{\mathrm {q} 1, q 2}\right) . \end{aligned}$$
(24)

The expression of the classical correlation is

$$\begin{aligned} C C\left( \rho _{q 1, q 2}\right) =S\left( \rho _{q 1}\right) -\min _{\left\{ \Pi _{k}^{q 2}\right\} }\left[ S\left( \rho _{q 1, q 2} \mid \left\{ \Pi _{k}^{q 2}\right\} \right) \right] , \end{aligned}$$
(25)

where \(S\left( \rho _{j}\right)\) is von Neumann entropy

$$\begin{aligned} S\left( \rho _{j}\right) =-T r_{j}\left( \rho _{j} \log _{2} \rho _{j}\right) =-\sum _{i} \lambda _{j}^{i} \log _{2} \lambda _{j}^{i}. \end{aligned}$$
(26)

\(\left\{ \lambda _{j}^{i}\right\}\) is the nonzero eigenvalue of \(\rho _{j}\), the subscript j refers to the subsystem 1 (2) or the total system, and the reduced density matrix of 1 (2) in the two atoms system is

$$\begin{aligned} \rho _{q1(q2)}={\text {Tr}}_{q2(q1)}\left( \rho _{q1, q2}\right) . \end{aligned}$$
(27)

The quantum conditional entropy is

$$\begin{aligned} S\left( \rho _{q 1, q 2} \mid \left\{ \Pi _{k}^{q 2}\right\} \right) =\sum _{k} p_{k} S\left( \rho _{k}^{q 1}\right) . \end{aligned}$$
(28)

Define \(\left\{ \Pi _{k}^{q 2}\right\}\) as a set of orthogonal complete projection operators locally acting on subsystem 2. k represents the outcomes of measurements, and

$$\begin{aligned} \begin{aligned} p_{k}={\text {Tr}}_{q 1, q 2}\left[ \left( I_{q 1} \otimes \Pi _{k}^{q 2}\right) \rho _{q 1, q 2}\left( I_{q 1} \otimes \Pi _{k}^{q 2}\right) \right] , \\ \rho _{k}^{q 1}=\frac{1}{p_{k}} {\text {Tr}}_{q 2}\left[ \left( I_{q 1} \otimes \Pi _{k}^{q 2}\right) \rho _{q 1, q 2}\left( I_{q 1} \otimes \Pi _{k}^{q 2}\right) \right] , \end{aligned} \end{aligned}$$
(29)

\(p_{k}\) and \(\rho _{k}^{q 1}\) refer to the probability of measurement and conditional density matrix, respectively, where \(I_{q 1}\) is the unit operator of subsystem 1. Substituting formulas (24) and (25) into (23), the quantum discord of the system can be expressed as

$$\begin{aligned} Q D\left( \rho _{q1, q2}\right) =S\left( \rho _{q2}\right) -S\left( \rho _{q1, q2}\right) +\min _{\left\{ \Pi _{k}^{q2}\right\} }\left[ \Sigma _{k} p_{k} S\left( \rho _{k}^{q1}\right) \right] . \end{aligned}$$
(30)

For the quantum system described by density matrix (17), QD can be simply expressed as [50]

$$\begin{aligned} \begin{aligned}&Q D\left( \rho _{q 1, q 2}\right) =\min \left\{ Q D_{1}, Q D_{2}\right\} , \\&Q D_{1}=\sum _{i=1}^{4} \gamma _{i} \log _{2} \gamma _{i}-\sum _{i=1}^{4} \rho _{i i} \log _{2} \rho _{i i}, \\&Q D_{2}=\Gamma \left( \rho _{11}+\rho _{33}\right) +\sum _{i=1}^{4} \gamma _{i} \log _{2} \gamma _{i}+ \\&\Gamma \left[ \left( 1+\sqrt{\left( \rho _{11}+\rho _{22}-\rho _{33}-\rho _{44}\right) ^{2}+4\left| \rho _{23}\right| ^{2}}\right) / 2\right] , \end{aligned} \end{aligned}$$
(31)

with

$$\begin{aligned} \begin{aligned}&\Gamma (x)=-x \log _{2} x-(1-x) \log _{2}(1-x), \\&\gamma _{1}=\rho _{11}, \gamma _{2}=\rho _{44}, \gamma _{3,4}\\&=\frac{\left( \rho _{22}+\rho _{33}\right) \pm \sqrt{\left( \rho _{22}-\rho _{33}\right) ^{2}+4\left| \rho _{23}\right| ^{2}}}{2} . \end{aligned} \end{aligned}$$
(32)

In particular, the classical correlation (CC) is

$$\begin{aligned} C C\left( \rho _{q 1, q 2}\right) =\max \left\{ C_{1}, C_{2}\right\} , \end{aligned}$$
(33)

and

$$\begin{aligned} \begin{aligned}&C_{j}=\Gamma \left( \rho _{11}+\rho _{22}\right) -B_{j}, \\&B_{1}=\Gamma \left[ \left( 1+\sqrt{\left( \rho _{11}+\rho _{22}-\rho _{33}-\rho _{44}\right) ^{2}+4\left| \rho _{23}\right| ^{2}+4\left| \rho _{14}\right| ^{2}}\right) / 2\right] , \\&B_{2}=-\sum _{i=1}^{4} \rho _{i i} \log _{2} \rho _{i i}-\Gamma \left( \rho _{11}+\rho _{33}\right) . \end{aligned} \end{aligned}$$
(34)

By applying the above results, we can discuss the time evolution behavior of the quantum correlation and classical correlation in the system.

3.3 Geometrical quantum discord

Quantum discord involves a difficult optimization process, and it is difficult to obtain analytical results of quantum discord except for a few classes of two qubits state. To overcome this difficulty, Dakić et al proposed a geometric measure of quantum discord [16], called geometrical quantum discord (GQD), which can be used to measure the quantum correlation between two subsystems [51]. Using geometric method, the geometrical quantum discord is defined as the nearest distance between a zero discord state and a given state, which can be described by Hilbert–Schmidt norm

$$\begin{aligned} D_{G}(\rho ) \equiv \min _{\chi \in \Omega _{0}}\Vert \rho -\chi \Vert ^{2}, \end{aligned}$$
(35)

where \(\Omega _{0}\) represents the set of zero discord states \(\chi\), \(\Vert \rho -\chi \Vert\) is the Hilbert–Schmidt norm of the Hermitian operator [52]. We consider the system of two atoms, whose density matrix can be expressed as

$$\begin{aligned}&\rho _{q1, q2}=\frac{1}{4}\left[ I \otimes I+\sum _{i=1}^{3}\left( A_{i} \sigma _{i} \otimes I+B_{i} I \otimes \sigma _{i}\right) \right. \nonumber \\&\quad \left. +\sum _{i, j=1}^{3}\left( P_{i j} \sigma _{i} \otimes \sigma _{j}\right) \right] , \end{aligned}$$
(36)

where I is the identity matrix, \(\sigma _{i}, \sigma _{j}\) \((i, j=x, y, z)\) represent Pauli matrices, and \(A_{i}\) and \(B_{i}\) are the components of the local Bloch vectors

$$\begin{aligned} \begin{aligned} A_{i}=&{\text {Tr}}\left[ \rho _{q 1, q 2}\left( \sigma _{i} \otimes I\right) \right] , \\ B_{i}=&{\text {Tr}}\left[ \rho _{q 1, q 2}\left( I \otimes \sigma _{i}\right) \right] , \end{aligned} \end{aligned}$$
(37)

and

$$\begin{aligned} P_{i j}={\text {Tr}}\left[ \rho _{q1, q2}\left( \sigma _{i} \otimes \sigma _{j}\right) \right] . \end{aligned}$$
(38)

Therefore, GQD is expressed as

$$\begin{aligned} \begin{aligned} D(t)=&\frac{1}{4}\left( \Vert A\Vert ^{2}+\Vert P\Vert ^{2}-\kappa _{\max }\right) , \\ \Vert A\Vert ^{2}=&\sum _{i=1}^{3} A_{i}^{2}, P=P_{i j},\Vert P\Vert ^{2}={\text {Tr}}\left( P^{T} P\right) . \end{aligned} \end{aligned}$$
(39)

The maximum eigenvalue of the matrix \(K=A A^{T}+P P^{T}\) is expressed as \(\kappa _{\max }\), and superscript T represents the transpose of the matrix P and the vector A. Based on the above theories, it can be concluded that

$$\begin{aligned} \begin{aligned}&A_{1}=0, A_{2}=0, A_{3}=\rho _{11}+\rho _{22}-\rho _{33}-\rho _{44}, \\&P_{11}=\rho _{23}+\rho _{32}, P_{12}=\mathrm {i}\left( \rho _{32}-\rho _{23}\right) , P_{13}=0, \\&P_{21}=\mathrm {i}\left( \rho _{23}-\rho _{32}\right) , P_{22}=\rho _{23}+\rho _{32}, P_{23}=0, \\&P_{31}=0, P_{32}=0, P_{33}=\rho _{11}-\rho _{22}-\rho _{33}+\rho _{44}, \end{aligned} \end{aligned}$$
(40)
$$\begin{aligned} \Vert A\Vert ^{2}=A_{3}^{2},\Vert P\Vert ^{2}=P_{11}^{2}+P_{12}^{2}+P_{21}^{2}+P_{22}^{2}+P_{33}^{2} . \end{aligned}$$
(41)

The three eigenvalues of the matrix K are

$$\begin{aligned} \begin{aligned} \kappa _{1}=&-\frac{1}{3} X_{1}-\frac{2}{3}\left( X_{1}^{2}-3 X_{2}\right) ^{1 / 2} \cos \frac{\gamma }{3}, \\ \kappa _{2}=&-\frac{1}{3} X_{1}+\frac{1}{3}\left( X_{1}^{2}-3 X_{2}\right) ^{1 / 2}\left( \cos \frac{\gamma }{3}+\sqrt{3} \sin \frac{\gamma }{3}\right) , \\ \kappa _{3}=&-\frac{1}{3} X_{1}+\frac{1}{3}\left( X_{1}^{2}-3 X_{2}\right) ^{1 / 2}\left( \cos \frac{\gamma }{3}-\sqrt{3} \sin \frac{\gamma }{3}\right) , \\ \gamma =&\arccos L, L=\frac{2 X_{1}^{3}+27 X_{3}-9 X_{1} X_{2}}{2\left( X_{1}^{2}-3 X_{2}\right) ^{3 / 2}}, \end{aligned} \end{aligned}$$
(42)

and

$$\begin{aligned} \begin{aligned}&X_{1}=-\left( Y_{1}+Y_{2}+Y_{3}\right) , \\&X_{2}=Y_{1} Y_{2}+Y_{2} Y_{3}+Y_{1} Y_{3}-Y_{4} Y_{5}, \\&X_{3}=Y_{3} Y_{4} Y_{5}-Y_{1} Y_{2} Y_{3}, \\&Y_{1}=P_{11}^{2}+P_{12}^{2}, Y_{2}=P_{21}^{2}+P_{22}^{2}, Y_{3}=A_{3}^{2}+P_{33}^{2}, \\&Y_{4}=P_{11} P_{21}+P_{12} P_{22}, Y_{5}=P_{21} P_{11}+P_{22} P_{12}, \\&Y_{6}=0, Y_{7}=0, Y_{8}=0, Y_{9}=0 . \end{aligned} \end{aligned}$$
(43)

According to the above formulae, GQD between two atoms is

$$\begin{aligned} D(t)=-\frac{1}{4}\left[ X_{1}+\max \left( \kappa _{1}, \kappa _{2}, \kappa _{3}\right) \right] . \end{aligned}$$
(44)

It is worth noting that GQD is sometimes regarded as the weak correlation measure since it may increase under some local operations. But the recent research show that it is more simple to measure experimentally [53].

4 Numerical results and discussion

In this section, we will focus on the numerical calculation and then analyze the obtained results. Here we express the ratio of the atom1-atom2 coupling to the atom2-field environment coupling as \(k \equiv g /\lambda\), and then \(g=k\lambda\). By changing k, viz., the coupling constant g and the mean photon number \(\bar{n}\) as well as the different intensity-dependent coupling parameter f(n), the time evolution processes of C, QD, GQD and CC are displayed and analyzed, respectively. For the convenience of calculation, the coupling constant \(\lambda\) is set to 10.

Case 1. The evolution curves of C, QD, GQD and CC are plotted versus the normalized time \(\lambda\) t on the three timescales.

Fig. 1
figure 1

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=1\), \(g=0.1\lambda\) and \(f(n)=\sqrt{n}\)

Full size image

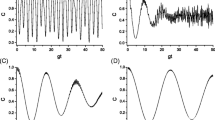
The quantum entanglement between two atoms is a periodic function of time for a completely isolated two-atom coupling system \((g=0)\) [41]. If we consider the interaction between the atoms and the thermal radiation field, the evolution process will be changed due to the influence of the external environment on quantum correlations or classical correlation. Therefore, the destructive effect of the small external environment can be estimated by observing the changes of the amplitudes of entanglement, the quantum and classical correlations during their evolution processes.

Now we consider the case where atom 2 is weakly coupled to the single-mode thermal radiation field \((g=0.1\lambda )\) and the average photon number is small \((\bar{n}=1)\) with \(f(n)=\sqrt{n}\). The evolution properties of quantum entanglement (C), quantum discord (QD), geometrical quantum discord (GQD) and classical correlation (CC) with time in three different timescales are given in Fig. 1. The initial values of C, QD, GQD and CC are zero \([t=0,\) \(C(0)=Q D(0)=G Q D(0)=C C(0)=0]\), which means that there is neither quantum correlation nor classical correlation between two atoms at the initial moment. It can be seen from Fig. 1 (a) that the time evolution behavior of C, QD and GQD is quite similar to each other, while the evolution curve of classical correlation CC is obviously different from those of the three quantities. Compared the evolution of C, QD, GQD with that of CC at the intermediate time scales, it has been observed in Fig. 1 (b) that the values of C, QD, GQD are degraded gradually and the value of CC fluctuates in the certain range. The periodic revivals of C, QD, GQD do not appear at the longer timescales as shown in Fig. 1 (c) when \(f(n)=\sqrt{n}\), in contrast to the case where the periodic revivals of them occur if \(f(n)=1\) corresponding to no intensity-dependent coupling. The above results signify that the intensity-dependent coupling factor f(n) may result in a destructive effect on periodic revivals of C, QD, GQD. The sudden death (SD) and sudden birth (SB) of C, QD and GQD occur during the whole evolution process. The SD and SB of CC appear only in the vicinity of time value 0.16, and its values are larger than zero in any other time intervals. The all-time evolution curves of C, QD, GQD and CC display the irregular oscillations in the observed periods.

Fig. 2
figure 2

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=10\), \(g=0.1\lambda\) and \(f(n)=\sqrt{n}\)

Full size image

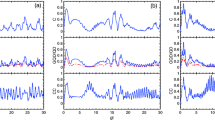
Figure 2 shows the evolution curves of C, QD, GQD and CC with time for \(g=0.1\lambda\), \(\bar{n}=10\) and \(f(n)=\sqrt{n}\). Compared with Fig. 1, the oscillating amplitudes of C, QD, GQD and CC become smaller and the fluctuations are more irregular for the larger value of the mean photon number. Figure 2 (a) shows the evolution of the four quantities in the short time domain, from which we can obviously observe the phenomena of entanglement sudden death (ESD) and sudden birth (ESB). Compared with the evolution processes of QD, GQD and CC, the values of C are not zero in only five isolated time intervals and remain at zero in any other time ones. However, the values of QD and GQD are zero only in a few shorter time periods. It is worth noting that the maximum values of QD, GQD are really smaller, but that of C are relatively larger when the time changes from 0.9 to 1.0 as shown in Fig. 2 (a) [see its panels]. It has been manifested that there are still the quantum correlation effects described by QD and GQD in the absence of quantum entanglement within the certain domains of time. By observing Fig. 2 (b) and (c), the evolution curves of C, QD and GQD exhibit the small-amplitude irregular oscillations with sudden death and sudden birth of entanglement and quantum correlations. However, the evolution behavior of the classical correlation is different from that of the quantum correlation. The values of CC are larger than zero in the selected time domains except for \(t=0\) moment.

Fig. 3
figure 3

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=1\), \(g=0.5\lambda\) and \(f(n)=\sqrt{n}\)

Full size image

We consider the case where atom 2 more strongly coupled to the thermal field \(g=0.5\lambda\). It means that the interaction strength between atom 2 and the thermal field will increase and the values of the other coefficients are the same as in Fig. 1. As shown in Fig. 3, the values of C are between 0 and 0.8, QD between 0 and 0.7, GQD from 0 to 0.35, and CC from 0 to 0.9. It can be seen that the amplitudes of the four quantities are generally lower than those in Fig. 1, but larger than in Fig. 2. The phenomena of sudden death and sudden birth for quantum entanglement and quantum correlations can still be observed in Fig. 3. According to Fig. 3 (a), the temporal evolution of C, QD and GQD is also similar to each other. The evolution curve of CC is significantly different from the others. The values of CC are always larger than zero when the time is larger than 0.17. For the intermediate and longer timescales as in Fig. 3 (b) and 3 (c), the evolution curves of the four quantities display intensely oscillating with time . The SD and SB of C, QD and GQD still occur during the evolution process and the phenomenon of the SD and SB of CC starts to appear in Fig. 3 (b) and 3 (c). It is clear that the stronger atom-environment coupling influences the evolution processes of the quantum and classical correlations between two atoms.

Fig. 4
figure 4

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=10\), \(g=0.5\lambda\) and \(f(n)=\sqrt{n}\)

Full size image

In Fig. 4, we take account of the case where there is a stronger atom-environment interaction (\(g=0.5\lambda\)), and the excitation of environment is the higher (\(\bar{n}=10\)). It has been shown in Fig. 4 (a) that the amplitudes of C, QD, GQD and CC become the lower than those in Fig. 2 (a) or Fig. 3 (a), and the time intervals having null entanglement remain longer as well as the values of CC vanish in some time intervals. Compared with the evolution of entanglement in Fig. 4 (a), it is clearly evident that the non-classical correlations captured by QD and GQD exist in some time intervals in the absence of the quantum entanglement. As plotted in Fig. 4 (b) and (c) in the intermediate and long timescales, all the evolution behavior of the four quantities displays the intensely oscillating one, and the amplitudes of them decrease gradually. The revivals of entanglement almost disappear at later times in Fig. 4 (c).

Case 2. The evolution curves of C, QD, GQD and CC are plotted versus the normalized time \(\lambda\) t on the three timescales.

Fig. 5
figure 5

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=1\), \(g=0.1\lambda\) and \(f(n)=\sqrt{3n}\)

Full size image

In Fig. 5, all the parameters are the same as in Fig. 1 except \(f(n)=\sqrt{3n}\). The evolution behavior of the four quantities in Fig. 5 (a) is similar to those in Fig. 1 (a), but the maximum values of them are lower compared to those in Fig. 1 (a). The evolution curves of C, QD, GQD and CC in Fig. 5 (b) are different from those in Fig. 1 (b), which also give the more details for the various evolution of the quantities in the intermediate scales. It has been seen clearly from Fig. 5 (c) that the more peaks of them occur in the longer timescales with rising the intensity-dependent coupling f(n). In Fig. 5 (c), it is shown that the oscillations of the four quantities tend to more intense fluctuating form in the long timescales. The SD and SB of C, QD, GQD and CC still occur during the evolution as shown in Fig. 5.

Fig. 6
figure 6

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=10\), \(g=0.1\lambda\) and \(f(n)=\sqrt{3n}\)

Full size image

The case is taken into account when \(\bar{n}=10\), \(g=0.1\lambda\) and \(f(n)=\sqrt{3n}\) as illustrated in Fig. 6. It is observed that the evolution curves of the four quantities shift evidently down compared to those in Figs. 2 and 5. It is clear that the zeros in entanglement and quantum correlations keep longer times, and the time intervals having null QD and GQD are still shorter than those in the absence of C. The SD and SB of CC occur during the evolution as shown in Fig. 6 (b) and (c). As we would expect, the larger mean excitation number of field attenuates further the effects of the various correlations, and rising the intensity-dependent coupling also brings about the destructive effect on the different correlations.

Fig. 7
figure 7

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=1\), \(g=0.5\lambda\) and \(f(n)=\sqrt{3n}\)

Full size image

In Fig. 7, we plot the case when \(\bar{n}=1\), \(g=0.5\lambda\) and \(f(n)=\sqrt{3n}\). For short timescales, it is shown in Fig. 7 (a) that the evolution curves of C, QD, GQD and CC display the different distributed forms compared to those in Fig. 5 (a), the time intervals having no entanglement become longer. For intermediate and long timescales, the evolution curves of the four quantities exhibit more intensely irregular oscillations in Fig. 7 (b) and (c) than those as plotted in Fig. 5 (b) and (c), and the SD and SB of C, QD, GQD, CC occur during the evolution.

Fig. 8
figure 8

The time evolution curves of C, QD, GQD and CC for the different timescales with \(\bar{n}=10\), \(g=0.5\lambda\) and \(f(n)=\sqrt{3n}\)

Full size image

In Fig. 8, we plot the evolution curves of the four quantities when the field mean excitation number increases (\(\bar{n}=10\)) with \(f(n)=\sqrt{3n}\). It is shown that all the values of C, QD, GQD and CC decay rapidly to the smaller ones with the increase of \(\bar{n}\), and there are some limited intervals having the weaker entanglement as plotted in Fig. 8 (a) and 8 (b), as well as the sudden-births of entanglement almost completely vanish in the longer times in Fig. 8 (c). Meanwhile, the evolution curves of QD, GQD and CC shift down, and the amplitudes of QD, GQD and CC become smaller with time going on. Compared with the entanglement, the sudden deaths and births of QD, GQD and CC may still occur during their evolution. It has been seen that the time intervals for the SD and SB of CC become longer with rising the intensity-dependent coupling.

5 Conclusions

In summary, we have investigated the time-dependent dynamics of quantum entanglement, quantum correlations and classical correlation in a system of two coupled two-level atoms interacting with a single mode thermal field to be regarded as a small external environment. By using four methods of measurement, the effects of the mean photon number of the thermal field, the coupling strength between the second atom and the thermal field and intensity-dependent coupling on the evolution behavior of C, QD, GQD and CC between two atoms are explored in detail. It has been shown that the amplitudes of the entanglement, the quantum and classical correlations degrade clearly with increasing the mean photon number of the thermal field, the coupling strength between the second atom and the thermal field and intensity-dependent coupling. The phenomena of the sudden deaths and births of the various correlations (entanglement, quantum and classical correlation) may be observed under the certain parameters’ conditions. It has been also found that there are still non-classical correlations measured by QD and GQD in some time intervals in the absence of entanglement, and the time evolution of CC are different from those of C, QD and GQD during the whole evolution. In addition, it has been pointed out that the maximal values of C, QD, GQD and CC become the less and less and the more peaks of them appear when the intensity-dependent coupling f(n) increases.