1 Introduction

Quantum entanglement and quantum correlation as an important resource in quantum information directly affects the efficiency and reliability of the quantum information processing, it is widely used in the field of quantum communication and quantum computing [1]. These two concepts of quantum entanglement and quantum correlation are closely related and differentiated. Each subsystem of a composite system in the measurement before don’t have a certain states, and once to measure makes it one of the subsystem collapse to a certain state, the other subsystems will collapse into the corresponding certain state, this phenomenon is quantum entangled. Through statistical measurement results of a subsystem, can get about the possibility of another subsystem information of the test results, This is the true meaning of the quantum correlation. Quantum entanglement cannot depict all the quantum correlation of a quantum system. The quantum entanglement exists there must be the quantum correlation. Even when entanglement is zero in a system, quantum correlation can still be finite. Whereupon, based on mutual information theory, think about classic mutual information there was a difference in the field of extend to the quantum, Olliver et al proposed the concept of quantum discord [2]. The quantum discord characterizes non-classical of correlations in quantum mechanics, similar to the entanglement, quantum discord can also capture the fundamental features of quantum states. Since the quantum discord is put forward, and soon it has been found the non-classical correlations are more widespread than the entanglement. The quantum discord was investigated quite intensively in recent years [3,4,5,6,7,8,9,10]. In practice, due to the quantum discord maximize involved in the calculation process, and it is difficult to get the analytic expression. In order to overcome this difficulty, Dakic et al. [11] put forward a new method of measuring quantum correlations, namely the geometrical quantum discord(GQD). The GQD is the use of between a given state and quantum discord for zero state the smallest Hilbert-schmidt distance of the definition. So far, some new research progress has been made for the GQD in different quantum system [12,13,14]. In the past work [15, 16], we studied the GQD and the entanglement dynamics of a quantum system which consists two two-level entangled atoms and the binomial optical field. In this paper, we investigate the quantum correlation and the quantum entanglement in a system of arbitrary two qubit atoms interacting with the coherent state optical field. For our purpose, we use the three criterions of the concurrence and the negative eigenvalue and the geometric quantum discord to measure the quantum correlation and the quantum entanglement between the two atoms by the means of numerical calculations. This paper is organized as follows. In the next section, we give our theoretical model and time-dependence wave function. In Section 3, we investigate the concurrence and the negative eigenvalue and the GQD of between two atoms. In Section 4, as examples we work out the concurrence and the negative eigenvalue and the GQD for three types of initial state of two atoms. We also are discussed numerical results. Finally, our results are summarized in Section 5.

2 Theoretical Model and Time-Dependence Wave Function

Consider a system composed of two identical two-level atoms resonantly interacting with a single-mode coherent state optical cavity simultaneously. Assume that the distance between atoms is greater than the wavelength of the cavity field, the dipole-dipole interaction between atoms can be neglected, and there are same couplings of the two atoms interacting with a coherent state optical field. Under these conditions, the Hamiltonian of the system in the rotating wave approximation can be written as \((\hbar = 1)\) [17]

$$\begin{array}{@{}rcl@{}} H={\Omega} a^{+}a+\frac{1}{2}\omega\sum\limits_{i=1}^{2}{\sigma_{i}^{z}}+g\sum\limits_{i=1}^{2} (a^{+}\sigma_{i}^{-}+a\sigma_{i}^{+}). \end{array} $$
(1)

Where a + and a are the creation and annihilation operators of the field mode of frequency Ω, ω is the atomic transition frequency, \({{\sigma _{i}^{z}}=|e_{i}\rangle \langle e_{i}|}\), \({\sigma _{i}^{+}=|e_{i}\rangle \langle g_{i}|}\), \({\sigma _{i}^{-}=|g_{i}\rangle \langle e_{i}|}\) are the inversion, rise and drop operators of i t h atom (i = 1,2), respectively. |e〉 denotes an excited state of atom, |g〉 denotes a ground state of atom, g is the atom-field coupling constant. For simplicity, we consider the resonant case (Ω = ω).

Let us suppose that the two atoms is initially prepared in two qubit state

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=a|e_{1}, e_{2}\rangle+b|g_{1}, g_{2}\rangle+c|e_{1}, g_{2}\rangle+d|g_{1}, e_{2}\rangle, \end{array} $$
(2)

where |a|2 + |b|2 + |c|2 + |d|2 = 1, the radiation field is initially prepared in a single-mode coherent state

$$\begin{array}{@{}rcl@{}} |{\Psi}_{f}(0)\rangle=\sum\limits_{n=0}^{\infty}F_{n}|n\rangle=\sum\limits_{n=0}^{\infty}e^{-\frac{1}{2}|\alpha|^{2}}\frac{\alpha^{n}}{\sqrt{n!}}|n\rangle, \end{array} $$
(3)

where α = |α|e iφ, |α| is the photon number of the mean square fluctuations of the coherent field, and φ is the phase angle of the coherent field (for convenience, we take φ = 0).

When two atoms interact with light field, the system state vector at any time evolved into

$$\begin{array}{@{}rcl@{}} |{\Psi}_{s}(t)\rangle=|\Re_{1}\rangle|e_{1},e_{2}\rangle +|\Re_{2}\rangle|g_{1},g_{2}\rangle +|\Re_{3}\rangle|e_{1},g_{2}\rangle +|\Re_{4}\rangle|g_{1},e_{2}\rangle. \end{array} $$
(4)

Over here

$$\begin{array}{@{}rcl@{}} |\Re_{1}\rangle&=&\sum\limits_{n=0}^{\infty}A(n,t)|n\rangle,\qquad |\Re_{2}\rangle=\sum\limits_{n=0}^{\infty}B(n,t)|n\rangle,\\ |\Re_{3}\rangle&=&\sum\limits_{n=0}^{\infty}C(n,t)|n\rangle,\qquad |\Re_{4}\rangle=\sum\limits_{n=0}^{\infty}D(n,t)|n\rangle. \end{array} $$
(5)

The initial conditions are A(n,0) = a F(n),B(n,0) = b F(n),C(n,0) = c F(n), D(n,0) = d F(n). In the interaction picture, the evolution of the state vector of the system obeys the Schrödinger equation

$$\begin{array}{@{}rcl@{}} i\frac{\partial}{\partial t}|{\Psi}_{s}(t)\rangle=H_{I}|{\Psi}_{s}(t)\rangle. \end{array} $$
(6)

Based on the initial condition, the solution of the Schrödinger equation is given by

$$\begin{array}{@{}rcl@{}} A(n,t)&=&aF_{n}-i\sqrt{\frac{n+1}{2(2n+3)}}(c+d)F_{n+1}\sin(\sqrt{2(2n+3)}g t)\\ &&-\,\sqrt{\frac{n+1}{2(2n+3)}}\left[\sqrt{\frac{2(n+1)}{2n+3}}aF_{n}+\sqrt{\frac{2(n+2)}{2n+3}}bF_{n+2}\right]\\ &&\times\, \left[1-\cos(\sqrt{2(2n+3)}g t)\right],\qquad n=0,1,2,\ldots, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} B(n,t)&=&bF_{n}-i\sqrt{\frac{n}{2(2n-1)}}(c+d)F_{n-1}\sin(\sqrt{2(2n-1)}g t)\\ &&-\,\sqrt{\frac{n}{2(2n-1)}}\left[\sqrt{\frac{2(n-1)}{2n-1}}aF_{n-2}+\sqrt{\frac{2n}{2n-1}}bF_{n}\right]\\ &&\times \,\left[1-\cos(\sqrt{2(2n-1)}g t)\right],\qquad n=2,3,4,\ldots,\\ B(1,t)&=&bF_{1}\sin(\sqrt{2}g t)-i\frac{1}{\sqrt{2}}(c+d)F_{0}\cos(\sqrt{2}g t),\\ B(0,t)&=&bF_{0}. \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} C(n,t)&=&\frac{1}{2}(c-d)F_{n}+\frac{1}{2}(c+d)F_{n}\cos(\sqrt{2(2n+1)}g t)\\ &&-\,i\frac{1}{2}\left[\sqrt{\frac{2n}{2n+1}}aF_{n-1}+\sqrt{\frac{2(n+1)}{2n+1}}bF_{n+1}\right]\\ &&\times \,\sin(\sqrt{2(2n+1)}g t),\qquad n=1,2,3,\ldots,\\ C(0,t)&=&\frac{1}{2}(c-d)F_{0}+\frac{1}{2}(c+d)F_{0}\cos(\sqrt{2}g t)\\ &&-\,i\frac{1}{2}\sqrt{2}bF_{1}\sin(\sqrt{2}g t). \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} D(n,t)&=&-\frac{1}{2}(c-d)F_{n}+\frac{1}{2}(c+d)F_{n}\cos(\sqrt{2(2n+1)}g t)\\ &&-\,i\frac{1}{2}\left[\sqrt{\frac{2n}{2n+1}}aF_{n-1}+\sqrt{\frac{2(n+1)}{2n+1}}bF_{n+1}\right]\\ &&\times \,\sin(\sqrt{2(2n+1)}g t),\qquad n=1,2,3,\ldots,\\ D(0,t)&=&-\frac{1}{2}(c-d)F_{0}+\frac{1}{2}(c+d)F_{0}\cos(\sqrt{2}g t)\\ &&-\,i\frac{1}{2}\sqrt{2}bF_{1}\sin(\sqrt{2}g t). \end{array} $$
(10)

3 Entanglement and Correlation Between the Two Atoms

We assumed that the two two-level atoms is initially prepared in a two qubit state, and the coherent field is initially prepared in a coherent state. Thus we can know that the atoms and the light field is initially in a non-entangled pure state. Using the three criterions of the concurrence and the negative eigenvalue and the geometrical quantum discord, we study the quantum entanglement and quantum correlation dynamic characteristic between the two two-level atoms.

  1. 1.

    The concurrence of between two atoms

    The concurrence is a measure of the entanglement of two bodies, it is suitable for both pure and mixed states, and is a common method to measure the entanglement between 2 × 2 system. For the 2 × 2 system described by the density matrix ρ, the degree of entanglement is defined as [18]

    $$\begin{array}{@{}rcl@{}} C(t)=\max\left\{0,\sqrt{\lambda_{1}}-\sqrt{\lambda_{2}}-\sqrt{\lambda_{3}}-\sqrt{\lambda_{4}}\right\}. \end{array} $$
    (11)

    Where λ 1 ≥ λ 2 ≥ λ 3 ≥ λ 4 is square root of eigenvalue of matrix M.

    $$\begin{array}{@{}rcl@{}} M=\hat{\rho}(\hat{\sigma_{y}}\otimes\hat{\sigma_{y}})\hat{\rho}^{\ast}(\hat{\sigma_{y}}\otimes\hat{\sigma_{y}}). \end{array} $$
    (12)

    Here \(\hat {\rho }^{\ast }\) denotes the complex conjugate of the density matrix \(\hat {\rho }\) and \(\hat {\sigma _{y}}\) is the Pauli matrix. It is shown that concurrence ranges from C(t) = 0 for a separable state and C(t) = 1 for a maximally entangled state.

  2. 2.

    The negative eigenvalue of between two atoms

    The negative eigenvalues of partial transposition of density matrix is a measurement of the degree of entanglement between the two subsystems. Consider a density matrix \({\hat {\rho }(t)}\) and its partial transposition \({\hat {\rho }^{T}(t)}\) for a systems of two spin-1/2, the measure of entanglement E(t) is then defined by [19, 20]

    $$\begin{array}{@{}rcl@{}} E(t)=-2\sum\limits_{i=1}\mu_{i}^{-}. \end{array} $$
    (13)

    Here \({\mu _{i}^{-}}\) is a negative eigenvalue of \({\hat {\rho }^{T}(t)}\). Then E(t) = 0 denotes that two atoms are separated. Then E(t) = 1 denotes that two atoms are in the maximum entangled state. Then 0 < E(t) < 1 denotes that two atoms are in entanglement state.

  3. 3.

    The GQD of between two atoms

    Therefore the GQD for two body systems is [11]

    $$\begin{array}{@{}rcl@{}} D(t)=\frac{1}{4}(\parallel A \parallel^{2}+\parallel P \parallel^{2}-K_{max}), \end{array} $$
    (14)

    here \(\parallel A \parallel ^{2}={\sum }_{i=1}^{3}{A_{i}^{2}}\), P = P i j is a matrix, ∥ P∥2 = T r(P T P), K m a x is the largest eigenvalue of the matrix K = A A T + P P T, superscript T denotes transpose of vector A or matrix P.

4 Numerical Results and Discussion

In this section, we will discuss the numerical calculation results of the C(t) and the E(t) and the D(t) given by (11), (13) and (14), when the atoms are initially in different state and different photon number of the mean square fluctuations. Industry to show that [15, 16, 21, 22], when and only when the two atoms are initially in the maximally entangled state \(|{\Psi }_{a}(0)\rangle =\frac {1}{\sqrt {2}}[|e_{1}, g_{2}\rangle -|g_{1}, e_{2}]\rangle \), the temporal evolution of the C(t) and the E(t) and the D(t) are not affected by the parameters, and always keep in is a fixed value, respectively. When the atoms are in the following three types of initial state, quantum properties of the system is significant. Namely

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle&=&\frac{1}{\sqrt{2}}[|e_{1}, e_{2}\rangle+|g_{1}, g_{2}]\rangle,\\ |{\Psi}_{a}(0)\rangle&=&|e_{1}, e_{2}\rangle,\\ |{\Psi}_{a}(0)\rangle&=&\frac{1}{2}[|e_{1}, e_{2}\rangle+|g_{1}, g_{2}\rangle+|e_{1}, g_{2}\rangle+|g_{1}, e_{2}\rangle]. \end{array} $$
(15)

The following mainly aimed at the above three kinds of initial condition were studied.

Case 1. :

We assume the two atoms are initially in the entangled state

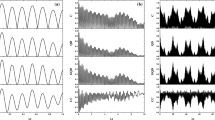
$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{\sqrt{2}}[|e_{1}, e_{2}\rangle+|g_{1}, g_{2}\rangle], \end{array} $$
(16)

the temporal evolution of the C(t) and the E(t) and the D(t) is shown as Figs. 1, 2 and 3.

Figures 1–3 are time evolution of the C(t) and the E(t) and the D(t) versus different |α| for the atoms are initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{\sqrt {2}}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle ]\), respectively. Here, photon number of the mean square fluctuations is |α| = 0.5,3.0,5.5,8.0. It is shown that: (1) The oscillation of the temporal evolution of the C(t) and the E(t) and the D(t) three factors has larger range and irregularity for smaller |α| value; (2) When we increase |α| value, the oscillation frequency speeds up the temporal evolution of three factors. On the other hand, oscillation of three factors is in a smaller range, and shows up regularity. This phenomenon shows that |α| value that is increased can lead to the entanglement weakened or even disentanglement.

Case 2. :

In case of the initial states of the two atoms are

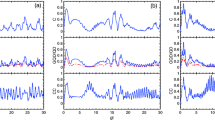
$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=|e_{1}, e_{2}\rangle. \end{array} $$
(17)

Similarly, we can see that two two-level atoms is in non-entangled state, the temporal evolution curves of the C(t) and the E(t) and the D(ρ(t)) between two atoms are shown in Figs. 4, 5 and 6.

In Figs. 4–6, the parameters of the photon number of the mean square fluctuations |α| is the same as Figs. 1– 3, that two two-level atoms is |Ψ a (0)〉 = |e 1,e 2〉. From Figs. 4–6, it is observed that the two two-level atoms are in non-entangled state, but have quantum correlation.

Case 3. :

Suppose the initial states of the two atoms are

$$\begin{array}{@{}rcl@{}} |{\Psi}_{a}(0)\rangle=\frac{1}{2}[|e_{1}, e_{2}\rangle+|g_{1}, g_{2}\rangle+|e_{1}, g_{2}\rangle+|g_{1}, e_{2}\rangle]. \end{array} $$
(18)

That is to say the two atoms are initially in a arbitrary two qubit states. Time evolution of the C(t) and the E(t) and the D(t) is shown as Figs. 7, 8 and 9.

Fig. 1
figure 1

Evolution of the C(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{\sqrt {2}}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 2
figure 2

Evolution of the E(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{\sqrt {2}}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 3
figure 3

Evolution of the D(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{\sqrt {2}}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 4
figure 4

Evolution of the C(t) with scaled time gt versus different |α| for the atoms initially in |Ψ a (0)〉 = |e 1,e 2〉. a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 5
figure 5

Evolution of the E(t) with scaled time gt versus different |α| for the atoms initially in |Ψ a (0)〉 = |e 1,e 2〉. a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 6
figure 6

Evolution of the D(t) with scaled time gt versus different |α| for the atoms initially in |Ψ a (0)〉 = |e 1,e 2〉. a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 7
figure 7

Evolution of the C(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{2}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle +|e_{1}, g_{2}\rangle +|g_{1}, e_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 8
figure 8

Evolution of the E(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{2}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle +|e_{1}, g_{2}\rangle +|g_{1}, e_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image
Fig. 9
figure 9

Evolution of the D(t) with scaled time gt versus different |α| for the atoms initially in \(|{\Psi }_{a}(0)\rangle =\frac {1}{2}[|e_{1}, e_{2}\rangle +|g_{1}, g_{2}\rangle +|e_{1}, g_{2}\rangle +|g_{1}, e_{2}\rangle ]\). a |α| = 0.5; b |α| = 3.0; c |α| = 5.5; d |α| = 8.0

Full size image

In Case 3, under certain parameters, the temporal evolution of the C(t) and the E(t) and the D(t) is obtained in Figs. 7–9. However, under the condition that two two-level atoms is initially in arbitrary two qubit states, the temporal evolution of the C(t) and the E(t) and the D(t), is dependence of the change of the parameter of photon number of the mean square fluctuations |α|.

5 Conclusions

In this paper, we have studied the concurrence and the negative eigenvalue and the geometric quantum discord evolution properties of the coherent field interacting with two qubit atoms. The influence of photon number of the mean square fluctuations on the temporal evolution of the concurrence and the negative eigenvalue and the geometrical quantum discord between two atoms are discussed for the two atoms are initially in specific three states, respectively. The result shows that two atoms always exist the correlation for different photon number of the mean square fluctuations. In addition, the temporal evolution of the concurrence and the negative eigenvalue and the geometrical quantum discord between the two atoms is always dependence of the change of photon number of the mean square fluctuations. The photon number of the mean square fluctuations can lead to the entanglement weakened or even disentanglement.