1 Introduction

In quantum mechanics a physical system is described by its wave function (i.e., quantum state), whose knowledge allows us to make predictions about the odds of the results of any measurement executed on the system. Also, all physical properties associated with the system can be derived from its wave function. The protocol of quantum teleportation proposed by Bennett et al. in 1993 [1] is to transmit the unknown wave function describing a system in one location (sender) to another system in a different place (receiver). At the end of the protocol the sender’s system is no longer described by its original wave function, while now describes the receiver’s system. In this process, the unknown wave function does not travel through the quantum channel, so this process does not have any classical analogue, and unconditional security of quantum key distribution [2] has been established [3]. The magical characteristics of quantum entanglement can be verified by using Bell theory [4, 5]. So far, quantum teleportation has drawn much attention of the scientific community, and consequently, a lot of generalized teleportation schemes such as schemes for quantum secret sharing [6,7,8,9,10], controlled teleportation [11,12,13], hierarchial quantum state sharing [15,15,16,17,18,19,20], quantum state preparation [21,22,23,24] have been presented. All these schemes may be viewed as modified teleportation protocols and can be verified by using recent nonlinear Bell inequalities [25,26,27]. Besides theoretical researches, some experimental performances [28,29,30] of quantum teleportation have been reported. Particularly, based on the hyper-entanglement Bell-state analysis, quantum teleportation can be extended for multiple degrees of freedom of a single photon encoding in the polarization and spatial modes degrees of freedom [31, 32]. Recently, the experiment realization of quantum teleportation of multiple degrees of freedom of a single photon encoding in the polarization and orbital angular momentum was reported [33].

The original scheme of quantum teleportation was a one-way scheme in which Alice transmits an unknown single-qubit wave function to Bob without sending any physical particle but with the aid of the previously shared entanglement and local operation as well as classical communication (LOCC). Subsequently, it was modified by Huelga et al. [34, 35] and others to get schemes for bidirectional quantum state teleportation (BST), where both Alice and Bob can simultaneously teleport unknown wave functions to each other. Recently, Zha et al. [36] extended the idea of BST and put forward the scheme of bidirectional controlled quantum teleportation (BCQT). In their scheme, Alice and Bob can simultaneously send a single-qubit unknown wave function to each other under the control of the supervisor Charlie. Soon after, Shukla [37], Chen [38], Dean [39] and Zhang [40] independently put forward a series of deterministic BCQT protocols. In these schemes, Alice and Bob can simultaneously exchange their unknown wave functions as in BST, but could not reconstruct the state received by them until the supervisor Charlie allows them to do so. Most notably, Shukla et al. [37] discussed some potential application of BCQT schemes in relation with the implementation of quantum remote control and quantum cryptography. As a generalization of BCQT, Peng et al. [41] proposed a protocol of bidirectional quantum states sharing.

In this paper, we propose a general procedure to investigate the possibility of an annular controlled teleportation (ACT), which is a generalization of bidirectional controlled quantum teleportation. The goal of ACT is as follows: under the control of the supervisor Bob, Alice1 transfers the wave function \( \mid {\xi}_1\Big\rangle {}_{A_1} \) to Alice2, Alice2 transfers the wave function \( \mid {\xi}_2\Big\rangle {}_{A_2} \) to Alice3, ⋯, Alicen transfers the wave function \( \mid {\xi}_n\Big\rangle {}_{A_n} \) to Alice1. We use a seven-qubit cluster state and a nine-qubit entangled state as the quantum channel respectively to illustrate the feasibility of our approach. Our schemes are easily modified into some hybrid versions of several different teleportations.

The rest of this paper is organized as follows. In Section 2, we described a generalized approach to study the possibility of ACT using (2n + 1)-qubit entangled state as quantum state and as examples we explicitly show that ACT is possible using seven-qubit cluster state and nine-qubit entangled state. Finally, discussion and summary are given in Section 3.

2 A Generalized for Annular Controlled Teleportation

As we all know, any arbitrary quantum entangled state \( \mid \mathcal{G}\Big\rangle \) can be written in the following form

$$ \mid \mathcal{G}\Big\rangle =\frac{1}{\sqrt{2}}\left(|a\Big\rangle {}_C|\mathcal{G}\Big\rangle {}_1+|b\Big\rangle {}_C|\mathcal{G}\Big\rangle {}_2\right), $$
(1)

where single-qubit states |a〉C and |b〉C satisfy 〈a|b〉 = δa, b, \( \mid \mathcal{G}\Big\rangle {}_1 \) and \( \mid \mathcal{G}\Big\rangle {}_2 \) are arbitrary states. Under certain conditions, \( \mid \mathcal{G}\Big\rangle {}_1 \) and \( \mid \mathcal{G}\Big\rangle {}_2 \) can be decomposed into the products of some quantum states.

Let us now start describing our protocol. Suppose that there are n + 1 legitimate users, say Alicei (i = 1,2,⋯ , n) and Bob. For any i ∈{1,2,⋯ , n}, Alicei has an arbitrary unknown single-qubit state, which is given by

$$ \mid {\xi}_i\Big\rangle {}_{A_i^{\prime }}=\frac{1}{\sqrt{2}}{\left({x}_i|0\Big\rangle +{y}_i|1\Big\rangle \right)}_{A_i^{\prime }}, $$
(2)

where the complex coefficients xi and yi satisfy the normalization condition |xi|2 + |yi|2 = 1.

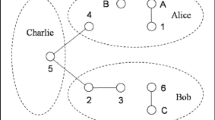
Under the control of the supervisor Bob, Alicei wishes to teleport the state of qubit \( {A}_i^{\prime } \) to Alicei+ 1 for any i ∈{1,2,⋯ , n}, and the convention Alicen+ 1 ≡ Alice1, as shown in Fig. 1. Obviously, the whole transmission route forms a closed ring, so we call it a annular controlled teleportation (ACT). It is clear that annular controlled teleportation is a generalization of bidirectional controlled teleportation.

Fig. 1
figure 1

A schematic transmission procedure of controlled cyclic teleportation

Full size image

Assume that these legitimate participants pre-share a (2n + 1)-qubit state of the form:

$$ \mid \mathcal{\mathscr{H}}\Big\rangle =\frac{1}{\sqrt{2}}\left(|a\Big\rangle {}_B\underset{i=1}{\overset{n}{\otimes }}|{\psi}_i\Big\rangle {}_{A_i{A}_{i+1}}\pm |b\Big\rangle {}_B\underset{i=1}{\overset{n}{\otimes }}|{\psi}_i^{\prime}\Big\rangle {}_{A_i{A}_{i+1}}\right), $$
(3)

where single-qubit states |a〉B and |b〉B satisfy 〈a|b〉 = δa, b, and \( \mid {\psi}_i\left\rangle, \mid {\psi}_i^{\prime}\right\rangle \in \left\{|{\Phi}^{+}\Big\rangle, |{\Phi}^{-}\Big\rangle, |{\Psi}^{+}\Big\rangle, |{\Psi}^{-}\Big\rangle \right\} \), \( \mid {\psi}_i\left\rangle \ne \mid {\psi}_i^{\prime}\right\rangle \) for any i ∈{1,2,⋯ , n}, \( \mid {\Phi}^{\pm}\left\rangle =\left(|00\Big\rangle \pm |11\Big\rangle \right)/\sqrt{2},\mid {\Psi}^{\pm}\right\rangle =\left(|01\Big\rangle \pm |10\Big\rangle \right)/\sqrt{2} \), and the convention An+ 1 ≡ A1. The subscripts Ai and B indicate the qubits of Alicei and Bob respectively. Thus \( \mid {\psi}_i\left\rangle, \mid {\psi}_i^{\prime}\right\rangle \) are the Bell states. The condition

$$ \mid {\psi}_i\left\rangle \ne \mid {\psi}_i^{\prime}\right\rangle, \kern2.00em i\in \left\{1,2,\cdots \kern0.3em ,n\right\} $$
(4)

ensures that Bob’s qubit is appropriately entangled with remaining 2n qubits. By appropriately entangled we mean that unless Bob measures his qubit in basis {|a〉,|b〉} and discloses the outcome, All Alice are unaware of the entangled states they share and consequently the receiver does not know upon the receipt of the measurement outcome of the sender which unitary operation is to be applied. In case \( \mid {\psi}_i\left\rangle =\mid {\psi}_i^{\prime}\right\rangle \) (1 ≤ i ≤ n) is allowed then the qubits of the state |ψi〉 are separable from the remaining qubits and consequently Bob has no control over the teleportation done using those two qubits. Now when the state (3) satisfies the condition (4) then on the disclosure of the outcome of Bob’s measurement on basis {|a〉,|b〉}, all Alice know with certainty which a set of Bell states they share and consequently they can use the conventional teleportation scheme to teleport unknown quantum states.

To accomplish this quantum task, we need to design the following three steps:

  1. (i)

    Each Alicei does a Bell-state measurement on her qubit pair \( \left({A}_1^{\prime },{A}_1\right) \), and tells Alicei+ 1 the measurement outcome by sending 2-cbit message.

  2. (ii)

    Bob performs a single-qubit measurement on his qubit B in basis {|a〉,|b〉}, and informs all the Alice of his measurement result by sending 1-cbit message.

  3. (iii)

    For any i ∈{1,2,⋯ , n}, Alicei+ 1 executes an appropriate operation to reconstruct Alicei’s quantum state \( \mid {\xi}_1\Big\rangle {}_{A_i^{\prime }} \) in accordance with the messages of Alicei and Bob.

Obviously, the task of ACT can been achieved successfully, and the probability of success is unit. This provides us the basic framework to investigate the possibilities of ACT in different quantum states. In the following subsections we will consider two specific cases and explicitly show that the above framework can be used to establish that ACT is possible with seven-qubit cluster staye and nine-qubit entangled state.

2.1 Case I: \( \mid \mathcal{\mathscr{H}}\Big\rangle \) is Seven-Qubit Cluster State

In 2001, Briegel and Raussendorf [31] introduced a kind of entangled state named as a cluster state, which can be created efficiently in any system with an Ising-type interaction, and the expression of one-dimensional cluster states can be written in the form as follows

$$ \mid {\mathcal{C}}_n\Big\rangle =\frac{1}{2^{n/2}}\underset{j=1}{\overset{n}{\otimes }}\left(|0\Big\rangle {}_j{\sigma}_z^{\left(j+1\right)}+|1\Big\rangle {}_j\right), $$
(5)

where σz = |0〉〈0|−|1〉〈1|, and the convention \( {\sigma}_z^{\left(n+1\right)}=I \). For n = 7, the cluster state can be given by

$$ \mid {\mathcal{C}}_7\left\rangle =\frac{1}{2\sqrt{2}}\right(\mid 0000000\left\rangle +\mid 1110000\right\rangle +\mid 1001100\left\rangle +\mid 0111100\right\rangle $$
(6)
$$ \kern2em +\mid 1000011\left\rangle +\mid 0110011\right\rangle +\mid 0001111\left\rangle +\mid 1111111\right\rangle \Big), $$
(7)

which has recently been used as a quantum channel for implementing bidirectional controlled teleportation [43]. The cluster states share the properties of both the GHZ states and W class entangled states. However, they still have some unique properties. For example, they have a large persistency of entanglement, that is, they (in the case of n > 4) are harder to be destroyed by local operations than GHZ class states.

Now, we describe our scheme as follows. Suppose that there are four legitimate users, say Alice, Bob, Charlie and David. Alice has an arbitrary unknown single-qubit state, which is given by

$$ \mid \xi \Big\rangle {}_A={\left(a|0\Big\rangle +b|1\Big\rangle \right)}_A, $$
(8)

at the same time, Bob has qubit B in an unknown state:

$$ \mid \eta \Big\rangle {}_B={\left(x|0\Big\rangle +y|1\Big\rangle \right)}_B $$
(9)

and Charlie has an arbitrary unknown state

$$ \mid \gamma \Big\rangle {}_C={\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_C, $$
(10)

where the complex coefficients a, b, x, y, α and β satisfy |a|2 + |b|2 = 1, |x|2 + |y|2 = 1 and |α|2 + |β|2 = 1.

Now, under the control of the supervisor David, Alice wants to transmit the state of qubit A to Bob, Bob intends to transmit the state of qubit B to Charlie and Charlie wants to transmit the state of qubit C to Alice. Obviously, this task requires to synchronously and circlewise transmit their quantum states, we call it the annular controlled teleportation (ACT). Assume that Alice, Bob, Charlie and David share a seven-qubit cluster state, which can be written as

$$ |{\mathcal{C}}_7\left\rangle {}_{D{A}_1{B}_1{B}_2{C}_1{C}_2{A}_2} =\frac{1}{2\sqrt{2}}\right(\mid 0000000\left\rangle +\mid 1110000\right\rangle +\mid 1001100\left\rangle +\mid 0111100\right\rangle $$
(11)
$$ \kern9.4em +\kern-.12em \mid 1000011\left\rangle \kern-.12em +\kern-.12em \mid 0110011\right\rangle \kern-.15em +\kern-.15em \mid 0001111\left\rangle \kern-.15em +\kern-.15em \mid 1111111\right\rangle \Big){}_{D{A}_1{B}_1{B}_2{C}_1{C}_2{A}_2} $$
(12)

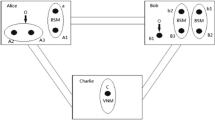
where the subscripts denote different qubits. In advance, these qubits are assumed to be safely distributed among all legitimate users; i.e., Alice has the the qubit pair (A1, A2), Bob the qubit pair (B1, B2), Charlie the qubit pair (C1, C2) and David the single-qubit D, respectively.

The initial state of the total system can be written as

$$ |\mathcal{T}\left\rangle = \mid \xi \right\rangle {}_A\otimes \mid \eta \left\rangle {}_B\otimes \mid \gamma \right\rangle {}_C\otimes \mid {\mathcal{C}}_7\Big\rangle {}_{D{A}_1{B}_1{B}_2{C}_1{C}_2{A}_2} $$
(13)
$$ = \sum \limits_{i,j,m,n,s,t=1}^2{\left(-1\right)}^{i\left(i+j\right)+m\left(m+n\right)+s\left(s+t\right)}\mid {\mathcal{B}}_{i,j}\left\rangle {}_{A{A}_1}\mid {\mathcal{B}}_{m,n}\right\rangle {}_{B{B}_2}\mid {\mathcal{B}}_{s,t}\Big\rangle {}_{C{C}_2} $$
(14)
$$ \kern3.5em \otimes \left\{{\sigma}_{B_1}^{\left(i,j\right)}{\sigma}_{C_1}^{\left(m,n\right)}{\sigma}_{A_2}^{\left(s,t\right)}{\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2}\mid {\mathcal{X}}_0\right\rangle {}_D $$
(15)
$$ \kern4em +{\sigma}_{B_1}^{\left(1\kern0.10em -i,1-j\right)}{\sigma}_{C_1}^{\left(1-m,1-n\right)}{\sigma}_{A_2}^{\left(1-s,1\kern0.10em -t\right)}{\left(a|0\Big\rangle \kern-.1em +\kern-.1em b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle \kern-.12em +\kern-.12em y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle \kern-.12em +\kern-.12em \beta |1\Big\rangle \right)}_{A_2}\mid {\mathcal{X}}_1\left\rangle {}_D\right\} $$
(16)

where

$$ \left\{\mid, {\mathcal{B}}_{i,j},\left\rangle, =,\frac{1}{\sqrt{2}},\right[,{\left(-1\right)}^i,\mid, i,,,j,\left\rangle, +,\mid, 1,\oplus, i,,,1,\oplus, j,\right\rangle, \Big],:,i,,,j,=,0,,,1\right\} $$
(17)

is Bell-state basis with ⊕ is the modulo-2-sum, the unitary operation

$$ {\sigma}^{\left(i,j\right)}={\left(-1\right)}^i\mid i\left\rangle \left\langle j|+|1-i\right\rangle \right\langle 1-j\mid \kern2.00em \left(i,j=0,1\right) $$
(18)

is usual Pauli operation, and the set

$$ \left\{\mid, {\mathcal{X}}_k,\left\rangle, =,\frac{1}{\sqrt{2}},\right[,{\left(-1\right)}^k,\mid, k,\left\rangle, +,\mid, 1,\oplus, k,\right\rangle, \Big],:,k,=,0,,,1\right\} $$
(19)

is a single-qubit basis.

In order to achieve the purpose of annular controlled teleportation task, Alice, Bob and Charlie firstly implement a Bell-state measurement on qubit pairs (A, A1), (B, B2) and (C, C2), respectively, and then Alice, Bob and Charlie notify Bob, Charlie and Alice of their measurements in turn by sending the 6-cbit messages (i, j), (m, n) and (s, t), respectively. As a priori agreement, the 6-cbit messages (i, j), (m, n) and (s, t) correspond to the Bell-states \( \mid {\mathcal{B}}_{i,j}\left\rangle {}_{A{A}_1}\mid {\mathcal{B}}_{m,n}\right\rangle {}_{B{B}_2} \) and \( \mid {\mathcal{B}}_{s,t}\Big\rangle {}_{C{C}_2} \), respectively, and vice versa.

After these measurements, the state of qubits B1, C1, A2 and D collapses one of the following states

$$ \begin{array}{rcl} |\mathcal{Q}\rangle_{ijmnst}&=&\sigma^{(i,j)}_{B_{1}}\sigma^{(m,n)}_{C_{1}}\sigma^{(s,t)}_{A_{2}} (a|0\rangle+b|1\rangle)_{B_{1}}(x|0\rangle+y|1\rangle)_{C_{1}}\\ &\otimes&(\alpha|0\rangle+\beta|1\rangle)_{A_{2}}|\mathcal{X}_{0}\rangle_{D} +\sigma^{(1-i,1-j)}_{B_{1}}\sigma^{(1-m,1-n)}_{C_{1}}\sigma^{(1-s,1-t)}_{A_{2}}\\ &\times &(a|0\rangle+b|1\rangle)_{B_{1}}(x|0\rangle+y|1\rangle)_{C_{1}} (\alpha|0\rangle+\beta|1\rangle)_{A_{2}}|\mathcal{X}_{1}\rangle_{D}, \end{array} $$
(20)

where i, j, m, n, s, t ∈{0,1}. Notice that, although they received the 6-qubit messages and henceforth know the state of qubits B1, C1 and A2 should be either \( \mid \Omega \Big\rangle {}_0={\sigma}_{B_1}^{\left(i,j\right)}{\sigma}_{C_1}^{\left(m,n\right)}{\sigma}_{A_2}^{\left(s,t\right)}{\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2} \) or \( \mid \Omega \Big\rangle {}_1={\sigma}_{B_1}^{\left(1-i,1-j\right)}{\sigma}_{C_1}^{\left(1-m,1-n\right)}{\sigma}_{A_2}^{\left(1-s,1-t\right)}{\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2} \), they do not clearly know which one it is exactly. This means that if they want to extract the conceivable state |Ω〉0 or |Ω〉1 from \( |\mathcal {Q}\rangle _{ijmnst} \), they must get some further assistance from David. In other words, they must collaborate to conclusively fulfill the ACT task.

If David allows for Alice, Bob and Charlie to reconstruct the initial states |γ〉C, |ξ〉A and |η〉B, respectively, he needs to carry out the single-measurement in the basis of \( \left\{|{\mathcal{X}}_k\Big\rangle =\frac{1}{\sqrt{2}}\left[{\left(-1\right)}^k|k\Big\rangle +|1\oplus k\Big\rangle \right]:k=0,1\right\} \) on qubit D, and tells his measured result to the receivers Alice, Bob and Charlie by sending 1-cbit message k. Likewise, the 1-cbit message k corresponds to the state \( \mid {\mathcal{X}}_k\Big\rangle {}_D \) and vice vera. If David’s measurement outcome is \( \mid {\mathcal{X}}_0\Big\rangle {}_D \), then the state of qubits B1, C1 and A2 collapses into the following state

$$ \mid \Omega \Big\rangle {}_0={\sigma}_{B_1}^{\left(i,j\right)}{\sigma}_{C_1}^{\left(m,n\right)}{\sigma}_{A_2}^{\left(s,t\right)}{\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2}. $$
(21)

After receiving the messages, Alice, Bob and Charlie perform the local operations \( {\sigma}_{A_2}^{\left(s,t\right)} \), \( {\sigma}_{B_1}^{\left(i,j\right)} \) and \( {\sigma}_{C_1}^{\left(m,n\right)} \) on qubits A2, B1 and C1, respectively. The corresponding collapse state of qubits qubits B1, C1 and A2 becomes

$$ {\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2}. $$
(22)

If David’s measurement result is \( \mid {\mathcal{X}}_1\Big\rangle {}_D \), then the state of qubits B1, C1 and A2 collapses into

$$ \mid \Omega \Big\rangle {}_1={\sigma}_{B_1}^{\left(1-i,1-j\right)}{\sigma}_{C_1}^{\left(1-m,1-n\right)}{\sigma}_{A_2}^{\left(1-s,1-t\right)}{\left(a|0\Big\rangle +b|1\Big\rangle \right)}_{B_1}{\left(x|0\Big\rangle +y|1\Big\rangle \right)}_{C_1}{\left(\alpha |0\Big\rangle +\beta |1\Big\rangle \right)}_{A_2}, $$
(23)

Alice, Bob and Charlie need to execute the local operations \( {\sigma}_{A_2}^{\left(1-s,1-t\right)} \), \( {\sigma}_{B_1}^{\left(1-i,1-j\right)} \) and \( {\sigma}_{C_1}^{\left(1-m,1-n\right)} \) on qubits A2, B1 and C1, respectively. After these local operations, we still obtain the same state in (11). This indicates that Alice’s, Bob’s and Charlie’s original states have simultaneously and successfully been transmitted under the control of supervisor David, and the probability of success of our scheme is unit.

Remark 1

  1. (i)

    The existing bidirectional controlled teleportation between Alice and Bob can be viewed as a ring-shaped controlled teleportation consisting of the controlled teleportation from Alice to Bob and the controlled teleportation from Bob to Alice. While our scheme is a ring-shaped controlled teleportation consisting of the controlled teleportation from Alice to Bob, the controlled teleportation from Bob to Charlie and the controlled teleportation from Charlie to Alice. Therefore, our scheme is a generalization of the existing bidirectional controlled teleportation.

  2. (ii)

    In the above scheme, if Charlie does not want to transmit the state |γ〉C to Alice, and he intends to transmit it to Bob, then a deterministic bidirectional controlled teleportation occurs between Charlie and Bob, while the quantum state transmission between Alice and Bob is the standard deterministic controlled teleportation. In the case, our protocol is a hybrid scheme of controlled teleportation and bidirectional controlled teleportation.

2.2 Case II: \( \mid \mathcal{\mathscr{H}}\Big\rangle \) is Nine-Qubit Entangled State

Recently, Li and Jin [44] prepared nine-qubit entangled state and used it as quantum channel to implement bidirectional controlled teleportation of arbitrary two-qubit states. This nine-qubit entangled state has the following form

$$ {\displaystyle \begin{array}{rcl}\mid \Theta \Big\rangle & =& \frac{1}{4\sqrt{2}}\left\{\mid 0\right\rangle {}_1{\left(|00\Big\rangle +|11\Big\rangle \right)}_{23}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{45}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{67}{\left(|00\Big\rangle +|11\Big\rangle \right)}_{89}\\ {}& & +\mid 1\left\rangle {}_1{\left(|01\Big\rangle -|10\Big\rangle \right)}_{23}{\left(|01\Big\rangle -|10\Big\rangle \right)}_{45}{\left(|01\Big\rangle -|10\Big\rangle \right)}_{67}{\left(|01\Big\rangle -|10\Big\rangle \right)}_{89}\right\}.\end{array}} $$
(24)

Now let us describe our scheme as follows. Suppose that Alice has a qubit A in a single-qubit state \( \mid {\zeta}_1\Big\rangle {}_A=\frac{1}{\sqrt{2}}{\left({\alpha}_1|0\Big\rangle +{\beta}_1|1\Big\rangle \right)}_A \), Bob has a qubit B in a single-qubit state \( \mid {\zeta}_2\Big\rangle {}_B=\frac{1}{\sqrt{2}}{\left({\alpha}_2|0\Big\rangle +{\beta}_2|1\Big\rangle \right)}_B \), Charlie has a qubit C in a state \( \mid {\zeta}_3\Big\rangle {}_C=\frac{1}{\sqrt{2}}{\left({\alpha}_3|0\Big\rangle +{\beta}_3|1\Big\rangle \right)}_C \), and David has a qubit D in a single-qubit state \( \mid {\zeta}_4\Big\rangle {}_D=\frac{1}{\sqrt{2}}{\left({\alpha}_4|0\Big\rangle +{\beta}_4|1\Big\rangle \right)}_D \). They pre-share a nine-qubit entangled state \( |\mathcal {Q}\rangle \) in (19) with Ellen, where the qubit pair (2,9) belongs to Alice, qubit pair (3,4) to Bob, qubit pair (5,6) to Charlie, qubit pair (7,8) to David, and qubit 1 to Ellen, respectively. Under the control of the supervisor Ellen, Alice wants to transmit the state |ζ1〉A of qubit A to Bob, Bob wishes to teleport the state |ζ2〉B of qubit B to Charlie, Charlie intents to transmit the state |ζ3〉C of qubit C to David, and David wants to transmit the state |ζ4〉D of qubit D to Alice. The initial state of the total system can be expressed as

$$ \mid \Gamma \left\rangle =\mid \Theta \right\rangle \otimes \mid {\zeta}_1\left\rangle {}_A\otimes \mid {\zeta}_2\right\rangle {}_B\otimes \mid {\zeta}_3\left\rangle {}_C\otimes \mid {\zeta}_4\right\rangle {}_D. $$
(25)

To achieve the ACT, Alice, Bob, Charlie and David simultaneously perform Bell-state measurements on own qubit pairs (A,2), (B,4), (C,6) and (D,8), respectively, and then Alice, Bob, Charlie and David inform Bob, Charlie, David and Alice of their measurement results in turn by sending 8-cbit messages (i, j),(k, l),(m, n) and (s, t), respectively. Before measurement, the initial state of the total system can be rewritten as

$$ {\displaystyle \begin{array}{rcl}\mid \Gamma \Big\rangle & =& \frac{1}{16\sqrt{2}}\sum \limits_{i,j,k,l,m,n,s,t}^2\mid {\mathcal{B}}_{i,j}\left\rangle {}_{A2}\mid {\mathcal{B}}_{k,l}\right\rangle {}_{B4}\mid {\mathcal{B}}_{m,n}\left\rangle {}_{C6}\mid {\mathcal{B}}_{i,j}\right\rangle {}_{D8}\\ {}& & \otimes \Big\{{\left(-1\right)}^{i\left(i+j\right)+k\left(k+l\right)+m\left(m+n\right)+s\left(s+t\right)}{\sigma}_3^{\left(i,j\right)}{\sigma}_5^{\left(k,l\right)}{\sigma}_7^{\left(m,n\right)}{\sigma}_9^{\left(s,t\right)}\\ {}& & \times {\left({\alpha}_1|0\Big\rangle +{\beta}_1|1\Big\rangle \right)}_3{\left({\alpha}_2|0\Big\rangle +{\beta}_2|1\Big\rangle \right)}_5{\left({\alpha}_3|0\Big\rangle +{\beta}_3|1\Big\rangle \right)}_7{\left({\alpha}_4|0\Big\rangle +{\beta}_4|1\Big\rangle \right)}_9\mid 0\Big\rangle {}_1\\ {}& & +{\left(-1\right)}^{\left(1+i+j\right)j+\left(1+k+l\right)l+\left(1+m+n\right)n+\left(1+s+t\right)t}{\sigma}_3^{\left(1\oplus i,j\right)}{\sigma}_5^{\left(1\oplus k,l\right)}{\sigma}_7^{\left(1\oplus m,n\right)}{\sigma}_9^{\left(1\oplus s,t\right)}\\ {}& & \times {\left({\alpha}_1|0\Big\rangle +{\beta}_1|1\Big\rangle \right)}_3{\left({\alpha}_2|0\Big\rangle +{\beta}_2|1\Big\rangle \right)}_5{\left({\alpha}_3|0\Big\rangle +{\beta}_3|1\Big\rangle \right)}_7{\left({\alpha}_4|0\Big\rangle +{\beta}_4|1\Big\rangle \right)}_9\mid 1\left\rangle {}_1\right\}.\end{array}} $$
(26)

It is dependent on the controller Ellen for the situation of that Alice, Bob, Charlie and David reconstruct the secret states. If Ellen allows them to restore the corresponding initial unknown states, she needs to carry out the single-qubit measurement in the basis of {|0〉,|1〉} on qubit 1 and tells her measured result to the receivers Alice, Bob, Charlie and David. When all measurements are done, the state of qubits 3,5,7 and 9 collapses into

$$ {\sigma}_3^{\left(i,j\right)}{\sigma}_5^{\left(k,l\right)}{\sigma}_7^{\left(m,n\right)}{\sigma}_9^{\left(s,t\right)}{\left({\alpha}_1|0\Big\rangle \kern-.1em +{\beta}_1|1\Big\rangle \right)}_3{\left({\alpha}_2|0\Big\rangle \kern-.2em +\kern-.2em {\beta}_2|1\Big\rangle \right)}_5{\left({\alpha}_3|0\Big\rangle +{\beta}_3|1\Big\rangle \right)}_7{\left({\alpha}_4|0\Big\rangle +{\beta}_4|1\Big\rangle \right)}_9, $$
(27)

or

$$ {\displaystyle \begin{array}{rcl}{\sigma}_3^{\left(1\oplus i,j\right)}{\sigma}_5^{\left(1\oplus k,l\right)}{\sigma}_7^{\left(1\oplus m,n\right)}{\sigma}_9^{\left(1\oplus s,t\right)}{\left({\alpha}_1|0\Big\rangle \kern-.13em +\kern-.13em {\beta}_1|1\Big\rangle \right)}_3{\left({\alpha}_2|0\Big\rangle \kern-.13em +\kern-.13em {\beta}_2|1\Big\rangle \right)}_5{\left({\alpha}_3|0\Big\rangle \kern-.13em +\kern-.13em {\beta}_3|1\Big\rangle \right)}_7{\left({\alpha}_4|0\Big\rangle \kern-.13em +\kern-.13em {\beta}_4|1\Big\rangle \right)}_9.& & \\ {}& & \end{array}} $$
(28)

By combining information from Alice, Bob, Charlie, David and Ellen, Alice make the unitary operation \( {\sigma}_9^{\left(s,t\right)} \) or \( {\sigma}_9^{\left(1\oplus s,t\right)} \) on qubit 9 to reconstruct the state |ζ4〉D, Bob performs the unitary operation \( {\sigma}_3^{\left(1\oplus i,j\right)} \) or \( {\sigma}_3^{\left(1\oplus i,j\right)} \) on qubit 3 to restore the state |ζ1〉A, Charlie executes the unitary operation \( {\sigma}_5^{\left(k,l\right)} \) or \( {\sigma}_5^{\left(1\oplus k,l\right)} \) on qubit 5 to recovery the state |ζ2〉B, and David implements the unitary operation \( {\sigma}_7^{\left(m,n\right)} \) or \( {\sigma}_7^{\left(1\oplus m,n\right)} \) on qubit 7 to reconstruct the state |ζ3〉C, respectively. In this way, this ACT task can be done faithfully and successfully, and the probability of success of our scheme is unit.

Remark 2

  1. (a)

    The general annular controlled teleportation, which is described in (2), (3) and (4), is called a n-annular controlled teleportation (n-ACT). Then the bidirectional controlled teleportation is a 2-ACT, the scheme in Section 2.1 is a 3-ACT, and the scheme in this subsection is a 4-ACT. Naturally, standard controlled teleportation can be considered as a 0-ACT.

  2. (b)

    The scheme in this section can be modified into several hybrid versions of different teleportations. For example, if qubit 9 doesn’t belong to Alice, but to Bob, in this case, the scheme is composed of a 0-ACT and a 3-ACT. If qubit 5 doesn’t belong to Charlie but to Alice, at the same time, qubit 9 doesn’t belong to Alice but to Charlie, then the scheme is composed of two 2-ACT, that is, it is a combination scheme consisting of two bidirectional controlled teleportations.

  3. (c)

    Up to now, we have unified the existing controlled teleportation schemes into the concept of n-ACT. In turn, we can use this concept to classify controlled teleportation schemes.

3 Discussion and Conclusion

Now let us make a summarization of our schemes from the following four: the resource consumption consisting of its classical and quantum parts, the necessary-operation complexity including its difficulty and intensity, the scheme success probability and the intrinsic efficiency of the scheme. We have already summarized the general scheme S1, two special schemes S2 and S3 in Table 1 with respect to the four aspects. The intrinsic efficiency of scheme is defined as η = qs/(qu + bt), where qs is the number of the qubits that consist of quantum information to be exchanged, qu is the number of qubits which are used as quantum channels, bt is the classical bits transmitted [45].

Table 1 Summarization of our three schemes S1, S2 and S3
Full size table

In Table 1, these schemes include TQS transferred quantum state, QRC quantum resource consumption, NO necessary oprations, CRC classical resource consumption, BM Bell-state measurement, SM single-qubit measurement, PO Pauli operation, P the final success probability. For example, in scheme S3, the TQS contains |ξ1〉A,|ξ2〉B,|ξ3〉C and |ξ4〉D, the QRC needed is nine-qubit entangled state, the NO contains four Bell-state measurements, one single-qubit measurement and four unitary operations, the CRC is nine cbits, the P is unit and η is 2/9. It is easy to see from Table 1 that the more participants, the greater efficiency. When n tends to infinity, η tends to 1/4 which is relatively high.

Now let us consider the security of our schemes via a simple analysis. It depends thoroughly on whether the legitimate participants have securely shared the entanglement beforehand. By virtue of the same matured check strategies in treating other similar quantum tasks [46, 47], then any evil outsider’ attack or insider’s cheating can be easily detected. For simplicity, here we do not repeat it. This means that the present schemes are conclusively secure, too. In addition, our schemes are controlled, it means that without the permission of the supervisor, any recipient alone will not be able to finally accomplish the reconstruction, which can be viewed as a scheme security protection in another manner.

The main doubt might arise from why such quantum channel is considered. Take scheme S2 as an example to illustrate the question, we know that in this ACT, there are three senders having qubits A, B and C, respectively, and a supervisor. Thus, the ACT scheme S2 should have at least seven parties (three senders, three receivers and a controller to ensure the quantum teleportation implementation and control), and therefore, we need at least a seven-qubit entangled channel for the performance of this ACT scheme. More importantly, the cluster states share the properties of both the GHZ states and W class entangled states. However, they still have some unique properties. For example, they have a large persistency of entanglement, that is, they (in the case that the number of particles is greater than 4) are harder to be destroyed by local operations than GHZ class states. In addition, they are the key ingredient in measurement-based quantum computing and one-way quantum computing [42], and generation of cluster states and its further applications have been proposed [48, 49]. This is why, we have used a seven-qubit cluster state as the quantum channel.

Finally let us simply discuss the question of the experimental implementation feasibility of our schemes. Obviously, the employed local unitary operations in our schemes are single-qubit operations. It is reported that the Bell-state measurement, single-qubit measurement and the single-qubit unitary operations have already been realized in various quantum systems, such as the cavity QED system [50], ion-trap system [51], optical system [52] and so on. Consequently, our schemes are completely feasible according to the present experimental technologies.

In summary, we have extended the idea of bidirectional controlled teleportation in this paper [31]. First, we have provided a general framework to study the annular controlled teleportation, where we use an appropriate (2n + 1)-qubit entangled state as the quantum channel to transfer \( \mid {\xi}_1\Big\rangle {}_{A_1^{\prime }} \) from Alice1 to Alice2, \( \mid {\xi}_2\Big\rangle {}_{A_2^{\prime }} \) from Alice2 to Alice3, ⋯, \( \mid {\xi}_n\Big\rangle {}_{A_n^{\prime }} \) from Alicen to Alice1 under the control of supervisor Bob. To illustrate the possibility of this general framework, we provide two specific protocols by using a seven-qubit cluster state and a nine-qubit entangled state as the quantum channel respectively. Further, some of their modified versions are discussed. Second, we have made a discussion of the quantum resource consumption (QRC), necessary operation (NO) complexity, classical resource consumption (CRC), success probability and the intrinsic efficiency. Finally, we have briefly explained the reasons for choosing quantum channels. Moreover, we have briefly shown that our schemes are secure and feasible with matured check methods and current experimental techniques.