1 Introduction

The cause of the accelerated expansion of universe, predicted by the observations of type Ia supernova [1,2,3,4], is the backbone of a big challenge in the modern physics. This phase of the universe expansion has been confirmed by observing the anisotropies of Cosmic Microwave Background (CMB) [5, 6]. The CMB observation can be considered as a signal to the universe flatness and claims that the energy density of the cosmic fluid is very close to the critical density [7]. Large-Scale Structure (LSS) [8,9,10,11], Baryon Acoustic Oscillations (BAO) in the Sloan Sky Digital Survey (SSDS) luminous galaxy sample [12, 13], and Plank data [14] are other observations supporting an accelerated universe.

Since the cosmic fluid, supporting the current accelerating universe, does not interact with light, it is called “dark energy”(DE), an oddity with negative pressure and negative equation of state parameter (EoS) ω< − 1/3. In general relativity (GR), there is a very simple model for describing the above mentioned picture called cosmological constant model. According to this model, there is an isotropic and homogeneous fluid with constant positive energy density and constant negative pressure with EoS parameter ω Λ = −1. Although the cosmological constant model of DE helps us in providing a well initial picture for the current accelerating phase, it suffers from some problems such as the fine-tuning and the coincidence problems [15].

In order to find a more realistic model of DE, various fluids with time varying EoS parameter have been introduced which are supported and constrained by the observational data [16,17,18,19]. Quintessence [20, 21], phantom (ghost) field [22,23,24], K-essence [25,26,27], Chaplygin gas [28, 29], holographic dark energy which originates from quantum gravity [30,31,32,33,34,35,36,37] and agegraphic DE [38,39,40,41,42,43,44,45,46,47,48,49,50] are some examples of DE models with time varying EoS parameter. On the other hand, in another approach, some physicists try to solve the DE problem by modifying the field equations of GR in such a way that the phase of acceleration is reproduced without including any new kind of energy [51,52,53,54]. Indeed, in the modified gravity approach, one may consider a new degree(s) of freedom leading to many unknown features and thus one should investigate their nature and new consequences in the universe meaning that this approach adds more complexity to the system. Therefore, it is impressive and economic if we can explain DE without entering the new degrees of freedom.

GDE is a model for DE wherein we do not need to introduce new degrees of freedom or modify gravity. This model is based on the Veneziano ghost field used in order to solve the so-called U(1) problem in QCD theory [55,56,57,58,59]. Although there is not any observable consequence from the ghost field in a Minkowskian spacetime, it produces a small vacuum energy density proportional to ρ D ∼ΛQCD3H ∼ (3 × 10−3 eV )4, which solves the fine-tuning problem [60], in curved spacetime. Here, Λ QCD ∼ 100MeV and H ∼ 10−33 eV are QCD mass scale and Hubble parameter, respectively [60]. Different features of GDE have been studied in ample details [61,62,63,64,65,66,67,68,69,70]. It has been found that the contribution of the Veneziano QCD ghost field to the vacuum energy is not exactly of order of H and there is also a second order term proportional to H 2 which contributes to the vacuum energy density [71]. Adding the H 2 correction term to the GDE model, one may study the GGDE model in which the energy density is taken as ρ D = αH + βH 2 [72,73,74].

Based on the cosmological principle, the universe is homogeneous and isotropic in scales larger than 100-Mpc and it can be open, flat or closed denoted by the curvature constant k = −1,0,1, respectively [15]. It is useful to mention here that although some observations indicate a flat universe, the nonflat case is not completely rejected by observations [15, 75,76,77,78,79,80,81,82,83,84,85]. In addition, there are also several observations which indicate a mutual interaction between DE and dark matter (DM) [86,87,88,89,90,91,92,93,94]. The initial simple models of the mutual interaction between DE and DM are linear functions of ρ D and ρ m [95,96,97,98,99,100,101,102,103,104], where ρ m is the energy density of DM.

Moreover, investigations confirm that the sign of the mutual interaction between DM and DE is changed during the history of universe [105]. In this regards, Wei [106, 107]. proposed a sign-changeable interaction term in the form \(Q=q(\alpha \dot {\rho }+3\beta H{\rho })\), where α and β are dimensionless constant and q is the deceleration parameter. It is obvious that the sign of Q is changed whenever the universe expansion phase is changed from a deceleration phase (q > 0) to an acceleration one (q < 0). It is also worth mentioning that, from the dimensional point of view, one may consider α = 0 and discard the \(\alpha \dot {\rho }\) term [107,108,109]. In fact, the sign-changeable interaction has attracted a lot of attentions [110,111,112,113,114,115,116,117,118,119]. For example, the Chaplygin gas model of DE with sign-changeable interaction has been investigated widely in the literatures [110,111,112,113,114,115,116]. The agegraphic and new agegraphic models of DE with the sign-changeable interaction have also been explored, respectively, in [117] and [118]. Very recently, we have studied the holographic DE model with the sign-changeable interaction term with various IR cutoffs [119].

In the present paper, we are interested in studying the effects of considering a mutual sign-changeable interaction between DM and the DE candidates, including GDE and GGDE, on the evolution history of universe. Indeed, we are going to investigate how a sign-changeable interaction affects the description of GDE and GGDE models of DE about the current phase of the cosmic expansion. We also investigate the evolution of the system parameters, such as the equation of state (EoS) parameter as well as the deceleration and dimensionless density parameters, during the cosmic evolution from the matter dominated era to the current accelerating epoch. In order to present our work, we organize the paper according to the following sections. In Section 2, we study GDE with the sign-changeable interaction in both flat and nonflat universes. Thereinafter, we extend our study to the sign-changeable interacting GGDE in both the flat and nonflat universes in Section 3 and investigate the cosmological implications of the model. In Section 4, we compare the EoS parameter of the sign-changeable interaction GDE and the standard GDE model. We summarize our results in Section 5.

2 GDE with the Sign-changeable Interaction

In this section, we study the GDE in the presence of the sign-changeable interaction term in both flat and nonflat universe.

2.1 Flat Universe

The first Friedmann equation in a flat homogeneous and isotropic FRW universe is written as [15]

$$ H^{2}=\frac{8\pi G}{3}(\rho_{m}+\rho_{D}), $$
(1)

where ρ D is the GDE density and ρ m is the energy density of DM. For the GDE density we have [60]

$$ \rho_{D}=\alpha H, $$
(2)

where α is a constant of order \({\Lambda }^{3}_{QCD} \) and Λ QCD is the QCD mass scale [60]. The fractional energy density parameters and the energy density ratio are defined as

$$ {\Omega}_{m}=\frac{\rho_{m}}{\rho_{cr}}=\frac{8\pi G\rho_{m}}{3H^{2}},\ \ \ ~~{\Omega}_{D}=\frac{\rho_{D}}{\rho_{cr}}=\frac{8\pi G\alpha }{3H}, $$
(3)

and

$$ r =\frac{\rho_{m} }{\rho_{D} }=\frac{{\Omega}_{m}}{{\Omega}_{D}}=\frac{1-{\Omega}_{D}}{{\Omega}_{D}}. $$
(4)

For an interacting universe in which there is a mutual interaction between dark sectors of cosmos, the energy-momentum conservation law can be written as

$$\begin{array}{@{}rcl@{}} &&\dot{\rho}_{m}+3H\rho_{m}=Q, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} &&\dot{\rho}_{D}+3H(1+\omega_{D})\rho_{D}=-Q. \end{array} $$
(6)

In the above equations, Q denotes the interaction term between DE and DM. Here, we consider the interaction term as [105, 107]

$$\begin{array}{@{}rcl@{}} Q = 3\beta Hq(\rho_{D}+\rho_{m}), \end{array} $$
(7)

where β is the coupling constant of interaction Q, and q is the deceleration parameter defined as

$$ q=-1-\frac{\dot{H}}{H^{2}}. $$
(8)

Let us note that although some negative values are allowed for the coupling constant β, we only focus on the β = b 2 > 0 case [105, 107]. Taking the time derivative of relation (2) and considering (1), we obtain

$$ \dot{\rho}_{D}=\rho_{D} \frac{\dot{H}}{H}=-4\pi G\alpha{\rho}_{D}(1+r+\omega_{D}). $$
(9)

Substituting (9) and (7) into (6) and bearing (4) in mind, one reaches at

$$ \omega_{D}=-\frac{1}{2-{\Omega}_{D}}\left( 1+\frac {2b^{2}q}{{\Omega}_{D}}\right). $$
(10)

If we set q = 1 in (7) and (10), then Q and ω D are reduced to relations obtained in Ref. [64]. In Fig. 1, considering the initial condition Ω D (z = 0) = 0.72, the evolution of ω D is plotted against the redshift parameter z. Intersetingly, the EoS parameter of the sign-changeable interacting GDE cannot cross the phantom divide (ω D = −1) at the late time where Ω D → 1. This is due to the fact that at the late time q becomes negative and hence w D = −(1 + 2b 2 q) ≥ −1. This is in contrast to the case of standard interacting GDE, where in the late time the EoS parameter of interacting GDE necessary crosses the phantom line, namely, w D = −(1 + 2b 2) < −1 independent of the value of coupling constant b 2 [64]. For example, taking Ω D = 0.72 for the present time, the phantom crossing take places provided b 2 > 0.1 [64].

Fig. 1
figure 1

The evolution of ω D versus redshift parameter z for the sign-changeable interacting GDE in flat universe

Full size image

Using (8) and (9), we find

$$ \frac{\dot{H}}{H^{2}}=-\frac{3}{2} {{\Omega}_{D}}({1+r+\omega_{D}}), $$
(11)

which can be combined with (10) and (8) to reach at

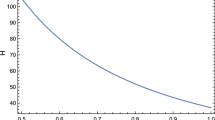
$$ q=\left( \frac{1}{2}-\frac{3{\Omega}_{D}}{2(2-{\Omega}_{D})}\right)\left[\frac{2-{\Omega}_{D}}{2-{\Omega}_{D}+3b^{2}}\right]. $$
(12)

Considering Ω D (z = 0) = 0.72 for the initial condition, we have plotted q against the redshift parameter in Fig. 2. As it is obvious, there is a transition from the deceleration phase to the acceleration one at z ≈ 0.6.

Fig. 2
figure 2

The evolution of q versus redshift parameter z for the sign-changeable interacting GDE in flat universe

Full size image

Taking the derivative with regard to time from Ω D = (8πGρ D )/3H 2 and combining the result with (6) and (25), one can find

$$ \frac{d{\Omega}_{D}}{d\ln a}=3{\Omega}_{D}\left[\frac{1-{\Omega}_{D}} {2-{\Omega}_{D}}\left( 1+\frac{2b^{2}q}{{\Omega}_{D}}\right)-\frac{b^{2}q}{{\Omega}_{D}}\right]=\frac{3}{2} {\Omega}_{D}\left[1-\frac{ {\Omega}_{D}}{2- {\Omega}_{D}}\left( 1+\frac{2b^{2}q}{{\Omega}_{D}}\right)\right]. $$
(13)

We have plotted the dynamics of dimensionless GDE density in Fig. 3. We observe that at the early time Ω D → 0 and at the late time Ω D → 1, as expected. It is easy to check that, as previous, the result of Ref. [64] are obtainable when q = 1. In summary, for the sign-changeable interacting GDE in flat universe, at the late time where z → 0, we have q → −1 and ω D ≥ −1.

Fig. 3
figure 3

The evolution of Ω D versus redshift parameter z for the sign-changeable interacting GDE in flat universe when Ω D (z = 0) = 0.72

Full size image

2.2 Nonflat Universe

Here we consider the sign-changeable interacting GDE in a nonflat universe. It has been argued that the flatness is not a necessary consequence of inflation if the number of e-folding is not very large [120]. The spatial curvature made a contribution to the energy components of cosmos which is constrained as − 0.0175 <Ω k < 0.0085 with 95% confidence level by current observations [121]. The first Friedmann equation in a nonflat homogeneous and isotropic FRW universe is

$$ H^{2}+\frac{k}{a^{2}}=\frac{8\pi G}{3}(\rho_{m}+\rho_{D}), $$
(14)

where k = −1,0,1 is the curvature parameter corresponding to open, flat, and closed universes, respectively. The curvature fractional density parameter is defined as Ω k = k/(a 2 H 2), and thus the Friedmann equation can be rewritten in the following form

$$ {\Omega}_{m}+{\Omega}_{D}=1+{\Omega}_{k}, $$
(15)

which also yields

$$ r =\frac{{\Omega}_{m}}{{\Omega}_{D}}=\frac{1+{\Omega}_{k}-{\Omega}_{D}}{{\Omega}_{D}}, $$
(16)

for the energy density ratio. Combining the time derivative of (14) with (15), we obtain

$$ \frac{\dot{H}}{H^{2}}={\Omega}_{k}-\frac{3}{2}{{\Omega}_{D}} ({1+r+\omega_{D}}). $$
(17)

Inserting the above relation into (6) and using (7) and (9), we reach at

$$ \omega_{D}=-\frac{1}{2-{\Omega}_{D}}\left( 1-\frac {{\Omega}_{k}}{3}+\frac{2qb^{2}}{{\Omega}_{D}}(1+{\Omega}_{k})\right), $$
(18)

for the EoS parameter of sign-changeable interacting GDE in a nonflat universe. Substituting (18) and (17) into (8), the deceleration parameter in a nonflat background is obtained as

$$ q=\left[\frac{1+{\Omega}_{k}}{2}-\frac{3{\Omega}_{D}}{2(2-{\Omega}_{D})}\left( 1-\frac{{\Omega}_{k}}{3}\right)\right]\left( \frac{2-{\Omega}_{D}}{2-{\Omega}_{D}+3b^{2}(1+{\Omega}_{k})}\right). $$
(19)

We plot the evolution of ω D and q against the redshift parameter (z) for GDE in the closed universe in Figs. 4 and 5, respectively. Again, we see that the universe has a phase transition from deceleration to an acceleration around z ≈ 0.6.

Fig. 4
figure 4

The evolution of ω D versus redshift parameter z for GDE in a nonflat universe when Ω D (z = 0) = 0.72 and k = 1

Full size image
Fig. 5
figure 5

The evolution of q versus redshift parameter z for GDE in a nonflat universe. Here we have taken ΩD0 = 0.72 and k = 1

Full size image

It is a matter of calculation to show that

$$ \frac{d{\Omega}_{D}}{d\ln a}=\frac{3{\Omega}_{D}}{2}\left[1+\frac{{\Omega}_{k}}{3}-\frac{{\Omega}_{D}}{2-{\Omega}_{D}}\left( 1-\frac{{\Omega}_{k}}{3}+\frac{2qb^{2}}{{\Omega}_{D}}(1+{\Omega}_{k})\right) \right], $$
(20)

where we used (17) and (6) to get the above equation. It is worthwhile to mention here that the results of flat case, obtained in previous subsection, are covered by setting Ω k = 0. The dynamics of GDE in terms of the redshift parameter is plotted in Fig. 6. Clearly, at the early time it shows Ω D → 0 and at the late time the DE dominates. In the following we can have q → −1 and ω D ≥ −1 at the late time where z → 0.

Fig. 6
figure 6

The evolution of Ω D versus redshift parameter z for the sign-changeable interacting GDE in nonflat universe when Ω D (z = 0) = 0.72 and k = 1

Full size image

3 GGDE with the Sign-changeable Interaction

In the previous section, we have assumed the energy density of GDE as ρ D = αH, while, in general, the vacuum energy of the Veneziano ghost field in QCD is of the form H + O(H 2) [71]. Motivated by the argument given in [122], one may expect that the subleading term H 2 in the GDE model might play a crucial role in the early evolution of the universe, acting as the early DE. It was shown [72,73,74] that taking the second term into account can give better agreement with observational data compared to the usual GDE. This mode is usually called the generalized ghost dark energy (GGDE) and our main task in this section is to investigate the properties of this model in the presence of the sign-changeable interacting term. Again, we first consider a flat universe and then generalize our study to the nonflat case.

3.1 Flat Universe

For the energy density of GGDE we have

$$ \rho_{D}=(\alpha H+\beta H^{2}), $$
(21)

where β is a constant [71, 72]. The fractional energy density parameters also take the below forms

$$ {\Omega}_{m}=\frac{\rho_{m}}{\rho_{cr}}=\frac{8\pi G\rho_{m}}{3H^{2}},\ \ \ ~~{\Omega}_{D}=\frac{\rho_{D}}{\rho_{cr}}=\frac{8\pi G(\alpha +\beta H)}{3H}. $$
(22)

Here, \(\rho _{cr}=\frac {3H^{2}}{8\pi G}\) denotes again the critical density. Finally, use (22) and (21) to obtain

$$ \frac{4\pi G}{3H}(\alpha+2\beta H)=\frac{{\Omega}_{D}}{2}+\frac{4\pi G \beta}{3}. $$
(23)

Taking the time derivative of (21), one can find

$$ \dot{\rho}_{D}=\dot{H}(\alpha+2\beta H), $$
(24)

combined with (22) to reach at

$$ \frac{\dot{H}}{H^{2}}=-\frac{3}{2} {{\Omega}_{D}}({1+r+\omega_{D}}), $$
(25)

finally leading to

$$ \dot{H}=-4\pi G{\rho_{D}}({1+r+\omega_{D}}), $$
(26)

where r is the energy density ratio (4). Substituting (24) and (7) into (6) and using (23), (4) and (26), we find out

$$ \omega_{D}=-\frac{1}{2-{\Omega}_{D}-\zeta}\left( 1+\frac {2b^{2}q}{{\Omega}_{D}}-\frac{\zeta}{{\Omega}_{D}}\right). $$
(27)

Here, \(\zeta =\frac {8\pi G \beta }{3}\). It is obvious that, as the flat case, this equation is reduced to the result of Ref. [73] in the q = 1 limit. The evolution of ω D has been plotted against the redshift parameter (z) for GGDE in Fig. 7.

Fig. 7
figure 7

The evolution of ω D versus redshift parameter z for the sign-changeable interacting GGDE in flat universe when Ω D (z = 0) = 0.72 , ζ = 0.1

Full size image

As the flat case, the EoS of sign-changeable interaction GGDE cannot cross the phantom division (ω D ≥ −1). Let us note that at the late time where the universe is in the accelerated phase, q becomes negative and considering the fact that ζ = .1, we arrive at \(\omega _{D}=-\left (1+\frac {2b^{2}q}{{\Omega }_{D}}-\frac {\zeta }{{\Omega }_{D}}\right )\geq -1\). Taking q = 1, we have \(\omega _{D}=-\left (1+\frac {2b^{2}}{{\Omega }_{D}}-\frac {\zeta }{{\Omega }_{D}}\right )<-1\), and the result of Ref. [73] is restored.

Substituting (25) in (8) and using (27), one can also obtain

$$ q=\frac{1-2{\Omega}_{D}+\zeta}{2-{\Omega}_{D}-\zeta+3b^{2}}. $$
(28)

It is easy to verify that the result of Ref. [73] is covered when b = 0. Moreover, for b = 0 and ζ = 0, we have \(q=\frac {1-2{\Omega }_{D}}{2-{\Omega }_{D}}=\frac {1}{2}-\frac {3}{2}{\frac {{\Omega }_{D}}{2-{\Omega }_{D}}}\) [63].

The behavior of q has also been plotted in Fig. 8, addressing a transition from the deceleration phase to the acceleration one at z ≈ 0.6. Finally, taking the time derivative of relation \({\Omega }_{D}=\frac {8\pi G\rho _{D} }{3H^{2}}\) and using (6) and (25), we find

$$ {\Omega}^{\prime}_{D}=3{\Omega}_{D}\left[\frac{1-{\Omega}_{D}} {2-{\Omega}_{D}-\zeta}\left( 1+\frac{2b^{2}q}{{\Omega}_{D}}-\frac{\zeta}{{\Omega}_{D}}\right)-\frac{b^{2}q}{{\Omega}_{D}}\right]. $$
(29)

It is also easy to check that the results of Refs. [63, 73] are obtainable from the above relations.

Fig. 8
figure 8

The evolution of q versus redshift parameter z for the sign-changeable interacting GGDE in flat universe when Ω D (z = 0) = 0.72, ζ = 0.1

Full size image

We have plotted the dynamics of density parameter in Fig. 9, and the behavior is similar to the previous case; at the early time Ω D → 0, while at the late time Ω D → 1.

Fig. 9
figure 9

The evolution of Ω D versus redshift parameter z for the sign-changeable interacting GGDE in flat universe when Ω D (z = 0) = 0.72 , ζ = .1

Full size image

3.2 Nonflat Universe

In order to find the EoS parameter of sign-changeable interacting GGDE in the non-flat universe, inserting (26) into (24) and combining the result with (6) and (16), we get

$$ \omega_{D}=-\frac{1}{2-{\Omega}_{D}-\zeta}\left[2-\left( 1+\frac {\zeta}{{\Omega}_{D}}\right)\left( 1+\frac{{\Omega}_{k}}{3}\right)+\frac{2b^{2}q}{{\Omega}_{D}}\left( 1+{\Omega}_{k}\right)\right]. $$
(30)

As one can see the EoS parameter cannot cross the phantom divide at the late time, because at this epoch we have Ω D → 1 and q becomes negative, therefore \(\omega _{D}=-\left (2-(1+\zeta )(1+\frac {{\Omega }_{k}}{3})+{2b^{2}q}(1+{\Omega }_{k})\right ) \geq -1\) (note that we have chosen ζ = .1 and Ω k = .01). If we set q = 1 we get \(\omega _{D}=-\left (2-(1+\zeta )(1+\frac {{\Omega }_{k}}{3})+{2b^{2}}(1+{\Omega }_{k})\right ) <-1\), which is the result of Ref. [73]. Thus in contrast to the EoS parameter of the usual interacting GGDE which the phantom regime can be achieved, in case of sign-changeable interaction term the EoS parameter of GGDE is always ω D ≥ −1.

Combining (30) with (17) and (8), one arrives at

$$ q=\left( \frac{1+{\Omega}_{k}}{2}-\frac{3{\Omega}_{D}}{2(2-{\Omega}_{D}-\zeta)}(1-\frac{{\Omega}_{k}}{3})\right)\left[\frac{2-{\Omega}_{D}}{2-{\Omega}_{D}+3b^{2}(1+{\Omega}_{k})}\right], $$
(31)

for the deceleration parameter. One can finally use (22), (6) and (17) in order to obtain

$$ {\Omega}^{\prime}_{D}=3{\Omega}_{D}\left[\frac{{\Omega}_{k}}{3}+ \frac{1-{\Omega}_{D}}{2-{\Omega}_{D}-\zeta}\left( 2-(1+\frac{\zeta}{{\Omega}_{D}})(1+\frac{{\Omega}_{k}}{3})+ \frac{2b^{2}q}{{\Omega}_{D}}(1+{\Omega}_{k})\right)-\frac{b^{2}q}{{\Omega}_{D}}(1+{\Omega}_{k})\right]. $$
(32)

It is worth mentioning that in the limit of Ω k = 0, all the obtained relations in this subsection restore their respective expressions in the previous subsections for flat universe. The behaviors of ω D and q against the redshift parameter for GGDE in the closed universe have also been plotted in Figs. 10 and 11. The main results of this figures are: (i) at late time, we have ω D ≥ −1 and q < −1. (ii) there is a transition from the deceleration phase to the accelerated one around z ≃ 0.6. We have also plotted the evolutionary of the GGDE density in Fig. 12.

Fig. 10
figure 10

The evolution of ω D versus redshift parameter z for the sign-changeable interacting GGDE in nonflat universe when Ω D (z = 0) = 0.72, ζ = 0.1 and k = 1

Full size image
Fig. 11
figure 11

The evolution of q versus redshift parameter z for the sign-changeable interacting GGDE in nonflat universe when Ω D (z = 0) = 0.72, ζ = 0.1 and k = 1

Full size image
Fig. 12
figure 12

The evolution of Ω D versus redshift parameter z for the sign-changeable interacting GGDE in nonflat universe when Ω D (z = 0) = 0.72, ζ = 0.1 and k = 1

Full size image

4 Comparison of EoS Parameter of Usual Interacting GDE and Sign-changeable Model

Finally, we compare the original interating GDE model with the sign-changeable interacting GDE model. For this purpose, we plot the evolution of ω D versus redshift parameter z in Figs. 13 and 14 for both of models GDE and GGDE in a flat and nonflat universe. The long-dash and dash-dot lines show the evolution of ω D for the sign-changeable interacting GDE model and the solid and dashed lines show the usual interacting GDE model with interaction term Q = 3b 2 H(ρ D + ρ m ). From these figures, we observe that the EoS parameter of both GDE and GGDE with sign-changeable interaction term cannot cross the phantom divide ω D = −1 and we always have ω D ≥ −1 at the late time. In contrast, the EoS parameter of the usual interacting GDE and GGDE can cross the phantom line, namely ω D < −1 at the late time.

Fig. 13
figure 13

The evolution of ω D versus redshift parameter z for GDE in a flat and nonflat universe when b 2 = .1,.04,Ω D (z = 0) = 0.72 and k = 1

Full size image
Fig. 14
figure 14

The evolution of ω D versus redshift parameter z for GGDE in a flat and nonflat universe when b 2 = .1,.04,Ω D (z = 0) = 0.72, ζ = 0.1 and k = 1

Full size image

5 Closing Remarks

The DE puzzle is undoubtedly one of the most important challenges of modern cosmology [123, 124]. In this paper, we considered a flat FRW universe filled by a DM and GDE interacting with each other through a sign-changeable interaction term. The generalization to the nonflat case is also investigated, which shows that, for a closed universe, although ω D ≥ −1 at late time, we have q < −1 for the deceleration parameter. Our studies show that, at the late time, we have q → −1 and ω D ≥ −1 meaning that this model does not cross the phantom line, a result which is consistent with the cosmological constant model of DE.

The values of the model parameters can be estimated by fitting the model with observational data. The observational data for coefficient β in original interaction model, Q = 3βH(ρ D + ρ m ), implies a positive value (β > 0), hence we consider β to be positive and can be rewritten β = b 2 > 0. We found out that if we select sign-changeable interaction model, Q = 3b 2 qH(ρ D + ρ m ), because q at the late time should have a negative value, we cannot have crossing phantom. Our studies here show that with the sign-changeable interaction term, only if coefficient β in Q is chosen as a negative value, we can reach the phantom regime. All of the studied cases indicate a transition from the deceleration phase to an accelerated one which take places around z ≈ 0.6.