1 Introduction

The accelerating cosmic expansion first inferred from the observations of distant type Ia supernovae (Riess et al. 1998; Perlmutter et al. 1999) has strongly confirmed by some other independent observations, such as the cosmic microwave background radiation (CMBR) (Spergel et al. 2007) and Sloan Digital Sky Survey (SDSS) (Tegmark et al. 2004). An exotic form of negative pressure matter called dark energy is used to explain this acceleration. The simplest candidate for dark energy is cosmological constant with equation of state (EoS) w Λ =−1. But one problem of this scenario is the coincidence problem, which is the problem why the dark energy density and matter density are at the same order today. Other possible forms of dark energy include quintessence (Wetterich 1988; Ratra and Peebles 1988), phantom (Caldwell 2002), modified gravity (Dvali et al. 2000; Nojiri and Odintsov 2003), holographic dark energy (Li 2004; Zhang and Wu 2005; Setare 2007a), generalized Chaplygin gas (GCG) (Bento et al. 2003; Makler et al. 2003; Zhai et al. 2006; Xu et al. 2012a) which is stemmed from the Chaplygin gas (CG) (Kamenshchik et al. 2001; Bilic et al. 2002), etc. In particular, Hao and Li (2005) have extended the EoS of GCG to w<−1 regime. GCG has an exotic EoS \(p_{gcg}=-A/\rho_{gcg}^{\alpha}\) with 0<α≤1. Also, the GCG model can be extended to the variable generalized Chaplygin gas (VGCG) model (Yang et al. 2007; Fu et al. 2009), which can be described by

$$ p_{\mathrm{vgcg}}=-A_{0}a^{-n}/ \rho_{\mathrm{vgcg}}^{\alpha} $$
(1)

where A 0, n and α are constants, and 0<α≤1. If n=0, then the EoS can reduce to the GCG scenario; if α=1, then the EoS reduces to the VCG model (Guo and Zhang 2007); and if n=0, α=1, then the EoS becomes CG scenario.

On the other hand, there are many other approaches to alleviate the coincidence problem. An interesting proposal is that dark energy is interacting with dark matter. Many interacting models have been studied (Zimdahl and Pavon 2001; Guo et al. 2005; Wei and Cai 2006; Cai and Wang 2005; Zhang and Zhu 2006; Wu and Yu 2007; Li et al. 2009; Chen et al. 2009; He et al. 2009; Chimento 2010; Setare 2006a, 2006b, 2007b, 2007c; Setare and Vagenas 2009; Wu et al. 2008; Bhadra and Debnath 2012; Jamil and Rashid 2008a, 2008b; Jamil 2010). A general interaction between dark energy and dark matter is described by \(\dot{\rho}_{m}+3H\rho_{m}=Q\) and \(\dot{\rho}_{\mathrm{de}}+3H(\rho_{\mathrm{de}}+p_{\mathrm{de}})=-Q\), where Q is the interacting term. The sign of Q determines the direction of energy transfer. A positive Q corresponds to the transfer of energy from dark energy to dark matter and the other way around for a negative one. Observationally the Abell cluster A586 provides evidence of the interaction between dark matter and dark energy (Bertolami et al. 2007). In the context of field theory and particle physics, it is customary and appealing to interpret the dark energy as some sort of particles that interact with the particles of the standard model very weakly. The weakness of the interaction is required since dark energy particles have not been produced in the accelerators and because dark energy has not yet been decayed into lighter or massless fields such as photons. The interaction between dark energy and other particles cannot be arbitrary since this interaction gives a fifth force with a range λ∼1/m 0, where m 0 is the mass of dark energy particle. In Carroll et al. (2003), it is proposed that the phantom particle can decay into one or more phantom plus an ordinary baryonic particle. Thus the above discussion shows that model of interacting dark energy is supported by both theoretical arguments and observational evidences.

There are various choices for the forms of Q. The most common choice is Q=3cHρ, where c is a coupling constant denoting the transfer strength, and ρ is taken to be the density of dark energy, dark matter, or the sum of them. Obviously, these interactions are always positive or negative and hence can not change their signs. Recently, Cai and Su (2010) investigated the interaction in a way independent of specific interacting forms by use of observational data (SNe, BAO, CMB and Hubble parameter). They found that the sign of interaction Q changed in the approximate redshift range of 0.45≤z≤0.9. Motivated by the work of Cai and Su (2010), Wei (2011a) has proposed a new type of interaction \(Q=q(\gamma\dot{\rho}+3\beta H\rho)\), where γ and β are both dimensionless constants. The key point of the new interaction is the deceleration parameter \(q\equiv-\ddot{a}a/\dot{a}^{2}\) in Q. This new feature gives the possibility that interaction Q can change its sign when the universe changes from deceleration (q>0) to acceleration (q<0) and brings different evolution to cosmology. Following Wei (2011a), we have studied a model with this type of interaction between GCG and dark matter and discuss its dynamics (Xu et al. 2012b). Since the term \(\gamma\dot{\rho}\) in Q is introduced from the dimensional point of view (Wei 2011a), one can remove this term by setting γ=0, and then Q becomes simply Q=3βqHρ (Wei 2011b).

In the present paper, we investigate the dynamical evolution of the model with the sign-changeable interaction between VGCG and dark matter. We are interested in the case of Q=3βqHρ tot=3βqH(ρ vgcg+ρ m ) (Wei 2011b). The dynamical analysis indicates that there exists a stable scaling attractor, which can help to alleviate the coincidence problem. Furthermore, when the parameters of the model take some fixed values, the attractor corresponds to the phase w=−0.939 and the equation of state of VGCG approaches it from either w>−1 or w<−1 depending on the choice of its initial cosmic density parameter and the ratio of pressure to critical energy density. Obviously, the phantom divide can be crossed. We find the interaction term Q can change its sign from Q<0 to Q>0 as the universe expands, which is different from the usual interaction. Also, we place constraints on the parameters from the point of view of dynamics.

The paper is organized as follow: In Sect. 2, we introduce a model with the sign-changeable interaction between VGCG and dark matter and investigate its dynamical evolution. The conclusions are summarized in Sect. 3.

2 The interacting model

In our scenario, we consider a spatially flat universe in which there are the VGCG (as dark energy) and dark matter, and postulate that dark matter and the VGCG interact through a sign-changeable interaction term Q. Thus the Einstein equation and continuity equations of dark matter and the VGCG can be written respectively as

(2)
(3)
(4)
(5)

where we have set 8πG=1, the subscripts vgcg and m denote the VGCG and dark matter respectively, H is the Hubble parameter, \(p_{\mathrm{vgcg}}=-A_{0}a^{-n}/\rho_{\mathrm{vgcg}}^{\alpha}\) is the pressure of the VGCG and the over dot represents the derivative with respect to the cosmic time. The sign-changeable interaction term Q is assumed to be Q=3βqH(ρ vgcg+ρ m ) (Wei 2011b), where β is a coupling constant. The key point of this type of interaction is the deceleration parameter q in Q. This new feature gives the possibility that interaction Q can change its sign when the universe changes from deceleration (q>0) to acceleration (q<0) and brings different evolution to cosmology.

A general study on the phase space system of quintessence and phantom in FRW universe has been given in Hao and Li (2004), Li et al. (2005), Liu and Li (2005). To analyze the dynamical system of the interacting VGCG model, we set

(6)

Thus Eqs. (2)–(5) can be rewritten as the following autonomous form:

(7)

From Eq. (3), we have

$$ \varOmega_{\mathrm{vgcg}}+\varOmega_{m}=1 $$
(8)

where Ω vgcg≡x and \(\varOmega_{m}\equiv \frac{\rho_{m}}{3H^{2}}\) are the cosmic density parameters for VGCG and dark matter, respectively. The EoS of VGCG could be expressed in terms of the new variables as

$$ w=\frac{p_{\mathrm{vgcg}}}{\rho_{\mathrm{vgcg}}}=\frac{y}{x} $$
(9)

The deceleration parameter reads

$$ q=-1-\frac{\dot{H}}{H^{2}}=-1+\frac{3}{2}(1+y) $$
(10)

and the interaction term Q satisfies

$$ \frac{Q}{H^{3}}=\frac{9}{2}\beta(1+3y) $$
(11)

The only critical point of the autonomous system (7) is

(12)
(13)

which are solutions of \(\frac{dx}{dN}=\frac{dy}{dN}=0\). For accelerating universe in the late time, \(q_{c}=-1+\frac{3}{2}(1+y_{c})\) must be negative, which implies n<2(1+α). In addition, since in a spatially flat universe, the physically meaningful range of x is 0<x≤1, so 0<x c ≤1, leading to \(-\frac{6(1+\alpha)-2n}{6(1+\alpha)-3n}<\beta\leq0\) and n<2(1+α), where 0<α≤1.

In what follows, we will investigate the stability of the critical point for the autonomous system. When linearizing the system near the critical point and translating the system to origin, we can give the first order perturbation equation as

$$ \frac{dU}{dN}=M\cdot U $$
(14)

where U is a 2-column vector consist of the perturbations of x and y. M is a 2×2 matrix at the critical point. The stability of the critical point is determined by the eigenvalues of the matrix M at the critical point. For the critical point, the two eigenvalues are

(15)

where

(16)

In order to obtain the stable critical point, the real parts of the eigenvalues must be negative. Note that

$$ \lambda_{1}\lambda_{2}=\frac{[3(1+\alpha)-n]^{2}}{1+\alpha}>0 $$
(17)

and

(18)

Since \(-\frac{6(1+\alpha)-2n}{6(1+\alpha)-3n}<\beta\leq0\), n<2(1+α) and 0<α≤1, it is easy to show that both the eigenvalues λ 1 and λ 2 will be negative if 3(1+α)(4+2α+4β+3αβ)−n(2+α)(2+3β)>0, and as a result, the critical point is a stable sink point (Feng et al. 2012) under condition \(-\frac{2[n-3(1+\alpha)]}{3[n-(1+\alpha)(4+3\alpha)/(2+\alpha)]}<\beta\leq0\), n<2(1+α) and 0<α≤1.

Furthermore, the stable attractor is a scaling solution since in the final state the ratio of cosmic density parameters \(\frac{\varOmega_{\mathrm{vgcg}}}{\varOmega_{m}}\) approaches the constant \(\frac{1-\varTheta}{\varTheta}\) except for β=0 (the case without interaction), where \(\varTheta=- [\frac{6(1+\alpha)-3n}{6(1+\alpha)-2n} ]\beta\). Note that 0≤Θ<1 because the physically meaningful range of x c is 0<x c ≤1. Thus, there exists a stable scaling solution in the model, which can help to alleviate the coincidence problem. Additionally, in the final state the EoS of VGCG is expressed by

$$ w= \biggl\{-1+\frac{n}{3(1+\alpha)} \biggr\}\Big/ \biggl\{1+ \frac{6(1+\alpha)-3n}{6(1+\alpha)-2n}\beta \biggr\} $$
(19)

When β=0 (the case without interaction), the stable attractor corresponds to the VGCG dark energy-dominated phase with Ω vgcg=1 and \(w=-1+\frac{n}{3(1+\alpha)}\).

If \(-\frac{6(1+\alpha)-2n}{6(1+\alpha)-3n}<\beta<- \frac{2[n-3(1+\alpha)]}{3[n-(1+\alpha)(4+3\alpha)/(2+\alpha)]}\), the two eigenvalues are positive and the critical point is an unstable source point. So our universe could be in the process of moving away from the critical point. However, observations show the value of the coupling parameter |β| should be small, therefore such evolution should be ruled out by observations.

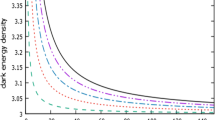
Next, we study the above dynamical system numerically. We choose the parameter as α=0.5, n=1 and β=−0.2. The initial x and y are chosen as shown in Table 1 and the results are contained in Figs. 1, 2, 3 and 4. From Fig. 1, we can observe that all orbits tend to an attractor which corresponds to w=−0.939. From Fig. 2, we can observe that for different initial ρ g and p g , the EoS w could approach to the attractor w=−0.939 from either w>−1 or w<−1 and the phantom divide is crossed. In Fig. 3, we show the evolution of the cosmic density parameter for Ω m and Ω vgcg, respectively, for different initial x and y. The evolution of \(\frac{Q}{H^{3}}\) is shown for different initial x and y in Fig. 4, from which we can observe that the sign of the interaction term Q changes from negative to positive, which is different from the usual interaction.

Fig. 1
figure 1

The phase diagram of the model with the sign-changeable interaction between VGCG and dark matter in terms of x and y for different initial x and y

Full size image
Fig. 2
figure 2

The evolution of the EoS of VGCG for different initial x and y. The curves from bottom to top correspond to the initial conditions specified in Table 1 from left to right respectively

Full size image
Fig. 3
figure 3

The evolution of the cosmic density parameter for Ω m and Ω vgcg respectively for different initial x and y

Full size image
Fig. 4
figure 4

The evolution of \(\frac{Q}{H^{3}}\) for different initial x and y

Full size image
Table 1 The initial values of x and y in the plots Figs. 1–4
Full size table

In Figs. 5, 6, we show the evolution of the EoS of the VGCG for different n and β, respectively. The smaller the values of n and β are, the smaller the value of w in the final state is.

Fig. 5
figure 5

The evolution of the EoS of VGCG for different n when taking x=0.15 and y=−0.18 as the initial values of x and y. We set α=0.5, β=−0.2 as well as n=1 (real line), 1.5 (dot line), 2 (dot-dashed line) and 2.5 (dashed line), respectively

Full size image
Fig. 6
figure 6

The evolution of the EoS of VGCG for different β when taking x=0.15 and y=−0.18 as the initial values of x and y. We set α=0.5, n=1 as well as β=−0.2 (real line), −0.15 (dot line), −0.1 (dot-dashed line) and −0.05 (dashed line), respectively

Full size image

3 Conclusion

In the present paper, we analyze the dynamical evolution of the cosmological model with the sign-changeable interaction between VGCG and dark matter. Here the interaction term Q is assumed to be Q=3βqHρ tot=3βqH(ρ vgcg+ρ m ) (Wei 2011b). The key point of this type of interaction is the deceleration parameter \(q\equiv-\ddot{a}a/\dot{a}^{2}\) in Q, which is different from the usual interaction. The dynamical analysis indicates that there exists a stable scaling attractor, which can help to alleviate the coincidence problem. Furthermore, when the parameters of the model take some fixed values, the attractor corresponds to the phase w=−0.939 and the EoS of VGCG approaches it from either w>−1 or w<−1 depending on the choice of its initial cosmic density parameter and the ratio of pressure to critical energy density. Obviously, the phantom divide can be crossed. Since different values of the parameters lead to different values of w, according to the observation data −1.33<w<−0.79 (Komatsu et al. 2009), we have the constraint \(-1.33< \{-1+\frac{n}{3(1+\alpha)} \}/ \{1+\frac{6(1+\alpha)-3n}{6(1+\alpha)-2n}\beta \}<-0.79\). Following (Hao and Li 2005), we have extended the EoS to w<−1 regime for the initial condition. The early universe is in matter-dominated epoch. We investigate the evolution of \(\frac{Q}{H^{3}}\) and find the interaction term Q can change its sign from Q<0 to Q>0 as the universe expands. Also from the point of view of dynamics, the parameters of the model should satisfy \(-\frac{2[n-3(1+\alpha)]}{3[n-(1+\alpha)(4+3\alpha)/(2+\alpha)]}<\beta\leq0\), n<2(1+α) and 0<α≤1.