1 Introduction

Strong evidences from the current cosmological observations such as SNeIa [1–4], SDSS [5], WMAP [6] converge upon the fact that the universe is spatially flat and there exists an exotic component called dark energy, which drives the speed-up expansion of the universe. Many scenarios have been proposed to explain the acceleration. One of the candidates for dark energy is generalized Chaplygin gas (GCG) [7–11] which is stemmed from the Chaplygin gas (CG) [12, 13]. In particular, Hao and Li [8] have extended the EoS of GCG to w<−1 regime. GCG can be extended to modified Chaplygin gas (MCG) model [14–19], which can also describe the current accelerating expansion of the universe. MCG has a simple EoS

$$ p_{g}=A\rho_{g}-\frac{B}{\rho_{g}^{\alpha}} $$
(1)

where A, B and α are constants, and 0<α≤1. It is obvious that when A is zero, the above equation corresponds to the EoS of GCG, whereas when B=0 it reduces to the EoS of barotropic fluid.

On the other hand, the interaction between dark energy and dark matter is widely studied to alleviate the coincidence problem [20–37]. Dark energy and dark matter interact through a coupling term Q, according to

(2)
(3)

where ρ m and ρ X are the densities of dark matter and dark energy respectively; p X is the pressure of dark energy; the overdot represents derivative with respect to cosmic time t, and H is Hubble parameter. The sign of Q determines the direction of energy transfer. A positive Q implies the transfer of energy from dark energy to dark matter, and vice versa. Since the format of interaction term Q can not be determined from fundamental physics, one can only discuss it to a phenomenological level. The most familiar interactions including Q=3c 1 Hρ m , Q=3c 2 Hρ X and Q=3cHρ tot =3cH(ρ m +ρ X ) are extensively considered. However, these interactions are always positive or negative and hence cannot change their signs.

Recently, Cai and Su [38] investigated the interaction in a way independent of specific interacting forms by use of observational data (SNe, BAO, CMB and Hubble parameter). They found that interaction Q may cross the non-interacting line (Q=0), i.e., the sign of Q changed in the approximate redshift range of 0.45≤z≤0.9. Noting this redshift range is coincident with the one of our universe changing from deceleration to acceleration [39, 40], Wei [41] find that the sign of Q can change when the universe changes from deceleration (q>0) to acceleration (q<0) if the interaction Q is proportional to the deceleration parameter \(q\equiv-\ddot{a}a/\dot{a}^{2}\). Noting that the deceleration parameter q is dimensionless, from Eqs. (2) and (3), \(Q\propto q\dot{\rho}\) and Q∝qHρ are both viable from the dimensional point of view, and then Wei [41] has proposed the linear combination of these two, namely \(Q=q(\bar{\alpha}\dot{\rho}+3\beta H\rho)\), where \(\bar{\alpha}\) and β are both dimensionless constants. The key point of the new interaction is the deceleration parameter q in the interaction term Q. This new feature gives the possibility that interaction Q can change its sign when the universe changes from deceleration (q>0) to acceleration (q<0) and brings different evolution to cosmology. Since the term \(\bar{\alpha}\dot{\rho}\) in Q is introduced from the dimensional point of view [41], one can remove this term by setting \(\bar{\alpha}=0\), and then Q becomes simply Q=3βqHρ. Following the literature [42], we are interested in three interactions of this type, namely Q=3βqHρ tot , Q=3βqHρ X and Q=3βqHρ m .

In the present paper, we investigate cosmological evolution of MCG with this new type of interactions. It is shown that the new interacting term Q can change its sign from Q<0 to Q>0 as the universe expands, which is different from the usual interaction. We find that there exist some stable scaling attractors, which can alleviate the coincidence problem. The EoS of MCG approaches the attractor phase from either w g >−1 or w g <−1 depending on the choice of its initial cosmic density parameter and the ratio of pressure to critical energy density. So, the phantom divide is crossed. We also find that there exist heteroclinic orbits [43] in the models, which connect MCG vacuum-energy-dominated attractor to MCG matter-dominated critical point.

The paper is organized as follow: In Sect. 2, MCG model with the new type of interaction in dark sector is introduced and the dynamical analysis of the model is investigated. We conclude in Sect. 3.

2 MCG Model with the Sign-Changeable Interactions

In our scenario, the universe is filled with two components, one is MCG component ρ g (as dark energy) with an EoS \(p_{g}=A\rho_{g}-\frac{B}{\rho_{g}^{\alpha}}\), and the other is dark matter component ρ m with w m =0, i.e., the total energy density ρ tot =ρ g +ρ m . In the flat FRW universe, the Friedmann and Raychaudhuri equations could be written as

(4)
(5)

where κ 2=8πG.

We assume the interaction between MCG and pressureless dark matter. Hence the energy balance equations for the interacting MCG and dark matter can be expressed as

(6)
(7)

Following the literature [42], we are interested in three new type of interactions including Q=3βqHρ tot , Q=3βqHρ g and Q=3βqHρ m . The key point of the new interaction is the deceleration parameter q in Q. This new feature gives the possibility that interaction Q can change its sign when the universe changes from deceleration (q>0) to acceleration (q<0) and brings different evolution to cosmology.

Case I::

Q=3βqHρ tot

Introducing the following dimensionless variables:

(8)

the equation system (4)–(7) can be rewritten as the following autonomous system:

(9)

Accordingly, the Friedman equation yields

$$ \varOmega_{g}+\varOmega_{m}=1 $$
(10)

where Ω g ≡x and \(\varOmega_{m}\equiv \frac{\kappa^{2}\rho_{m}}{3H^{2}}\) are the cosmic density parameters for MCG and dark matter, respectively. The EoS of MCG could be expressed in terms of the new variables as

$$ w_{g}=\frac{p_{g}}{\rho_{g}}=\frac{y}{x} $$
(11)

and the sound speed is

$$ c_s^2= -\alpha\frac{y}{x}+(1+\alpha)A $$
(12)

The new interaction Q satisfies

$$ \frac{2\kappa^{2}}{9H^{3}}Q=\beta(1+3y) $$
(13)

From the autonomous system (9), we can find three critical points and present them in Table 1.

Table 1 Critical points for the case of Q=3βqHρ tot
Full size table

Since in a spatially flat universe, the physically meaningful range is 0<Ω g ≤1, consequently 0<x c ≤1. Moreover, x c and y c must be real. Together with the constraint of the sound velocity \(0\leq c_{s}^{2}<1\), we can analyze the existence conditions of the critical points in Table 1. For Point (T.1), it can exist under condition −1<β≤0 and \(-\frac{\alpha}{(1+\alpha)(1+\beta)}\leq A<\frac{1+\beta-\alpha}{(1+\alpha)(1+\beta)}\). Point (T.2) can exist for 0<A<1, \(-\frac{2}{3}<\beta<0\) and 8β+A(2+3β)2≥0. Point (T.3) can exist for 0<A<1, \(-\frac{2}{3}<\beta\leq0\) and 8β+A(2+3β)2≥0.

To study the stability of the critical point \((x_{c}^{(i)}, y_{c}^{(i)}), i=1,2,3\), we linearize the system near the critical points and then translate the system to origin, we could readily write the first order perturbation equation as

$$ \frac{dU}{dN}=M^{(i)}\cdot U $$
(14)

where U is a 2-column vector consist of the perturbations of x and y. M (i) is a 2×2 matrix at the critical point \((x_{c}^{(i)}, y_{c}^{(i)})\). The stability of the critical points is determined by the eigenvalues of the matrix M (i) at the critical point \((x_{c}^{(i)}, y_{c}^{(i)})\). For the point \((x_{c}^{(1)}, y_{c}^{(1)})\), the two eigenvalues are

(15)

where

(16)

It is easily shown that the two eigenvalues of \((x_{c}^{(1)},y_{c}^{(1)})\) are negative for −1<β≤0 and \(-\frac{\alpha}{(1+\alpha)(1+\beta)}\leq A<\frac{1+\beta-\alpha}{(1+\alpha)(1+\beta)}\). So, Point (T.1) is a stable sink [44] point. For the point \((x_{c}^{(2)}, y_{c}^{(2)})\), the two eigenvalues are \(\lambda_{1}^{(2)}=-6s_{2}\) and \(\lambda_{2}^{(2)}=3(1+s_{1}-s_{2})(1+\alpha)\). For the point \((x_{c}^{(3)}, y_{c}^{(3)})\), the two eigenvalues are \(\lambda_{1}^{(3)}=6s_{2}\) and \(\lambda_{2}^{(3)}=3(1+s_{1}+s_{2})(1+\alpha)\), where s 1=A(2+3β)/4 and \(s_{2}=\sqrt{A}\sqrt{8\beta+A(2+3\beta)^{2}}/4\). Noting that the existence of \((x_{c}^{(2)}, y_{c}^{(2)})\) requires 0<A<1, \(-\frac{2}{3}<\beta<0\) and 8β+A(2+3β)2≥0, one has \(\lambda_{1}^{(2)}\leq0\) and \(\lambda_{2}^{(2)}>0\). So, Point (T.2) is a saddle point, namely the usual matter-dominated phase is unstable. We have \(\lambda_{1}^{(3)}\geq0\) and \(\lambda_{2}^{(3)}>0\) if \((x_{c}^{(3)}, y_{c}^{(3)})\) exists. So, Point (T.3) is a source [44] point, namely the MCG matter-dominated phase is unstable.

For the case with interaction Q=3βqHρ tot , we find that there exists a stable scaling attractor (T.1) with \(w_{g}=-\frac{1}{1+\beta}\) and Ω g =1+β, which can help to alleviate the cosmological coincidence problem.

Case II::

Q=3βqHρ g

Introducing (8), the corresponding equation system (4)–(7) can be rewritten as the following autonomous system:

(17)

The new interaction Q satisfies

$$ \frac{2\kappa^{2}}{9H^{3}}Q=\beta x(1+3y) $$
(18)

From the autonomous system (17), we can find two critical points and present them in Table 2.

Table 2 Critical points for the case of Q=3βqHρ g
Full size table

Now, we analyze the existence conditions and stability of the critical points in Table 2. It is shown that Point (G.1) can exist and be a stable sink point under condition β≤0 and \(-\frac{\alpha(1-\beta)}{1+\alpha}\leq A<\frac{1-\alpha(1-\beta)}{1+\alpha}\). Point (G.2) can exist for 0<A<1 and −2A<β≤0, but it is an unstable saddle point if it exists. Point (G.2) corresponds to MCG matter-dominated phase.

For the case with interaction Q=3βqHρ g , we find that there exists a stable scaling attractor (G.1) with w g =−1+β and \(\varOmega_{g}=\frac{1}{1-\beta}\) , which can help to alleviate the cosmological coincidence problem.

Case III::

Q=3βqHρ m

Introducing (8), the corresponding equation system (4)–(7) can be rewritten as the following autonomous system:

(19)

The new interaction Q satisfies

$$ \frac{2\kappa^{2}}{9H^{3}}Q=\beta(1-x)(1+3y) $$
(20)

From the autonomous system (19), we can find three critical points and present them in Table 3.

Table 3 Critical points for the case of Q=3βqHρ m
Full size table

Now, we analyze the existence conditions and stability of the critical points in Table 3. For Point (M.1), noting that its existence requires \(-\frac{\alpha}{1+\alpha}\leq A<\frac{1-\alpha}{1+\alpha}\), it is a stable sink point for β≥−1. For Point (M.2), noting that its existence requires 0≤A<1, it is an unstable saddle point for \(\beta<-\frac{2A}{1+3A}\), whereas it is an unstable source point for \(\beta\geq-\frac{2A}{1+3A}\). Point (M.2) corresponds to MCG matter-dominated phase. For Point (M.3), noting that its existence requires \(0<-\frac{\beta}{2+3\beta}\leq A<1\), it is an unstable saddle point, which corresponds to the usual matter-dominated phase.

For the case with interaction Q=3βqHρ m , we find that there exists a MCG vacuum-energy-dominated attractor (M.1) with w g =−1 and Ω g =1, namely de Sitter attractor.

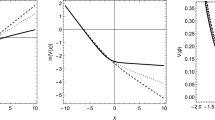
In the following, we study the above dynamical system numerically. For definite, we choose the parameters as A=0.1, α=0.5 and β=−0.2. The initial x and y are chosen as shown in Table 4 and the results are contained in Figs. 1–10. From Fig. 1, we can observe that for the case with interaction Q=3βqHρ tot , the EoS w g could approach to the attractor w g =−1.25 from either w g >−1 or w g <−1. The corresponding cosmic density parameter Ω g could tend to 0.8 for different initial conditions in Fig. 4. From Fig. 2, we can observe that for the case with interaction Q=3βqHρ g , the EoS w g could approach to the attractor w g =−1.2 from either w g >−1 or w g <−1. The corresponding cosmic density parameter Ω g could tend to 0.83 for different initial conditions in Fig. 5. From Fig. 3, we can observe that for the case with interaction Q=3βqHρ m , the EoS w g could approach to the attractor w g =−1 from either w g >−1 or w g <−1. The corresponding cosmic density parameter Ω g could tend to 1 for different initial conditions in Fig. 6. From Figs. 7, 8, 9, we can observe that the new interaction Q has a transition from Q<0 to Q>0, which is different from the usual interaction. From Fig. 10, we can observe that for the case without interaction Q=0 (β=0), the EoS w g could approach to the attractor w g =−1 from either w g >−1 or w g <−1. We find there exists difference in global structure of phase diagram between models with and without these interactions. For MCG model with the sign-changeable interactions, the EoS w can cross the cosmological constant boundary w=−1. While for the case without interaction Q=0, the EoS w can not cross −1.

Fig. 1
figure 1

The evolution of the EoS of MCG for different initial x and y in the case of Q=3βqHρ tot , where we have taken A=0.1, α=0.5 and β=−0.2. The curves from bottom to top correspond to the initial conditions specified in Table 4 from left to right respectively

Full size image
Fig. 2
figure 2

The evolution of the EoS of MCG for different initial x and y in the case of Q=3βqHρ g , where we have taken A=0.1, α=0.5 and β=−0.2. The curves from bottom to top correspond to the initial conditions specified in Table 4 from left to right respectively

Full size image
Fig. 3
figure 3

The evolution of the EoS of MCG for different initial x and y in the case of Q=3βqHρ m , where we have taken A=0.1, α=0.5 and β=−0.2. The curves from bottom to top correspond to the initial conditions specified in Table 4 from left to right respectively

Full size image
Fig. 4
figure 4

The evolution of the cosmic density parameter for Ω m and Ω g respectively for different initial x and y in the case of Q=3βqHρ tot , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 5
figure 5

The evolution of the cosmic density parameter for Ω m and Ω g respectively for different initial x and y in the case of Q=3βqHρ g , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 6
figure 6

The evolution of the cosmic density parameter for Ω m and Ω g respectively for different initial x and y in the case of Q=3βqHρ m , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 7
figure 7

The evolution of \(\frac{2\kappa^{2}Q}{9H^{3}}\) for different initial x and y in the case of Q=3βqHρ tot , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 8
figure 8

The evolution of \(\frac{2\kappa^{2}Q}{9H^{3}}\) for different initial x and y in the case of Q=3βqHρ g , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 9
figure 9

The evolution of \(\frac{2\kappa^{2}Q}{9H^{3}}\) for different initial x and y in the case of Q=3βqHρ m , where we have taken A=0.1, α=0.5 and β=−0.2

Full size image
Fig. 10
figure 10

The evolution of the EoS of MCG without interaction (Q=0) for different initial x and y , where we have taken A=0.1, α=0.5 and β=0. The curves from bottom to top correspond to the initial conditions specified in Table 4 from left to right respectively

Full size image
Table 4 The initial values of x and y in the plots Figs. 1–10
Full size table

Critical points are always exact constant solutions in the context of autonomous dynamical system. Theses points are often the extreme points of the orbits and therefore describe the asymptotic behavior. If the solutions interpolate between critical points they can be divided into a heteroclinic orbit [43]. Therefore, we consider the possibility of forming heteroclinic orbit. For MCG model with interaction Q=3βqHρ tot , heteroclinic orbits can be found in Fig. 11, where we choose A=0.3, α=0.5 and β=−0.02. From Fig. 11, we can see that the universe can evolve from MCG matter-dominated phase to MCG vacuum-energy-dominated phase. Other models possess with similar characteristics.

Fig. 11
figure 11

The attractor property of the MCG with Q=3βqHρ tot , where we have taken A=0.3, α=0.5 and β=−0.02. The heteroclinic orbits connect MCG vacuum-energy-dominated attractor T.1 to MCG matter-dominated critical point T.3

Full size image

3 Conclusions

In the present paper, the cosmological evolution of MCG model with the sign-changeable interactions including Q=3βqHρ tot , Q=3βqHρ g and Q=3βqHρ m is studied. We find that the EoS of MCG approaches the attractor phase from either w g >−1 or w g <−1 depending on the choice of its initial cosmic density parameter and the ratio of pressure to critical energy density. So, the phantom divide is crossed. While for MCG without interaction (Q=0), the EoS w g can not cross −1. For the two cases of Q=3βqHρ tot and Q=3βqHρ g (β≠0), the EoS of MCG remains less than −1 in the final state, but both energy densities of MCG and dark matter are constant with the cosmic expansion since all the increased MCG energy has transferred into dark matter, thus the big rip does not appear. Therefore, there exists the stable scaling solution for the above two cases, which can alleviate the coincidence problem. However, for the case of Q=3βqHρ m , there exists a MCG dominated attractor with w g =−1 and Ω g =1, namely de Sitter attractor. Moreover, we show numerically the evolution of \(\frac{2\kappa^{2}}{9H^{3}}Q\) with the proper parameters and find the new interaction Q has a transition from Q<0 to Q>0 as the universe expands, which is different from the usual interaction. The numerical calculation also shows that a heteroclinic orbit can interpolate between MCG matter-dominated phase and MCG vacuum-energy-dominated attractor.