Analysis of QCD ghost $F(\tilde{R})$ gravity

Abstract

We work on reconstruction scenario of recently proposed dark energy model call QCD ghost with modified Horava-Lifshitz F(R) gravity. We construct the $F(\tilde{R})$ model by taking well-known power law form of scale factor. It is found that this model satisfies the realistic condition. Also, the effective equation of state parameter shows quintom-like behavior from quintessence to phantom era by crossing the vacuum era of the universe. The squared speed of sound represents the instability of the model. In this context, the cosmological planes such as $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ and statefinder show consistency with the accelerated expansion of the universe. We also investigate the generalized second law of thermodynamics on the Hubble horizon which remains valid for all cases of scale factor parameter n.

1 Introduction

Recent developments in the subject of cosmology have led many interesting discoveries about the evolution of the universe. Accelerating expansion of the universe is one of the distinguished events which has brought many challenges in this subject. There are two different teams of astronomers who have evidenced about the accelerated phenomenon of the universe through different observational schemes (Riess et al. 1998; Perlmutter et al. 1999; Caldwell and Doran 2004; Koivisto and Mota 2006; Fedeli et al. 2009). The collected data through these observations suggest that a mysterious form of force named as dark energy (DE) takes part in this phenomenon which dominates overall energy density of the universe. Although current observations favor the presence of DE but its unknown nature is the biggest puzzle in astronomy.

The question about the ambiguous nature of DE is curious as well as interesting for researchers. The most appealing candidate of DE is the cosmological constant which has remained under consideration in the relativistic cosmology throughout its history. However, it faces two main problems, i.e., the fine tuning and cosmic coincidence problems. In order avoid these problems, two alternatives approaches have been used extensively to illustrate the present status of the universe, i.e., dynamical DE models and modified (or extra dimensional) theories of gravity. In the first approach, the modification of matter part of the Einstein field equations takes place by specifying different forms of the energy-momentum tensor including quintessence, k-essence and perfect fluid models (Amendola and Tsujikawa 2010). The perfect fluid models with specific form of EoS include family of Chaplygin gas (Kamenshchik et al. 2001; Bento et al. 2002), holographic (Li 2004), agegraphic (Cai 2007), new agegraphic (Wei and Cai 2008), PDE (Wei, 2012; Sharif and Jawad, 2013a, 2013b, 2014), QCD ghost DE (in different versions) (Urban and Zhitnitsky, 2009a, 2009b; Urban and Zhitnitsky, 2010a, 2010b, 2011; Cai et al., 2012; Garcia-Salcedo et al., 2013) etc. A detail discussion on dynamical DE models have been given in the reviews (Copeland et al. 2006; Bamba et al. 2012).

It is well-known that dynamical DE models play an important role in describing the accelerated expansion of the universe. The Veneziano ghost DE is one of the dynamical DE model which is proposed on the basis of Veneziano ghost of choromodynamics (QCD) which helps in solving the U(1) problem in QCD. The Veneziano ghost (being unphysical in quantum field theory formulation in the Minkowski spacetime) provides non-trivial physical effects in FRW universe (Rosenzweig et al. 1980; Nath and Arnowitt 1981). Although, QCD ghost possesses small contribution in describing vacuum energy density which is proportional to $\varLambda^{3}_{QCD}H$ (here Λ _QCD ∼100 MeV is the smallest QCD scale), but this contribution plays important role in the discussion of evolutionary universe. It is also investigated that this model also helps in alleviating two major problems of DE called fine tuning and cosmic coincidence problem (Urban and Zhitnitsky, 2009a, 2009b, 2010a, 2010b, 2011; Forbes and Zhitnitsky, 2008). Many authors have investigated/tested this model through different cosmological parameters theoretically (Ebrahimi and Sheykhi 2011; Sheykhi and Sadegh 2012; Sheykhi and Bagheri 2011; Rozas-Fernandez 2012; Karami and Fahimi 2013) and different observational schemes (Cai et al. 2011).

It is observed that the Veneziano ghost field in QCD of the form H+O(H²) has ability in producing enough vacuum energy to explain the accelerated expansion of the universe (Zhitnitsky 2012), but only leading term (i.e., H) involved in ordinary ghost DE model. It is suggested (Cai et al. 2012) that the contribution of the term H² in the ordinary ghost DE may be useful in describing the early evolution of the universe which is known as generalized ghost DE. Recently, its new version has been proposed in which it is shown that QCD GDE energy density can be related with the radius of the trapping horizon (Garcia-Salcedo et al. 2013) which defined as follows

$$\begin{aligned} \rho_{\vartheta}=\frac{\alpha(1-\epsilon)}{\tilde{r}_T}= \alpha(1-\epsilon) \sqrt{H^2+\frac{k}{H^2}},\quad \epsilon\equiv\frac{\dot{\tilde{r}}_T}{2H\tilde{r}_T}. \end{aligned}$$

(1)

Nowadays, the reconstruction scenario between dynamical DE models and modified theories of gravity has been investigated in detail. A number of works has been carried on reconstruction scheme adopting different scenarios in modified gravity theories (Nojiri and Odintsov, 2006, 2007; Nojiri et al., 2006, 2009). We have also explored different cosmological parameters through reconstruction scenario via different modified theories of gravity as well as dynamical DE models (Jawad et al., 2013a, 2013b, 2013c, 2013d, 2014). Recently, Chattopadhyay has explored this phenomenon by using F(T) and F(G) gravities and QCD ghost DE and found interesting results (Chattopadhyay, 2014a, 2014b).

In this paper, we reconsider the reconstruction scenario by choosing modified Horava-Lifshitz F(R) gravity (MFRHL) gravity (Chaichian 2010) and QCD ghost DE (Garcia-Salcedo et al. 2013). We find the $F(\tilde{R})$ model through correspondence of MFRHL gravity and DE model and then discuss the behavior of EoS and squared speed of sound parameters as well as $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ and r–s planes. We also discuss the generalized second law of thermodynamics (GSLT). Rest of the paper has been arranged as follows. In the next section, we provide basic scenario of MFRHL and QCD ghost DE in the flat universe. In Sect. 3, we discuss the behavior of cosmological parameters as well as cosmological planes. Also, it contains the discussion of GSLT in this gravity on Hubble horizon. We summarize these outcomes in the last section.

2 Modified F(R) Horava-Lifshitz gravity

The action of MFRHL gravity ($F(\tilde{R})$ gravity) is given by (Nojiri and Odintsov 2007, 2011; Nojiri et al. 2009; Elizalde et al. 2011; Carloni et al. 2010; Chaichian 2010)

$$\begin{aligned} S_{F(\tilde{R})}=\int d^{4}\sqrt{g^{(3)}}N F(\tilde{R}) \end{aligned}$$

with

$$\begin{aligned} \tilde{R} =&K^{ij}K_{ij}-\lambda K^{2}+2\mu \nabla_{\mu} \bigl(n^{\mu}\nabla_{\nu}n^{\nu}-n^{\nu} \nabla_{\nu}n^{\mu } \bigr) \\ &{}-E^{ij}\mathcal{G}_{ijkl}E^{kl}, \end{aligned}$$

is known as modified Ricci scalar. It takes the following form in the context of flat FRW universe

$$\begin{aligned} \tilde{R} =&\frac{(3-9\lambda)H^2}{N^2}+\frac{6\mu}{a^3 N}\frac{d}{dt} \biggl( \frac{Ha^3}{N} \biggr)\\ =&\frac{ (3-9\lambda+18\mu )H^2}{N^2}+ \frac{6\mu}{N}\frac{d}{dt} \biggl(\frac{H}{N} \biggr). \end{aligned}$$

For λ=μ=1, $\tilde{R}\rightarrow R$, and hence we recover usual f(R) gravity. For the action stated earlier, we get by variation over $g_{ij}^{(3)}$ and by setting N=1:

$$\begin{aligned} 0 =&F(\tilde{R})-2(1-3\lambda+3\mu) \bigl(\dot{H}+3H^2 \bigr)F'(\tilde {R}) \\ &{}-2(1-3\lambda)H\frac{dF'(\tilde{R})}{dt}+2\mu \frac{d^2F'(\tilde{R})}{dt^2}+p. \end{aligned}$$

(2)

In above equation, prime represents the differentiation with respect to its argument and also the matter contribution is involved as pressure p. Taking ρ as the matter density and the conservation equation is

$$\begin{aligned} \dot{\rho}+3H(\rho+p)=0. \end{aligned}$$

(3)

Using Eq. (2) and Eq. (3), we get

$$\begin{aligned} 0 =&F(\tilde{R})-6 \bigl[(1-3\lambda+3\nu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H\frac{dF'(\tilde{R})}{dt}- \rho-Ca^{-3} \end{aligned}$$

(4)

where C is an integration constant. Thus, the density corresponding to MFRHL gravity with C=0 turns out to be

$$\begin{aligned} \rho_{\tilde{R}} =&F(\tilde{R})-6 \bigl[(1-3\lambda+3 \mu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H \frac{dF'(\tilde{R})}{dt}. \end{aligned}$$

(5)

To realize the role of DE in modified gravity, a very useful technique is proposed by Nojiri and Odintsov (2006, 2007), Nojiri et al. (2006, 2009) and also extended for several cosmological scenarios. There exists several DE EoS in the literature, however, the authors (Nojiri and Odintsov, 2005; Capozziello et al., 2006) have discussed the more general forms of DE inhomogeneous EoS. In view of these EoS, they have usefully remarked that the more general form may contain the derivative of H, like $\dot{H}, \ddot{H},\ldots$ in principle, it is given by

$$\begin{aligned} F(p,\rho,H,\dot{H},\ddot{H})=0. \end{aligned}$$

This form contains a family of Chaplygin gas and much more complicated EoS. The interested feature of this form as addressed by Nojiri and Odintsov (2005) is that one can recover Friedmann equations through its trivial condition. They have also investigated its non-trivial scenario and sketched a useful picture of cosmological implications. They pointed out that the inhomogeneous term in EoS helps to realize the crossing of phantom barrier. They have also discussed the future behavior of the universe through singularity analysis by taking the several specific examples of above general form of EoS.

However, the DE EoS as mentioned in the above paragraph are much complicated, hence we apply reconstruction scenario on a specific model called QCD ghost DE. Our aim in this work is to reconstruct $f(\tilde{R})$ for PDE in flat FRW Universe. In flat universe, the QCD ghost DE model turns out to be

$$\begin{aligned} \rho_{\vartheta}=\alpha \biggl(1+\frac{\dot{H}}{2H^2} \biggr)H. \end{aligned}$$

(6)

By setting $\rho_{\tilde{R}}=\rho_{\vartheta}$, we obtain

$$\begin{aligned} &{6\mu H\dot{\tilde{R}}F''(\tilde{R})-6 \bigl[(1-3\lambda+3\mu)H^{2}+\mu \dot{H} \bigr]F'( \tilde{R}) }\\ &{\quad{} +F(\tilde{R})=\alpha \biggl(1-\frac{\dot {H}}{2H^2} \biggr)H.} \end{aligned}$$

(7)

This equation is much complicated to obtain analytic solution, but we are interested in finding out analytic solution, so we choose the well-known scale factor

$$\begin{aligned} a(t)=a_0(t_s-t)^{-n},\quad t_s>t. \end{aligned}$$

(8)

Here a₀ and n appear as constant parameters while t _s represent the finite future singularity time.

As, we have considered the DE universe model which contain finite-time, future singularities. It is clear that depending on the content of the model such singularities may behave in different ways. That is why it is useful to classify the future singularities in the following way (Nojiri et al. 2005):

• Type I: for t→t _s , a→∞, ρ,|p|→∞, this singularity corresponds to Big Rip singularity.

• Type II: for t→t _s , a→a _s , ρ→ρ _s , |p|→∞, this singularity corresponds to sudden future singularity.

• Type III: for t→t _s , a→a _s , ρ,|p|→∞.

• Type IV: for t→t _s , a→a _s , ρ,|p|→0.

Our scenario correspond to Type I singularity which describes the Big Rip singularity. It is strongly believed that universe undergoes the big rip singularity, where all the gravitationally bounded objects dispersed due to phantom DE. With the help of this scale factor and Eq. (7), we get

$$\begin{aligned} F(\tilde{R})=c_1\tilde{R}^{\beta_-}+c_2 \tilde{R}^{\beta_+}+\gamma \sqrt{\tilde{R}}, \end{aligned}$$

(9)

which is required MFRHL DE model with QCD ghost filled in the universe. Also, c₁ and c₂ are integration constants while β and γ are given as follows

$$\begin{aligned} &{\beta_{\mp}=\frac{1}{2}\bigl(1-\delta\mp\sqrt{1-2 \delta+\delta^2-4\xi}\bigr),}\\ &{\gamma=-\frac{4b}{(-\delta+\sqrt{1-2\delta+\delta^2-4\xi}) (\delta+\sqrt{1-2\delta+\delta^2-4\xi})}} \end{aligned}$$

with

$$\begin{aligned} &{\delta=-\frac{1}{12\mu}(n-3\lambda n+9\mu n-2\mu),}\\ &{\xi= \frac{3}{4\mu}(n-3\lambda n+6\mu n+2\mu),} \\ &{b=-\frac{\alpha(1+2n)}{24\mu}\sqrt{3n\bigl(n-3\lambda n+\mu(2+6n)\bigr)}.} \end{aligned}$$

It is observed that reconstructed model (9) characterizes as a realistic one because it satisfies the following sufficient condition

$$\begin{aligned} \lim_{\tilde{R}\rightarrow0}F(\tilde{R})=0. \end{aligned}$$

(10)

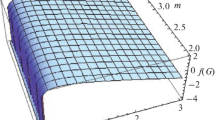
To analyze the behavior of constructed model $F(\tilde{R})$, we plot it against its argument $\tilde{R}$ for three different values of n as shown in Fig. 1. Also, we choose μ=1, λ=−4, c₁=2, c₂=1.5, α=0.91. It can be observed that behavior of $F(\tilde{R})$ shows consistency with realistic condition. Also, it shows increasing with respect to its argument and remains positive throughout.

Fig. 1

Plot of $f(\tilde{R})$ versus t with n=2 (red), n=2.2 (green) and n=2.4 (blue)

3 Cosmological analysis

In order to check the viability of this model, we will discuss the basic cosmological parameters (EoS and squared speed of sound) as well as cosmological planes ($\omega_{\tilde{R}}\mbox{--}\omega'_{\tilde{R}}$ and r–s).

3.1 Equation of state parameter

We use effective EoS parameter for analyzing the behavior of $F(\tilde{R})$ in the present day universe. In effective form, EoS takes form

$$\begin{aligned} \omega_{eff}=\frac{p_{\tilde{R}}}{\rho_{\tilde{R}}+\rho_m}. \end{aligned}$$

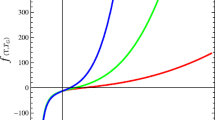
The plot of EoS parameter with respect to cosmic time for three different values of n is shown in Fig. 2. It can be observed that EoS parameter shows evolution of the universe from dust like matter towards phantom DE era by evolving quintessence and vacuum eras. In this scenario, quintom-like behavior is also observed from quintessence to phantom era by crossing the vacuum era of the universe. Also, it is noted that EoS parameter attains maximum phantom value and then shifted towards minimum phantom value.

Fig. 2

Plot of ω _eff versus t for reconstructed MFRHL QCD model with n=2 (red), n=2.2 (green) and n=2.4 (blue)

3.2 Squared speed of sound

Now, we use squared speed of sound for the stability analysis of $F(\tilde{R})$ model. In terms of effective pressure and density, the squared speed of sound takes the form

$$\begin{aligned} \upsilon_{s}^2=\frac{p'_{eff}}{\rho'_{eff}}. \end{aligned}$$

(11)

The sign of $v_{s}^{2}$ is very important to see the stability of background evolution of the model. A positive value indicates a stable model whereas instability of a given perturbation corresponds to the negative value of $v^{2}_{s}$. We can obtained the squared speed of sound in this scenario, by using values of pressure and energy density from Eqs. (2) and (5) along with reconstructed model $F(\tilde{R})$ in Eq. (11). We plot it against t as shown in Fig. 3 by keeping the same values of constant cosmological parameters. It can be observed that the squared speed of sound remains less than zero exhibits the instability of the model.

Fig. 3

Plot of $v^{2}_{s}$ versus t for reconstructed MFRHL QCD model with n=2 (red), n=2.2 (green) and n=2.4 (blue)

3.3 $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ plane

The $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ plane is used to discuss the dynamical property of DE models, where $\omega'_{\vartheta}$ is the evolutionary form of ω _ϑ with prime indicates derivative with respect to lna. Firstly, this method was proposed by Caldwell and Linder (2005) in order to analyzing the behavior of quintessence scalar field DE model. It was pointed by them that $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ plane can be classified into two categories of thawing and freezing regions. In thawing region, EoS parameter begins nearly from −1 and increases with time while its evolution remains positive. In freezing region, EoS parameter remains negative and decreases with time while its evolution also remains negative. In other words, the thawing region is described as $\omega'_{\vartheta}>0$ for ω _ϑ <0 while freezing region as $\omega'_{\vartheta}<0$ for ω _ϑ <0.

This study was extended in a wide range by several authors for analyzing the dynamical nature of various DE models such as more general form of quintessence (Scherrer 2006), quintom (Guo et al. 2006), phantom (Chiba 2006), holographic (Setare 2007), polytropic DE (Sahni et al. 2003), modified gravity theories (Sharif and Rani, 2014) and PDE (Wei, 2012; Sharif and Jawad, 2013a, 2013b, 2014) models. In this scenario, we also develop $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ plane for three different values of n as shown in Figs. 4–6. Figure 4 shows that the $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ plane corresponds to freezing as well as thawing regions. In Figs. 5 and 6, it can be observed that planes correspond to freezing region only. Hence, $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ planes corresponding to n=2.2, 2.4, 2.6 show consistency with the accelerated expansion of the universe.

Fig. 4

Plot $\omega_{\vartheta}'$ versus ω _ϑ for reconstructed MFRHL QCD model with n=2

Fig. 5

Plot $\omega_{\vartheta}'$ versus ω _ϑ for reconstructed MFRHL QCD model with n=2.2

Fig. 6

Plot $\omega_{\vartheta}'$ versus ω _ϑ for reconstructed MFRHL QCD model with n=2.4

3.4 r–s plane

Various models of DE have been proposed for analyzing the DE phenomenon in the accelerated expansion of the universe. It is need to differentiate these models so that one can decide which one provides better explanation for the current status of the universe. Because many DE models provide the same present value of the deceleration and Hubble parameter, so these parameters could not be able to discriminate the DE models. For this purpose, Sahni et al. (2003) introduced two new dimensionless parameters as follows

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3}, \qquad s=\frac{r-1}{3(q-\frac{1}{2})}, \end{aligned}$$

(12)

where q represents the scale factor. The statefinders are useful in the sense that we can find the distance of a given DE model from ΛCDM limit. The well-known regions described by these cosmological parameters are as follows: (r,s)=(1,0) indicates ΛCDM limit, (r,s)=(1,1) shows CDM limit, while s>0 and r<1 represent the region of phantom and quintessence DE eras.

In the present work, we also develop r–s planes for different values of n is shown in Figs. 7, 8 and 9. It can be observed that all plots correspond to ΛCDM limit. It can be observed that the r–s planes correspond to all n shows correspondence with DE regions (quintessence and phantom) and chaplygin gas model.

Fig. 7

Trajectory of r–s for reconstructed MFRHL QCD model with n=2

Fig. 8

Trajectory of r–s for reconstructed MFRHL QCD model with n=2.2

Fig. 9

Trajectory of r–s for reconstructed MFRHL QCD model with n=2.4

3.5 Generalized second law of thermodynamics

Here, we discuss GSLT (the entropy of matter inside the horizon plus the entropy of the horizon must not decrease in time) in MFRHL gravity on the Hubble horizon ($\tilde{r}_{A}=\frac{1}{H}$). It was pointed out by Bamba and Geng (2009) that an f(R) gravity model with phantom divide behavior can satisfy the GSLT in the phantom phase as well as non-phantom. The same authors (Bamba and Geng 2011) investigated thermodynamics of the apparent horizon in f(T) gravity with both equilibrium and non-equilibrium descriptions. Further, Karami and Abdolmaleki (2012) investigated the validity of the GSLT in the framework of f(T) gravity. Moreover, Chattopadhyay and Ghosh (2012) explored the validity of GSLT in the modified f(R) Horava-Lifshitz gravity. We follow the procedure of Karami and Abdolmaleki (2012) and draw the graph of $\dot{S}_{tot}$ against cosmic time t as shown in Fig. 10. It can be observed that $\dot{S}_{tot}$ rapidly decreases with the passage of time and approaches to zero with the passage of time. This behavior shows the validity of GSLT for all cases of n.

Fig. 10

Plot of $\dot{S}_{total}$ versus t with n=2 (red), n=2.2 (green) and n=2.4 (blue)

4 On unification of inflation with Dark Energy in $f(\tilde{R})$

Here, we provide reconstruction scenario for realizing the unification of $f(\tilde{R})$ to unify the early inflationary epoch with the late time de-Sitter era. The framework of unification of inflation with DE in modified gravities was firstly provided in f(R) gravity. It was examined in Nojiri-Odintsov model (Nojiri and Odintsov 2003), which was subsequently generalized to more realistic versions (Nojiri and Odintsov 2007; Cognola et al. 2008). The singularity is an important problem in describing the early universe which is investigated by Nojiri and Odintsov (2008). Actually, it has been pointed out that there exists a class of non-singular exponential gravity to unify the early and late-time accelerated expansion of the Universe (Elizalde et al. 2011). The detailed analysis is given in Nojiri and Odintsov (2011). For this purpose, we consider the inflationary solution

$$\begin{aligned} H=\frac{H_1}{t} \end{aligned}$$

(13)

which provides the following solution of

$$\begin{aligned} F(t) =&\frac{1}{t^{1+\frac{H_1}{2}(19H_1-1)}} \biggl[C_1t^{-\sqrt {4+4H_1+H^2_1(1-19H_1)^2}}\\ &{}+C_2t^{\sqrt{4+4H_1+H^2_1(1-19H_1)^2}} \\ &{}+\frac{\alpha(2+n(-23+38H_1))}{6H_1(H_1+1)}t^{1+\frac {H_1}{2}(19H_1-1)} \biggr]. \end{aligned}$$

This is an inflationary solution. At inflationary (early) Universe, when t≪t₀, the dominant part of the F(t) turns out to be

$$\begin{aligned} F(t)\sim C_1t^{-1-\frac{H_1}{2}(19H_1-1)-\sqrt{4+4H_1+H^2_1(1-19H_1)^2}}, \end{aligned}$$

(14)

where C₁ and C₂ are appear as integration constants. In this limit, the reconstructed $f(\tilde{R})$ for inflationary era takes the form

$$\begin{aligned} f(\tilde{R}) =& \frac{C_1}{\sqrt{3H_1(19H_1-2)}} \\ &{}\times \Bigl[\tilde{R}^{-\frac{1}{2}-\frac {H_1}{4}(19H_1-1) -\frac{1}{2}\sqrt{4+4H_1+H^2_1(1-19H_1)^2}} \Bigr]. \end{aligned}$$

(15)

Hence, $F(\tilde{R})$ produces also the inflationary (phantom) solution.

At late time, i.e., in the de-Sitter epoch when H(t)∼H₀, we have

$$\begin{aligned} \dot{F}_{\tilde{R}}=\dot{\tilde{R}} F_{\tilde{R},\tilde{R}}|_{H=H_0}=0. \end{aligned}$$

(16)

In this scenario, the $F(\tilde{R})$ model turns out to be

$$\begin{aligned} F(\tilde{R})=C_3e^{\frac{1}{96H^2_0}\tilde{R}}+H_0\alpha, \end{aligned}$$

(17)

where C₃ appears as integration constant. The above $F(\tilde{R})$ reproduces de-Sitter (late time) epoch.

5 Concluding remarks

In this work, we reconstruct $F(\tilde{R})$ model through correspondence phenomenon of MFRHL gravity and QCD ghost DE model in the presence of well-known power law form scale factor. In order to analyze the reliability of this reconstructed model, we investigate two cosmological parameters such as the EoS and squared speed of sound. We also develop two well-known cosmological planes called $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ and r–s. We also develop GSLT in this scenario on the Hubble horizon. We summarize our results as follows.

• It can be observed that the behavior of $F(\tilde{R})$ shows consistency with realistic condition as shown in Fig. 1. Also, it shows increasing behavior with respect to its argument and remains positive throughout.

• The EoS parameter shows evolution of the universe from dust like matter towards phantom DE era by evolving quintessence and vacuum eras. In this scenario, quintom-like behavior is also observed from quintessence to phantom era by crossing the vacuum era of the universe. Also, it is noted that EoS parameter attains maximum phantom value and then shifted towards minimum phantom value.

• The squared speed of sound remains less than zero for all values of n which exhibits the instability of the model.

• Figure 4 shows that the $\omega_{\vartheta}-\omega '_{\vartheta}$ plane corresponds to freezing as well as thawing regions. In Figs. 5 and 6, it can be observed that planes correspond to freezing region only. Hence, $\omega_{\vartheta}\mbox{--}\omega'_{\vartheta}$ planes corresponding to n=2.2, 2.4, 2.6 show consistency with the accelerated expansion of the universe.

• The $\dot{S}_{total}$ rapidly decreases and approaches to zero with the passage of time. This behavior shows the validity of GSLT for all cases of n.