An iterated greedy metaheuristic for the blocking job shop scheduling problem

Abstract

In this paper we consider a job shop scheduling problem with blocking (BJSS) constraints. Blocking constraints model the absence of buffers (zero buffer), whereas in the traditional job shop scheduling model buffers have infinite capacity. There are two known variants of this problem, namely the blocking job shop scheduling with swap allowed (BWS) and the one with no swap allowed (BNS). This scheduling problem is receiving an increasing interest in the recent literature, and we propose an Iterated Greedy (IG) algorithm to solve both variants of the problem. IG is a metaheuristic based on the repetition of a destruction phase, which removes part of the solution, and a construction phase, in which a new solution is obtained by applying an underlying greedy algorithm starting from the partial solution. A comparison with recent published results shows that the iterated greedy algorithm outperforms other state-of-the-art algorithms on benchmark instances. Moreover it is conceptually easy to implement and has a broad applicability to other constrained scheduling problems.

1 Introduction

The job shop scheduling problem is one of the most studied problems in combinatorial optimization. In this problem, a set of jobs must be processed on a set of machines and the sequence of machines for each job is prescribed. The processing of a job on a machine is called an operation and cannot be interrupted. Each machine can host only one job at a time, and whenever two jobs require the same machine, a processing order must be defined between the incompatible operations. The problem consists of scheduling all operations on all machines to minimize the completion time of all jobs. The classical version of the problem assumes that jobs can be stored in a buffer of infinite capacity between consecutive operations. However, there are many practical situations in which the buffer capacity has to be taken into account. This is the case, for example, when there is no buffer to store work-in-progress or it is not convenient to store jobs due to economic considerations. Among industrial applications from the literature in which these situations occur we cite the production of concrete (Grabowski and Pempera 2000) and steel (Pacciarelli 2004; Pacciarelli and Pranzo 2004), the management of robotic systems (Levner et al. 1997), as well as surgical case scheduling (Pham and Klinkert 2008), container handling (Meersmans 2002), and railway traffic management (D’Ariano et al. 2007, 2010).

The blocking constraint models the complete absence of storage capacity between consecutive machines (Hall and Sriskandarajah 1996). In this setting, a machine is released by a job only when the subsequent machine is available for processing it. When the subsequent machine is unavailable the job remains on the current machine, thus blocking it, even after its operation is completed. For example, in railway traffic management one can view a train as a job and a rail track segment between two signals as a machine that can host at most one job at a time. A blocking constraint arises since each train, having reached the end of a track segment can enter the next segment only if this is empty. Otherwise it must wait, thus preventing other trains from entering its current segment. Therefore, regulating the traffic on a train networks corresponds to scheduling jobs on blocking machines.

Two versions of the job shop scheduling problems with blocking can be distinguished: the blocking with swap (BWS) and the blocking no-swap (BNS) versions. The need to swap operations between machines arises whenever there is a circular set of blocking operations in which each operation is waiting for a machine occupied by another operation in the set. The only way to solve such situation is that all operations in the set swap, i.e., move simultaneously to their subsequent machines so that all corresponding subsequent operations can start at the same time. In other words, a circular set of mutually blocked operations can occur in the BWS case, while it must be avoided in the BNS case, when swap is not allowed. Railway traffic management is one example of the BNS case, since a train can start moving to the next segment only after that this has been emptied. Mascis and Pacciarelli (2002) show that the problem of deciding whether a feasible schedule exists, when a certain partial schedule is given, is polynomially solvable for the BWS case and it is NP-complete for the BNS version, while the BJSS problem of finding the minimum completion time is NP-hard in both cases.

Despite the practical relevance of the BJSS problem, only in the last years few algorithmic contributions on job shop scheduling problems with blockings have been proposed in the literature. One successful approach is based on the alternative graph formulation (Mascis and Pacciarelli 2002), which allows to model the BJSS problem in both variants, with and without swaps. In Mascis and Pacciarelli (2002) a branch and bound algorithm is proposed to sove the problem exploiting the generalization to the blocking case of some properties holding for the traditional JSS problem with infinite buffer capacity. In Pranzo et al. (2003) a family of heuristics (AGH) extending the ones introduced in Mascis and Pacciarelli (2002) has been proposed and tested. Based on the AGH heuristics, in Meloni et al. (2004) a rollout algorithm is proposed for solving four variants of the job shop scheduling problem including, among the others, the BWS and the BNS versions. In Liu and Kozan (2011), a constructive algorithm with local search improvement is proposed for solving the blocking job shop scheduling problem with parallel-machines and applied to solve a train scheduling problem. Computational results for the BWS case are also reported.

The literature on the blocking job shop scheduling problem includes several recent algorithmic contributions specially tailored for the BWS version of the problem. Gröflin and Klinkert (2009) propose a tabu search algorithm in which the solution feasibility is recovered after every move. In Gröflin et al. (2011), the neighborhood is enlarged to take into account machine flexibility and improved results are presented. A complete local search with memory is proposed by Zhu and Li (2011) which compares favourably with the greedy heuristic algorithms presented in Mascis and Pacciarelli (2002). Recently, Oddi et al. (2012) presented an iterative flattening search for the BWS problem obtaining state-of-the-art results.

The literature for the BNS case experienced a smaller number of contributions. Mati et al. (2001a, b) study a flexible manufacturing system and model the production scheduling problem as a BNS job shop scheduling problem in which each operation may require more than a resource at a time to be executed. They develop a geometric approach to optimally solve the BNS problem with two jobs. Mati and Xie (2011) extend the previous works to include resource flexibility. They propose an insertion heuristic based on the geometric approach for the problem with two jobs and incorporate this algorithm in a tabu search framework to produce deadlock-free schedules for the problem with $n$ jobs.

In this paper, we discuss and apply a conceptually very simple technique, known as Iterated Greedy (IG), which aims at improving the performance of a greedy constructive heuristic procedure in short computation times.

The paper is organized as follows. In Sect. 2 we formulate job shop scheduling problems with blocking constraints using the alternative graph formulation. In Sect. 3 we present our iterated greedy algorithm for solving the problem modeled by means of the alternative graph formulation. Computational results on a set of benchmark instances are presented in Sect. 4, and finally some conclusions follow.

2 The job shop scheduling problem with blocking constraints

In the job shop scheduling problem a set of jobs $J$ must be processed on a set of machines $M$, each processing at most one job at a time. The processing of a job on a machine is called an operation and cannot be interrupted. We let $\{o_1, \ldots , o_n\}$ be the set of all operations. The sequence of operations for each job is prescribed, while the sequence of operations for each machine has to be determined in such a way that the time needed to complete all operations, called the makespan, is minimum. More formally, the scheduling problem consists in assigning a starting time $t_i$ to operation $o_i$, $i=1,\ldots ,n$, such that: $(i)$ precedence constraints between consecutive operations of the same job are satisfied; $(ii)$ each machine hosts at most one job at a time; and $(iii)$ the makespan is minimized.

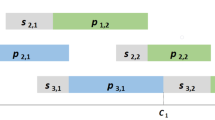
In the blocking job shop scheduling problem no intermediate storage is allowed between two consecutive machines. Hence, once a job completes processing on machine $M_h$ it either moves to the subsequent machine $M_k$ (if it is available) or it remains on $M_h$, thus blocking it (if $M_k$ is not available). The blocking job shop scheduling problem can be modeled by using the alternative graph model of Mascis and Pacciarelli (2002). An alternative graph is a triple ${\mathcal {G}}=(N,F,A)$. $N=\{0,1,\ldots ,n+1\}$ is a set of nodes, and each node $i\in N$ is associated to operation $o_i$. Two additional nodes start $0$ and finish $n+1$ (dummy operations $o_0$ and $o_{n+1}$) model the beginning and the completion of the schedule, i.e., $o_0$ precedes all other operations while $o_{n+1}$ follows all other operations. $F$ is a set of fixed directed arcs and $f_{ij}$ is the length of the fixed arc $(i,j) \in F$. A fixed arc $(i,j)$ represents a precedence constraint on the starting time of operation $o_j$, which is constrained to start at least $f_{ij}$ time units after $o_i$, i.e., $t_j \ge t_i + f_{ij}$. Finally, $A$ is a set of $m$ pairs of alternative directed arcs, and $a_{ij}$ is the length of the alternative arc $(i,j)$. If $((i,k),(h,j))\in A$, then arcs $(i,k)$ and $(h,j)$ form an alternative pair. Alternative pairs are used to model precedence relations between pairs of operations to be processed on the same machine. Let $o_i$ and $o_j$ be two operations to be processed on the same machine, and let $o_h$ and $o_k$ be the operations immediately following $o_i$ and $o_j$ in their respective jobs (see Fig. 1). The blocking constraint states that if $o_i$ is processed before $o_j$, operation $o_j$ can start the processing only after the starting time of $o_h$ (i.e., when $o_i$ leaves the machine). Hence, we represent this situation with the alternative arc $(h,j)$. Conversely, arc $(k,i)$ represents operation $o_j$ preceding $o_i$.

Fig. 1

a The alternative pair of blocking operations with swaps allowed. b The alternative pair of blocking operations when swaps are not allowed

A selection $S$ is a set of arcs obtained from $A$ by choosing at most one arc from each pair, and ${\mathcal {G}}(S)$ indicates the graph $(N, F \cup S)$. The selection is feasible if there are no positive length cycles in the resulting graph ${\mathcal {G}}(S)$. In fact, a positive length cycle represents an operation preceding itself, which is not feasible. A selected alternative arc $(i,j)$ represents the precedence relation $t_j \ge t_i + a_{ij}$.

When swaps are allowed (Fig. 1a) the length of all the alternative arcs is set to zero. In fact given an alternative pair $((i,k),(h,j))\in A$, $o_j$ can start immediately after the start of $o_h$, i.e., $a_{hj}=0$. Note that, in this case, a cycle of alternative arcs has total length zero, and it is therefore feasible. In the no-swap case a deadlock is infeasible. Since a deadlock corresponds to a cycle of alternative arcs (see Fig. 2), this infeasibility is achieved by setting the length of alternative arcs to a small positive value $\varepsilon$ (Fig. 1b). Positive length models the fact that an operation can start processing on a machine strictly after that the previous operations has left it.

Fig. 2

a A simple swap cycle between two operations. b The alternative graph model with swaps allowed. c The alternative graph model when swaps are not allowed

Given a feasible selection $S$, we denote the length of a longest path from $i$ to $j$ in ${\mathcal {G}}(S)$ by $l^S(i,j)$ (if there is no path from $i$ to $j$ we assume $l^S(i,j)= -\infty$). A solution $S$ is a selection of $|A|$ alternative precedence relations, exactly one from each pair in $A$. A feasible solution is optimal if the length $l^S(0,n+1)$ of a longest path from $0$ to $n+1$ is minimum over all feasible solutions.

Finally, given a feasible selection $S$, we define $L^S_{ij}$ as the length of a critical (i.e., longest) path passing through the alternative arc $(i,j)$:

$$\begin{aligned} L^S_{ij} = l^S(0,i) + a_{ij} + l^S(j,n+1). \end{aligned}$$

$L^S_{ij}$ represents a rough lower bound of the longest path between $0$ and $n+1$ (i.e., of the makespan) in any feasible solution obtained starting from the selection $S\cup \{(i,j)\}$.

We also make use of static implications. Two alternative pairs $((k,i),(h,j))$ $((d,a),(c,b))$ are statically implied if there is no feasible solution in which arcs $(k,i)$ and $(c,b)$ are selected or arcs $(h,j)$ and $(d,a)$ are selected. In other words, the selection of arc $(d,a)$ implies the selection of arc $(k,i)$, and the selection of arc $(h,j)$ implies the selection of arc $(c,b)$. Given an alternative arc $(h,i)$, we define the set $I(h,j)$ as the set of alternative arcs statically implied by $(h,j)$. Whenever an alternative arc pair $(h,j)$ is selected/deselected also all arcs in $I(h,i)$ are selected/deselected.

The following simple result allows to establish a correspondence between the selection of arcs from different alternative pairs.

Proposition 1

(Implication) Given a selection $S$ and two unselected alternative pairs $((d,a),(c,b))$ and $((h,j),(k,i))$, if $l^S(a,h)\ge 0$ and $l^S(j,d)\ge 0$ then there is no feasible solution in which arcs $(d,a)$ and $(h,j)$ are both selected in $S$.

Proposition 1 can be applied in particular with the empty selection $S=\emptyset$, when the graph $\mathcal {G}(\emptyset )=(N,F)$ is composed of a set of chains of fixed arcs. Then, the paths $l^S(a,h)\ge 0$ and $l^S(j,d)\ge 0$ can be composed only by fixed arcs, i.e., the paths exist only if nodes $a,h$ refer to a same job $J_1$, and $j,d$ refer to another job $J_2$, sharing some machines with $J_1$. We call this implication static since it holds for any selection $S$. The conditions of Proposition 1 hold for $S=\emptyset$ in the following two cases:

• $J_1$ and $J_2$ pass both through two consecutive machines $M_1$ and $M_2$ in the same order. In this case $c \equiv i$ and $d \equiv j$ (see Fig. 3a).

• $J_1$ and $J_2$ pass both through $M_1$ and $M_2$ consecutively, although in the opposite order (see Fig. 3b).

Fig. 3

a Jobs passing in the same order. b Jobs passing in opposite order

Whenever one of the two above situations occurs, the selection of arc $(d,a)$ implies the selection of arc $(k,i)$, and the selection of arc $(h,j)$ implies the selection of arc $(c,b)$. Therefore $I(d,a)=\{(k,i)\}$, $I(k,i)=\{(d,a)\}$, $I(h,j)=\{(c,b)\}$ and $I(c,b)=\{(h,j)\}$.

Static implications can be computed off-line very efficiently and have been successfully applied to train scheduling problems (D’Ariano et al. 2007).

3 Iterated greedy

Iterated Greedy is a conceptually very simple approach that can be used to improve the performance of a greedy heuristic, which is used as a black box within the algorithm. The basic idea is to iterate a Destruction–Construction cycle. A sketch of the algorithm is given in Fig. 4. A Destruction–Construction cycle consists of three different phases, namely destruction (some components of the incumbent solution are removed), construction (starting from the partial solution a new complete solution is built by the greedy heuristic) and acceptance criterion (the new solution is evaluated and possibly accepted as a new incumbent). Finally a stopping criterion is adopted to terminate the search.

Fig. 4

The pseudocode of an iterated greedy algorithm

Given its simple structure, the IG algorithm has been independently developed by different research communities under different names, such as Ruin and Recreate (2000), Adaptive Large Neighborhood Search (Shaw 1997) or Iterated Flattening Search (Cesta et al. 2000). IG algorithms have been successfully applied to the Set Covering Problem (Marchiori and Steenbeek 2000), to some variants of the Vehicle Routing Problem (Ropke and Pisinger 2006a, b), to the permutation flowshop scheduling in both versions without and with blocking (Ruiz and Stützle 2007, 2008; Ribas et al. 2011) and to the BJSS problem (Oddi et al. 2012).

One of the main advantages of the iterated greedy algorithm is that it does not rely on specific properties of the problem addressed, but all the problem specific knowledge is embedded in the underlying heuristic solution procedure. This is particularly useful when dealing with very general problems that suffer from a lack of specific properties to be used in the design of efficient solution algorithms. Moreover, the framework is easy to implement once a construction heuristic procedure is available. In the remaining part of this section we describe the three phases of our iterated greedy algorithm for the blocking job shop problem with or without swaps.

3.1 Initial solution

The first incumbent solution is obtained by simply ordering the jobs from $1$ to $|J|$ and then, for each alternative pair involving jobs $J_i$ and job $J_j$ with $i<j$, selecting the arc in which $J_i$ precedes $J_j$. Is it easy to show that the initial solution constructed in this way is always feasible in the BWS and BNS cases, since a cycle in ${\mathcal {G}}(S)$ would require at least one arc from $J_j$ to $J_i$, with $i<j$. This is relevant since, starting from a partial selection, the problem of deciding whether a feasible solution exists is a $NP$-complete problem for the BNS case (Mascis and Pacciarelli 2002). However we observe as the solution found by this initial heuristic has typically very poor quality.

3.2 Destruction

In the Destruction phase a portion of the current selection $S$ (representing the incumbent solution) is deselected, and a new partial selection $S'$ is obtained. More precisely, each alternative pair is randomly deselected with probability $p$. The probability $p$ is a parameter of the Destruction procedure called perturbation strength and in our test we set it to 0.8, i.e., in the destruction phase 80 % of all alternative arcs are deselected. Recall that, since we use static implications, every time the algorithm deselects the alternative arc $(i,j) \in ((i,j),(h,k))$ all the implied alternative arcs in $I(i,j)$ are also deselected. Thus the actual fraction of removed arcs is at least $p$.

Notice that, in our model, $k$ operations that must be processed on the same machine lead to $k(k-1)/2$ alternative pairs. Clearly, only $(k-1)$ of them are necessary, while all the others are redundant. Removing a redundant arc would not lead to a different solution, since a redundant arc is implied by the others and construction algorithm would select it immediately. Hence, in order to reach a new solution, the destruction phase must remove a large number of arcs, most of which are redundant.

3.3 Construction

Given a partial selection $S$, a constructive greedy procedure is applied to extend $S$ at each step with a new alternative arc $(i,j)$, i.e., $S=S\cup \{(i,j)\}\cup I(i,j)$, until a new feasible solution $S'$ is obtained or an infeasibility is detected. The latter case arises when there is an alternative pair $((i,j),(h,k))$ such that both ${\mathcal {G}}(S\cup \{(i,j)\}\cup I(i,j))$ and ${\mathcal {G}}(S\cup \{(h,k)\}\cup I(h,k))$ contain a positive cycle, and we say that $S$ is infeasible even if ${\mathcal {G}}(S')$ does not contain any cycle.

As constructive heuristic we next describe a family of greedy heuristics described in Fig. 5, differing from each other for a selection criterion $\mathcal {C}$. We investigate three criteria, named AMCC (Avoid Maximum Current Completion time), AMSP (Avoid Max Sum Pair) and SMBP (Select Most Balanced Pair). The first is introduced in Mascis and Pacciarelli (2002) while the others are introduced in Pranzo et al. (2003). The rationale behind this choice is that moving from the former to the latter the probability of finding feasible schedules increase at the price of a deteriorating makespan. The AMCC heuristic chooses at each step the alternative pair $((i,j),(h,k)) \in A$ such that $\max \{ L^S_{ij},L^S_{hk} \}$ is maximum over all unselected alternative pairs. In other words, AMCC avoids the selection of the arc that would increase most the completion time of the current partial schedule. This choice has been demonstrated to be quite effective with different versions of the job shop scheduling problem (Laborie 2003; Gabel and Riedmiller 2007; D’Ariano et al. 2007). The AMSP heuristic chooses at each step the alternative pair $((i,j),(h,k)) \in A$ such that $L^S_{ij}+L^S_{hk}$ is maximum over all unselected alternative pairs, while the SMBP heuristic chooses at each step the alternative pair $((i,j),(h,k)) \in A$ such that $|L^S_{ij}-L^S_{hk}|$ is minimum. Once the pair is chosen, in all cases the heuristic selects the most promising arc of the pair, i.e., if $L^S_{ij} < L^S_{hk}$, then $(i,j)\cup I(i,j)$ is selected.

Fig. 5

Sketch of the constructive algorithm

If the selection of arc $(i,j)$ would cause a positive length cycle in the graph, then the arc $(h,k)$ is selected. If also the selection of $(h,k)$ would lead to a positive length cycle the algorithm terminates and returns the (acyclic but infeasible) partial selection.

Observe that, as stand-alone heuristic, AMCC often fails in finding a feasible solution for large instances of both the BWS and BNS case. Hence, the use of a metaheuristic scheme is particularly useful to achieve the feasibility of the solutions, besides improving their quality.

3.4 Acceptance criterion

Once a candidate solution is built, the algorithm decides whether to accept it as the new incumbent or to discard it and retain the previous incumbent. Among the acceptance criteria defined in the literature, in our experiments we assessed the following two:

• Random Walk (RW). When RW is adopted every feasible candidate solution generated by the constructive phase is always accepted. If the construction phase does not terminate with a feasible solution then the IG maintains the previous incumbent solution.

• Simulated Annealing like (SA). In the Simulated Annealing criterion (Ruiz and Stützle 2007; Ropke and Pisinger 2006b) a new feasible solution $S'$ is always accepted if it is not worst than the incumbent $S$, i.e., if $C_{max}(S') \le C_{max}(S)$. If $C_{max}(S') > C_{max}(S)$, then the candidate solution $S'$ is accepted with probability $e^{[C_{max}(S) - C_{max}(S')]/T}$ where T is a parameter called the temperature. In our experiments we set $T = 0.5$.

3.5 Stopping criterion

Different stopping criteria can be devised, such as a time limit, a maximum number of iterations and so on. In our tests we set a maximum time limit of computation of 60 s for each run. To avoid stagnation and to improve the performance of the algorithm we run the IG for 10 independent runs and retain the best solution found.

4 Computational results

We tested the performance of our algorithm on the 58 benchmark instances for the job shop scheduling problem by Fisher and Thompson (1963), Lawrence (1984), Applegate and Cook (1991), Adams et al. (1988), adapted to the BWS and BNS cases (for a total of 116 instances). The optimum for these instances is known only for the 18 BWS and 18 BNS instances with 10 jobs and 10 machines (Mascis and Pacciarelli 2002). The time needed to prove the optimality ranges from few minutes up to 30 hours on a Pentium II at 350 MHz. In what follows we refer to this algorithm as BB.

In this section, we first briefly discuss the preliminary test phase. Since the results obtained in this phase often improve the best known solutions from the literature, we show the updated best known upper bound for each instance. Then we compare the performance of the two selected IG configurations against the best performing algorithms for both the BWS (Sect. 4.1) and BNS (Sect. 4.2) problems.

In a preliminary test phase, we tested 12 different parameters setting configurations, retaining the best solution found for all the runs. More specifically we considered three perturbation strength $\{0.4, 0.6, 0.8\}$ two acceptance criteria (Random Walk and Simulated Annealing) and two different construction phases (running the AMCC or taking the best among three independent runs using AMCC, AMSP and SMBP criteria.

From this preliminary test phase we selected the two configurations exhibiting the best performance:

• Destruction In the destruction phase we set perturbation strength equal to 0.8.

• Construction The chosen constructive greedy heuristic is the AMCC algorithm.

• Acceptance Criterion The two best configurations differ for the acceptance criterion, which is Random Walk (RW) in one configuration and Simulated Annealing (SA) in the other.

• Stopping Criterion As stopping criterion we use a time limit of computation equal to 10 min. After every 60 s the current run is interrupted and a new independent run is started.

We refer to these algorithms as IG.RW and IG.SA, respectively. The algorithm is implemented in C++, uses a single thread and runs on an 3.0 GHz Core Duo Intel processor equipped with 2 Gb of RAM.

In the Appendix of the paper (Table 5) we report on the number of iterations executed by IG in a second of computation. This value varies from more than one thousand for the smallest $(10 \times 5)$ instances to less than ten for the largest $(30 \times 10)$ instances. To give an idea of the dynamic behavior of IG during its execution, for the two instances ft10 (with and without swap allowed) on average after 10,000 moves, the percentage of failures in the construction phase (when AMCC fails in finding a feasible solution) is about 31 % for IG.SA and 44 % for IG.RW, the improving moves (new solution feasible and better than the previous incumbent) are 8 % for IG.SA and 14 % for IG.RW, the side-ways moves (the new incumbent has the same makespan than the previous one) are more than 44 % for IG.SA and about 32 % for IG.RW, the worsening moves are about 10 % for IG.RW and 18 % for IG.SA, 8 % of which of the latter are accepted.

4.1 Performance analysis on blocking with swap

In this section, we compare our results with the best known solutions available in the literature. As a benchmark for the BWS case, we consider two tabu search algorithms (Gröflin and Klinkert 2009; Gröflin et al. 2011), a rollout algorithm (Meloni et al. 2004), a complete local search with memory (Zhu and Li 2011), simple heuristic techniques reported in Pranzo et al. (2003), Liu and Kozan (2011) and the recent algorithms presented in Oddi et al. (2012). The best performing algorithms described in these papers are the tabu search algorithm by Gröflin and Klinkert (2009) and Gröflin et al. (2011) (denoted as GK and GPB respectively), the iterated flattening scheme algorithm (Oddi et al. 2012) denoted as IFS and the CP-OPT constraint programming solver of IBM Ilog (Oddi et al. 2012) which implements the approach described in Laborie and Godard (2007). Note that the two latter algorithms have the same structure of the IG, as they both repeat a destruction–construction cycle, although with different components. Specifically, in Oddi et al. (2012) two destruction criteria are analyzed, namely a random selection of the relaxed activities and a slack-based destruction procedure, which restricts the pool of relaxable activities to the subset containing those activities that are closer to the critical path. The construction component has the same structure of our constructive heuristic, but the criterion ${\mathcal {C}}$ is different from the ones used by AMCC, SMBP, AMSP. Finally, a solution is then accepted only if it improves the current best solution. Laborie and Godard (2007) use a portfolio of destruction and construction components. At each destruction–construction iteration, a learning algorithm chooses the specific component to use by taking into account the quality of the improvements and the computation times attained in the previous iterations.

In Table 1 we compare the results found by our IG against the best known solutions from the literature. The first two columns report the instance name and size (number of jobs $\times$ number of machines). The reference to the paper and the best known solution for each instance are shown in Column 3 and 4, respectively. Finally, in Column 5 we show the best result found by all the tested configurations of IG, highlighted in bold when some configuration of the IG improves or attains the best known solution.

Table 1 Comparisons between the best known solutions for BWS from the literature and the best solutions found by IG

The overall CPU time required for each instance by the 12 configurations of IG to obtain the results in Table 1 is 7,200 s on a 3.0 GHz processor. The CPU times required by the other best performing algorithms are as follows. GK performs 5 independent runs of 1,800 s each on a 2.8 GHz processor, for a total of 9,000 s. IFS requires two runs of 1,800 s each. Since 16 configurations of IFS are presented in Oddi et al. (2012) and Table 1 shows the best result, the total computation time required by IFS for one instance is 16 hours of computation. CP-OPT performs a single run of 1,800 s. Both the IFS and CP-OPT run on a AMD Phenom II X4 Quad 3.5 GHz.

The 12 configurations of IG presented in this paper are able to attain or to improve the best solution known in the literature in 42 over 58 benchmark instances. Over the 40 instances for which a proven optimum is not known, IG finds a new best known in 19 cases. Among the other 18 instances for which the optimum is given in Mascis and Pacciarelli (2002), IG achieves the optimum in 17 cases.

Table 2 compares the results of the two best configurations of IG with the three best performing algorithms from the literature: GPB, IFS and CP-OPT. We restrict the comparison to the 40 BWS instances of the Lawrence benchmark, the only instances for which a published result is available for all the three benchmark algorithms. Under IFS we report the results of the best performing configuration among the 16 proposed variants presented in Oddi et al. (2012), namely the one using the slack-based procedure and with $\gamma =0.5$.

Table 2 Performance of IG.RW and IG.SA compared to the best known solutions (Column 3) and the best performing algorithms [GPB Gröflin et al. (2011), CP-OPT and IFS Oddi et al. (2012)] for BWS on Lawrence instances

In Table 2, columns from 1 to 4 show the instance name, size, the value of the best known solution from Table 1 and the paper in which the solution has been presented, respectively. Columns 5, 6 and 7 report the results obtained by GBP, IFS and CP-OPT, respectively. Finally, Columns 8 and 9 report the results achieved by two Iterated Greedy configurations IG.RW and IG.SA. The bold values in the table show the IG configuration attaining the new best known result. For each algorithm we present, in the last row of Table 2, the relative percentage error over the best known solutions ($error = 100 \times (found-best)/best$) from the literature. The computation times of the algorithms are as follows: GPB uses 5 independent runs of 1,800 s each on a 3.0 GHz processor. IFS’12 requires two runs of 1,800 s each on a 3.5 GHz processor. CP-OPT performs a single run of 1,800 s on a 3.5 GHz processor. Finally, the computation time of the IG.RW and IG.SA is 600 s for both algorithms, obtained with 10 independent runs of 60 s each on a 3.0 GHz processor.

From Table 2, it turns out that both IG.RW and IG.SA outperform on average the other algorithms in terms of solution quality and computation time. More in detail, when considering the aggregated performance of each algorithm over the instances of the same size (see Table 6 in the Appendix), we observe a less consistent behavior. IFS is the best performing algorithm over the $(20 \times 5)$ instances, while CP-OPT is the best performing algorithm over the $(30 \times 10)$ instances. With all the other instances both versions of IG outperform the other algorithms. In fact, both the computation time of IG.RW and its average distance from the best known is one third of the best performing algorithm from the literature (CP-OPT), i.e., 600 against 1,800 s and 1.25 % against 3.84 %, respectively. Moreover, the two IGs are able to improve the best known solution in 11 out of 40 benchmark instances (the values are shown in bold in the table).

In the Appendix of the paper (Table 7) we provide additional details on the performance of the two IG algorithms across the ten repetitions on each BWS instance (average, best, worst results and standard deviation). From Table 7, it can be noticed that even a single one-minute run of the IG yields similar average performance compared to GPB and IFS.

4.2 Performace analysis on blocking no swap

In this section we focus on the BNS case. As in the previous section, we first compare the overall performance of the 12 configurations of IG with the current state-of-the-art. We next compare the two best performing configurations against the best algorithm for JSP with blocking and no swaps. To the best of our knowledge, besides the exact approach in Mascis and Pacciarelli (2002) referred to as BB, the only available heuristic results on JSP in the BNS case are a tabu search algorithm by Mati and Xie (2011) referred to as MX, a rollout algorithm (Meloni et al. 2004) and simple heuristic techniques (Pranzo et al. 2003). Among these approaches the tabu search of Mati and Xie (MX) is the best performing algorithm. Thus we omit the other approaches in the comparison.

In Table 3 we show the current state-of-the-art performance on BNS instances of JSP. The instance name and its size are reported in the first two columns. The best known solution from the literature is shown in Column 3, while Column 4 shows the paper reporting first the best solution. Finally, in Column 5 (Best IG) we report the best solution found by the 12 IG configurations. In bold are highlighted the new best values. The proposed IG configurations are able to attain or to improve the best known solution in all but 3 instances. For the 40 instances for which a proven optimum is not known, IG finds a new best known solution in 29 cases. Moreover, for the 18 known optima, IG attains the optimum in 16 cases. Regarding the CPU times, the algorithm MX described in Mati and Xie (2011) requires a shorter CPU time since the results are obtained after 2,000 s on a 2.8 GHz processor, while the 12 IG configurations require in total 2 h on a 3 GHz processor.

Table 3 Comparisons between the best known solutions for BNS from the literature and the best solutions found by IG

In Table 4 we compare the performance obtained by the two best configurations of IG, namely IG.RW and IG.SA, against that of MX over the 40 BNS instances of the Lawrence benchmark. Columns 1 and 2 show the instance name and size, respectively. The best known solutions are shown in Column 3. Except for the 5 instances with 10 jobs and 10 machines for which a proven optimum is known (Mascis and Pacciarelli 2002), the best known is given by MX. In columns 4, 5 and 6 we report the results for MX, IG.RW and IG.SA. The bold values in the table show the IG configuration attaining the new best known result. For each algorithm, the last row of Table 4 report the relative percentage error ($error = 100\times (found-best)/best$) over the best known solution from the literature. A negative value corresponds to a performance improving on average the best known solutions. The computation times of the algorithms are as follows: MX performs 10 independent runs of 200  s on a 2.8 GHz processor, for a total of 2,000 s, while the IG is the best over 10 independent runs of 60 s on a 3.0  GHz processor, for a total of 600 s.

Table 4 Performance of IG.RW and IG.SA compared to the best known solutions (Column 3)and the best performing algorithm (MX Mati and Xie (2011)) for BNS on Lawrence instances

The results show that IG clearly outperforms MX both in terms of computation time and quality of the solutions. In particular, the two IG algorithms improve the best known solutions 28 times out of the 35 instances for which the proven optimum is not known. The best average results are attained by the IG.SA ($-$2.25 % on average).

In the Appendix of the paper (Table 9) we provide additional details on the performance of the two IG algorithms across the ten repetitions on each BNS instance (average, best, worst results and standard deviation). Table 6 shows that also when considering the aggregated performance of each algorithm over the instances of the same size, both versions of IG clearly outperform MX.

5 Conclusions

In this paper we developed an Iterated Greedy metaheuristic to solve the job shop scheduling problem with blocking constraints, in the two variants with and without swaps. The main advantages of the iterated greedy algorithm are the ease of implementation and the independence of the framework from specific properties of the problem addressed.

Even if the proposed approach is conceptually very simple and easy to implement, the performance obtained clearly outperforms all the previously published algorithms from the literature. A new best known solution has been found for 20 BWS instances and for 29 BNS instances. It is also important to notice that the Iterated Greedy has a broad applicability since it can be easily applied to any complex scheduling problem modeled by means of the alternative graph formulation.

Future research directions should address the study of local search based approaches for the blocking job shop scheduling problem and the adaptation of the IG algorithms to real world applications with more complex constraints.

Appendix

See Tables 5, 6, 7, 8 and 9.

Table 5 Speed of the proposed IG algorithms

Table 6 Comparisons focused on different instance sizes between GPB, CP-OPT, IFS, IG.RW and IG.SA algorithms for the BWS

Table 7 Details on the performance of the IG algorithms for the BWS case on the Lawrence testbed

Table 8 Comparisons focused on different instance sizes between MX, IG.RW, IG.SA algorithms for the BNS

Table 9 Details on the performance of the IG algorithms for the BNS case on the Lawrence testbed