1 Introduction

Sequencing and scheduling can be defined as allocating resources to perform tasks over time. This type of problem is so general that it appears almost everywhere. Unfortunately, proposing feasible solutions in real-world situations is not always easy. In complex environments, scheduling problems often involve tasks competing for resources along with several embedded constraints and objectives, making them very hard to solve (Pinedo 2016; T’kindt and Billaut 2006). Furthermore, the pressure to overcome this challenge is ever-increasing, since failing to use available resources efficiently or respond quickly to customer demands in today’s competitive markets can be the end of any business. This makes a well-chosen scheduling strategy play a crucial role in present times. In this context, we study the m-machine flow shop scheduling problem (FSP). In order to propose more realistic solutions for complex scenarios, the problem is addressed with a multiple criteria approach. Specifically, a multi-objective function is applied to minimize total tardiness subject to an upper bound on makespan. In addition, the FSP is considered with no-wait (NWT) and sequence dependent setup times (SDST). These objectives and constraints are common in productions systems and have never been considered together in this problem before. To solve the problem, a new algorithm is proposed and compared with the current best methods for similar applications.

The m-machine FSP is a system where a set of jobs have to be processed through a series of machines in the same processing routing. Each machine processes one job at a time. No job can overtake other jobs (first-in-first-out) and therefore only permutation schedules are allowed. When the NWT constraint is in place, there is no waiting time between successive operations. Therefore, no job is permitted to utilize a buffer or to wait in an upstream machine. NWT may occur due to process requirements or unavailability of waiting space. Having setup constraints means that a machine requires some preparation before processing a particular job. This preparation may include cleaning, retooling, adjustments, inspection and rearrangement of the workstation. When setup times are sequence-dependent, the length of these times depends on the difficulty involved in switching from one processing configuration to another. SDST are common in multipurpose machines or where a single facility produces a variety of products. In those situations, instead of absorbing the setup times in the processing times, it is recommended to make explicit considerations to address the problem (Baker and Trietsch 2019; Pinedo 2016; Emmons and Vairaktarakis 2013).

Total tardiness and makespan are two important performance measures in the field of scheduling. Total tardiness is the sum of all delays related to not meeting due dates. Minimizing total tardiness implies that delays can be subjected to penalties, but there are no benefits from completing jobs in advance. Makespan represents the maximal completion time among all jobs in the system. Minimizing makespan is appropriate when a complete batch of jobs needs to be dispatched as quickly as possible. A reduced makespan is also important to have an efficient utilization of resources, that is, to decrease equipment idle time (Baker and Trietsch 2019; Pinedo 2016). Total tardiness and makespan are addressed here as the hierarchical objective \(TT \mid C_{max} \le K\). A hierarchical function \(A \mid B \le K\) minimizes A subject to an upper bound K on B. This formulation is appropriate when there is no need to optimize objective B as long as it does not exceed the upper bound (Emmons and Vairaktarakis 2013).

The NWT-FSP is proved to be NP-hard. Since using exact methods in this case can be impractical, heuristic methods have been developed to speed up the process of finding reasonable solutions for this problem. Some researchers have proposed algorithms to minimize makespan and total tardiness in NWT-FSP-SDST. The most relevant studies include greedy algorithms (Bianco et al. 1999; Xu et al. 2012; Li et al. 2018), simulated annealing (Lee and Jung 2005; Aldowaisan and Allahverdi 2015), hybrid genetic algorithm (Franca et al. 2006), constructive heuristics (Ara and Nagano 2011), greedy randomized adaptive search procedure and evolutionary local search based (Zhu et al. 2013b), iterative algorithms (Zhu et al. 2013a), hybrid evolutionary cluster search (Nagano and Araújo 2014), hybrid greedy algorithm (Zhuang et al. 2014), particle swarm optimization (Samarghandi and ElMekkawy 2014), genetic algorithms (Samarghandi 2015a, b; Aldowaisan and Allahverdi 2015) and local search (Miyata et al. 2019).

The literature on multi-objective optimization of NWT-FSP is relatively limited, especially when hierarchical objectives are addressed. Allahverdi (2004) proposed an insertion-based iterative algorithm to minimize a weighted sum of makespan and maximum tardiness with an upper bound on maximum tardiness. Framinan and Leisten (2006) proposed a heuristic based on a dominance property over the job of maximum tardiness to minimize makespan subject to maximum tardiness. To minimize makespan subject to mean completion time (or the equivalent total completion time), Aydilek and Allahverdi (2012) presented several heuristics based on simulated annealing and local searches and Nagano et al. (2020) proposed an iterated greedy. Allahverdi and Aydilek (2013) develop an iterated local search and a genetic algorithm to minimize total completion time subject to makespan, and Allahverdi and Aydilek (2014) proposed—among others—a heuristic based on simulated annealing for the same problem with separate setup times. Recently, Allahverdi et al. (2018) proposed an algorithm which combines simulated annealing and an insertion algorithm to solve the NWT-FSP with total tardiness subject to makespan, and Allahverdi et al. (2020) presented a similar method for the same problem with separate setup times.

As can be noted, many applications and research have independently investigated different variations of the no-wait flow shop scheduling problem. And since most of them have not been compared, it is unclear which solution methodology performs better and under what conditions [see the related surveys presented by for more information]. However, the literature highlights the most frequently used high-performance techniques. Based on this information, we propose a new iterated greedy algorithm called \(IG_{A}\). An iterated greedy algorithm fundamentally has a construction mechanism and a destruction mechanism that are repeatedly executed in an alternating order. It is a very flexible and malleable method that can easily be combined with other techniques and reach very high performance when applied to basically any combinatorial optimization problem. The iterated greedy was initially proposed to solve the FSP by Ruiz and Stützle (2007). After that, different extensions have been published considering additional constraints, e.g., sequence-dependent setup times (Ruiz and Stützle 2008), no-idle mixed no-idle (Pan and Ruiz 2014), no-wait (Yamada et al. 2021) and blocking (Tasgetiren et al. 2017). Other optimization criteria have also been addressed apart from makespan such as total tardiness and total flowtime. The iterated greedy has also been effective to solve multi-objective scheduling problems (Dubois-Lacoste et al. 2011; Minella et al. 2011; Ciavotta et al. 2013). Given the wide applicability, the flexibility, and the often high performance of iterated greedy, we decided to use this strategy to develop \(IG_{A}\).

In this work, the no-wait flow shop problem to minimize total tardiness subject to makespan is addressed for the first time with sequence-dependent setup times, which is a more complex scenario in production systems where machine setup times depend on the sequencing of jobs and decisions taken in previous periods. We present an original iterated greedy algorithm. The novelty of this method includes a new mechanism capable of using some search-dependent properties to calibrate the algorithm during execution. Specifically, the algorithm adjusts its destruction intensity according to the instance size and number of iterations to improve convergence to a global optimum. Extensive computational experiments were conducted to evaluate the proposed approach against two recent methods for similar problems: algorithm AA (no setup) by Allahverdi et al. (2018) and algorithm PA (simple setup) by Allahverdi et al. (2020). The two literature methods are adapted to solve the problem with sequence-dependent setup times. The results show that the proposed algorithm outperforms the best literature method by about 35% on average under the same computational conditions.

The remaining content is structured as follows. Section 2 is dedicated to the problem definition. The algorithms are described in Sect. 3. Section 4 presents the computational experiments. The final conclusions and some future directions are given in Sect. 5.

2 Problem definition

The FSP consists of a set \(M = \left\{ 1,\ldots , m \right\} \) of m work stations that process a set \(N = \left\{ 1,\ldots , n \right\} \) of n independent jobs sequentially. In addition, there are some assumptions made on jobs and machines: all operational requirements are known; all jobs are available to be processed from time zero; there is only one machine on each work station (m-machine); no machine can process two or more jobs at the same time; no job can be processed on more than one machine simultaneously; each operation must be performed without interruption (no preempt); after an operation is completed, a job is immediately available for the next operation; each machine must process a job only once (no recirculation); all processing times are positive; and all jobs are processed in the same order on all machines (permutation). The goal consists of finding the best possible sequence that optimizes the objective function.

The problem can be addressed as follows. Let \(p_{i,j}\) denote the processing time of job \(j \in N\) on machine \(i \in M\). Furthermore, let \(s_{i,j}\) represent the setup time required on machine i for job j after job \(j-1\) is completed. Then, the start time of job j on the first machine, denoted by \(S_{j}\), can be defined as

$$\begin{aligned} S_{j} = \max \limits _{1 < k \le m} \left\{ S_{j-1} + \sum _{i=1}^{k} p_{i,j-1} + s_{k,j} - \sum _{i=1}^{k-1} p_{i,j} \right\} , \quad j = 2,\ldots , n \end{aligned}$$

where \(S_{1} = s_{1,1}\) and \(j = 0\) is a dummy job with processing times and setup times of zero length. Now, let \(C_{j}\) denote the completion time of job j on the last machine. Then, \(C_{j}\) can be defined as

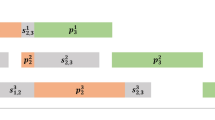
$$\begin{aligned} C_{j} = S_{j} + \sum _{i=1}^{m} p_{i,j} \;, \; \; \; \; j = 1,\ldots , n. \end{aligned}$$

In addition, let TT and \(C_{max}\) denote total tardiness and makespan, respectively. Finally, let \(d_{j}\) be the due date of job j. Total tardiness is defined as \(TT = \sum _{j=1}^{n} T_{j}\), where \(T_{j} = max\{C_{j}-d_{j};0\}\). Makespan is defined as \(C_{max} = C_{n}\). Figure 1 illustrates two adjacent jobs on the NWT-FSP-SDST.

Fig. 1
figure 1

Two adjacent jobs on the NWT-FSP-SDST

Full size image

Using the classification system \(\alpha /\beta /\gamma \) introduced by the m-machine NWT-FSP-SDST to minimize total tardiness subject to makespan can be written as

$$\begin{aligned} \textit{Fm} \; / \; \textit{nwt}, s_{i,j} \; / \; \left( \textit{TT} \mid \textit{C}_{max} \le \textit{K}\right) , \end{aligned}$$

where Fm and nwt represent flow shop and no-wait, respectively. Thus, the problem consists of finding the best possible sequence so that total tardiness is minimized and makespan does not exceed a predefined K value. In real problems, the initial solution and K must be provided by the scheduler. For the experiments performed here, these data are generated using the Transposition local search presented by Algorithm  1. Starting from a random sequence, the Transposition method returns the best solution of \((n - 1)\) permutations produced by swapping successive pairs of adjacent jobs. The upper bound K is defined as the makespan value of the returned sequence.

figure a

3 Heuristic algorithms

The problem of \(\textit{Fm} / \textit{nwt} / \left( \textit{TT} \mid \textit{C}_{max} \le \textit{K}\right) \) has already been addressed in the literature by Allahverdi et al. (2018, 2020). In this work, the algorithm presented in each study is implemented to solve the problem with sequence-dependent setup times. The two methods are briefly explained in the next subsection, followed by a complete description of the proposed algorithm.

3.1 Literature algorithms

Allahverdi et al. (2018) proposed the algorithm AA to solve the NWT-FSP with the objective of minimizing total tardiness subject to makespan. They adapt many existing algorithms for this problem and prove that AA performs better than all of them. In summary, the algorithm AA is composed by a simulating annealing (SA) algorithm and an insertion local search. Starting from an initial sequence obtained from EDD (Earliest Due Date) rule, the SA is performed to reduce TT using a random pairwise exchange operator. Then, if the solution does not satisfy the constraint \(C_{max} \le K\), the insertion local search tries to improve the sequence to obtain a feasible solution. The algorithm repeats these steps until the stopping criterion is satisfied.

Allahverdi et al. (2020) studied the same problem with separate setup times. These setups can be classified as simple because the preparation times do not depend on production in previous periods. They propose the algorithm PA, which was shown to outperform different existing algorithms modified for this environment. PA starts the initial solution as the best sequence between the EDD rule and the NEH minimizing TT. The optimization process has three phases. In the first phase, an SA algorithm utilizes block insertion and block exchange operators to reduce TT. In the second phase, an insertion local search is performed as an attempt to find a feasible solution for the condition \(C_{max} \le K\). In the third phase, total tardiness is minimized by inserting the job having the maximum tardiness into all other positions.

It should be noted that at the start of both, AA and PA, the optimization of total tardiness takes place without imposing the upper bound on makespan. Only then does a local search try to satisfy this constraint, but this time without accepting worse values for total tardiness. For this reason, these algorithms tend to get stuck, as optimizing total tardiness and makespan are often competing objectives. In other words, both methods may not be able to generate a feasible solution. This fact is confirmed in the experiments carried out. To avoid fundamental changes in the algorithms, the initial solution is returned each time AA or PA are not able to produce a feasible solution.

3.2 Iterated greedy algorithm (\(IG_{A}\))

The proposed method, called \(IG_{A}\), optimizes an initial solution through a destruction and construction process. In the destruction phase, a set of random jobs is removed from the incumbent solution. This simple stochastic method provides fast destruction and at the same time reduces the chance of trapping in local optima. The construction phase tries to reinsert the removed jobs through a process based on the NEH mechanism, Nawaz et al. (1983) to produce a new candidate solution. Next, an acceptance criterion updates the incumbent with the candidate if the new sequence is a better feasible solution (or in other words, if the candidate is complete, has lowest total tardiness and satisfies the upper bound constraint on makespan). The method is composed of Algorithms  2 and  3.

figure b
figure c

Algorithm  2 runs at the highest level. In line 1, the necessary parameters (N and P) and the initial sequence (\(s_{0}\)) are defined. The next two lines initialize the incumbent variables \(\pi \) and F that receive copies of \(s_{0}\) and its total tardiness \(TT(s_{0})\), respectively. In line 4, the factor \(f \in \{0, 1\}\) is calculated using N and P. A copy of f is made to initialize the variable d in line 5. Lines 6–14 make up the main loop, which is responsible for the optimization itself. First, Algorithm  3 is called on line 7. It takes \(\pi \) and d as arguments and returns the candidate solution \(\pi '\). Then, an acceptance process is carried out from line 8–12. In this process, the auxiliary variable \(F'\) is initialized with \(TT(\pi ')\) in line 8. If in line 9 the statement \(F' < F\) is true, that is, \(TT(\pi ') < TT(\pi )\), then \(\pi \) and F are updated with \(\pi '\) and \(F'\) in lines 10 and 11, respectively. After the acceptance process, the factor f is used to update d in line 13. If the time limit is not reached in line 14, the main loop starts another iteration from line 6. Otherwise, the iterations terminate and the incumbent sequence \(\pi \) is returned in line 15.

Algorithm  3 runs at the lowest level. It generates a candidate solution through the destruction and construction process. In line 1, the sequence \(\pi \) and the coefficient d are both initialized. In line 2, a copy of \(\pi \) is made to initialize the auxiliary variable \(\pi _d\). The number of jobs to be removed from \(\pi _d\) is calculated and assigned to D in line 3. In line 4, the sequence \(\pi _e\) is initialized with D random jobs removed from \(\pi _d\). In lines 5–7, a loop tries to reinsert the removed jobs, one by one, from \(\pi _e\) to \(\pi _d\) through a NEH-based process where the job to be inserted is tested in all possible positions. The best feasible solution is taken at the end of each iteration. These steps are repeated until all jobs are reinserted or no feasible solution is produced. When the reinsertion process can generate a feasible solution, \(\pi \) is updated with \(\pi _d\) (line 9). Finally, \(\pi \) is returned in line 11.

It is important to note that d is not fixed across different instance sizes or while the algorithm is solving a problem. Instead, some search-dependent properties are used by the algorithm to modify this value in order to find an appropriate balance between search diversification and intensification. Diversification is explored by removing a large number of jobs to drive the search to rather distant solutions in the construction phase. Intensification, on the other hand, is explored by removing few jobs to focus the search on more localized regions. Some initial experiments suggested that a diversification strategy is more effective at the beginning of the search and have the cost of higher computation times for large problems. Considering this observation, the algorithm was designed so that the initial value of d is inversely proportional to the number of jobs and it decreases after each iteration. The adjustment is made at the end of each loop by multiplying d by the constant f defined as

$$\begin{aligned} f = \frac{1}{exp (ln(2) \times (n/P)^{Q})} \;, \end{aligned}$$

where n is the number of jobs. The values P and Q are parameters that have to be calibrated. The parameter P defines the number of jobs needed for f to reach 50%. Q is the parameter used to attenuate the change rate of the function. Figure 2 illustrates the function with some values set for P and Q.

Fig. 2
figure 2

Examples of function f(n)

Full size image

The IRACE software package (Lopez-Ibanez et al. 2016) is used to determine the appropriate parameter settings. This package automatically finds the most appropriate parameter values for optimization algorithms given a set of instances and parameter ranges. A set of 120 instances was created for this purpose, composed by all combinations of \(n \in \) {5, 10, 20, 40, 80, 160} and \(m \in \) {4, 8, 12, 16}, with 5 different problems for each combination \(n \times m\). It was considered for calibration \(N \in \) {150, 300, 450, 600, 750, 900} and \(P \in \) {\(4^{-1}, 3^{-1}, 2^{-1}, 1, 2, 3, 4\)}. The processing times have a uniform distribution in the range [1, 99]. The sequence dependent setup times are at most 10% of the maximum processing times. In order to generate due dates, a uniform distribution between \(L(1 - T - R/2)\) and \(L(1 - T + R/2)\) was used where T represents a tardiness factor, R represents the due date range, and L denotes an approximate value for makespan. This is a consolidate approach in literature to generate due dates (e.g., Aldowaisan and Allahverdi 2012; Fernandez-Viagas and Framinan 2015; Framinan and Perez-Gonzalez 2018). The values 0.25 and 1.0 were defined for T and R, respectively. The tuning was performed using a computation time limit of \(n \times (m/2) \times 25\) ms as stopping criterion (see Ruiz and Stützle 2008). The best parameter values obtained are \(P = 300\) and \(Q = 2\).

4 Computational experiments

All algorithms were implemented in C++. The computer used was a PC with an AMD Quad-Core Processor A12-9720P 3.60 GHz and 8 GB RAM running under a Windows 10 operating system. This study considers the test problems proposed by Minella et al. (2008) and Ruiz and Stützle (2008), which are extensions of the benchmarks of Taillard (1993). The processing times have a uniform distribution in the range [1, 99]. We use five instance sets with ratio of setup times \(s \in \) {0, 10, 50, 100, 125} of the maximum processing times. Each set consists of 10 problems for each combination \(n \times m\) of {20, 50, 100} \(\times \) {5, 10, 20} and 200 \(\times \) {10, 20}. The first set called SDST0 is taken from Minella et al. (2008) and has no setup times. The remaining sets called SDST10, SDST50, SDST100, and SDST125 are taken from Ruiz and Stützle (2008) and have times uniformly distributed in the range [1, 9], [1, 49], [1, 99] and [1, 124], respectively. Thus, there are 550 instances in total. In order to provide an easy and fair comparison, all methods were tested by using the same initial solutions (and K values) obtained from Algorithm  1.

The stopping criterion used was the CPU time limit defined as \(n \times (m/2) \times t\) ms. The experiments were performed for \(t \in \{10, 20, 30, 40\}\) to analyze the algorithms in different available computational times. The solutions were evaluated by using the average relative percentage deviation (ARPD) defined as

$$\begin{aligned} ARPD_{h} = \frac{100}{N} \sum _{i=1}^{N} \frac{TT_{i}^{h} - TT_{i}^{best}}{TT_{i}^{h}}, \end{aligned}$$

where \(ARPD_{h}\) represents the performance of a heuristic h. In other words, this measure consists of the arithmetic mean of the deviations of a heuristic h from each best known solution. Therefore, the best heuristic is the one with the lowest ARPD value.

Table 1 ARPD results
Full size table
Fig. 3
figure 3

ARPD versus jobs and machines

Full size image
Fig. 4
figure 4

ARPD versus setup and time

Full size image
Table 2 Multiple comparison of means—Tukey’ HSD test
Full size table
Fig. 5
figure 5

Multiple comparisons between all pairs (Tukey)

Full size image

The ARPD results over jobs and machines are presented in Table 1(a). Table 1(b) gives the results over setup and time factors. It should be noted that the ARPD values of \(IG_{A}\) are disproportionately higher for time factor \(t = 10\). The reason for this is that the time limits generated in this condition may not be sufficient for the algorithm to complete the first iteration, especially in cases with small instances. Others minor differences can be explained by the fact that the benchmarks used have due dates produced by different strategies. Despite that, the performance behaviors and their differences are very clear as can be seen in Figs. 3 and 4. As noted, the differences between the algorithms tend to decrease when the setup factor and especially the number of jobs increase. On the other hand, in general, the errors get bigger when the number of machines increases. Variations in the time factor do not appear to have much effect for values above 10. In all cases, \(IG_{A}\) has a significant advantage over the other methods. The overall ARPD values of \(IG_{A}\), PA, and AA are 4.23, 39.98 and 56.28, respectively.

The Tukey’ honestly significant difference (HSD) test was conducted to analyze the statistic difference between the methods. The null hypothesis that two algorithms have equal performances was tested at a significance level of 5%. The results in Table 2 show that all algorithms are statistically different from each other. The differences at a confidence interval of 95% are illustrated in Fig. 5. As can be noted, \(IG_{A}\) outperform the second best method by about 35% and the third best by about 52%.

5 Conclusion

In this work, the NWT-FSP-SDST is addressed. The objective is to minimize total tardiness subject to the constraint that makespan does not exceed a maximum acceptable value. An iterated greedy algorithm was proposed to solve the problem. The proposed approach was tested against the existent algorithms AA and PA, which are designed to solve the most similar problems found in the literature. Experiments under the same computational conditions show that \(IG_{A}\), PA and AA obtained overall ARPD values of 4.23, 39.98 and 56.28, respectively. Therefore, \(IG_{A}\) outperforms the literature methods.

There are some issues that can be investigated in the future. First, the proposed algorithm was compared with the best literature methods for similar problems. However, adapting other methods for different applications in future experiments could be promising. Another option is to consider additional factors like number of machines to determine the destruction strength of the proposed algorithm. In this work, only the number of jobs was considered for this purpose and therefore it may be possible to get better results with a broader approach. Additionally, the diversification/intensification behavior of the heuristic can be further explored. For example, it can be favorable to examine new strategies that combine greedy searching with random perturbations, both in destruction and construction phases.