Keywords

1 Problem Definition

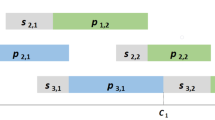
We are engaged in this research with generating an efficient optimization technique for the subsequent scheduling problem. Each of N jobs from the job set \(J={1; 2;\ldots ; N}\) has to be processed on m consecutive machines from the machine set \(M=(j=1,2,\ldots ,m)\) during a \(p_{ij}\) time units. The process of each job on each machine is exactly the same and once the process is started it may not be broken down. A job i can have a given due date \(D_{i}\) corresponding to the perfect time that it should be completed. Besides, each job can be processed only on one machine at a time and each machine can process at most one job at a time. No passing is allowed.

Considering the above assumptions, we are facing some blocking constraints: buffers between consecutive pair of machines are stated with zero capacity. That is a current machine j may be blocked by the job it has processed if the next machine is not discharged. This environment is completely different from the No-wait Flow Shop setting where when a job is started on the first machine, it must be constantly processed till its achievement on the last machine without interruption.

This research deals with the Blocking Flow Shop Scheduling Problem (BFSP) to minimize the total tardiness of jobs, denoted as \(Fm|block|\sum {T_{j}}\) according to the notation proposed in [1]. This variant of flow shop problems has important impact in manufacturing systems since when a job is not finished by its due date then supplementary costs are incurred.

The tardiness is defined as the maximum time between zero and the lateness of a job settled as the difference between the completion time of a job and its fixed due date. In general, the \(Fm|block|C_{max}\) is strongly NP-hard [2]. This is an immediate consequence of the NP-hardness of the \(Fm||C_{max}\). The case of two machines (\(m=2\)) may be easily solved using Gilmore and Gomory’s scheme [3].

Formally, the BFSP may be formulated using the following equations [4], where \(C_{\pi _{i},M}=d_{\pi _{i},M}\) is the completion time of job \(\pi _{i}\) on machine M, \(d_{\pi _{i},j}\) \((i=1,2,\ldots ,N; j=0,1,2,\ldots ,M)\) represents the departure time of job \(\pi _{i}\) on machine j, and \(\varPi :=(\pi _{1},\pi _{2},\ldots ,\pi _{N})\) is a solution for the problem.

$$\begin{aligned} d{_{\pi _{1},0}}=0 \end{aligned}$$
(1)
$$\begin{aligned} d{_{\pi _{1},j}}=\sum {_{k=1}^{j}}p_{\pi _{1,k}}~~~~j=1,2,\ldots ,M-1 \end{aligned}$$
(2)
$$\begin{aligned} d{_{\pi _{i},0}}=d{_{\pi _{i-1},1}}~~~~i=2,\ldots ,N \end{aligned}$$
(3)
$$\begin{aligned} d{_{\pi _{i},j}}=max\{{d{_{\pi _{i},j-1}}+p{_{\pi _{i},j}},d{_{\pi _{i-1},j+1}}}\}~~~~i=2,\ldots ,N;j=1,2,\ldots ,M-1 \end{aligned}$$
(4)
$$\begin{aligned} d{_{\pi _{i},M}}=d{_{\pi _{i},M-1}}+p{_{\pi _{i},M}}~~~~i=1,2,\ldots ,N \end{aligned}$$
(5)
$$\begin{aligned} TT(\varPi )=\sum _{i=1}^{n} (max\{0,(C_{\pi _{i}}-D_{i}\}) \end{aligned}$$
(6)

The literature regarding a BFSP is not extensive. Indeed, the tardiness criterion has been studied fewer than the makespan and total flow time criteria. We rapidly review the related literature.

As a constructive heuristics, we refer to the Profile Fitting (PF) [5], the Nawaz-Enscore-Ham heuristic (NEH) [6], the MinMax (MM) and combination of MM and NEH (MME) and combination of PF and NEH (PFE) [7] techniques. In [8, 9] the NEH-WPT heuristic and a constructive and a GRASP-based heuristics for the BFSP were introduced, respectively.

Concerning meta-heuristics, we refer to the Genetic Algorithm (GA) proposed in [10], the (Ron) algorithm developed in [11], and the Tabu Search (TS) and the enhanced TS techniques used in [12]. Meanwhile, we cite the Hybrid Discrete Differential Evolution (HDDE) algorithm introduced in [13] which was compared to the Hybrid Differential Evolution (HDE) algorithm developed in [14], and the Iterated Greedy (IG) method in [15].

Thus far, it was proven that RON, HDDE, and IG algorithms give competitive results and may be considered as top techniques for the BFSP under makespan.

Now, under the total flow time criterion, we refer to the hybrid modified global-best Harmony Search (hmgHS) algorithm and the Discrete Artificial Bee Colony algorithm (DABC_D) technique presented in [8, 16], respectively, and the Greedy Randomized Adaptive Search Procedures (GRASP) hybridized with the Variable Neighbourhood Search (VNS) technique in [17].

Besides, we cite the effective hybrid discrete artificial bee colony algorithms proposed in [18], and the Revised Artificial Immune Systems (RAIS) technique in [19]. A three-phase algorithm under \(C_{max}\) is presented in [20] and a Discrete Particle Swarm Optimization algorithm with self-adaptive diversity control was treated in [21].

Also, we cite the Memetic Algorithm (MA) in [22], the chaos-induced discrete self organizing migrating algorithm in [23], the Iterated Local Search algorithm (ILS) coupled with a Variable Neighbourhood Search (VNS) in [24], and the Blocking Genetic Algorithm (BGA) and Blocking Artificial Bee Colony (BABC) algorithms in [25].

Under tardiness measure, few papers were found. Basically, the Tabu Search method proposed in [26], the NEH-based method called (FPDNEH) and the Greedy Randomized Adaptive Search Procedure(GRASP) developed in [9], and the Iterated Local Search algorithm (ILS) hybridized with the Variable Neighbourhood Search (VNS) technique in [24].

Therefore, it is interesting to intensify research to develop simple algorithms which are easy to adapt and implement in practical applications. In this paper we propose an Iterated Greedy algorithm (IG) to minimize the tardiness of scheduled jobs in a flow shop environment with blocking. We restrict our attention solely to permutation schedules.

Following this brief definition, the paper is structured as follows. The IG algorithm under blocking is explained in Sect. 2. Section 3 presents the numerical experiments, and Sect. 4 summarizes the conclusions.

2 Iterated Greedy Algorithm for the Blocking Flow Shop Problem

The iterated greedy algorithm is very well adapted to solve combinatory problems, and especially various flow shop instances [27]. In an iterative way, the greedy method uses constructive techniques to generate new solution based on some other fixed solution, and then decides if it will be accepted and replace the old one based on some acceptance criterion.

The destruction and construction stages are employed to obtain a sequence of solution. The destruction stage deletes some elements from the designated solution. After that, a new sequence is obtained by reforming a whole solution based on constructive heuristic, which rearranges the removed elements in some order to form a final sequence. Optionally, the obtained sequence (final) may be subjected to local search stage for enhancement.

One important point to note is that IG is closely related to the Iterated Local Search (ILS). The difference between them is that in IG the perturbation of an incumbent solution is done by means of the destruction and construction phases, whereas in ILS the perturbation is done just for escaping from local optimum.

Now, details of the algorithms are presented below.

2.1 Seed Sequence

To yield the initial sequence, the PF-NEH(x) heuristic proposed in [25] has been used. Nevertheless, instead of generating x solutions at the end of the heuristic, we select only the permutation with the minimum tardiness value. With a probability \(P_{ls}\), we have also used a local search technique based on the insertion operator to generate neighboring solution. A fixed job is removed from its first position and reinserted in all feasible places. Then, the new obtained sequence is recorded only when there is an enhancement in the objective value. The final permutation \(\varPi ^{s}\) thus generated forms the seed sequence.

2.2 Destruction and Construction Phases

The destruction stage is started based on the initial seed sequence generated as explained earlier. Iteratively, the current stage starts with a whole sequence \(\varPi ^{s}\) and then removes [\(q*\varPi ^{s}\)] randomly jobs from \(\varPi ^{s}\). The degree of destruction q is drawn in the range [0,1]. This yields two sub-solutions: the first one models the removed jobs \(\varPi ^{r}\), and the second represents the rest of the sequence after deleting jobs \(\varPi ^{s}\).

In the construction stage, a final solution \(\varPi ^{c}\) is then reformed by replacing the previously extracted jobs in the order in which they were removed.

The procedures of the destruction and construction stages are as in Tables 1 and 2.

Table 1 Procedure destruction stage (\(\varPi ^{s}\), q)
Full size table
Table 2 Procedure construction stage (\(\varPi ^{q}\), \(\varPi ^{r}\))
Full size table

2.3 Acceptance Measure and Final IG Algorithm Under Blocking

An acceptance measure is applied to decide wether the generated sequence will be accepted or not. As in [27, 28], we have used the Simulated Annealing (SA) acceptance measure to approve ‘bad’ solutions with some fixed probability.

This acceptance criterion is employed with a certain temperature value depending on the number of jobs, machines, and on other tractable parameter \(\lambda \):

$$\begin{aligned} Tempt=\lambda *\frac{\sum _{i=1}^{N}\sum _{j=1}^{M}p_{ij}}{10*M*N} \end{aligned}$$
(7)

Let \(TT(\varPi ^{s})\) and \(TT(\varPi ^{c})\) be respectively the total tardiness values of the current incumbent solution and the new reconstructed solution. Also, let rand() be a function returning a random number sampled from a uniform distribution between 0 and 1.

If \(TT(\varPi ^{c})\ge TT(\varPi ^{s})\), Then \(\varPi ^{c}\) is accepted as the new incumbent solution if:

$$\begin{aligned} rand()\le exp\{TT(\varPi ^{c})-TT(\varPi ^{s})/Tempt\} \end{aligned}$$
(8)

Considering all previous subsections, the proposed IG algorithm under blocking goes as in Table 3.

Table 3 IG algorithm under blocking
Full size table

3 Numerical Experiments

This section focuses on computational experience with the proposed IG algorithm under blocking. Its performance obtained by comparing the resulting solutions (total tardiness) with respect to one competitive algorithm from the literature was investigated. We performed experiments on a well-known set of benchmark instances [9]. These instances are composed of 5 groups which are a combination of 20, 50, 100, 200 and 500 jobs with 5, 10 and 20 machines. The processing times of jobs and due dates are uniformly distributed between [29, 99] and \(P(1-T-R/2)\) and \(P(1-T+R/2)\), respectively. T is the tardiness factor, R is the due-date range [30], and P is a valid LB [31].

As well, the Relative Percentage Deviation (RPD) is numbered once an instance is launched (with 10 replications) and calculated according to the following recursion. \(TT^{A}\) is the tardiness value obtained using the proposed technique and \(TT^{Min}\) represents the minimum tardiness value obtained among the two compared algorithms.

$$\begin{aligned} RPD(A)= \frac{(TT^{A}-TT^{Min})\times 100}{TT^{Min}} \end{aligned}$$
(9)

The IG algorithm under blocking is coded in Visual C++ and run on an Intel Pentium IV 2.4 GHz PC with 512 MB of memory. Our technique establishes a relatively simple mechanism where there are basically four parameters which must be properly established. These are the MCN, \(P_{ls}\), \(\lambda \), and q. We analyzed these parameters using one generated instance with \(n=150\) and \(m=10\). The due dates of the jobs were generated following the TWK rule [32]. We fix this size since it represents a challenge given the number of jobs and machines that must be satisfied (large instance). For each analysis, we vary only the parameter of interest to study its impact on the final solution and on the convergence rate of the IG. After extensive testing, parameters were set to the following values: \(MCN=100\), \(P_{ls}=0.2\), \(\lambda =2\), and \(q=3\).

3.1 Evaluation of the IG Algorithm Under Blocking

To prove the good quality of our presented IG for the BFSP, we wanted to compare our technique to other meta-heuristics that are already used in the literature for dealing with our problem. Our IG was compared against the obtained results by the GA algorithm based on the path relinking technique (GA_PR) in [33]. This technique has shown higher efficiencies in solving benchmark for large scale instances. Therefore, this technique was selected for comparison with the IG under blocking. In fact, Table 4 summarizes the computational results of the two compared techniques for all combination of jobs and machines, and where the total tardiness solutions were averaged (comparisons were made based on the ARPD metric).

Table 4 ARPD values under total tardiness measure
Full size table

By analyzing Table 4, it can be seen that IG algorithm presents better average results than the \(GA\_PR\) in the different scenarios. For all test instances, with \(N*M\) varying from (20*5) up to (500*20), the greedy technique enhanced all results. The tested algorithm outperforms the \(GA\_PR\) algorithm in \(97\,\%\) of the classes, and considering the number of superior results, our method outperformed the \(GA\_PR\) in 398 of the 480 test-problems.

4 Final Remarks

Different from other sophisticated techniques, this greedy algorithm has few parameters to be adjusted, which makes it more simpler to be implemented and used to solve the BFSP. Also, the IG under blocking presented a significant improvement in all test instances. Its superiority against \(GA_PR\) algorithm should be attributed to the smart combination of greedy stages (destruction and construction), local search, as well as to the use of new version of the PF-NEH heuristic. Future work involving the tardiness criterion could include designing another procedure for comparing algorithms. We also expect to apply the IG for multi-objective scheduling problems.