Heuristics for flow shop rescheduling with mixed blocking constraints

Abstract

In the flow shop rescheduling literature, many papers consider unlimited buffer capacities between successive machines. In real fact, these capacities may be limited, or no store may exist. Thus, a blocking situation is inducted. Diverse types of blocking constraints are studied in the flow shop scheduling problems. However, in dynamic environments, only few papers deal with these kinds of constraints. The aim of this paper is to investigate a problem of rescheduling the jobs in a flowshop environment and mixed blocking as a constraint, considering simultaneously schedule efficiency and stability as a performance measure, and job arrival as a disruption. An iterative methodology based on the predictive–reactive strategy is implemented for dealing with this rescheduling problem. The problem has first been modeled as a Mixed Integer Linear Programing (MILP) model. Experimental results show that the MILP resolution is only possible for small-sized instances. Hence, inspired by NEH algorithm, we proposed four heuristics for solving large-sized instances of this problem. Eventually, we discussed the performance of the proposed heuristics for different blocking situations, both in terms of solution efficiency and resolution time.

1 Introduction and literature review

The adoption of digital technology in services companies has completely changed the customer’s practices (Mula and Bogataj 2021). From now on, a customer can, in real time, create, modify, or cancel an order using new technological tools, such as mobile phone applications or companies’ websites. To keep a competitive edge, the companies must be adapted to these orders uncertainties. In fact, the possibility to change the order’s information has an impact on the production scheduling (Şenyiğit et al. 2022). Although traditional scheduling properly organizes the production system planning (Pitombeira-Neto and Prata 2020), this one will be invalid when a new disruption occurs. Therefore, the decision-makers must quickly react so as not to stop completely the production. As a consequence, the process of revising an existing schedule in response to disruptions, referred to as rescheduling, becomes a major issue for the enterprises, as well as an interesting research area.

Several papers have already established literature reviews of the rescheduling problems. Vieira et al. (2003) is among the well-known works that have provided a detailed definition of this process, and described its framework, methods, and strategies. The following works can also be noticed, Li et al. (2020), Serrano-Ruiz et al. (2021) and recently Mohan et al. (2022). In the scheduling literature, different types of machines environments have been studied, such as single machine representing a single workstation (Hall and Potts 2004; Prata et al. 2021), resources constrained (Machado-Dominguez et al. 2022), parallel machines representing identical or non-identical workstations (Kovalyov et al. 2019; Akyol Ozer and Sarac 2019; De La Vega et al. 2023), job shop (Yan et al. 2018; Serrano-Ruiz et al. 2022), flexible job Shop problem (Auer et al. 2021), and open shop (Liu and Zhou 2013; Ozolins 2021). Numerous papers are also dealing with flow shop rescheduling. Rahmani and Ramezanian (2016) investigated a flexible flowshop rescheduling problem, with the arrival of new jobs as a disruption, the weighted tardiness as an efficiency measure, and the absolute deviation of completion times as a stability measure. The authors adopted a predictive–reactive rescheduling strategy and designed a variable neighborhood search algorithm to solve their problem. Katragjini et al. (2013) considered a permutation flow shop rescheduling problem. They assumed three simultaneous random disruptions, the arrival of new jobs, machine breakdowns, and release time delays. Makespan is considered as the schedule efficiency criterion, and the number of starting times altered tasks as the stability measure. The authors proposed an iterated greedy algorithm to solve the described problem. The following papers also present interesting studies about flow shop scheduling problems, Uhlmann et al. (2022) and Bautista-Valhondo and Alfaro-Pozo (2020).

The scheduling problems generally use classical efficiency criteria to assess the schedule performance. For instance, the makespan (Sayed et al. 2020; Valledor et al. 2022), the total completion time (Druetto et al. 2022), the total tardiness (Zhang et al. 2022a, b), the total weighted tardiness (Haroune et al. 2022), the number of tardy jobs (Zhang et al. 2013), and the multiple efficiency measures (Kacem and Dammak 2021) are criteria that have already been studied. However, in dynamic environments, other measures can also be considered. Stability criteria, limiting the deviation from the initial schedule, are often associated with the efficiency criterion. They measure the penalty induced by moving jobs due to disruptions. In fact, the schedule movement generates supplementary costs, like reallocation costs, or raw materials reordering costs. Akkan (2015) considered a single machine rescheduling problem, disrupted by new jobs arrival. The authors associated the schedule efficiency and stability. They considered the maximum tardiness as an efficiency criterion, and the sum of the absolute starting time deviations as a stability measure, which is the sum of the absolute difference between the starting time of a job before and after the rescheduling. Other stability criteria have already been investigated in the rescheduling literature, for example the number of jobs that change of machine after rescheduling (He et al. 2020), change in human resources assignments (Xiao et al. 2010), and the maximum time disruption (delivery times of jobs to customers changes) (Liu and Ro 2014). Different from existing literature, this work investigates two performance measures. At first, regarding the schedule efficiency, the Total Weighted Waiting Time (TWWT) is used as a criterion. This measure is inspired from real-life systems, it represents the job waiting time in front of a workstation, or the patient waiting time in the case of hospital system (Braune et al. 2022), assuming the weight as the customer priority. Tighazoui et al. (2021a) considered a problem of the TWWT minimization combined with a stability criterion in a flowshop rescheduling problem. The authors explain that the problem can be an illustration of real-life systems. For example, in production systems, it can be regarded as the waiting period of a product in front of an installation and the weight as the product priority. In hospital systems, it can represent the delay between a patient’s arrival and his actual treatment, considering the emergency level as a weight. Guo and Xie (2017) formulated two MILP models for a single machine rescheduling problem with the total waiting time as an objective. The studied problem came from a quartz glass factory, considering that the waiting time is the waiting of materials before the welding step. Kan (1976) classified the problem of the minimization of the average waiting time as NP-hard for a single machine scheduling. Second, concerning the schedule stability, the Total Weighted Completion Time Deviation (TWCTD) is considered as a criterion. It consists of assessing the deviation between the completion times of a job, when it is scheduled for the first time and after the rescheduling, associating a weight for each job, to penalize more largely the important orders (Tighazoui et al. 2020). This association of criteria has already been introduced in Tighazoui et al. (2021b) for the parallel machines rescheduling problem. The authors observed that due to a proactive effect, the stability measure provides better solutions compared to a mono criterion considering only the efficiency. Now, the aim is to analyze the criterion behavior in a flow shop rescheduling problem with blocking constraints.

Most of flow shop rescheduling problems assume that the buffer spaces capacities between successive machines are unlimited. In actual industrial systems, the store between successive machines is generally limited or no store space may exist. Thus, a blocking situation is generated, referred to as blocking constraint. In the rescheduling literature, only few papers are interested in this question (Kecman et al 2013; Tao and Liu 2019). Different types of blocking constraints have already been investigated in static flow shop scheduling. The classical RSb (Release when Starting Blocking) constraint for example has been introduced in Wang et al. (2006). It describes the case where a machine is blocked by a job, until the job starts on the following machine. RCb or RCb* (Release when Completing Blocking) describes the case where a machine is blocked by a job, until this one ends on the following machine (RCb*) (Yuan et al. 2009; Trabelsi et al. 2011) or starts on the further next one (RCb) (Martinez et al. 2006). Mixed blocking constraints represent the case where successive machines can be simultaneously subject to any combination of previous blocking constraints (Trabelsi et al. 2012). To fill the void, the present paper treats a flow shop rescheduling problem with different types of constraints mixed in one production system. The aim is to study a general case in which the decision-maker can choose the type of blocking constraint to apply between two successive machines. An example of mixed blocking constraints can be found in the cider brewing process. In this application, it is not possible to simultaneously brew apples for different customers. In this process, pouring the apples into the vat represents stage 1, grinding the apples is stage 2, and pressing the apples to make juice is stage 3. Between stage 1 and 2, there is an RSb constraint since all the apples must be poured before starting the grinding. Between stages 2 and 3, there is an RCb constraint since the apples of a new customer cannot be poured into the vat until all the apples of the first customer have been pressed.

Rescheduling strategies are classified in two basic categories (Herrmann 2006). Dynamic scheduling strategy consists in dispatching the jobs, using some rules at the moment of dispatching. In this strategy, heuristics are used to choose the sequence of the jobs that will be proceeded on the machine (Wu et al. 2022; Zhang et al. 2022a, b). Predictive–reactive scheduling strategy consists of generating an initial schedule at the first step, then updating it at each time a disruption occurs (Manzini et al. 2022). Gürel et al. (2010) used a predictive–reactive strategy on a parallel non-identical machines’ problem with controllable processing times. In the predictive phase, an initial schedule is generated to minimize the total manufacturing costs of the jobs. In the reactive phase, after a disruption caused by machines breakdowns, the schedule is repaired. In our paper, the predictive–reactive scheduling strategy is also adopted. In the predictive step, the flow shop scheduling problem with mixed blocking constraints is solved with the objective of minimizing the TWWT. After disruption occurrence, the reactive step starts, solving the rescheduling problem, but considering this time the TWWT as a criterion combined with the TWCTD. These two criteria are associated by the efficiency–stability coefficient α, representing a ponderation between both parts of the objective function (α TWWT + (1 − α) TWCTD).

The present work addresses a problem of rescheduling the jobs in a flowshop environment, mixed blocking as a constraint, and the arrival of the jobs as a disruption. A MILP formulation is designed to describe the problem, as well as an iterative methodology based on the predictive–reactive scheduling strategy. Experimental results show that the MILP resolution is only possible for little size instances. Hence, inspired by NEH algorithm, we proposed four heuristics for solving large size instances of this problem. These heuristic methods have been compared to the resolution based on the MILP model, both in terms of accuracy and computation time. To the best of our knowledge, no other work was interested in studying this kind of problem. The main contributions of this paper are:

• Investigating for the first time a flow shop rescheduling problem with mixed blocking constraints.

• Simultaneously integrating the schedule efficiency and stability in the described problem.

• Designing a MILP model for this problem, and heuristic methods allowing to browse more jobs in a reasonable time.

The outline of the paper is as follows: Sect. 2 presents a description of the problem and the predictive–reactive strategy adopted to tackle it. Section 3 explains the MILP formulation of the offline problem, and the additional equation used to solve the online problem. In Sect. 4, heuristic methods are described. In Sect. 5, experimental results are presented and discussed. Finally, a conclusion and some perspectives are given in Sect. 6.

2 Problem description and methodology

In this section, the problem is described, as well as the predictive–reactive scheduling strategy proposed to handle the disruptions.

2.1 Problem description

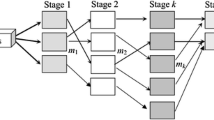
A flow shop rescheduling problem with different types of blocking constraints is studied in this section. The system is also disrupted by the arrival of new jobs. To each job, j is associated a processing time on the machine m, p_jm, a weight w_j and a release date r_j. Preemption is not assumed in this problem. Thus, when a job j starts its execution in the system, it proceeds up to the completion time CT_jm. Efficiency measure, stability measure, and blocking constraints are explained hereafter.

The efficiency measure: W_j is the waiting time of the job j. It represents the total period that the job j waits in the system before its complete execution.

In Fig. 1, the red lines represent the total period that job j waits in the system before its complete execution, it also represents the sum of the waiting periods that a job waits in front of the successive machines (workstations). Hence, the waiting time W_j is defined as: $W_j = {\text{CT}}_{j\,nm} - r_j - \sum_{m = 1}^{nm} {p_{jm} } \,$, where CT_{j nm} is the job j completion time on the last machine.

Fig. 1

Waiting time of a job j

It is assumed that N = {1, 2, …, n} is the set of jobs, and M = {1, 2, …, nm} is the set of machines. At time t = 0, the set of jobs N are already available. Thus, the initial problem to solve before the disruptions consists in minimizing $\sum_{j = 1}^n {w_j W_j }$, referred to as the TWWT.

The stability measure: let CTo_jm be the original completion time of the job j on the machine m. It corresponds to the job j completion time when it is scheduled for the first time. After the occurrence of new jobs, the schedule may change, and the job j may then actually end at CT_jm, its actual completion time. Thus, the difference between CT_jm and CTo_jm is the completion time deviation. In addition, the weight w_j is associated to each job j to penalize more largely the deviation of the important orders. In order to normalize this criterion with respect to the efficiency measure, it is divided by the number of machines nm. So, the stability measure is then defined as $\frac{1}{nm}\sum_{j = 1}^n {\sum_{m = 1}^{nm} {w_j ({\text{CT}}_{jm} - {\text{CTo}}_{jm} )} }$, referred to as the TWCTD.

Both parts of the objective function are associated with α, the efficiency–stability coefficient. Thereby, the function simultaneously considers the schedule efficiency and the stability is:

$$\alpha \sum_{j = 1}^{n^{\prime}} {w_j W_j } + (1 - \alpha )\frac{1}{nm}\sum_{j = 1}^n {\sum_{m = 1}^{nm} {w_j ({\text{CT}}_{jm} - {\text{CTo}}_{jm} )} }$$

As can be seen, only the set N of jobs are concerned by the stability criterion. N contains the jobs existing before the occurrence of a disruption. N’ = {1, 2, …, n’} is the set of jobs which contains the currently unexecuted jobs (i.e., the jobs that have not started) combined with the newly arrived ones.

The mixed blocking constraints: Most of flow shop rescheduling problems consider unlimited buffer space capacities between successive machines. This case is referred to as without blocking constraint (Wb). There is also the case of classical blocking constraints RSb when the machine is blocked by a job until this one starts in the following machine. Specific constraint RCb* can also be considered. It describes the case where a machine is blocked by a job until this one is finished on the following machine. RCb constraint is a particular case where a machine is blocked by a job, until this one is finished and left the next machine, this time then corresponds to the starting time of the job on the third machine. To illustrate the difference among these blocking constraints, we present in Fig. 2 an example with four jobs and five machines. The matrix of processing times is given by:

Fig. 2

Flowshop with different blocking constraints. a Wb, b RCb*, c RSb, d RCb

$$pjm = \left(\begin{array}{c}\begin{array}{ccc}1& 1& \begin{array}{ccc}2& 1& 2\end{array}\\ 1& 3& \begin{array}{ccc}2& 2& 1\end{array}\\ 1& 1& \begin{array}{ccc}2& 2& 1\end{array}\end{array}\\ \begin{array}{ccc}3& 2& \begin{array}{ccc}1& 1& 1\end{array}\end{array}\end{array}\right)\; j \epsilon \left\{1,..,4\right\}, m \;\epsilon \{1,..,5\}$$

In Fig. 2a, there is no blocking situation. Thus, each machine is available to treat a job as soon as the previous job is finished. In Fig. 2c, job J₃ remains blocked on machine M₁ while the machine M₂ is executing job J₂. In Fig. 2b, illustrates the case when job J₃ blocks the machine M₁ until the operation J₃ on M₂ will finish. In Fig. 2d, illustrates the case when job J₃ blocks the machine M₁ until the operation J₃ on M₂ will finish and it will leave this machine. This date corresponds to the operation beginning of job J₃ on the machine M₃.

In this work, we assume that all those described constraints can be mixed in one production system, with any combination. Thereby, a vector V is introduced, to describe a sequence of constraints between the successive machines of the problem. For instance, V = (RCb, RSb, RCb*, Wb) can be a blocking constraints vector for the 5-machines problem presented on Fig. 3. Different combinations of the vector V are studied in the experimental results section.

Fig. 3

Mixed blocking constraints with the vector V(RCb, RSb, RCb*, Wb)

2.2 Predictive-reactive scheduling strategy

In order to solve the flow shop rescheduling problem, we implemented a predictive–reactive scheduling strategy. It consists in solving at first, a problem of minimization of the TWWT efficiency measure. At the appearance of a new job, this one will be combined with the yet uninitiated jobs and the schedule will be updated. The new objective function contains a part of schedule efficiency measured with TWWT, as well as a part for assessing the schedule instability TWCTD. For simulating this matter, a finite time horizon [0, T] is defined, and discretized into periods Δt. The occurrence of a job may be possible only at these periods. It is assumed that Δt = 1 unit of time, and one job can arrive per period. In several industrial cases, it is common to urgently treat the arrival of one order. When a job arrives at time t, this date will correspond to its release date. Accordingly, the variable β(t) is defined, equal to one if a job appears and zero otherwise.

$$\beta (t) = \left\{ \begin{gathered} 1\quad {\text{if}}\,{\text{a}}\,{\text{job}}\,{\text{appears}} \hfill \\ 0\quad {\text{Otherwise}} \hfill \\ \end{gathered} \right.$$

(1)

The flowchart presented in Fig. 4 describes the proposed predictive–reactive scheduling strategy. This methodology consists of going through the simulation horizon step by step and checks whether a job appears thanks to the state of β(t). If β(t) = 1, the problem data, constraints, and the objective function are updated. Then, the new problem is solved.

Fig. 4

Predictive–reactive scheduling strategy

3 Mathematical models

According to the chart presented in Fig. 4, two phases of resolution are implemented. The first is before the disruption, referred to as the offline resolution. The second operates after the occurrence of the disruptions and is referred to as the online resolution. Accordingly, the two mathematical models corresponding to both phases are described in this section.

3.1 The offline mathematical formulation

To build our mathematical formulation, we adapted the parallel machine model presented in Tighazoui et al. (2020) to a flow shop environment with mixed blocking constraints. The presented model is based on assigning jobs to positions. Variables, parameters, and constraints are given hereafter:

3.1.1 Parameters

N: set of jobs {1, 2, …, n}.

K: set of positions {1, 2, …, n}.

M: set of machines {1, 2, …, nm}.

j: index of job, j = 1, 2, …, n.

k: index of position, k = 1, 2, …, n.

m: index of machine, m = 1, 2, …, nm.

w_j: weight of job j.

r_j: The release date of job j.

p_jm: processing time of job j on machine m.

$$B_{hm} = \left\{ \begin{gathered} 1\,\,\,\,{\text{if}}\,{\text{there}}\,{\text{is}}\,{\text{a}}\,{\text{blocking}}\,{\text{constraint}}\,{\text{of}}\,{\text{type}}\,h\,{\text{between}}\,{\text{the}}\,{\text{machine}}\,m\,{\text{and}}\,m + {1} \hfill \\ 0\,\,\,{\text{Otherwise}} \hfill \\ \end{gathered} \right.$$

with: h = 1 if there is no blocking constraint between the machine m and m + 1.

h = 2 if there is a blocking of type RSb between the machine m and m + 1.

h = 3 if there is a blocking of type RCb* between the machine m and m + 1.

h = 4 if there is a blocking of type RCb between the machine m and m + 1.

bigM: big value.

3.1.2 Decision variables

$$X_{jk} = \left\{ \begin{gathered} 1\quad {\text{if}}\,{\text{the}}\,{\text{job}}\,j\,{\text{is}}\,{\text{assigned}}\,{\text{to}}\,k{\text{th}}\,{\text{position}} \hfill \\ 0\quad {\text{Otherwise}} \hfill \\ \end{gathered} \right.$$

S_km: Starting time of the job in kth position on machine m.

C_km: Completion time of the job in kth position on machine m.

CT_jm: Completion time of job j on machine m.

W_j: Waiting time of job j.

Objective function ${f}_{1}={\sum }_{j=1}^{n}{w}_{j}{W}_{j}$, the objective is to ${\mathrm{Minimize} f}_{1}$ subject to:

$$\sum_{k = 1}^n {X_{jk} } = 1\,\,\,\forall j \in N$$

(2)

$$\sum_{j = 1}^n {X_{jk} } = 1\,\,\,\forall k \in K$$

(3)

$$C_{k{\text{m}} } = S_{k\,m} + \sum_{j = 1}^n {p_{j\,m} X_{jk} } \,\,\forall k \in K,\,\forall m \in M$$

(4)

$$S_{k{\text{m}} } \ge \,\,C_{k\,m - 1} \,\,\forall k \in K,\,\forall m \in \left\{ {2,\,\,...,nm} \right\}$$

(5)

$$\begin{gathered} S_{k{\text{m}} } \ge C_{k - 1\,\,m} \cdot B_{1m} \, + S_{k - 1\,\,m + 1} \cdot B_{2m} + C_{k - 1\,\,m + 1} \cdot B_{3m} + S_{k - 1\,\,m + 2} \cdot B_{4m} \, \hfill \\ \,\forall k \in \left\{ {2,\,\,...,n} \right\},\,\forall m \in \left\{ {1,\,\,...,nm - 2} \right\} \hfill \\ \end{gathered}$$

(6)

$$S_{k\,nm - 1} \ge C_{k - 1\,\,nm - 1} \cdot B_{1\,nm - 1} \, + S_{k - 1\,\,nm} \cdot B_{2\,nm - 1} + C_{k - 1\,\,nm} \cdot B_{3\,\,nm - 1} \,\,\forall k \in \left\{ {2,\,\,...,n} \right\}$$

(7)

$$S_{k\,nm} \ge C_{k - 1\,\,nm} \,\,\forall k \in \left\{ {2,\,\,...,n} \right\}$$

(8)

$$S_{km} \ge \sum_{j = 1}^n {r_j X_{jk} } \,\,\forall k \in K,\,\forall m \in M$$

(9)

$${\text{CT}}_{j\,m} \ge C_{k\,m} - bigM(1 - X_{jk} )\quad \forall j \in N,k \in K,\forall m \in M$$

(10)

$${\text{CT}}_{j\,m} \le C_{k\,m} + bigM(1 - X_{jk} )\quad \forall j \in N,k \in K,\forall m \in M$$

(11)

$$W_j = CT_{j\,nm} - r_j - \sum_{m = 1}^{nm} {p_{jm} } \quad \forall j \in N$$

(12)

$$X_{jk} \in \left\{ {0,1} \right\},\quad \forall j \in N,\,\,\forall k \in K$$

(13)

$$S_{km} ,C_{km} ,CT_{jm} ,W_j \ge 0\quad \forall j \in N,k \in K,\,\,\forall m \in M$$

(14)

Constraint (2) specifies that each job is assigned to one position. Constraint (3) specifies that each position is occupied by only one job. Constraint (4) defines the completion time of the position k. Constraint (5) an operation on a machine starts after its completion on the previous machine. Constraint (6) defines the starting time of a position. It depends on different types of blocking constraints, depending on the parameter B_hm. Constraint (7) defines the starting time of a position in the penultimate machine where there is no RCb constraint, as it depends on the two following machines. Constraint (8) defines the starting time in the last machine which can only be without blocking. Constraint (9) makes the starting time of an operation greater than or equal its release date. Constraints (10) and (11) associates the job completion time to the position completion time, where bigM must be sufficiently large. Constraint (12) defines the waiting time of job j, according to its completion time in the last machine, release date, and processing time. Constraint (13) constraints the variable X_jk to be a binary decision variable. Constraints (14) are non-negativity constraints, making all decision variables greater than or equal to zero.

3.2 Online mathematical formulation

This second mathematical formulation is used after a disruption. Thus, all jobs that have already begun their execution before t (the time of disruption) are omitted from the set of jobs. The new parameters are presented hereafter:

3.2.1 Parameters of the online mathematical formulation

Nj: number of new jobs (we assumed in this work that only one job arrives per period nj = 1).

nt: number of unexecuted jobs at time t.

n′ = nt + nj

N’:set of jobs {1, 2, …, n′}.

K’: set of positions {1, 2, …, n′}.

j: index of job j = 1, 2, …, n′.

k: index of position k = 1, 2, …, n′.

CTo_jm: original completion time of job j on machine m.

α: efficiency–stability coefficient.

The same decision variables as previously described are used for this second model. Thus, the new objective function is defined as:

$$f_2 \, = \,\alpha \sum_{j = 1}^{n^{\prime}} {w_j W_j } + (1 - \alpha )\frac{1}{nm}\sum_{j = 1}^n {\sum_{m = 1}^{nm} {w_j ({\text{CT}}_{jm} - {\text{CTo}}_{jm} )} }$$

4 Heuristic methods

The proposed heuristics are based on the initial solution to insert the new job on schedule. The heuristics browse in the simulation horizon step by step, at each step t, if β(t) = 1, a job arrives. This job will be combined with the set of unexecuted jobs, its release date will correspond to the time t, and the last position in the existing schedule will be assigned to it. Then, one of the proposed heuristic methods will be applied. The following algorithm describes this process.

The proposed heuristics are based on the NEH heuristic. This latter is one of the best well known in the scheduling problem since its effectiveness is proven (Nawaz et al. 1983). It is also very simple to implement. NEH algorithm is widely accepted as one of the best simple heuristics for makespan minimization in flow shop scheduling problems (Sauvey and Sauer 2020). As NEH is based on job insertion, it is wise to use it in the case of a disruption due to job arrival, since the new job is inserted into the existing schedule. In our case, we use NEH algorithm evaluating the new objective function f₂. NEH pseudo-code is recalled below:

4.1 Heuristic H1

Description of H1: We consider the list of jobs sequenced in the order of the previous schedule and we insert the new job in all possible positions, starting by the last position. The solution that minimizes the objective function is selected.

Improvement of H1: We consider the sequence obtained by H1 and we put the last job in all possible positions. We select the solution if it is better. We repeat the same operation, while the value of the objective function is improved. We call this heuristic H1*.

Example illustrating H1 and H1*: In Table 1, the processing times p_jm, the release dates r_j and the weights w_j for the 4 jobs are presented. The first 3 jobs are considered in the initial schedule (in offline), for which all information is known in advance, then job 4 arrives at t = 3 (in online). There is no blocking constraints between the machines V(Wb,Wb), and α = 0.5.

Table 1 Problem data of the illustrative example

Optimal initial sequence is 1-2-3 with f₁ = 15. Table 2 presents the obtained solutions with H1 and H1* after the apparition of job 4.

Table 2 Obtained solutions with H1 and H1*

H1 placed job 4 in all possible positions, except for the first one since the job 1 has already started its execution when job 4 arrived at time t = 3. The best solution provided by H1 is f₂ = 19.83 instead of 18.5 given by H1*, which improves H1 by repeating the same operations, as long as a better result is obtained. However, the computing time of H1* is bigger than H1.

4.2 Heuristic H2

Description of H2: We consider a list of jobs sequenced by the order obtained in the previous schedule and put temporarily the new job in the last position. We apply NEH for sequencing this list. The solution that minimizes the objective function is selected.

Improvement of H2: We consider the sequence obtained by H2 and apply the algorithm of NEH recursively as for H1*, while an improvement is found. We call this heuristic H2*.

Example illustrating H2 and H2*: We study here an illustration of H2 and H2*, with the same example as the one presented in Table 1. The obtained results are presented in Table 3.

Table 3 Obtained solutions with H2 and H2*

H2 considers the list 1–2-3–4. Exempt the jobs that already started their execution (job 1 in this example), H2 puts the jobs of the list, one by one, in the partial schedule applying NEH method. The best solution provided by H2 is f₂ = 19.83 instead of 18.5 given by H2*, which improves H2 by repeating the same operations as long as the result is better. However, the computing time of H2* is bigger than H2.

4.3 Heuristic H3

Description of H3: We consider a list of jobs sequenced by the order obtained in the previous schedule and put temporarily the new job in the first position. We apply NEH to sequence this list. The solution that minimizes the objective function is selected.

Improvement of H3: We consider the sequence obtained by H3 and apply the algorithm of NEH recursively as for H1*, while an improvement is found. We call this heuristic H3*.

Example illustrating H3 and H3*: We study here an illustration of H3 and H3*, with the same example as the one presented in Table 1. The obtained results are presented in Table 4.

Table 4 Obtained solutions with H3 and H3*

H3 considers the list 1–4-2–3. Exempt the jobs that already started their execution (job 1 in this example), H3 puts the jobs of the list, one by one, in the partial schedule applying NEH method. The best solution provided by H3 and H3* is f₂ = 18.5. However, the computing time of H3* is bigger than H3.

4.4 Heuristic H4

Description of H4: We consider the list of jobs sequenced by descending order of w_j and we apply NEH to sequence this list. The solution that minimizes the objective function is selected.

Improvement of H4: We consider the sequence obtained by H4 and apply the algorithm of NEH recursively as for H1*, while an improvement is found. We call this heuristic H4*.

Example illustrating H4 and H4*: We study here an illustration of H4 and H4*, with the same example as the one presented in Table 1. The obtained results are presented in Table 5.

Table 5 Obtained solutions with H4 and H4*

H4 considers the list of jobs sequenced by descending order of w_j, 4-3-1-2. Exempt the jobs that already started their execution (job 1 in this example), H4 puts the jobs of the list, one by one, in the partial schedule applying NEH method. The best solution provided by H4 and H4* is f₂ = 18.5. However, the computing time of H4* is bigger than H4.

5 Experimental results

In this section, numerical results obtained for a flow shop system composed by 5 machines are presented. The data used are explained in Table 6.

Table 6 Parameter values

The chosen data are adapted for real industrial cases. The simulation is over 8-h’ time horizon (480 min), representing a factory opening time. It is assumed that Δt = 1 unit of time (ut), and 1 ut is equivalent to 10 min. Thus, T = 8 h = 480 min = 48 ut. The weight values w_j represent 5 priority levels of customers. The processing times p_jm represent the durations of product manufacturing times. It is assumed that it follows a discrete uniform distribution with values between 1 and 4, obtaining durations between 1 ut (10 min) and 4 ut (40 min). In the offline phase, the release dates are generated following a discrete uniform distribution, providing values between 0 and 2, U ~ (0, 2), to have an initial solution on which we have generated the disruptions. In the online phase, the variable β(t) is used for generating the arrival of new jobs, its value is randomly generated with the Bernoulli distribution. At each time t, the value 1 is generated with probability p_β, and 0 with probability 1-p_β, where p_β is the appearance frequency of the jobs. Different values of p_β are tested.

50 different instances are randomly generated according to p_jm and w_j. For each instance, we scheduled the first five jobs in the offline phase, considering that the information is known at time t = 0. Then, the schedule will be disrupted by the arrival of new jobs. For each instance, we tested three scenarios of α (0.5, 0.75 and 1) and four scenarios of p_β (0.2, 0.5, 0.8 and 1). In total, we investigated 50*3*4 = 600 scenarios. Thus, three vectors of constraints are studied, in order to analyze the impact of the blocking constraints on the solution.

5.1 Without blocking constraints case

In this case, a vector without any blocking constraint V(Wb, Wb, Wb, Wb) is considered. It represents a classical flowshop rescheduling problem. Two studies are conducted in this section. We firstly made a comparison between the proposed heuristics and their improved versions, to quantify the improvement process, both in terms of efficiency and computing time. Secondly, the heuristics are compared with the method based on the MILP model (B-MILP).

5.1.1 Heuristics versus improved heuristics

A comparison of the heuristics (H) and their improved versions (H*) has been established. Ten instances are generated, accordingly to Table 6. For each heuristic, the Number of Times when H* ≤ H (NT), the Improvement Rate (IR), and the Time Difference Rate (TDR) are calculated. Averages are presented in Table 7.

Table 7 Comparison between the heuristics and their improved versions

$$\mathrm{IR}=\frac{\mathrm{Solution\;given\;by\;} H-\mathrm{Solution\;given\;by\;} {H}^{*}}{\mathrm{Solution\;given\;by\;} H}$$

$$\mathrm{TDR}=\frac{\mathrm{Time\;of\;} {H}^{*}-\mathrm{Time\;of\;} H}{\mathrm{Time\;of\;} H}$$

The improvement rate is, in most of cases, positive. That proves the efficiency of the improved versions of the heuristics. However, in some particular cases, this rate can be negative. By applying the improvement on some steps, we certainly get a better solution. But, in the next step, the methodology consists in fixing the already executed jobs in the previous step and rescheduling. In this case, if the set of jobs fixed by H and H* is not the same, the problem to solve in the next steps becomes different. Thus, the improved version can provide a bad result in the final step, but the value of IR when it is negative is relatively small. On the other hand, the average of the number of times when H* ≤ H (NT) is 7.8.

Time difference rate is always positive, since the improvement consists of repeating the operations of the heuristic if the solution is better. Thus, the computing time increases. Thanks to their effectiveness, in the rest of the experimental results, the improved heuristics are used for the resolution methods comparison.

5.1.2 Resolution methods comparison

We compared for the 50 generated instances, four improved heuristics with the B-MILP in terms of solution quality and computing time. Averages are presented in Tables 8 and 9.

Table 8 Resolution methods comparison in the case of V(Wb, Wb, Wb, Wb)

Table 9 Percentage error and standard deviation with the best solution in the case of V(Wb, Wb, Wb, Wb)

As can be seen, when p_β increases, the number of arrived jobs at each period increase too, the problem then will be difficult to solve in a reasonable time with the B-MILP. Only the heuristics can provide solutions when p_β exceeds 0.5. The Maximum Duration of Iteration (MDI) is the maximum computation duration that the method takes, at each iteration, to provide a solution. It estimates the period between the occurrence of a job and the establishment of the new schedule. As shown in Table 8, the MDI of the B-MILP is large when p_β = 0.5.

When p_β = 0.2, as there are few disruptions, the heuristics and B-MILP provide close solutions. In this case, the percentage errors and standard deviations presented in Table 9 becomes small. The percentage error is the difference between the best solution and provided solution, as a percentage of the best solution.

$$\mathrm{percentage\;error}=\frac{\mathrm{provided\;solution}-\mathrm{best\;solution}}{\mathrm{best\;solution}}\times 100$$

When p_β = 0.5, as the disruptions are medium, the B-MILP takes more time to provide a solution compared to the heuristics. The method based on MILP (B-MILP) is also a heuristic consisting in generating at each disruption the MILP for solving the problem. The B-MILP method may sometimes produce inferior solutions compared to heuristics. This occurs because the B-MILP method finds a locally optimal solution, which may not be the optimal solution for the entire problem (when all the jobs have appeared). In the predictive–reactive strategy, which is an iterative process, the solution obtained with B-MILP is used as a basis for solving the next problem in the subsequent iteration. However, in this process, all the jobs that have already started their execution before time t are excluded from the set of jobs. So, B-MILP and heuristics schedule a different set of jobs. Thus, the obtained solutions are different, sometimes in favor of the heuristics.

In dynamic environments, decision-makers need to establish a new plan after each disruption. This planning process should be initiated as quickly as possible, preferably before the occurrence of another disruption. In our case, based on the discretization assumption, we have made, a new job can potentially arrive at every time interval of Δt. Therefore, if the Maximum Duration of Iteration (MDI) exceeds Δt, it is considered as an unacceptable time frame. In our experiments, we have assumed that Δt is equivalent to 10 min, which is equal to 600 s. Therefore, if the MDI exceeds 600 s, it is considered as an unreasonable duration. However, we only interrupt the simulations after 12 h, regardless of the MDI exceeding 600 s. With p_β = 0.8 and 1, the B-MILP fails to give a solution in a reasonable time. Heuristics quickly provide solutions, generally the fours heuristics are close in terms of computing time.

H4* considers a list of jobs sequenced by descending order of w_j and use NEH method to reschedule this list of jobs. It provides better solutions when α = 1 since the schedule stability is not considered. The jobs weights are very influential in this case. H2* considers a list of jobs sequenced by the order obtained in the previous schedule and uses NEH method to reschedule this list of jobs. It provides better solutions when α = 0.75. As the schedule stability is considered in this case, the previous sequence is often maintained, and the new arrived job is often placed in the last positions, depending on its weight. This is already the principle of H2*, which explains its adaptation to this case. When α = 0.5, the schedule stability is more considered. According to Table 9, the number of times that H2* provides the best solution becomes very high. This approves the superiority of H2* when the schedule stability is more considered. H1* only puts the new job in all possible positions without using NEH method. In most cases, it provides a bad solution than others since H2*, H3* and H4* are improved versions of H1*.

As a conclusion, one of the best choices that the decision-maker can do is to use, for each case, a heuristic among the proposed heuristics. Ideally, H4* when α = 1, and H2* when α = 0.5 or α = 0.75.

5.2 The case of V(Wb, RSb, RCb*, RCb)

A vector of V(Wb, RSb, RCb*, RCb) is studied in this sub-section, and the average results of the 50 different instances are presented in Tables 10 and 11.

Table 10 Resolution methods comparison in the case of V(Wb, RSb, RCb*, RCb)

Table 11 Percentage error and standard deviation in the case of V(Wb, RSb, RCb*, RCb)

When the blocking constraints are simultaneously mixed in one production system, the space of feasible solutions reduces since there are many constraints to satisfy at the same time. As can be seen in Table 10, the computing time and the MDI becomes large compared to the case without blocking constraints. The B-MILP can hardly provide solutions when p_β = 0.5.

The B-MILP and the heuristics still give very close results when p_β = 0.2. The results differ when the system is subjected to more disruptions, p_β > 0.2. Also, according to Table 10, we always observe a superiority of H4* when α = 1, and H2* when α = 0.75 and α = 0.5. Therefore, the interpretation established in Sect. 5.1 about the impact of α on the solutions performance remains still correct.

However, a diminution of the percentage errors and standard deviations is observed in Table 11, in comparison with Table 9. As the mixed blocking constraints are used in this example, the space of feasible solutions reduces. Thus, the heuristic solutions become close to each other. H2*, H3*, H4* converge in most of the cases toward the same solution, compared with the case without blocking. H1* which does not use NEH method, has a higher percentage error, compared to other heuristics.

The constraint RCb* describes the case where a machine is blocked by a job, until this one will finish on the following machine. According to Sauvey et al (2020), this blocking constraint links together two machines around the same job since it considers at least the next operation to schedule an in‐course operation. Therefore, in the next sub-section we consider RCb* introduced between the first and the second machine, followed by two successive Wb. This, for evaluating the impact of this particular situation on the computing time and the percentage errors of the proposed methods.

5.3 The case of V(RCb*, Wb, Wb, RSb)

The vector V (RCb*, Wb, Wb, RSb) is studied in this sub-section, the average results of the 50 instances are presented in Tables 12 and 13.

Table 12 Resolution methods comparison in the case of V(RCb*, Wb, Wb, RSb)

Table 13 Percentage error and standard deviation in the case of V(RCb*, Wb, Wb, RSb)

Having RCb* constraint introduced between the first and the second machine, makes the problem difficult to solve. Since this blocking considers the next operation to schedule an in-course one, the B-MILP needs more time to find the best solution. Therefore, the B-MILP can only provide solutions when the system is subjected to little disruptions. When p_β exceeds 0.2, it fails to give solutions in a reasonable time. The simulation has been interrupted after 12 h. Heuristics still provide solutions in a short time. However, the computing time and the MDI are long compared to the blocking case previously studied.

On the other hand, a diminution of the percentage errors and standard deviations is observed in Table 13, in comparison with Table 11. As the RCb* is introduced between the first and the second machine, the space of feasible solutions becomes even smaller. H2*, H3*, and H4* are based on NEH method for rescheduling jobs, converge even more toward the same solution. H1* has a large percentage error compared to other heuristics. Since it only puts the new job in all possible positions without using NEH method, it fails in most of cases to provide the best solution.

In this particular blocking case, H4* is still efficient when the stability is not considered (α = 1). H2* is also still efficient when the schedule stability is more considered. H3* provides better results compared to the blocking cases previously studied.

6 Conclusion and perspectives

This paper investigates a flow shop rescheduling problem when different blocking constraints are mixed in one production system. Two aspects are simultaneously investigated to measure the schedule performance. First, regarding the efficiency, the total weighted waiting time is considered as a criterion. Second, in terms of stability, the total weighted completion time deviation is used as a criterion to limit the difference from the initial schedule. At each period, the established schedule can be disrupted by the arrival of a new job. Using the predictive–reactive strategy, the schedule is updated in response to this disruption. The problem has first been solved using a MILP model. Experimental results show that the MILP resolution is only possible for little size instances. Hence, inspired by NEH algorithm, we proposed four heuristics for solving large size instances of this problem. The comparison of these methods has been discussed in the experimental results section, where three different blocking constraints vectors have been evaluated. The main conclusions of this work are:

• The appearance frequency of the jobs p_β has a major impact on the computing time. The more arriving jobs increase, the more the resulting computing time increases. The increase in computing time depends also on the type of successive blocking constraints between the machines.

• When the schedule stability is not considered, improved Heuristic 4 (H4*) which sequences the set of jobs by descending order of w_j and uses NEH method for rescheduling, provides better solutions since the jobs weights have a major impact on the results. However, when the schedule stability is more considered, improved Heuristic 2 (H2*) which consists in maintaining the previous order and in using NEH method for rescheduling, gives better solutions since the deviation from the previous schedule is limited by the stability criterion. One of the best choices that the decision-maker can do, is to use, for each case, a heuristic among the proposed heuristics. Ideally, H4* when α = 1, and H2* when α = 0.5 or α = 0.75.

• Considering blocking constraints mixed in one flow shop system, reduces the space of feasible solutions since there are many constraints to satisfy. This increases the resolution time, but it reduces the percentage errors of the resolution methods. The B-MILP and the proposed heuristics converge in most of the cases toward the same solution. This matter has been clearly shown when RCb* constraint has been considered as a first constraint in the flow shop system.

This work can be of great interest, not only for the researchers facing with flow shop rescheduling problems, but also for a broader audience, such as industrial decision-makers. As perspectives, we intend to improve our methods by adapting it to consider, at each period, more than one job. Indeed, the decision-makers must quickly react for providing a new schedule in response to disruptions, even if several ones arrive at the same time. On the other hand, the proposed heuristics accelerate the getting of solutions. However, the decision-makers must choose among the proposed heuristics, the best adapted to their case, depending on the efficiency-stability coefficient value. In future work, it will be interesting to design a metaheuristic that can be smartly adapted to all cases. Finally, we will study the behavior of the TWWT combined with the TWCTD in the case of job shop or open shop environments, considering the blocking constraints.