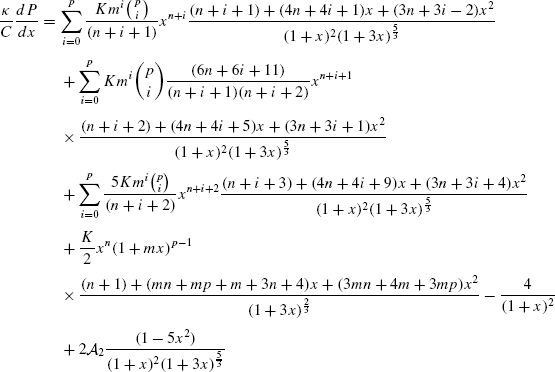1 Introduction

The vital importance of analytical solutions of Einstein–Maxwell equations in the description of electrically charged self-bound star have been discussed by several authors previously [2–7]. The best-known example of self-bound stars results from the Bodmer–Witten hypothesis also known as the strange quark matter hypothesis. Self-bound stars have significant finite density, larger than normal nuclear matter density, but zero pressure at their surfaces [8–10].

The structure of normal stars or self-bound stars can be obtained by reference to applicable analytic solutions of the relativistic stellar structure equations. Although over 100 static spherically symmetric analytic solutions to Einstein’s equations are known [11], nearly all of them are physically unrealistic.

In recent years several authors have presented various analytical models of electrically charged compact self-bound stars within the framework of linear equation of state (EOS) based on MIT bag model [12–15] and nonlinear EOS based on particular choice of metric potential [16–19]. Some nonsingular charged solutions, obtained previously for different suitable choices of electric charge distributions, have been summarized in Table 1 of Sect 3. With this motivation and continuation of previous work [paper I] some new classes of exact static spherically symmetric perfect fluid solutions of Einstein–Maxwell field equations are presented here to model self-bound stars by satisfying applicable boundary conditions.

Table 1 Some Exact static spherically symmetric perfect fluid solutions of Einstein-Maxwell equations using charge distributions (2.9a)–(2.9c)
Full size table

2 Interior Solutions of Einstein–Maxwell Field Equations

2.1 Field Equations

As in paper I, we intend to study static spherically symmetric relativistic stellar objects whose spacetime metric in Schwarzschild-like coordinates x μ=(t,r,θ,φ) is given by,

$$ ds^{2} = e^{\nu(r)} dt^{2} - e^{\lambda(r)} dr^{2} - r^{2} \bigl( d\theta^{2} + \sin^{2} \theta d\varphi^{2} \bigr) $$
(2.1)

It has been shown [20–25] that for the uncharged case the ansatz for the metric function

$$ e^{\nu} = \mathcal{B}_{N} \bigl( 1+C r^{2} \bigr)^{N} $$
(2.2)

where N is a positive integer, produces an infinite family of analytic solutions of the self-bound type. Some of those were previously known (N=1,2,3,4, and 5). The most relevant case is for N=2, for which the velocity of sound \({\approx}1/ \sqrt{3}\) throughout most of the star, similar to the behavior of strange quark matter.

The objective of this work is to derive some new charged analogues of Wyman-Adler solution in general relativity and use these solutions to model self-bound stars. The interior problem of a static charged fluid sphere with density ρ, the pressure P and the proper charge density ρ ch for the metric (2.1) Einstein-Maxwell field equations lead to the following set of relevant equations:

$$\begin{aligned} &\frac{\nu'}{r} e^{- \lambda} - \frac{ ( 1 - e^{- \lambda} )}{ r^{2}} = \kappa P - \frac{q^{2}}{r^{4}} \end{aligned}$$
(2.3)
$$\begin{aligned} & \biggl( \frac{\nu''}{2} - \frac{\nu' \lambda'}{4} + \frac{\nu^{\prime 2}}{ 4} + \frac{\nu' - \lambda'}{2 r} \biggr) e^{- \lambda} = \kappa P + \frac{q^{2}}{r^{4}} \end{aligned}$$
(2.4)
$$\begin{aligned} &\frac{\lambda'}{r} e^{- \lambda} + \frac{ ( 1 - e^{- \lambda} )}{r^{2}} = \kappa\rho+ \frac{q^{2}}{r^{4}} \end{aligned}$$
(2.5)

where,

$$ q ( r ) = 4 \pi\int_{0}^{r} e^{\frac{\lambda}{2}} \rho_{\mathrm{ch}} u^{2} du $$
(2.6)

Eliminating the pressure, P, from the Eqs. (2.3) and (2.4), one obtains the following equation of “pressure isotropy”,

$$ \biggl( \frac{\nu''}{2} - \frac{\nu' \lambda'}{4} + \frac{\nu^{\prime 2}}{ 4} - \frac{\nu' + \lambda'}{2r} \biggr) e^{- \lambda} + \frac{ ( 1 - e^{- \lambda} )}{r^{2}} = \frac{2 q^{2}}{r^{4}} $$
(2.7)

Introducing an auxiliary variable x=Cr 2, where C>0, and with the help of Eq. (2.2), Eq. (2.7) yield the following solution [paper I],

$$\begin{aligned} e^{-\lambda} =& \frac{x}{ ( 1+x )^{N-2} [ 1+ ( 1+N ) x ]^{\frac{2}{ ( 1+N )}}} \int\frac{ ( 1+x )^{N-1} [ 1+ ( 1+N ) x ]^{\frac{ ( 1-N )}{ ( 1+N )}}}{x^{2}} \biggl( \frac{2C q^{2}}{x} - 1 \biggr) dx \\ &{}+ \mathcal{A}_{N} \frac{x}{ ( 1+x )^{N-2} [ 1+ ( 1+N ) x ]^{\frac{2}{ ( 1+N )}}} \end{aligned}$$
(2.8)

where \(\mathcal{A}_{N}\) is a constant of integration will be determined by imposing appropriate physical boundary conditions.

2.2 Models of Electric Charge Distribution

To perform the integration in Eq. (2.8) and express e −λ in terms of x explicitly we consider the following models electric charge distributions,

$$\begin{aligned} &\mbox{Model I:}\quad \frac{2C q^{2}}{x^{2}} =K x^{n+1} ( 1+x )^{1-N} \end{aligned}$$
(2.9a)
$$\begin{aligned} &\mbox{Model II:}\quad \frac{2C q^{2}}{x^{2}} = K x^{n+1} ( 1+mx )^{p} \bigl[ 1+ ( 1+N ) x \bigr]^{\frac{ ( N-1 )}{ ( N+1 )}} \end{aligned}$$
(2.9b)
$$\begin{aligned} &\mbox{Model III:}\quad \frac{2C q^{2}}{x^{2}} =K x^{n+1} ( 1+mx )^{p} ( 1+ x )^{1 - N} \bigl[ 1+ ( 1+ N ) x \bigr]^{\frac{ ( N - 1 )}{ ( N +1 )}} \end{aligned}$$
(2.9c)

where n>0 (n is positive integer for model I), K>0, m is any real number and p is a non-negative integer. The term 2Cq 2/x 2 is chosen, in term of x, in such a way that electric field intensity vanishes at the center and remains continuous and bounded in the interior of the star for a wide range of values of the parameters. Thus these choices are physically reasonable and useful in the study of the gravitational behavior of charged stellar objects. Table 1 summarizes the solutions Eq. (2.1) obtained previously for variety of charge distributions of different values of N, K, n, m, and p.

3 New Charged Analogues of Wyman-Adler solution (N=2)

To present the complete solution of the Einstein–Maxwell system (2.3)–(2.6) we choose N=2 in (2.2) and (2.8):

Case I: :

Model I with n=1

$$\begin{aligned} &e^{\nu} = \mathcal{B}_{2} ( 1+x )^{2} \end{aligned}$$
(3.1a)
$$\begin{aligned} &e^{- \lambda} = \frac{K}{10} \bigl( 2 x^{2} -x \bigr) +1+ \mathcal{A}_{2} \frac{x}{ ( 1+3x )^{\frac{2}{3}}} \end{aligned}$$
(3.1b)
$$\begin{aligned} &\frac{2C q^{2}}{x^{2}} =K \frac{x^{2}}{ ( 1+x )} \end{aligned}$$
(3.1c)
$$\begin{aligned} &\frac{\kappa}{C} P= \frac{K}{10} \frac{ ( -1-3x+15 x^{2} )}{ ( 1+x )} + \frac{4}{ ( 1+x )} + \mathcal{A}_{2} \frac{ ( 1+5x )}{ ( 1+x ) ( 1+3x )^{\frac{2}{3}}} \end{aligned}$$
(3.1d)
$$\begin{aligned} &\frac{\kappa}{C} \rho= \frac{K}{10} \frac{ ( 3-7x-15 x^{2} )}{ ( 1+x )} - \mathcal{A}_{2} \frac{ ( 3+5x )}{ ( 1+3x )^{\frac{5}{3}}} \end{aligned}$$
(3.1e)
Case II: :

Model II with n>0

$$\begin{aligned} &e^{\nu} = \mathcal{B}_{2} ( 1+x )^{2} \end{aligned}$$
(3.2a)
$$\begin{aligned} &e^{- \lambda} =K \sum_{i=0}^{p} {p\choose i}m^{i} \frac{x^{n+i+2}}{ ( 1+3x )^{\frac{2}{3}}} \biggl[ \frac{1}{ ( n+i+1 )} + \frac{x}{ ( n+i+2 )} \biggr] \\ &\phantom{e^{- \lambda} =}{}+ 1 + \mathcal{A}_{2} \frac{x}{ ( 1+3x )^{\frac{2}{3}}} \end{aligned}$$
(3.2b)
$$\begin{aligned} &\frac{2C q^{2}}{x^{2}} =K x^{n+1} ( 1+3x )^{\frac{1}{3}} ( 1+mx )^{p} \end{aligned}$$
(3.2c)
(3.2d)
(3.2e)
Case III: :

Model III with n>0

$$\begin{aligned} &e^{\nu} = \mathcal{B}_{2} ( 1+x )^{2} \end{aligned}$$
(3.3a)
(3.3b)
$$\begin{aligned} &\frac{2C q^{2}}{x^{2}} =K \frac{x^{n+1} ( 1+3x )^{\frac{1}{3}} ( 1+mx )^{p}}{ ( 1+x )} \end{aligned}$$
(3.3c)
(3.3d)
(3.3e)

4 Physical Boundary Conditions

4.1 Determination of the Arbitrary Constant \(\mathcal{A}_{2}\)

To specify \(\mathcal{A}_{2}\) the boundary condition P(r=R)=0 can be utilized, where R is the radius of the fluid sphere.

$$\begin{aligned} &\mathcal{A}_{2} = \frac{K}{10} \frac{ ( 1+3X-15 X^{2} ) ( 1+3X )^{\frac{2}{3}}}{ ( 1+5X )} - \frac{4 ( 1+3X )^{\frac{2}{3}}}{ ( 1+5X )}\quad (\mathrm{Model}\ \mathrm{I} ) \\ &\mathcal{A}_{2} =- \frac{K X^{n+1}}{2 ( n+1 ) ( n+2 )} \frac{ ( n^{2} +5n+4 ) + ( 4 n^{2} +24n+30 ) X+ ( 3 n^{2} +19n+16 ) X^{2}}{ ( 1+5X )} \\ &\phantom{\mathcal{A}_{2} =}{}-4 \frac{ ( 1+3X )^{\frac{2}{3}}}{ ( 1+5X )}\quad ( \mathrm{Model}\ \mathrm{II} ) \\ &\mathcal{A}_{2} = - \frac{K}{2 ( n+1 )} \frac{X^{n+1} [ ( n+3 ) + ( 3n+13 ) X ]}{ ( 1+5X )} - \frac{4 ( 1+3X )^{\frac{2}{3}}}{ ( 1+5X )}\quad ( \mathrm{Model}\ \mathrm{III} ) \end{aligned}$$

where X=CR 2.

4.2 Determination of the Total Mass and Charge

The total mass M and the total charge Q of the fluid sphere can be determined by matching the obtained solutions with the exterior Reissner–Nordström metric:

$$ ds^{2} = \biggl( 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}} \biggr) dt^{2} - \biggl( 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}} \biggr)^{- 1} dr^{2} - r^{2} \bigl( d \theta^{2} + \sin^{2} \theta d\varphi^{2} \bigr) $$
(4.2)

And this requires the continuity of the metric functions e ν, e λ and the charge q across the boundary r=R

$$ e^{\nu(r)} = e^{-\lambda ( r )} = \biggl( 1 - \frac{2M}{r} + \frac{Q^{2}}{r^{2}} \biggr)\quad r\geq R $$
(4.3)
$$q ( R ) =Q $$

For our models, at the boundary r=R,

$$ e^{\nu(R)} = \mathcal{B}_{2} ( 1+X )^{2} = \biggl( 1 - \frac{2M}{ R} + \frac{Q^{2}}{R^{2}} \biggr) $$
(4.2)

and

where X=CR 2.

And the constant \(\mathcal{B}_{N}\) can be specified by the boundary condition e ν(R)=e −λ(R) which gives,

$$\mathcal{B}_{N} = ( 1+X )^{-N} e^{-\lambda ( R )} $$

5 Physical Analysis of the Models

A physically acceptable interior solution of Einstein–Maxwell field equations must comply with the certain (not necessarily mutually independent) physical conditions [58, 59]. Further details are in paper I and not repeated here.

In the following subsection we report the necessary equations to investigate the behaviors of the models numerically.

5.1 Pressure and Density gradients

Differentiating Eqs. (3.2d, 3.2e) and (3.3d, 3.3e) with respect to the auxiliary variable x we obtain the pressure and density gradients for each model equations of state.

Model I: :
$$\frac{\kappa}{C} \frac{dP}{dx} = \frac{K}{10} \frac{ ( -2+30x+15 x^{2} )}{ ( 1+x )^{2}} - \frac{4}{ ( 1+x )^{2}} +2 \mathcal{A}_{2} \frac{ ( 1 - 5 x^{2} )}{ ( 1+x )^{2} ( 1+3x )^{\frac{5}{3}}} $$
$$\frac{\kappa}{C} \frac{d\rho}{dx} = - \frac{K}{2} \frac{ ( 2+6x+3 x^{2} )}{ ( 1+x )^{2}} +10 \mathcal{A}_{2} \frac{ ( 1+x )}{ ( 1+3x )^{\frac{8}{3}}} $$
Model II: :
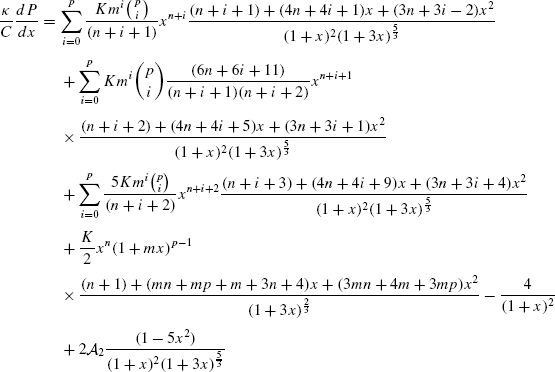$$\begin{aligned} \frac{\kappa}{C} \frac{d\rho}{dx} =& - \sum_{i=0}^{p} K m^{i} {p\choose i} \frac{ ( 2n+2i+5 )}{ ( n+i+1 )} x^{n+i} \frac{ ( n+i+1 ) + ( 3n+3i-2 ) x}{ ( 1+3x )^{\frac{8}{3}}} \\ &{} - \sum_{i=0}^{p} K m^{i} {p \choose i} \biggl[ \frac{ ( 6n+6i+11 )}{ ( n+i+1 )} + \frac{ ( 2n+2i+7 )}{ ( n+i+2 )} \biggr] x^{n+i+1}\\ &{}\times\frac{ ( n+i+2 ) + ( 3n+3i+1 ) x}{ ( 1+3x )^{\frac{8}{3}}} \\ &{}- \sum_{i=0}^{p} K m^{i} {p \choose i} \frac{ ( 6n+6i+17 )}{ ( n+i+2 )} x^{n+i+2} \frac{ ( n+i+3 ) + ( 3n+3i+4 ) x}{ ( 1+3x )^{\frac{8}{3}}} \\ &{}- \frac{K}{2} x^{n} ( 1+mx )^{p-1}\\ &{}\times\frac{ ( n+1 ) + ( mn+mp+m+3n+4 ) x+ ( 3mn+4m+3mp ) x^{2}}{ ( 1+3x )^{\frac{2}{3}}} \\ &{}+10 \mathcal{A}_{2} \frac{ ( 1+x )}{ ( 1+3x )^{\frac{8}{3}}} \end{aligned}$$
Model III: :
$$\begin{aligned} \frac{\kappa}{C} \frac{dP}{dx} =& K \sum_{i=0}^{p} {p\choose i} \frac{m^{i}}{ ( n+i+1 )} x^{n+i} \frac{ ( n+i+1 ) + ( 4n+4i+1 ) x+ ( 3n+3i-2 ) x^{2}}{ ( 1+x )^{2} ( 1+3x )^{\frac{5}{3}}} \\ &{}+5K \sum_{i=0}^{p} {p\choose i} \frac{m^{i}}{ ( n+i+1 )} x^{n+i+1} \\ &{}\times\frac{ ( n+i+2 ) + ( 4n+4i+5 ) x+ ( 3n+3i+1 ) x^{2}}{ ( 1+x )^{2} ( 1+3x )^{\frac{5}{3}}} \\ &{}+ \frac{K}{2} \frac{x^{n} ( 1+mx )^{p-1}}{( 1+x )^{2} ( 1+3x )^{\frac{2}{3}}} \bigl[( n+1 ) + ( mn+mp+m+4n+4 ) x\\ &{}+ ( 4mn+4mp+4m+3n+1) x^{2}+ ( 3mn+3mp+m ) x^{3}\bigr]\\ &{}-\frac{4}{ ( 1+x )^{2}} +2 \mathcal{A}_{2} \frac{ ( 1 - 5 x^{2} )}{ ( 1+x )^{2} ( 1+3x )^{\frac{5}{3}}} \end{aligned}$$
$$\begin{aligned} \frac{\kappa}{C} \frac{d\rho}{dx} =& -K \sum_{i=0}^{p} {p\choose i} \frac{m^{i} ( 2n+2i+5 ) ( n+i+1 )}{ ( n+i+1 )} \frac{x^{n+i}}{ ( 1+3x )^{\frac{8}{3}}} \\ &{}-K \sum_{i=0}^{p} {p\choose i} \frac{m^{i} ( 2n+2i+5 ) ( 3n+3i-2 ) + ( 6n+6i+11 ) ( n+i+2 )}{ ( n+i+1 )} \\ &{}\times\frac{x^{n+i+1}}{ ( 1+3x )^{\frac{8}{3}}} \\ &{} -K \sum_{i=0}^{p} {p\choose i} \frac{m^{i} ( 6n+6i+11 ) ( 3n+3i+1 )}{ ( n+i+1 )} \frac{x^{n+i+2}}{ ( 1+3x )^{\frac{8}{3}}} \\ &{}- \frac{K}{2} \frac{x^{n} ( 1+mx )^{p-1}}{( 1+x )^{2} ( 1+3x )^{\frac{2}{3}}} \bigl[( n+1 ) + ( mn+mp+m+4n+4 ) x\\ &{}+ ( 4mn+4mp+4m+3n+1 ) x^{2}+ ( 3mn+3mp+m ) x^{3}\bigr]\\ &{}+10 \mathcal{A}_{2} \frac{ ( 1+x )}{ ( 1+3x )^{\frac{8}{3}}} \end{aligned}$$

5.2 Charge to Radius Ratio

From Eq. (2.9a)–(2.9c), using X=CR 2, we obtain the charge to radius ratio.

$$\frac{Q^{2}}{R^{2}} = \frac{K}{2} X^{n+2} ( 1+X )^{1-N}\quad ( \mathrm{Model}\ \mathrm{I} ) $$
$$\frac{Q^{2}}{R^{2}} = \frac{K}{2} X^{n+2} ( 1+3X )^{\frac{1}{3}} ( 1+mX )^{p}\quad ( \mathrm{Model}\ \mathrm{II} ) $$
$$\frac{Q^{2}}{R^{2}} = \frac{K}{2} \frac{X^{n+2} ( 1+3X )^{\frac{1}{3}} ( 1+mX )^{p}}{ ( 1+X )}\quad ( \mathrm{Model}\ \mathrm{III} ) $$

5.3 Mass to Radius Ratio (Compactness Parameter)

With the help of Eqs. (3.2b) and (3.3b) we can establish the equation of mass to radius ratio (compactness parameter).

$$\frac{2M}{R} =- \frac{K}{10} \bigl( 2 X^{2} -X \bigr) + \frac{K}{2} \frac{X^{3}}{ ( 1+X )} - \mathcal{A}_{2} \frac{X}{ ( 1+3X )^{\frac{2}{3}}} \quad ( \mathrm{Model}\ \mathrm{I} ) $$
$$\begin{aligned} \frac{2M}{R} =&- \sum_{i=0}^{p} \frac{K m^{i} {p\choose i}}{ ( n+i+1 )} \frac{X^{n+i+2}}{ ( 1+3X )^{\frac{2}{3}}} - \sum_{i=0}^{p} \frac{K m^{i} {p\choose i}}{ ( n+i+2 )} \frac{X^{n+i+3}}{ ( 1+3X )^{\frac{2}{3}}} \\ &{}+ \frac{K}{2} X^{n+2} ( 1+3X )^{\frac{1}{3}} ( 1+mX )^{p} - \mathcal{A}_{2} \frac{X}{ ( 1+3X )^{\frac{2}{3}}}\quad ( \mathrm{Model}\ \mathrm{II} ) \end{aligned}$$
$$\begin{aligned} \frac{2M}{R} =&- K \sum_{i=0}^{p} \frac{{p\choose i} m^{i}}{ ( n+i+1 )} \frac{X^{n+i+2}}{ ( 1+3X )^{\frac{2}{3}}} + \frac{K}{2} \frac{X^{n+2} ( 1+3X )^{\frac{1}{3}} ( 1+mX )^{p}}{ ( 1+X )} \\ &{}- \mathcal{A}_{2} \frac{X}{ ( 1+3X )^{\frac{2}{3}}}\quad ( \mathrm{Model}\ \mathrm{III} ) \end{aligned}$$

5.4 Stellar Surface Density

Using X=CR 2 in the Eqs. (3.2e) and (3.3e) the equation of stellar surface density can be constructed as the following,

$$\kappa R^{2} \rho_{s} = \frac{K}{10} \frac{ ( 3-7X-15 X^{2} )}{ ( 1+X )} - \mathcal{A}_{2} \frac{ ( 3+5X )}{ ( 1+3X )^{\frac{5}{3}}} =L\quad ( \mathrm{Model}\ \mathrm{I} ) $$

For the particular values of N, n, m, and p, the basic inputs to the above equations are K and X. In our study the values of parameters have been set in a way for which the energy density ρ, the pressure P and the electric charge Q remain positive and satisfy the necessary physical conditions.

For the numerical investigations the physical variables may be determined by three ways: for a given (i) radius, (ii) surface density, and (iii) central density. Only the case (ii) will be discussed. Thus for a given surface density, ρ s , in our model calculation we prefer ρ s =4.6888×1014 g cm−3 (paper I) the radius of the fluid sphere can be calculated by,

$$R = \sqrt{\frac{LX}{8\pi\rho_{s}}} $$

The maximum mass and corresponding radius of compact self-bound charged fluid spheres, obtained from the models considered, are reported in Table 2.

Table 2 Maximum mass and the various physical parameters of charged fluid spheres for different charge distribution for surface density ρ s =4.6888×1014 g cm−3
Full size table

5.5 Discussions

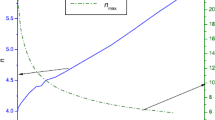
The metric functions e ν and e λ are plotted in Figs. 1(a) and 1(b) respectively which show the continuity of those quantities. In Figs. 1(c) and 1(d) we have the behaviors of isotropic pressure and energy density which are positive and monotonically decreasing functions in the interior of the star. The pressure to density ratio, for fluid sphere obtained by assigning values of the parameters (p,m,n,K,X)=(1,−0.5,0.2,0.691,0.729), is presented in Fig. 1(e). The behaviors of the quantities \(\frac{\kappa}{C} \frac{dP}{dx},\ \frac{\kappa}{C} \frac{d\rho}{dx}\) are shown in Figs. 1(f)–1(g). It can be observed from the behavior of \(\sqrt{\frac{dP}{d\rho}}\), Fig. 1(h), that the speed of sound is always less than the speed of light and causality is maintained. The electric charge distribution for the same fluid sphere is plotted in Fig. 2, which is zero at the center and monotonically increasing towards the boundary. Figure 3 demonstrates the pressure-density relation.

Fig. 1
figure 1figure 1

Behaviors of (a) e ν, (b) e λ, (c) P (MeV fm−3), (d) ρ (MeV fm−3), (e) \(\frac{P}{\rho}\), (f) \(\frac{\kappa}{C} \frac{dP}{dx}\), (g) \(\frac{\kappa}{C} \frac{d \rho}{dx}\), (h) \(\sqrt{\frac{dP}{d\rho}}\) within fluid sphere described by the input (p,m,n,K,X)=(1,−0.5,0.2,0.691,0.729) using the charge distribution model II. The fractional radius \(( \frac{r}{R} )\) is plotted along the horizontal axis

Full size image
Fig. 2
figure 2

Charge distribution within fluid sphere described by the same input as in Fig. 1. The fractional radius \(( \frac{r}{R} )\) and the charge Q (km) are plotted along the horizontal and vertical axes respectively

Full size image
Fig. 3
figure 3

Pressure-density profile for fluid sphere described by the same input as in Fig. 1. The pressure P (MeV fm−3) and density ρ (MeV fm−3) are plotted along the horizontal and vertical axes respectively

Full size image

The mass to radius ratio of charged fluid spheres are found to satisfy Böhmer–Harko limit [60], the lower limit of the allowable mass-to-radius ratio (M/R) for charged fluid sphere

$$\frac{3}{2} \frac{Q^{2}}{R^{2}} \frac{ ( 1+ \frac{Q^{2}}{18 R^{2}} )}{ ( 1+ \frac{Q^{2}}{12 R^{2}} )} \leq\frac{2M}{R} $$

Also the mass of the charged fluid sphere satisfies Andréasson [61] inequality, the charged analogue of Buchdahl inequality,

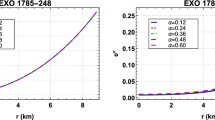
$$\sqrt{M} \leq\frac{\sqrt{R}}{3} + \sqrt{\frac{R}{9} + \frac{Q^{2}}{3R}} $$

The mass-radius relation for the particular set of values (p,m,n,K)=(1,−0.5,0.2,0.691) and 0<X≤0.729, using model II, is graphed in Fig. 4. The behavior of Fig. 4 reproduces that of other quark star models (e.g., [12]).

Fig. 4
figure 4

Mass-radius relation for the input (p,m,n,K)=(1,−0.5,0.2,0.691) and 0≤X≤0.729 (model II). The radius R (km) and total mass M (in the unit of M ⊙) are plotted along the horizontal and vertical axes respectively

Full size image

6 Conclusion

In this work some new families of exact solutions to the Einstein–Maxwell equations for a static spherically symmetric distribution of charged perfect fluid for particular forms of charge distribution were obtained and used to construct electrically charged self-bound stellar models. The relevant equations of state are also determined. These classes comprise some nonsingular stellar models, which have finite values for both the physical and metric variables at the stellar center. The method used in this paper to obtain new charged analogues to the neutral solutions depends crucially on the choice for the metric potential e ν and the forms electric charge distribution. It would be desirable to seek physically reasonable solutions, with new forms of e −λ.

The relationships between the total mass M, the total charge Q, and the constants \(\mathcal{B}_{N}\), C have been determined by the continuity of the metric coefficients across the boundary of the star to the unique exterior Reissner–Nordström solution. It has been showed that a wide range of charged spheres, with nonsingular potentials and matter variables, are possible for relevant choices of parameters.