Relativistic star in higher dimensions with Finch and Skea geometry

Abstract

We study relativistic solutions of compact objects with Finch and Skea (FS) metric of a hydrodynamical stable star in four and in higher dimensions. The solutions obtained in the usual four and in higher dimensions will be employed to construct stellar models. We study variation of different physical parameters inside the star. It is noted that a compact star in 4-dimensions with Finch and Skea geometry is always isotropic here which however is anisotropic if the space time is higher dimensional. The plausibility of such stars are studied here.

1 Introduction

The success of superstring theories in the last couple of decades led to a considerable research activities in understanding issues both in cosmology and in astrophysics in higher dimensions. The results obtained in the usual four dimensions are generalized in higher dimensions in addition to exploring scope of new physics. The history of higher dimensions goes back to the work done by Kaluza (1921) and Klein (1926) independently by introducing the concept of extra dimensions in addition to the usual four dimensions to unify gravity with the electromagnetic interaction. On the other hand, it is also very important to generalize the results obtained in four dimensional General theory of Relativity (GTR) in higher dimensional context and to probe the effects due to incorporation of extra space-time dimensions in the theory. The study of higher-dimensional gravity has no recorded observational and experimental support till now but it remains an academics interest today. A number of work in astrophysics with Finch and Skea (1989) metric is studied in $D = 4$ dimensions. The motivation of the paper is to study for stellar models by considering a higher dimensional FS metric. Finch and Skea (1989) metric was originally developed by Duorah and Ray (1987). This space-time geometry has got much attention in the modeling of relativistic compact star as the solution is well behaved and satisfies all criteria of physical acceptability (Delgaty and Lake 1998). The Finch-Skea metric has been used by many to study a large variety of stellar bodies by introducing electromagnetic field and anisotropic pressure. It is also generalized to study astrophysical objects in lower as well as in higher dimensional gravitational aspects, considering isotropic pressure distribution.

Kalam et al. (2013) obtained a model for strange quark star in Finch and Skea metric with the help of MIT Bag model, which later extended for two-fluids model. The above solution satisfies all the energy conditions. Banerjee et al. (2013) employed Finch and Skea metric to obtain a class of interior solutions corresponding to the BTZ (Banados et al. 1992) exterior solution, which is useful for the description of compact objects in $(3+1)$-dimensions. In ($2+1$)-dimensions Bhar et al. (2014) proposed a new class of solutions of anisotropic stars in Finch and Skea space time making use of the MIT bag model, which corresponds to the BTZ black hole. Tikekar and Jotania (2007) applied this space-time geometry to find two-parameters family of physically viable relativistic models of neutron stars and found the possibilities of describing strange stars and other highly compact objects. Recently, Jafry et al. (2017) investigated theoretically the nature of the massive pulsar J0348+0432 in a compact relativistic binary by considering it as isotropic one. The space-time of the pulsar is described by Finch and Skea metric in four dimensions to obtain stellar models taking into its mass as was considering (Antoniadis et al. 2013). Hansraj and Maharaj (2006) obtained charged analogue model of the Finch-Skea solution which can describe a realistic charged stellar body. The relativistic solution for the Einstein-Maxwell equations can be described by Bessel functions and modified Bessel functions in addition to elementary function with electric field intensity $E\ne0$ (except at the center) and $E = 0$ throughout the interior space-time. Recently, Maharaj et al. (2017) derived a master equation which governs an anisotropic and charged compact star description with a Finch and Skea geometry and find the solutions of that equation in terms of Bessel and modified Bessel functions which can be reduced to an elementary function for certain choice in the model. Consequently, an infinite family of exact solutions can be obtained from the master equation in terms of elementary functions. Pandya et al. (2015) taken up a modified Finch and Skea geometry, which is compatible with the observed masses and radii of a wide variety of compact stars. The stellar models in the above cases predict masses and radii of the pulsars which are in agreement with objects that might filled up with exotic strange matter used by Dey et al. (1998) and Gangopadhyay et al. (2013). The Finch-Skea ansatz has also been taken up in higher dimensional gravitational theories by Hansraj (2017), Dadhich et al. (2017), Molina et al. (2017). In a recent paper, assuming the Finch-Skea ansatz as a seed solution, Hansraj et al. (2017) constructed a stellar model with static spherical distribution of perfect fluid using trace-free Einstein gravity where the solution admit only for isotropic fluid distribution.

Furthermore, Chilambwe et al. (2015) also studied the Finch and Skea metric in $n$-dimensional context considering the space-time geometry isotropic in nature. A class of solutions of compact objects in five dimensional EGB gravity has been also found by Sardar (2016) in Finch-Skea geometry.

The motivation of the present work is to explore the stellar models both in usual four dimensions as well as in higher dimensions to accommodate isotropic and anisotropic stars respectively. Variations of different physical parameters will be probed, considering the technique given by Paul (2004). The relativistic compact star solution in higher dimensions will also be studied considering a spherically symmetric space-time. The motivation of the paper is to study highly compact stars, consequently relativistic stellar solutions are obtained describing anisotropic matter distribution whose geometry will be characterized by the Finch and Skea ansatz. The reason for incorporating anisotropy is due to the fact that in the high-density regime of compact stars the radial pressure $(p_{r})$ and the transverse pressure ($p_{t}$) need not be equal which was invented by Ruderman (1972), Canuto (1974). Kippenhahn and Weigert (1990) proposed that in relativistic stars anisotropy might occur due to the existence of a solid core or type 3A super fluid. Weber (1999) pointed out that strong magnetic field in a compact star may generate an anisotropic pressure. Anisotropy might occur in astrophysical objects for various reasons namely, viscosity, phase transition (Sokolov 1980), pion condensation (Sawyer 1972) and the presence of strong electromagnetic field (Usov 2004). The shear of the fluid may be considered as another reason for the origin of anisotropy in a self-gravitating body (Prisco et al. 2007). It is also assumed that anisotropy may develop due to the slow rotation of fluids (Herrera and Santos 1995), a mixture of perfect and a null fluid also originates an effective anisotropic fluid model in a compact star Letelier (1980).

In this work we study the Finch and Skea stellar models can be extended to the case of an anisotropic matter distribution in higher dimensional aspects. The system of field equations has been solved to generate analytic solutions which are physically important.

The paper is organized as follows: In Sect. 2, we have discussed the Einstein field equations for a static spherically symmetric and anisotropic fluid distribution in $n$-dimensions. In Sect. 3, we redact the conditions for a physically realistic model. Then, in Sect. 4, we studied features of compact objects e.g. density and radial pressure in the usual form and more than four dimensions, anisotropy parameter, mass radius relation, stability and in Sect. 5 equation of states are presented. In Sect. 6, we illustrated the range of different metric parameters and their variations with dimensions. Finally, in Sect. 7 we summarized the results.

2 Field equation in higher dimensions and solution

The Einstein’s field equation is given by,

$$ R_{ab}-\frac{1}{2}g_{ab} R =\frac{8\pi G_{D}}{c^{2}} T_{ab} $$

(1)

where, $D$ is the total no. of Dimensions, $G_{D}= G V_{D-4}$ is the gravitational constant in $D$-dimension. $G$ denotes the 4-dimensional gravitational constant and ${ V_{D-4}}$ is the volume of the extra space. ${R_{ab}}$ is Ricci tensor and ${T_{ab}}$ is the energy-momentum tensor in $D$-dimension. We consider the metric of a higher dimensional spherically symmetric, static space-time is given by,

$$ ds^{2}=-e^{2\nu(r)}dt^{2}+e^{2\lambda(r)}dr^{2}+r^{2}\Omega_{n}^{2} $$

(2)

where, $\nu(r)$ and $\lambda(r)$ are the two unknown metric functions, $n={D-2}$ and $d\Omega_{n}^{2}={d\theta_{1} ^{2}+\sin^{2}\theta_{1} d\theta_{2} ^{2}}+\sin^{2}\theta_{2}(d\theta _{3}^{2}+\cdots+\sin^{2}\theta_{n-1}d\theta_{n}^{2})$ represents the metric on the $n$-sphere in polar coordinates. The energy momentum tensor for an anisotropic star in the most general form is given by,

$$ T_{ab}= \operatorname{diag} (-\rho,p_{r},p_{t},p_{t},\ldots,p_{t}) $$

(3)

where, $\rho$ is the energy density, $p_{r}$ is the radial pressure and $p_{t}$ is the tangential pressure. $\Delta= p_{r}-p_{t}$ is the measure of pressure anisotropy in this model, which depends on metric potential $\lambda(r)$ and $\nu(r)$.

Using Eqs. (1) and (2), Einsteins field equation reduces to the following set of equations:

$$\begin{aligned}& \frac{8\pi G_{D}\rho}{c^{2}} = \frac{n(n-1)\left(1-e^{-2\lambda}\right )}{2r^{2}}+\frac{n\lambda'e^{-2\lambda}}{r} \end{aligned}$$

(4)

$$\begin{aligned}& \frac{8\pi G_{D}p_{r}}{c^{2}} = \frac{n\nu'e^{-2\lambda}}{r}-\frac {n(n-1)\left(1-e^{-2\lambda}\right)}{2r^{2}} \end{aligned}$$

(5)

$$\begin{aligned}& \frac{8\pi G_{D}p_{t}}{c^{2}}= e^{-2\lambda} \left(\nu^{\prime\prime}+{\nu^{\prime}}^{2}-\nu ^{\prime }\lambda^{\prime}-\frac{(n-1)(\lambda^{\prime}-\nu^{\prime })}{r}\right) \\& \phantom{\frac{8\pi G_{D}p_{t}}{c^{2}}=\,\,}{} -\frac{(n-1) (n-2)\left(1-e^{-2\lambda}\right)}{2r^{2}} \end{aligned}$$

(6)

where, overheads dash denotes the derivative w.r.t $r$. Using Eqs. (5) and (6), the pressure anisotropy condition ($\Delta = p_{t}-p_{r}$) gives rise to,

$$\begin{aligned}& \nu^{\prime\prime}+{\nu^{\prime}}^{2}-\nu^{\prime}\lambda ^{\prime}-\frac{(n-1)\lambda^{\prime}}{r}-\frac{\nu^{\prime }}{r}-\frac{(n-1)\left(1-e^{2\lambda}\right)}{r^{2}} \\& \quad =\Delta e^{2\lambda} \end{aligned}$$

(7)

We consider the interior space-time given by Finch and Skea metric as,

$$\begin{aligned}& e^{2\lambda(r)}=(1+C r^{2}) \end{aligned}$$

(8)

$$\begin{aligned}& e^{2\nu(r)}= D^{2}[(B-A\sqrt{1+C r^{2}}) \operatorname{Cos}\sqrt{1+C r^{2}} \\& \phantom{e^{2\nu(r)}=\,\,}{}+ (A+B\sqrt{1+C r^{2}}) \operatorname{Sin}\sqrt{1+C r^{2}}]^{2} \end{aligned}$$

(9)

where $A$, $B$, $C$ and $D$ are constants, prescribing the specific geometries for the 3-Space of the interior space-time of the star and discussed the various features. Therefore, in $D$ (i.e. ${n+2 }$)-dimension, the physical parameters relevant in this model are given below:

$$\begin{aligned}& \frac{8\pi G_{D} \rho}{c^{2}} = \frac{C n (1 + n-C r^{2} + C n r^{2})}{2 (1 + C r^{2})^{2}} \end{aligned}$$

(10)

$$\begin{aligned}& \frac{8\pi G_{D} p_{r}}{c^{2}}=\frac{-n C [n X+ X' ]}{2 K^{2} X} \end{aligned}$$

(11)

where, $K= \sqrt{1 + C r^{2}}$, $X= (B-A K) \operatorname{Cos} K+ (A+B K) \operatorname{Sin} K$ and $X' = \operatorname{Cos} K (A K-3 B)-\operatorname{Sin} K (B K+3 A)$

$$ \Delta= \frac{C^{2}(n-2) r^{2}}{(1+C r^{2})^{2}} $$

(12)

Here, $n=2$ correspondingly $\Delta= 0$ is obtained but $\Delta\ne0$ for $n \ne 2$. Equations (10) to (13) will be employed here to study exact compact stellar objects in higher dimension.

The total mass contained within radius $r$ in $D$-dimension is,

$$ m(r) = A_{n}\int_{0}^{r} r^{\prime\,D-2} \rho(r') dr' $$

(13)

where, $A_{n}= \frac{2 \pi^{\frac{n+1}{2}}}{\Gamma(\frac{n+1}{2})}$ and $\rho(r')$ represents the energy density at $r= r'$. The actual mass of a star can be obtained by using Eq. (14) and then integrating upto $r= b$, i.e., the maximum size of the compact object.

3 Conditions for obtaining physically realistic stellar model

A comparatively reasonable set of conditions includes:

• (i) At the boundary of the star $(i.e. r = b)$, the interior solution should be matched with the exterior Schwarzschild solution. This determines the metric at the surface, $e^{2\nu(r = b)} = e^{-2\lambda(r=b)} = (1-\frac{K}{b^{n-1}})$ where K is a constant related to the mass of the star which is given by $M= \frac{n A_{n} K}{16\pi G_{D}}$. In four dimensions ($D= 4$), $K= 2 M$ and in five dimension ($D= 5$), $K= 0.84848$ $MG_{5}$ where $G_{5} = G V_{1}$ and $V_{1}$ is the volume of extra space in five dimensions. In general, $V_{n} =\frac{ 2\pi^{\frac{n+1}{2}} r^{n+1}}{(n+1)\Gamma {\frac{n+1}{2}}}$. In $D= 5$, it becomes $V_{1} = 2 r$.

• (ii) In addition, the radial pressure drops from its maximum value (at center) to zero at the boundary, i.e., at $r= b$, $p_{r} = 0$.

• (iii) The density and the pressures should be positive inside the star. For $\rho$ this coincides with the null energy condition (NEC). At the center, they should be finite $\rho(0) = \rho_{0}$, $p_{r}(0) = p_{r0}$. Moreover, $p_{r0} = p_{t0}$.

• (iv) The solution should satisfy the dominant energy condition (DEC) at the center, $\rho_{0} > | p_{0}|$.

• (v) Inside the star the stellar model should satisfy the condition, $v^{2} = \frac{dp}{d\rho} \leqslant1$, for the sound propagation to be causal.

• (vi) The gradient of the pressure and energy-density should be negative inside the stellar configuration, i.e., $\frac{dp_{r}}{dr} < 0$, $\frac{dp_{t}}{dr} < 0$ and $\frac{d\rho}{dr} < 0$.

The above conditions are used to obtain physically viable stellar models.

4 Physical analysis of compact objects

In this section we investigate the following features of the compact object:

• Density and pressure of a compact object and variation with dimension

From Eq. 10, the energy-density in $D=4$ dimension is,

$$ \frac{8\pi G \rho_{4}}{c^{2}} = \frac{C (3+C r^{2})}{(1+C r^{2})^{2}} $$

(14)

Whereas, in $D= 5$ dimension,

$$ \frac{8\pi G_{5}\rho_{5}}{c^{2}}= \frac{3 C (2+C r^{2})}{(1+C r^{2})^{2}} $$

(15)

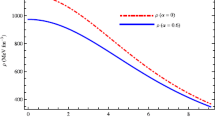
For the both cases, clearly, at the center, the density of the star is maximum and it decreases radially outward. In Fig. 1, we plot variation of energy density $(\rho)$ inside the compact objects with different space-time dimensions using Eqs. (15) and (16). It is found that the energy density is more in five dimensions than that in four dimensions. Therefore, it is evident that a star of same radius accommodates more mass in the case of higher dimensions.

Fig. 1

Radial variation of energy-density ($\rho$) for $D= 4$ (Black) and $D= 5$ (Red)

Similarly, in $D=4$ dimension, the radial pressure $(p_{r4})$ becomes,

$$ \frac{8\pi G p_{r4}}{c^{2}}=\frac{C[(B+A K)\operatorname{Cos} K +(A-B K) \operatorname{Sin}K ]}{K^{2} X} $$

(16)

In $D=5$ dimension, the radial pressure $(p_{r5})$ becomes

$$ \frac{8\pi G_{5} p_{r5}}{c^{2}} = \frac{3 C[A \operatorname{Cos} K-B \operatorname{Sin} K ]}{K X} $$

(17)

where, $K= \sqrt{1 + Cr^{2}}$ and $X= (B-A K) \operatorname{Cos} K+ (A+B K) \operatorname{Sin}K$.

In the case of radial pressure plotted in Fig. 2, it is evident that the radial pressure increases with increase of space-time dimensions. Thus, the energy density and the pressure are found well behaved inside the compact object. The plot of variation of the energy-density and radial pressure gradients with dimensions in Figs. 3 and 4 are negative.

Fig. 2

Radial variation of pressure ($p_{r}$) for $D= 4$ (Black) and $D= 5$ (Red)

Fig. 3

Radial variation of the energy-density gradient $\frac{d\rho }{dr}$ for $D= 4$ (Black) and $D= 5$ (Red)

Fig. 4

Radial variation of pressure gradient $\frac{dP_{r}}{dr}$ for $D = 4$ (Black) and $D= 5$ (Red)

• Anisotropy parameter

From Eq. (13), it is shown that when $n = 2$, i.e., in 4-dimension $\Delta=0$, it represent an isotropic star always. However it is found that if we extend the space-time dimensions, it is possible to accommodate anisotropy in star for $n\ne2$. We noted from Fig. 5 that the anisotropy ($\Delta$) increases with dimensions. Therefore, the FS solution admits anisotropic star in higher dimensions which however is isotropic in 4-dimensions. Now, the transverse pressure is defined as, $p_{t} = p_{r}+\Delta$. From Fig. 5 it is evident that at the center of the star anisotropy ($\Delta$) vanishes for all dimensions, whereas it attains a maximum value at the surface. Though the nature of radial variation of $\Delta$ is same, it picks up higher values in higher dimensions. But different situations arises with ($2+1$) dimension, as shown in Fig. 5.

Fig. 5

Variation of compact object for different dimensions namely: $D = 5$ (Black) and $D= 6$ (Green), $D=(2+1)$ (Blue)

• Stability

The stability of a stellar model is studied by computing $\frac {dp}{d\rho}$ insider the star. The effect of increase in space time dimensions on stability on a compact object is studied here, which is presented in Table 1. From Table 1, it is shown that a star with $r= 10~\mbox{km}$ in $D=4$ dimensions as well as in $D=6$ dimensions are not allowed. Similarly, for $r=12~\mbox{km}$, $D<4$ and $D>6$ are not allowed and for $r=14~\mbox{km}$, $D<4$ and $D>6$ are also not permitted for a given set of values of $A$, $B$ and $C$. The variation of the sound speed inside the star for $D=4$ and $D=5$ are plotted in Fig. 6. It is found that $\frac{dp}{d\rho}$ decreases with increasein radius for a particular dimension. It is also noted that $\frac {dp}{d\rho}$ is maximum at the center and gradually it decreases outward.

Fig. 6

Variation of the sound speed at the stellar interior for $D=4$ (Black) and $D=5$ (Red)

Table 1 Variation of $\frac{dp}{d\rho}$ with dimensions ($n$) for different values of radius ($r$)

• Mass-radius relation The total mass contained within radius $r$ in $D$-dimension is,

$$ m_{D}(r) = A_{n}\int_{0}^{r} r^{\prime\,D-2} \rho(r') dr' $$

(18)

For Pulsar J0348+0432, the observed mass is $2.01\pm 0.04~M_{\odot}$. Now, plotting observed mass in mass-radius curve one can find the radius of pulsar in the frame of $D= 4$ and $D= 5$ dimensions using Finch-Skea metric.

In $D= 4$ dimension, from Eq. (14) the gravitational mass ($M$) in terms of the energy density ($\rho_{4}$) can be expressed as (taking $c=1$ and $G=1$),

$$ m_{4}(r) = A_{2}\int_{0}^{r} r^{\prime\,2} \rho_{4}(r') dr' = \frac{Cr^{3}}{2+2 Cr^{2}} $$

(19)

Similarly, in $D=5$ dimension, the mass will be,

$$\begin{aligned} m_{5}(r) =& A_{3}\int_{0}^{r} r^{\prime\,2} \rho_{5}(r') dr' \\ =& \frac{3\pi[r-\frac {r}{2(1+Cr^{2})}-\frac{\tan^{-1}(\sqrt{C}r)}{2\sqrt{C}}]}{8} \end{aligned}$$

(20)

Conventionally, the mass-radius curves are plotted in Fig. 7 for a given density function in a particular dimension, where the mass of a star is fixed. The radius is estimated for the Pulsar J0348+0432 is in the range of $13.92~\mbox{km} < r< 14.16~\mbox{km}$ for $D=4$ dimension and $10.44~\mbox{km} < r < 10.58~\mbox{km}$ for $D =5$ dimension respectively with $\mbox{mass} = 2.01 \pm 0.04~M_{\odot}$.

Fig. 7

Nature of the mass function at the stellar interior of the Pulsar J0348+0432 for $D= 4$ (Black) and $D=5$ (Red)

5 Equation of state

Using the above model parameters we plot the radial variation of density and radial pressure vied Eqs. (4) and (5). However, it may be pointed out here that an analytic function of pressure with density in known form cannot be obtained exactly here because of non-linearity terms. We study numerically to obtain a best fitted relation between the energy density ($\rho$) and radial pressure ($p_{r}$), which vary with dimensions. Equation of state for a compact object is plotted in Figs. 8 and 9 corresponding to $D=4$ and $D = 5$ respectively.

Fig. 8

Equation of State of the Pulsar in our model in different dimensions $D= 4$ (Black) and $D= 5$ (Red)

Fig. 9

Nature of the mass function at the stellar interior of the Pulsar HER X1 (Purple), SAX J-SS1 (Orange) and SAX J-SS2 (Green) (for $D= 4$ (Black) and $D=5$ (Red))

6 Variations of metric parameters with dimensions

The metric parameters $A$, $B$ and $C$ for $D = 4$ and $D= 5$ dimensions both for an acceptable range of radius of compact objects (i.e. from $R= 10~\mbox{km}$ to $R= 14~\mbox{km}$) using Finch-Skea metric are shown in Table 2. These will be used to understand the physical properties of a compact object in more general way.

Table 2 Different values of parameters $A$, $B$, $C$ in $D= 4$ and $D= 5$

7 Discussion

In this paper we study compact objects in hydrodynamical equilibrium for different dimensions with Finch and Skea metric (1989) as the interior space of the object. But it is quite interesting that one determines various physical aspects with a similar kind of solutions in different dimensions. The interior geometry is described by Finch and Skea metric both in four and in higher dimensions and we have analyzed the effect of higher dimensions on the physically relevant Finch-Skea model of a spherically symmetric compact object in the standard Einstein gravitational theory. We note the following:

• (i) In Fig. 1, we plot the variation of energy density $(\rho)$ with radial distance and found that energy density is more in five dimensions than that in four dimension. It is evident that a star of same radius accommodates more mass in case of higher dimensions.

• (ii) In Fig. 2, we plot the variation of radial pressure away from the center to the boundary and found that the radial pressure $(p_{r})$ increases with an increase in space-time dimensions ($D$).

• (iii) Here, the density and the radial pressure in $D = 4$ and also in higher dimensions are all decreasing away from the center. At the center, density and radial pressure are found to be more than that in four dimensions. But, the radial pressure becomes zero at the boundary (i.e. at $r= R$). Here, also energy-density and pressure gradients is negative (see Figs. 3 and 4).

• (iv) The squared speed of sound ($v^{2} = \frac{dp}{d\rho}$) with radius $r$ for different dimensions is presented in Table 1. From Table 1, it is shown that a star with $r= 10~\mbox{km}$ in $D=4$ dimensions as well as in $D=6$ dimensions are not allowed. Similarly, for $r=12~\mbox{km}$, $D<4$ and $D>6$ are not allowed and for $r=14~\mbox{km}$, $D<4$ and $D>6$ are also not permitted for a given set of values of A, B and C. Therefore, it is found that for fixed values $A$, $B$ and $C$ there exist a upper bound of dimensions for a physically viable stellar model. It is also noted that for a particular dimension, $\frac {dp}{d\rho}$ is maximum at the center which however found to decrease radially outward and decreases with increasing dimensions in Finch-Skea geometry which is in agreement with Chilambwe et al. (2015). It’s observed that inside the star $v^{2} = \frac{dp}{d\rho} \leqslant1$, which shows that the stellar model is stable.

• (v) It is found the EoS satisfies a linear relation $p =\alpha+ \beta \rho$. In $D = 4$, $\alpha=-0.00214163$ and $\beta= 0.322546$ and similarly, in $D =5$, $\alpha=-0.0127792$ and $\beta= 0.565581$. The plot of $p$ vs. $\rho$ are shown in Figs. 8 and 9 for $D =4$ and $D = 5$ respectively.

• (vi) The most interesting result in this model is that the relativistic solution in $D =4$, which was obtained for isotropic fluid, is found anisotropic when the space time dimensions is increased, which is shown in Fig. 5. At the center of the star, the anisotropy $(\Delta)$ vanishes both in $D= 5$, $D= 6$ and also in $D = 3$, whereas at the surface it attains a maximum value. Though the nature of radial variations of $\Delta$ is same, but situation becomes completely flipped when $D = (2+1)$.

• (vii) In Table 2, we tabulated the range of the values of $A$, $B$ and $C$, which vary with dimensions. It is evident that for a particular radius, $A$ increases with dimensions, whereas $B$ and $C$ decreases with dimensions.

• (viii) Again, from Table 2, it is evident that for both $D = 4$ and $D = 5$ as radius increases, $B$ increases and $C$ decreases simultaneously. But $A$ is found to play different role. For $D = 4$, $A$ decreases with increasing radius, where for $D =5$ it increases with radius.

• (ix) From Fig. 7, it is also found that for a particular radius, the mass of the compact object increases with increasing dimensions. It is also worthy to mention here that our model is well applicable to other Pulsars also such as HER X1, SAX J-SS1 and SAX J-SS2 etc., which is shown in Fig. 9. More interestingly, if we starts from the center with a certain central density, the structure of a pulsar can be determined by stopping at any radius where pressure becomes zero.

• (x) For Pulsar J0348+0432, we estimate the radius in $D=4$ and $D=5$ dimensions. In Fig. 7, we obtain the radii: $13.92~\mbox{km} < r< 14.16~\mbox{km}$ for $D=4$ dimension and $10.44~\mbox{km} < r < 10.58~\mbox{km}$ for $D =5$ dimension respectively. It is evident that if the dimension is increased, the lower and upper limit of radius of a compact object are found to decrease accommodating same mass. So in higher dimensions a massive compact object can be accommodated.