1 Introduction

Ever since the formulation of Einstein-Maxwell field equations, the relativists have been proposing different models of immensely gravitating astrophysical objects by considering the distinct nature of matter or radiation (energy-momentum tensor) present in them. Einstein-Maxwell field equations have more importance over Einstein field equations due to following rationale justifications:

  • The presence of some charge may avert the catastrophic gravitational collapse by counter balancing the gravitational attraction by the electric repulsion in addition to the pressure gradient.

  • The inclusion of charge inhibits the growth of space time curvature which has a great role to avoid singularities (Ivanov 2002; de Felice et al. 1995).

  • Bonnor (1965), pointed out that a dust distribution of arbitrarily large mass and small radius can remain in equilibrium against the pull of gravity by a repulsive force produced by a small amount of charge.

  • The solutions of Einstein-Maxwell equations are useful to study the cosmic matter.

  • The charge dust models and electromagnetic mass models are providing some clue about the structure of electron (Bijalwan 2011) and Lepton model (Kiess 2013).

  • Several solutions which do not satisfy some or all the conditions for well behaved nature can be renewed into well behaved nature by charging them.

Thus it is desirable to study the insinuations of Einstein-Maxwell field equations with reference to the general relativistic prediction of gravitational collapse. For this purpose charged fluid ball models are required. The external field of such ball is to be matched with Reissener-Nordström solution. The solutions of Einstein-Maxwell field equations successfully explain the characteristics of massive objects like neutron star, quark star or other super-dense objects. Further, these stars are specified in terms of their masses and densities:

  1. (a)

    A Neutron Star has surface density ρ b =2×1014 g/cm3 (Brecher and Caporaso 1976) or 2.7×1014 g/cm3 (Astashenok et al. 2013) and mass 1.4M ⊙–2.9M ⊙. However, Astashenok et al. (2013) established that f(R) models with realistic equation of state of neutron star has upper limit mass 2.0M ⊙ and minimal radius close to 9 km.

  2. (b)

    A Strange Quark Star has surface density ρ b =4.6888×1014 g/cm3 (Fatema and Murad 2013; Zdunik 2000) and possible maximum mass 2M ⊙. However, Dong et al. (2013) established that due to presence of half skyrmions in the dense baryonic matter the stable Strange Quark Star can have upper mass limit 2.4M ⊙.

2 Conditions for well behaved solution

For well behaved nature of the solution in isotropic coordinates, the following conditions should be satisfied:

  1. (i)

    The solution should be free from physical and geometrical singularities i.e. finite and positive values of central pressure, central density and non zero positive values of e ω and e υ.

  2. (ii)

    The solution should have positive and monotonically decreasing expressions for pressure and density (p and ρ) with the increase of r. The solution should have positive value of ratio of pressure-density and less than 1 (weak energy condition) and less than 1/3 (strong energy condition) throughout within the star, monotonically decreasing as well.

  3. (iii)

    The causality condition should be obeyed i.e. velocity of sound should be less than that of light throughout the model. In addition to the above the velocity of sound should be decreasing towards the surface i.e.

    $$\frac{d}{dr} \biggl( \frac{dp}{d\rho} \biggr) < 0\quad \mathrm{or}\quad \biggl( \frac{d^{2}p}{d\rho^{2}} \biggr) > 0 $$

    for 0≤r≤r b i.e. the velocity of sound is increasing with the increase of density. In this context it is worth mentioning that the equation of state at ultra-high distribution, has the property that the sound speed is decreasing outwards (Canuto and Lodenquai 1975).

  4. (iv)

    \(\frac{p}{\rho} \le\frac{dp}{d\rho}\), everywhere within the ball.

    $$\gamma=\frac{d\log_{e}p}{d\log_{e} \rho} = \frac{\rho}{p} \frac{dp}{d\rho} \quad \Rightarrow\quad \frac{dp}{d\rho} = \gamma\frac{p}{\rho}, $$

    for realistic matter γ≥1.

  5. (v)

    The red shift Z should be positive, finite and monotonically decreasing in nature with the increase of r.

  6. (vi)

    Electric intensity E, such that E (r=0)=0, is taken to be monotonically increasing.

Under these conditions, we have to assume the one of the gravitational potential components in such a way that the field equation (8) can be integrated and solution should be well behaved. Further, the mass of the such modeled super dense object can be maximized by assuming surface density, for Neutron star (Brecher and Caporaso 1976) ρ b =2×1014 g/cm3 and for SQM, Strange Quark star (Fatema and Murad 2013; Zdunik 2000) ρ b =4.6888×1014 g/cm3.

Keeping in view this aspect, several authors obtained the parametric class of exact solutions; Das et al. (2011), Pant et al. (2011a, 2011b), Pant and Negi (2012), Kiess (2012), Gupta and Maurya (2011), Maurya and Gupta (2011), Pant (2011a, 2011b), Murad and Fatema (2013), Takisa and Maharaj (2013) etc. These coupled solutions are well behaved with some positive values of charge parameter K and completely describe the interior of the super-dense astrophysical object with charged matter. However, the works of Pant (2011b), Kiess (2012), Gupta and Maurya (2011) and Fatema and Murad (2013) are well behaved with their neutral counterparts. Most of the findings are in curvature coordinates. By motivation of Ivanov (2012) and in continuation our previous work (Pradhan and Pant 2014), in this paper we present a new family of solutions of Einstein-Maxwell field equations in isotropic coordinates for perfect fluid assuming a particular form of one of the metric potentials and suitable choice of electric intensity.

3 Field equations in isotropic coordinates

We consider the static and spherically symmetric metric in isotropic co-ordinates

$$ ds^{2} = - e^{\omega} \bigl[ dr^{2} + r^{2}\bigl(d\theta^{2} + \sin^{2}\theta d \phi^{2}\bigr)\bigr] + c^{2}e^{\upsilon} dt^{2} $$
(1)

where, ω and υ are functions of r.

Einstein-Maxwell field equations of gravitation for a non empty space-time are

$$\begin{aligned} R_{j}^{i} - \frac{1}{2}R\delta_{j}^{i} &= - \frac{8\pi G}{c^{4}}T_{j}^{i} \\ & = - \frac{8\pi G}{c^{4}}\biggl[\bigl(p + \rho c^{2} \bigr)v^{i}v_{j} - p\delta_{j}^{i} \\ &\quad {} + \frac{1}{4\pi} \biggl( - F^{im}F_{jm} + \frac{1}{4} \delta_{j}^{i}F_{mn}F^{mn}\biggr)\biggr] \end{aligned}$$
(2)

where R ij is Ricci tensor, T ij is energy-momentum tensor, R is the scalar curvature and F jm is the electromagnetic field tensor, p denotes the pressure distribution, ρ the density distribution and v i the velocity vector, satisfying the relation

$$ g_{ij}v^{i}v^{j} = 1 $$
(3)

Since the field is static, therefore

$$ v^{1} = v^{2} = v^{3} = 0 \quad \mathrm{and}\quad v^{4} = \frac{1}{\sqrt{g_{44}}} $$
(4)

Thus we find that for the metric (1) under these conditions and for matter distributions with isotropic pressure the field equation (2) reduces to the following Das et al. (2011):

$$\begin{aligned} & \frac{8\pi G}{c^{4}}p = e^{ - \omega} \biggl[\frac{(\omega')^{2}}{4} + \frac{\omega'}{r} + \frac{\omega'\upsilon'}{2} + \frac{\upsilon'}{r}\biggr] + \frac{q^{2}}{r^{4}} \end{aligned}$$
(5)
$$\begin{aligned} & \frac{8\pi G}{c^{4}}p = e^{ - \omega} \biggl[\frac{\omega''}{2} + \frac{\upsilon''}{2} + \frac{(\upsilon')^{2}}{4} + \frac{\omega'}{2r} + \frac{\upsilon'}{2r} \biggr] - \frac{q^{2}}{r^{4}} \end{aligned}$$
(6)
$$\begin{aligned} & \frac{8\pi G}{c^{2}}\rho= - e^{ - \omega} \biggl[ \omega'' + \frac{(\omega')^{2}}{4} + \frac{2\omega'}{r}\biggr] - \frac{q^{2}}{r^{4}} \end{aligned}$$
(7)

where, prime (′) denotes differentiation with respect to r. From Eqs. (5) and (6) we obtain following differential equation in ω and υ.

$$ e^{ - \omega} \biggl(\omega'' + \nu'' + \frac{(\upsilon')^{2}}{2} - \frac{(\omega')^{2}}{2} - \omega'\upsilon' - \frac{\omega'}{r} - \frac{\upsilon'}{r}\biggr) - 4\frac{q^{2}}{r^{4}} = 0 $$
(8)

Our task is to explore the solutions of Eq. (8) and obtain the fluid parameters p and ρ from Eq. (5) and Eq. (7). To solve the above equation we consider a seed solution as Pant et al. (2013), Murad and Pant (2014) and the electric intensity E of the following form:

$$ \frac{E^{2}}{C} = \frac{q^{2}}{Cr^{4}} = \frac{KCr^{2} ( 1 + Cr^{2} )^{\frac{2 - 2n}{n}}}{B^{2}} $$
(9)

where K is a positive constant. The electric intensity is so assumed that the model is physically significant and well behaved i.e. E remains regular and positive throughout the sphere. In addition, E vanishes at the center of the star and increases towards the boundary.

4 Boundary conditions in isotropic coordinates

For exploring the boundary conditions, we use the principle that the metric coefficients g ij and their first derivatives g ij,k in interior solution (I) as well as in exterior solution (E) are continuous upto and on the boundary B. The continuity of metric coefficients g ij of I and B on the boundary is known first fundamental form. The continuity of derivatives of metric coefficients g ij of I and B on the boundary is known second fundamental form.

The exterior field of a spherically symmetric static charged fluid distribution is described by Reissner-Nordström metric given by

$$\begin{aligned} ds^{2}& = \biggl( 1 - \frac{2GM}{c^{2}R} + \frac{q^{2}}{R^{2}} \biggr) c^{2} dt^{2} \\ &\quad {} - \biggl( 1 - \frac{2GM}{c^{2} R} + \frac{q^{2}}{R^{2}} \biggr)^{ - 1}dR^{2} - R^{2}d \theta^{2} \\ &\quad {} - R^{2} \sin^{2}\theta d \phi^{2} \end{aligned}$$
(10)

where M is the mass of the ball as determined by the external observer and R is the radial coordinate of the exterior region.

Since Reissner-Nordström (10) is considered as the exterior solution, thus we shall arrive at the following conclusions by matching first and second fundamental forms:

$$\begin{aligned} & e^{\upsilon_{b}}=\biggl[1 - 2\frac{GM}{c^{2}R_{b}} + \frac{q_{b}^{2}}{R_{b}^{2}}\biggr] \end{aligned}$$
(11)
$$\begin{aligned} & R_{b} = r_{b}.e^{\frac{\omega_{b}}{2}}\quad \mathrm{and}\quad q_{(\mathrm{at}\ r = r_b)} = q_{b} \end{aligned}$$
(12)
$$\begin{aligned} & \frac{1}{2} \biggl( \omega' + \frac{2}{r} \biggr)_{b} r_{b} = \biggl( 1 - 2\frac{GM}{c^{2}R_{b}} + \frac{q_{b}^{2}}{R_{b}^{2}} \biggr)^{1 / 2} \end{aligned}$$
(13)
$$\begin{aligned} & \frac{1}{2} \bigl( \nu' \bigr)_{b} r_{b} = \biggl(\frac{GM}{c^{2}R_{b}} - \frac{q_{b}^{2}}{R_{b}^{2}}\biggr) \biggl( 1 - 2\frac{GM}{c^{2}R_{b}} + \frac{q_{b}^{2}}{R_{b}^{2}} \biggr)^{ - 1 / 2} \end{aligned}$$
(14)

Equations (11) to (14) are four conditions, known as boundary conditions in isotropic coordinates. Moreover, (12) and (14) are equivalent to zero pressure of the interior solution on the boundary.

5 A new class of solution

Equation (8) is solved by assuming the seed solution as Hajj-Boutros (1986), Murad and Pant (2014) and the electric intensity E in such a manner that the solution can be obtained and physically viable. Thus we have,

$$ \begin{aligned} & e^{\omega/2} = B \bigl( 1 + Cr^{2} \bigr)^{ - \frac{1}{n}},\quad x = Cr^{2},\quad y = \frac{d\upsilon}{dx}\quad \mathrm{and} \\ & q^{2} = \frac{K}{B^{2}C}x^{3}(1 + x)^{\frac{2 - 2n}{n}} \end{aligned} $$
(15)

On substituting the above in Eq. (8), we get the following Riccati differential equation in y,

$$ \frac{dy}{dx} + \frac{2}{n}\frac{1}{(1 + x)}y + \frac{1}{2} y^{2} = - \frac{2n - 2}{n^{2}}\frac{1}{ ( 1 + x )^{2}} + \frac{K}{(1 + x)^{2}} $$
(16)

Which yields the following solution,

$$ e^{\frac{\nu}{2}} = \frac{ \{ 1 + A ( 1 + Cr^{2} )^{\frac{2S}{2n}} \} ( 1 + Cr^{2} )^{\frac{n - 2 - S}{2n}}}{B^{2}} $$
(17)

where A, B, C and K are arbitrary constants and

$$ S = \sqrt{2n^{2}K + n^{2} - 8n + 8} $$
(18)
$$ \begin{aligned} & S\ \mbox{is real for } K>\frac{8n-n^2-8}{2n^2}\\ & K\ \mbox{is non-zero for }4 - 2 \sqrt{2} < n < 4 + 2 \sqrt{2} \end{aligned} $$
(18a)

The expressions for density and pressure are given by

$$\begin{aligned} & \frac{8\pi G\rho}{c^{2}} = \frac{C}{n^{2}B^{2}f^{4n - 4}}\bigl(12n+ (4n-4)Cr^2-n^2 KCr^2\bigr) \end{aligned}$$
(19)
$$\begin{aligned} & \frac{8\pi Gp}{c^{4}} \\ &\quad = \frac{C}{n^{2}B^{2}f^{4n - 4}\{ 1 + Af^{2S}\}} \\ &\qquad {}\times \bigl[ Cr^{2}\bigl[Af^{2S}\bigl(n^{2}K + 2n^{2} - 12n + 12 + 2nS - 4S\bigr) \\ &\qquad {} + \bigl(n^{2}K + 2n^{2} - 12n + 12 - 2nS + 4S\bigr)\bigr] \\ &\qquad {} + 2n\bigl[Af^{2S}(n - 4 + S) + (n - 4 - S)\bigr] \bigr] \end{aligned}$$
(20)
$$\begin{aligned} & \mbox{where}, f = \bigl(1 + Cr^{2} \bigr)^{\frac{1}{2n}} \end{aligned}$$
(21)

6 Properties of the new solution

The central values of pressure and density are given by

$$\begin{aligned} & \biggl( \frac{8 \pi G p}{c^{4}} \biggr)_{r = 0} = \frac{2C}{nB^{2} (1 + A)} \bigl[ (n - 4) (1 + A) + S(A - 1) \bigr] \end{aligned}$$
(22)
$$\begin{aligned} & \biggl( \frac{8 \pi G \rho}{c^{2}} \biggr)_{r = 0} = \frac{12 C}{nB^{2}} \end{aligned}$$
(23)

The central values of pressure and density will be non zero positive definite, if the following conditions will be satisfied.

$$ A > (S-n+4)/(S+n-4),\qquad C > 0. $$
(24)

In view of (19) and (20) the ratio of pressure-density is given by

$$\begin{aligned} \frac{p}{\rho c^{2}} &= \bigl(Cr^{2}\bigl[Af^{2S} \bigl(n^{2}K + 2n^{2} - 12n + 12 + 2nS - 4S\bigr) \\ &\quad {} + \bigl(n^{2}K + 2n^{2} - 12n + 12 - 2nS + 4S\bigr)\bigr] \\ &\quad {}+ 2n \bigl[Af^{2S}(n - 4 + S) + (n - 4 - S)\bigr]\bigr) \\ &\quad {}\times \bigl(\bigl(1 + Af^{2S}\bigr)\bigl[12n + (4n - 4)Cr^{2} - n^{2}KCr^{2} \bigr]\bigr)^{-1} \end{aligned}$$
(25)

Subjecting the condition that positive value of ratio of pressure-density and less than 1 at the centre i.e. \(\frac{p_{0}}{\rho_{0} c^{2}} \le1\) which leads to the following inequality,

$$\begin{aligned} \biggl\{ \frac{p}{\rho c^{2}}\biggr\} _{r = 0} &= \frac{(n - 4)(1 + A) + SA - S}{6(1 + A)} \\ & = \frac{n - 4}{6} - \frac{S(1 - A)}{6(1 + A)} \end{aligned}$$
(26)

All the values of A which satisfy Eq. (24), will also lead to the condition \(\frac{p_{0}}{\rho_{0} c^{2}} \le1\).

Differentiating (20) with respect to r, we get

$$\begin{aligned} &\frac{8\pi G}{c^4} \frac{dp}{dr} \\ &\quad =\frac{C^2 r}{n^3 B^2 \{1+Af^{2S}\}^2 f^{6n-4}} \bigl[-Cr^2(2n-4) \\ &\qquad {}\times\bigl[A^2f^{4S} \bigl\{ n^2K+2n^2-12n+12+(2n-4)S\bigr\} \\ &\qquad {}+ \bigl\{ n^2K+2n^2-12n+12-(2n-4)S\bigr\} \\ &\qquad {}+2Af^{2S} \bigl(n^2K+2n^2-12n+12-2S^2\bigr)\bigr] \\ &\qquad {} +2n \bigl[A^2f^{4S}\bigl\{ n^2K-2n^2+8n-4-2nS \bigr\} \\ &\qquad {}+\bigl(n^2K-2n^2+8n-4+2nS\bigr) \\ &\qquad {} +2Af^{2S} \bigl(n^2K-2n^2+8n-4+2S^2\bigr)\bigr]\bigr] \end{aligned}$$
(27)

Thus it is found that extrema of p occur at the centre i.e.

$$ p' = 0 \quad \Rightarrow\quad r = 0\quad\mbox{and} \quad \frac{8 \pi G}{c^{4}} \bigl( p'' \bigr)_{r = 0} = - ve $$
(28)

Thus the expression of right hand side of Eq. (28) is negative for all values of A satisfying condition (24), showing thereby that the pressure (p) is maximum at the centre and monotonically decreasing.

Now differentiating Eq. (19) with respect to r we get

$$\begin{aligned} \frac{8\pi G}{c^{2}}\frac{d\rho}{dr} &= \frac{C^{2}r}{n^{3}B^{2}f^{6n - 4}} \bigl[ - 40n^{2} + 40n - 2n^{3}K \\ &\quad {}- 8\bigl(n^{2} - 3n + 2 \bigr)Cr^{2} + \bigl(2n^{3} - 4n^{2} \bigr)KCr^{2} \bigr] \end{aligned}$$
(29)

Thus the extrema of ρ occur at the centre if

$$\begin{aligned} & \rho' = 0 \quad \Rightarrow\quad r = 0 \\ & \frac{8 \pi G}{c^{2}} \bigl( \rho'' \bigr)_{r = 0} = \frac{( - 40n^{2} + 40n - 2n^{3}K)C^{2}}{ n^{3}B^{2}} \end{aligned}$$
(30)

Thus, the expression of right hand side of (30) is negative showing thereby that the density ρ is maximum at the centre and monotonically decreasing.

The square of adiabatic sound speed at the centre, \(\frac{1}{c^{2}} ( \frac{dp}{d\rho} )_{r = 0}\), is given by

$$\begin{aligned} & \frac{1}{c^{2}} \biggl( \frac{dp}{d\rho} \biggr)_{r = 0} = \frac{ ( n^{2}K - 2n^{2} + 8n - 4)(1 + A)^{2} + 2nS + 4AS^{2} - 2nSA^{2} )}{(20 - 20n - n^{2}K)(1 + A)^{2}} < 1\quad \mbox{and positive} \end{aligned}$$
(31)

The causality condition is obeyed at the centre for all values of constants satisfying condition (24).

Due to cumbersome expressions of (25) and (31), the trend of pressure-density ratio and adiabatic sound speed is studied analytically after applying the boundary conditions.

Applying the boundary conditions from (11) to (14), we get the values of the arbitrary constants in terms of Schwarzschild parameters \(u = \frac{GM}{c^{2}R_{b}}\) and radius of the star R b .

$$\begin{aligned} C & = \frac{n(1 - d)}{(nd - n + 2) r_{b}^{2}} > 0\quad \mathrm{for}\quad u \le\frac{2n - 2}{n^{2}} + \frac{q_{b}^{2}}{2R_{b}^{2}} \end{aligned}$$
(32)
$$\begin{aligned} A & = \frac{n.(u - \frac{q_{b}^{2}}{R_{b}^{2}}).(1 + Cr_{b}^{2})^{\frac{n - 2 - S}{2n}} - (n - 2 - S).Cr_{b}^{2}.d.(1 + Cr_{b}^{2})^{\frac{ - n - 2 - S}{2n}}}{(n - 2 + S).d.Cr_{b}^{2}.(1 + Cr_{b}^{2})^{\frac{ - n - 2 + S}{2n}} - n(u - \frac{q_{b}^{2}}{R_{b}^{2}}).(1 + Cr_{b}^{2})^{\frac{n - 2 + S}{2n}}} \end{aligned}$$
(33)
$$\begin{aligned} B & = \sqrt{\frac{(1 + Cr_{b}^{2})^{\frac{n - 2 - S}{2n}} + A(1 + Cr_{b}^{2})^{\frac{n - 2 + S}{2n}}}{d}} \end{aligned}$$
(34)

where we define a new parameter called as Reissner-Nordström parameter ‘d’ given by

$$ d = \sqrt{1 - 2u + \frac{q_{b}^{2}}{R_{b}^{2}}} $$
(35)

Whose value lies between (n−2)/n<d<1 for \(Cr_{b}^{2} > 0\).

Surface density is given by

$$ \frac{8\pi G}{c^2}\rho_b R_b^2= \frac{Cr_b^2 [12n+4(n-1)Cr_b^2 -n^2KCr_b^2]}{n^2(1+Cr_b^2)^2} $$
(36)

Central red-shift is given by

$$ Z_{0} = \biggl[ \frac{B^{2}}{1 + A} - 1 \biggr] $$
(37)

The surface red shift is given by

$$ Z_{b} = \bigl[e^{ - \frac{\nu_{b}}{2}} - 1\bigr] $$
(38)

7 Discussions

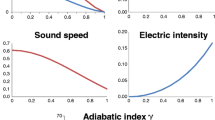
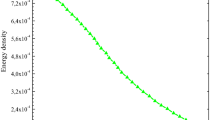
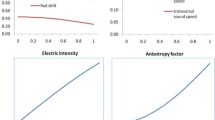
In view of Table 1 and Fig. 1 it has been observed that all the physical parameters (p, ρ, \(\frac{p}{\rho c^{2}}\), \(\frac{dp}{d\rho}\), z, γ and E) are positive at the centre and within the limit of realistic equation of state and the conditions for well behaved nature are satisfied. Our solution is well behaved for the all values of n satisfying the inequalities \(4 < n \le4(4 + \sqrt{2} )\) and K satisfying the inequalities 0≤K≤0.24988. However, for \(n > 4(4+\sqrt{2})\), there exist no value of K for which the nature of adiabatic sound speed is monotonically decreasing from centre to pressure free interface. In view of Fig. 2: With the increase of n the maximum mass decreases.

Fig. 1
figure 1

The variation of p, \(\rho,\frac{p}{\rho c^{2}}\), \(Z,\frac{1}{c^{2}} ( \frac{dp}{d\rho} )\), γ and E from centre to surface for n=4.001 and K=0.24988 is shown in the following graphs

Full size image
Fig. 2
figure 2

Variation of maximum mass M of quark star with n

Full size image
Table 1 The march of pressure, density, pressure-density ratio, square of adiabatic speed of sound, γ, red shift and electric field intensity within the ball corresponding to n=4.001 for which K max=K min=0.24988, d min=0.6552 and u max=0.3448
Full size table

In Table 2, we present a neutron star modeling based on the particular solution; corresponding to n=4.001 for which K max=0.24988 and u max=0.3448 the maximum mass of neutron star for surface density 2×1014 gm/cc is found to be M=3.58M ⊙ and radius R=15.37 km and that for surface density 2.7×1014 gm/cc is found to be M=3.08M ⊙ and radius R=13.23 km.

Table 2 The variation of maximum mass of neutron star, corresponding radius R b , surface red shift and electric field with u for n=4.001 and K=0.24988
Full size table

In Table 3, we present a quark star modeling based on the particular solution; corresponding to n=4.001 for which K max=0.24988 and u max=0.3448 and by assuming the surface density the maximum mass of quark star M=2.335M ⊙ and radius R=10.04 km.

Table 3 Variation of maximum mass of quark star (surface density ρ b =4.6888×1014 g/cc) and its radius with u for n=4.001 and K=0.24988
Full size table

8 Conclusion

We find that all the physical parameters (p, ρ, \(\frac{p}{\rho c^{2}}\), \(\frac{dp}{d\rho}\), Z, γ and E) are showing the desired trend in our range for K(0≤K≤0.24988) and for the prescribed value for n; \(4(4+\sqrt{2}) \geq n>4\). However, for \(4+2\sqrt{2} \geq n >4\), we observe that with the increase of K, i.e. increasing the charge, the mass of the star increases. This is consistent with the observed phenomena. The ratio of mass/radius is increasing as we increase the charge i.e. with increasing charge; the proportion of mass to the radius of the star is increasing. Hence the denser star can be stabilized with the increase of charge. Second important aspect of the solutions is that the range of well behaved nature of solutions of Murad and Pant (2014) (Neutral solutions) is augmented substantially from \(4 (4+\sqrt{2}) \geq n > 4+2 \sqrt{2}\ \mathrm{to}\ 4 (4+\sqrt{2}) \geq n > 4\). The maximum mass of the quark star is very close to the value suggested by Dong et al. (2013). Further, for some suitable choices of input parameters n and u, we have generated in Table 3 compact fluid spheres similar to the mass and radius of some possible strange star candidates like Her X-1, 4U 1538–52, LMCX-4, SAX J1808.4–3658 (Gangopadhyay et al. 2013).