1 Introduction

Astronomers have obtained cosmological data from different observational schemes such as SNela, SDSS, WMAP and CMB radiation anisotropous, X-ray and suggested that our universe undergoes accelerated expansion (De Bernardis et al. 2002; Perlmulter et al. 1999; Riess et al. 1998; Bernnelt et al. 2003; Ade et al. 2014; Tegmark et al. 2004; Allen et al. 2004). These observations also represents that our universe is spatially flat and consists of about 70 percent dark energy (DE) with negative pressure, 30 percent dust matter (cold dark matter plus baryons) and negligible radiation. To explain the phenomenon of accelerated expansion of universe, researchers used two different representative ways. Firstly, in general relativity, introduces dynamical DE models and secondly, modification of Einstein’s gravity. A number of scientists observed the cosmic accelerated expansion universe. For example, cosmological constant (with \(\omega =-1\)), dynamical DE models with varying equation of state (EoS) parameter and \(f(R)\), \(f(T)\) theories etc. are proposed for this accelerated expansion (Martin 2008; Tsujikawa 2013).

It is observed that DE models may be associated with scalar field which arises in string theory. Mostly DE models are carried out for canonical scalar field and non-canonical scalar field model for DE (Das and Mamon 2015; Fang et al. 2007). The non-canonical scalar field model provides good solution of large number of cosmological problems. Usually, a large number of scalar field DE models assume the field to be non-interacting. In present framework, we take DE density interacts with that of dark matter which can be easily dealt by taking a suitable interaction term. In the history of universe expansion, to obtain very reasonable evaluation of interaction term is assumed (Berger and Shojaei 2006; Cai and Wang 2005; Zimdahl 2005; Hu and Ling 2006) where the decay rat is assumed to be proportional to the present value of Hubble parameter. Moreover, the problem of breaking of the Lorentz and CPT symmetries is intensively studied now. Among a great number of possible Lorentz-CPT breaking modification of gravities (Kostelecky 2004), the four dimensional gravitational Chern-Simons term originally introduced in Alexander and Yunes (2009) is certainly the most popular one. The main reasons for it are its relatively simple form, evident gauge symmetry and straightforward analogies with the three-dimensional gravitational Chern-Simons term (Deser et al. 1982).

A lot number of issues treating different aspects of the four-dimensional gravitational Chern-Simons term has been studied for a general review. In particular, in Mariz et al. (2004) it was shown to emerge as a quantum correction. The most important line of studies of this term is actually devoted to searching for the solutions of the equations of motion in the modified theory whose action is a sum of the usual Einstein-Hilbert action and of the gravitational Chern-Simons term. It was shown that a lot of well-known solutions of the usual Einstein equations, in particular, spherically symmetric and cylindrically symmetric ones, such as Schwarzschild, Reissner-Nordstrom and FRW metrics resolve the modified Einstein equations as well (Grumiller and Yunes 2008). However, the Kerr metric failed to solve the modified Einstein equations. To circumvent this difficulty, in Grumiller and Yunes (2008) and Smith et al. (2008), the concept of the dynamical Chern-Simons coefficient was introduced. The modified Chern-Simons gravity has not randomly extension which is described in Calldwell and Linder (2005). The modified Chern-Simons gravity is motivated from string theory of low energy limit which comprises as a necessary anomaly-canceling for correction of Einstein-Hilbert action and for describing modified Chern-Simons gravity as an effective theory. The accelerated expansion of the universe taking various DE models and thermodynamics (Jawad and Majeed 2015; Jawad 2014a, 2014b, 2015; Jawad et al. 2013a, 2013b, 2014, 2016; Jawad and Sohail 2015; Jawad and Rani 2015) have been discussed in this theory.

Sharif and Jawad (2015) studied the generalized second law of thermodynamics with thermal equilibrium and non-equilibrium processes in a flat as well as in a closed Kaluza-Klein universe. Recently, Das et al. (2015) considered a non-canonical scalar field DE model interacting with dark matter and investigated the validity of GSLT with and without entropy corrected terms. We consider the non-canonical scalar field model in the framework of modified Chern-Simons gravity and discuss the validity of GSLT. The paper is organized as follows: In Sect. 2, we briefly discuss Chern-Simons modified gravity and non-canonical scalar field model. In Sect. 3, we construct the field equation for underlying scenario taking interaction between scalar field model and dark matter. Also, we check the stability of the model using squared speed of sound parameter. We check the validity of GSLT for the model without and with corrected entropy models (logarithmic and power law entropy corrections) in Sect. 4. In the last section, we summarize the results.

2 Dynamical Chern-Simons modified gravity and non-canonical scalar field model

In this section, we give a brief review of dynamical Chern-Simons modified gravity and a discussion about non-canonical scalar field model. The action which describes the Chern-Simons theory is defined as follows

$$\begin{aligned} \mathcal{S} =&\frac{1}{16\pi G} \int d^{4}x \biggl[ \sqrt{-g}R+\frac{ \ell }{4}\theta {^{\star }R}^{\rho \sigma \mu \nu }R_{\rho \sigma \mu \nu } \\ &{}-\frac{1}{2} g^{\mu \nu }\nabla_{\mu }\theta \nabla_{\nu } \theta +v(\theta ) \biggr] +\mathcal{S}_{m}, \end{aligned}$$
(1)

where \(R\), \({^{\star }R}^{\rho \sigma \mu \nu }R_{\rho \sigma \mu \nu }\), \(\ell \), \(\theta \), \(\mathcal{S}_{m}\) and \(v (\theta )\) represent the Ricci scalar, a topological invariant called the Pontryagin term, coupling constant, dynamical variable, action of matter and the potential, respectively. For simplicity, we consider the potential \(v(\theta )\) to be zero. Varying the action Eq. (1) with respect to \(g_{\mu \nu }\) and scalar field \(\theta \), we obtain field equations as follows

$$\begin{aligned} &G_{\mu \nu }+lC_{\mu \nu } =8\pi G T_{\mu \nu }, \end{aligned}$$
(2)
$$\begin{aligned} &g^{\mu \nu }\nabla_{\mu }\nabla_{\nu }\theta =- \frac{l}{64\pi } {^{\star }R}^{\rho \sigma \mu \nu }R_{\rho \sigma \mu \nu }. \end{aligned}$$
(3)

Here \(G_{\mu \nu }\) is the Einstein tensor while \(C_{\mu \nu }\) denotes the Cotton tensor and defined as follows

$$ C^{\mu \nu }=-\frac{1}{2\sqrt{-g}}\bigl((\nabla_{\rho } \theta ) \varepsilon^{\rho \beta \tau (\mu }{\nabla_{\tau }R^{\nu }_{\beta }} \bigr)+( \nabla_{\sigma }\nabla_{\rho }\theta ) {^{\star }R}^{\rho \sigma \mu \nu }. $$
(4)

For external field part, the energy momentum tensor is defined as

$$\begin{aligned} T^{\theta }_{\mu \nu } =&\nabla_{\mu }\theta \nabla_{\nu }\theta - \frac{1}{2}g_{\mu \nu }\nabla^{\rho } \theta \nabla_{\rho }\theta , \end{aligned}$$
(5)

where \(T^{\theta }_{\mu \nu }\) represents the scalar field contribution.

Moreover, we assume the action of scalar field model

$$ \mathcal{L}= \int \sqrt{-g}dx^{4} \biggl[ \frac{R}{2}+\mathcal{L}( \phi ,X) \biggr] +\mathcal{L}_{mat}. $$
(6)

The Lagrangian density \(\mathcal{L}(\varPhi ,X)\) is an arbitrary function of the scalar field \(\phi \) which is a function of time only and whose kinetic term \(X\) is given by

$$ X=\frac{1}{2}\partial_{\mu }\phi \partial^{\mu }\phi . $$
(7)

The Einstein field equations take the following form

$$ G_{\mu \nu }=T^{\theta }_{\mu \nu }+T^{\phi }_{\mu \nu }+T^{m}_{ \mu \nu }, $$
(8)

where the energy momentum tensors for scalar field \(\phi \) and matter part composed of perfect fluid are defined as

$$\begin{aligned} T^{\phi }_{\mu \nu } =& \frac{\partial \mathcal{L}}{\partial X} \partial_{\mu }\phi \partial_{\nu }\phi -g_{\mu \nu } \mathcal{L}, \end{aligned}$$
(9)
$$\begin{aligned} T^{m}_{\mu \nu } =&(\rho_{cdm}+p_{cdm})U_{\mu }U_{\nu }+p_{cdm}g_{ \mu \nu }, \end{aligned}$$
(10)

where \(U_{\mu }\) denotes the four-velocity of the fluid and \(\rho_{cdm}\), \(p_{cdm}\) are energy density and pressure of matter components of the universe respectively. The energy density and pressure of scalar field are defined as

$$ \rho_{\phi }=2X\frac{\partial \mathcal{L}}{\partial X}-\mathcal{L}, \qquad p_{\phi }= \mathcal{L}. $$
(11)

Under the variation of action (7) with respect to scalar field \(\phi \) yields the differential equation as

$$\begin{aligned} &\ddot{\phi } \biggl[ \biggl( \frac{\partial \mathcal{L}}{\partial X} \biggr) +2X \biggl( \frac{\partial^{2}\mathcal{L}}{\partial X^{2}} \biggr) \biggr] + \biggl[ 3H \biggl( \frac{\partial \mathcal{L}}{\partial X}+ \dot{\phi }\frac{ \partial^{2}\mathcal{L}}{\partial \phi \partial X} \biggr) \biggr] \dot{\phi } \\ &\quad{}- \biggl( \frac{\partial \mathcal{L}}{\partial \phi } \biggr) =0. \end{aligned}$$
(12)

In order to find out this equation, we need to consider a proper form of Lagrangian density ℒ. Fang et al. (2007) proposed the density for the non-canonical scalar field as, \(\mathcal{L}(\varPhi ,X)=F(X)-V( \phi )\) where \(F(X)\) is an arbitrarily chosen function for different cosmological solutions. Here, we consider the following form

$$ \mathcal{L}(\varPhi ,X)=X^{2}-V(\phi ). $$
(13)

3 Field equations and stability analysis

We construct the field equations and discuss the stability analysis of the model in this section. Let us consider isotropic and homogeneous spatially flat FRW metric which is given by line element

$$ ds^{2}=dt^{2}-a^{2}(t) \bigl[ dr^{2}+r^{2}d\theta^{2}+r^{2} \sin^{2} \theta d\phi^{2} \bigr] $$
(14)

where \(a(t)\) is the scale factor of universe depending on cosmic time \(t\). Here, we consider the spatially flat FRW universe as indicated by the anisotropy of CMBR measurement (De Bernardis et al. 2000). With the help of Eq. (13), the pressure and energy density associated with scalar field become

$$\begin{aligned} \rho_{\phi } =&3X^{2}+V(\phi )= \frac{3}{4}\dot{\phi }^{4}+V(\phi ), \end{aligned}$$
(15)
$$\begin{aligned} p_{\phi } =&X^{2}-V(\phi )=\frac{1}{4} \dot{\phi }^{4}-V(\phi ). \end{aligned}$$
(16)

The scalar field given in Eq. (4) results \(g^{\mu \nu }\nabla _{\mu }\nabla_{\nu }\theta =g^{\mu \nu }[\partial_{\mu }\partial_{ \nu }\theta ]=0\) where term \({^{\star }R}^{\rho \sigma \mu \nu }R_{ \rho \sigma \mu \nu }\) vanishes for FRW spacetime. Taking \(\theta = \theta (t)\) in this equation, we find the differential equation as

$$\begin{aligned} \ddot{\theta }+3H\dot{\theta } =&0, \end{aligned}$$
(17)

yields the solution \(\dot{\theta }=b^{2}a^{-3}\) where \(b\) is an arbitrary constant and \(T^{\theta }_{\mu \nu }=\frac{1}{2} \dot{\theta }^{2}\). The Friedmann equations take the form

$$\begin{aligned} &3H^{2} =\rho_{cdm}+\rho_{\phi }+ \frac{1}{2}\dot{\theta }^{2}, \end{aligned}$$
(18)
$$\begin{aligned} &{-}\bigl(2\dot{H}+3H^{2}\bigr) =p_{\phi }+p_{cdm}. \end{aligned}$$
(19)

Generally, it is said that there exists no interaction between the dark matter and scalar field components. However, due to unknown nature of DE, we may assume an interaction between these components of matter which may provide a more general scenario. According to this scenario in underlying case, we consider that dark matter interacts with scalar field by means of a source term \(Q\). Taking into account \(p_{cdm}=0\), the continuity equations for scalar field and matter are given by

$$\begin{aligned} &\dot{\rho }_{\phi }+3H(1+\omega_{\phi }) \rho_{\phi } =Q, \end{aligned}$$
(20)
$$\begin{aligned} &\dot{\rho }_{cdm}+3H\rho_{cdm} =-Q, \end{aligned}$$
(21)

where \(Q\) is the interaction term between the scalar field and dark energy mater which will be defined as the rate of flow of energy between the two components. The unknown nature of DE as well as CDM leads to the basic problem for the choice of interaction term. It is difficult to describe interaction via first principle. However, the continuity equation provides a clue about the form of interaction, i.e., it must be a function of the product of energy density and a term with units of time (such as Hubble parameter). With this idea, different forms for interaction have been proposed. We take the following form of this interaction term (Ferreira et al. 2014; Das and Mamon 2015)

$$ Q= \varepsilon H \dot{\phi }^{4},\quad \varepsilon ~ \text{is constant}. $$
(22)

with \(b^{2}\) serves as interaction parameter which exchanges the energy between CDM and DE components. This form of interaction term has been explored for energy transfer through different cosmological constraints. The sign of coupling constant decides the decay of energies either DE decays into CDM (when the interacting parameter is positive) or CDM decays into DE (when the interacting parameter is negative). The present analysis from different aspects imply that the phenomenon of DE decays into CDM which is more acceptable and favors the observational data (Amendola 2007; Guo et al. 2007; Xu et al. 2011). It was argued that negative coupling does not help in solving the cosmic coincidence problem (Pavon and Wang 2007) and the second law of thermodynamics also violated (Sen and Pavon 2008; Karwan 2008). Feng et al. (2008) explored the impact of interaction on the compatibility of observational data. They arrived at the conclusion that small positive value of interacting parameter provides more reliable compatibility with observational data while its higher value gives poorer compatibility. Their results also showed consistency with that found independently by galaxy cluster analysis (Abdalla et al. 2009).

Observationally, the value of EoS parameter for DE era lies in the range \(-1<\omega <-\frac{1}{3}\), presenting accelerating expansion of the universe. This shows that allowed range of EoS is very small. So, we may take EoS parameter \(\omega_{\phi }\) as constant (Das et al. 2015) and is given by the relation

$$\begin{aligned} \omega_{\phi }=\frac{p_{\phi }}{\rho_{\phi }}= \frac{X^{2}-V}{3X^{2}+V} = \omega_{c}\quad \text{(constant)}, \end{aligned}$$
(23)

which leads to

$$\begin{aligned} \dot{\phi }^{4}=4V\biggl(\frac{1+\omega_{c}}{1-3\omega_{c}} \biggr). \end{aligned}$$
(24)

Using this equation along with Eqs. (15) and (16), we get (changing argument from \(t\) to \(a\))

$$\begin{aligned} p_{\phi }(z)=\frac{4\omega_{c}}{1-3\omega_{c}}V(z),\qquad \rho_{\phi }(z)=\frac{4}{1-3 \omega_{c}}V(z), \end{aligned}$$
(25)

where \(1+z=\frac{a_{0}}{a}\) with \(a_{0}\) representing present-day value of the scale factor. Substituting these values and interaction term in Eq. (20), it yields

$$\begin{aligned} V(z)= V_{0}(1+z)^{\epsilon }. \end{aligned}$$
(26)

Here \(V_{0}\) represents arbitrary positive constant and \(\epsilon =(1+ \omega_{c})(3-\varepsilon )\). The Hubble parameter takes the form

$$\begin{aligned} H^{2} =&\gamma (1+z)^{\epsilon }+\delta (+z)^{3} \end{aligned}$$
(27)

where \(\delta \) is a positive constant and \(\gamma =\frac{4 \omega _{c} V_{0}}{(3-\epsilon )(3 \omega_{c}-1)}\) is for the sake of simplicity. Inserting all corresponding values in Eq. (18), we get

$$\begin{aligned} \rho_{cdm}(z) =&\biggl(3\gamma - \frac{4V_{0}}{1-3\omega_{c}}\biggr) (1+z)^{ \epsilon }+3\delta (1+z)^{3} \\ &{}-\frac{1}{2}b^{2}(1+z)^{6}. \end{aligned}$$
(28)

The expressions for effective components of the universe i.e., effective pressure and effective energy density take the following form

$$\begin{aligned} \rho_{eff}(z) =&3H^{2}-\frac{1}{2}b^{2}(1+z)^{6}, \end{aligned}$$
(29)
$$\begin{aligned} p_{eff}(z) =&p_{\phi }(z). \end{aligned}$$
(30)

Using Eqs. (20), (21) and (27), we can obtain expression for first derivative of Hubble parameter in terms of \(p_{eff}\) and \(\rho_{eff}\). It is given by

$$\begin{aligned} \dot{H} =&-\frac{1}{2}(p_{eff}+ \rho_{eff})-\frac{1}{4}b^{2}(1+z)^{6}. \end{aligned}$$
(31)

In order to check the stability of the interacting non-canonical scalar field model in the framework of Chern-Simons gravity, we use squared speed of sound parameter. This parameter is defined by the ratio of first derivative of pressure and energy density components \((C_{s} ^{2}=\frac{\dot{p}}{\dot{\rho }})\). The detailed discussion is as follows. In the linear perturbation theory, the density perturbation is described by Kim et al. (2008)

$$ \rho (t,\textbf{x})= \rho (t)+\delta \rho (t,\textbf{x}) $$
(32)

with \(\rho (t)\) the background value. Then the conservation law for the energy-momentum tensor of \(\nabla_{\nu }T^{\mu \nu }= 0\) yields

$$ \delta \ddot{\rho }= C_{{s}}^{2} \nabla^{2}\delta \rho (t,\textbf{x}), $$
(33)

where \(T_{0}^{0}=-\rho (t)-\delta \rho (t,\textbf{x})\) and

$$ C_{{s}}^{2}= \frac{\partial p}{\partial \rho }. $$
(34)

For \(C_{{s}}^{2} > 0\), Eq. (34) becomes a regular wave equation whose solution is given by \(\delta \rho = \delta {\rho_{0}} e^{i \omega t+i\textbf{k.x}}\). Hence the positive squared speed (real value of speed) shows a regular propagating mode for a density perturbation. For \(C_{{s}}^{2} < 0\), the perturbation becomes an irregular wave equation whose solution is given by \(\delta \rho = \delta {\rho_{0}} e ^{i\omega t+i\textbf{k.x}}\). Hence the negative squared speed (imaginary value of speed) shows an exponentially growing mode for a density perturbation. That is, an increasing density perturbation induces a lowering pressure, supporting the emergence of instability.

Das and Mamon (2015) checked the stability of non-canonical scalar field model and pointed out the existence of two stable points while unstable for remaining points. For the present model, the effective speed of sound is given by

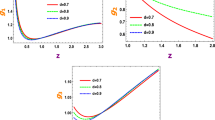
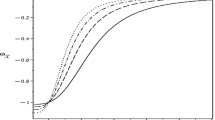
$$ C_{{s}}^{2}=\frac{\frac{\partial p_{eff}}{\partial z}}{\frac{ \partial \rho_{eff}}{\partial z}}= \frac{\frac{4\omega_{c} V_{0} \epsilon }{1-3\omega_{c}}}{3\gamma \epsilon +9\delta (1+z)^{3-\epsilon }-3b^{2}(1+z)^{6-\epsilon }}. $$
(35)

In the present model, we significantly rewrite the stability analysis of the present model depend upon the different cosmological parameters. Here we take specific values of different cosmological parameters to discuss the stability as \(\omega_{c}=-0.9\), \(B=2\), \(b=0.2\), \(\epsilon =1, 1.8, 1.2\) (see Fig. 1). For this choice of parameters, the squared speed of sound shows the stable behavior because \(C_{{s}}^{2}> 0\). Hence, this behavior of squared speed (real value of speed) leads to a regular propagating mode for a density perturbation. This stability analysis make more realistic current model.

Fig. 1
figure 1

Plot of \(C_{s}^{2}\) versus \(z\) for \(\epsilon =1,1.8,2.1\)

Full size image

4 Generalized second law of thermodynamics

In this section, we check the validity of GSLT taking into account apparent horizon as the boundary of universe which states that the sum of the rate of change of horizon entropy and entropy of total matter inside the horizon does not decrease with time. We will check the validity into three different versions, e.g., with usual entropy-area relation, logarithmic and power law entropy corrections.

4.1 With usual entropy-area relation

The first law of thermodynamics can be defined as (Bardeen et al. 1973)

$$ TdS=dE+pdV, $$
(36)

Cai and Kim (2005) investigated the same formalism and considered the first law of thermodynamics at apparent horizon for FRW flat universe and derived the Friedmann equation. By assuming the universe as thermodynamical system, Gibbons and Hawking (1977) has firstly observed the thermodynamics in the form of de Sitter spacetime. It has been investigated that specially for the flat universe, the apparent and Hubble horizon are coincided. Wang et al. (2005) has observed that first law and GSLT hold on apparent horizon. Till now, a lot of work has been done on the validity of first and GSLT on apparent and event horizons (Setare and Shafei 2006; Izquierdo and Pavon 2004; Frolov and Kofman 2003; Gong et al. 2007; Sheykhi and Wang 2009; Wang and Wu 2009; Akbar and Cai 2006; Sadjadi 2007).

In order to find out the internal entropy of the system, we use Gibb’s equation (36) which takes the form

$$\begin{aligned} T_{A}\dot{S}_{I}=4\pi R^{2}_{A}( \dot{R}_{A}-HR_{A}) (\rho_{eff}+p _{eff}), \end{aligned}$$
(37)

where \(T_{A}\) and \(R_{A}\) represent the temperature and radius of the apparent horizon, respectively. The radius of apparent horizon for flat FRW universe is defined by Cai and Wang (2005)

$$ R_{A}=\frac{1}{H}, \quad \dot{R}_{A}= \frac{\dot{H}}{H^{2}}. $$
(38)

It is suggested that the horizon entropy is directly proportional to surface area of its horizon (in units \(c = G= \hbar = 1\)) which is defined as

$$ S_{A}=\frac{A}{4G}, $$

where \(A=4\pi R^{2}_{A}\) is the surface area and \(R_{A}\) is the radius of apparent horizon. The rate of change of entropy of horizon on the apparent horizon leads to (Cai and Wang 2005; Davis et al. 2007; Bhattacharya and Debnath 2011)

$$\begin{aligned} T_{A}\dot{S_{A}} =&4\pi R^{3}_{A}H(p_{eff}+\rho_{eff}). \end{aligned}$$
(39)

Using Eqs. (37) and (39), the total time rate of change of entropy function becomes

$$ T_{A}\dot{S}_{tot}=4\pi R^{2}_{A}H(p_{eff}+ \rho_{eff}) \dot{R_{A}}. $$
(40)

Inserting all the corresponding values in Eq. (40), we get the GSLT as

$$\begin{aligned} T_{A}\dot{S}_{tot} =&\biggl[2\pi \biggl(3\gamma (1+z)^{\epsilon }+3 \delta (1+z)^{3} \\ &{}-\frac{1}{2}b^{2}(1+z)^{6}+\frac{4\omega_{c} V_{0}(1+z)^{ \epsilon }}{1-3\omega_{c}}\biggr)^{2}\biggr] \\ &\times\biggl(\gamma (1+z)^{ \epsilon }+\delta (1+z)^{3}\biggr)^{-2} \\ &{}+\pi b^{2}(1+z)^{6}\biggl[3\gamma (1+z)^{\epsilon }+3 \delta (1+z)^{3} \\ &{}-\frac{b ^{2}}{2}(1+z)^{6}+\frac{4\omega_{c} V_{0}(1+z)^{\epsilon }}{1-3\omega _{c}}\biggr] \\ &\times\biggl(\gamma (1+z)^{\epsilon }+\delta (1+z)^{3}\biggr)^{-2}. \end{aligned}$$
(41)

The plot of \(T_{A}\dot{S}_{tot}\) verses \(z\) for same values of constant parameters as for stability analysis is shown in Fig. 2 for \(\epsilon = 1,1.8,2.1\). It is noted that the \(T_{A}\dot{S}_{Atot}\) shows increasing behavior as well as remains positive at early, present and later epoch of the universe and GSLT satisfied for this scenario of entropy.

Fig. 2
figure 2

Plots of \(T_{A}\dot{S}_{Atot}\) versus \(z\)

Full size image

4.2 With entropy corrections

It has been found that in quantum mechanics (quantum correction namely power law and logarithmic correction) provided the relationship of entropy area and curvature correction in the Einstein-Hilbert action and vice visa (Zhu and Ren 2009; Cai et al. 2009). The logarithmic correction arises from the loop quantum gravity due to the thermal equilibrium and quantum fluctuations (Miessner 2004; Sadjadi and Jamil 2010). The logarithmic entropy correction (Wei 2009) can be defined as follows

$$\begin{aligned} S_{LE} =&\frac{A}{4G}+\alpha \ln \biggl( \frac{A}{4G}\biggr)+\frac{4G \beta }{A}+\gamma , \end{aligned}$$

where \(\alpha \), \(\beta \) and \(\gamma \) are dimensionless constants. The temperature on the apparent horizon is defined through surface gravity \(\kappa \) and is given by Cai and Wang (2005)

$$\begin{aligned} T_{A}=\frac{|\kappa |}{2\pi } =&\frac{1}{2\pi R_{A}} \biggl(1-\frac{ \dot{R_{A}}}{2H R_{A}}\biggr) \\ =&\frac{1}{4\pi } R_{A}\bigl( \dot{H}+2H^{2}\bigr). \end{aligned}$$
(42)

Taking into account Eqs. (30), (31), (41) and (42) yield

$$\begin{aligned} T_{A}\dot{S}_{A} =& \frac{f'(A)(2\pi (p_{eff}+\rho_{eff})+ \pi b^{2}(1+z)^{6})}{(\frac{1}{3}\rho_{eff}+ \frac{1}{6}b^{2}(1+z)^{6})^{2}} \\ &{}\times \biggl(\frac{1}{6}(\rho_{eff}-3p_{eff}) + \frac{1}{12}b^{2}(1+z)^{6}\biggr), \end{aligned}$$
(43)

where

$$\begin{aligned} & f(A) =A+\frac{\alpha }{2\pi } \ln (2\pi A)+\frac{\beta }{4\pi^{2} A}+ \frac{ \gamma }{2\pi }, \\ &f'(A) = 1+\frac{\alpha }{2\pi }\frac{1}{A}- \frac{\beta }{4\pi^{2}}\frac{1}{A ^{2}}. \end{aligned}$$

Similarly, the rate of change of internal entropy inside the apparent horizon is obtained as

$$ T_{A}\dot{S}_{I}=\frac{4\pi (p_{eff}+\rho_{eff}) [ \frac{1}{6}(\rho_{eff}+3p_{eff} +\frac{1}{12}b^{2}(1+z)^{6} ]}{ (\frac{1}{3}\rho_{eff}+ \frac{1}{6}b^{2}(1+z)^{6} )^{2}}. $$
(44)

Adding Eqs. (43) and (44), the rate of change of total entropy is as follows

$$\begin{aligned} T_{A}\dot{S}_{tot} =& \biggl[ \bigl(2 \pi (p_{eff}+\rho_{eff})+\pi b ^{2}(1+z)^{6} \bigr) \\ &{}\times \biggl(\frac{1}{6}(\rho_{eff}-3p_{eff}) +\frac{1}{12}b^{2}(1+z)^{6} \biggr) \biggr] \\ &{}\times \biggl\{ \frac{f'}{( \frac{1}{3}\rho_{eff}+ \frac{1}{6}b^{2}(1+z)^{6})^{2}} \biggr\} \\ &{}+4\pi (p_{eff}+\rho_{eff}) \\ &{}\times \biggl\{ \frac{1}{6}( \rho_{eff}+3p_{eff})+\frac{1}{12}b^{2}(1+z)^{6} \biggr\} \\ &{}\times \biggl( \frac{1}{3}\rho_{eff}+\frac{1}{6}b^{2}(1+z)^{6} \biggr)^{-2} . \end{aligned}$$
(45)

Inserting the values of \(\rho_{eff}\), \(p_{eff}\) and \(f'(A)\) in Eq. (45), we plot \(T_{A}\dot{S}_{Atot}\) versus \(z\) taking different set of parameters \(\alpha \) and \(\beta \) as (\(\alpha =1\), \(\beta =1\)), (\(\alpha =1\), \(\beta =-1\)), (\(\alpha =1\), \(\beta =0\)), (\(\alpha =-1\), \(\beta =1\)), (\(\alpha =-1\), \(\beta =-1\)), (\(\alpha =-1\), \(\beta =0\)), (\(\alpha =0\), \(\beta =1\)), (\(\alpha =0\), \(\beta =-1\)), (\(\alpha =0\), \(\beta =0\)) while remaining parameters are same given after Eq. (35) with \(\epsilon =2.1\) as shown in Fig. 3. The behavior of \(T_{A}\dot{S}_{Atot}\) remains positive for the present day value of redshift as well as remains positive in near future. It is noted that the case (\(\alpha =0\), \(\beta =0\)) reduces the logarithmic corrected entropy to the case with \(f\rightarrow A\). It is noted that the \(T_{A}\dot{S}_{Atot}\) shows the decreasing behavior in the near past, while exhibits increasing at the present as well as near future. However, \(T_{A}\dot{S}_{Atot}\) remains positive at the past, present and future which represents that all the models are realistic for the current choice of parameters. Thus, GSLT holds for the logarithmic corrected entropy for the non-canonical scalar field model in the framework of Chern-Simons gravity.

Fig. 3
figure 3

Plots \(T_{A}\dot{S}_{tot}\) for logarithmic entropy corrected versus \(z\)

Full size image

The power law entropy correction is defined by the entanglement of quantum field inside and outside the horizon (Zhu and Ren 2009; Cai et al. 2009). This can be defined as (Bhattacharya and Debnath 2011; Sheykhi and Jamil 2011)

$$ S_{PE}=\frac{A}{4G} \bigl[1-k_{\lambda } A^{1-\frac{\lambda }{2}} \bigr], $$
(46)

where \(k_{\lambda }= \frac{\lambda (4\pi )^{\frac{\lambda }{2}}-1}{(4- \lambda )r_{c}^{2-\lambda }}\) and \(r_{c}\) is crossover scale and \(\lambda \) is dimensionless constant. In this case,

$$\begin{aligned} &f(A)= A\bigl(1-k_{\lambda }A^{1-\frac{\lambda }{2}} \bigr)\quad \Rightarrow \\ & f'(A)=1-k_{\lambda }A^{1-\frac{\lambda }{2}} \biggl(2-\frac{\lambda }{2}\biggr). \end{aligned}$$
(47)

One can obtained the rate of change of total entropy for power law entropy correction by inserting the values of \(\rho_{eff}\), \(p_{eff}\) and \(f'(A)\) in Eq. (45). Figure 4 shows the variation of \(T_{A}\dot{S}_{Atot}\) with \(z\) for power law corrected entropy for different values of parameter \(\lambda =3,3.5,3.9\) while all other constant parameters are same as utilized in previous plots. It is noted that \(T_{A}\dot{S}_{Atot}\) shows the increasing behavior at the early, present as well as later epoch. However, \(T_{A}\dot{S}_{Atot}\) remains positive at the early, present as well as later epoch which represents that all the models are realistic for the current choice of parameters.

Fig. 4
figure 4

Plots \(T_{A}\dot{S}_{Atot}\) for power law corrected entropy verses \(z\)

Full size image

5 Conclusion

In this paper, we have studied the scalar field DE model possessing a non-canonical kinetic term in the framework of modified Chern-Simons gravity. We have taken the flat FRW universe model with interaction between dark matter and non-canonical DE part. The chosen interacting term is well-suitable according to recent accelerated expansion of the universe. That is, the DE should dominates dark matter during evolving universe. Under this interacting scenario, we have constructed the potential and develop the effective energy density and pressure. By utilizing these effective pressure and energy density, we have discussed the instability of the model and then evaluated the GSLT in the current scenario by assuming the usual entropy density and its corrected forms (power law as well as logarithmic corrected entropies). In order to check the validity of GSLT for non-canonical scalar field model in the framework of Chern-Simons gravity, we have considered apparent horizon as the boundary of the universe.

We have analyzed the behavior of the squared speed of sound for the specific choice of parameters which leads to the stable behavior of the current system because \(C^{2}_{s} > 0\). Also, this behavior of squared speed (real value of speed) leads to a regular propagating mode for a density perturbation. This stability analysis make more realistic current system. We have also observed from Figs. 2, 3 and 4 that \(T_{A}\dot{S}_{Atot}\) exhibits the increasing behavior at the present as well as later epoch. Also, \(T_{A}\dot{S}_{Atot}\) remains positive at the early, present and later epochs which leads to the validity of GSLT. It can be remarked that all the models corresponding to specific choice of parameters are realistic in dynamical Chern-Simons modified gravity because squared speed of sound remains positive as well as GSLT remains satisfied for the cases without any modification and with modification in terms of logarithmic and power law forms in area-entropy relationship.