1 Introduction

The current accelerated expansion of the universe has been confirmed via different well-known cosmological tests (Riess et al. 1998; Perlmutter et al. 1999; Miller et al. 1999; de Bernardis et al. 2000; Astier et al. 2006). Several approaches have been proposed till date for explaining the accelerated phenomenon of the universe in the late time. One of these approaches consists of an unknown component of energy characterized by large negative pressure which is named as “dark energy” (DE). Extensive reviews on DE have been presented in the references (Copeland et al. 2006; Sami 2009; Frieman et al. 2008; Bamba et al. 2012). A second approach consists in modified versions of Einstein’s gravity has been witnessed in recent years. The idea behind this approach is that a gravitational description of dark energy can be obtained (Brevik et al. 2005). Furthermore, the modification of Einstein-Hilbert action in large scale provides f(R) gravity which is a scalar non-linear function of the Ricci scalar curvature (Caramêsa and de Mellob 2009).

Another important feature of modified gravity is that it explains both scenarios i.e., early inflation and late time accelerated expansion (Caramêsa and de Mellob 2009). Carroll et al. (2005) have discussed on such features of modified gravity. Different classes of modified gravity have been reviewed in the references (Nojiri and Odintsov 2005, 2011; Olmo 2011). In the exhaustive review, Nojiri and Odintsov (2011) presented an elaborate discussion on various well-known modified gravity models. Assuming flat FRW cosmology, Nojiri and Odintsov (2011) investigated the unified scenario of the universe through modified gravity background evolution. The popular modified gravity models include: f(R) gravity, \(f(\mathcal{G})\) gravity, f(T) gravity and Horava-Lifshitz gravity. A review on f(T) gravity is available in Myrzakulov (2011).

The present study is focused on modified f(R) Horava-Lifshitz gravity (MFRHL) (Carloni et al. 2010; Chaichian 2010; Nojiri and Odintsov 2011; Kluson et al. 2011). Mathematical overview of the MFRHL would be presented in the subsequent section. The basic aim of the current work is to reconstruct the MFRHL under holographic DE (HDE) scenario. Based on the idea of quantum field theory that a short distance cut-off is related to a long distance cut-off due to the limit set by formation of a black hole, the proposal of HDE was generated (Li 2004; Elizalde et al. 2005; Nojiri and Odintsov 2006a, 2006b; Jamil et al. 2009; Jamil and Farooq 2010; Bamba et al. 2012; Sheykhi et al. 2012). The HDE model is defined as (Li 2004):

$$ \rho_{\varLambda}=3c^{2}M_{p}^{2}L^{-2}, $$
(1)

where L is the IR cut-off scale with a dimension of length. Here, 3c 2 appears as a constant and M p indicates the reduced Plank mass satisfying the relation \(M_{p}^{-2}=8\pi G_{N}\) (where G N represents the gravitational constant). Holographic reconstruction of DE models has been attempted in a handful of works. Setare (2007a) studied cosmological implication of HDE in the Brans-Dicke (BD) framework and explored a relation between the HDE scenario in flat universe and the phantom DE in BD framework with potential. In another work, Setare (2007b) reconstructed the potential and the dynamics of the scalar field which describe the Chaplygin cosmology. Reconstruction of modified gravity theories has also been attempted in different references. Reconstruction of f(R) gravity theory has been carried out in the works of Nojiri and Odintsov (2007a, 2007b). Jawad et al. (2013) considered a correspondence between HDE and f(G) gravity.

A holographic reconstruction of f(T) gravity via power-law solution of scale factor was attempted in the reference (Chattopadhyay and Pasqua 2013). Another HDE based reconstruction of modified gravity model is a very recent work by Houndjo and Piattella (2012), where cosmological evolution in f(R,T) scenario is considered and the function f(R,T) is reconstructed in view of HDE model.

The paper is organized as follows. In Sect. 2 we have presented a mathematical outline of MFRHL gravity in Sect. 2.1. In Sect. 2.2 we have presented our methodology of reconstruction of the \(f(\widetilde{R})\) of MFRHL. In Sect. 2.3 we have presented the stability analysis of the reconstructed MFRHL by means of \(v_{s}^{2}\) i.e. the squared speed of sound. In Sect. 2.4, we have inserted a comparison of our work with other works and we write the conclusions of our work.

2 HDE based reconstruction of MFRHL gravity

2.1 Overview of MFRHL

The class of modified gravity models are also known as extended theories of gravity in which modification of action of gravitational fields takes place (Kluson 2009a). The clue about these theories comes from an extension of the Einstein-Hilbert action by introducing some curvature invariants of higher order and/or minimally or non-minimally coupled scalar fields to the dynamics. The f(R) theories mainly explain the mysterious acceleration of the universe and provide modification of the Einstein theory on large scales. Kluson (2009b) introduced a new class of f(R) gravity based on the principle of detailed balance and dubbed it as “Horava-Lifshitz f(R) gravity”. In Kluson (2009b), Horava-Lifshitz f(R) theory of gravity was discussed both with and without projectability condition. Kluson (2009a) discussed the limitations of the f(R) gravity theories and introduced new models of f(R) theories of gravity that are a generalization of Horava-Lifshitz gravity and extended his own work in Kluson (2009b). Chaichian (2010) proposed a general approach for the construction of modified gravity which is invariant under foliation-preserving diffeomorphisms.

The action for Horava-Lifshitz f(R) is given by Kluson (2009a):

(2)

Here δ is a real constant in the ‘generalised De Witt metric’ or ‘super-metric’ (‘metric of the space of metric’):

$$ {\mathcal{G}}_{ijkl}=\frac{1}{2}\bigl(g^{(3)ik}g^{(3)jl}+g^{(3)il}g^{(3)jk} \bigr)-\delta g^{(3)ij}g^{(3)kl}, $$
(3)

defined on three-dimensional hyperspace Σ t , E ij can be defined by the so-called detailed balanced condition by using an action \(W[g^{3}_{kl}]\) on the hypersurface Σ t :

$$ \sqrt{g^{(3)}}E^{ij}=\frac{\delta W[g^{(3)}_{kl}]}{\delta g_{ij}}, $$
(4)

and the inverse of \(\mathcal{G}^{ijkl}\) is written as:

$$ {\mathcal{G}}_{ijkl}=\frac{1}{2}\bigl(g^{(3)}_{ik}g^{(3)}_{jl}+g^{(3)}_{il}g^{(3)}_{jk} \bigr)-\tilde{\delta} g^{(3)}_{ij}g^{(3)}_{kl}, \quad \tilde{\delta}=\frac{\delta}{3\delta-1}. $$
(5)

In the HL-like f(R) gravity proposed by Kluson (2009a) as stated above, the lapse N was assumed to be a function of t only, which represents the projectability condition. Chaichian (2010) explored a new very general HL-like f(R) gravity, which is a general approach for the construction of modified gravity which is invariant under foliation-preserving diffeomorphism. For the new form generalized gravity i.e. “modified f(R) Horava-Lifshitz gravity” (MFRHL), Chaichian (2010) proposed the following action:

$$ S_{f(\tilde{R})}=\int d^{4}\sqrt{g^{(3)}}N f(\tilde{R}), $$
(6)

where

(7)

In flat FRW universe, the form of \(\tilde{R}\) comes out to be

(8)

Here \(\tilde{R}\) reduces to R and we recover f(R) gravity from this theory for δ=ν=1 for flat FRW universe. For the action stated earlier, we get by variation over \(g_{ij}^{(3)}\) and by setting N=1:

(9)

In Eq. (9), prime indicates the differentiation with respect to its argument. In the above equation, the matter contribution is involved as pressure p. Taking ρ as the matter density, the conservation equation is given by:

$$ \dot{\rho}+3H(\rho+p)=0. $$
(10)

Using Eqs. (9) and (10), we get

(11)

where C is an integration constant. The IR cut-off L in Eq. (1) becomes the future event horizon with radius \(R_{h}=a\int^{\infty}_{t}\frac{dt}{a}\). For the reconstructed scenario, we consider the solution of the field equation in exact power-law form given by:

$$ a(t)=a_0(t_s-t)^n,\quad t_s>t. $$
(12)

Here a 0, t s and n are constants. The term t s is distinguished as the finite future singularity time and the scale factor (12) is used to check the type II (sudden singularity) or type IV (corresponds to \(\dot{H}\)) for positive values of n. From Eq. (12), we get \(\ddot{a}=a_{0} n(n-1)(t_{s}-t)^{n-2}\). If t→t s with 1<n<2, then \(\ddot{a}\rightarrow +\infty\). If n>2 and t→t s , then \(\ddot{a}\rightarrow 0\). If n<1 and t→t s , then \(\ddot{a}\rightarrow -\infty\). However, as the singularity time t s is approached, H \((=\frac{-n}{t_{s}-t} )\) and therefore, the \(\tilde{R}=\frac{3n(n-3\delta n+\nu(6n-2))}{(t_{s}-t)^{2}}\) diverges. Here t is not equal to t s , thus a(t) does not show zero expansion or static universe. As concern with t<t s case, since we have mentioned that t s is the finite future singularity time, whereas t represents cosmic time for the present universe. We cannot neglect the t if we discuss the present era of the universe towards future era. However, for the future era, we may neglect the t and emphasize on t s . We may say that by choosing t s >t, we discuss the behavior of expanding universe in present towards near future. Using this scale factor with \(a_{0}=M_{p}^{2}=1\) (for the sake of simplicity), we obtain the expressions of R h and ρ Λ as follow:

$$ R_h=\frac{t_s-t}{1-n},\qquad \rho_{\varLambda}= \frac{3c^2(n-1)^2}{(t_s-t)^2}. $$
(13)

The objective of the present work is to reconstruct the \(f(\tilde{R})\) based on Eq. (1) using the exact power-law solution (12). In this reconstructed context, we replace the energy density (ρ) of MFRHL by the energy density of HDE (ρ Λ ) in Eq. (11). Taking C=0 (Chaichian 2010) and inserting Eq. (13) in Eq. (11), it yields the solution:

(14)

where c 1, c 2 are constants come through integration and:

This reconstructed model may correspond to the model investigated by Elizalde et al. (2010) with a similar form of Hubble parameter and specific choices of model parameters. Elizalde et al. (2010) studied the modified f(R) Horava-Lifshitz gravity and provided a unified description of early-time inflation and late-time acceleration in this theory. The finite-time future singularities are investigated and it is shown that these singularities are cured by adding a higher order derivative term. However a difference of first term is appeared in model (14) due to neglect the matter part in the latter model (Elizalde et al. 2010).

2.2 Reconstruction methodology

In this subsection, we discuss the reconstructed scenario of the HDE based MFRHL gravity via graphical representation following the method of Carloni et al. (2010) and Nojiri and Odintsov (2007a).

We observe that the reconstructed model (14) satisfied the following condition (Rastkar et al. 2012):

$$ \lim_{\tilde{R}\rightarrow0}f(\tilde{R})=0, $$
(15)

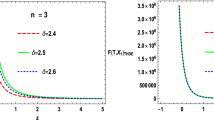
which is the sufficient condition to be a realistic model. However, the MFRHL gravity is not a realistic gravity due to breaking of Lorentz symmetry. Hence, in view of the above equation (15), we state that it may yield fair qualitative description of some cosmological era for the underlying scenario. The behavior of this model versus its argument is shown in Fig. 1. We chose some specific values of constants, δ=3, ν=2, c=2 and integration constants are taken as c 1=c 2=2. We perform this geometrical interpretation for different values of n, i.e. n=2, 2.5, 3, 3.5. Initially, the model represents a decaying behavior for all values of n roughly for the range \(\tilde{R}<0.5\). After that, the model expresses an increasing evolution for \(\tilde{R}\geq0.5\). Thus the reconstructed model \(f(\tilde{R})\) from MFRHL gravity with HDE model incorporating power-law scale factor establishes a consistency evidence and increasing behavior with \(\tilde{R}\).

Fig. 1
figure 1

Evolution of \(f(\tilde{R})\) for reconstructed MFRHL gravity with n=2 (red), n=2.5 (green), n=3 (blue), n=3.5 (black)

Full size image

To examine the evolution of the accelerated expansion of the universe, we adopt the phenomenon of the equation of state (EoS) parameter (ω) which is the ratio of pressure to energy density. This parameter designates different phases of the acceleration and deceleration of the expanding universe. The stiff fluid phase corresponds to ω=1, the value \(\omega=\frac{1}{3}\) indicates the radiation dominated phase, the matter dominated universe is observed for ω=0 and recent DE phase corresponds to the negative values corresponding to \(\omega<-\frac{1}{3}\). The DE phase is further distinguished into different eras with EoS parameter such as \(-1<\omega<-\frac{1}{3}\) gives the quintessence era, the cosmological constant dominated universe is indicated for the ω=−1 whereas the phantom dominated universe is expressed by ω<−1.

Taking into account Eqs. (9) and (11) and using the reconstructed model \(f(\tilde{R})\), we get the expression for EoS parameter \(\omega_{\tilde{R}}\) for MFRHL gravity based on HDE model. We draw this parameter versus t as shown in Fig. 2 for the same values of constants as for Fig. 1. Presently, the graph shows the evolution of the universe from matter dominated towards the DE era. For approximately t>3, it meets the quintessence dominated era of the DE phase for all values of n. As time elapses, it shows that universe remains in this era and does not meet or cross the cosmological constant era. The quintessence behavior is clear for n=2 whereas for higher value of n, the graphs show a small flatness. It leads to an accelerated expanding universe for a far future if we increase n. Thus, the reconstructed model through EoS parameter represents initially a matter dominated universe and soon nearly converges to quintessence era (particularly) for smaller values of n.

Fig. 2
figure 2

Evolution of EoS parameter for reconstructed MFRHL gravity with n=2 (red), n=2.5 (green), n=3 (blue), n=3.5 (black)

Full size image

2.3 Analysis of stability

In order to check the stability of the reconstructed model, we adopt the squared speed of sound phenomenon defined by \(v_{s}^{2}=\frac{dp}{d\rho}\). Detailed discussion in this regard is available in Kim et al. (2008), Sharif and Jawad (2012). Since the underlying scenario becomes time-dependent due to power-law scale factor, hence its definition becomes \(v_{s}^{2}=\frac{\dot{p}}{\dot{\rho}}\). The sign of \(v_{s}^{2}\) is very important to see the stability of background evolution of the model. A positive value indicates a stable model whereas instability of a given perturbation corresponds to the negative value of \(v^{2}_{s}\). It is found that squared speed of sound for HDE with future event horizon as IR cut-off is always negative and gives instability of the model (Myung 2007). Using values of pressure and energy density from Eqs. (9) and (11) along with reconstructed model \(f(\tilde{R})\), we can obtain an expression for \(v_{s}^{2}\). We plot its obtained expression versus t represents in Fig. 3 taking same values of the constants in the model as for above figures. Initially the squared speed of sound bears a decreasing behavior but with positive sign which shows the stable model. As a small interval of time passed, all the curves related to n becomes zero during 0.5<t<0.9. After this range, these curves exhibit negative behavior in nearly future. Thus for the reconstructed model \(f(\tilde{R})\) from MFRHL gravity and HDE model is found the stability for a small time and then becomes instable with the passage of time.

Fig. 3
figure 3

Behavior of \(v_{s}^{2}\) for reconstructed MFRHL gravity with n=2 (red), n=2.5 (green), n=3 (blue), n=3.5 (black)

Full size image

2.4 Comparison and conclusion

The results obtained graphically in Figs. 1, 2 and 3 are now discussed. In Fig. 1, we have plotted the reconstructed \(f(\tilde{R})\) against the its argument \(\tilde{R}\). The reconstruction methodology is stated in the earlier section. We observe that in general, \(f(\tilde{R})\) is increasing with \(\tilde{R}\). However, the increasing behavior is apparent after some initial decaying pattern. For a specific condition n=1, the density of the HDE model becomes zero and model may correspond to the reconstructed model for phantom cosmology (Bamba et al. 2012). Also, this model (14) corresponds to the reconstructed HDE f(R) model (Karami and Khaledian 2011) with only difference of constants of models.

The EoS parameter \(\omega_{\tilde{R}}\) is plotted against cosmic time t in Fig. 2. We observe that it crosses −1/3 after roughly t≈3 and after that \(-1<\omega_{\tilde{R}}<-1/3\). However, for the present universe, \(\omega_{\tilde{R}}>-1/3\) i.e. the strong energy condition is satisfied. At this juncture, we refer the work entitled “Reconstructing dark energy” by Sahni and Starobinsky (2006), where, modified gravity was referred to as “Geometrical DE”. In Sahni and Starobinsky (2006) it was shown that “for physical DE, the EoS makes physical sense. However, this is not so for geometrical DE for which the acceleration of the universe is caused by the fact that the field equations describing gravity are not Einsteinian.” It was further stated in Sahni and Starobinsky (2006) that the EoS may not robust for determining DE properties in the case of modified gravity. Here also we find our results consistent with that stated in Sahni and Starobinsky (2006) on the EoS in modified gravity. Also, the WMAP, BAO and SNe Ia data has indicated that the value of constant EoS parameter keeps the range −1.24≤ω≤−0.96. Thus the EoS parameter (Fig. 2) for reconstructed model has shown consistent result.

To further discern the behavior of the holographic-modified f(R) Horava-Lifshitz gravity, we analyze its stability through the squared speed of sound whose relevance is already discussed in the earlier section. Figure 3 shows that initially, and roughly up to t≈0.9, \(v_{s}^{2}\) stays at positive level and after that it shifts to negative level. This indicates that the holographic-modified f(R) Horava-Lifshitz gravity is classically stable for the present universe and in later stages it becomes unstable.

The holographically reconstructing model with modified f(R) Horava-Lifshitz gravity consider power law solution of the scale factor, the crisp conclusions are:

  • The reconstructed \(f(\tilde{R})\), when plotted against its argument with power law solution of the scale factor, exhibits an increasing pattern after initial decay.

  • The holographic DE based reconstruction of modified f(R) Horava-Lifshitz gravity, with scale factor in power-law form, describes the present dark energy dominated universe evolving from matter dominated universe as far as the EoS parameter is concerned.

  • The holographic-modified f(R) Horava-Lifshitz gravity is classically stable initially and becomes instable for nearly future in the accelerated expanding universe.